Tolerance Modelling of Vibrations and Stability for Periodic Slender Visco-Elastic Beams on a Foundation with Damping. Revisiting
Abstract
1. Introduction
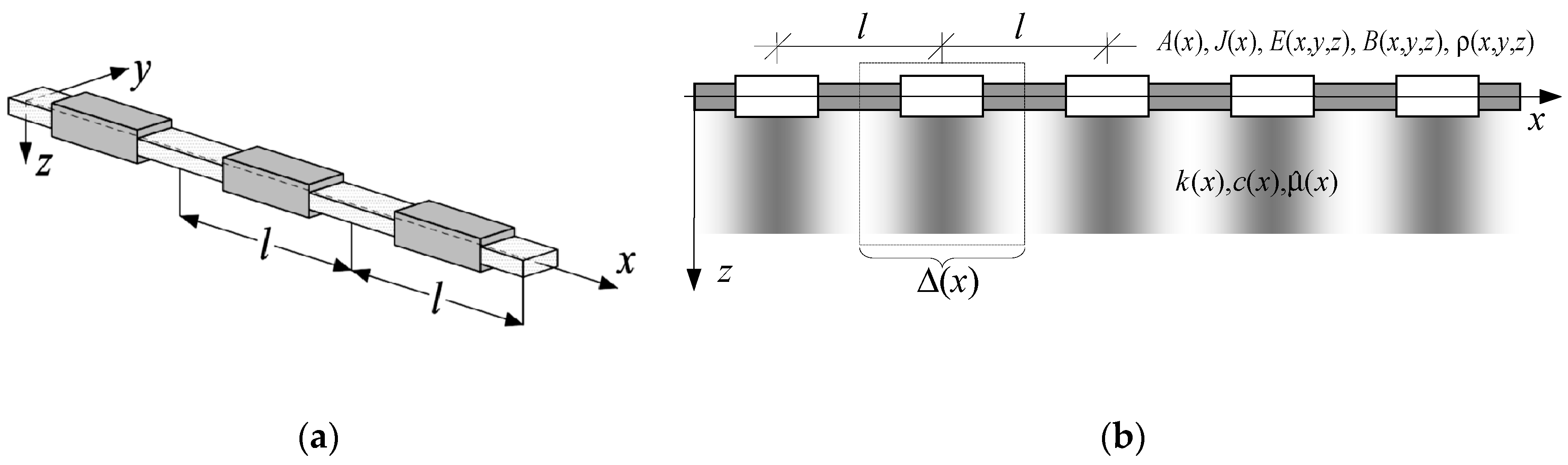
2. Modelling Approach
2.1. Modelling Preliminaries
2.2. Introductory Concepts of the Tolerance Modelling
- ;
- .
- ;
- .
- ;
- .
- ;
- .
- .
- ∂kg ∈ O(lα−k) for k = 0,1, …,α, α = 2, ∂0g ≡ g;
- <g>(x) ≈ 0 for every ,
2.3. Tolerance Modelling Assumptions
- ∂kgA∈O(l2−k) for k = 0, 1, …, 2;
- <μgA> = 0;
- <μgAgB> = 0 for A ≠ B, A, B = 1, …,P.
2.4. The Outline of the Tolerance Modelling Procedure
3. Results—The Governing Equations
3.1. The General Tolerance Model Equations
- The general tolerance constitutive equations.
- The general tolerance equations of motion.
3.2. The (Standard) Tolerance Model Equations
- The standard tolerance constitutive equations.
- The standard tolerance equations of motion.
3.3. The Asymptotic Model Equations
- The asymptotic constitutive equations.
- The asymptotic equations of motion.
4. Results—A Simple Theoretical Example
4.1. Introduction
4.2. Example—Frequencies of a Travelling Wave
4.2.1. The General Tolerance Model
4.2.2. The Standard Tolerance Model
4.2.3. The Asymptotic Model
4.3. Comments on the Example
5. Remarks
- The tolerance modelling method allows one to derive averaged equations of models of slender visco-elastic beams on a periodic damping foundation with constant coefficients, which replace the classic equations with non-continuous, periodic coefficients.
- Using various definitions of concepts of the weakly-slowly-varying function and the slowly-varying function. two different tolerance models can be derived in the framework of the tolerance approach—the general tolerance model and the standard tolerance model.
- The governing equations of both the tolerance models involve terms which describe the effect of the microstructure size on overall dynamic and stability behavior of these beams; hence both models allow one to analyze dynamic and stability problems of the beams under consideration on the macro-and the micro-level.
- The form of the model equations depends on the class of slowly-varying, basic, unknown functions. The weakly-slowly-varying functions lead to the general tolerance model equations, which involve additional terms depending on the microstructure parameter; but the slowly-varying functions lead to the standard tolerance model equations.
- In contrast to the governing equations of the standard tolerance model for slender visco-elastic beams on a periodic damping foundation, the equations of the general tolerance model for these beams include additional terms describing the effect of the microstructure size also in stationary problems.
- In contrast, the asymptotic model allows one to analyze dynamic and stability problems of the beams under consideration only at the macro-level, without the effect of the microstructure.
- Based on the presented simple example, it can be observed that the proposed general tolerance model also allows one in such a simple case not only to analyze the effect of microstructure in the form of higher order vibrations (microvibrations), but also to consider and relate this effect with the fundamental lower order vibrations (macrovibrations).
Funding
Conflicts of Interest
References
- Bensoussan, A.; Lions, J.L.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; North-Holland: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Kohn, R.V.; Vogelius, M. A new model for thin plates with rapidly varying thickness. Int. J. Solids Struct. 1984, 20, 333–350. [Google Scholar] [CrossRef]
- Kolpakov, A. Calculation of the characteristics of thin elastic rods with a periodic structure. J. Appl. Math. Mech. 1991, 55, 358–365. [Google Scholar] [CrossRef]
- Kolpakov, A. Application of homogenization method to justification of 1-D model for beam of periodic structure having initial stresses. Int. J. Solids Struct. 1998, 35, 2847–2859. [Google Scholar] [CrossRef]
- Kolpakov, A. The governing equations of a thin elastic stressed beam with a periodic structure. J. Appl. Math. Mech. 1999, 63, 495–504. [Google Scholar] [CrossRef]
- Matysiak, S.J.; Nagórko, W. Microlocal parameters in the modelling of microperiodic plates. Ing. Arch. 1989, 59, 434–444. [Google Scholar] [CrossRef]
- Hajianmaleki, M.; Qatu, M.S. Vibrations of straight and curved composite beams: A review. Compos. Struct. 2013, 100, 218–232. [Google Scholar] [CrossRef]
- Roque, C.M.C.; Fidalgo, D.S.; Ferreira, A.J.M.; Reddy, J.N. A study of a microstructure-dependent composite laminated Timoshenko beam using a modified couple stress theory and a meshless method. Compos. Struct. 2013, 96, 532–537. [Google Scholar] [CrossRef]
- Batra, R.C.; Xiao, J. Finite deformations of curved laminated St. Venant–Kirchhoff beam using layer-wise third order shear and normal deformable beam theory (TSNDT). Compos. Struct. 2013, 97, 147–164. [Google Scholar] [CrossRef]
- Grygorowicz, M.; Magnucki, K.; Malinowski, M. Elastic buckling of a sandwich beam with variable mechanical properties of the core. Thin Walled Struct. 2015, 87, 127–132. [Google Scholar] [CrossRef]
- Wittenbeck, L.; Grygorowicz, M.; Paczos, P. Numerical analysis of sandwich beam with corrugated core under three-point bending. AIP Conf. Proc. 2015, 1648, 800007. [Google Scholar]
- Grygorowicz, M.; Magnucka-Blandzi, E. Mathematical modeling for dynamic stability of sandwich beam with variable mechanical properties of core. Appl. Math. Mech. 2016, 37, 1361–1374. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H.; Fraska, A. Torsion of elliptical composite beams with auxetic phase. Phys. Status Solidi Basic Res. 2016, 253, 1359–1368. [Google Scholar] [CrossRef]
- Jopek, H.; Strek, T. Torsion of a two-phased composite bar with helical distribution of constituents. Phys. Status Solidi 2017, 254, 1700050. [Google Scholar] [CrossRef]
- Pawlus, D. Stability of three-layered annular plate with composite facings. Appl. Compos. Mater. 2017, 24, 141–158. [Google Scholar] [CrossRef]
- Arruda, M.R.T.; Castro, L.M.S.; Ferreira, A.J.M.; Garrido, M.; Gonilha, J.; Correia, J.R. Analysis of composite layered beams using Carrera unified formulation with Legendre approximation. Compos. Part B Eng. 2018, 137, 39–50. [Google Scholar] [CrossRef]
- Bui, T.Q.; Khosravifard, A.; Zhang, C.; Hematiyan, M.R.; Golu, M.V. Dynamic analysis of sandwich beams with functionally graded core using a truly meshfree radial point interpolation method. Eng. Struct. 2013, 47, 90–104. [Google Scholar] [CrossRef]
- Murin, J.; Aminbaghai, M.; Hrabovsky, J.; Kutiš, V.; Kugler, S. Modal analysis of the FGM beams with effect of the shear correction function. Compos. Part B 2013, 45, 1575–1582. [Google Scholar] [CrossRef]
- Carpentieri, G.; Tornabene, F.; Ascione, A.; Fraternali, F. An accurate one-dimensional theory for the dynamics of laminated composite curved beams. J. Sound Vibration 2015, 336, 96–105. [Google Scholar] [CrossRef]
- Roque, C.M.C.; Martins, P.A.L.S.; Ferreira, A.J.M.; Jorge, R.M.N. Differential evolution for free vibration optimization of functionally graded nano beams. Compos. Struct. 2016, 156, 29–34. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F. Strong formulation isogeometric analysis (SFIGA) for laminated composite arbitrarily shaped plates. Compos. Part B Eng. 2016, 96, 173–203. [Google Scholar] [CrossRef]
- Liu, B.; Ferreira, A.J.M.; Xing, Y.F.; Neves, A.M.A. Analysis of composite plates using a layerwise theory and a differential quadrature finite element method. Compos. Struct. 2016, 156, 393–398. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Krysko, V.A.; Pavlov, S.P.; Zhigalov, M.V.; Krysko, A.V. On natural frequencies of non-uniform beams modulated by finite periodic cells. Int. J. Solids Struct. 2017, 117, 39–50. [Google Scholar] [CrossRef]
- Kołakowski, Z.; Mania, R.J. Influence of the coupling matrix B on the interactive buckling of FML-FGM columns with closed cross-sections under axial compression. Compos. Struct. 2017, 173, 70–77. [Google Scholar] [CrossRef]
- Mania, R.J.; Madeo, A.; Zucco, G.; Kubiak, T. Imperfection sensitivity of post-buckling of FML channel section column. Thin Walled Struct. 2017, 114, 32–38. [Google Scholar] [CrossRef]
- Jouneghani, F.Z.; Dimitri, R.; Tornabene, F. Structural response of porous FG nanobeams under hygro-thermo-mechanical loadings. Compos. Part B Eng. 2018, 152, 71–78. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. Bending and vibration analyses of coupled axially functionally graded tapered beams. Nonlinear Dyn. 2018, 91, 17–28. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Vibration analysis of shear-deformable AFG imperfect beams. Compos. Struct. 2018, 200, 910–920. [Google Scholar] [CrossRef]
- Brillouin, L. Wave Propagation in Periodic Structures; Dover Pub. Inc.: Dover, UK, 1953. [Google Scholar]
- Robinson, C.W.; Leppelmeier, G.W. Experimental verification of dispersion relations for layered composites. J. Appl. Mech. 1974, 41, 89–91. [Google Scholar] [CrossRef]
- Xiang, H.J.; Shi, Z.F. Analysis of flexural vibration band gaps in periodic beams using differential quadrature method. Comput. Struct. 2009, 87, 1559–1566. [Google Scholar] [CrossRef]
- Cheng, Z.B.; Xu, Y.G.; Zhang, L.L. Analysis of flexural wave bandgaps in periodic plate structures using differential quadrature element method. Int. J. Mech. Sci. 2015, 100, 112–125. [Google Scholar] [CrossRef]
- Yu, D.; Wen, J.; Shen, H.; Xiao, Y.; Wen, X. Propagation of flexural wave in periodic beam on elastic foundations. Phys. Lett. A 2012, 376, 626–630. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, X.; Wang, W.; Wang, L.; Peng, F.; Li, B. On natural frequencies of non-uniform beams modulated by finite periodic cells. Phys. Lett. A 2016, 380, 3278–3283. [Google Scholar] [CrossRef]
- Chen, T. Investigations on flexural wave propagation of a periodic beam using multi-reflection method. Arch. Appl. Mech. 2013, 83, 315–329. [Google Scholar] [CrossRef]
- Wu, Z.J.; Li, F.M.; Wang, Y.Z. Vibration band gap properties of periodic Mindlin plate structure using the spectral element method. Meccanica 2014, 49, 725–737. [Google Scholar] [CrossRef]
- Zhou, X.Q.; Yu, D.Y.; Shao, X.; Wang, S.; Tian, Y.H. Band gap characteristics of periodically stiffened-thin-plate based on center-finite-difference-method. Thin Walled Struct. 2014, 82, 115–123. [Google Scholar] [CrossRef]
- Zhou, X.Q.; Yu, D.Y.; Shao, X.; Wang, S.; Zhang, S.Q. Simplified-super-element-method for analyzing free flexural vibration characteristics of periodically stiffened-thin-plate filled with viscoelastic damping material. Thin Walled Struct. 2015, 94, 234–252. [Google Scholar] [CrossRef]
- Woźniak, C.; Wierzbicki, E. Averaging Techniques in Thermomechanics of Composite Solids. Tolerance Averaging Versus Homogenization; Publishing House of Częstochowa University of Technology: Częstochowa, Poland, 2000. [Google Scholar]
- Thermomechanics of Heterogeneous Solids and Structures; Woźniak, C., Michalak, B., Jędrysiak, J., Eds.; Publishing House of Łódź University of Technology: Łódź, Poland, 2008. [Google Scholar]
- Woźniak, C. Mathematical Modelling and Analysis in Continuum Mechanics of Microstructured Media; Publishing House of Łódź University of Technology: Gliwice, Poland, 2010. [Google Scholar]
- Mazur-Śniady, K. Macro-dynamic of micro-periodic elastic beams. J. Theor. Appl. Mech. 1993, 31, 781–793. [Google Scholar]
- Dell’Isola, F.; Rosa, L.; Woźniak, C. A micro-structural continuum modelling compacting fluid-saturated grounds. Acta Mech. 1998, 127, 165–182. [Google Scholar] [CrossRef]
- Wierzbicki, E.; Woźniak, C. On the dynamics of combined plane periodic structures. Arch. Appl. Mech. 2000, 70, 387–398. [Google Scholar] [CrossRef]
- Jędrysiak, J. On the stability of thin periodic plates. Eur. J. Mech. A Solids 2000, 19, 487–502. [Google Scholar] [CrossRef]
- Michalak, B. The meso-shape functions for the meso-structural models of wavy-plates. ZAMM 2001, 81, 639–641. [Google Scholar] [CrossRef]
- Nagórko, W.; Woźniak, C. Nonasymptotic modelling of thin plates reinforced by a system of stiffeners. Electr. J. Polish Agric. Univ. Civil Eng. 2002, 5, 8. [Google Scholar]
- Baron, E. On dynamic behaviour of medium-thickness plates with uniperiodic structure. Arch. Appl. Mech. 2003, 73, 505–516. [Google Scholar] [CrossRef]
- Jędrysiak, J. The length-scale effect in the buckling of thin periodic plates resting on a periodic Winkler foundation. Meccanica 2003, 38, 435–451. [Google Scholar] [CrossRef]
- Jędrysiak, J. Free vibrations of thin periodic plates interacting with an elastic periodic foundation. Int. J. Mech. Sci. 2003, 45, 1411–1428. [Google Scholar] [CrossRef]
- Mazur-Śniady, K.; Woźniak, C.; Wierzbicki, E. On the modelling of dynamic problems for plates with a periodic structure. Arch. Appl. Mech. 2004, 74, 179–190. [Google Scholar] [CrossRef]
- Tomczyk, B. A non-asymptotic model for the stability analysis of thin biperiodic cylindrical shells. Thin Walled Struct. 2007, 45, 941–944. [Google Scholar] [CrossRef]
- Tomczyk, B. Dynamic stability of micro-periodic cylindrical shells. Mech. Mech. Eng. 2010, 14, 137–150. [Google Scholar]
- Jędrysiak, J. Geometrically nonlinear vibrations of thin visco-elastic periodic plates on a foundation with damping: Non-asymptotic modelling. J. Theor. Appl. Mech. 2016, 54, 945–961. [Google Scholar] [CrossRef]
- Domagalski, Ł.; Jędrysiak, J. Nonlinear vibrations of periodic beams. J. Theor. Appl. Mech. 2016, 54, 1095–1108. [Google Scholar] [CrossRef]
- Marczak, J.; Jędrysiak, J. Some remarks on modelling of vibrations of periodic sandwich structures with inert core. Compos. Struct. 2018, 202, 752–758. [Google Scholar] [CrossRef]
- Jędrysiak, J.; Ostrowski, P. The effect of uncertain material properties on free vibrations of thin periodic plates. Meccanica 2017, 52, 3713–3730. [Google Scholar] [CrossRef]
- Michalak, B.; Wirowski, A. Dynamic modelling of thin plate made of certain functionally graded materials. Meccanica 2012, 47, 1487–1498. [Google Scholar] [CrossRef][Green Version]
- Perliński, W.; Gajdzicki, M.; Michalak, B. Modelling of annular plates stability with functionally graded structure interacting with elastic heterogeneous subsoil. J. Theor. Appl. Mech. 2014, 52, 485–498. [Google Scholar]
- Wirowski, A.; Michalak, B.; Gajdzicki, M. Dynamic modelling of annular plates of functionally graded structure resting on elastic heterogeneous foundation with two modules. J. Mech. 2015, 31, 493–504. [Google Scholar] [CrossRef]
- Jędrysiak, J.; Kaźmierczak-Sobińska, M. On free vibration of thin functionally graded plate bands resting on an elastic foundation. J. Theor. Appl. Mech. 2015, 53, 629–642. [Google Scholar] [CrossRef]
- Michalak, B. 2D tolerance and asymptotic models in elastodynamics of a thin-walled structure with dense system of ribs. Arch. Civil Mech. Eng. 2015, 15, 449–455. [Google Scholar] [CrossRef]
- Ostrowski, P.; Michalak, B. The combined asymptotic-tolerance model of heat conduction in a skeletal micro-heterogeneous hollow cylinder. Compos. Struct. 2015, 134, 343–352. [Google Scholar] [CrossRef]
- Pazera, E.; Jędrysiak, J. Effect of microstructure in thermoelasticity problems of functionally graded laminates. Compos. Struct. 2018, 202, 296–303. [Google Scholar] [CrossRef]
- Jędrysiak, J. Tolerance modelling of free vibration frequencies of thin functionally graded plates with one-directional microstructure. Compos. Struct. 2017, 161, 453–468. [Google Scholar] [CrossRef]
- Tomczyk, B.; Szczerba, P. A new asymptotic-tolerance model of dynamic and stability problems for longitudinally graded cylindrical shells. Compos. Struct. 2018, 202, 473–481. [Google Scholar] [CrossRef]
- Jędrysiak, J. Tolerance modelling of free vibrations of medium thickness functionally graded plates. Compos. Struct. 2018, 202, 1253–1262. [Google Scholar] [CrossRef]
- Jędrysiak, J. General and standard tolerance models of thin two-directional periodic plates. In Shell Structures: Theory and Applications; Pietraszkiewicz, W., Witkowski, W., Eds.; Taylor & Francis: London, UK, 2018; Volume 4, pp. 101–104. [Google Scholar]
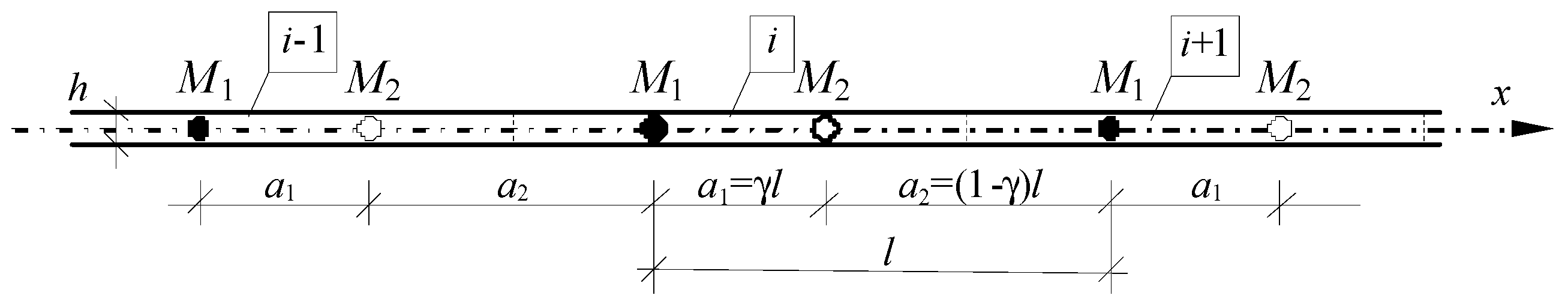

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jędrysiak, J. Tolerance Modelling of Vibrations and Stability for Periodic Slender Visco-Elastic Beams on a Foundation with Damping. Revisiting. Materials 2020, 13, 3939. https://doi.org/10.3390/ma13183939
Jędrysiak J. Tolerance Modelling of Vibrations and Stability for Periodic Slender Visco-Elastic Beams on a Foundation with Damping. Revisiting. Materials. 2020; 13(18):3939. https://doi.org/10.3390/ma13183939
Chicago/Turabian StyleJędrysiak, Jarosław. 2020. "Tolerance Modelling of Vibrations and Stability for Periodic Slender Visco-Elastic Beams on a Foundation with Damping. Revisiting" Materials 13, no. 18: 3939. https://doi.org/10.3390/ma13183939
APA StyleJędrysiak, J. (2020). Tolerance Modelling of Vibrations and Stability for Periodic Slender Visco-Elastic Beams on a Foundation with Damping. Revisiting. Materials, 13(18), 3939. https://doi.org/10.3390/ma13183939



