Accurate, Efficient and Rigorous Numerical Analysis of 3D H-PDLC Gratings
Abstract
1. Introduction
2. Physical Model
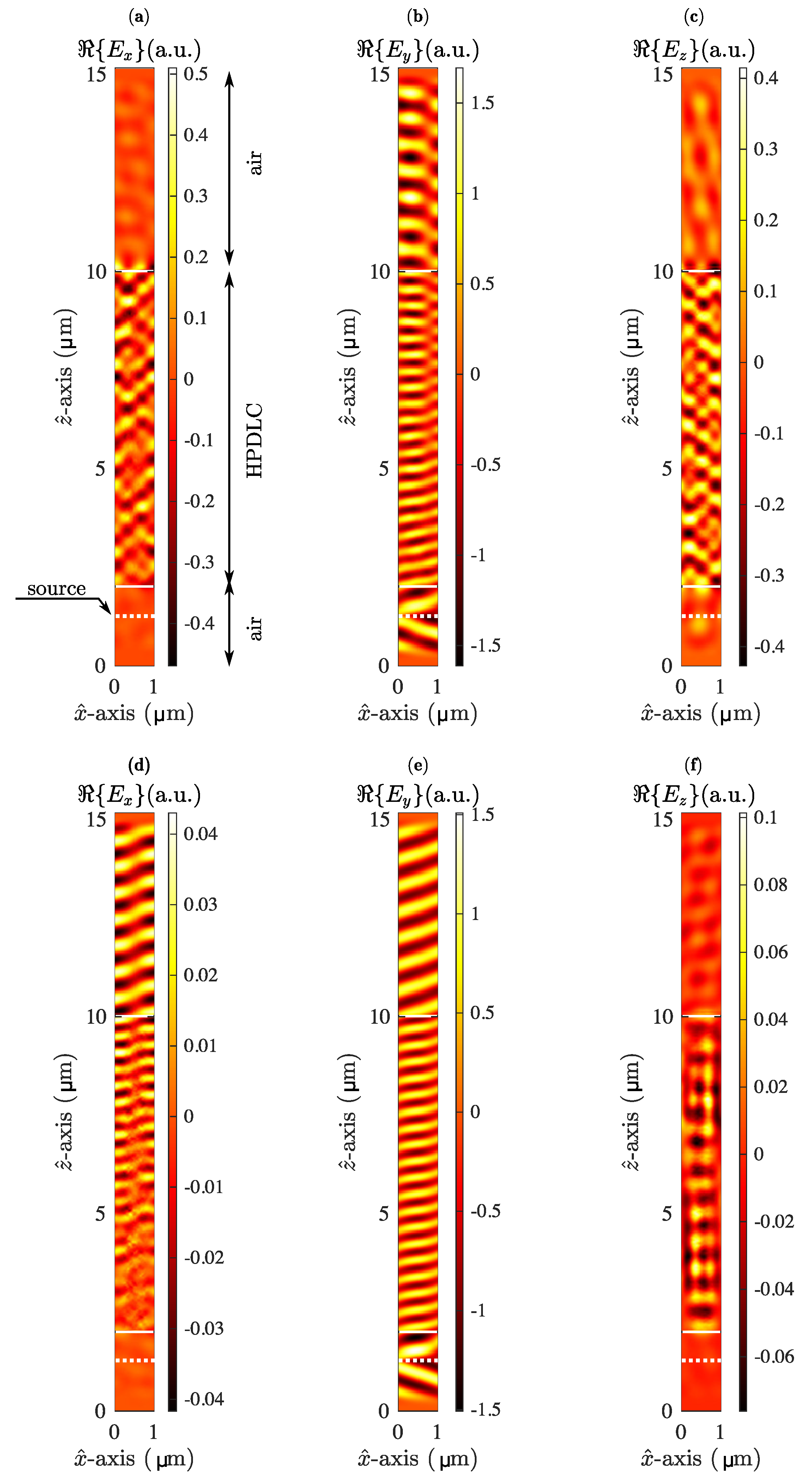
2.1. Numerical Solution of the Optical Field
2.2. Director Distribution of the LC Droplets
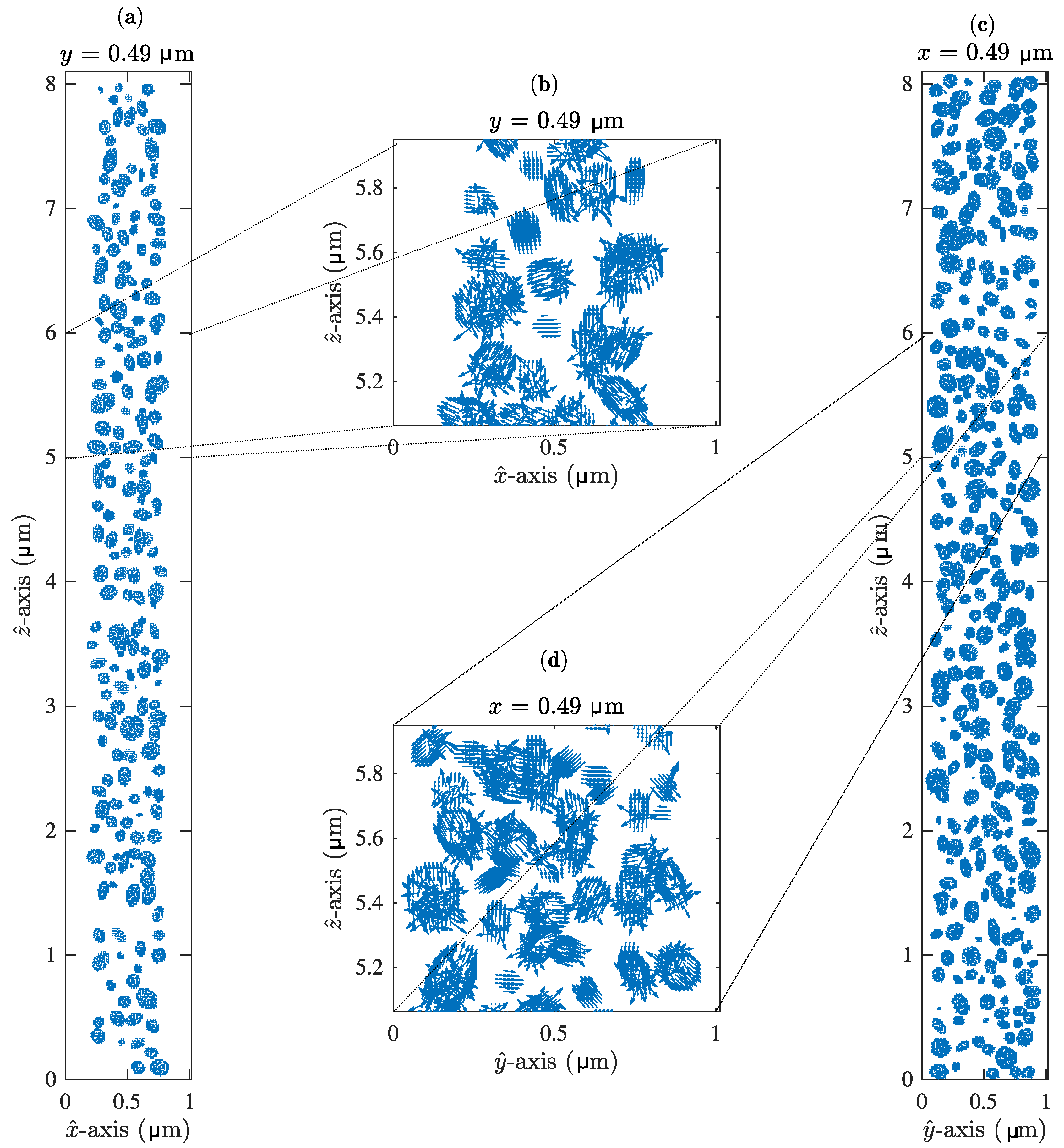
2.3. Random H-PDLC Sample Created by Packing Ellipsoids
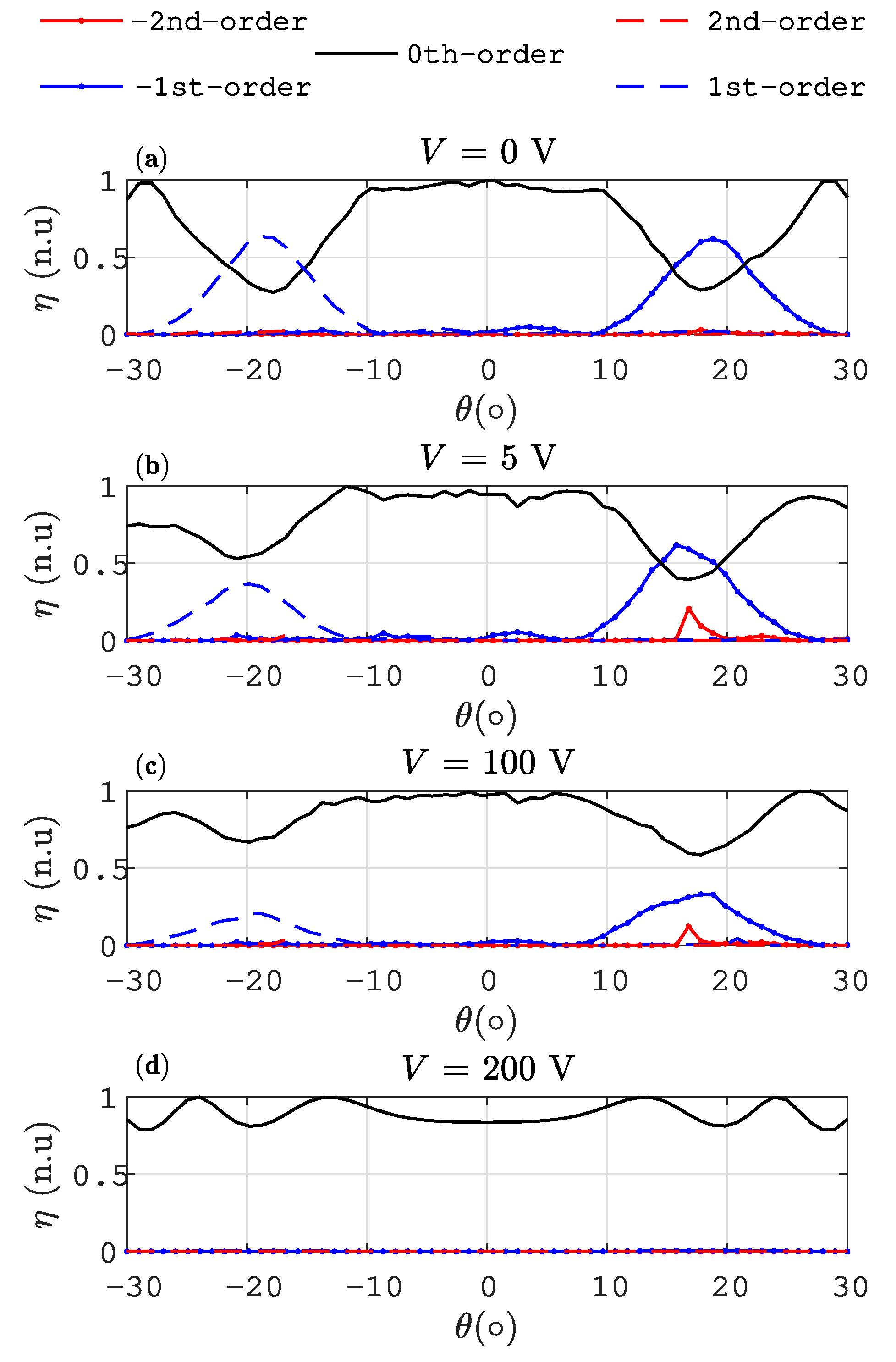
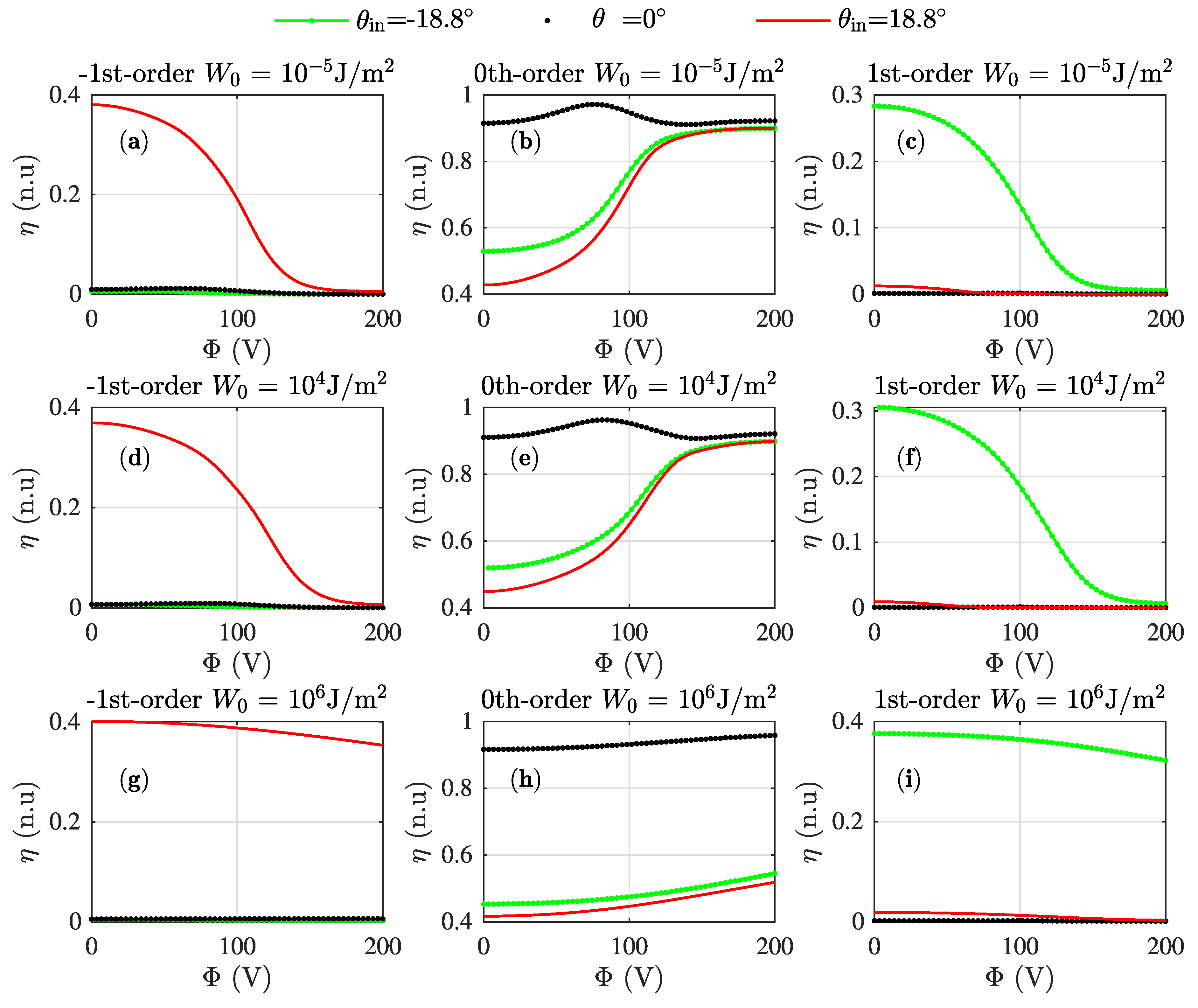
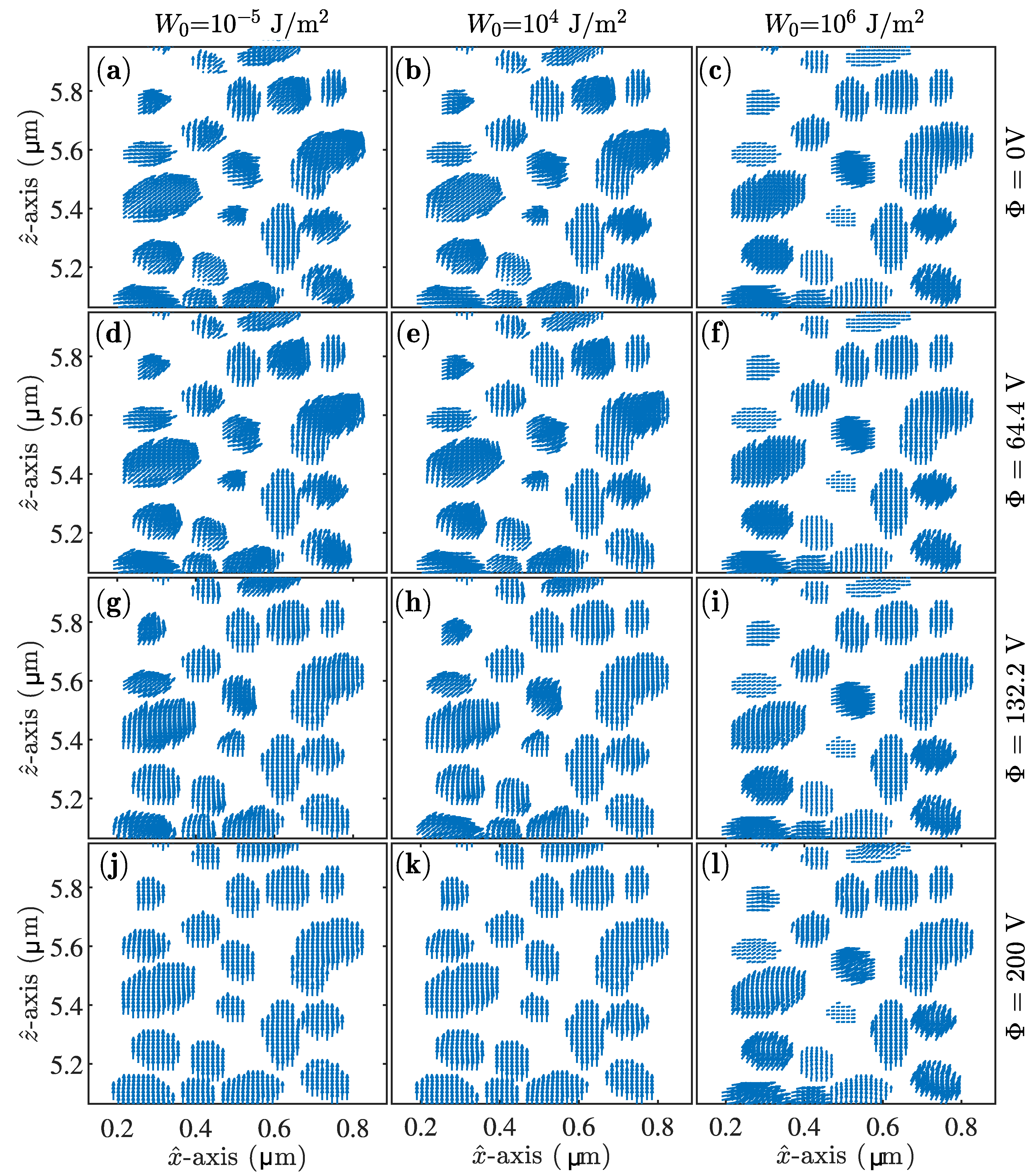
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| H-PDLC | Holographic polymer dispersed liquid crystal |
| SF-FDTD | Split field finite-difference time-domain |
References
- Shen, T.; Cai, Z.; Liu, Y.; Zheng, J. Switchable pupil expansion propagation using orthogonal superposition varied-line-spacing H-PDLC gratings in a holographic waveguide system. Appl. Opt. 2019, 58, 6622–6628. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zheng, J.; Shen, T.; Wang, K.; Zhuang, S. Diffusion kinetics investigations of Nano Ag-doped holographic polymer dispersed liquid crystal gratings. Liq. Cryst. 2019, 46, 1852–1860. [Google Scholar] [CrossRef]
- You-Rong, L.; Ji-Hong, Z.; Kun, G.; Kang-Ni, W.; Song-Lin, Z. Equivalent circuit modeling of non-uniformly distributed nano Ag doped Holographic polymer dispersed Liquid Crystal Grating. J. Infrared Millim. Waves 2017, 36, 599–605. [Google Scholar] [CrossRef]
- Wang, K.; Zheng, J.; Liu, Y.; Gao, H.; Zhuang, S. Electrically tunable two-dimensional holographic polymer-dispersed liquid crystal grating with variable period. Opt. Commun. 2017, 392, 128–134. [Google Scholar] [CrossRef]
- Zheng, J.; Wang, K.; Gao, H.; Lu, F.; Sun, L.; Zhuang, S. Multi-wavelength sensitive holographic polymer dispersed liquid crystal grating applied within image splitter for autostereoscopic display. In Proceedings of the Photonic Fiber and Crystal Devices: Advances in Materials and Innovations in Device Applications X, San Diego, CA, USA, 28–29 August 2016; Yin, S., Guo, R., Eds.; SPIE: Bellingham, WA, USA, 2016; Volume 9958. [Google Scholar] [CrossRef]
- Wang, K.; Zheng, J.; Gao, H.; Lu, F.; Sun, L.; Yin, S.; Zhuang, S. Tri-color composite volume H-PDLC grating and its application to 3D color autostereoscopic display. Opt. Express 2015, 23, 31436. [Google Scholar] [CrossRef] [PubMed]
- Montemezzani, G.; Zgonik, M. Light diffraction at mixed phase and absorption gratings in anisotropic media for arbitrary geometries. Phys. Rev. E 1997, 55, 1035–1047. [Google Scholar] [CrossRef]
- Sutherland, R.L. Polarization and switching properties of holographic polymer-dispersed liquid-crystal gratings. I. Theoretical model. J. Opt. Soc. Am. B 2002, 19, 2995–3003. [Google Scholar] [CrossRef]
- Wu, B.G.; Erdmann, J.H.; Doane, J.W. Response times and voltages for PDLC light shutters. Liq. Cryst. 1989, 5, 1453–1465. [Google Scholar] [CrossRef]
- Sutherland, R.L.; Tondiglia, V.P.; Natarajan, L.V.; Lloyd, P.F.; Bunning, T.J. Coherent diffraction and random scattering in thiol-ene–based holographic polymer-dispersed liquid crystal reflection gratings. J. Appl. Phys. 2006, 99, 123104. [Google Scholar] [CrossRef]
- Kubitskiy, V.; Reshetnyak, V.; Galstian, T. Electric Field Control of Diffraction Efficiency in Holographic Polymer Dispersed Liquid Crystal. Mol. Cryst. Liq. Cryst. 2005, 438, 283/[1847]–290/[1854]. [Google Scholar] [CrossRef]
- Kubytskyi, V.; Reshetnyak, V. Finite-difference time-domain method calculation of light propagation through H-PDLC. Semicond. Phys. Quantum Electron. Optoelectron. 2007, 10, 83–87. [Google Scholar] [CrossRef]
- Wang, B.; Wang, X.; Bos, P.J. Finite-difference time-domain calculations of a liquid-crystal-based switchable Bragg grating. J. Opt. Soc. Am. A 2004, 21, 1066–1072. [Google Scholar] [CrossRef] [PubMed]
- Gui, K.; Zheng, J.; Wang, K.; Li, D.; Zhuang, S. FDTD modelling of silver nanoparticles embedded in phase separation interface of H-PDLC. J. Nanomater. 2015, 2015. [Google Scholar] [CrossRef]
- Hällstig, E.; Martin, T.; Sjöqvist, L.; Lindgren, M. Spatial Light Modulator for Phase Modulation. J. Opt. Soc. Am. A 2005, 22, 177–184. [Google Scholar] [CrossRef]
- Moser, S.; Ritsch-Marte, M.; Thalhammer, G. Model-based compensation of pixel crosstalk in liquid crystal spatial light modulators. Opt. Express 2019, 27, 25046. [Google Scholar] [CrossRef]
- Wang, X. Liquid Crystal Diffractive Optical Elements: Applications and Limitations. PhD Thesis, Kent State University, Kent, OH, USA, 2005. [Google Scholar]
- Wang, X.; Wang, B.; Bos, P.J.; McManamon, P.F.; Pouch, J.J.; Miranda, F.A.; Anderson, J.E. Modeling and design of an optimized liquid-crystal optical phased array. J. Appl. Phys. 2005, 98. [Google Scholar] [CrossRef]
- Bleda, S.; Francés, J.; Gallego, S.; Márquez, A.; Neipp, C.; Pascual, I.; Beléndez, A. Numerical Analysis of H-PDLC Using the Split-Field Finite-Difference Time-Domain Method. Polymers 2018, 10, 465. [Google Scholar] [CrossRef]
- Aste, T.; Weaire, D. The Pursuito of Perfect Packing, 2nd ed.; Taylor & Francis: Boca Raton, FL, USA, 2008. [Google Scholar]
- Delaney, G.W.; Cleary, P.W. The packing properties of superellipsoids. EPL (Europhys. Lett.) 2010, 89, 34002. [Google Scholar] [CrossRef]
- Brouwers, H.J. Particle-size distribution and packing fraction of geometric random packings. Phys. Rev. E-Stat. Nonlinear Soft Matter Phys. 2006, 74, 1–15. [Google Scholar] [CrossRef]
- Bagatin, A.C.; Petit, J.M. Effects of the Geometric Constraints on the Size Distributions of Debris in Asteroidal Fragmentation. Icarus 2001, 149, 210–221. [Google Scholar] [CrossRef]
- Bernal, J.D.; Mason, J. Packing of Spheres: Co-ordination of Randomly Packed Spheres. Nature 1960, 188, 910–911. [Google Scholar] [CrossRef]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Oh, C.; Escuti, M.J. Time-domain analysis of periodic anisotropic media at oblique incidence: An efficient FDTD implementation. Opt. Express 2006, 14, 11870–11884. [Google Scholar] [CrossRef] [PubMed]
- Oh, C.; Escuti, M.J. Numerical analysis of polarization gratings using the finite-difference time-domain method. Phys. Rev. A 2007, 76, 043815. [Google Scholar] [CrossRef]
- Miskiewicz, M.N.; Bowen, P.T.; Escuti, M.J. Efficient 3D FDTD analysis of arbitrary birefringent and dichroic media with obliquely incident sources. In Physics and Simulation of Optoelectronic Devices XX; SPIE: Bellingham, WA, USA, 2012; Volume 8255, p. 82550W. [Google Scholar] [CrossRef]
- Francés, J.; Bleda, S.; Neipp, C.; Márquez, A.; Pascual, I.; Beléndez, A. Performance analysis of the {FDTD} method applied to holographic volume gratings: Multi-core {CPU} versus {GPU} computing. Comput. Phys. Commun. 2013, 184, 469–479. [Google Scholar] [CrossRef]
- Abdulhalim, I.; Menashe, D. Approximate analytic solutions for the director profile of homogeneously aligned nematic liquid crystals. Liq. Cryst. 2010, 37, 233–239. [Google Scholar] [CrossRef]
- Shahmansouri, A.; Rashidian, B. GPU implementation of split-field finite-difference time-domain method for Drude-Lorentz dispersive media. Prog. Electromagn. Res. 2012, 125, 55–77. [Google Scholar] [CrossRef][Green Version]
- Yang, D.K.; Wu, S.T. Fundamentals of Liquid Crystal Devices; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Žumer, S.; Kralj, S. Influence of k24 on the structure of nematic liquid crystal droplets. Liq. Cryst. 1992, 12, 613–624. [Google Scholar] [CrossRef]
- Kralj, S.; Žumer, S. Fréedericksz transitions in supra-m nematic droplets. Phys. Rev. A 1992, 45, 2461–2470. [Google Scholar] [CrossRef]
- Roden, J.; Gedney, S.; Kesler, M.; Maloney, J.; Harms, P. Time-domain analysis of periodic structures at oblique incidence: Orthogonal and nonorthogonal FDTD implementations. IEEE Trans. Microw. Theory Tech. 1998, 46, 420–427. [Google Scholar] [CrossRef]
- Shahmansouri, A.; Rashidian, B. Comprehensive three-dimensional split-field finite-difference time-domain method for analysis of periodic plasmonic nanostructures: Near- and far-field formulation. JOSA B 2011, 28, 2690. [Google Scholar] [CrossRef]
- Francés, J.; Bleda, S.; Álvarez, M.L.; Martínez, F.J.; Márquez, A.; Neipp, C.; Beléndez, A. Acceleration of split-field finite difference time-domain method for anisotropic media by means of graphics processing unit computing. Opt. Eng. 2013, 53, 011005. [Google Scholar] [CrossRef]
- Francés, J.; Tervo, J.; Neipp, C. Split-field finite-difference time-domain scheme for Kerr-type nonlinear periodic media. Prog. Electromagn. Res. 2013, 134, 559–579. [Google Scholar] [CrossRef]

| Parameter Description | Symbol | Value |
|---|---|---|
| Frank-Oseen elastic coefficients | 6.82 pN, 3.9 pN, 5.74 pN, 4.00 pN | |
| refractive indices LC | 1.84, 1.54 | |
| refractive index of the polymer | 1.53 | |
| relative dielectric permittivity | 14, 8.5 | |
| thickness of the grating | d | 8 m |
| cell size | 12.67 nm | |
| maximum voltage | 200 V | |
| Wavelength | 633 nm | |
| Time step |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Francés, J.; Bleda, S.; Puerto, D.; Gallego, S.; Márquez, A.; Neipp, C.; Pascual, I.; Beléndez, A. Accurate, Efficient and Rigorous Numerical Analysis of 3D H-PDLC Gratings. Materials 2020, 13, 3725. https://doi.org/10.3390/ma13173725
Francés J, Bleda S, Puerto D, Gallego S, Márquez A, Neipp C, Pascual I, Beléndez A. Accurate, Efficient and Rigorous Numerical Analysis of 3D H-PDLC Gratings. Materials. 2020; 13(17):3725. https://doi.org/10.3390/ma13173725
Chicago/Turabian StyleFrancés, Jorge, Sergio Bleda, Daniel Puerto, Sergi Gallego, Andrés Márquez, Cristian Neipp, Inmaculada Pascual, and Augusto Beléndez. 2020. "Accurate, Efficient and Rigorous Numerical Analysis of 3D H-PDLC Gratings" Materials 13, no. 17: 3725. https://doi.org/10.3390/ma13173725
APA StyleFrancés, J., Bleda, S., Puerto, D., Gallego, S., Márquez, A., Neipp, C., Pascual, I., & Beléndez, A. (2020). Accurate, Efficient and Rigorous Numerical Analysis of 3D H-PDLC Gratings. Materials, 13(17), 3725. https://doi.org/10.3390/ma13173725











