Nonlinear XFEM Modeling of Mode II Delamination in PPS/Glass Unidirectional Composites with Uncertain Fracture Properties
Abstract
1. Introduction
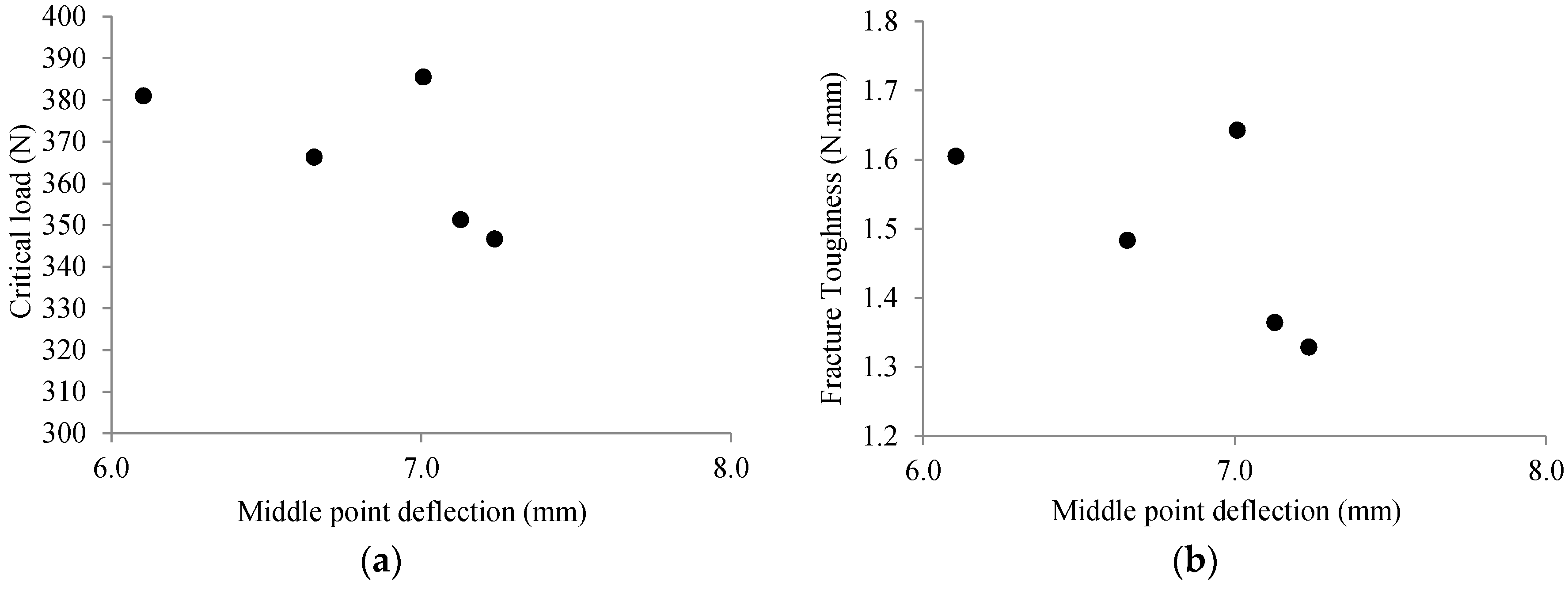
2. Experimental
3. XFEM Modeling of Delamination
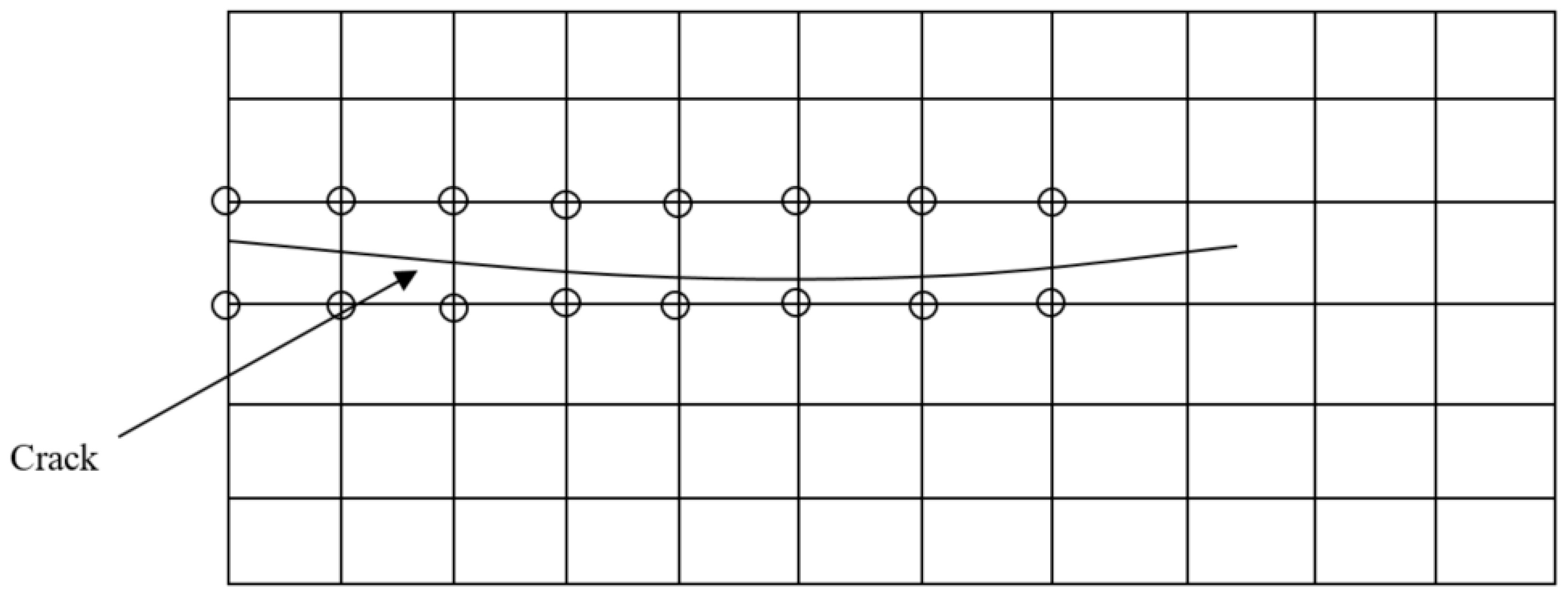
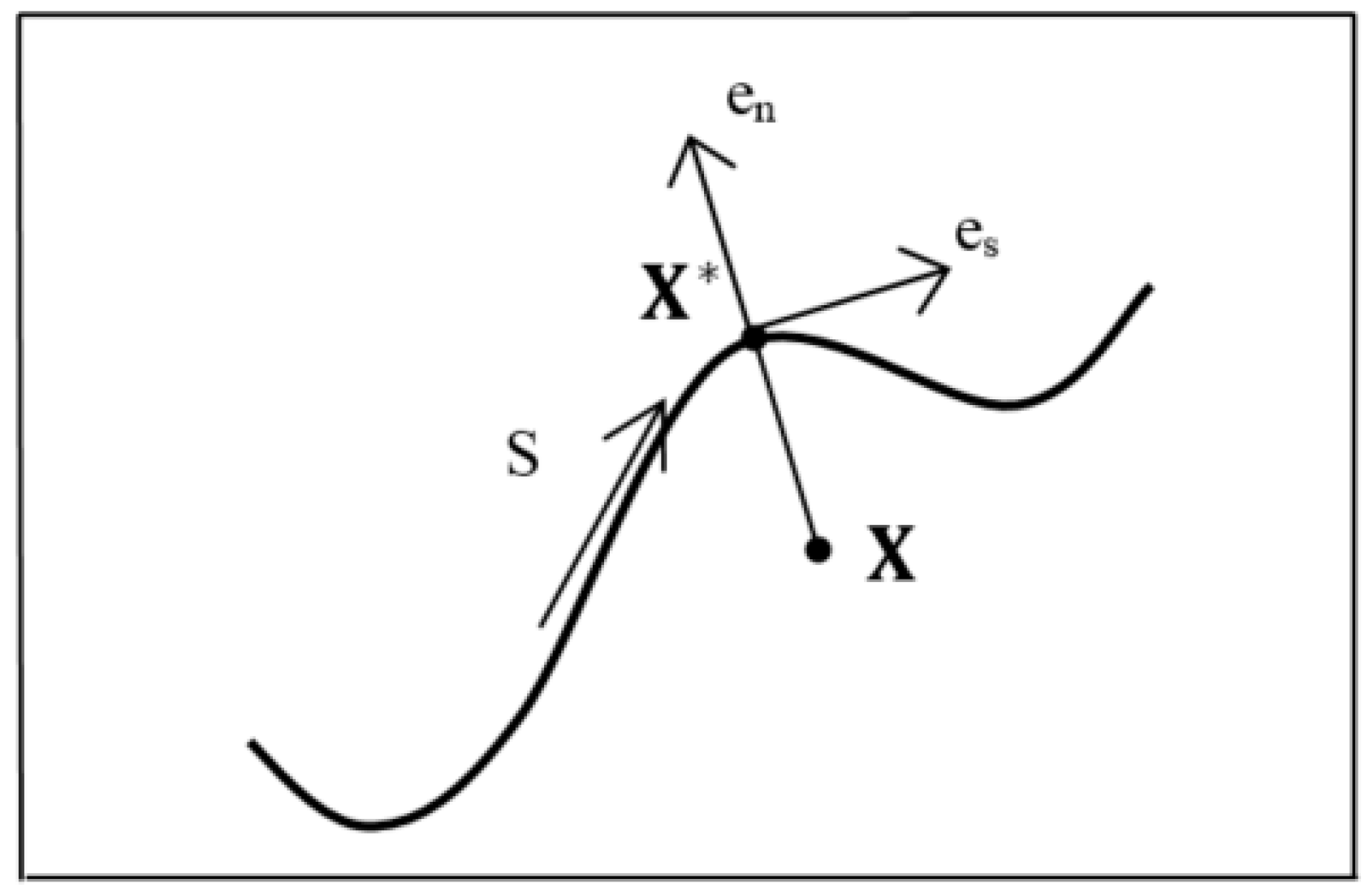
3.1. Modeling Cracks in XFEM
3.2. Modeling Contact on Material Interfaces Using XFEM
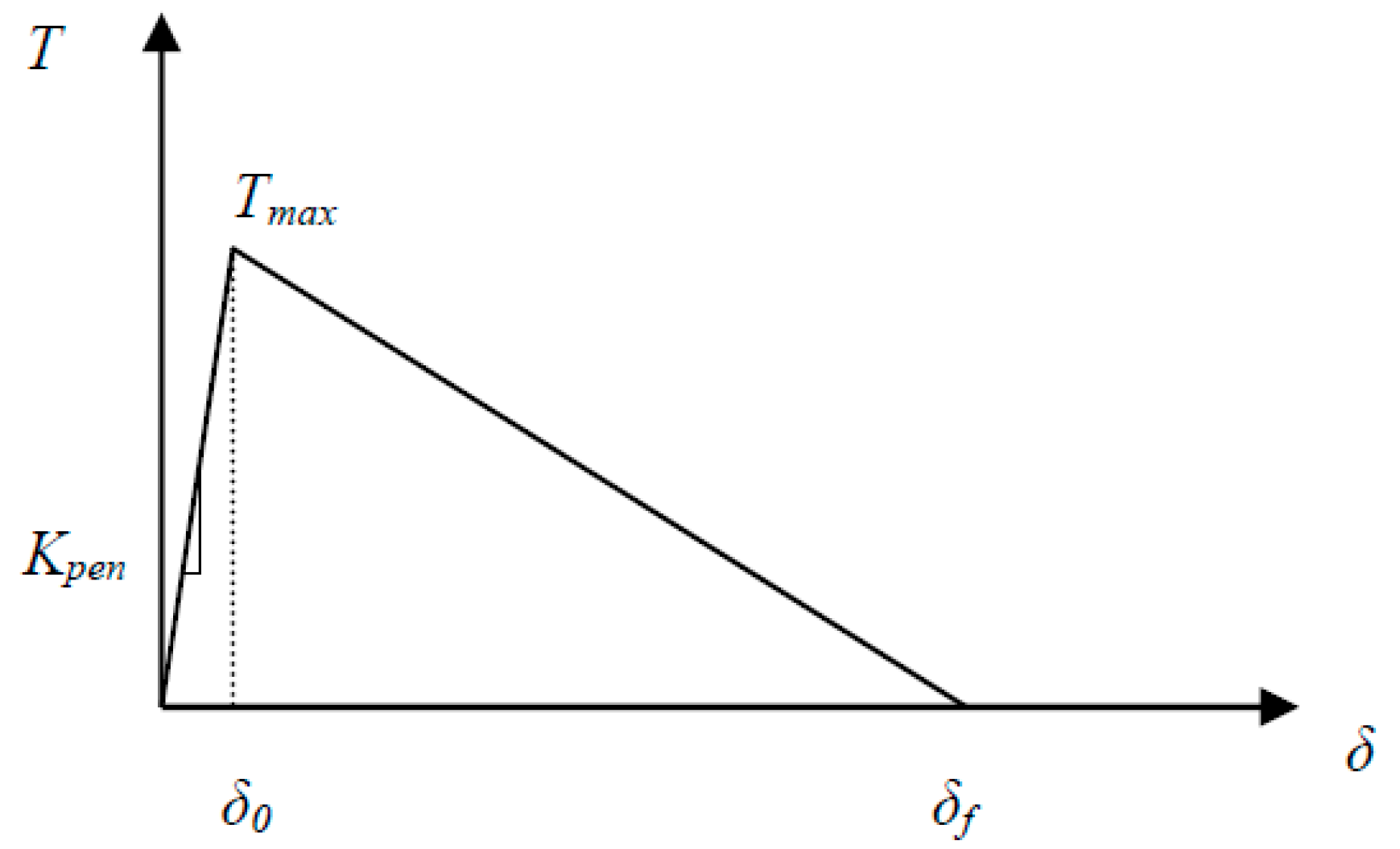
3.3. Cohesive Zone Implementation
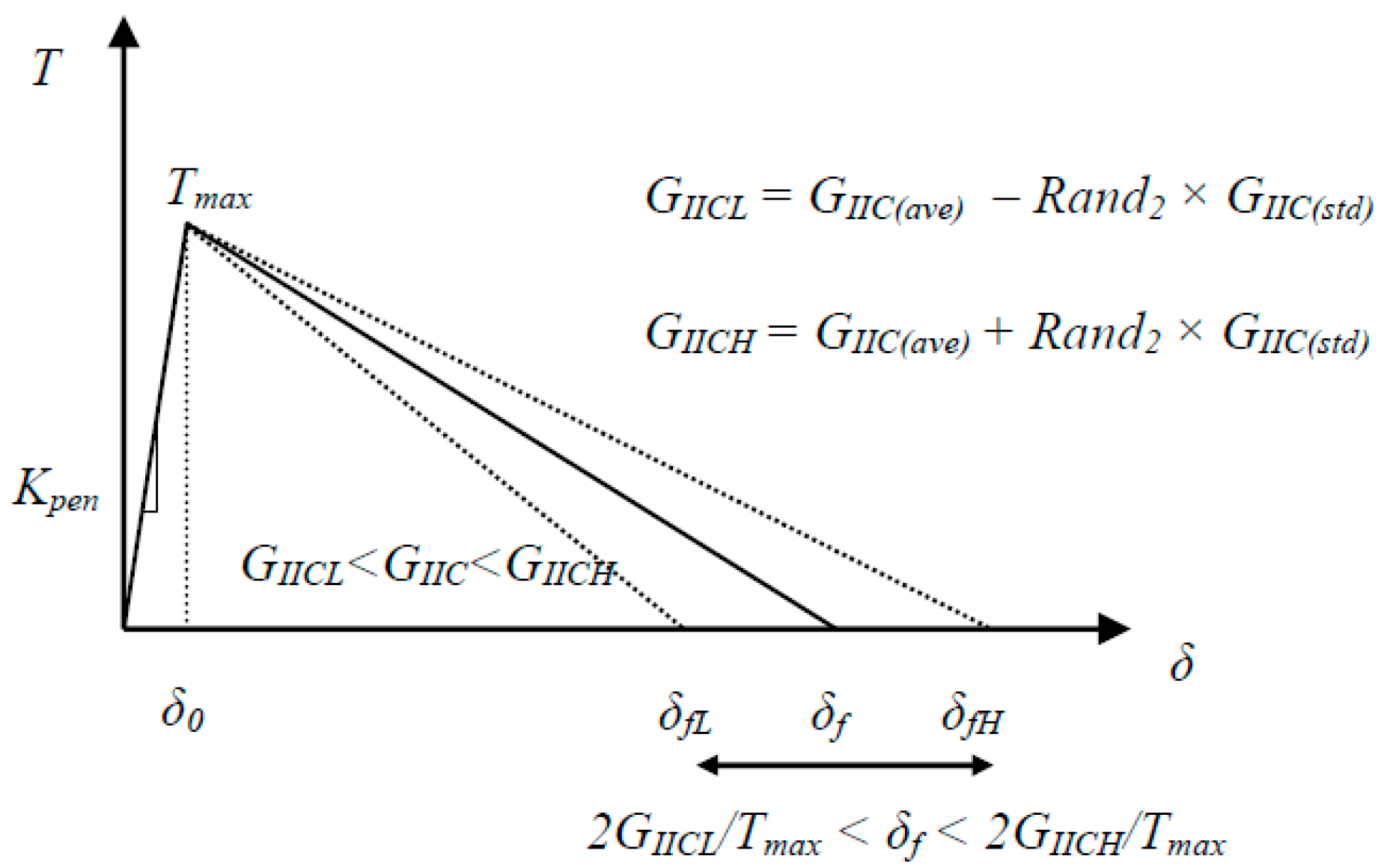
3.4. Stochastic Fracture Properties
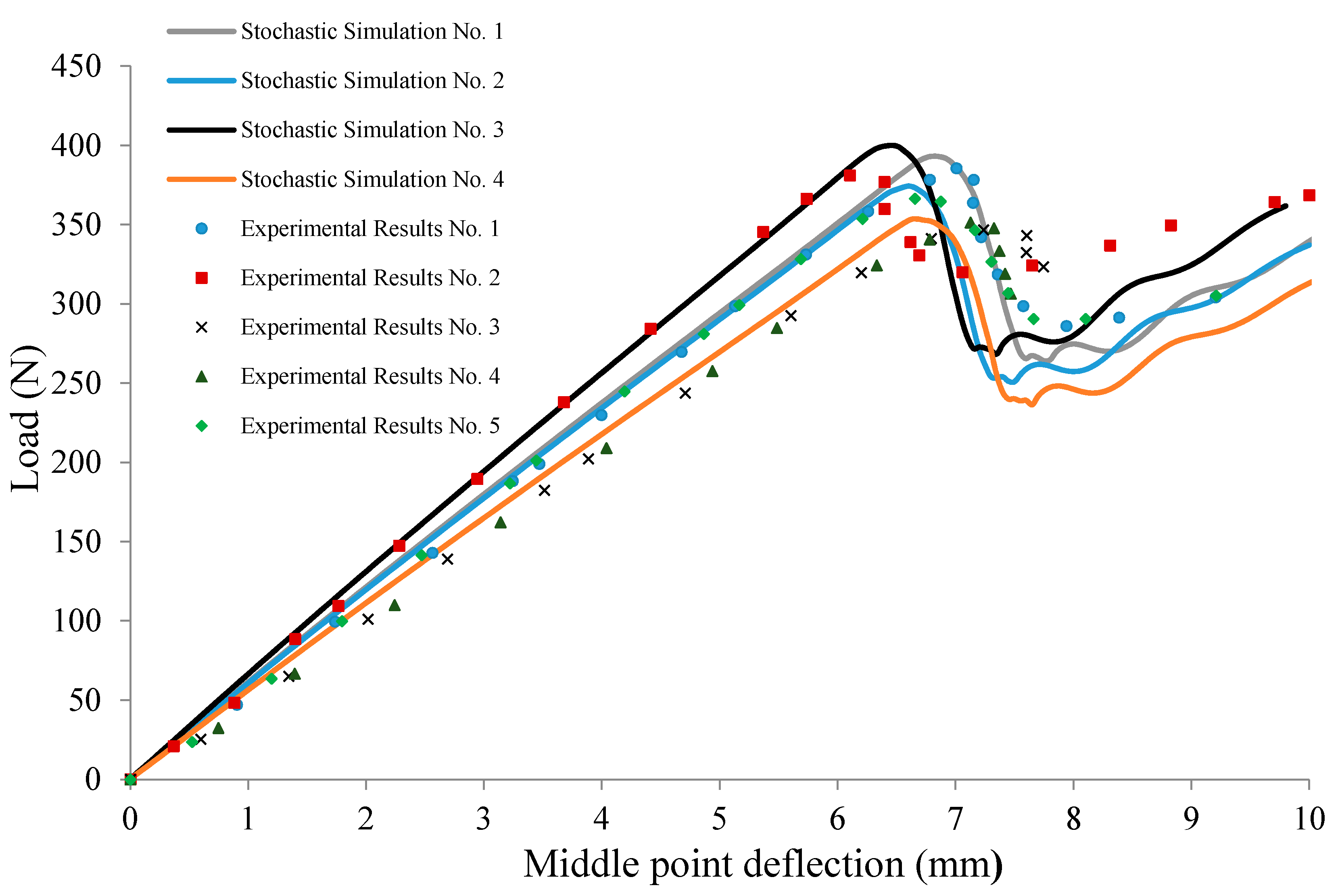
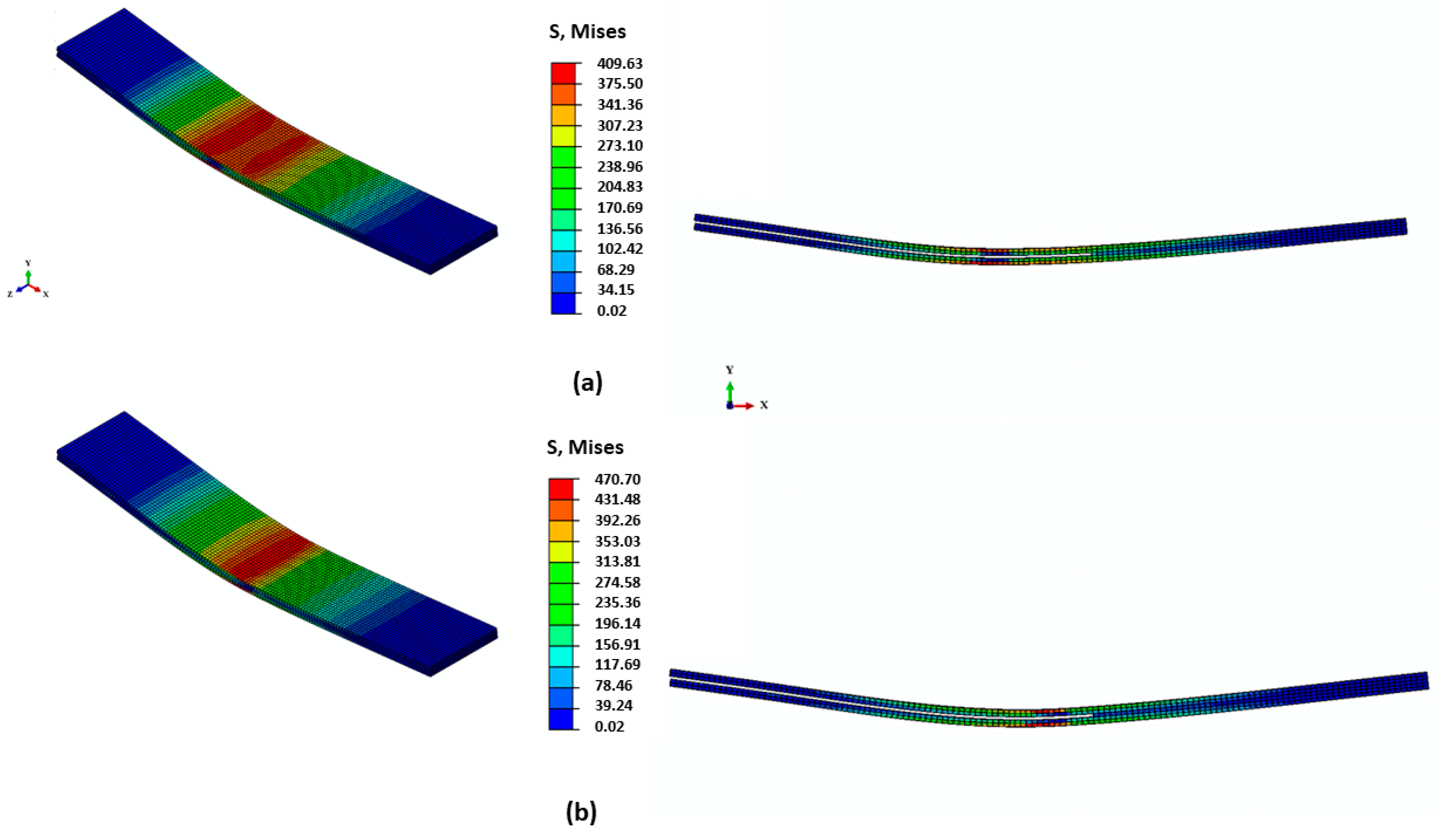
4. Results and Discussion
5. Conclusion
Author Contributions
Funding
Conflicts of Interest
References
- Prasad, M.S.; Venkatesha, C.S.; Jayaraju, T. Experimental methods of determining fracture toughness of fiber reinforced polymer composites under various loading conditions. J. Miner. Mater. Charact. Eng. 2011, 10, 1263–1275. [Google Scholar] [CrossRef]
- Gaggar, S.; Broutman, L.J. Fracture toughness of random glass fiber epoxy composites: An experimental investigation. Flaw Growth Fract. ASTM STP 1977, 631, 310–330. [Google Scholar]
- Mower, T.M.; Li, V.C. Fracture characterization of short fiber reinforced thermoset resin composites. Eng. Fract. Mech. 1987, 26, 593–603. [Google Scholar] [CrossRef]
- Russell, A.J. On the Measurement of Mode II Interlaminar Fracture Energies; Material Report 82; Defence Research Establishment Pacific: Victoria, BC, Canada, 1982. [Google Scholar]
- Murri, G.B.; Obrien, T. Interlaminar GIIC evaluation of toughened resin matrix composites using the end-notched flexure test. In Proceedings of the 26th AIAA/ASME/ASCE/AHS Structures, Structural Dynamics, and Materials Conference, Orlando, FL, USA, 15–17 April 1985. [Google Scholar]
- Harper, P.W.; Hallett, S.R. Cohesive zone length in numerical simulations of composite delamination. Eng. Fract. Mech. 2008, 75, 4774–4792. [Google Scholar] [CrossRef]
- Fan, C.; Jar, P.Y.B.; Cheng, J.R. Cohesive zone with continuum damage properties for simulation of delamination development in fibre composites and failure of adhesive joints. Eng. Fract. Mech. 2008, 75, 3866–3880. [Google Scholar] [CrossRef]
- Silberschmidt, V.V. Matrix cracking in cross-ply laminates: Effect of randomness. Compos. A Appl. Sci. Manuf. 2005, 36, 129–135. [Google Scholar] [CrossRef]
- Skordos, A.; Sutcliffe, M. Stochastic simulation of woven composites forming. Compos. Sci. Technol. 2008, 68, 283–296. [Google Scholar] [CrossRef]
- Ashcroft, I.A.; Khokar, Z.R.; Silberschmidt, V.V. Modelling the effect of micro-structural randomness on the mechanical response of composite laminates through the application of stochastic cohesive zone elements. Comput. Mater. Sci. 2012, 52, 95–100. [Google Scholar] [CrossRef]
- Jumel, J. Crack propagation along interface having randomly fluctuating mechanical properties during DCB test finite difference implementation–Evaluation of Gc distribution with effective crack length technique. Compos. Part B Eng. 2017, 116, 253–265. [Google Scholar] [CrossRef]
- ASTM Standard. D7905/D7905M–14. Standard Test Method for Determination of the Mode II Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites; ASTM Standard: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Park, S.J.; Seo, M.K. Modeling of Fiber–Matrix Interface in Composite Materials. In Interface Science and Technology; Elsevier: Amsterdam, The Netherlands, 2011; Volume 18, pp. 739–776. [Google Scholar]
- Motamedi, D. Nonlinear XFEM Modeling of Delamination in Fiber Reinforced Composites Considering Uncertain Fracture Properties and Effect of Fiber Bridging. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2013. [Google Scholar]
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703. [Google Scholar] [CrossRef]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin methods. Int. J. Numer. Methods Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Coates, R.T.; Schoenberg, M. Finite-difference modeling of faults and fractures. Geophysics 1995, 60, 1514–1526. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method: Solid Mechanics; Butterworth-Heinemann: Oxford, UK, 2000; Volume 2. [Google Scholar]
- Mi, Y.; Aliabadi, M.H. Dual boundary element method for three-dimensional fracture mechanics analysis. Eng. Anal. Bound. Elem. 1992, 10, 161–171. [Google Scholar] [CrossRef]
- Douillet-Grellier, T.; Jones, B.D.; Pramanik, R.; Pan, K.; Albaiz, A.; Williams, J.R. Mixed-mode fracture modeling with smoothed particle hydrodynamics. Comput. Geotech. 2016, 79, 73–85. [Google Scholar] [CrossRef]
- Liu, P.F.; Zheng, J.Y. Recent developments on damage modeling and finite element analysis for composite laminates: A review. Mater. Des. 2010, 31, 3825–3834. [Google Scholar] [CrossRef]
- Barenblatt, G.I. The formation of equilibrium cracks during brittle fracture. General ideas and hypotheses. Axially-symmetric cracks. J. Appl. Math. Mech. 1959, 23, 622–636. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Molnár, G.; Gravouil, A. 2D and 3D Abaqus implementation of a robust staggered phase-field solution for modeling brittle fracture. Finite Elem. Anal. Des. 2017, 130, 27–38. [Google Scholar] [CrossRef]
- Leguillon, D. Strength or toughness? A criterion for crack onset at a notch. Eur. J. Mech. A Solids 2002, 21, 61–72. [Google Scholar] [CrossRef]
- Doitrand, A.; Martin, E.; Leguillon, D. Numerical implementation of the coupled criterion: Matched asymptotic and full finite element approaches. Finite Elem. Anal. Des. 2020, 168, 103344. [Google Scholar] [CrossRef]
- Melenk, J.M.; Babuška, I. The partition of unity finite element method: Basic theory and applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 289–314. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Moёs, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Motamedi, D.; Milani, A.S.; Komeili, M.; Bureau, M.N.; Thibault, F.; Trudel-Boucher, D. A stochastic XFEM model to study delamination in PPS/Glass UD composites: Effect of uncertain fracture properties. Appl. Compos. Mater. 2014, 21, 341–358. [Google Scholar] [CrossRef]
- Khoei, A.R.; Biabanaki, S.O.R.; Anahid, M. A Lagrangian extended finite element method in modeling large plasticity deformations and contact problems. Int. J. Mech. Sci. 2009, 51, 384–401. [Google Scholar] [CrossRef]
- Unger, J.F.; Eckardta, S.; Könke, C. Modelling of cohesive crack growth in concrete structures with the extended finite element method. Comput. Methods Appl. Mech. Eng. 2007, 196, 4087–4100. [Google Scholar] [CrossRef]
- Khokhar, Z.R.; Ashcroft, I.A.; Silberschmidt, V.V. Simulations of delamination in CFRP laminates: Effect of microstructural randomness. Comput. Mater. Sci. 2009, 46, 607–613. [Google Scholar] [CrossRef]
- Motamedi, D.; Milani, A.S. 3D nonlinear XFEM simulation of delamination in unidirectional composite laminates: A sensitivity analysis of modeling parameters. Open J. Compos. Mater. 2013, 3, 113–126. [Google Scholar] [CrossRef][Green Version]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Motamedi, D.; Takaffoli, M.; S. Milani, A. Nonlinear XFEM Modeling of Mode II Delamination in PPS/Glass Unidirectional Composites with Uncertain Fracture Properties. Materials 2020, 13, 3548. https://doi.org/10.3390/ma13163548
Motamedi D, Takaffoli M, S. Milani A. Nonlinear XFEM Modeling of Mode II Delamination in PPS/Glass Unidirectional Composites with Uncertain Fracture Properties. Materials. 2020; 13(16):3548. https://doi.org/10.3390/ma13163548
Chicago/Turabian StyleMotamedi, Damoon, Mahdi Takaffoli, and Abbas S. Milani. 2020. "Nonlinear XFEM Modeling of Mode II Delamination in PPS/Glass Unidirectional Composites with Uncertain Fracture Properties" Materials 13, no. 16: 3548. https://doi.org/10.3390/ma13163548
APA StyleMotamedi, D., Takaffoli, M., & S. Milani, A. (2020). Nonlinear XFEM Modeling of Mode II Delamination in PPS/Glass Unidirectional Composites with Uncertain Fracture Properties. Materials, 13(16), 3548. https://doi.org/10.3390/ma13163548





