Modeling and Experimental Analysis of Shear-Slitting of AA6111-T4 Aluminum Alloy Sheet
Abstract
1. Introduction
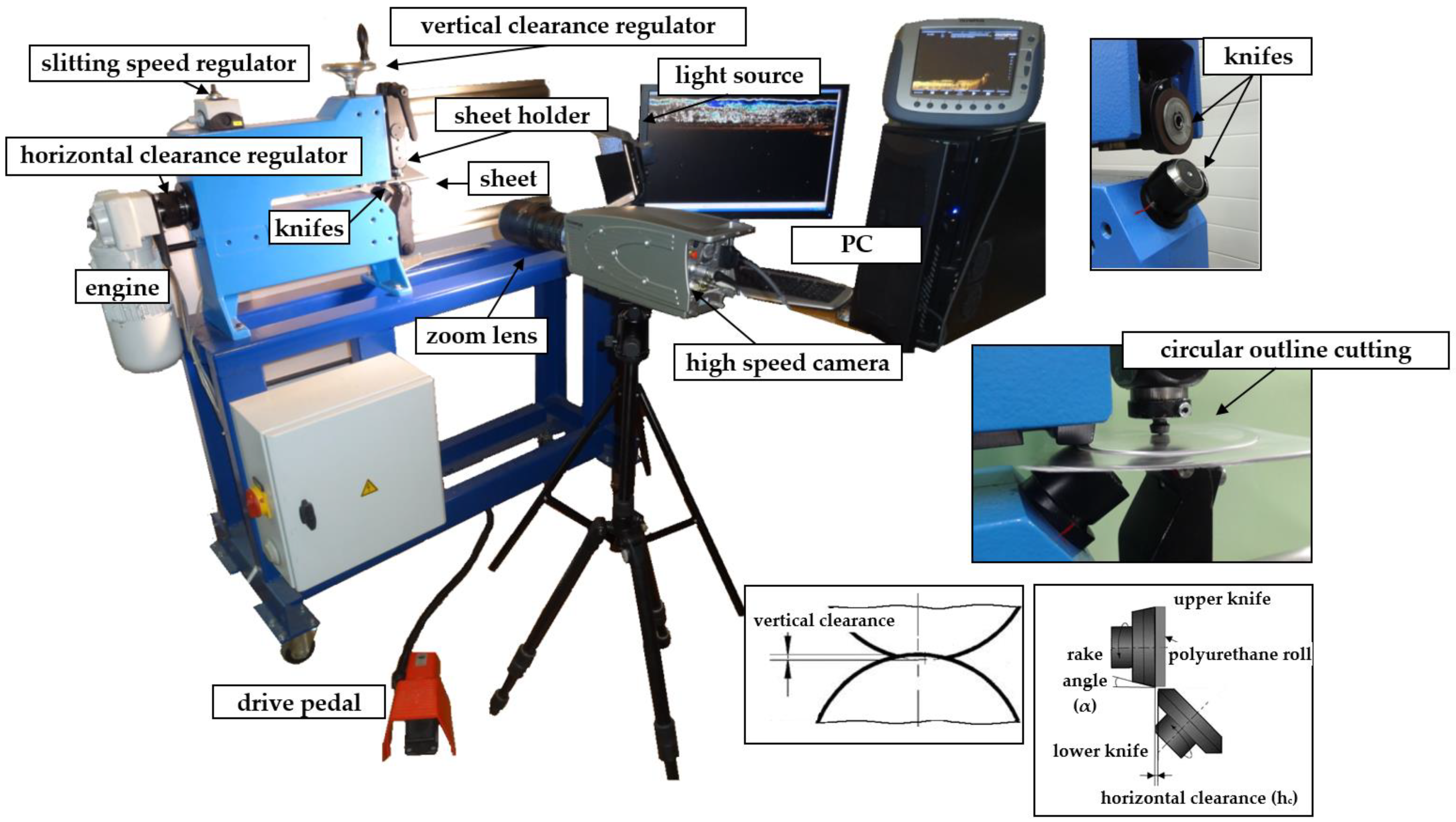
2. Experiment Setup and Results
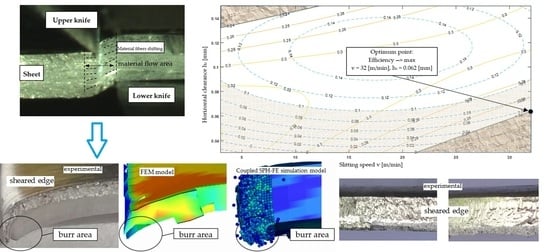
2.1. Mechanism of Slit Edges Generation
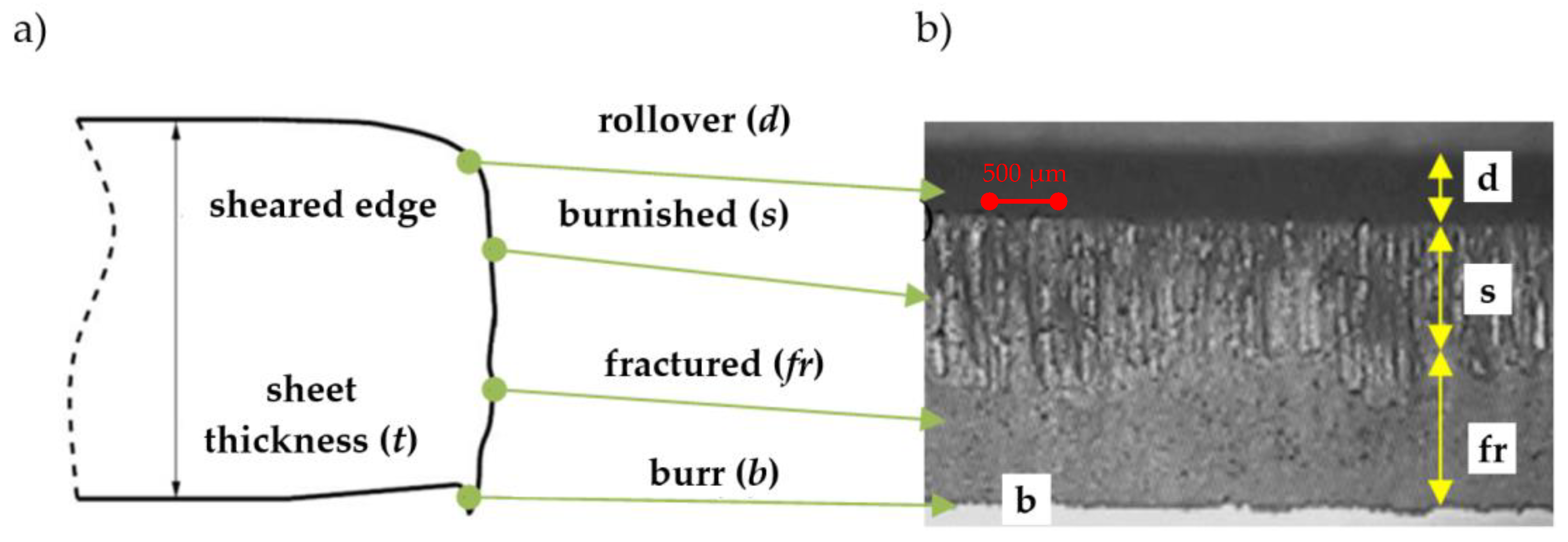
2.2. Quality of Sheared Edge
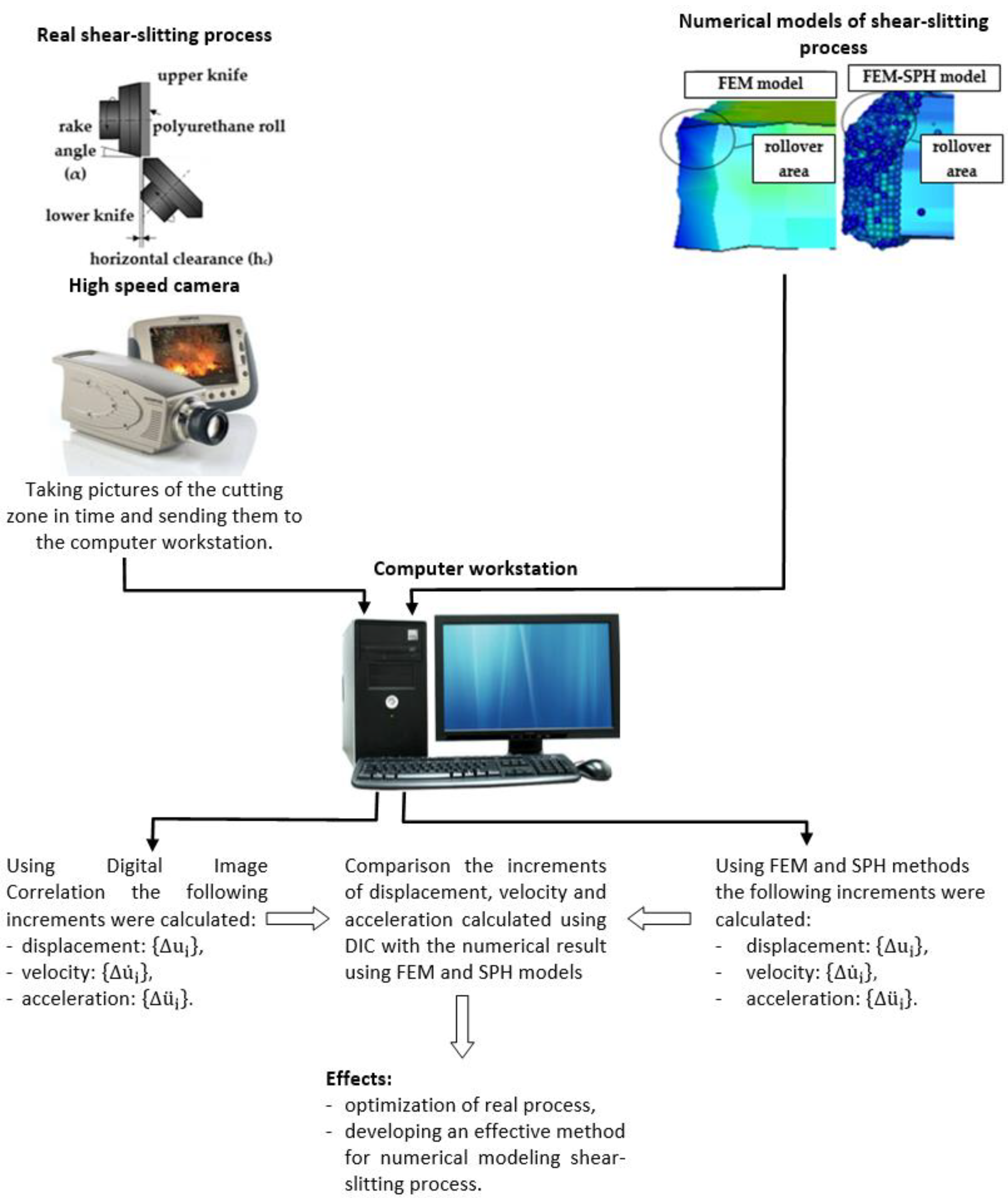
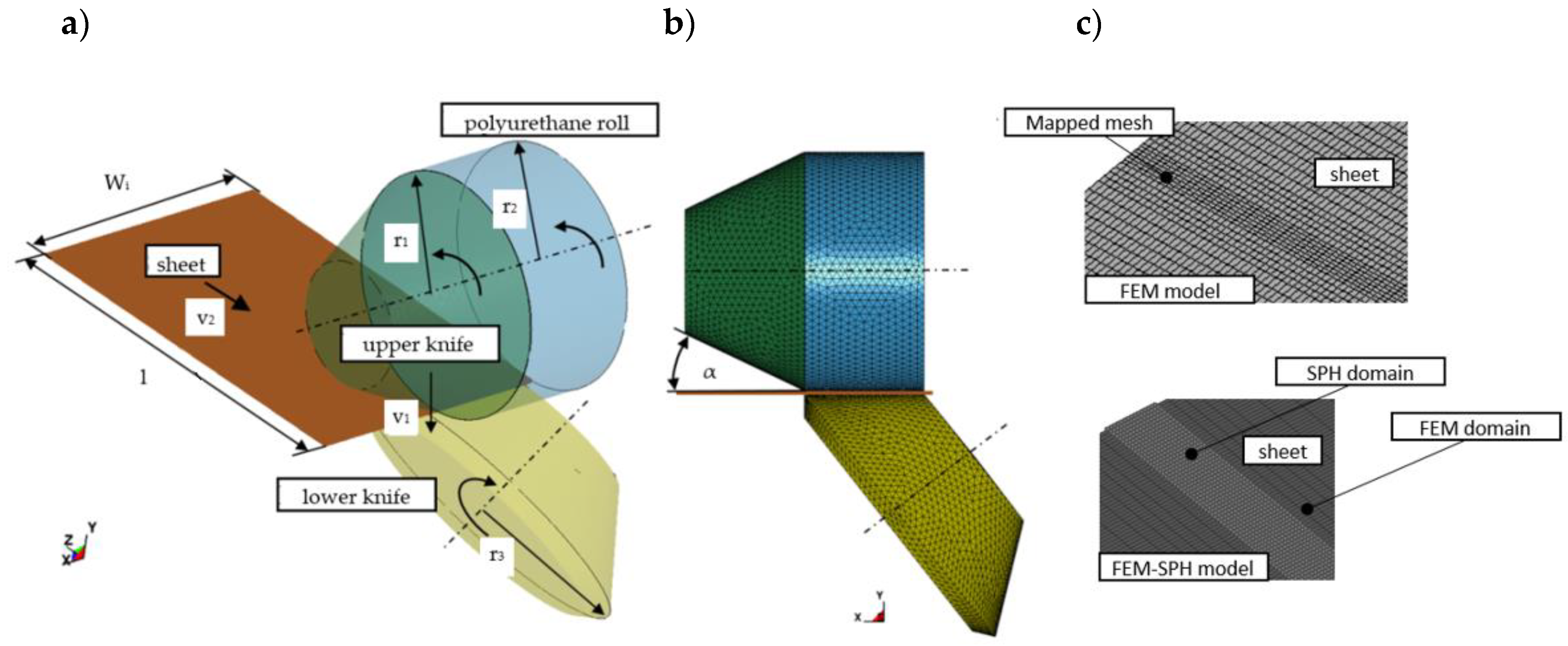
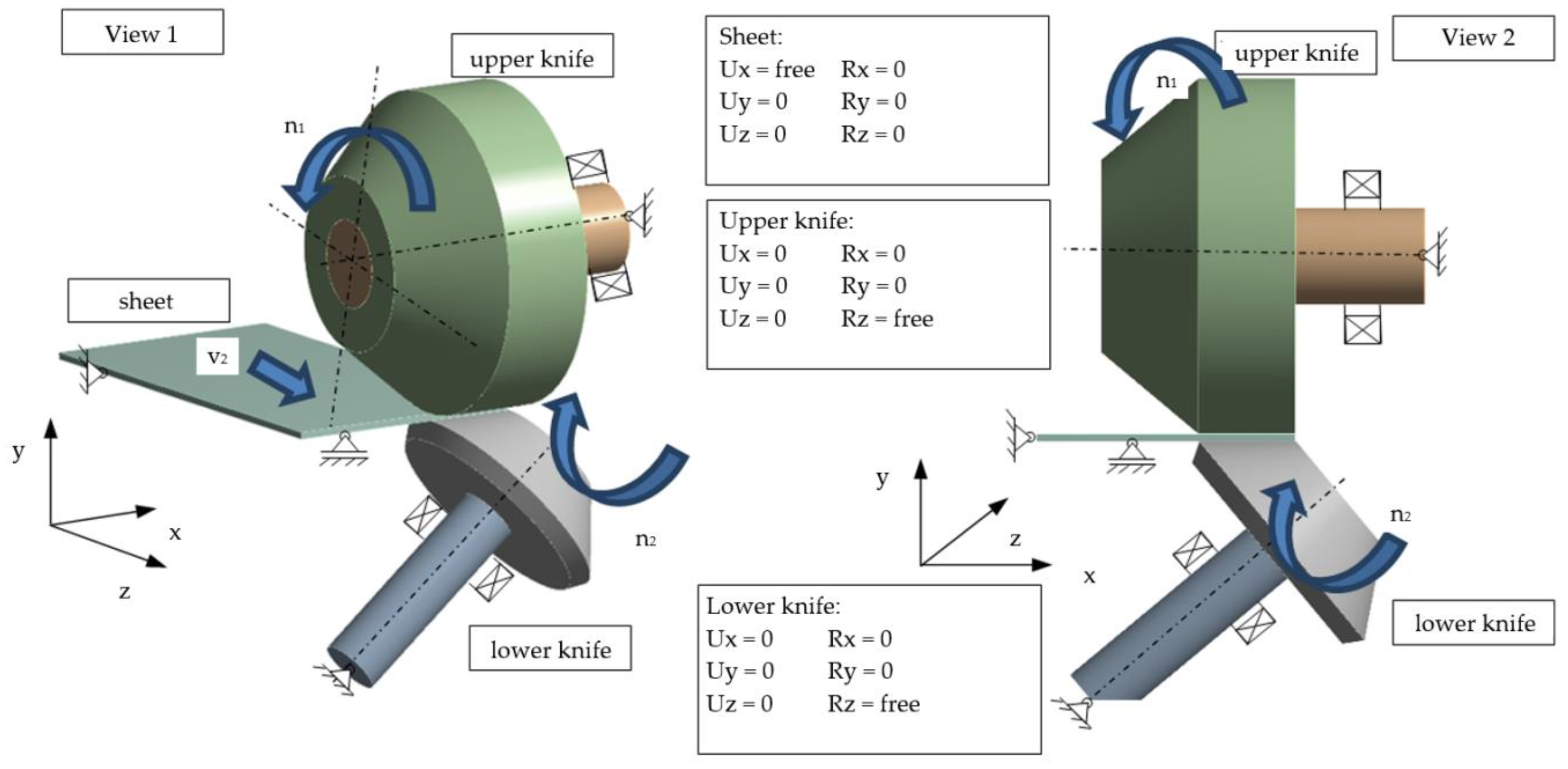
3. FE and SPH Modeling
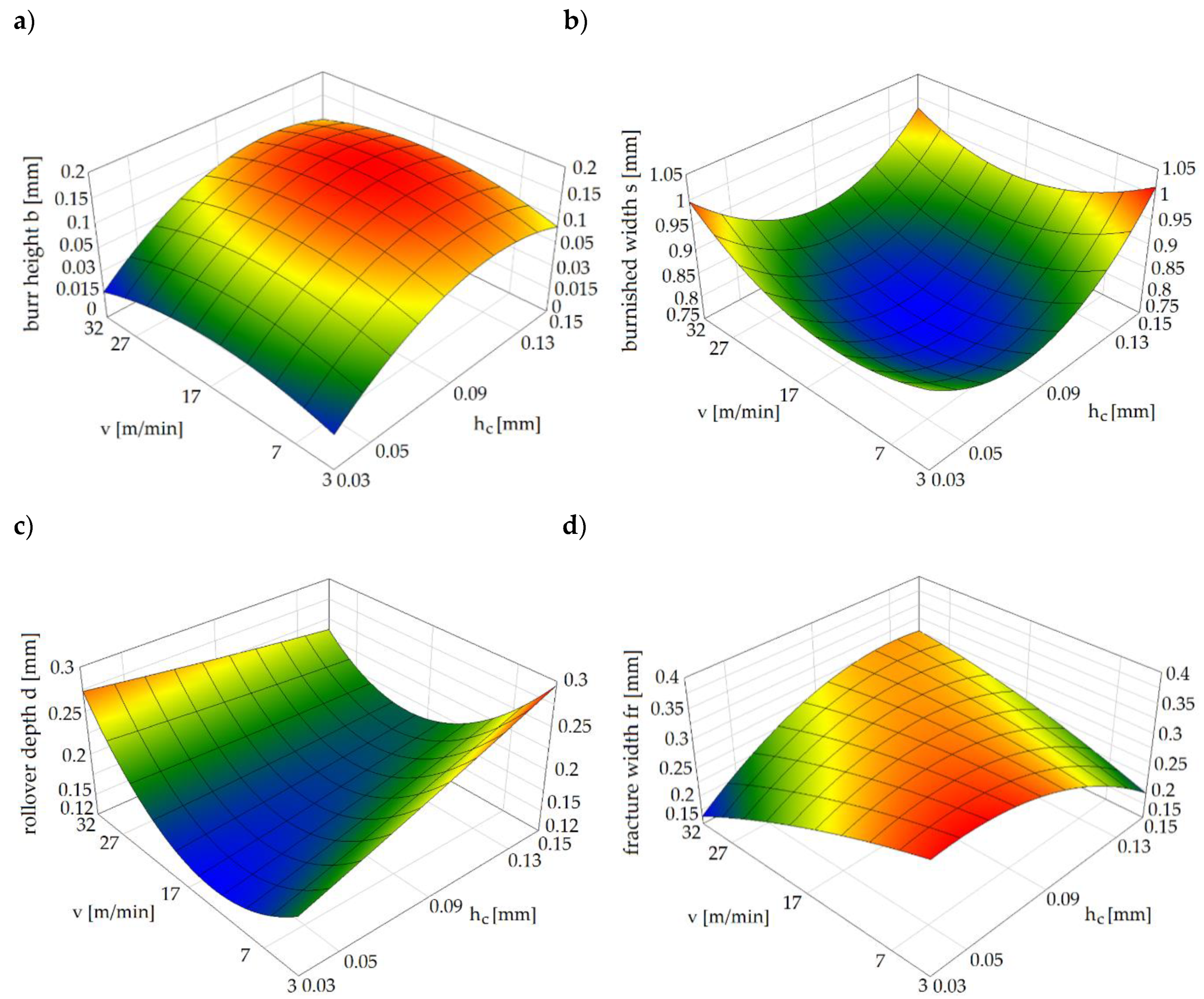
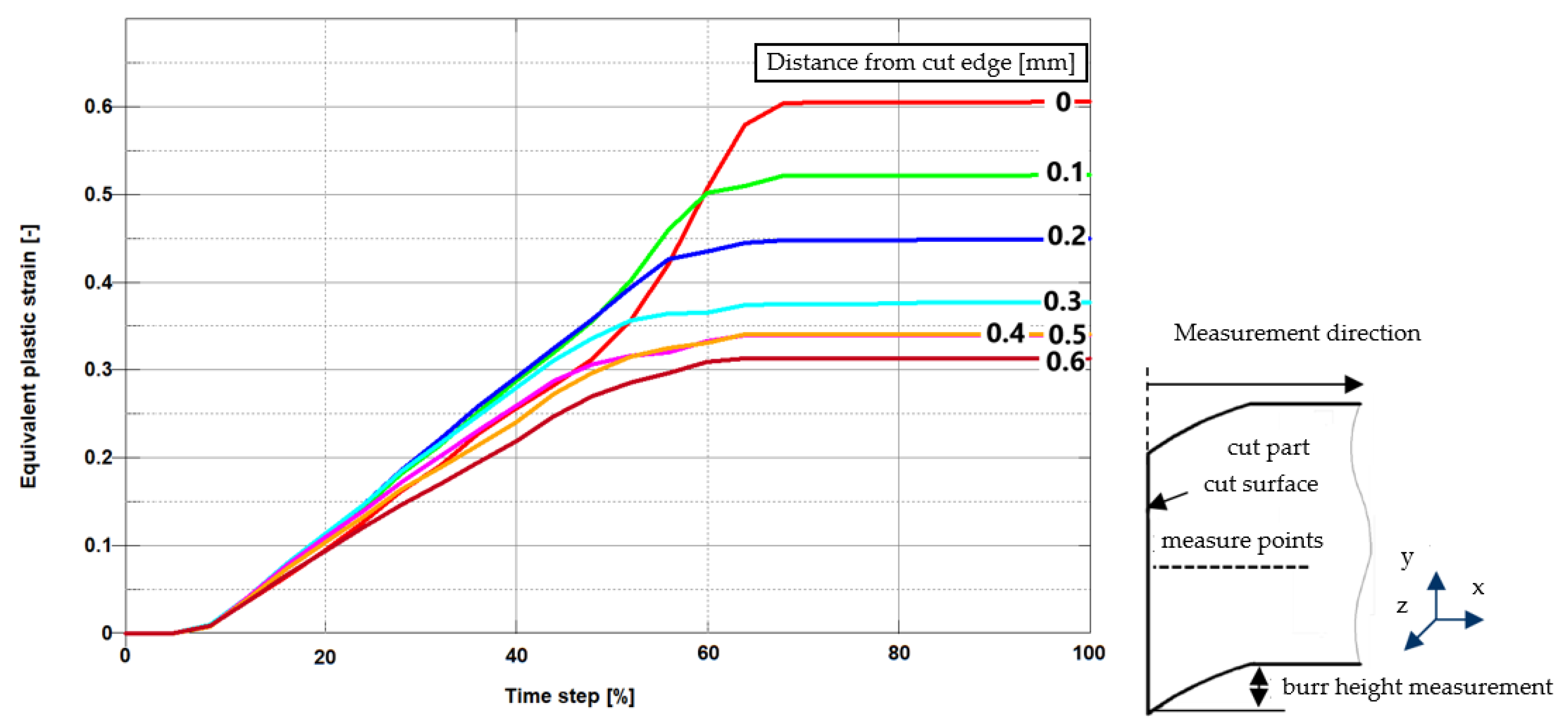
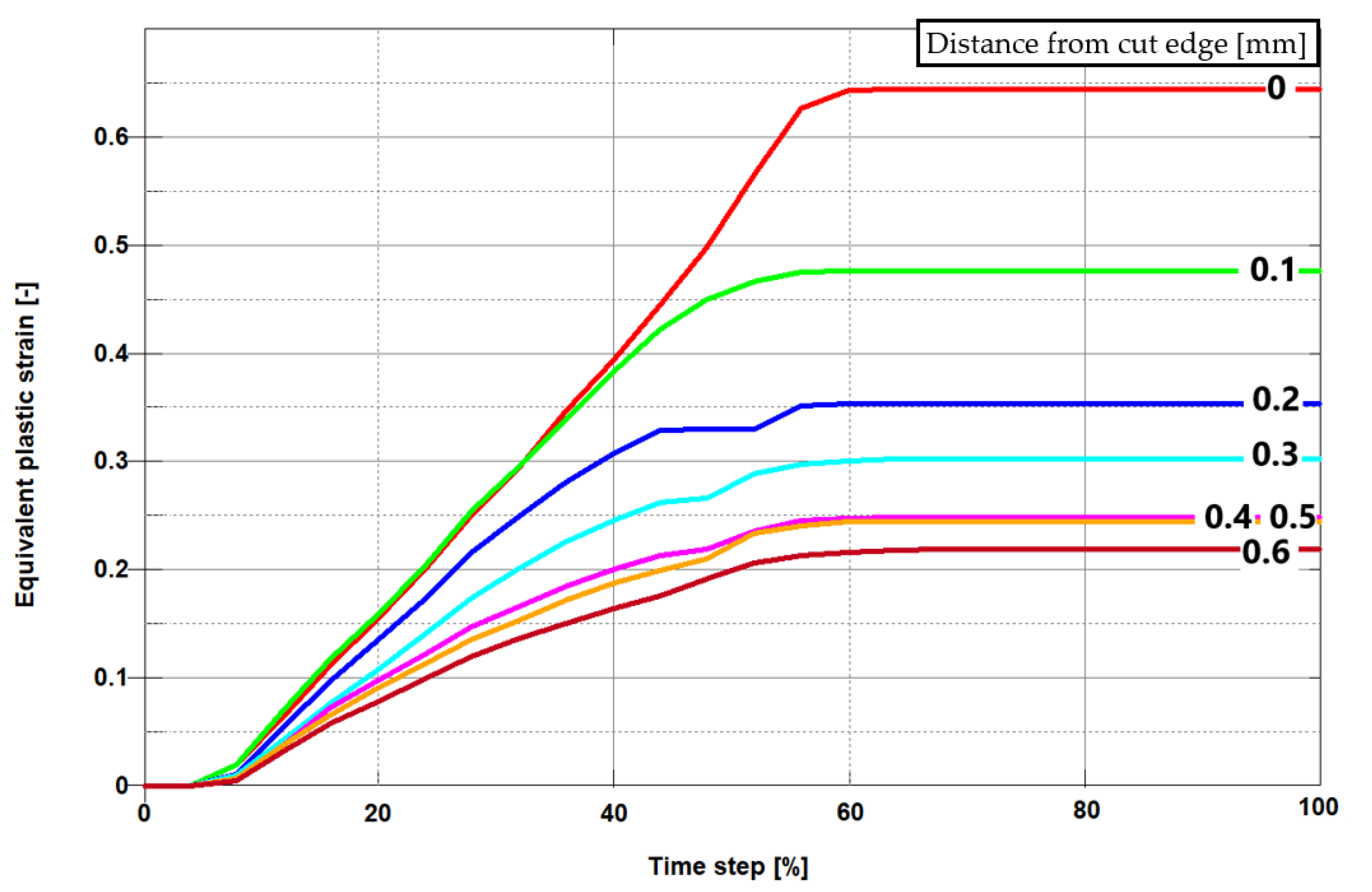
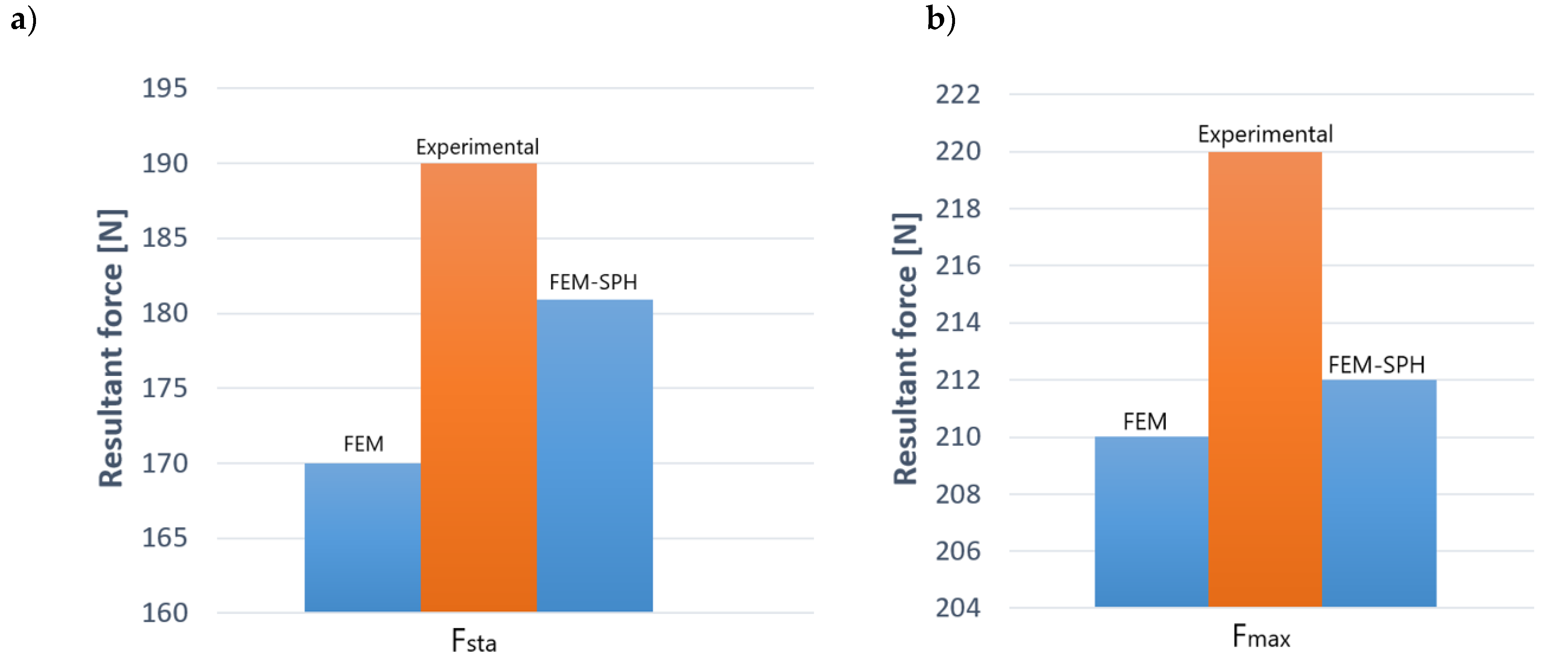
4. Numerical Results
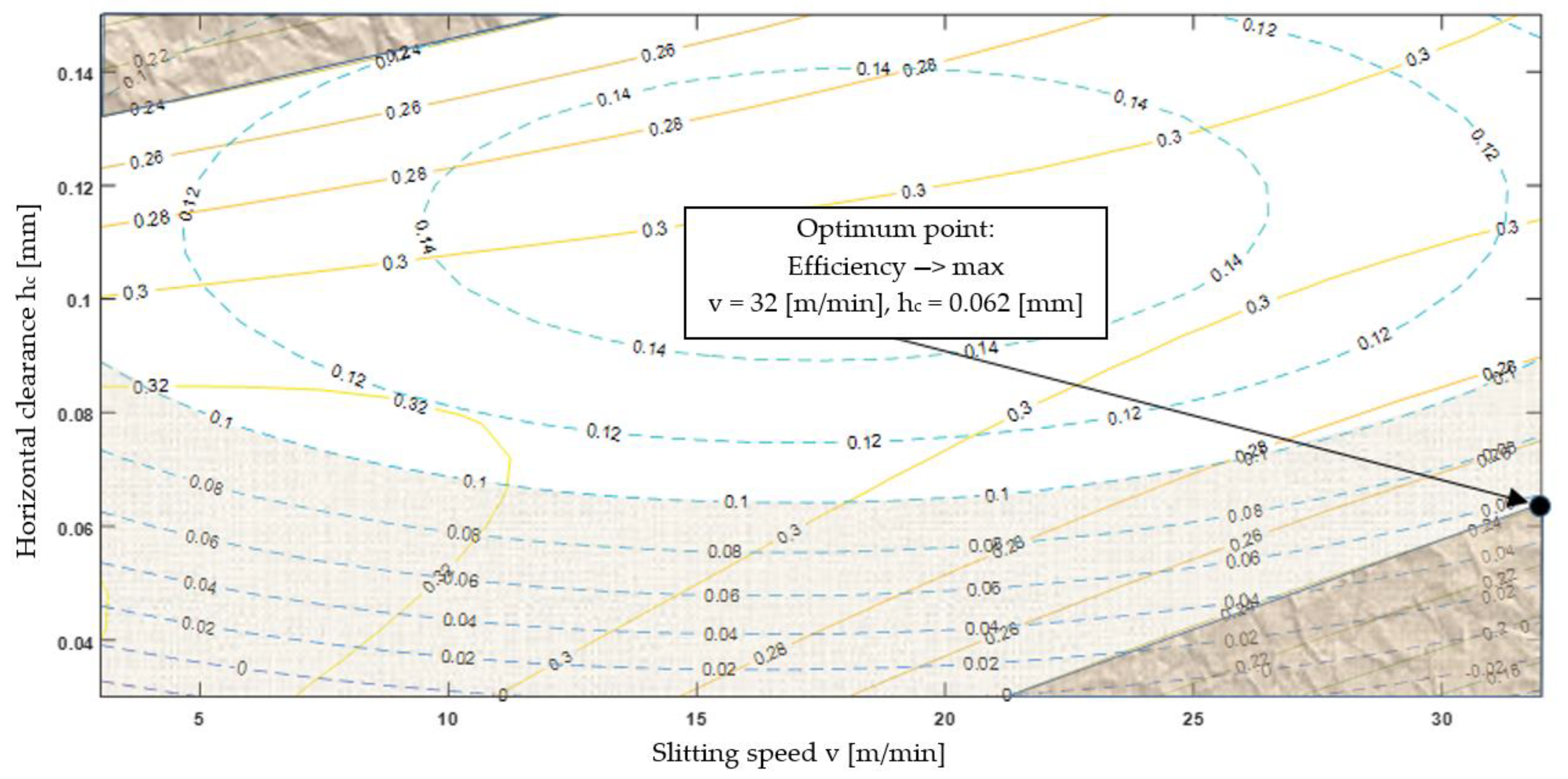
5. Optimization
6. Conclusions
- The use of two FEM and SPH numerical methods, enabled gaining new knowledge about shear-slitting processes, which can help in choosing the best and the most accurate numerical method to simulate similar processes, especially those ones in which strong deformation, structure fracture and separation occurs.
- The conducted experimental research using vision systems allowed for observing the physical phenomena occurring within very small areas and running at high speeds. Thanks to that, it was possible to learn them more accurately, as well as to use the recorded images to validate simulation models in individual cutting phases. So far, the validation of simulation models has involved comparative analysis of cutting forces and the quality of the cut edge with the experiment offline (after the process). The presented method enables the analysis of accuracy and correctness of simulation models, in unstable phases inclusive, e.g., during separation, online.
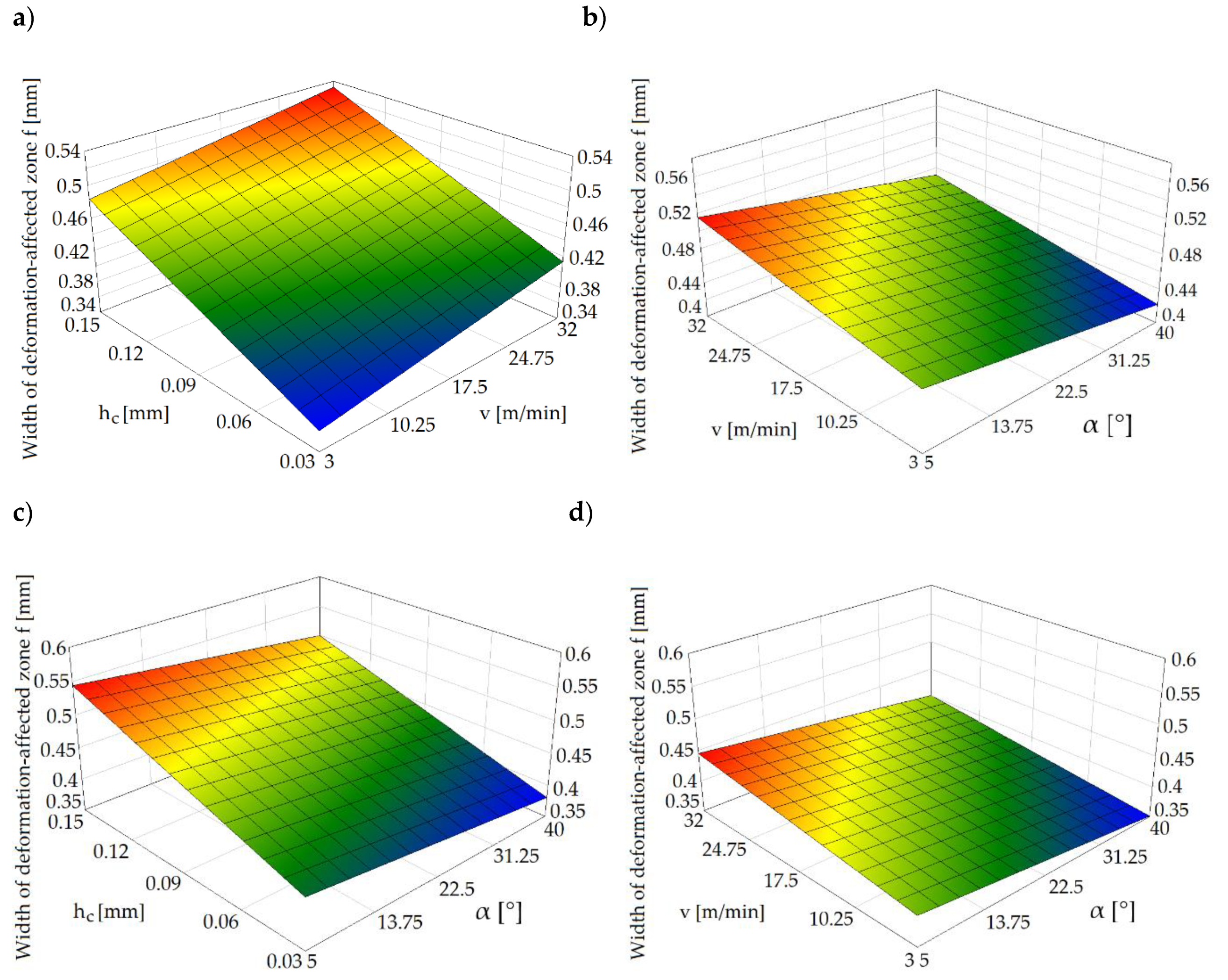
- The most important and controllable parameters affecting the quality of the sheared edge include the slitting speed and the horizontal clearance. The results indicate a significant effect of the clearance on the deformation zone’s width. Along with the increase in the clearance value, the deformation zone increased. Conditions affecting burr formation on the edge were also specified. The highest burrs were obtained when the slitting speed was set to v = 17 m/min and the clearance was set to hc = 6%t.
- The use of graphic optimization has enabled the determination of process conditions that allow for obtaining the highest quality of the cut edge for the given criteria. The most favorable conditions were obtained for v = 32 m/min, hc = 0.062 mm and α = 30°. The proposed methodology can be used to analyze various materials of different thicknesses formed by mechanical cutting.
Author Contributions
Funding
Conflicts of Interest
References
- Legutko, S. Development Trends in Machines Operation Maintenance. Eksploat. i Niezawodn. -Maint. Reliab. 2009, 2, 8–16. [Google Scholar]
- Kumar, R.; Chatopadhyaya, S.; Hloch, S.; Krolczyk, G.; Legutko, S. Wear characteristics and defects analysis of friction stir welded joint of aluminum alloy 6061-T6. Eksploat. i Niezawodn. -Maint. Reliab. 2016, 18, 128–135. [Google Scholar] [CrossRef]
- Maruda, R.W.; Feldshtein, E.; Legutko, S.; Krolczyk, G.M. Research on Emulsion Mist Generation in the Conditions of Minimum Quantity Cooling Lubrication (MQCL). Tehnicki Vjesn. -Tech. Gaz. 2015, 22, 1213–1218. [Google Scholar]
- Saanouni, K. Virtual metal forming including the ductile damage occurrence. Actual state of the art and main perspectives. J. Mater. Process. Technol. 2006, 177, 19–25. [Google Scholar] [CrossRef]
- Bohdal, L. The application of the smoothed particle hydrodynamics (SPH) method to the simulation and analysis of blanking process. Mechanika 2016, 22, 380–387. [Google Scholar] [CrossRef]
- Gontarz, S.; Gumiński, R. New approach to the evaluation of the effort state of steel based on magneto-mechanical effects. Mech. Res. Comm. 2017, 82, 14–20. [Google Scholar] [CrossRef]
- Kukielka, L. Mathematical modelling and numerical simulation of non-linear deformation of the asperity in the burnishing cold rolling operation. In Computational Methods in Contact Mechanics V: Proceedings of the 5th International Conference on Computational Methods in Contact Mechanics, Seville, Spain, 7 June 2001; Book Series: Computational and Experimental Methods; WIT Press: Ashurst, UK, 2001; pp. 317–326. [Google Scholar]
- Aggarwal, S.H.; Bhushan, B.; Katsube, N. Three-dimensional finite element analysis of the magnetic tape slitting process. J. Mater. Process. Technol. 2005, 170, 71–88. [Google Scholar] [CrossRef]
- Liu, C.; Lu, H.; Huang, Y. Dynamic steady-state stress field in a web during slitting. ASME J. App. Mech. 2005, 72, 157–164. [Google Scholar] [CrossRef]
- Lu, H.; Wang, B.; Iqbal, J. Deformation in shear slitting of polymeric webs. In Proceedings of the 6th International Conference on Web Handling, Stillwater, OK, USA, 10–13 June 2001; pp. 389–402. [Google Scholar]
- Krinninger, M.; Steinlehner, F.; Opritescu, D.; Golle, R.; Volk, W. On the influence of different parameters on the characteristic cutting surface when shear cutting aluminum. Procedia CIRP 2017, 63, 230–235. [Google Scholar] [CrossRef]
- Li, M. Micromechanisms of deformation and fracture in shearing aluminum alloy sheet. Int. J. Mech. Sci. 2000, 42, 889–906. [Google Scholar] [CrossRef]
- Golovashchenko, S.F. A study on trimming of aluminum autobody sheet and development of a new robust process eliminating burrs and slivers. Int. J. Mech. Sci. 2006, 48, 1384–1400. [Google Scholar] [CrossRef]
- Ma, J.; Lu, H.; Li, M.; Wang, B. Burr height in shear slitting of aluminum webs. ASME J. Man. Sci. Eng. 2006, 128, 46–55. [Google Scholar] [CrossRef]
- Wang, J.P. A novel fine-blanking approach. Int. J. Adv. Man. Technol. 2015, 78, 1015–1019. [Google Scholar] [CrossRef]
- Wang, N.; Golovashchenko, S.F. Mechanism of fracture of aluminum blanks subjected to stretching along the sheared edgel. J. Mater. Proc. Technol. 2016, 233, 142–160. [Google Scholar] [CrossRef]
- Mao, H.; Zhou, F.; Liu, Y.; Hua, L. Numerical and experimental investigation of the discontinuous dot indenter in the fine-blanking process. J. Man. Proc. 2016, 24, 90–99. [Google Scholar] [CrossRef]
- Shih, H.C.; Shi, M.F. An innovative shearing process for AHSS edge stretchability improvements. J. Man. Sci. Eng. 2011, 133, 061018. [Google Scholar] [CrossRef]
- Du, H.; Fan, W.F.; Zhang, Z.M. Comparative study of the process fracture between fine-blanking with negative clearance and conventional blanking. Adv. Mater. Res. 2010, 97–101, 191–194. [Google Scholar] [CrossRef]
- Le, Q.B.; de Vries, J.A.; Golovashchenko, S.F.; Bonnen, J.F. Analysis of Sheared Edge Formability of Aluminum. J. Mater. Process. Technol. 2014, 214, 876–891. [Google Scholar] [CrossRef]
- Nasheralahkami, S.; Golovashchenko, S.F.; Pan, K.; Brown, L.; Gugnani, B. Characterization of Trimmed Edge of Advanced High Strength Steel; SAE Technical Paper No. 2016-01-0358; SAE International: Warrendale, PA, USA, 2016; pp. 1–7. [Google Scholar]
- Golovashchenko, S.F. Quality of trimming and its effect on stretch flanging of automotive panels. J. Mater. Eng. Perform. 2008, 17, 316–325. [Google Scholar] [CrossRef]
- Hilditch, T.B.; Hodgson, P.D. Development of the sheared edge in the trimming of steel and light metal sheet: Part 1—Experimental observations. J. Mater. Proc. Technol. 2005, 169, 184–191. [Google Scholar] [CrossRef]
- Hilditch, T.B.; Hodgson, P.D. Development of the sheared edge in the trimming of steel and light metal sheet: Part 2—Mechanisms and modeling. J. Mater. Proc. Technol. 2005, 169, 192–198. [Google Scholar] [CrossRef]
- Kaczmarczyk, J.; Grajcar, A. Numerical Simulation and Experimental Investigation of Cold-Rolled Steel Cutting. Materials 2018, 11, 1263. [Google Scholar] [CrossRef]
- Gąsiorek, D. The application of the smoothed particle hydrodynamics (SPH) method and the experimental verification of cutting of sheet metal bundles using a guillotine. J. Theor. Appl. Mech. 2013, 51, 1053–1065. [Google Scholar]
- Bohdal, Ł.; Kułakowska, A.; Patyk, R. Analysis of Slitting of Aluminum Body Panels in the Aspect of Scrap Reduction. Ann. Set Env. Prot. 2014, 16, 105–114. [Google Scholar]
- Bohdal, L.; Kukielka, L. Application of variational and FEM methods to the modelling and numerical analysis of the slitting process for geometrical and physical nonlinearity. J. Theor. Appl. Mech. 2015, 53, 487–500. [Google Scholar] [CrossRef]
- Bohdal, L. Application of FEM and vision-based methods to analysis of shearing processes in the aspect of scrap reduction. Ann. Set Environ. Prot. 2015, 17, 90–103. [Google Scholar]
- Hubert, C.; Dubar, L.; Dubar, M.; Dubois, A. Experimental simulation of strip edge cracking in steel rolling sequences. J. Mater. Proc. Technol. 2010, 210, 1587–1597. [Google Scholar] [CrossRef]
- Górszczyk, J.; Malicki, K.; Zych, T. Application of digital image correlation (DIC) method for road material testing. Materials 2019, 12, 2349. [Google Scholar] [CrossRef]
- Górszczyk, J.; Malicki, K. Digital Image Correlation Method in monitoring deformation during geogrid testing. Fibres Text. East. Eur. 2019, 27, 84–90. [Google Scholar] [CrossRef]
- Malesa, M.; Malowany, K.; Kujawińska, M. Multi-camera DIC system with a spatial data stitching procedure for measurements of engineering objects. Photonics Lett. Pol. 2014, 6, 157–159. [Google Scholar]
- Dai, S.; Liu, X.; Nawnit, K. Experimental study on the fracture process zone characteristics in concrete utilizing DIC and AE methods. Appl. Sci. 2019, 9, 1346. [Google Scholar] [CrossRef]
- Jang, L.; Smith, L.; Gothekar, A.; Chen, X. Measure Strain Distribution Using Digital Image Correlation (DIC) for Tensile Tests; Oakland University: Rochester, MI, USA, 2010. [Google Scholar]
- Wattrisse, B.; Chrysochoos, A.; Muracciole, J.M.; Nemoz-Gaillard, M. Analysis of strain localization during tensile tests by digital image correlation. Exp. Mech. 2001, 41, 29–39. [Google Scholar] [CrossRef]
- Goijaerts, A.; Govaert, L.; Baaijens, F. Evaluation of ductile fracture models for diferent metals in blanking. J. Mater. Process. Technol. 2001, 110, 312–323. [Google Scholar] [CrossRef]
- Ghadbeigi, H.; Al-Rubaye, A.; Robinson, F.C.J.; Hawezy, D.; Birosca, S.; Atallah, K. Blanking induced damage in thin 3.2% silicon steel sheets. Prod. Eng. 2020, 14, 53–64. [Google Scholar] [CrossRef]
- Hu, X.H.; Sun, X.; Golovashchenko, S.F. Predicted tensile stretchability of trimmed AA6111-T4 sheets. Comp. Mater. Sci. 2014, 85, 409–419. [Google Scholar] [CrossRef]
- Yu, S.; Zhao, J. Investigation on blanking of thick sheet metal using the ductile fracture initiation and propagation criterion. J. Shanghai Jiaotong Univ. (Sci.) 2012, 17, 531–536. [Google Scholar] [CrossRef]
- Niu, Y.; Shao, S.; Park, S.B.; Kao, C. A novel speckle-free digital image correlation method for in situ warpage characterization. IEEE Trans. Compon. Packag. Manuf. Technol. 2017, 7, 276–284. [Google Scholar] [CrossRef]
- Suliman, S.M.A. An experimental investigation of guillotining of aluminum alloy 5005. Mater. Man. Proc. 2001, 16, 673–689. [Google Scholar] [CrossRef]
- Meehan, R.R.; Burns, S.J. Mechanics of slitting and cutting webs. Exp. Mech. 1998, 38, 103–109. [Google Scholar] [CrossRef]
- Wisselink, H.; Hue’tink, J. 3D FEM simulation of stationary metal forming processes with applications to slitting and rolling. J. Mater. Process. Technol. 2004, 148, 328–341. [Google Scholar] [CrossRef]
- Lu, H.; Ma, J.; Li, M. Edge trimming of aluminum sheets using shear slitting at a rake angle. ASME J. App. Mech. 2006, 128, 866–873. [Google Scholar] [CrossRef]
- Hatanaka, N.; Yamaguchi, K.; Takakura, N. Finite element simulation of the shearing mechanism in the blanking of sheet metal. J. Mater. Process. Technol. 2003, 139, 64–70. [Google Scholar] [CrossRef]
- Bohdal, Ł.; Patyk, R.; Tandecka, K.; Gontarz, S.; Jackiewicz, D. Influence of shear-slitting parameters on workpiece formation, cut edge quality and selected magnetic properties for grain-oriented silicon steel. J. Man. Proc. Part A 2020, 56, 1007–1026. [Google Scholar] [CrossRef]
- Zhao, B.; Gao, G.; Gao, H.; Yan, Y. Finite Element Simulation of Shearing Force in Disc Slitting Process. Adv. Mater. Res. 2014, 1027, 150–155. [Google Scholar]
- Zhang, M. Calculation and selection of energetic parameters for disc shears. Heavy Mach. 2010, 4, 42–45. [Google Scholar]
- Ding, M.; Wu, D.; Qin, Q. Finite Element Modeling of Shear-Slitting Process. Adv. Mater. Res. 2012, 459, 3–6. [Google Scholar]
- Ghozzi, Y.; Labergere, C.; Saanouni, K.; Parrico, A. Modelling and numerical simulation of thick sheet double slitting process using continuum damage mechanics. Int. J. Dam. Mech. 2014, 23, 1150–1167. [Google Scholar] [CrossRef]
- Bohdal, L.; Kukiełka, L. Application of variational and FEM methods to the modelling and numerical analysis of guillotining process for geometrical and physical nonlinearity. Mechanika 2014, 20, 197–204. [Google Scholar] [CrossRef]
- Kleiber, M. Finite Element Method in Non-Linear Solid Mechanics; IPPT PAN, PWN: Warsaw, Poland; Poznan, Poland, 1985. [Google Scholar]
- Kukiełka, L.; Geleta, K.; Kukiełka, K. Modelling of initial and boundary problems with geometrical and physical nonlinearity and its application in burnishing processes. In Steel Research International, Metal Forming 2012; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2012; pp. 1375–1378. [Google Scholar]
- Kukiełka, L.; Kułakowska, A.; Patyk, R. Numerical Modeling and Simulation of the Movable Contact Tool-Worpiece and Application in Technological Processes. J. Syst. Cyb. Inf. 2010, 8, 36–41. [Google Scholar]
- Kukiełka, L. New damping models of metallic materials and its application in non-linear dynamical cold processes of metal forming. In Steel Research International, Proceedings of the 13th International Conference Metal Forming 2010, Toyohashi, Japan, 19–22 September 2010; Special Edition 2010; Verlag Stahleisen GmbH: Düsseldorf, Germany, 2010; Volume 81, Number 9; pp. 1482–1485. ISBN 978-3-514-00774-1. [Google Scholar]
- Kukiełka, L.; Geleta, K.; Kukiełka, K. Modelling and analysis of nonlinear physical phenomena in the burnishing rolling operation with electrical current. In Steel Research International, Metal Forming 2012; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2012; pp. 1379–1382. [Google Scholar]
- Kułakowska, A.; Kukiełka, L.; Patyk, R. Numerical analysis and experimental researches of burnishing rolling process of workpieces with real surface. In Proceedings of the 5th International Symposium on Management, Engineering and Informatics: MEI 2009, The 13th Multi-Conference on Systemics, Cybernetics and Informatics: WMSCI 2009, Orlando, FL, USA, 10–13 July 2009. [Google Scholar]
- Bohdal, L.; Kukiełka, L.; Radchenko, A.M.; Patyk, R.; Kułakowski, M.; Chodór, R. Modelling of guillotining process of grain oriented silicon steel using FEM. AIP Conf. Proc. 2019, 2078, 020080. [Google Scholar]
- Bohdal, L.; Kukiełka, L.; Świłło, S.; Radchenko, A.M.; Kułakowska, A. Modelling and experimental analysis of shear-slitting process of light metal alloys using FEM, SPH and vision-based methods. AIP Conf. Proc. 2019, 2078, 020060. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Bohdal, Ł. Teoretyczne i Doświadczalne Podstawy Optymalizacji Procesów Cięcia Mechanicznego Stopów Metali Lekkich i stali Elektrotechnicznych; Monografia Wydziału Mechanicznego nr 344; Wydawnictwo Uczelniane Politechniki Koszalińskiej: Koszalin, Poland, 2018; ISSN 0239-7129; ISBN 978-83-7365-481-5. (In Polish) [Google Scholar]
- Gasiorek, D.; Baranowski, P.; Malachowski, J.; Mazurkiewicz, L.; Wiercigroch, M. Modelling of guillotine cutting of multi-layered aluminum sheets. J. Man. Proc. 2018, 34, 374–388. [Google Scholar] [CrossRef]
- Bohdal, L.; Kukielka, L.; Kukielka, K.; Kulakowska, A.; Malag, L.; Patyk, R. Three Dimensional Finite Element Simulation of Sheet Metal Blanking Process. Appl. Mech. Mater. 2014, 474, 430–435. [Google Scholar] [CrossRef]
- Kulakowska, A.; Patyk, R.; Bohdal, L. Application of Burnishing Process in Creating Environmental Product. Ann. Set Environ. Prot. 2014, 16, 323–335. [Google Scholar]





| Young’s Modulus, E | 70 GPa |
| Elongation, A100 | 28% |
| Shear Modulus, G | 26–26.5 GPa |
| Poisson’s Ratio, ν | 0.33 |
| Tensile Strength, Rm | 265–285 MPa |
| Fracture Toughness, KIC | 22–35 MPa·√m |
| Yield Strength Rp0.2, Rp0.2 | 150–170 MPa |
| Coefficient of Thermal Expansion, α | 1.6E-5–2.4E-5 1/K |
| Specific Heat Capacity, cp | 887–963 J/(kg·K) |
| Thermal Conductivity, λ | 170–220 W/(m·K) |
| Si | Cu | Zn | Cr | Mn | Ti | Mg | Fe |
|---|---|---|---|---|---|---|---|
| 0.6–1.1 | 0.5–0.9 | 0.15 | 0.1 | 0.1–0.45 | 0.1 | 0.5–1 | 0.4 |
| Horizontal Clearance, hc | 0.03–0.15 mm |
| Vertical Clearance, cv | 0.15 mm |
| Slitting Speed, v2 | 3–32 m/min |
| Rake Angle of the Upper Knife, α | 5°–40° |
| Upper Knife, Polyurethane Roll Radius, r1, r2 | 15 mm |
| Lower Knife Radius, r3 | 20 mm |
| Plan Level | Coded Variables | Real Variables | ||||
|---|---|---|---|---|---|---|
| hc [mm] | v2 [m/min] | α [°] | ||||
| 1 | − | − | − | 0.054 | 8.87 | 12.09 |
| 2 | + | − | − | 0.125 | 8.87 | 12.09 |
| 3 | − | + | − | 0.054 | 26.12 | 12.09 |
| 4 | + | + | − | 0.125 | 26.12 | 12.09 |
| 5 | − | − | + | 0.054 | 8.87 | 32.9 |
| 6 | + | − | + | 0.125 | 8.87 | 32.9 |
| 7 | − | + | + | 0.054 | 26.12 | 32.9 |
| 8 | + | + | + | 0.125 | 26.12 | 32.9 |
| 9 | +α = 1.682 | 0 | 0 | 0.15 | 17.5 | 22.5 |
| 10 | −α = −1.682 | 0 | 0 | 0.03 | 17.5 | 22.5 |
| 11 | 0 | +α = 1.682 | 0 | 0.09 | 32 | 22.5 |
| 12 | 0 | −α = −1.682 | 0 | 0.09 | 3 | 22.5 |
| 13 | 0 | 0 | +α = 1.682 | 0.09 | 17.5 | 40 |
| 14 | 0 | 0 | −α = −1.682 | 0.09 | 17.5 | 5 |
| 15 | 0 | 0 | 0 | 0.09 | 17.5 | 22.5 |
| 16 | 0 | 0 | 0 | 0.09 | 17.5 | 22.5 |
| 17 | 0 | 0 | 0 | 0.09 | 17.5 | 22.5 |
| 18 | 0 | 0 | 0 | 0.09 | 17.5 | 22.5 |
| 19 | 0 | 0 | 0 | 0.09 | 17.5 | 22.5 |
| 20 | 0 | 0 | 0 | 0.09 | 17.5 | 22.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bohdal, Ł.; Kukiełka, L.; Legutko, S.; Patyk, R.; Radchenko, A.M. Modeling and Experimental Analysis of Shear-Slitting of AA6111-T4 Aluminum Alloy Sheet. Materials 2020, 13, 3175. https://doi.org/10.3390/ma13143175
Bohdal Ł, Kukiełka L, Legutko S, Patyk R, Radchenko AM. Modeling and Experimental Analysis of Shear-Slitting of AA6111-T4 Aluminum Alloy Sheet. Materials. 2020; 13(14):3175. https://doi.org/10.3390/ma13143175
Chicago/Turabian StyleBohdal, Łukasz, Leon Kukiełka, Stanisław Legutko, Radosław Patyk, and Andrii M. Radchenko. 2020. "Modeling and Experimental Analysis of Shear-Slitting of AA6111-T4 Aluminum Alloy Sheet" Materials 13, no. 14: 3175. https://doi.org/10.3390/ma13143175
APA StyleBohdal, Ł., Kukiełka, L., Legutko, S., Patyk, R., & Radchenko, A. M. (2020). Modeling and Experimental Analysis of Shear-Slitting of AA6111-T4 Aluminum Alloy Sheet. Materials, 13(14), 3175. https://doi.org/10.3390/ma13143175