Memetic Cuckoo-Search-Based Optimization in Machining Galvanized Iron
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Details
2.2. Regression Analysis
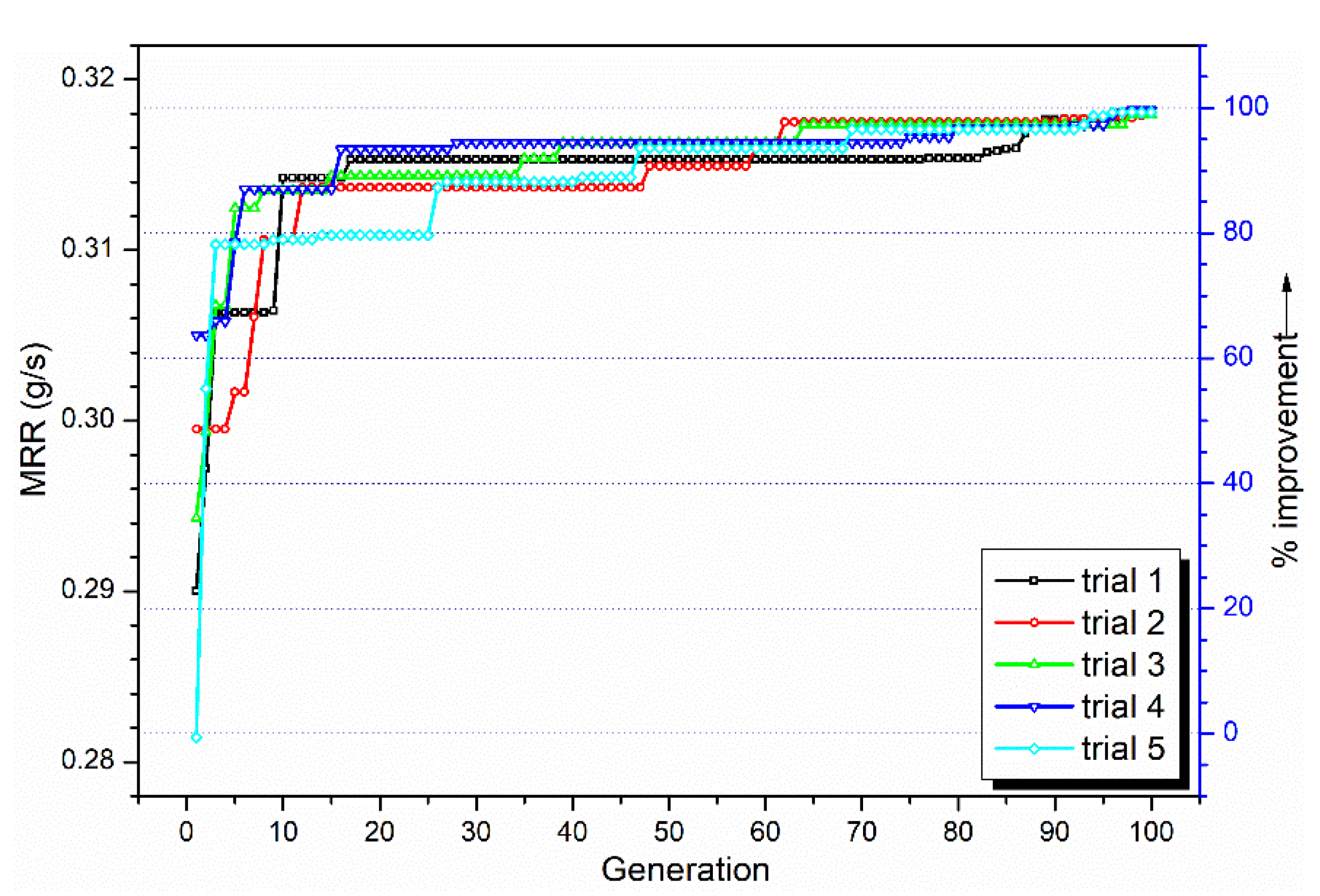
2.3. Optimization Using Improved Cuckoo Search
3. Results and Discussion
3.1. Building the Regression Model
3.2. ANOVA of the Regression Model
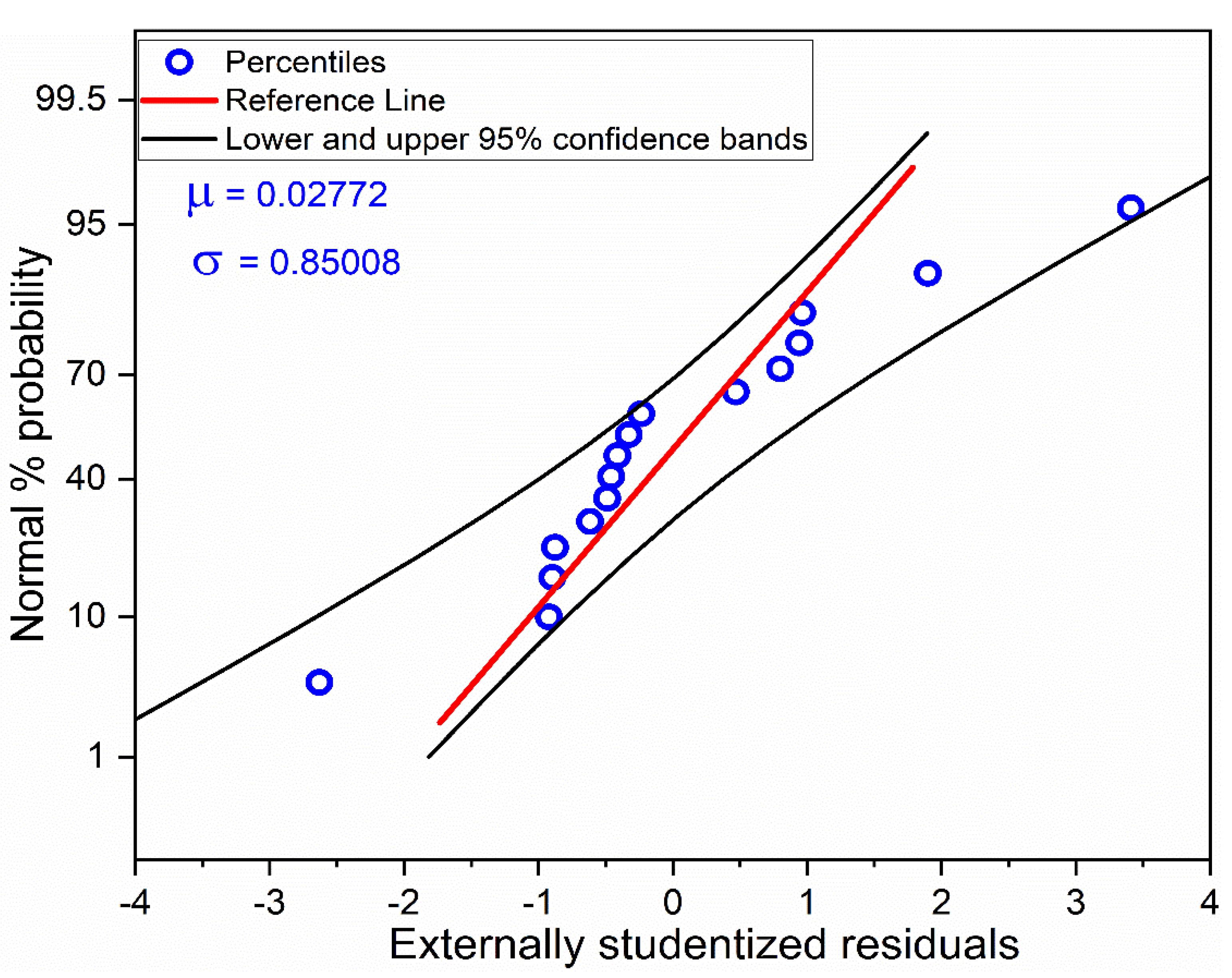
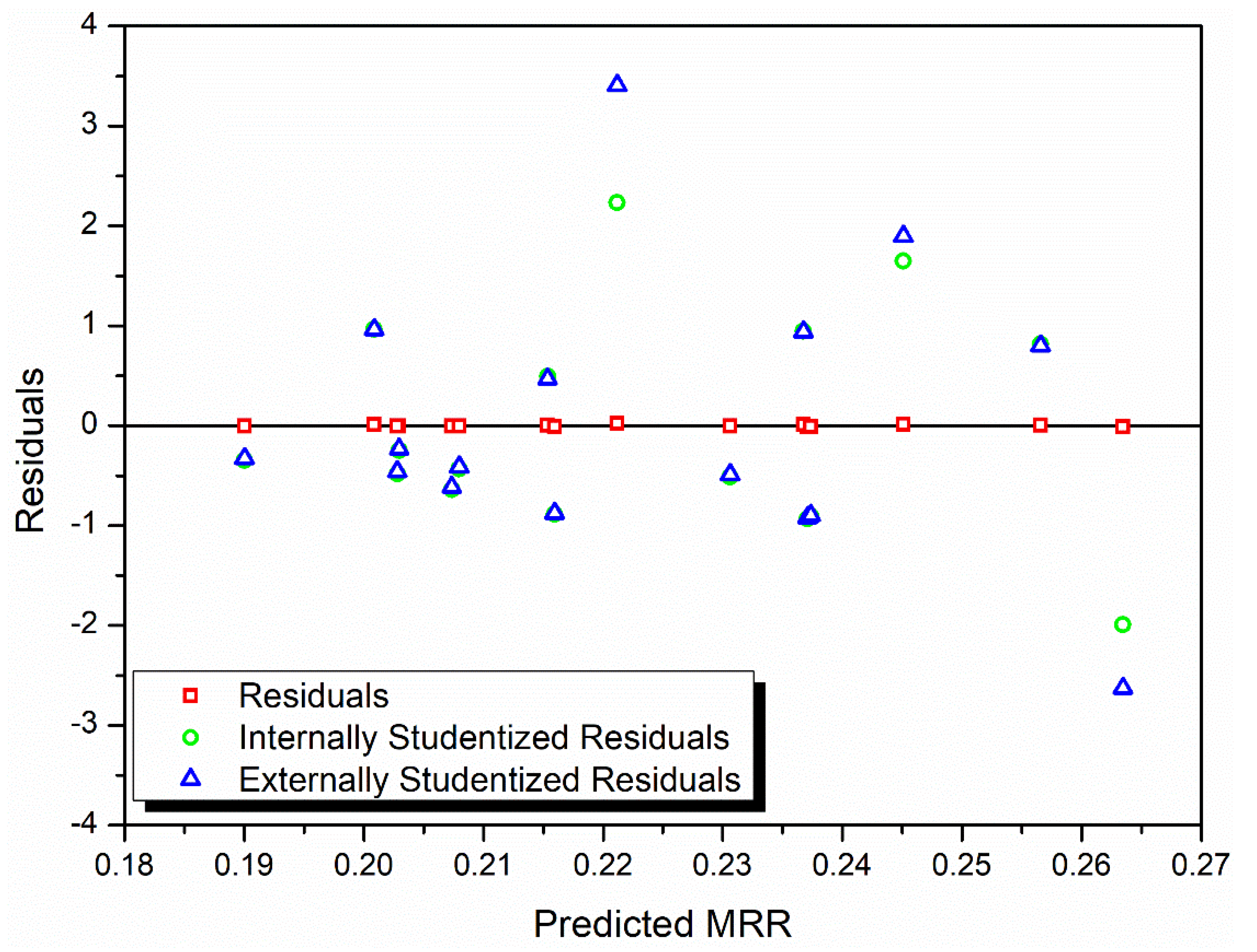
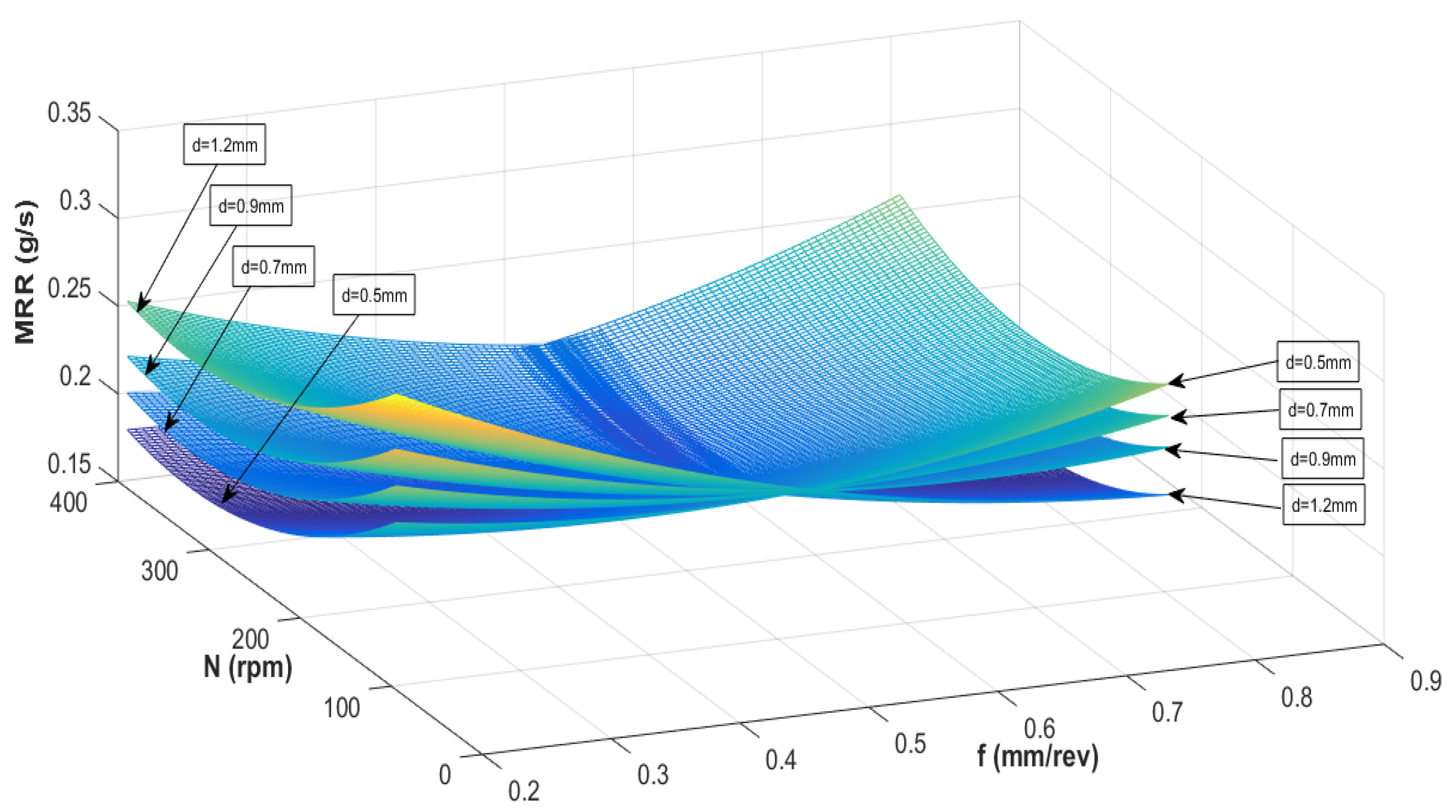
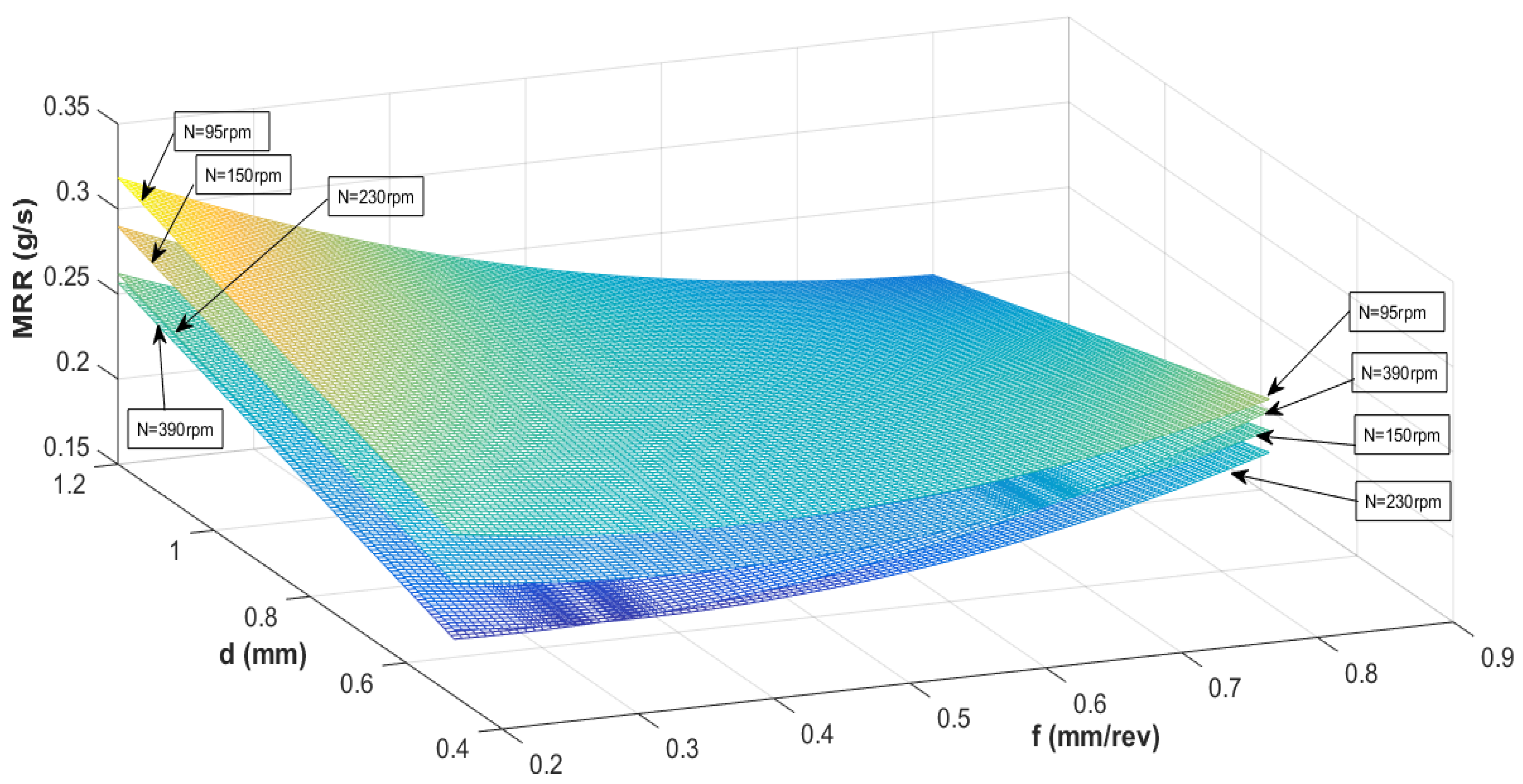
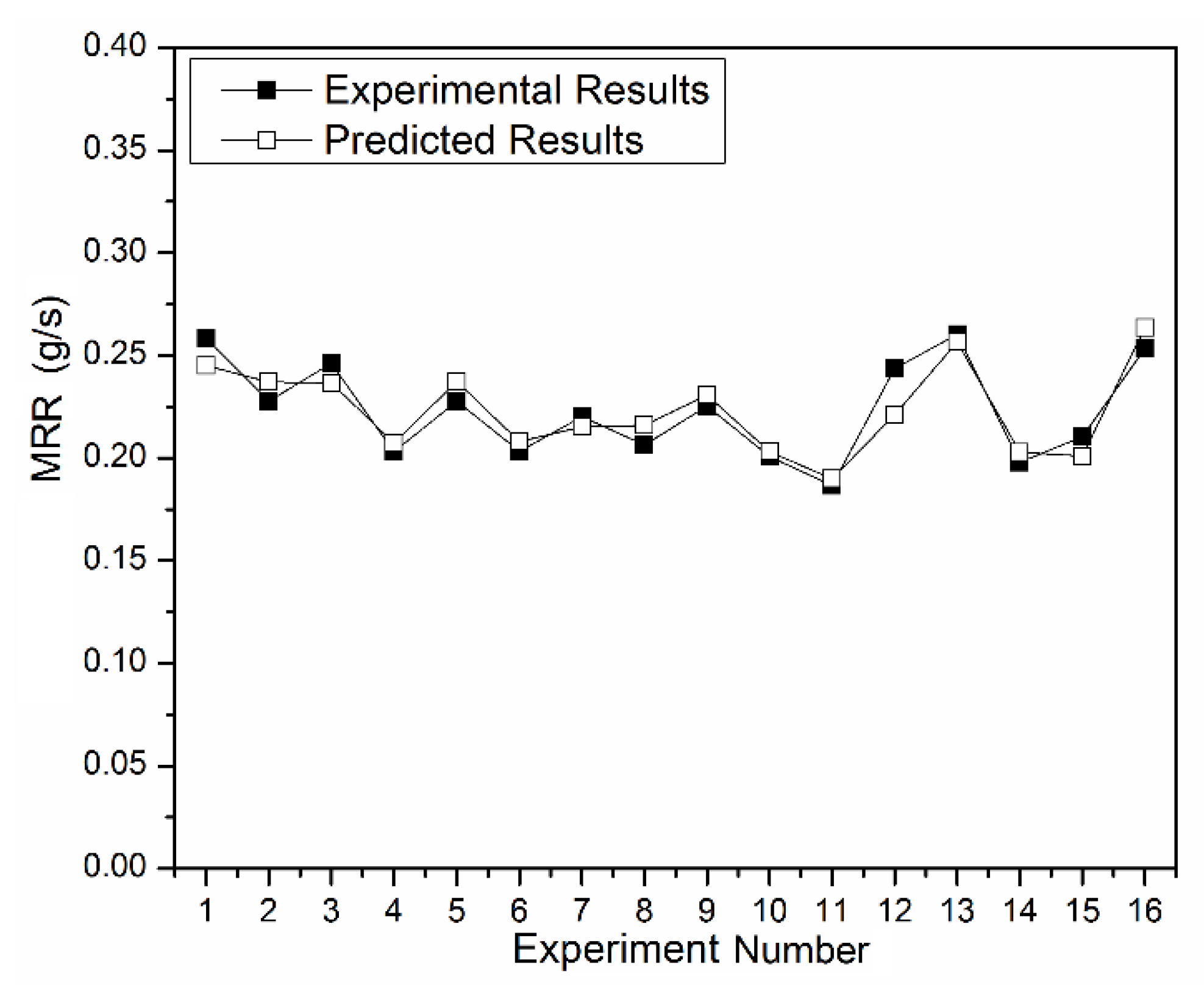
3.3. Analyzing the Regression Model
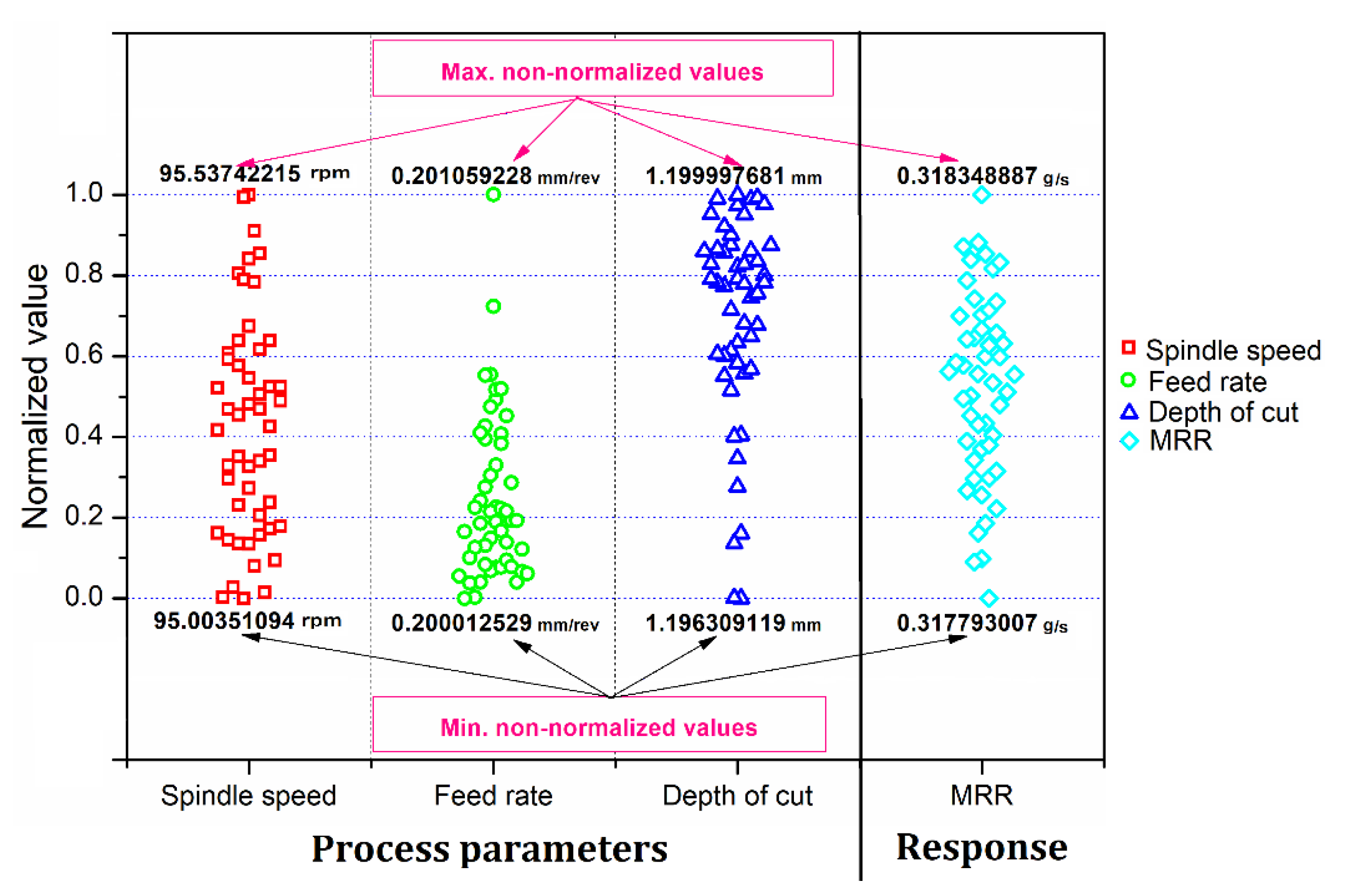
3.4. Process Parameter Optimization with CHP
0.2 ≤ f ≤ 0.8
0.5 ≤ d ≤ 1.2
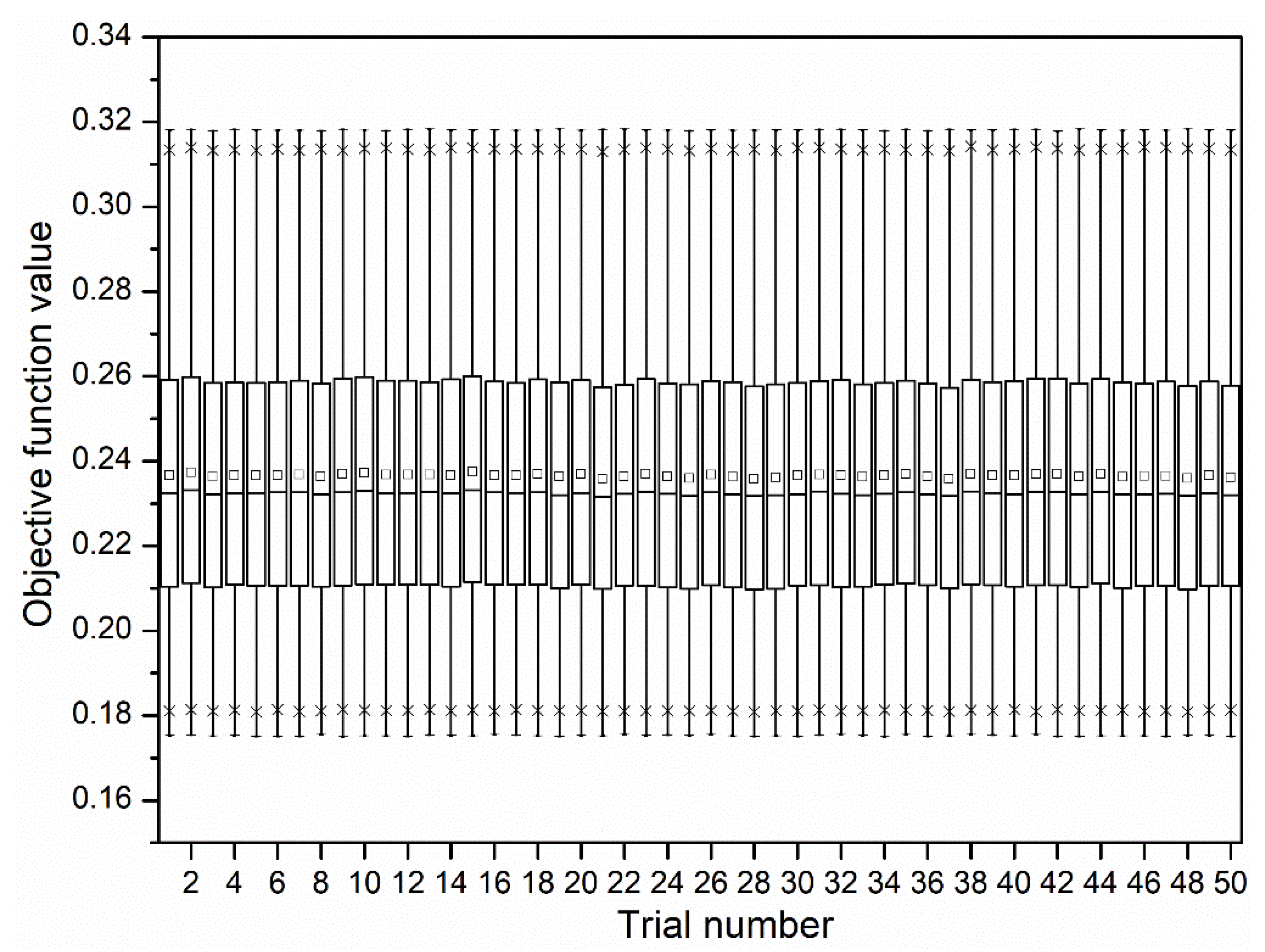
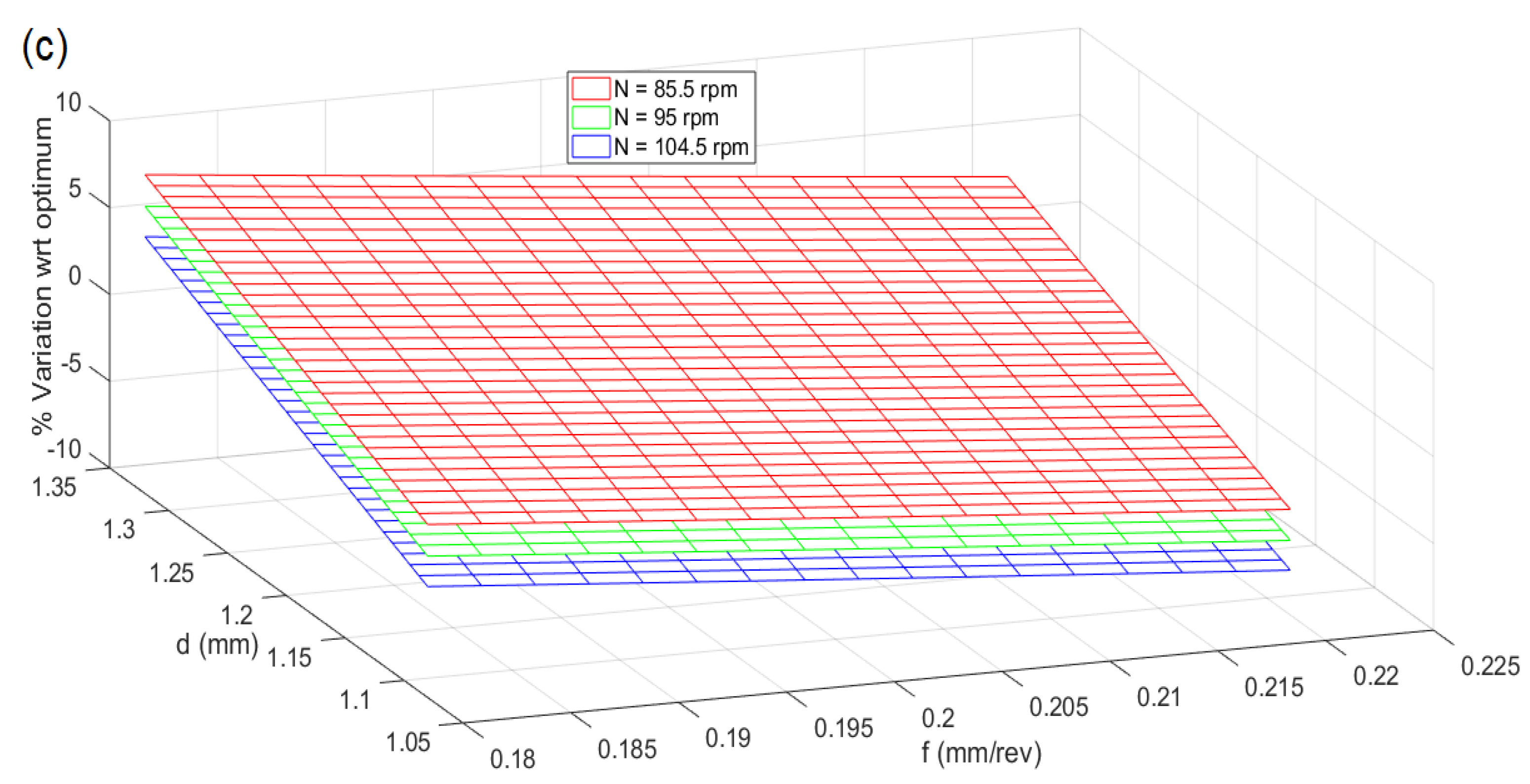
3.5. Robustness of CHP Solution
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Das, P.P.; Gupta, P.; Ghadai, R.K.; Ramachandran, M.; Kalita, K. Optimization of turning process parameters by taguchi-based six sigma. Mech. Mech. Eng. 2017, 21, 649–656. [Google Scholar]
- Santhanakrishnan, M.; Sivasakthivel, P.S.; Sudhakaran, R. Modeling of geometrical and machining parameters on temperature rise while machining Al 6351 using response surface methodology and genetic algorithm. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 487–496. [Google Scholar] [CrossRef]
- Suresh, P.; Venkatesan, R.; Sekar, T.; Elango, N.; Sathiyamoorthy, V. Optimization of intervening variables in Micro EDM of Ss 316L using a genetic algorithm and response-surface methodology. Stroj. Vestn. J. Mech. Eng. 2014, 60, 656–664. [Google Scholar] [CrossRef]
- Prabhu, S.; Vinayagam, B.K. Optimization of carbon nanotube-based electrical discharge machining parameters using full factorial design and genetic algorithm. Aust. J. Mech. Eng. 2016, 14, 161–173. [Google Scholar] [CrossRef]
- Ghadai, R.K.; Kalita, K.; Gao, X.Z. Symbolic regression metamodel based multi-response optimization of EDM process. Fme Trans. 2020, 48, 405. [Google Scholar] [CrossRef]
- Behera, R.R.; Ghadai, R.K.; Kalita, K.; Banerjee, S. Simultaneous prediction of delamination and surface roughness in drilling GFRP composite using ANN. Int. J. Plast. Technol. 2016, 20, 424–450. [Google Scholar] [CrossRef]
- Cus, F.; Balic, J.; Zuperl, U. Hybrid ANFIS-ants system based optimization of turning parameters. J. Achiev. Mater. Manuf. Eng. 2009, 36, 79–86. [Google Scholar]
- Ning, J.; Liang, S.Y. Inverse identification of Johnson-Cook material constants based on modified chip formation model and iterative gradient search using temperature and force measurements. Int. J. Adv. Manuf. Technol. 2019, 102, 2865–2876. [Google Scholar] [CrossRef]
- Ning, J.; Nguyen, V.; Huang, Y.; Hartwig, K.T.; Liang, S.Y. Inverse determination of Johnson–Cook model constants of ultra-fine-grained titanium based on chip formation model and iterative gradient search. Int. J. Adv. Manuf. Technol. 2018, 99, 1131–1140. [Google Scholar] [CrossRef]
- Zuo, K.T.; Chen, L.P.; Zhang, Y.Q.; Yang, J. Manufacturing-and machining-based topology optimization. Int. J. Adv. Manuf. Technol. 2006, 27, 531–536. [Google Scholar] [CrossRef]
- Kilickap, E.; Huseyinoglu, M. Selection of optimum drilling parameters on Burr Height using response surface methodology and genetic algorithm in drilling of AISI 304 stainless steel. Mater. Manuf. Process. 2010, 25, 1068–1076. [Google Scholar] [CrossRef]
- Kilickap, E.; Huseyinoglu, M.; Yardimeden, A. Optimization of drilling parameters on surface roughness in drilling of Aisi 1045 using response surface methodology and genetic algorithm. Int. J. Adv. Manuf. Technol. 2011, 52, 79–88. [Google Scholar] [CrossRef]
- Kalita, K.; Shivakoti, I.; Ghadai, R.K. Optimizing process parameters for Laser Beam Micro-Marking using genetic algorithm and particle swarm optimization. Mater. Manuf. Process. 2017, 32, 1101–1108. [Google Scholar] [CrossRef]
- Kalita, K.; Mallick, P.K.; Bhoi, A.K.; Ghadai, R. Optimizing drilling induced delamination in GFRP composites using genetic algorithm & particle swarm optimisation. Adv. Compos. Lett. 2018, 27, 1–9. [Google Scholar]
- Saidi, R.; Fathallah, B.B.; Mabrouki, T.; Belhadi, S.; Yallese, M.A. Modeling and optimization of the turning parameters of cobalt alloy (Stellite 6) based on RSM and desirability function. Int. J. Adv. Manuf. Technol. 2019, 100, 2945–2968. [Google Scholar] [CrossRef]
- Mia, M.; Królczyk, G.; Maruda, R.; Wojciechowski, S. Intelligent optimization of hard-turning parameters using evolutionary algorithms for smart manufacturing. Materials 2019, 12, 879. [Google Scholar] [CrossRef] [PubMed]
- Warsi, S.S.; Agha, M.H.; Ahmad, R.; Jaffery, S.H.I.; Khan, M. Sustainable turning using multi-objective optimization: A study of Al 6061 T6 at high cutting speeds. Int. J. Adv. Manuf. Technol. 2019, 100, 843–855. [Google Scholar] [CrossRef]
- Mia, M.; Dhar, N.R. Prediction and optimization by using SVR, RSM and GA in hard turning of tempered AISI 1060 steel under effective cooling condition. Neural Comput. Appl. 2019, 31, 2349–2370. [Google Scholar] [CrossRef]
- Laouissi, A.; Yallese, M.A.; Belbah, A.; Belhadi, S.; Haddad, A. Investigation, modeling, and optimization of cutting parameters in turning of gray cast iron using coated and uncoated silicon nitride ceramic tools. Based on ANN, RSM, and GA optimization. Int. J. Adv. Manuf. Technol. 2019, 101, 523–548. [Google Scholar] [CrossRef]
- Kalita, K.; Nasre, P.; Dey, P.; Haldar, S. Metamodel based multi-objective design optimization of laminated composite plates. Struct. Eng. Mech. 2018, 67, 301–310. [Google Scholar]
- Ragavendran, U.; Ghadai, R.K.; Bhoi, A.; Ramachandran, M.; Kalita, K. Sensitivity analysis and optimization of EDM process parameters. Trans. Can. Soc. Mech. Eng. 2018, 43, 13–25. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Cuckoo search via Levy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 210–214. [Google Scholar] [CrossRef]
- Mishra, S.K. Global optimization of some difficult benchmark functions by host-parasite coevolutionary algorithm. Econ. Bull. 2013, 33, 1–18. [Google Scholar]
- Kalita, K.; Dey, P.; Haldar, S.; Gao, X.Z. Optimizing frequencies of skew composite laminates with metaheuristic algorithms. Eng. Comput. 2020, 36, 741–761. [Google Scholar] [CrossRef]
- Bártol, I.; Karcza, Z.; Moskát, C.; Røskaft, E.; Kisbenedek, T. Responses of great reed warblers Acrocephalus arundinaceus to experimental brood parasitism: The effects of a cuckoo Cuculus canorus dummy and egg mimicry. J. Avian Biol. 2002, 33, 420–425. [Google Scholar] [CrossRef]
- Kalita, K.; Dey, P.; Haldar, S. Search for accurate RSM metamodels for structural engineering. J. Reinf. Plast. Compos. 2019, 38, 995–1013. [Google Scholar] [CrossRef]
- Ghadai, R.K.; Kalita, K.; Mondal, S.C.; Swain, B.P. PECVD process parameter optimization: Towards increased hardness of diamond-like carbon thin films. Mater. Manuf. Process. 2018, 33, 1905–1913. [Google Scholar] [CrossRef]
- Tibadia, R.; Patwardhan, K.; Shah, D.; Shinde, D.; Chaudhari, R.; Kalita, K. Experimental investigation on hole quality in drilling of composite pipes. Trans. Can. Soc. Mech. Eng. 2018, 42, 147–155. [Google Scholar] [CrossRef]


| Level | Spindle Speed, N (rpm) | Feed Rate, f (mm/rev) | Depth of Cut, d (mm) |
|---|---|---|---|
| 1 | 95 | 0.2 | 0.5 |
| 2 | 150 | 0.45 | 0.7 |
| 3 | 230 | 0.5 | 0.9 |
| 4 | 390 | 0.8 | 1.2 |
| Experiment Number | N (rpm) | f (mm/rev) | d (mm) | Average MRR (g/s) |
|---|---|---|---|---|
| 1 | 95 | 0.2 | 0.5 | 0.2584 |
| 2 | 95 | 0.45 | 0.7 | 0.2277 |
| 3 | 95 | 0.5 | 0.9 | 0.2463 |
| 4 | 95 | 0.8 | 1.2 | 0.2030 |
| 5 | 150 | 0.2 | 0.7 | 0.2277 |
| 6 | 150 | 0.45 | 0.5 | 0.2033 |
| 7 | 150 | 0.5 | 1.2 | 0.2203 |
| 8 | 150 | 0.8 | 0.9 | 0.2065 |
| 9 | 230 | 0.2 | 0.9 | 0.2253 |
| 10 | 230 | 0.45 | 1.2 | 0.2007 |
| 11 | 230 | 0.5 | 0.5 | 0.1867 |
| 12 | 230 | 0.8 | 0.7 | 0.2437 |
| 13 | 390 | 0.2 | 1.2 | 0.2603 |
| 14 | 390 | 0.45 | 0.9 | 0.1980 |
| 15 | 390 | 0.5 | 0.7 | 0.2103 |
| 16 | 390 | 0.8 | 0.5 | 0.2533 |
| Source | Standard Deviation | R2 | Adjusted R2 |
|---|---|---|---|
| Linear | 0.025 | 5.67% | −17.91% |
| 2FI | 0.024 | 36.77% | −5.39% |
| Quadratic | 0.014 | 84.87% | 62.18% |
| Source | Full Quadratic | Reduced Quadratic | ||||
|---|---|---|---|---|---|---|
| Sum of Squares | F Value | Prob > F | Sum of Squares | F Value | Prob > F | |
| Model | 0.0070 | 3.7404 | 0.0612 | 0.0069 | 5.6642 | 0.0130 |
| N | 0.0008 | 3.6799 | 0.1035 | 0.0012 | 6.9765 | 0.0297 |
| f | 0.0000 | 0.0149 | 0.9067 | 0.0004 | 2.4203 | 0.1584 |
| d | 0.0001 | 0.6400 | 0.4542 | 0.0000 | 0.1592 | 0.7003 |
| Nf | 0.0005 | 2.6404 | 0.1553 | 0.0004 | 2.4493 | 0.1562 |
| Nd | 0.0001 | 0.6587 | 0.4480 | - | - | - |
| fd | 0.0018 | 8.4281 | 0.0272 | 0.0023 | 13.5467 | 0.0062 |
| N2 | 0.0020 | 9.4189 | 0.0220 | 0.0021 | 11.9810 | 0.0086 |
| f2 | 0.0021 | 9.8556 | 0.0201 | 0.0022 | 12.8268 | 0.0072 |
| d2 | 0.0000 | 0.0093 | 0.9262 | - | - | - |
| Residual | 0.0012 | 0.0014 | ||||
| Cor Total | 0.0083 | 0.0083 | ||||
| Standard Deviation | 0.0140 | 0.0132 | ||||
| Mean | 0.2200 | 0.2232 | ||||
| Coefficient of Variation% | 6.4700 | 5.90 | ||||
| R2 | 84.87% | 83.21% | ||||
| Adjusted R2 | 62.18% | 68.52% | ||||
| N (rpm) | f (mm/rev) | d (mm) | Predicted MRR (g/s) | Experiment MRR (g/s) |
|---|---|---|---|---|
| 95 | 0.2 | 1.2 | 0.318 | 0.326 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalita, K.; Ghadai, R.K.; Cepova, L.; Shivakoti, I.; Bhoi, A.K. Memetic Cuckoo-Search-Based Optimization in Machining Galvanized Iron. Materials 2020, 13, 3047. https://doi.org/10.3390/ma13143047
Kalita K, Ghadai RK, Cepova L, Shivakoti I, Bhoi AK. Memetic Cuckoo-Search-Based Optimization in Machining Galvanized Iron. Materials. 2020; 13(14):3047. https://doi.org/10.3390/ma13143047
Chicago/Turabian StyleKalita, Kanak, Ranjan Kumar Ghadai, Lenka Cepova, Ishwer Shivakoti, and Akash Kumar Bhoi. 2020. "Memetic Cuckoo-Search-Based Optimization in Machining Galvanized Iron" Materials 13, no. 14: 3047. https://doi.org/10.3390/ma13143047
APA StyleKalita, K., Ghadai, R. K., Cepova, L., Shivakoti, I., & Bhoi, A. K. (2020). Memetic Cuckoo-Search-Based Optimization in Machining Galvanized Iron. Materials, 13(14), 3047. https://doi.org/10.3390/ma13143047








