Crystal-Plasticity-Finite-Element Modeling of the Quasi-Static and Dynamic Response of a Directionally Solidified Nickel-Base Superalloy
Abstract
1. Introduction
2. Materials and Methods
2.1. Material Description
2.2. Mechanical Characterisation
2.2.1. Quasi-Static Tensile Tests
2.2.2. Dynamic Tensile Tests
2.3. Numerical Modelling
2.3.1. Crystal Plasticity Model
2.3.2. Numerical Set-Up
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CP | Crystal plasticity |
| CPFEM | Crystal-plasticity-finite-element method |
| DS | Directionally solidified |
| FCC | Face centred cubic |
| SX | Single crystal |
| Melting temperature | |
| VPSC | Visco plastic self consistent |
| SHTB | Split Hopkinson tension bar |
| fps | Frames per second |
| CRSS | Critical-resolved-shear stress |
| RVE | Representative volume element |
| C3D8 | Eight-node fully-integrated hexahedral element |
| Probability density function |
References
- Davis, J.R. ASM Specialty Handbook: Heat-Resistant Materials; ASM International: Novelty, OH, USA, 1997. [Google Scholar]
- Pope, D.; Ezz, S.S. Mechanical properties of Ni3AI and nickel-base alloys with high volume fraction of γ′. Int. Metals Rev. 1984, 29, 136–167. [Google Scholar]
- Stoloff, N.S.; Davies, R.G. The mechanical properties of ordered alloys. Progress Mater. Sci. 1968, 13, 1–84. [Google Scholar] [CrossRef]
- Thornton, P.; Davies, R. The temperature dependence of the flow stress of gamma prime phases having the Ll 2 structure. Metall. Mater. Trans. B 1970, 1, 549–550. [Google Scholar] [CrossRef]
- Ashby, M.; Verrall, R. Diffusion-accommodated flow and superplasticity. Acta Metall. 1973, 21, 149–163. [Google Scholar] [CrossRef]
- Coble, R. A model for boundary diffusion controlled creep in polycrystalline materials. J. Appl. Phys. 1963, 34, 1679–1682. [Google Scholar] [CrossRef]
- Kassner, M.E. Fundamentals of Creep in Metals and Alloys; Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar]
- Lacaze, J.; Hazotte, A. Directionally Solidified Materials: Nickel-Base Superalloys for Gas Turbines. Textures Microstruct. 1990, 13, 1–14. [Google Scholar] [CrossRef]
- Zhou, Y.Z.; Green, N.R. Competitive grain growth in directional solidification of a nickel-base superalloy. Proc. Int. Symp. Superalloys 2008, 56, 317–324. [Google Scholar] [CrossRef]
- Shenoy, M.M.; McDowell, D.L.; Neu, R.W. Transversely isotropic viscoplasticity model for a directionally solidified Ni-base superalloy. Int. J. Plast. 2006, 22, 2301–2326. [Google Scholar] [CrossRef]
- Shi, D.; Dong, C.; Yang, X. Constitutive modeling and failure mechanisms of anisotropic tensile and creep behaviors of nickel-base directionally solidified superalloy. Mater. Des. 2013, 45, 663–673. [Google Scholar] [CrossRef]
- Sabar, H.; Berveiller, M.; Favier, V.; Berbenni, S. A new class of micro–macro models for elastic–viscoplastic heterogeneous materials. Int. J. Solids Struct. 2002, 39, 3257–3276. [Google Scholar] [CrossRef]
- Martin, G.; Ochoa, N.; Saï, K.; Hervé-Luanco, E.; Cailletaud, G. A multiscale model for the elastoviscoplastic behavior of Directionally Solidified alloys: Application to FE structural computations. Int. J. Solids Struct. 2014, 51, 1175–1187. [Google Scholar] [CrossRef]
- Kashinga, R.J.; Zhao, L.G.; Silberschmidt, V.V.; Farukh, F.; Barnard, N.C.; Whittaker, M.T.; Proprentner, D.; Shollock, B.; McColvin, G. Low cycle fatigue of a directionally solidified nickel-based superalloy: Testing, characterisation and modelling. Mater. Sci. Eng. A 2017, 708, 503–513. [Google Scholar] [CrossRef]
- Lin, B.; Zhao, L.G.; Tong, J. A crystal plasticity study of cyclic constitutive behaviour, crack-tip deformation and crack-growth path for a polycrystalline nickel-based superalloy. Eng. Fract. Mech. 2011, 78, 2174–2192. [Google Scholar] [CrossRef]
- Guan, Y.; Chen, B.; Zou, J.; Britton, T.B.; Jiang, J.; Dunne, F.P. Crystal plasticity modelling and HR-DIC measurement of slip activation and strain localization in single and oligo-crystal Ni alloys under fatigue. Int. J. Plast. 2017, 88, 70–88. [Google Scholar] [CrossRef]
- Knezevic, M.; Carpenter, J.S.; Lovato, M.L.; McCabe, R.J. Deformation behavior of the cobalt-based superalloy Haynes 25: Experimental characterization and crystal plasticity modeling. Acta Mater. 2014, 63, 162–168. [Google Scholar] [CrossRef]
- Shahba, A.; Ghosh, S. Crystal plasticity FE modeling of Ti alloys for a range of strain-rates. Part I: A unified constitutive model and flow rule. Int. J. Plast. 2016, 87, 48–68. [Google Scholar] [CrossRef]
- Ghosh, S.; Shahba, A.; Tu, X.; Huskins, E.L.; Schuster, B.E. Crystal plasticity FE modeling of Ti alloys for a range of strain-rates. Part II: Image-based model with experimental validation. Int. J. Plast. 2016, 87, 69–85. [Google Scholar] [CrossRef]
- Sehitoglu, H.; Boismier, D. Thermo-Mechanical Fatigue of Mar-M247: Part 1-Experiments, Part 2-Life Prediction. J. Eng. Mater. Technol. Dated Jan. 1990, 5, 239–254. [Google Scholar]
- Kupkovits, R.A.; Neu, R.W. Thermomechanical fatigue of a directionally-solidified Ni-base superalloy: Smooth and cylindrically-notched specimens. Int. J. Fatigue 2010, 32, 1330–1342. [Google Scholar] [CrossRef]
- Moore, Z.; Neu, R. Creep fatigue of a directionally solidified Ni-base superalloy–smooth and cylindrically notched specimens. Fatigue Fract. Eng. Mater. Struct. 2011, 34, 17–31. [Google Scholar] [CrossRef]
- Huang, H.E.; Koo, C.H. Characteristics and Mechanical Properties of Polycrystalline CM 247 LC Superalloy Casting. Mater. Trans. 2004, 45, 562–568. [Google Scholar] [CrossRef]
- Liao, J.H.; Bor, H.Y.; Chao, C.G.; Liu, T.F. Effects of rhenium on microstructure and phase stability of MAR-M247 Ni-base fine-grain superalloy. Mater. Trans. 2010, 51, 810–817. [Google Scholar] [CrossRef]
- Segurado, J.; Llorca, J. Simulation of the deformation of polycrystalline nanostructured Ti by computational homogenization. Comput. Mater. Sci. 2013, 76, 3–11. [Google Scholar] [CrossRef]
- Haouala, S.; Segurado, J.; LLorca, J. An analysis of the influence of grain size on the strength of FCC polycrystals by means of computational homogenization. Acta Mater. 2018, 148, 72–85. [Google Scholar] [CrossRef]
- Harris, K.; Erickson, G.; Schwer, R. MAR M 247 derivations—CM 247 LC DS alloy, CMSX® single crystal alloys, properties and performance. In Proceedings of the 5th International Symposium on Superalloys, Seven Springs, PA, USA, 7–11 October 1984; pp. 221–230. [Google Scholar]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671. [Google Scholar] [CrossRef] [PubMed]
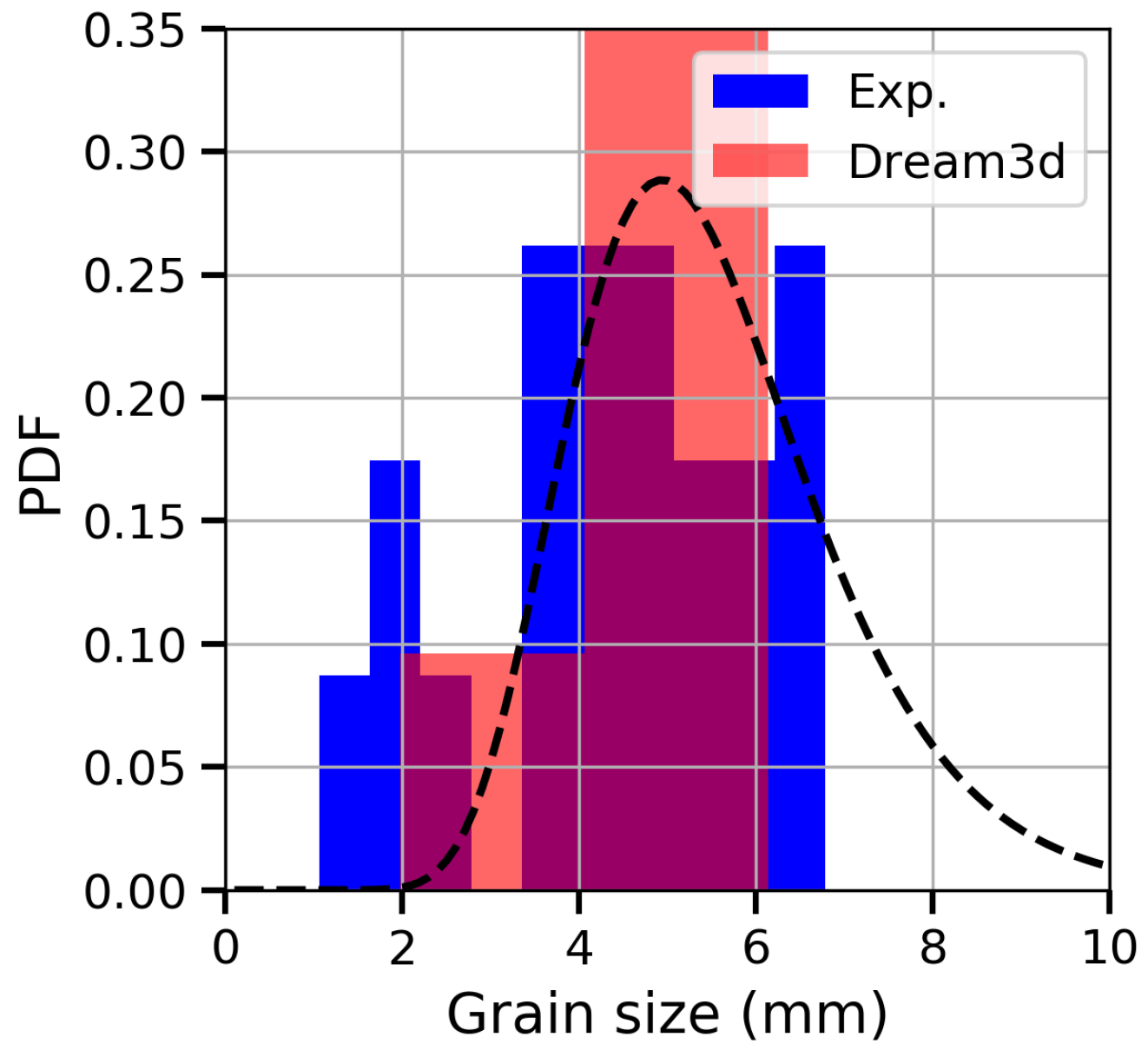
- Groeber, M.A.; Jackson, M.A. DREAM. 3D: A digital representation environment for the analysis of microstructure in 3D. Integr. Mater. Manuf. Innov. 2014, 3, 5. [Google Scholar] [CrossRef]
- User Manual-eCorr-Digital Image Correlation Tool. Available online: https://www.ntnu.edu/kt/ecorr (accessed on 1 July 2019).
- Harding, J.; Wood, E.; Campbell, J. Tensile testing of materials at impact rates of strain. J. Mech. Eng. Sci. 1960, 2, 88–96. [Google Scholar] [CrossRef]
- Kolsky, H. Stress Waves in Solids; Dover Publications: Mineola, NY, USA, 1963. [Google Scholar]
- Chen, Y.; Clausen, A.; Hopperstad, O.; Langseth, M. Application of a split-Hopkinson tension bar in a mutual assessment of experimental tests and numerical predictions. Int. J. Impact Eng. 2011, 38, 824–836. [Google Scholar] [CrossRef]
- Erice, B.; Gálvez, F. A coupled elastoplastic-damage constitutive model with Lode angle dependent failure criterion. Int. J. Solids Struct. 2014, 51, 93–110. [Google Scholar] [CrossRef]
- Lee, E.; Liu, D. Finite-strain elastic—plastic theory with application to plane-wave analysis. J. Appl. Phys. 1967, 38, 19–27. [Google Scholar] [CrossRef]
- Weber, G.R.; Ghosh, S. Thermo-mechanical deformation evolution in polycrystalline Ni-based superalloys by a hierarchical crystal plasticity model. Mater. High Temp. 2016, 33, 401–411. [Google Scholar] [CrossRef]
- Raabe, D. Modelling of active slip systems, Taylor factors and grain rotations during rolling and compresssion deformation of plycrystalline intermetallic L12 compounds. Acta Metall. Mater 1995, 43, 1531–1540. [Google Scholar] [CrossRef]
- Nembach, E. The high temperature peak of the yield strength of γ′-strengthened superalloys. Mater. Sci. Eng. A 2006, 429, 277–286. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. Material rate dependence and localized deformation in crystalline solids. Acta Metall. 1983, 31, 1951–1976. [Google Scholar] [CrossRef]
- Bertin, N.; Capolungo, L.; Beyerlein, I.J. Hybrid dislocation dynamics based strain hardening constitutive model. Int. J. Plast. 2013, 49, 119–144. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. An analysis of nonuniform and localized deformation in ductile single crystals. Acta Metall. 1982, 30, 1087–1119. [Google Scholar] [CrossRef]
- Kaufman, M. Properties of cast Mar-M-247 for turbine blisk applications. In Proceedings of the 5th International Symposium on Superalloys, Seven Springs, PA, USA, 7–11 October 1984; pp. 43–52. [Google Scholar]
- Kuhn, H.A.; Sockel, H.G. Comparison between experimental determination and calculation of elastic properties of nickel-base superalloys between 25 and 1200 C. Phys. Status Solidi (a) 1988, 110, 449–458. [Google Scholar] [CrossRef]
- Caillard, D.; Martin, J.L. Thermally Activated Mechanisms in Crystal Plasticity; Elsevier: Oxford, UK, 2003. [Google Scholar]





| Cr | Co | Al | Ti | W | Ta | Mo | C | Hf | Ni |
|---|---|---|---|---|---|---|---|---|---|
| 8.00 | 10.0 | 5.50 | 1.00 | 10.0 | 3.00 | 0.60 | 0.15 | 1.5 | Bal. |
| m | ||||||
|---|---|---|---|---|---|---|
| 258.6 GPa | 167.0 GPa | 125.0 GPa | 1.36 | 2.26 | 0.0015 | |
| 0.001 s | 1.00 | 1.00 | 5.38 | 0.68 | 1.12 | 0.96 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sancho, R.; Segurado, J.; Erice, B.; Pérez-Martín, M.-J.; Gálvez, F. Crystal-Plasticity-Finite-Element Modeling of the Quasi-Static and Dynamic Response of a Directionally Solidified Nickel-Base Superalloy. Materials 2020, 13, 2990. https://doi.org/10.3390/ma13132990
Sancho R, Segurado J, Erice B, Pérez-Martín M-J, Gálvez F. Crystal-Plasticity-Finite-Element Modeling of the Quasi-Static and Dynamic Response of a Directionally Solidified Nickel-Base Superalloy. Materials. 2020; 13(13):2990. https://doi.org/10.3390/ma13132990
Chicago/Turabian StyleSancho, Rafael, Javier Segurado, Borja Erice, María-Jesús Pérez-Martín, and Francisco Gálvez. 2020. "Crystal-Plasticity-Finite-Element Modeling of the Quasi-Static and Dynamic Response of a Directionally Solidified Nickel-Base Superalloy" Materials 13, no. 13: 2990. https://doi.org/10.3390/ma13132990
APA StyleSancho, R., Segurado, J., Erice, B., Pérez-Martín, M.-J., & Gálvez, F. (2020). Crystal-Plasticity-Finite-Element Modeling of the Quasi-Static and Dynamic Response of a Directionally Solidified Nickel-Base Superalloy. Materials, 13(13), 2990. https://doi.org/10.3390/ma13132990






