Theoretical and Experimental Studies on Thermal Properties of Polyester Nonwoven Fibrous Material
Abstract
1. Introduction
2. Review of Thermal Conductivity Models
2.1. Semi-Empirical Models
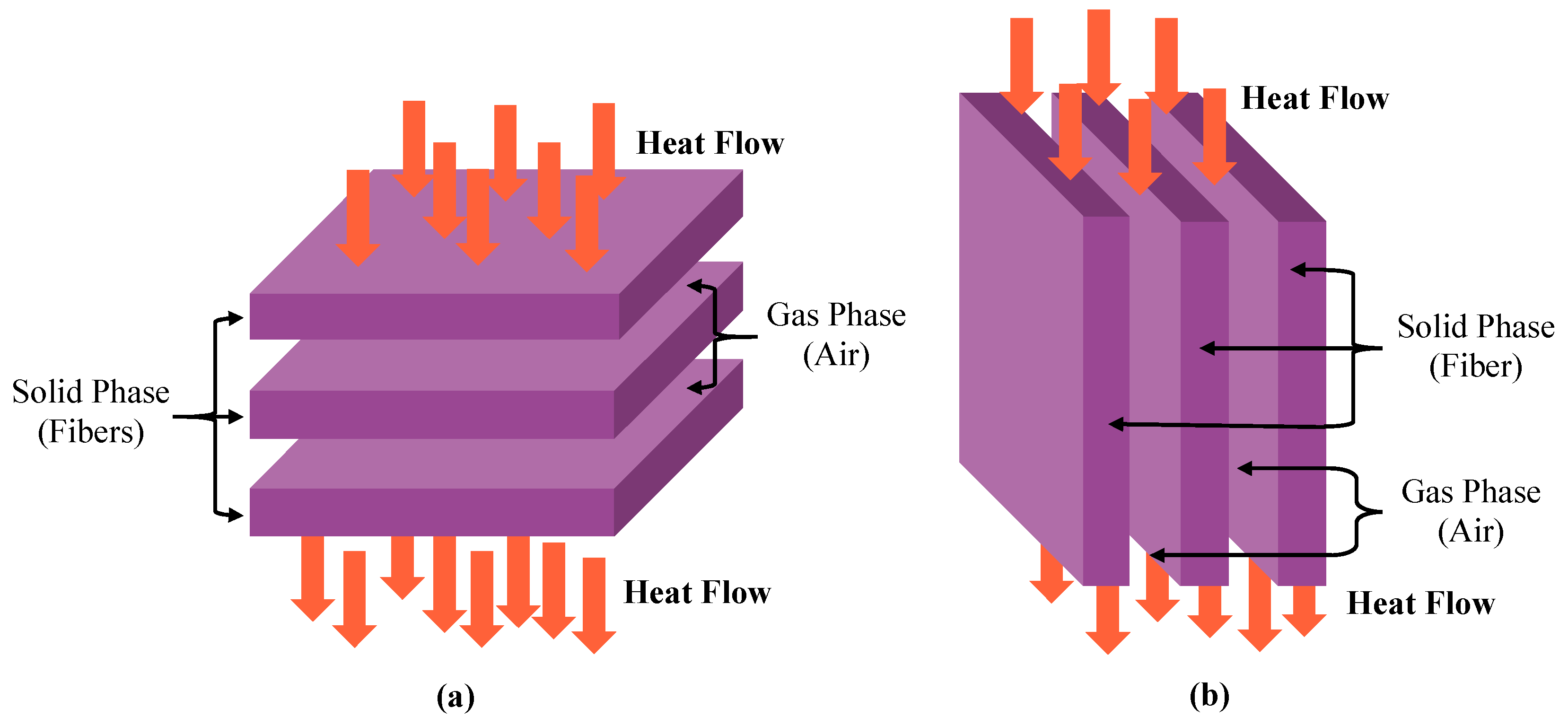
2.2. Models Based on Thermal-Electrical Analogy
3. Materials and Methods
3.1. Materials
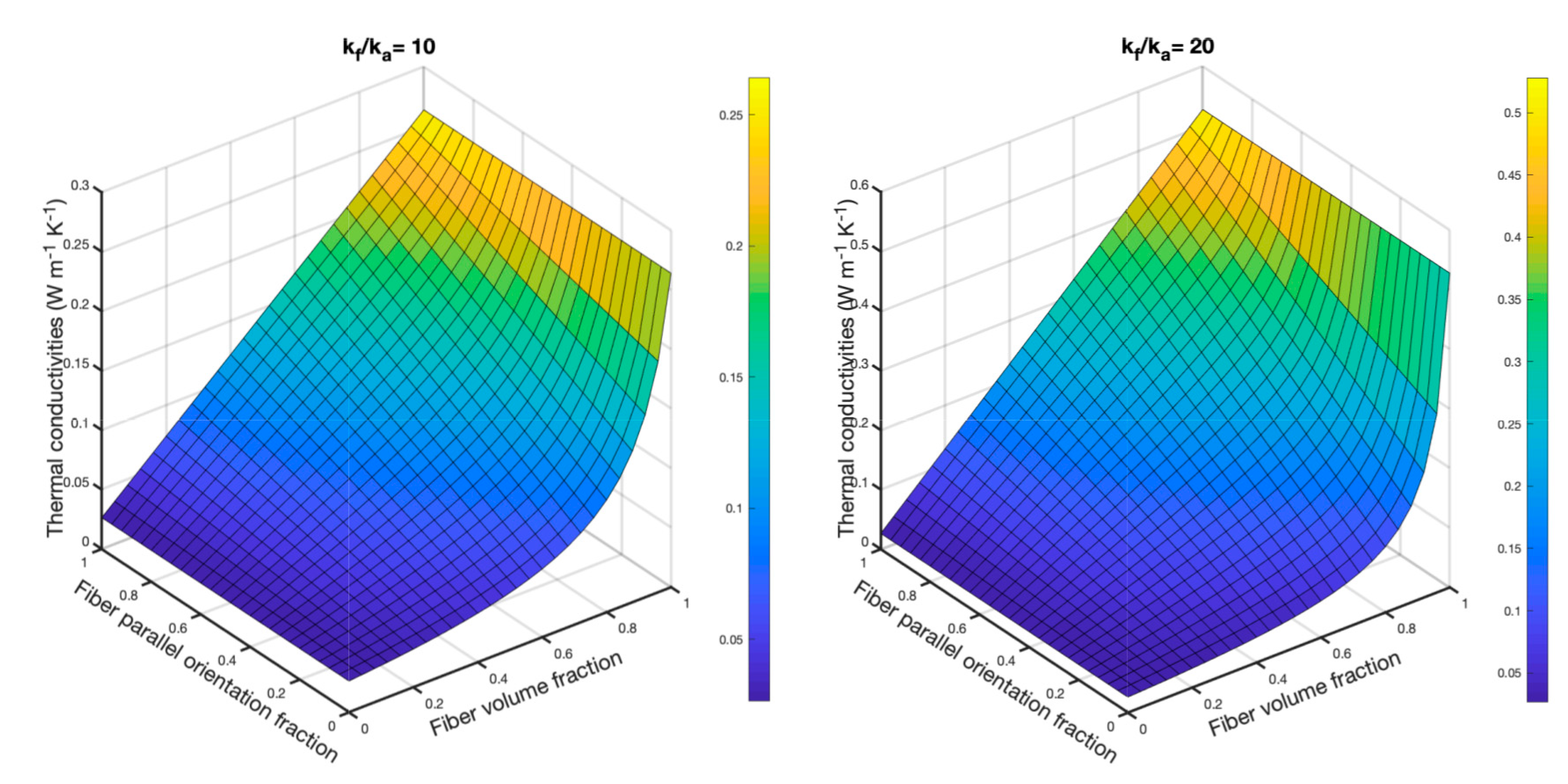
3.2. Theoretical Study
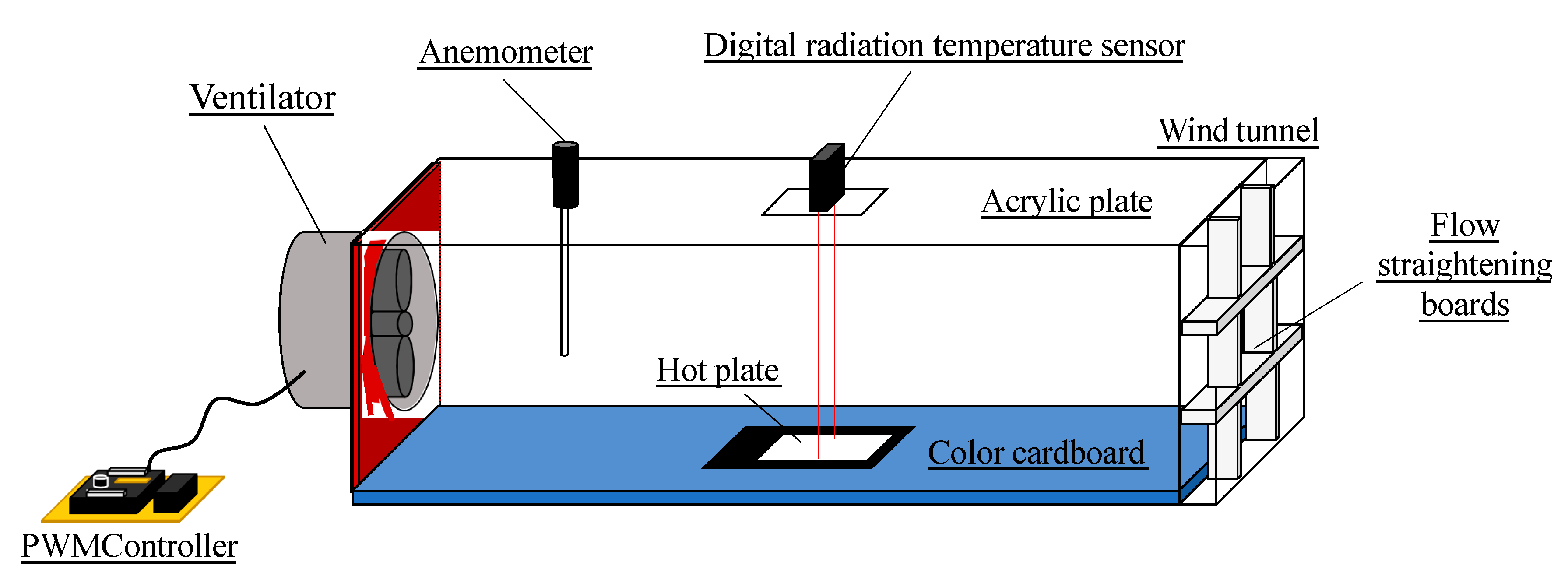
3.3. Experimental Study
4. Results and Discussion
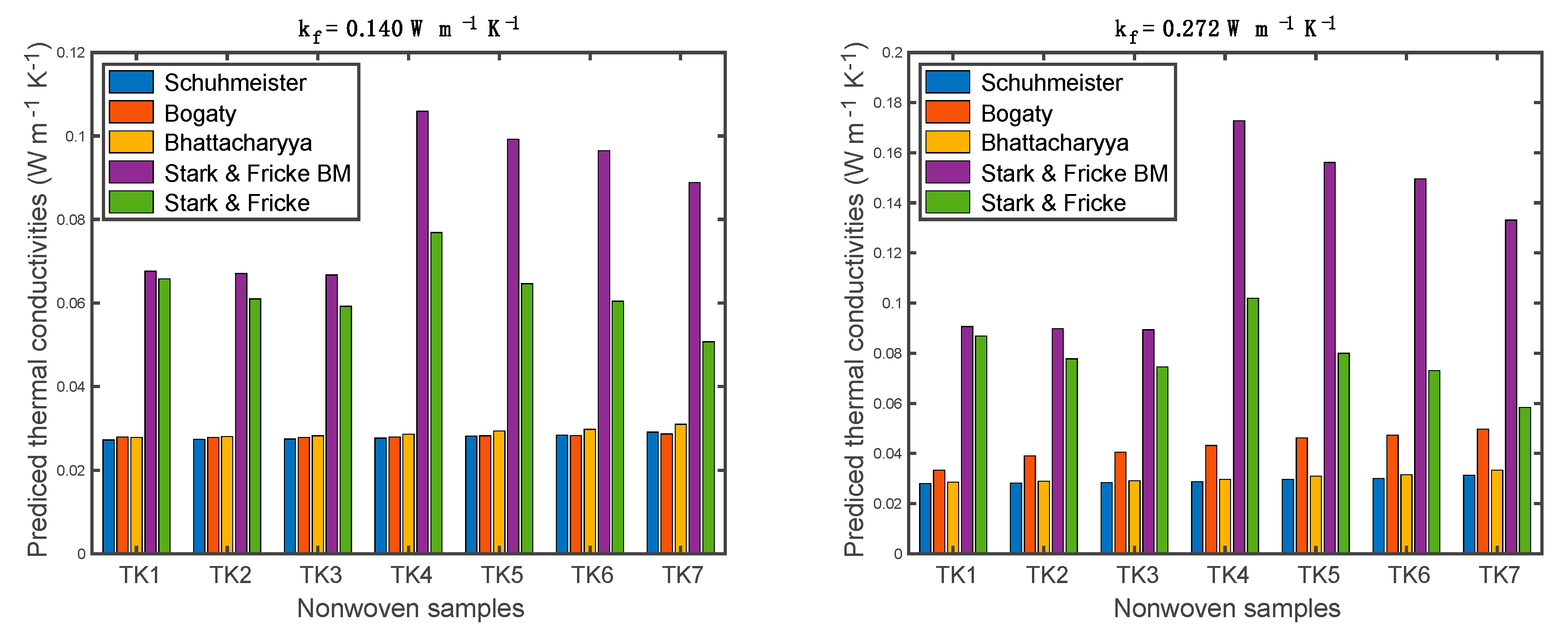
4.1. Predictions of Thermal Conductivity of Nonwoven Samples
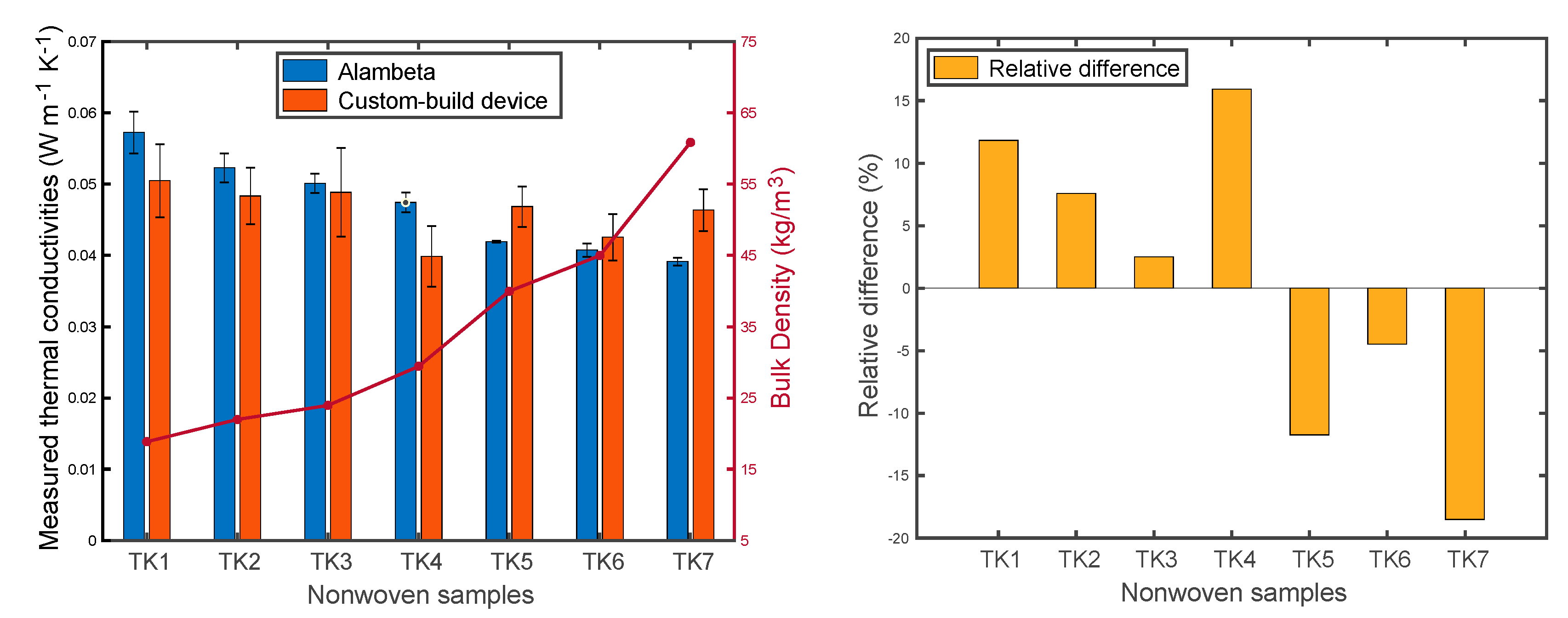
4.2. Measured Thermal Conductivity of Nonwoven Samples
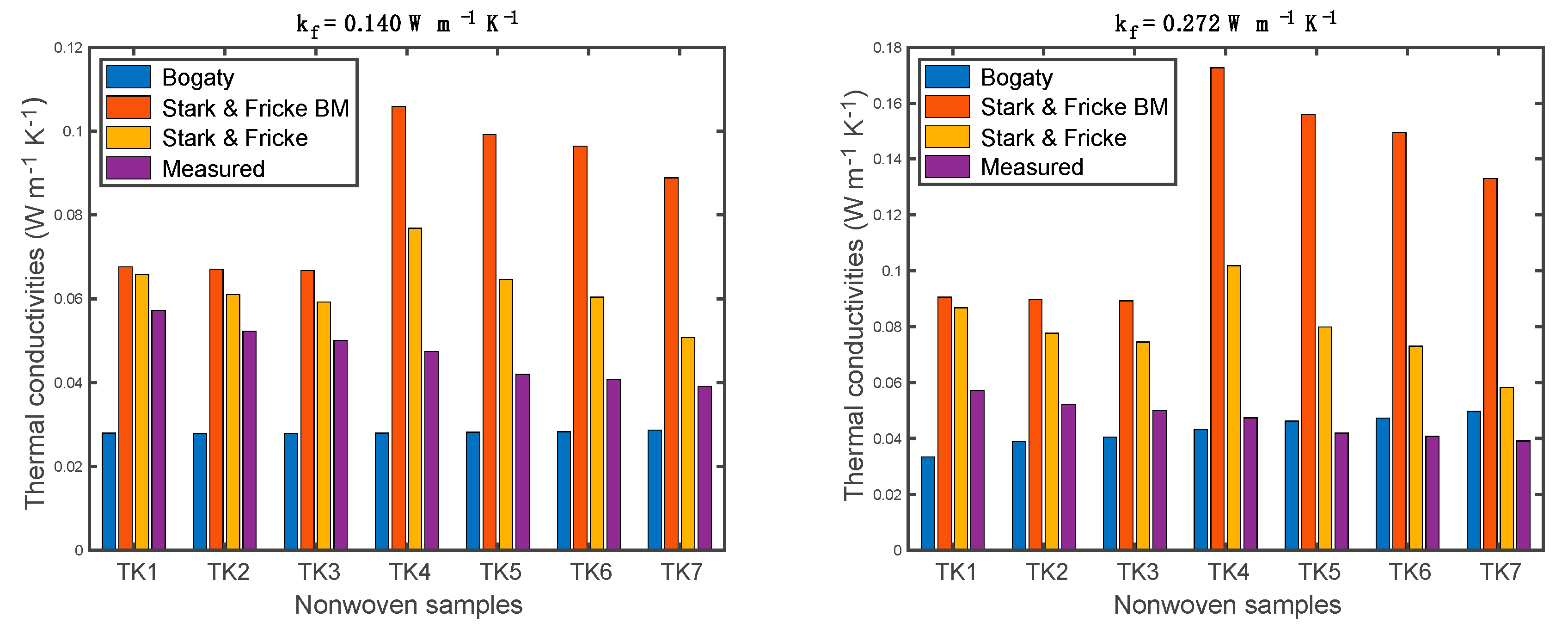
4.3. Validation of Thermal Conductivity Models
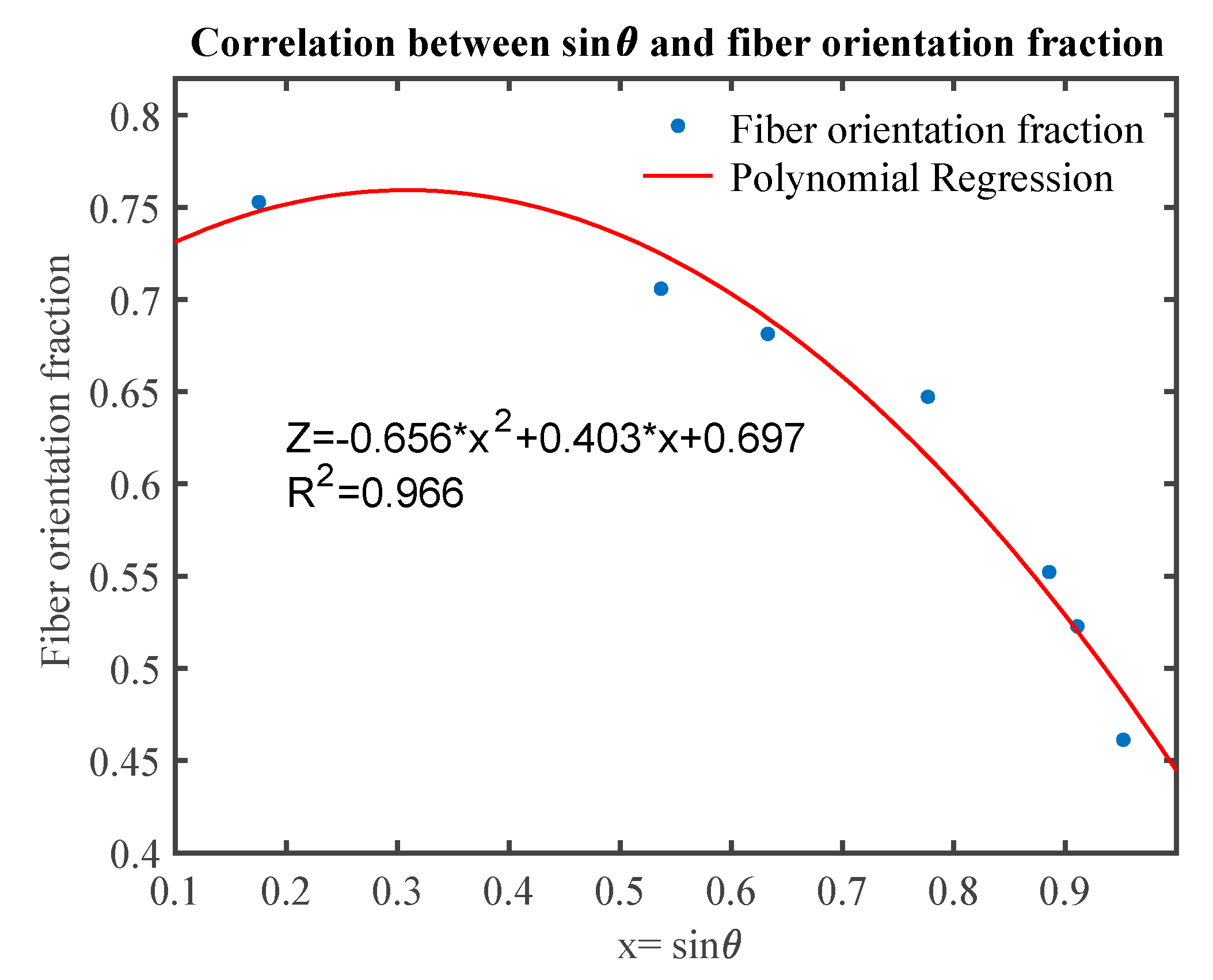
4.4. Modification on Stark-Fricke Basic Model
5. Conclusions
- Predicted thermal conductivities of nonwoven samples exhibited big differences among the models. Changing of fiber thermal conductivity had a small effect on the results from the Schuhmeister and Bhattacharyya models. The Bogaty model was not suitable for nonwoven materials with a low fiber volume fraction (i.e., <0.1). The two models proposed by Stark et. al. showed much higher predictions compared to the other models.
- Measured thermal conductivities from the Alambeta device and the custom-built device had varying relative differences between the samples. The value was between −18.50% and 15.92%, which is reasonable due to the measurement uncertainties, different environments, and other factors. Although sample density increased the thermal conductivity decreased. This is because the fiber orientation turns more perpendicular to the direction of heat flow when the sample density increased.
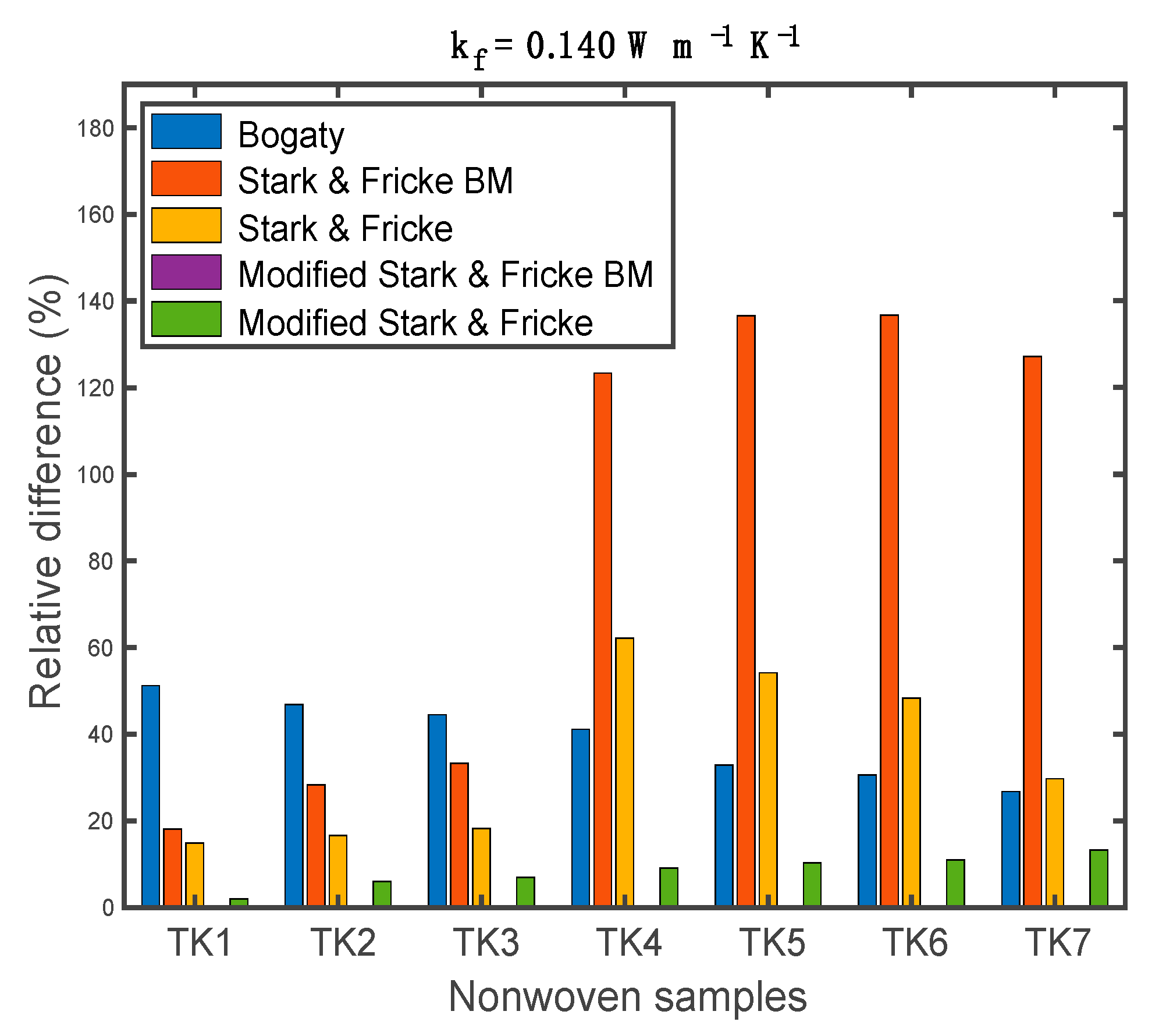
- Two Stark-Fricke models overestimated the thermal conductivities of the nonwoven samples. The Bogaty model exhibited a relatively low difference with the values ranging from 26.73% to 51.21%. The original Stark-Fricke basic model showed a big relative difference (i.e., 18.13–127.18%). The modified model could accurately predict the thermal conductivities with a very small relative difference and can provide a reliable prediction of the thermal conductivity of polyester nonwoven fibrous materials.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| h | Material thickness (m) |
| k | Thermal conductivity (W m−1 K−1) |
| ka | Thermal conductivity of air (W m−1 K−1) |
| kf | Thermal conductivity of fiber (W m−1 K−1) |
| ks−f | Thermal conductivity of staple PET fiber (W m−1 K−1) |
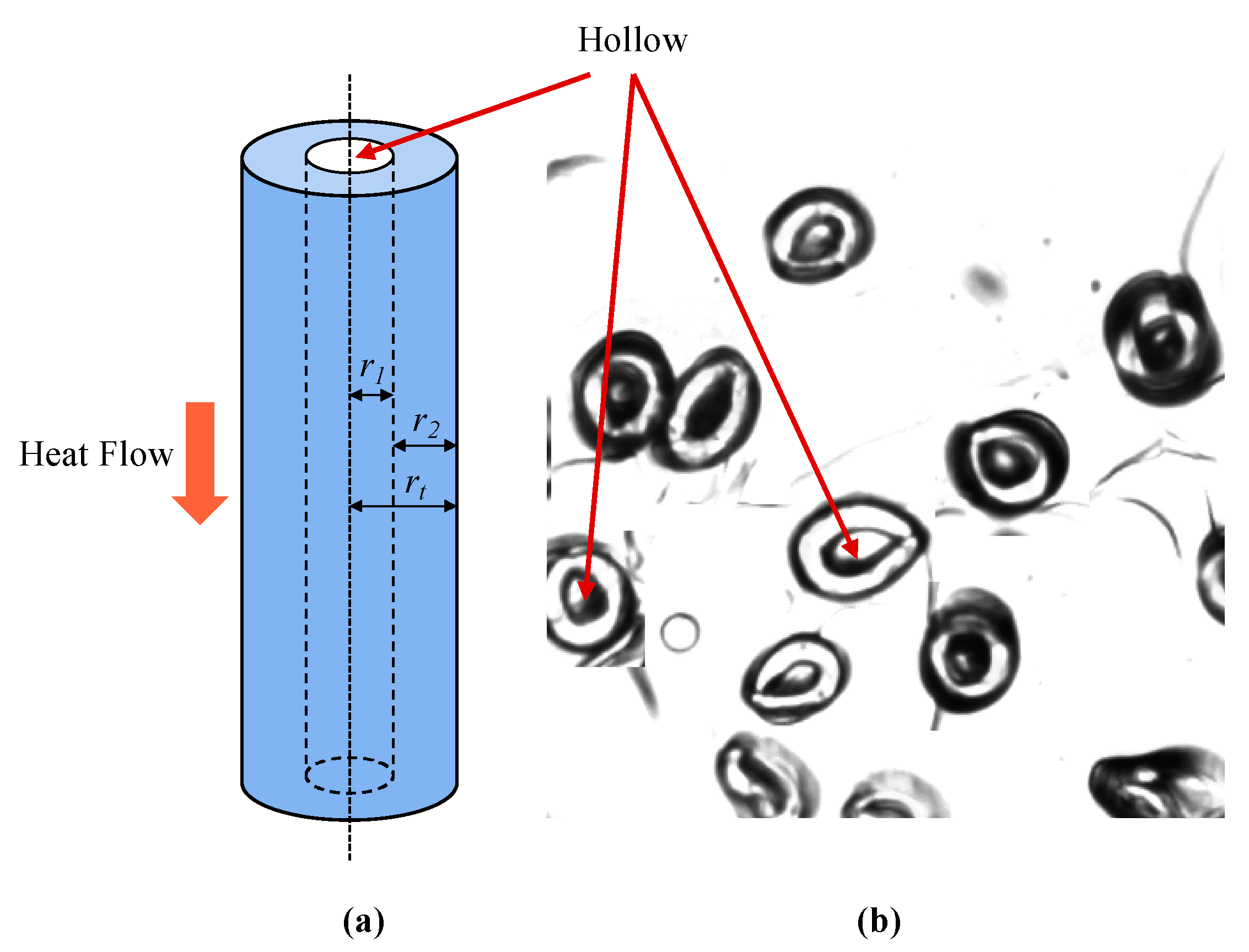
| kh−f | Thermal conductivity of hollow PET fiber (W m−1 K−1) |
| kb−f | Thermal conductivity of bi-component PET fiber (W m−1 K−1) |
| kalam | Measured thermal conductivity on an Alambeta device (W m−1 K−1) |
| kCust | Measured thermal conductivity on a custom-build device (W m−1 K−1) |
| kmeas | Measured thermal conductivity (W m−1 K−1) |
| kpred | Predicted thermal conductivity (W m−1 K−1) |
| l | Fiber length (m) |
| m | Empirical coefficient |
| R | Thermal resistance (W m−1 K) |
| va | Volume fraction of air |
| vf | Volume fraction of fiber |
| x | Fraction of fibers parallel to heat flow direction () |
| y | Fraction of fibers perpendicular to heat flow direction |
| z | Factor of fibers orientation to the heat flow direction |
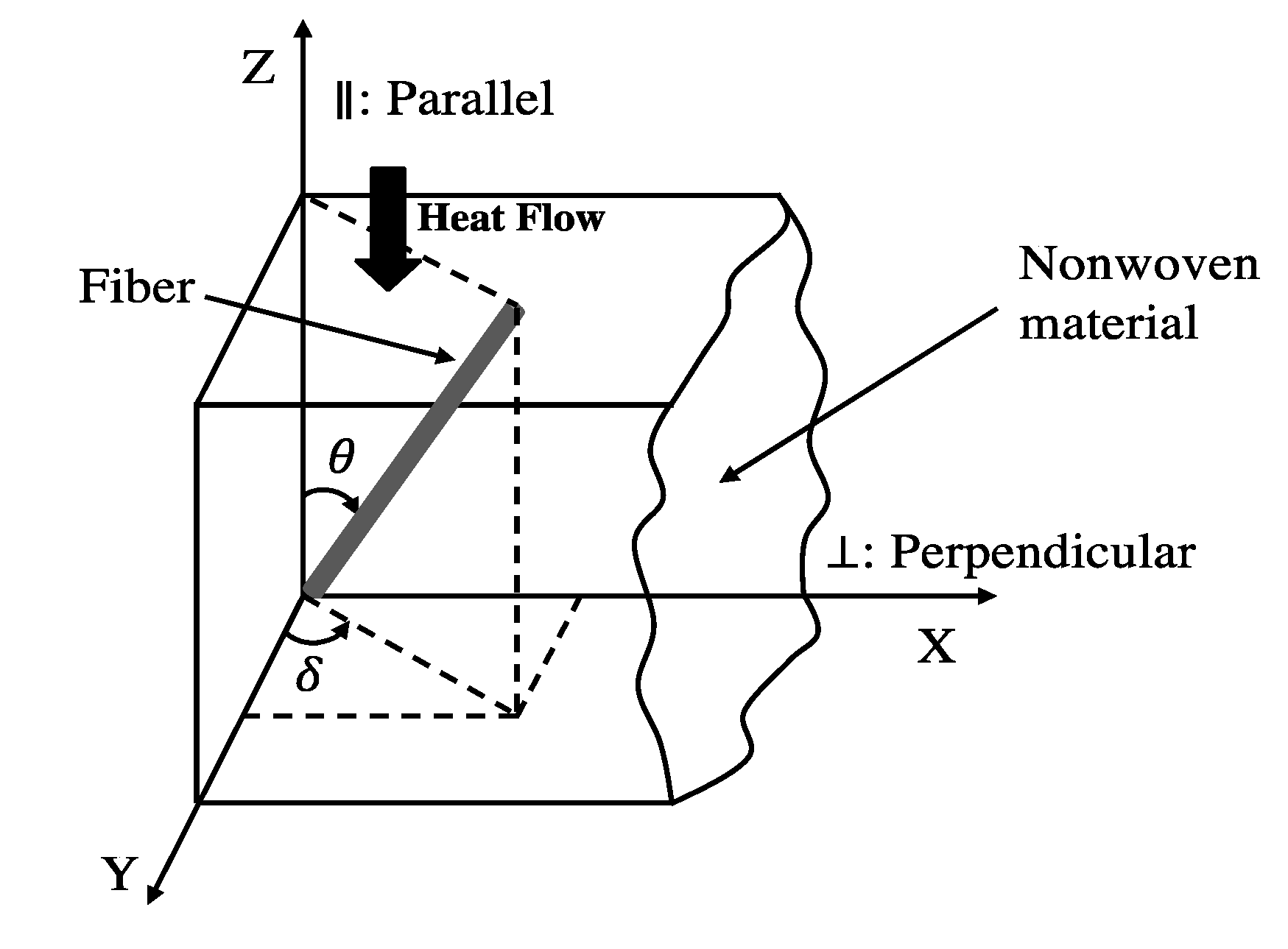
| δ | Fiber in-plane orientation angle (°) |
| θ | Fiber through-plane orientation angle (°) |
| ψ | Critical fiber orientation angle (°) |
| Δ | Relative difference |
References
- Patnaik, A.; Mvubu, M.; Muniyasamy, S.; Botha, A.; Anandjiwala, R.D. Thermal and sound insulation materials from waste wool and recycled polyester fibers and their biodegradation studies. Energy Build. 2015, 92, 161–169. [Google Scholar] [CrossRef]
- Yang, T.; Xiong, X.; Mishra, R.; Novák, J.; Militký, J. Acoustic evaluation of Struto nonwovens and their relationship with thermal properties. Text. Res. J. 2018, 88, 426–437. [Google Scholar] [CrossRef]
- Papadopoulos, A.M. State of the art in thermal insulation materials and aims for future developments. Energy Build. 2005, 37, 77–86. [Google Scholar] [CrossRef]
- Kymäläinen, H.R.; Sjöberg, A.M. Flax and hemp fibres as raw materials for thermal insulations. Build. Environ. 2008, 43, 1261–1269. [Google Scholar] [CrossRef]
- Tilioua, A.; Libessart, L.; Lassue, S. Characterization of the thermal properties of fibrous insulation materials made from recycled textile fibers for building applications: Theoretical and experimental analyses. Appl. Therm. Eng. 2018, 142, 56–67. [Google Scholar] [CrossRef]
- Cerkez, I.; Kocer, H.B.; Broughton, R.M. Airlaid nonwoven panels for use as structural thermal insulation. J. Text. Inst. 2018, 109, 17–23. [Google Scholar] [CrossRef]
- Xiong, X.; Yang, T.; Mishra, R.; Kanai, H.; Militky, J. Thermal and compression characteristics of aerogel-encapsulated textiles. J. Ind. Text. 2018, 47, 1998–2013. [Google Scholar] [CrossRef]
- Shabaridharan, M.; Das, A. Study on heat and moisture vapour transmission characteristics through multilayered fabric ensembles. Fibers Polym. 2012, 13, 522–528. [Google Scholar] [CrossRef]
- Jirsak, O.; Sadikoglu, T.G.; Ozipek, B.; Pan, N. Thermo-Insulating Properties of Perpendicular-Laid Versus Cross-Laid Lofty Nonwoven Fabrics. Text. Res. J. 2000, 70, 121–128. [Google Scholar] [CrossRef]
- Wang, M.; He, J.; Yu, J.; Pan, N. Lattice Boltzmann modeling of the effective thermal conductivity for fibrous materials. Int. J. Therm. Sci. 2007, 46, 848–855. [Google Scholar] [CrossRef]
- Křemenáková, D. Selected Properties of Functional Materials; Fakulta textilní, Technická univerzita v Liberci: Liberec, Czech Republic, 2013; pp. 294–300. [Google Scholar]
- Van Krevelen, D.W. Properties of Polymers; Elsevier: Amsterdam, The Netherlands, 1997; pp. 645–653. [Google Scholar]
- Carvajal, S.A.; Garboczi, E.J.; Zarr, R.R. Comparison of Models for Heat Transfer in High-Density Fibrous Insulation. J. Res. Natl. Inst. Stand. Technol. 2019, 124, 1–21. [Google Scholar] [CrossRef]
- Sun, Z.; Pan, N. Thermal conduction and moisture diffusion in fibrous materials. In Thermal and Moisture Transport in Fibrous Materials; Pan, N., Gibson, P., Eds.; Woodhead Publishing Ltd: Sawston, UK, 2006; p. 225. [Google Scholar]
- Stark, C.; Fricke, J. Improved heat-transfer models for fibrous insulations. Int. J. Heat Mass Transf. 1993, 36, 617–625. [Google Scholar] [CrossRef]
- Bhattacharyya, R.K. Heat-Transfer Model for Fibrous Insulations. In Thermal Insulation Performance, ASTM STP 718; MeElroy, D.L., Tye, R.P., Eds.; American Society for Testing and Materials: West Conshohocken, PA, USA, 1980; pp. 272–286. [Google Scholar]
- Arambakam, R.; Tafreshi, H.V.; Pourdeyhimi, B. Modeling performance of multi-component fibrous insulations against conductive and radiative heat transfer. Int. J. Heat Mass Transf. 2014, 71, 341–348. [Google Scholar] [CrossRef]
- Xiong, X.; Yang, T.; Mishra, R.; Huang, J.; Kotresh, T.M.; Militký, J. Heat Transfer through Thermal Insulation Materials Part I—Nonwoven Fabrics. In Recent Developments in Fibrous Material Science; Ops Publishing: Kenosha, WI, USA, 2015; ISBN 978-80-87269-45-9. [Google Scholar]
- Nouri, N. Radiative Conductivity Analysis of Low-Density Fibrous Materials. Master’s Thesis, University of Kentucky, Lexington, KY, USA, 2015. [Google Scholar]
- Lawson, D.I.; Mcguire, J.H. The Solution of Transient Heat-flow Problems by Analogous Electrical Networks. Proc. Inst. Mech. Eng. 1953, 167, 275–290. [Google Scholar] [CrossRef]
- Fricke, H.I.J. A Mathematical Treatment of the Electrical conductivity and Capacity of Disperse Systems. Phys. Rev. 1924, 24, 678–681. [Google Scholar] [CrossRef]
- Schuhmeister, J. Ber. K Akad Wien (Math-Naturw Klasse) 1877, 76, 283. [Google Scholar]
- Baxter, S. The Thermal Conductivity of Textiles. Proc. Phys. Soc. 1946, 58, 105–118. [Google Scholar] [CrossRef]
- Verschoor, J.D.; Greebler, P. Heat transfer by gas conduction and radiation in fibrous insulation. Trans. Am. Soc. Mech. Eng. 1952, 74, 961–968. [Google Scholar]
- Tavman, I.H. Effective thermal conductivity of polymer composites. Int. Comm. Heat Mass Transf. 1998, 25, 723–732. [Google Scholar] [CrossRef]
- Militký, J.; Křemenáková, D. A Simple Methods for Prediction of Textile Fabrics Thermal Conductivity. In Proceedings of the 5th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, Sun City, South Africa, 1–4 July 2007; p. PJ4. [Google Scholar]
- Bogaty, H.; Hollies, N.R.S.; Harris, M. Some Thermal Properties of Fabrics: Part I: The Effect of Fiber Arrangement. Text. Res. J. 1957, 27, 445–449. [Google Scholar] [CrossRef]
- Militký, J.; Křemenáková, D. Prediction of fabrics thermal conductivity. In Proceedings of the 5th International Textile, Clothing & Design Conference—Magic World of Textiles, Dubrovnik, Croatia, 3–6 October 2010; pp. 1–6. [Google Scholar]
- Mao, N.; Russell, S.J. The thermal insulation properties of spacer fabrics with a mechanically integrated wool fiber surface. Text. Res. J. 2007, 77, 914–922. [Google Scholar] [CrossRef]
- Arambakam, R.; Vahedi Tafreshi, H.; Pourdeyhimi, B. A simple simulation method for designing fibrous insulation materials. Mater. Des. 2013, 44, 99–106. [Google Scholar] [CrossRef]
- Bicerano, J. Prediction of Polymer Properties; CRC Press: London, UK, 2002. [Google Scholar]
- Yang, T.; Saati, F.; Horoshenkov, K.V.; Xiong, X.; Yang, K.; Mishra, R.; Marburg, S.; Militký, J. Study on the sound absorption behavior of multi-component polyester nonwovens: Experimental and numerical methods. Text. Res. J. 2019, 89, 3342–3361. [Google Scholar] [CrossRef]
- Kawabata, S. Measurement of Anisotropic Thermal Conductivity of Single Fiber. J. Text. Mach. Soc. Jpn. 1986, 39, T184–T186. [Google Scholar] [CrossRef]
- Morton, W.E.; Hearle, J.W.S. Physical Properties of Textile Fibers; The Textile Institute: Manchester, UK, 1986; pp. 174–175. [Google Scholar]
- Daryabeigi, K.; Cunnington, G.R.; Knutson, J.R. Heat transfer modeling for rigid high-temperature fibrous insulation. J. Thermophys. Heat Transf. 2013, 27, 414–421. [Google Scholar] [CrossRef]
- Hes, L.; de Araujo, M.; Djulay, V.V. Effect of Mutual Bonding of Textile Layers on Thermal Insulation and Thermal Contact Properties of Fabric Assemblies. Text. Res. J. 1996, 66, 245–250. [Google Scholar] [CrossRef]
- Hes, L.; Dolezal, I. New method and equipment for measuring thermal properties of textiles. Sen’i Kikai Gakkaishi J. Text. Mach. Soc. Jpn. 1989, 42, 124–128. [Google Scholar] [CrossRef]
- Kaneko, H.; Sakuma, A. Evaluation of heat transfer kinetics on layers of air-rich soft materials in their natural state. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Pittsburgh, PA, USA, 9–15 November 2018; pp. 1–6. [Google Scholar]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]




| No. | Thermal Conductivity | Reference |
|---|---|---|
| 1 | Schuhmeister [22] | |
| 2 | Baxter [23] | |
| 3 | Verschoor and Greebler [24] | |
| 4 | Tavman [25] |
| No. | Thermal Conductivity | Fiber Orientation to the Direction of Heat Flow | Reference |
|---|---|---|---|
| 5 | Parallel | Bogaty et al. [27] | |
| 6 | Perpendicular | Bogaty et al. [27] | |
| 7 | Bhattacharyya [16] | ||
| 8 | Random | Bogaty et al. [27] | |
| 9 | Bhattacharyya [16] |
| Samples Code | Thickness (mm) | Bulk Density (kg/m3) | Porosity (%) | Mean Fiber Orientation Angle (°) |
|---|---|---|---|---|
| TK1 | 26.93 | 18.85 | 98.350 | 10.09 |
| TK2 | 23.08 | 21.99 | 98.074 | 32.46 |
| TK3 | 21.18 | 23.96 | 97.901 | 39.26 |
| TK4 | 17.23 | 29.46 | 97.420 | 50.96 |
| TK5 | 12.7 | 39.96 | 96.500 | 62.36 |
| TK6 | 11.28 | 44.99 | 96.060 | 65.65 |
| TK7 | 8.34 | 60.85 | 94.671 | 72.25 |
| Reference | |
|---|---|
| 0.140 | Baxter [23] |
| 0.272 | Militký et.al. [26] |
| 0.260 | Stark et.al. [15] |
| Referred Values [23,26] (W m−1 K−1) | Staple and Bi-Component Fibers (W m−1 K−1) | Hollow Fiber (W m−1 K−1) | Fiber Unity (W m−1 K−1) | Bogaty Models [27] |
|---|---|---|---|---|
| 0.140 | 0.140 | 0.1187 | 0.1324 | Parallel |
| 0.272 | 0.272 | 0.2261 | 0.2556 | Parallel |
| TK1 | TK2 | TK3 | TK4 | TK5 | TK6 | TK7 | |
|---|---|---|---|---|---|---|---|
| 0.9835 | 0.9807 | 0.9790 | 0.9742 | 0.9650 | 0.9606 | 0.9467 | |
| 0.0165 | 0.0193 | 0.0210 | 0.0258 | 0.0350 | 0.0394 | 0.0533 | |
| 0.8489 | 0.6112 | 0.5503 | 0.4478 | 0.3439 | 0.3116 | 0.2425 | |
| 0.1511 | 0.3888 | 0.4497 | 0.5522 | 0.6561 | 0.6884 | 0.7575 |
| Models | Predicted Thermal Conductivity of Nonwovens (W m−1 K−1) | |||||||
|---|---|---|---|---|---|---|---|---|
| TK1 | TK2 | TK3 | TK4 | TK5 | TK6 | TK7 | ||
| :0.140 | Schuhmeister | 0.0272 | 0.0274 | 0.0274 | 0.0277 | 0.0281 | 0.0284 | 0.0291 |
| Bogaty | 0.0279 | 0.0278 | 0.0278 | 0.0279 | 0.0282 | 0.0283 | 0.0287 | |
| Bhattacharyya | 0.0278 | 0.0280 | 0.0282 | 0.0286 | 0.0294 | 0.0298 | 0.0310 | |
| Stark & Fricke BM | 0.0676 | 0.0671 | 0.0667 | 0.1059 | 0.0992 | 0.0964 | 0.0889 | |
| Stark & Fricke | 0.0658 | 0.0610 | 0.0592 | 0.0769 | 0.0646 | 0.0604 | 0.0507 | |
| :0.272 | Schuhmeister | 0.0279 | 0.0282 | 0.0283 | 0.0288 | 0.0296 | 0.0301 | 0.0314 |
| Bogaty | 0.0334 | 0.0390 | 0.0405 | 0.0432 | 0.0462 | 0.0473 | 0.0497 | |
| Bhattacharyya | 0.0285 | 0.0289 | 0.0291 | 0.0297 | 0.0309 | 0.0315 | 0.0334 | |
| Stark & Fricke BM | 0.0906 | 0.0898 | 0.0893 | 0.1727 | 0.1561 | 0.1495 | 0.1331 | |
| Stark & Fricke | 0.0868 | 0.0777 | 0.0745 | 0.1019 | 0.0799 | 0.0730 | 0.0583 | |
| Methods | Measured Thermal Conductivity of Nonwoven Samples (W m−1 K−1) | ||||||
|---|---|---|---|---|---|---|---|
| TK1 | TK2 | TK3 | TK4 | TK5 | TK6 | TK7 | |
| Alambeta | 0.05726 | 0.0523 | 0.0501 | 0.04742 | 0.04194 | 0.04074 | 0.03912 |
| SD | 0.00293 | 0.00204 | 0.00135 | 0.00139 | 0.00013 | 0.00092 | 0.00053 |
| Custom-build device | 0.05049 | 0.04834 | 0.04885 | 0.03987 | 0.04686 | 0.04256 | 0.04636 |
| SD | 0.00512 | 0.00398 | 0.00623 | 0.00426 | 0.00284 | 0.00326 | 0.00294 |
| TK1 | TK2 | TK3 | TK4 | TK5 | TK6 | TK7 | |
|---|---|---|---|---|---|---|---|
| Fiber orientation angle (°) | 10.09 | 32.49 | 39.26 | 50.96 | 62.34 | 62.34 | 72.25 |
| Original Z | 0.83 | 0.83 | 0.83 | 1 | 1 | 1 | 1 |
| Optimized Z | 0.7530 | 0.7059 | 0.6814 | 0.6473 | 0.5523 | 0.5228 | 0.4613 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Xiong, X.; Petrů, M.; Tan, X.; Kaneko, H.; Militký, J.; Sakuma, A. Theoretical and Experimental Studies on Thermal Properties of Polyester Nonwoven Fibrous Material. Materials 2020, 13, 2882. https://doi.org/10.3390/ma13122882
Yang T, Xiong X, Petrů M, Tan X, Kaneko H, Militký J, Sakuma A. Theoretical and Experimental Studies on Thermal Properties of Polyester Nonwoven Fibrous Material. Materials. 2020; 13(12):2882. https://doi.org/10.3390/ma13122882
Chicago/Turabian StyleYang, Tao, Xiaoman Xiong, Michal Petrů, Xiaodong Tan, Hiroki Kaneko, Jiří Militký, and Atsushi Sakuma. 2020. "Theoretical and Experimental Studies on Thermal Properties of Polyester Nonwoven Fibrous Material" Materials 13, no. 12: 2882. https://doi.org/10.3390/ma13122882
APA StyleYang, T., Xiong, X., Petrů, M., Tan, X., Kaneko, H., Militký, J., & Sakuma, A. (2020). Theoretical and Experimental Studies on Thermal Properties of Polyester Nonwoven Fibrous Material. Materials, 13(12), 2882. https://doi.org/10.3390/ma13122882








