Improvements to the Sink Strength Theory Used in Multi-Scale Rate Equation Simulations of Defects in Solids
Abstract
1. Introduction
2. Results
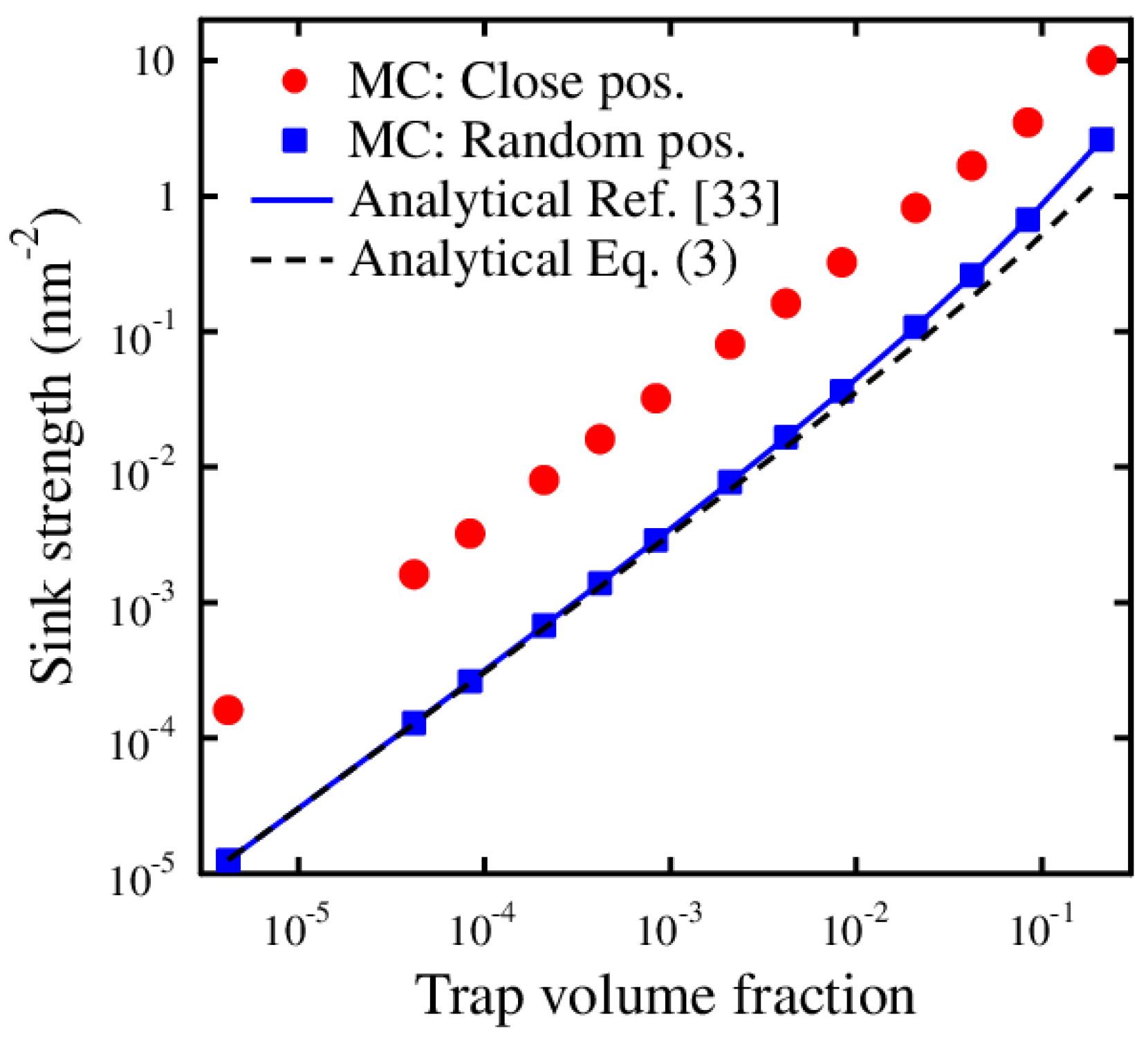
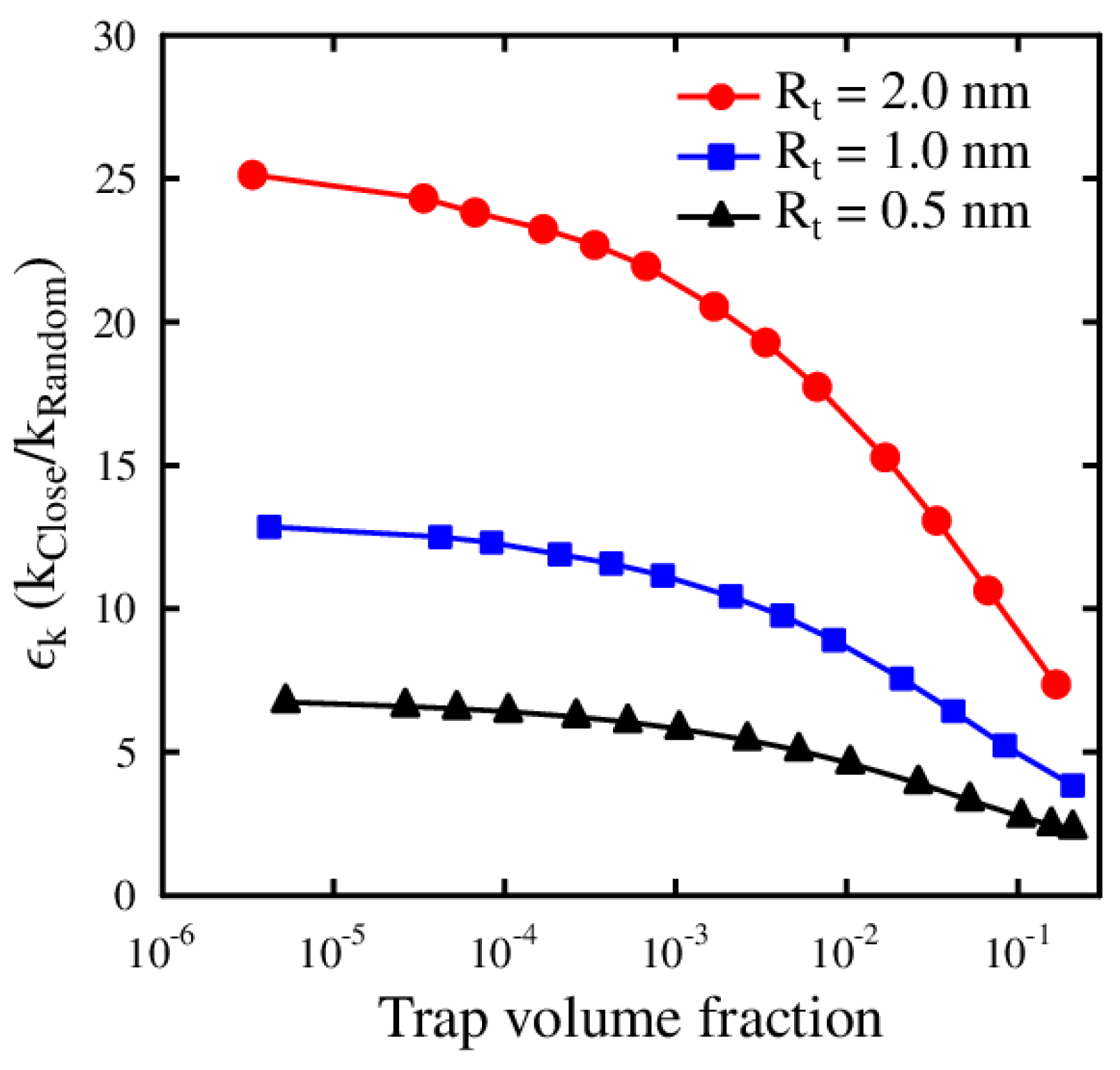
2.1. Theory
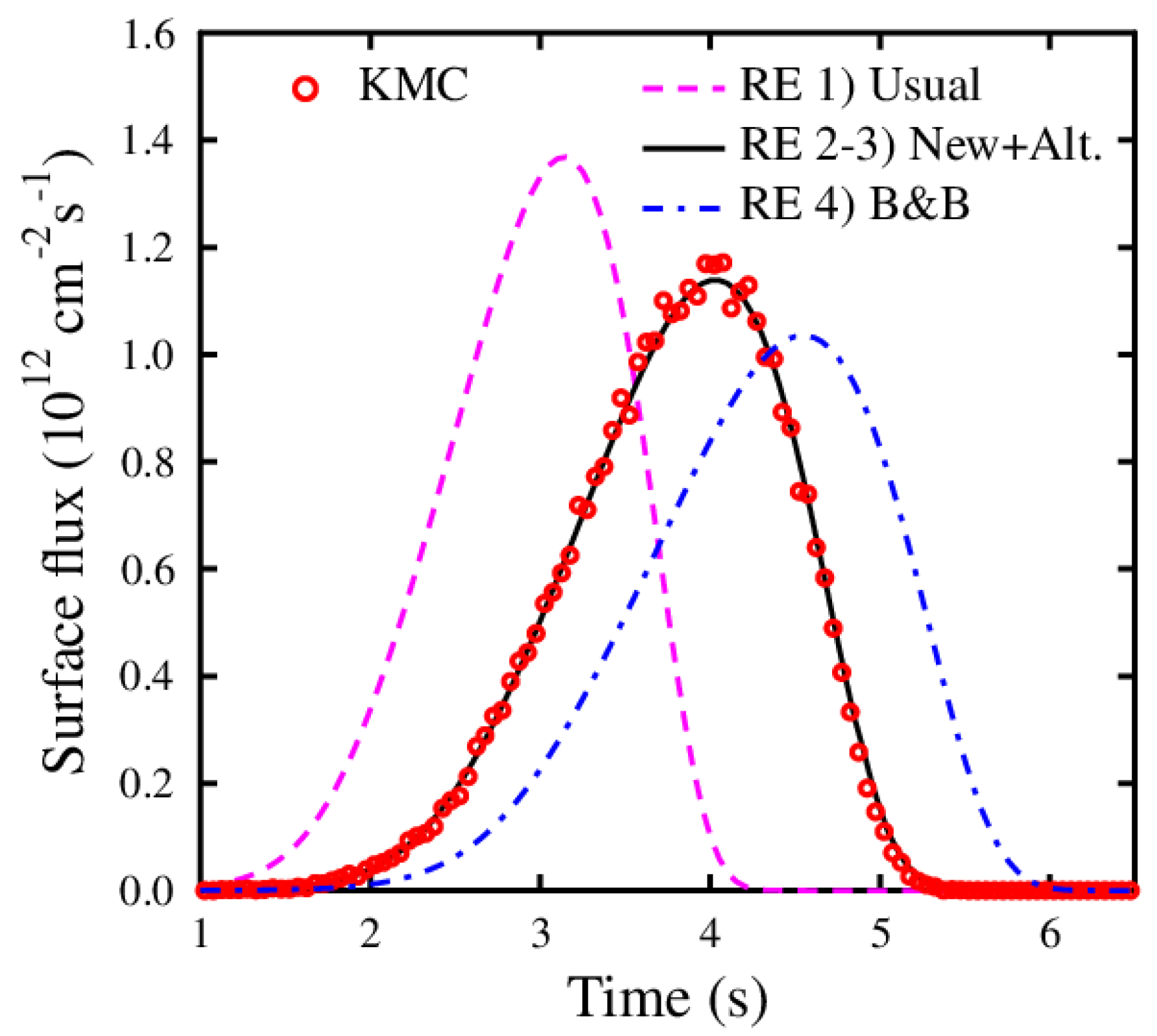
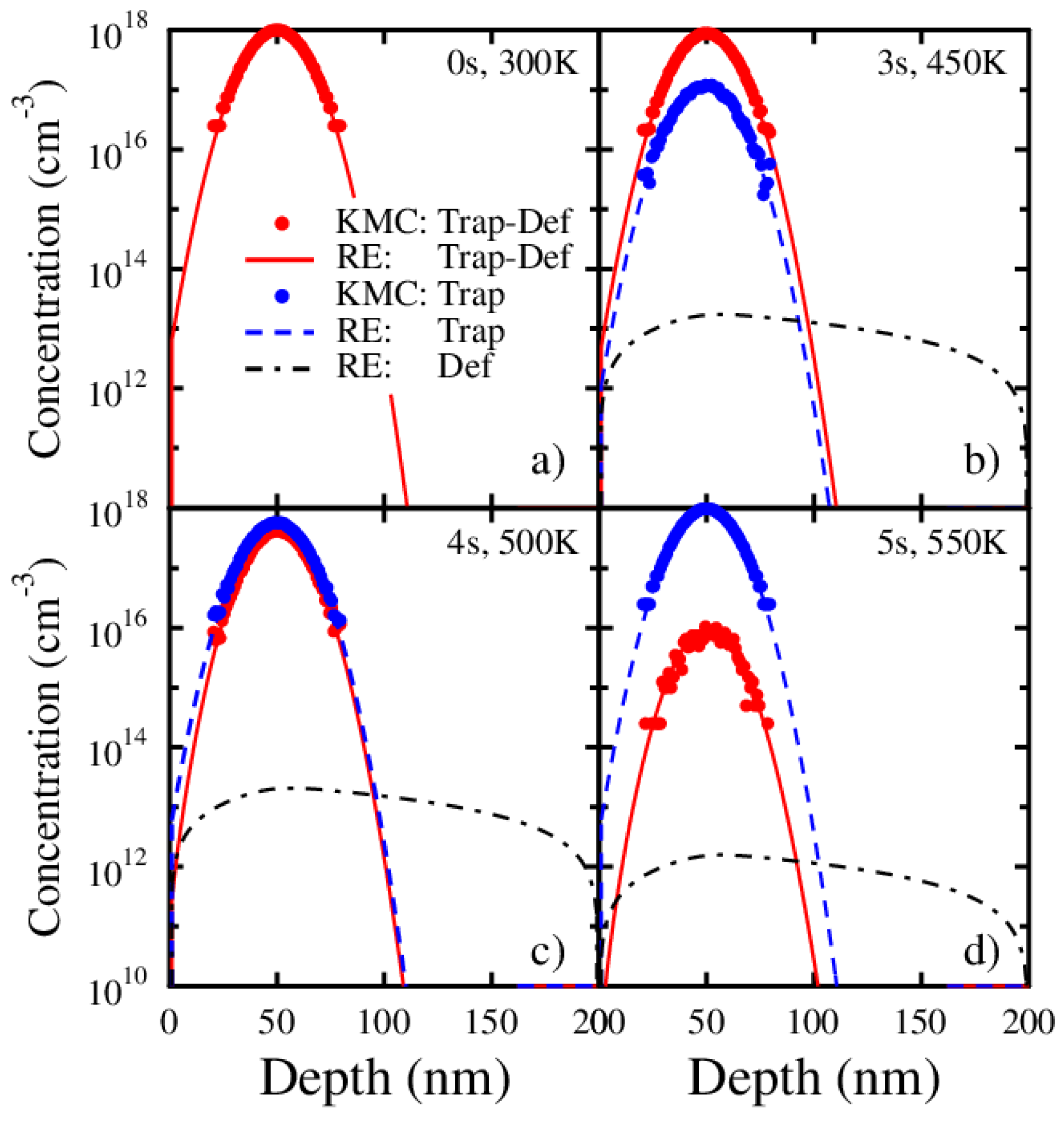
2.2. Rate Equation Simulations
3. Discussion
4. Materials and Methods
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Derlet, P.M.; Nguyen-Manh, D.; Dudarev, S.L. Multiscale modeling of crowdion and vacancy defects in body-centered-cubic transition metals. Phys. Rev. B 2007, 76, 054107. [Google Scholar] [CrossRef]
- McNabb, A.; Foster, P.K. A new analysis of the diffusion of hydrogen in iron and ferritic steels. Trans. Metall. Soc. AIME 1963, 227, 618. [Google Scholar]
- Wiedersich, H. On the theory of void formation during irradiation. Radiat. Eff. 1972, 12, 111–125. [Google Scholar] [CrossRef]
- Freeman, G. Kinetics of Nonhomogeneous Processes, LK Mansur: Mechanisms and Kinetics of Radiation Effects in Metals and Alloys; John Wiley and Sons: New York, NY, USA, 1987. [Google Scholar]
- Ahlgren, T.; Heinola, K.; Vörtler, K.; Keinonen, J. Simulation of irradiation induced deuterium trapping in tungsten. J. Nucl. Mater. 2012, 427, 152–161. [Google Scholar] [CrossRef]
- Baskes, M.I.; Wilson, W.D. Kinetics of helium self-trapping in metals. Phys. Rev. B 1983, 27, 2210–2217. [Google Scholar] [CrossRef]
- Myers, S.M.; Nordlander, P.; Besenbacher, F.; Nørskov, J.K. Theoretical examination of the trapping of ion-implanted hydrogen in metals. Phys. Rev. B 1986, 33, 854–863. [Google Scholar] [CrossRef]
- Katoh, Y.; Muroga, T.; Kohyama, A.; Stoller, R.E.; Namba, C. Rate theory modeling of defect evolution under cascade damage conditions: The influence of vacancy-type cascade remnants on defect evolution. J. Nucl. Mater. 1996, 233–237, 1022–1028. [Google Scholar] [CrossRef]
- Rottler, J.; Srolovitz, D.J.; Car, R. Point defect dynamics in bcc metals. Phys. Rev. B 2005, 71, 064109. [Google Scholar] [CrossRef]
- Ortiz, C.J.; Caturla, M.J. Simulation of defect evolution in irradiated materials: Role of intracascade clustering and correlated recombination. Phys. Rev. B 2007, 75, 184101. [Google Scholar] [CrossRef]
- Wilson, W.D.; Baskes, M.I.; Bisson, C.L. Atomistics of helium bubble formation in a face-centered-cubic metal. Phys. Rev. B 1976, 13, 2470–2478. [Google Scholar] [CrossRef]
- Wang, Z.; Sang, C.; Liu, S.; Chang, M.; Sun, J.; Wang, D. Modeling of fuel retention in the pre-damaged tungsten with MeV W ions after exposure to D plasma. Nucl. Mater. Energy 2017, 13, 1–7. [Google Scholar] [CrossRef]
- Coenen, J.; Berger, M.; Demkowicz, M.; Matveev, D.; Manhard, A.; Neu, R.; Riesch, J.; Unterberg, B.; Wirtz, M.; Linsmeier, C. Plasma-wall interaction of advanced materials. Nucl. Mater. Energy 2017, 12, 307–312. [Google Scholar] [CrossRef]
- Wert, C.; Zener, C. Interference of Growing Spherical Precipitate Particles. J. Appl. Phys. 1949, 21, 5. [Google Scholar]
- Brailsford, A.; Bullough, R. The rate theory of swelling due to void growth in irradiated metals. J. Nucl. Mater. 1972, 44, 121–135. [Google Scholar] [CrossRef]
- Barnard, L.; Tucker, J.; Choudhury, S.; Allen, T.; Morgan, D. Modeling radiation induced segregation in Ni–Cr model alloys from first principles. J. Nucl. Mater. 2012, 425, 8–15. [Google Scholar] [CrossRef]
- Heinola, K.; Ahlgren, T.; Brezinsek, S.; Vuoriheimo, T.; Wiesen, S. Modelling of the effect of ELMs on fuel retention at the bulk W divertor of JET. Nucl. Mater. Energy 2019, 19, 397–402. [Google Scholar] [CrossRef]
- Schmid, K.; von Toussaint, U.; Schwarz-Selinger, T. Transport of hydrogen in metals with occupancy dependent trap energies. J. Appl. Phys. 2014, 116, 134901. [Google Scholar] [CrossRef]
- Hodille, E.A.; Ferro, Y.; Fernandez, N.; Becquart, C.S.; Angot, T.; Layet, J.M.; Bisson, R.; Grisolia, C. Study of hydrogen isotopes behavior in tungsten by a multi trapping macroscopic rate equation model. Phys. Scr. 2016, 2016, 014011. [Google Scholar] [CrossRef]
- Markelj, S.; Založnik, A.; Schwarz-Selinger, T.; Ogorodnikova, O.; Vavpetič, P.; Pelicon, P.; Čadež, I. In situ NRA study of hydrogen isotope exchange in self-ion damaged tungsten exposed to neutral atoms. J. Nucl. Mater. 2016, 469, 133–144. [Google Scholar] [CrossRef]
- Swaminathan, N.; Morgan, D.; Szlufarska, I. Ab initio based rate theory model of radiation induced amorphization in β-SiC. J. Nucl. Mater. 2011, 414, 431–439. [Google Scholar] [CrossRef]
- Pisarev, A.A.; Voskresensky, I.D.; Porfirev, S.I. Computer modeling of ion implanted deuterium release from tungsten. J. Nucl. Mater. 2003, 313–316, 604. [Google Scholar] [CrossRef]
- Poon, M.; Haasz, A.; Davis, J. Modelling deuterium release during thermal desorption of D+-irradiated tungsten. J. Nucl. Mater. 2008, 374, 390–402. [Google Scholar] [CrossRef]
- Gasparyan, Y.; Ogorodnikova, O.; Efimov, V.; Mednikov, A.; Marenkov, E.; Pisarev, A.; Markelj, S.; Čadež, I. Thermal desorption from self-damaged tungsten exposed to deuterium atoms. J. Nucl. Mater. 2015, 463, 1013–1016. [Google Scholar] [CrossRef]
- Grigorev, P.; Matveev, D.; Bakaeva, A.; Terentyev, D.; Zhurkin, E.E.; Oost, G.V.; Noterdaeme, J.M. Modelling deuterium release from tungsten after high flux high temperature deuterium plasma exposure. J. Nucl. Mater. 2016, 481, 181–189. [Google Scholar] [CrossRef]
- Arrhenius, S. Über die Reaktionsgeschwindigkeit bei der Inversion von Rohrzucker durch Säuren. Z. Phys. Chem. (Leipzig) 1889, 4, 226. [Google Scholar]
- Wigner, E. On the penetration of potential energy barriers in chemical reactions. Z. Phys. Chem. Abt. B 1932, 19, 203. [Google Scholar]
- Eyring, H. The activated complex in chemical reactions. J. Chem. Phys. 1935, 3, 107. [Google Scholar] [CrossRef]
- Brailsford, A.D.; Bullough, R. Theory of sink strengths. Philos. Trans. R. Soc. Lond. 1981, 302, 87. [Google Scholar]
- Rouchette, H.; Thuinet, L.; Legris, A.; Ambard, A.; Domain, C. Quantitative phase field model for dislocation sink strength calculations. Comput. Mater. Sci. 2014, 88, 50–60. [Google Scholar] [CrossRef]
- Malerba, L.; Becquart, C.S.; Domain, C. Object kinetic Monte Carlo study of sink strengths. J. Nucl. Mater. 2007, 360, 159. [Google Scholar] [CrossRef]
- Jansson, V.; Malerba, L.; Backer, A.D.; Becquart, C.S.; Domain, C. Sink strength calculations of dislocations and loops using OKMC. J. Nucl. Mater. 2013, 442, 218–226. [Google Scholar] [CrossRef]
- Ahlgren, T.; Bukonte, L. Sink strength simulations using the Monte Carlo method: Applied to spherical traps. J. Nucl. Mater. 2017, 496, 66. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahlgren, T.; Heinola, K. Improvements to the Sink Strength Theory Used in Multi-Scale Rate Equation Simulations of Defects in Solids. Materials 2020, 13, 2621. https://doi.org/10.3390/ma13112621
Ahlgren T, Heinola K. Improvements to the Sink Strength Theory Used in Multi-Scale Rate Equation Simulations of Defects in Solids. Materials. 2020; 13(11):2621. https://doi.org/10.3390/ma13112621
Chicago/Turabian StyleAhlgren, Tommy, and Kalle Heinola. 2020. "Improvements to the Sink Strength Theory Used in Multi-Scale Rate Equation Simulations of Defects in Solids" Materials 13, no. 11: 2621. https://doi.org/10.3390/ma13112621
APA StyleAhlgren, T., & Heinola, K. (2020). Improvements to the Sink Strength Theory Used in Multi-Scale Rate Equation Simulations of Defects in Solids. Materials, 13(11), 2621. https://doi.org/10.3390/ma13112621






