Asymmetric Hysteresis Modeling Approach Featuring “Inertial System + Shape Function” for Magnetostrictive Actuators
Abstract
1. Introduction
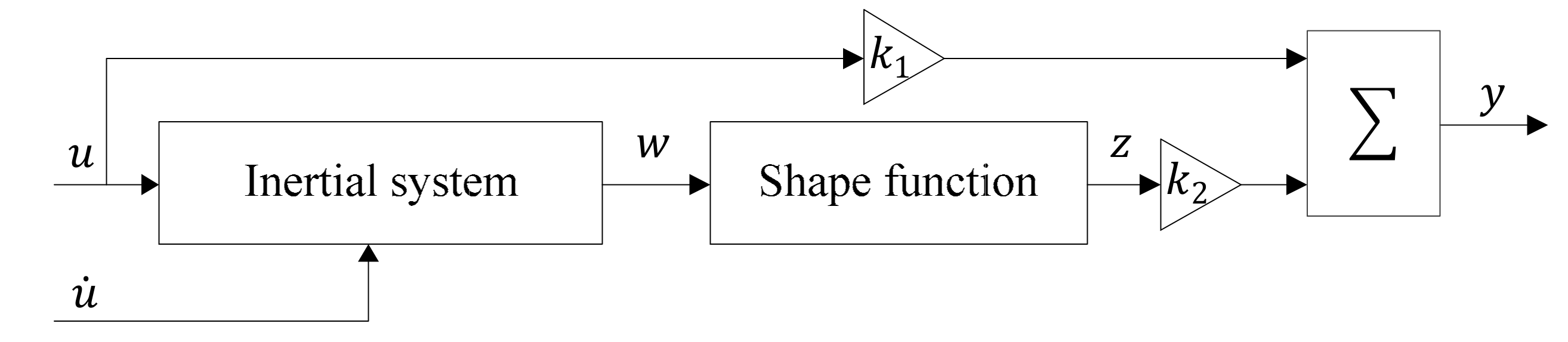
2. ISSF-Duhem Model
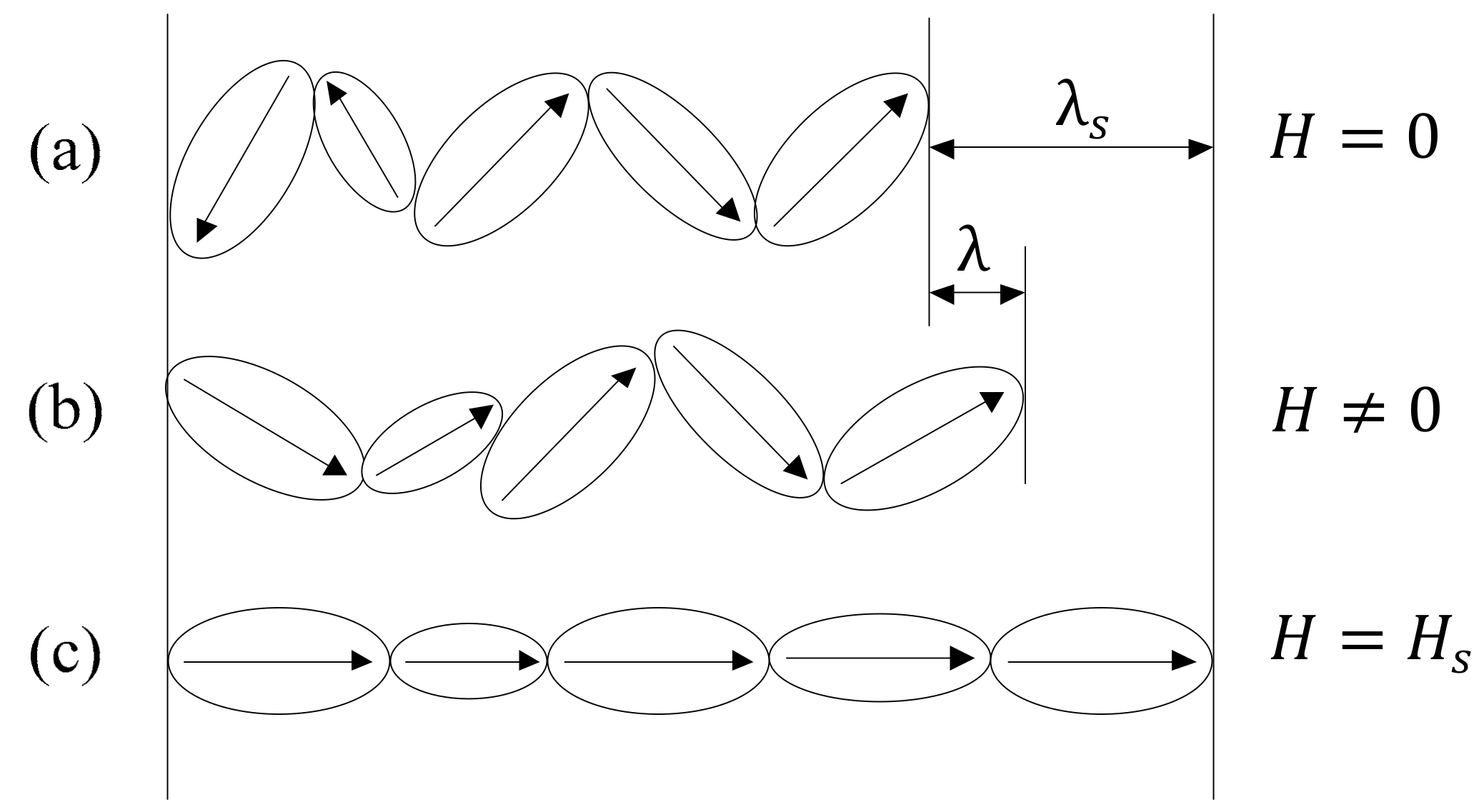
2.1. Hysteresis in an Inertial System
2.2. Construction of Inertial System
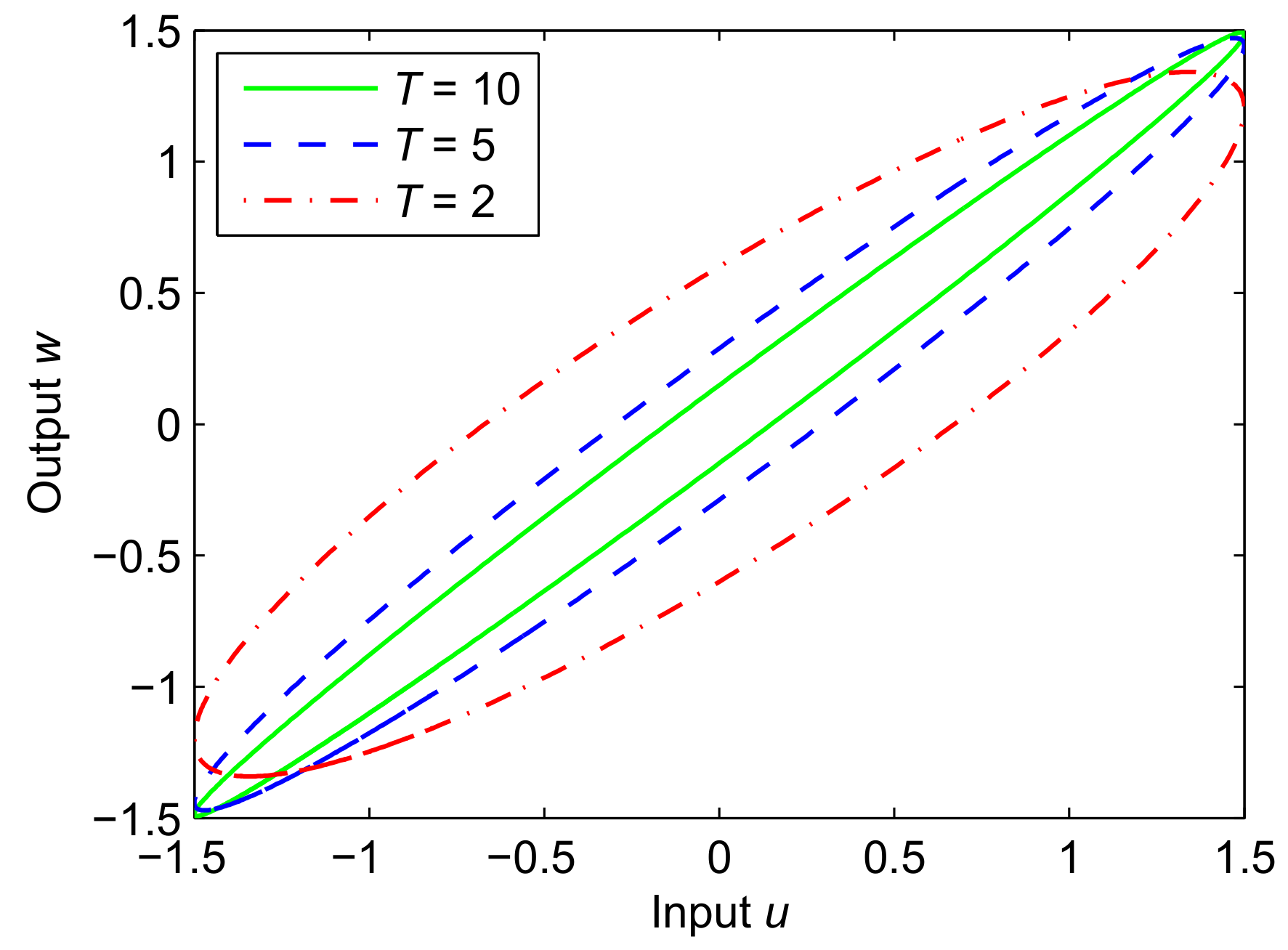
2.3. Construction of Shape Function
2.3.1. Grompertz Function-Based Shape Function
2.3.2. Modified Hyperbolic Tangent Function-Based Shape Function
2.3.3. One-Sided Dead-Zone Operator-Based Shape Function
3. Experimental Validation
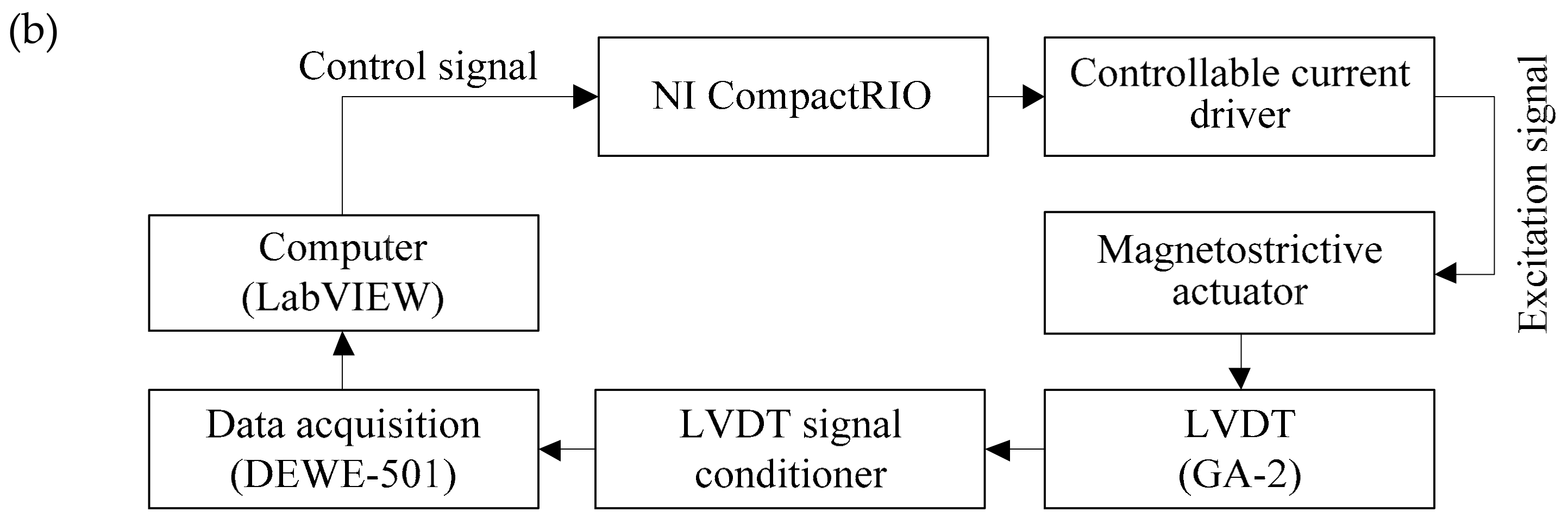
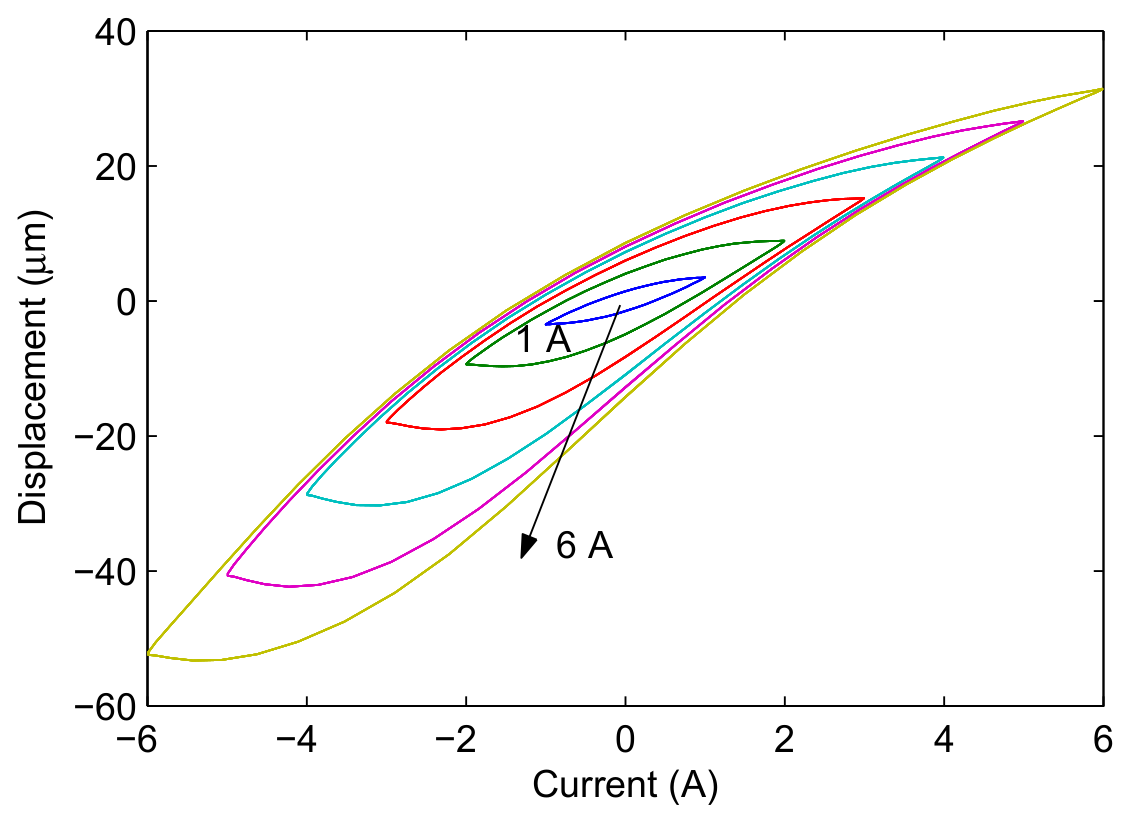
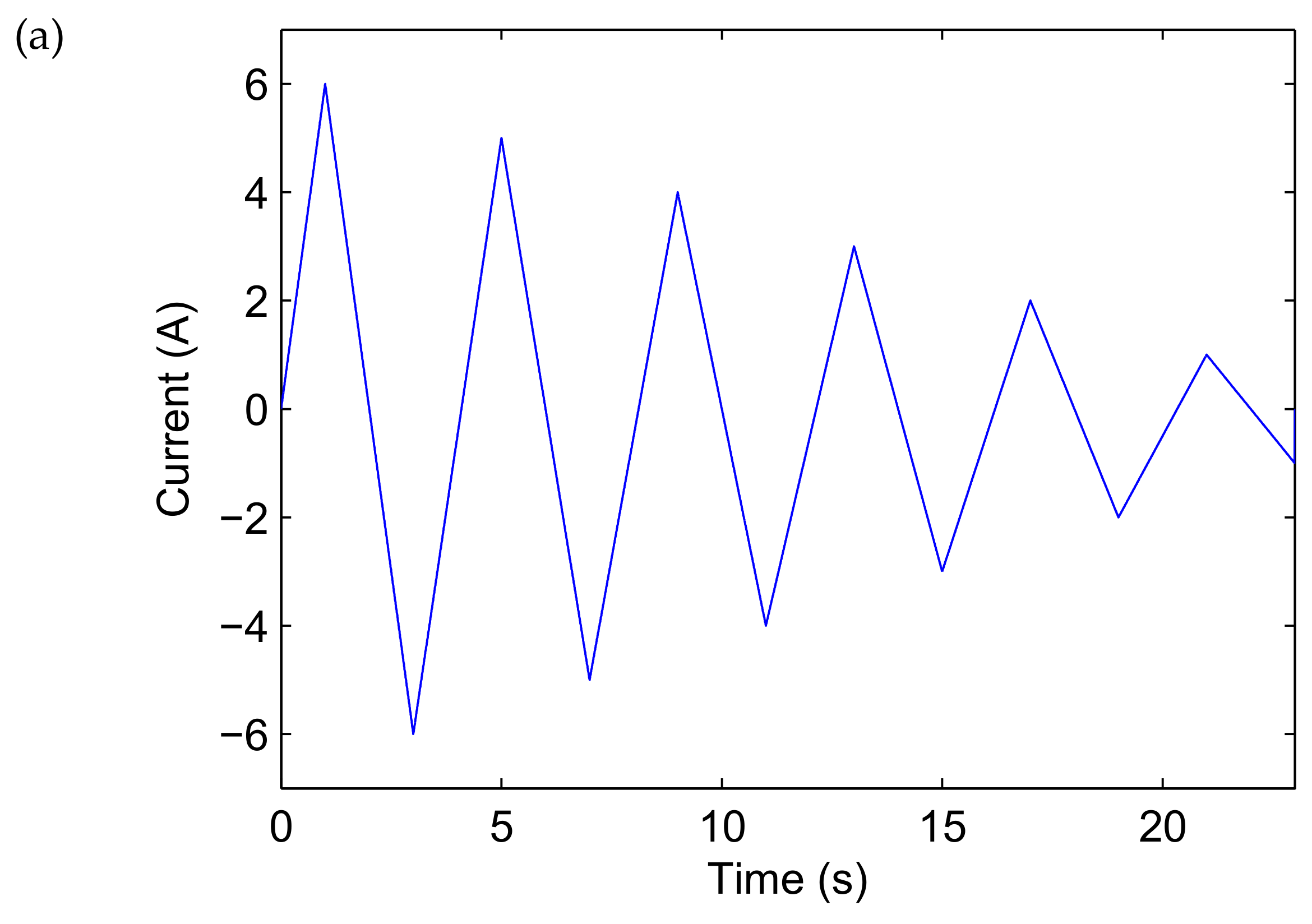
3.1. Experimental Setup and Hysteresis Loop Test
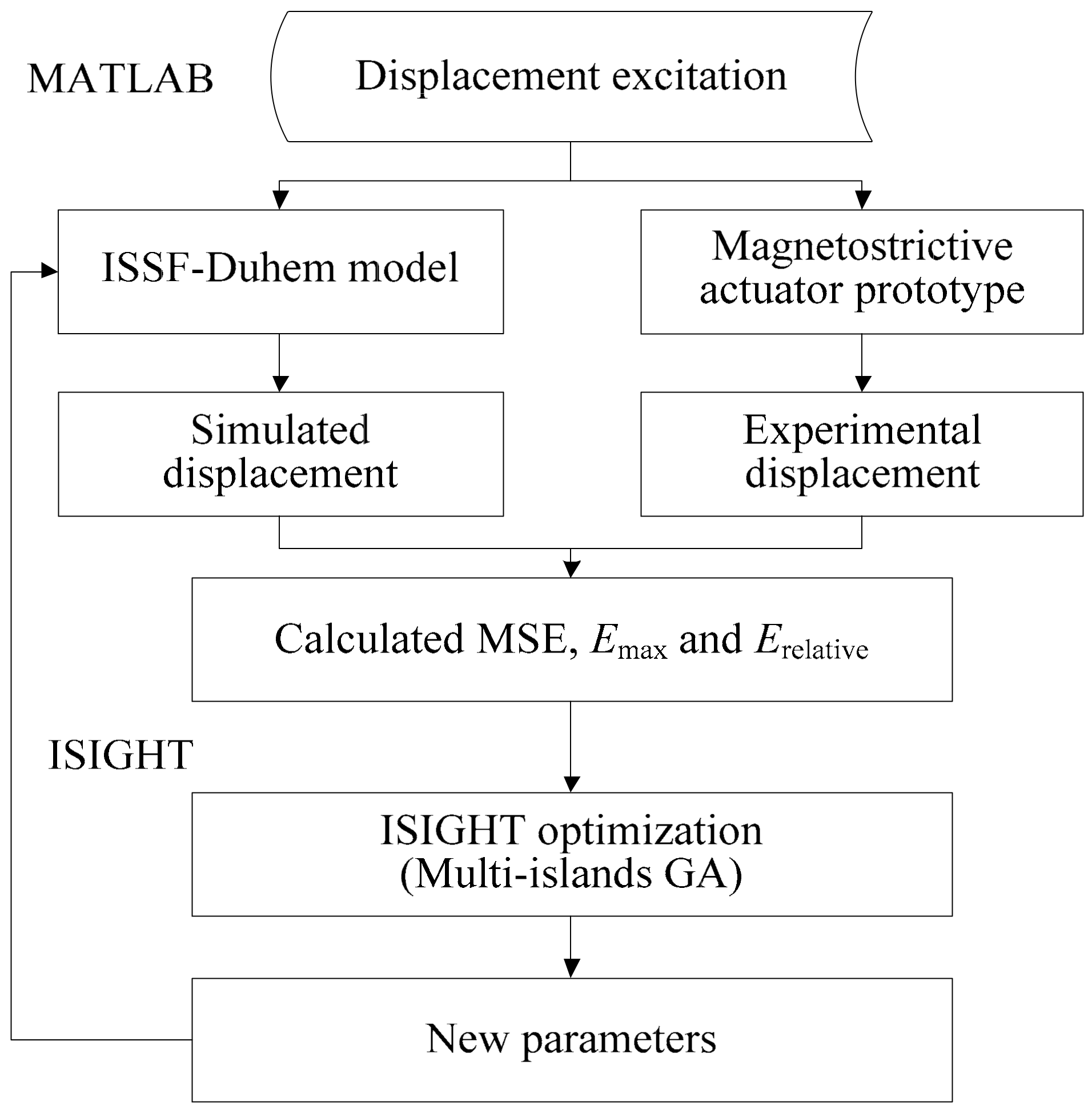
3.2. Parameter Identification
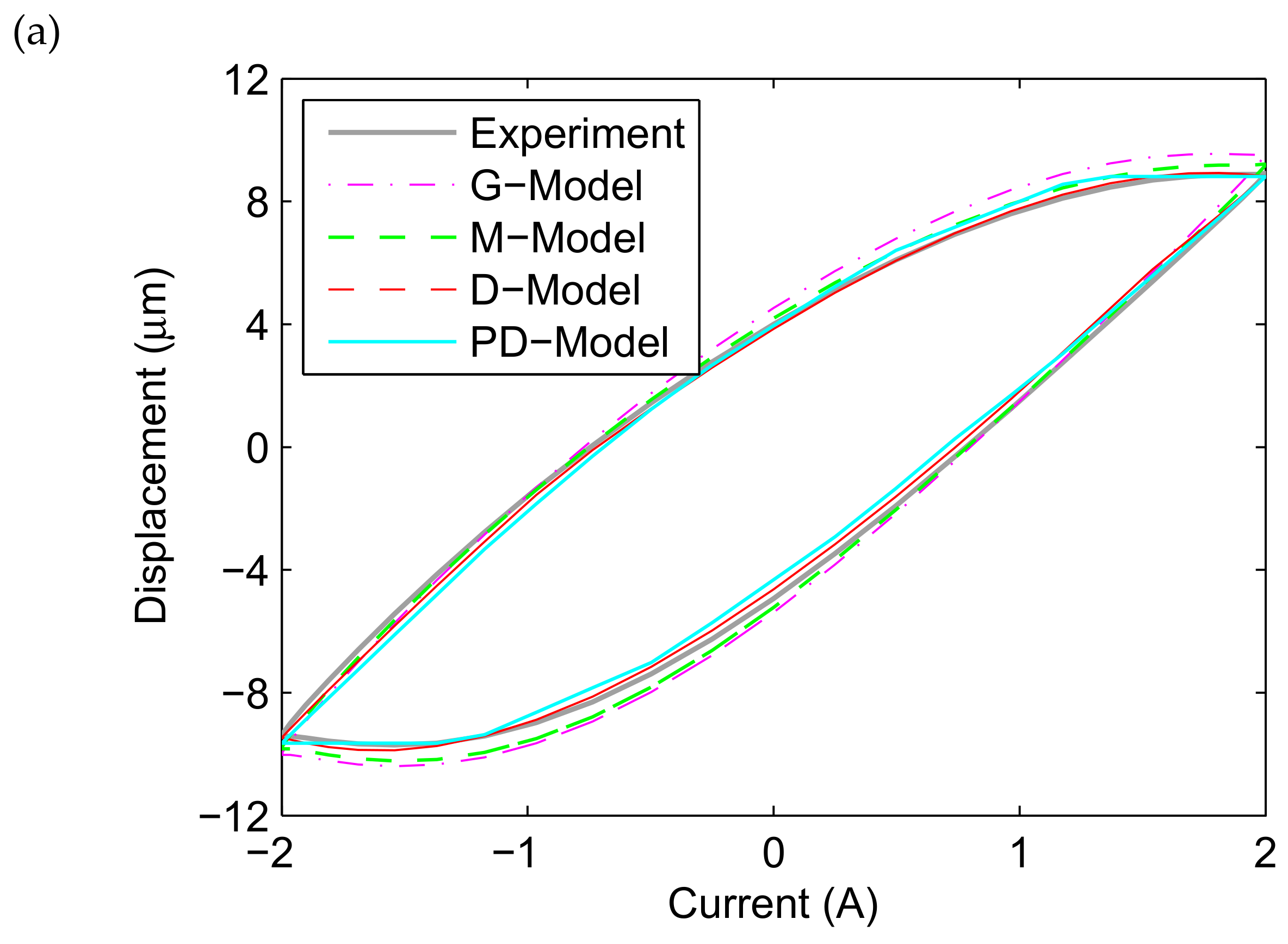
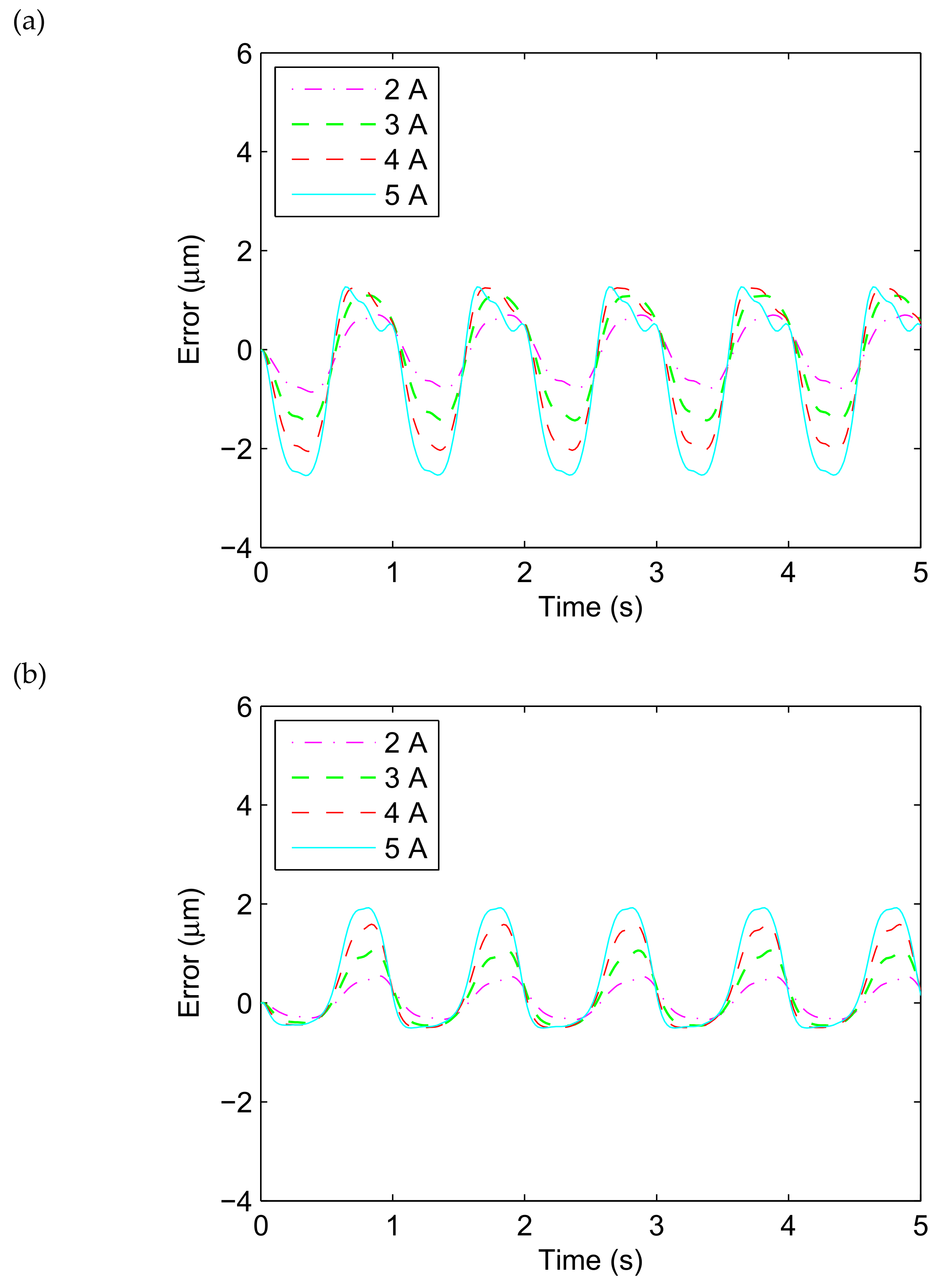
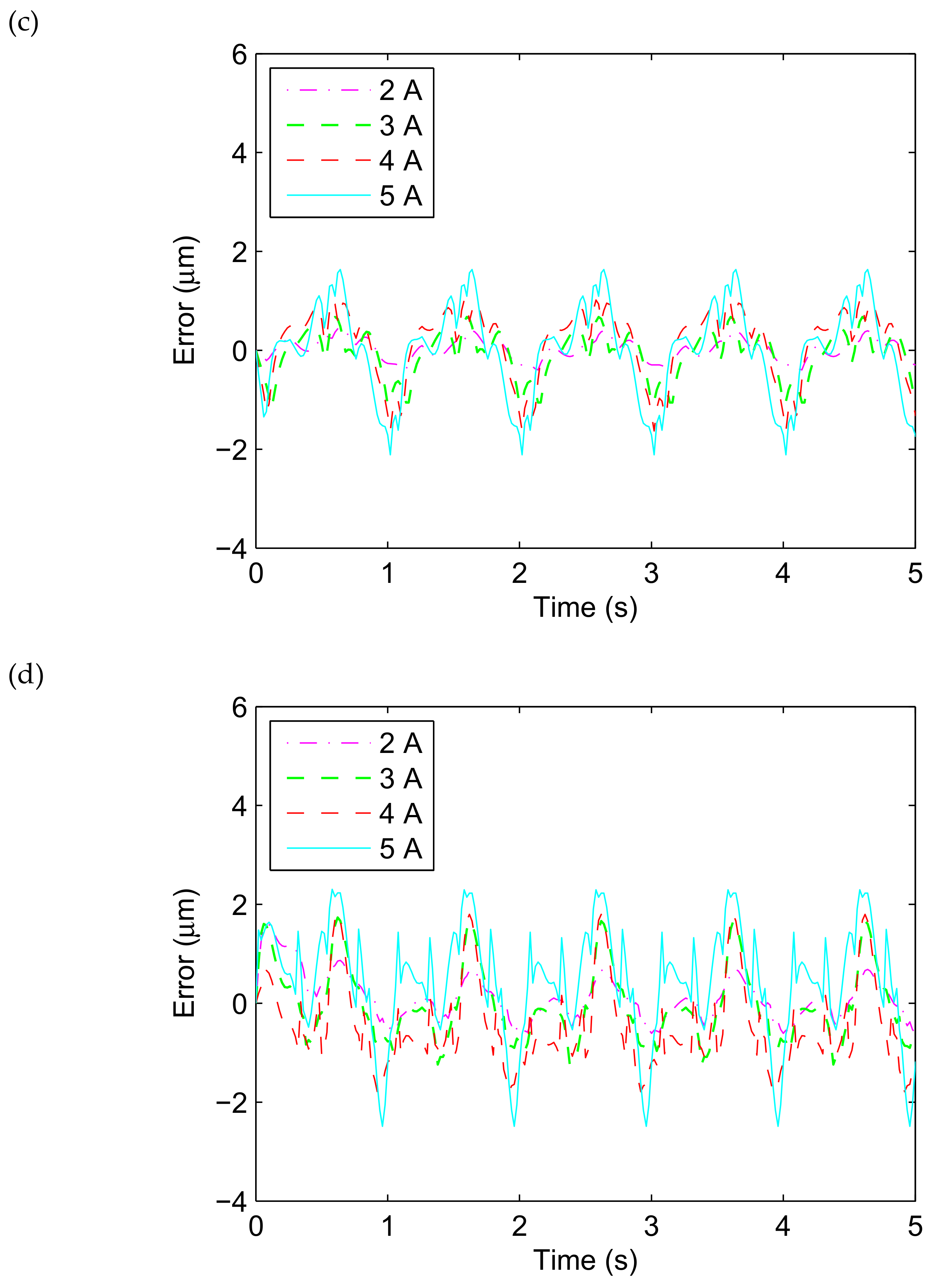
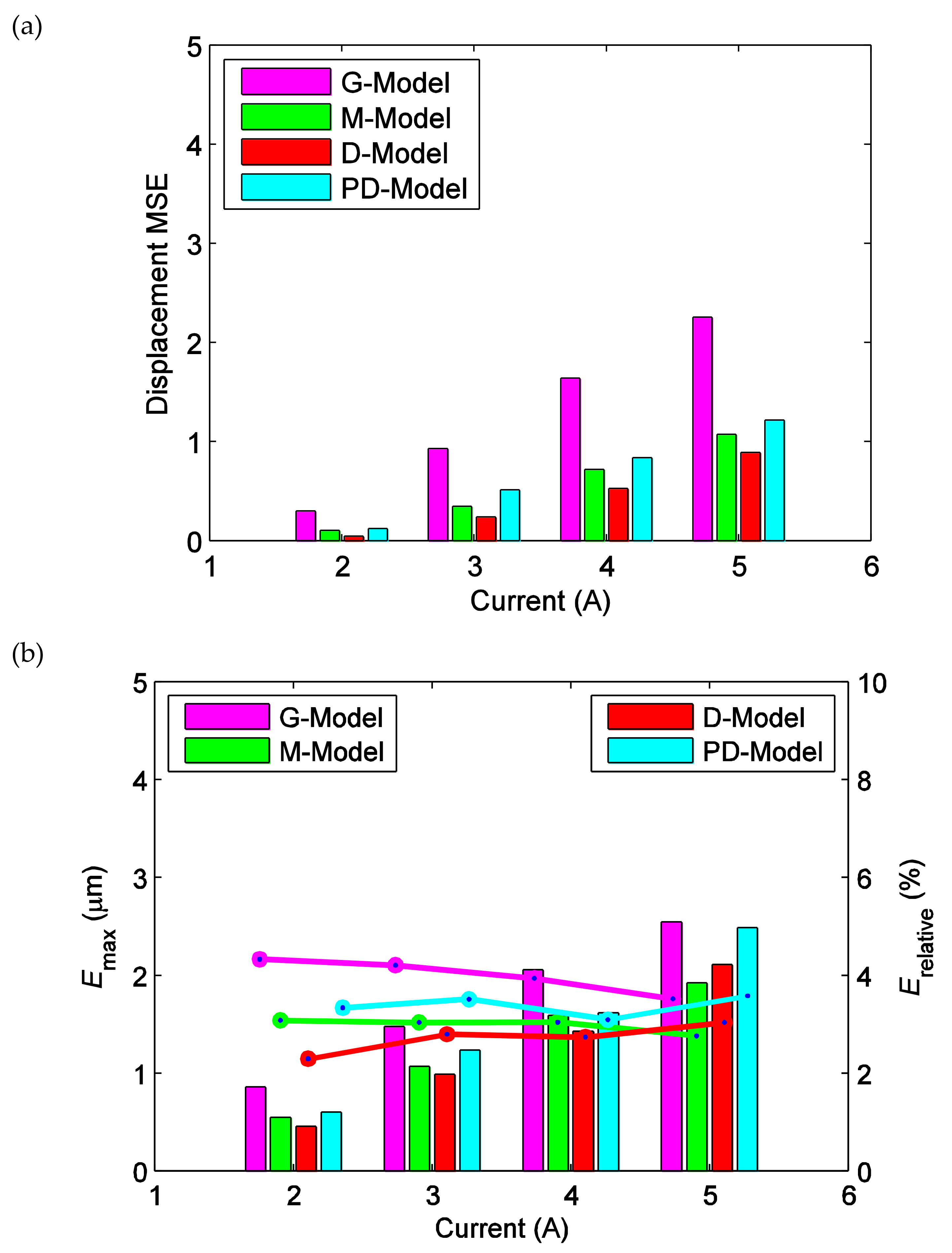
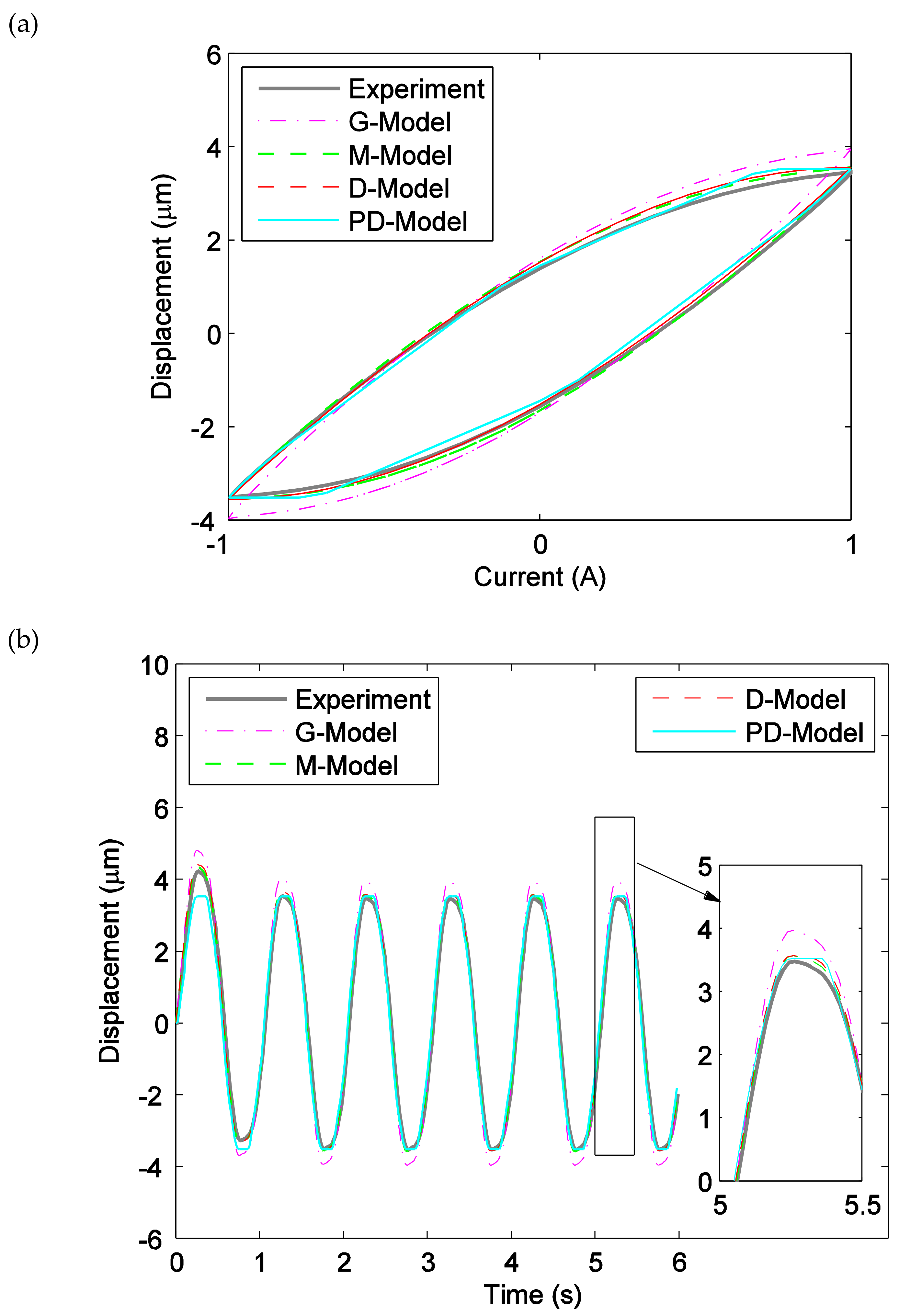
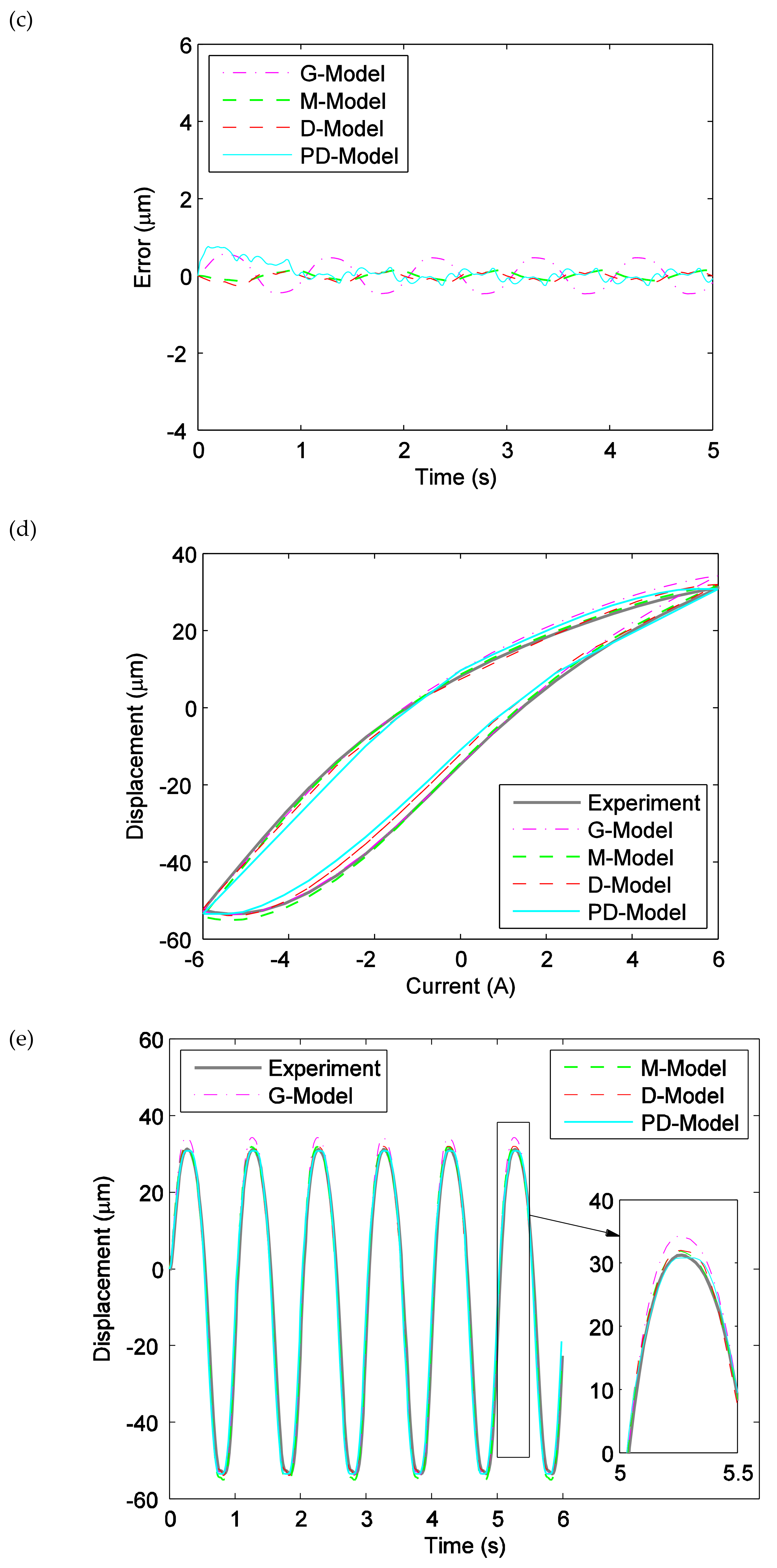
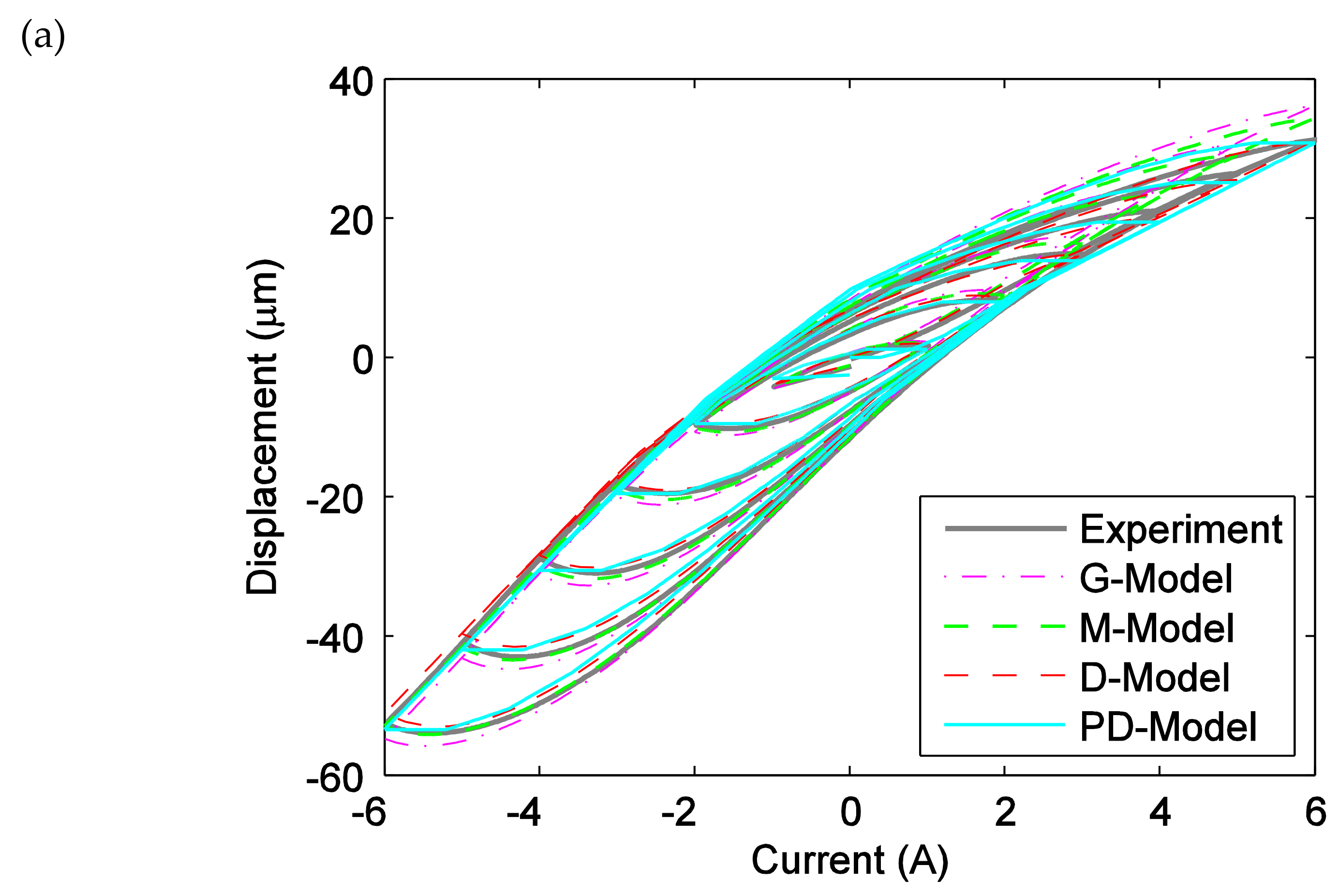
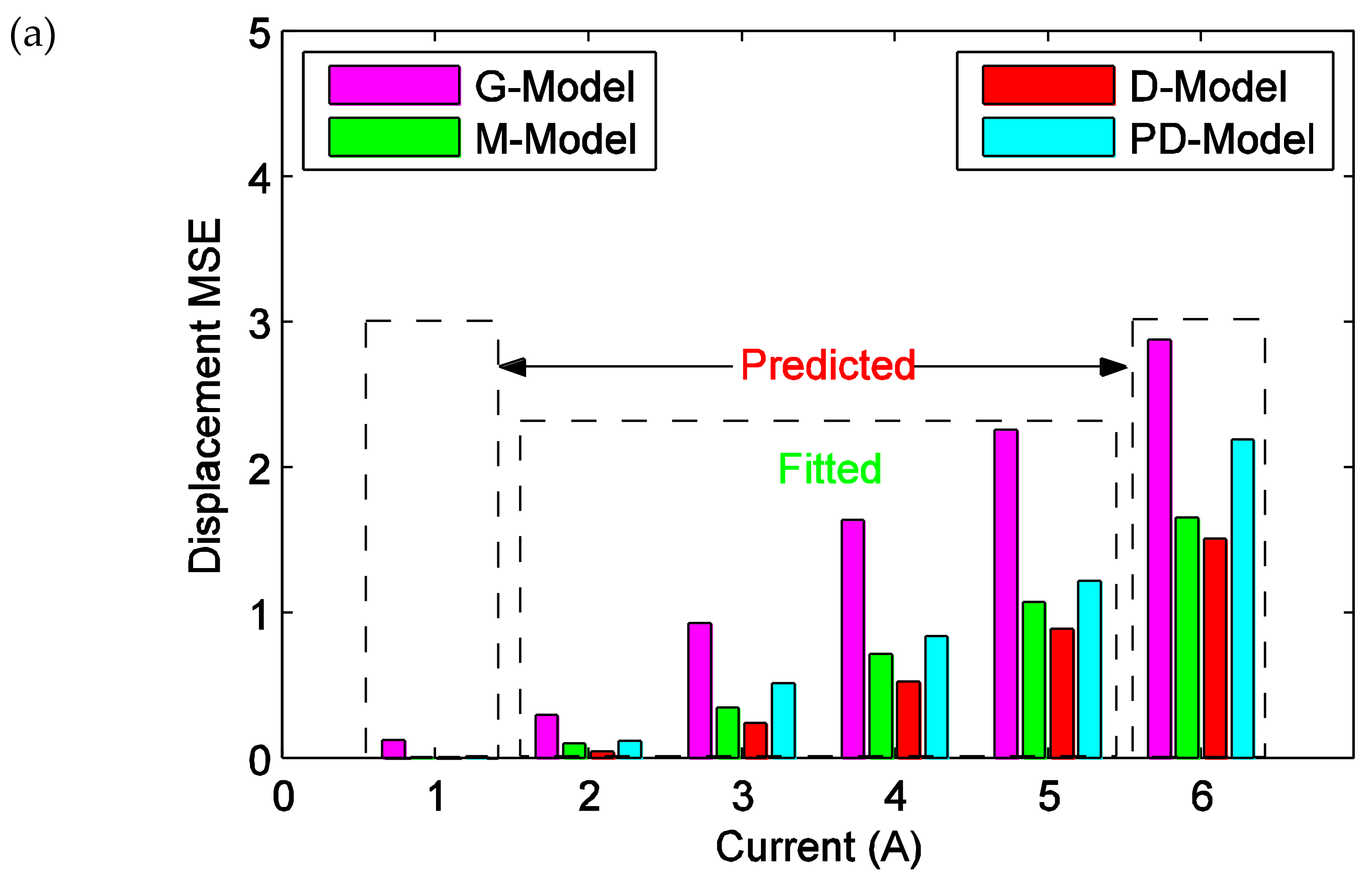
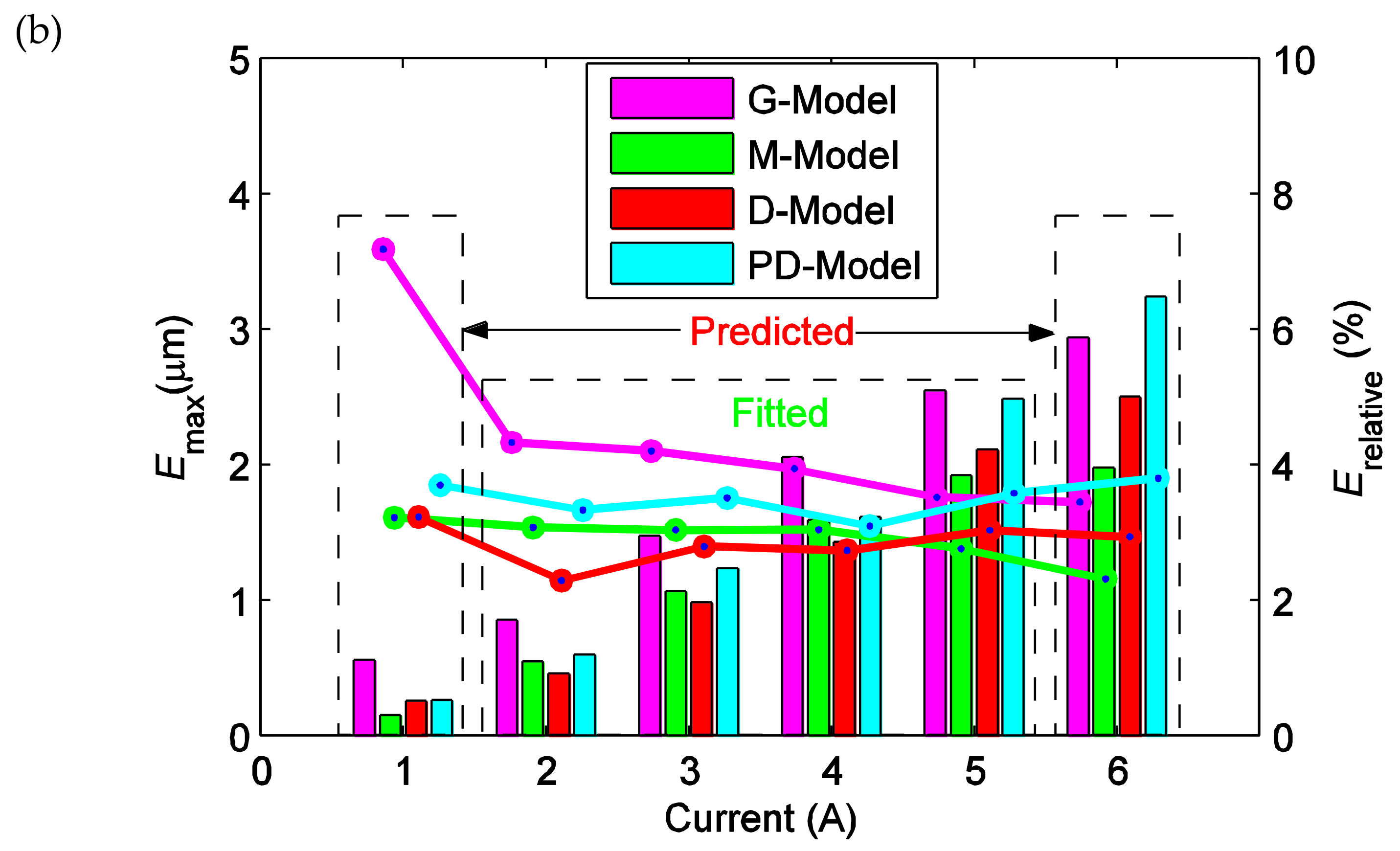
3.3. Prediction Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Claeyssen, F.; Lhermet, N.; Le Letty, R.; Bouchilloux, P. Actuators, transducers and motors based on giant magnetostrictive. J. Alloy. Compd. 1997, 258, 61–73. [Google Scholar] [CrossRef]
- Yi, S.; Yang, B.; Meng, G. Microvibration isolation by adaptive feedforward control with asymmetric hysteresis compensation. Mech. Syst. Signal Process. 2019, 114, 644–657. [Google Scholar] [CrossRef]
- Calkins, F.T.; Smith, R.C.; Flatau, A.B. Energy-based hysteresis model for magnetostrictive transducers. IEEE Trans. Magn. 2000, 36, 429–439. [Google Scholar] [CrossRef]
- Hassani, V.; Tjahjowidodo, T. Structural response investigation of a triangular-based piezoelectric drive mechanism to hysteresis effect of the piezoelectric actuator. Mech. Syst. Signal Process. 2013, 36, 210–223. [Google Scholar] [CrossRef]
- Minorowicz, B.; Leonetti, G.; Stefanski, F.; Binetti, G.; Naso, D. Design, modelling and control of a micro-positioning actuator based on magnetic shape memory alloys. Smart Mater. Struct. 2016, 25, 075005. [Google Scholar] [CrossRef]
- Zakerzadeh, M.R.; Sayyaadi, H. Precise position control of shape memory alloy actuator using inverse hysteresis model and model reference adaptive control system. Mechatronics 2013, 23, 1150–1162. [Google Scholar] [CrossRef]
- Zhou, M.; He, S.; Hu, B.; Zhang, Q. Modified KP model for hysteresis of magnetic shape memory alloy actuator. IETE Tech. Rev. 2015, 32, 29–36. [Google Scholar] [CrossRef]
- Zhu, W.; Yang, F.; Rui, X. Robust independent modal space control of a coupled nano-positioning piezo-stage. Mech. Syst. Signal Process. 2018, 106, 466–478. [Google Scholar] [CrossRef]
- Olabi, A.G.; Grunwald, A. Design and application of magnetostrictive materials. Mater. Des. 2008, 29, 469–483. [Google Scholar] [CrossRef]
- Tan, X.; Baras, J.S. Modeling and control of hysteresis in magnetostrictive actuators. Automatica 2004, 40, 1469–1480. [Google Scholar] [CrossRef]
- Jiles, D.C.; Atherton, D.L. Theory of ferromagnetic hysteresis. J. Magn. Magn. Mater. 1986, 61, 48–60. [Google Scholar] [CrossRef]
- Jiles, D.C. Frequency dependence of hysteresis curves in conducting magnetic materials. J. Appl. Phys. 1994, 76, 5849–5855. [Google Scholar] [CrossRef]
- Dapino, M.J.; Smith, R.C.; Faidley, L.E.; Flatau, A.B. A coupled structural-magnetic strain and stress model for magnetostrictive transducers. J. Intell. Mater. Syst. Struct. 2000, 11, 135–152. [Google Scholar] [CrossRef]
- Baghel, A.P.; Chwastek, K.; Kulkarni, S.V. Modeling of minor hysteresis loops in rolling and transverse directions of grain-oriented laminations. IET Electr. Power Appl. 2015, 9, 344–348. [Google Scholar] [CrossRef]
- Jiles, D.C. A self consistent generalized model for the calculation of minor loop excursions in the theory of hysteresis. IEEE Trans. Magn. 1992, 28, 2602–2604. [Google Scholar] [CrossRef]
- Valadkhan, S.; Morris, K.; Shum, A. A new load-dependent hysteresis model for magnetostrictive materials. Smart Mater. Struct. 2010, 19, 125003. [Google Scholar] [CrossRef]
- Zhu, Y.; Yang, X.; Wereley, N.M. Research on hysteresis loop considering the prestress effect and electrical input dynamics for a giant magnetostrictive actuator. Smart Mater. Struct. 2016, 25, 085030. [Google Scholar] [CrossRef]
- Li, J.W.; Xu, M.Q. Modified Jiles-Atherton-Sablik model for asymmetry in magnetomechanical effect under tensile and compressive stress. J. Appl. Phys. 2011, 110, 063918. [Google Scholar] [CrossRef]
- Iyer, R.V.; Tan, X.; Krishnaprasad, P.S. Approximate inversion of the Preisach hysteresis operator with application to control of smart actuators. IEEE Trans. Autom. Control 2005, 50, 798–810. [Google Scholar] [CrossRef]
- Mayergoyz, I. Mathematical models of hysteresis. IEEE Trans. Magn. 1986, 22, 603–608. [Google Scholar] [CrossRef]
- Kuhnen, K.; Krejci, P. Compensation of complex hysteresis and creep effects in piezoelectrically actuated systems—A new Preisach modeling approach. IEEE Trans. Autom. Control 2009, 54, 537–550. [Google Scholar] [CrossRef]
- Mayergoyz, I.D. Dynamic Preisach models of hysteresis. IEEE Trans. Magn. 1988, 24, 2925–2927. [Google Scholar] [CrossRef]
- Koutný, J.; Kružík, M.; Kurdila, A.J.; Roubíček, T. Identification of Preisach-Type Hysteresis Operators. Numer. Funct. Anal. Optim. 2008, 29, 149–160. [Google Scholar] [CrossRef]
- Al Janaideh, M.; Aljanaideh, O. Further results on open-loop compensation of rate-dependent hysteresis in a magnetostrictive actuator with the Prandtl-Ishlinskii model. Mech. Syst. Signal Process. 2018, 104, 835–850. [Google Scholar] [CrossRef]
- Feng, Y.; Li, Z.; Rakheja, S.; Jiang, H. A modified Prandtl-Ishlinskii hysteresis modeling method with load-dependent delay for characterizing magnetostrictive actuated systems. Mech. Sci. 2018, 9, 177–188. [Google Scholar] [CrossRef]
- Li, Z.; Su, C.Y.; Chen, X. Modeling and inverse adaptive control of asymmetric hysteresis systems with applications to magnetostrictive actuator. Control Eng. Pract. 2014, 33, 148–160. [Google Scholar] [CrossRef]
- Al Janaideh, M.; Su, C.Y.; Rakheja, S. Development of the rate-dependent Prandtl–Ishlinskii model for smart actuators. Smart Mater. Struct. 2008, 17, 035026. [Google Scholar] [CrossRef]
- Yang, M.J.; Li, C.X.; Gu, G.Y.; Zhu, L.M. A Modified Prandtl-Ishlinskii Model for Rate-dependent Hysteresis Nonlinearity Using m th-power Velocity Damping Mechanism. Int. J. Adv. Robot. Syst. 2014, 11, 163. [Google Scholar] [CrossRef]
- Kuhnen, K. Modelling, identification, and compensation of complex hysteretic and log (t)-type creep nonlinearities. Control Intell. Syst. 2005, 33, 134–147. [Google Scholar] [CrossRef]
- Lin, C.J.; Yang, S.R. Precise positioning of piezo-actuated stages using hysteresis-observer based control. Mechatronics 2006, 16, 417–426. [Google Scholar] [CrossRef]
- Zhu, W.; Bian, L.X.; Cheng, L.; Rui, X.T. Non-linear compensation and displacement control of the bias-rate-dependent hysteresis of a magnetostrictive actuator. Precis. Eng. 2017, 50, 107–113. [Google Scholar] [CrossRef]
- Bai, X.X.; Cai, F.L.; Chen, P. Resistor-capacitor (RC) operator-based hysteresis model for magnetorheological (MR) dampers. Mech. Syst. Signal Process. 2019, 117, 157–169. [Google Scholar] [CrossRef]
- Chen, P.; Bai, X.X.; Qian, L.J.; Choi, S.B. An approach for hysteresis modeling based on shape function and memory mechanism. IEEE/ASME Trans. Mechatron. 2018, 23, 1270–1278. [Google Scholar] [CrossRef]
- Coleman, B.D.; Hodgdon, M.L. On a class of constitutive relations for ferromagnetic hysteresis. Arch. Ration. Mech. Anal. 1987, 99, 375–396. [Google Scholar] [CrossRef]
- Macki, J.W.; Nistri, P.; Zecca, P. Mathematical models for hysteresis. Siam Rev. 1993, 35, 94–123. [Google Scholar] [CrossRef]
- Oh, J.; Bernstein, D.S. Semilinear Duhem model for rate-independent and rate-dependent hysteresis. IEEE Trans. Autom. Control 2005, 50, 631–645. [Google Scholar]
- Su, C.Y.; Stepanenko, Y.; Svoboda, J.; Leung, T.P. Robust adaptive control of a class of nonlinear systems with unknown backlash-like hysteresis. IEEE Trans. Autom. Control 2000, 45, 2427–2432. [Google Scholar] [CrossRef]
- Kciuk, M.; Chwastek, K.; Kluszczyński, K.; Szczygłowski, J. A study on hysteresis behaviour of SMA linear actuators based on unipolar sigmoid and hyperbolic tangent functions. Sens. Actuators A Phys. 2016, 243, 52–58. [Google Scholar] [CrossRef]
- Bai, X.X.; Chen, P.; Qian, L.J. Principle and validation of modified hysteretic models for magnetorheological dampers. Smart Mater. Struct. 2015, 24, 085014. [Google Scholar] [CrossRef]
- Li, W.; Chen, X.; Li, Z. Inverse compensation for hysteresis in piezoelectric actuator using an asymmetric rate-dependent model. Rev. Sci. Instrum. 2013, 84, 115003. [Google Scholar] [CrossRef]
- Nugroho, P.W.; Li, W.; Du, H.; Alici, G.; Yang, J. An adaptive neuro fuzzy hybrid control strategy for a semiactive suspension with magneto rheological damper. Adv. Mech. Eng. 2014, 6, 487312. [Google Scholar] [CrossRef]
- Weber, F.; Bhowmik, S.; Høgsberg, J. Extended neural network-based scheme for real-time force tracking with magnetorheological dampers. Struct. Control Health Monit. 2014, 21, 225–247. [Google Scholar] [CrossRef]
- Zong, L.H.; Gong, X.L.; Guo, C.Y.; Xuan, S.H. Inverse neuro-fuzzy MR damper model and its application in vibration control of vehicle suspension system. Veh. Syst. Dyn. 2012, 50, 1025–1041. [Google Scholar] [CrossRef]





| Parameters | G-Model | M-Model | D-Model |
|---|---|---|---|
| 3.037 | 2.950 | 2.979 | |
| 34.925 | 33.102 | 0.778 | |
| 0.593 | 0.612 | 0.575 | |
| 3.468 | 3.322 | 1.859 | |
| 0.059 | — | — | |
| 0.988 | — | — | |
| — | 0.061 | — | |
| — | 1.251 | — | |
| — | — | 0.452 | |
| — | — | 2.378 | |
| — | — | 0.098 | |
| — | — | 0.587 | |
| — | — | 3.997 | |
| — | — | 0.214 | |
| — | — | 6 |
| Error | MSE | Emax (μm) | Erelative (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | 1 A | 6 A | Tri | 1 A | 6 A | Tri | 1 A | 6 A | Tri | |
| G-Model | 0.123 | 2.8783 | 2.8227 | 0.5583 | 2.9368 | 4.6929 | 7.20 | 3.46 | 5.50 | |
| M-Model | 0.0184 | 1.6529 | 1.1267 | 0.2504 | 1.9796 | 2.9526 | 3.23 | 2.34 | 3.46 | |
| D-Model | 0.0097 | 1.5047 | 0.9210 | 0.2584 | 2.5032 | 1.2861 | 3.24 | 2.95 | 1.53 | |
| PD-Model | 0.014 | 2.1883 | 1.4272 | 0.2613 | 3.2383 | 2.3738 | 3.72 | 3.82 | 2.82 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Si, Z.-Y.; Bai, X.-X.‘F.; Qian, L.-J. Asymmetric Hysteresis Modeling Approach Featuring “Inertial System + Shape Function” for Magnetostrictive Actuators. Materials 2020, 13, 2585. https://doi.org/10.3390/ma13112585
Si Z-Y, Bai X-X‘F, Qian L-J. Asymmetric Hysteresis Modeling Approach Featuring “Inertial System + Shape Function” for Magnetostrictive Actuators. Materials. 2020; 13(11):2585. https://doi.org/10.3390/ma13112585
Chicago/Turabian StyleSi, Zhi-Yuan, Xian-Xu ‘Frank’ Bai, and Li-Jun Qian. 2020. "Asymmetric Hysteresis Modeling Approach Featuring “Inertial System + Shape Function” for Magnetostrictive Actuators" Materials 13, no. 11: 2585. https://doi.org/10.3390/ma13112585
APA StyleSi, Z.-Y., Bai, X.-X. ‘F., & Qian, L.-J. (2020). Asymmetric Hysteresis Modeling Approach Featuring “Inertial System + Shape Function” for Magnetostrictive Actuators. Materials, 13(11), 2585. https://doi.org/10.3390/ma13112585






