The Influence of the Strain and Stress Gradient in Determining Strain Fatigue Characteristics for Oscillatory Bending
Abstract
1. Introduction
2. Materials and Methods
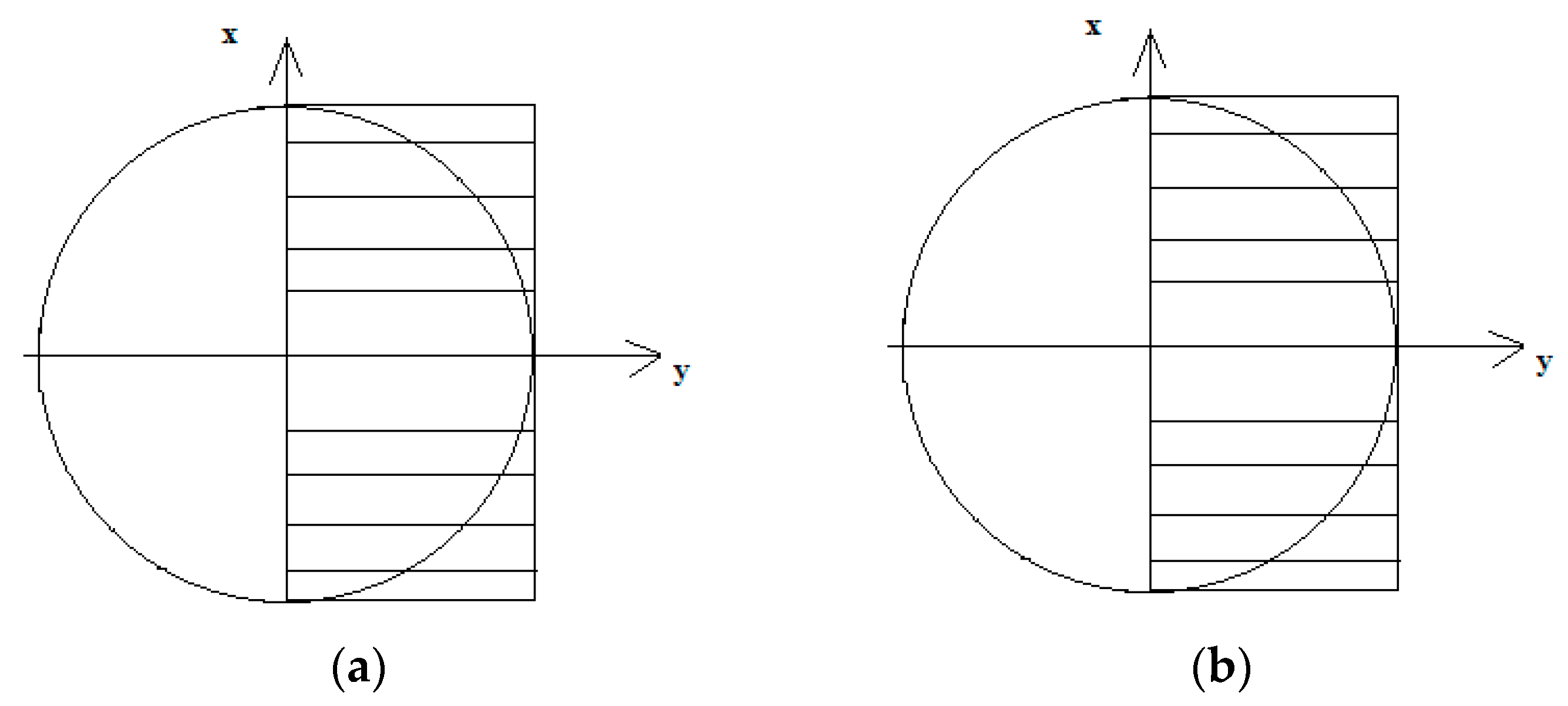
2.1. Stress and Strain Gradient
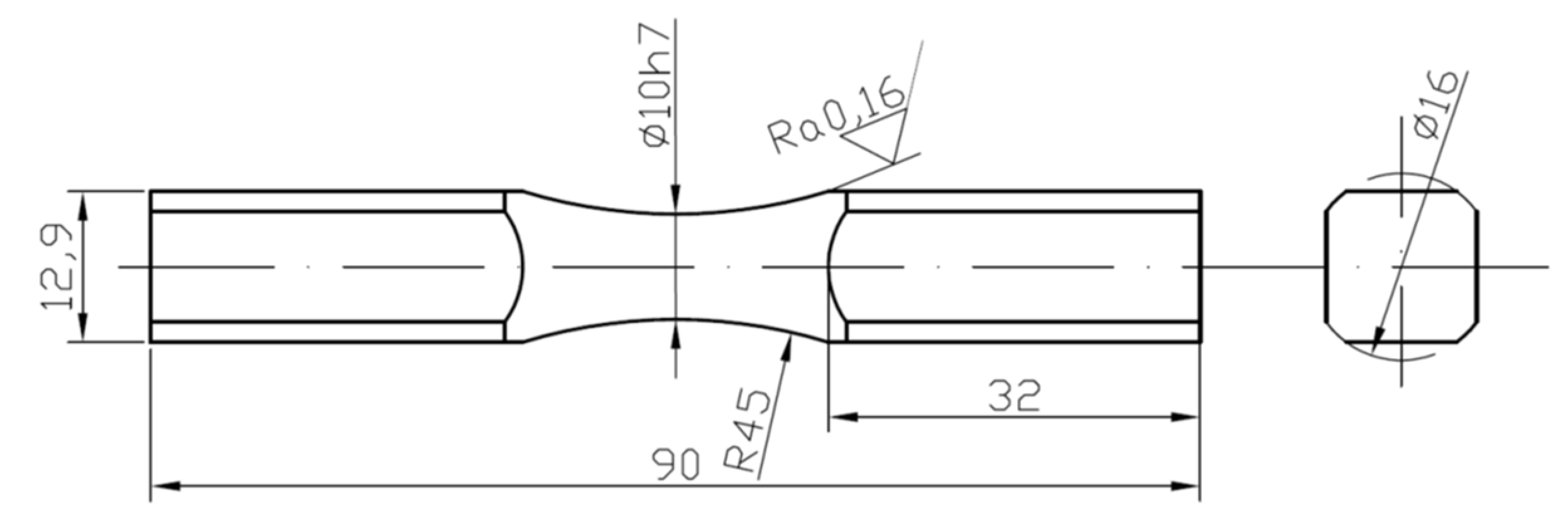
2.2. Experimental Tests
2.3. Analysis
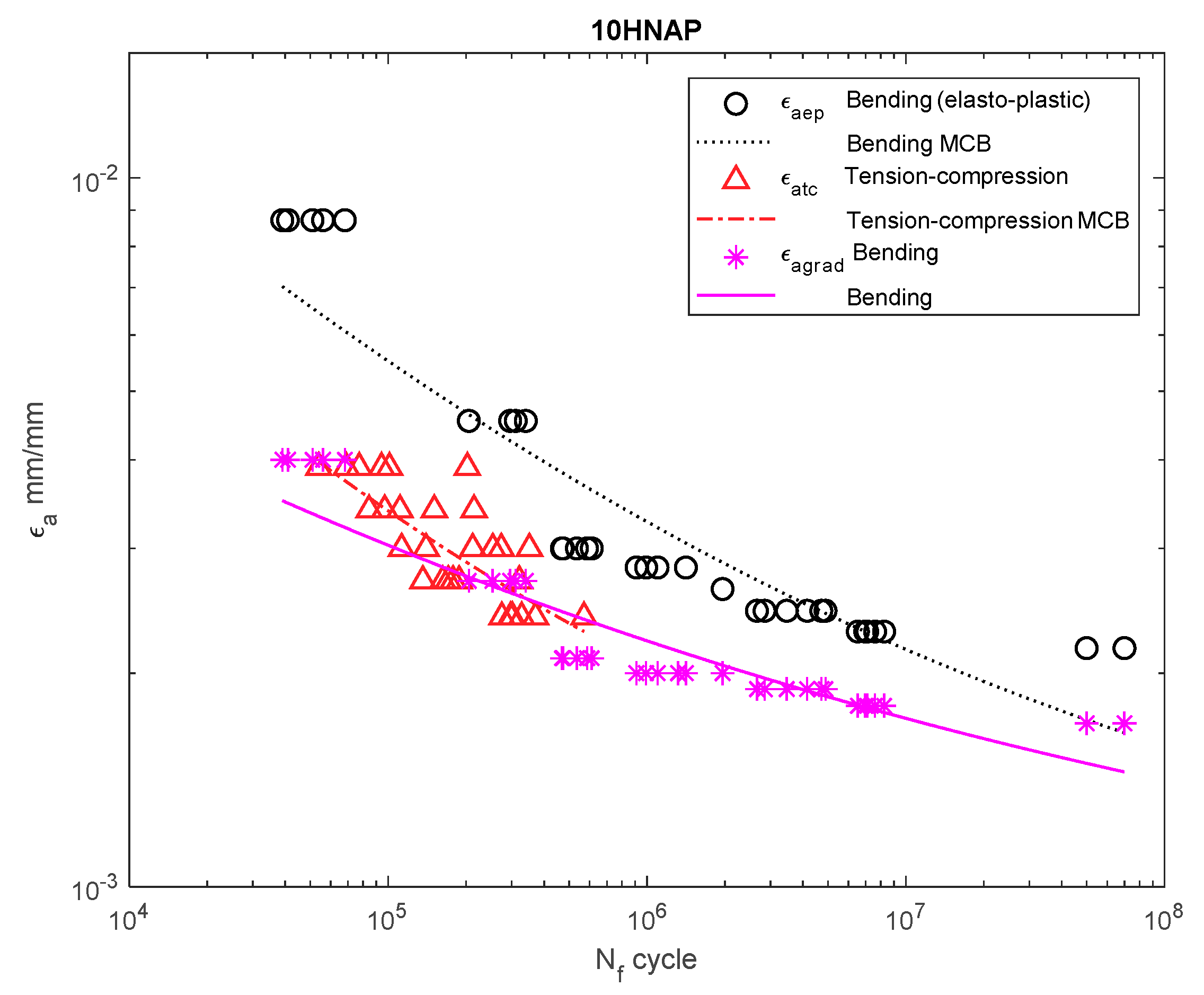
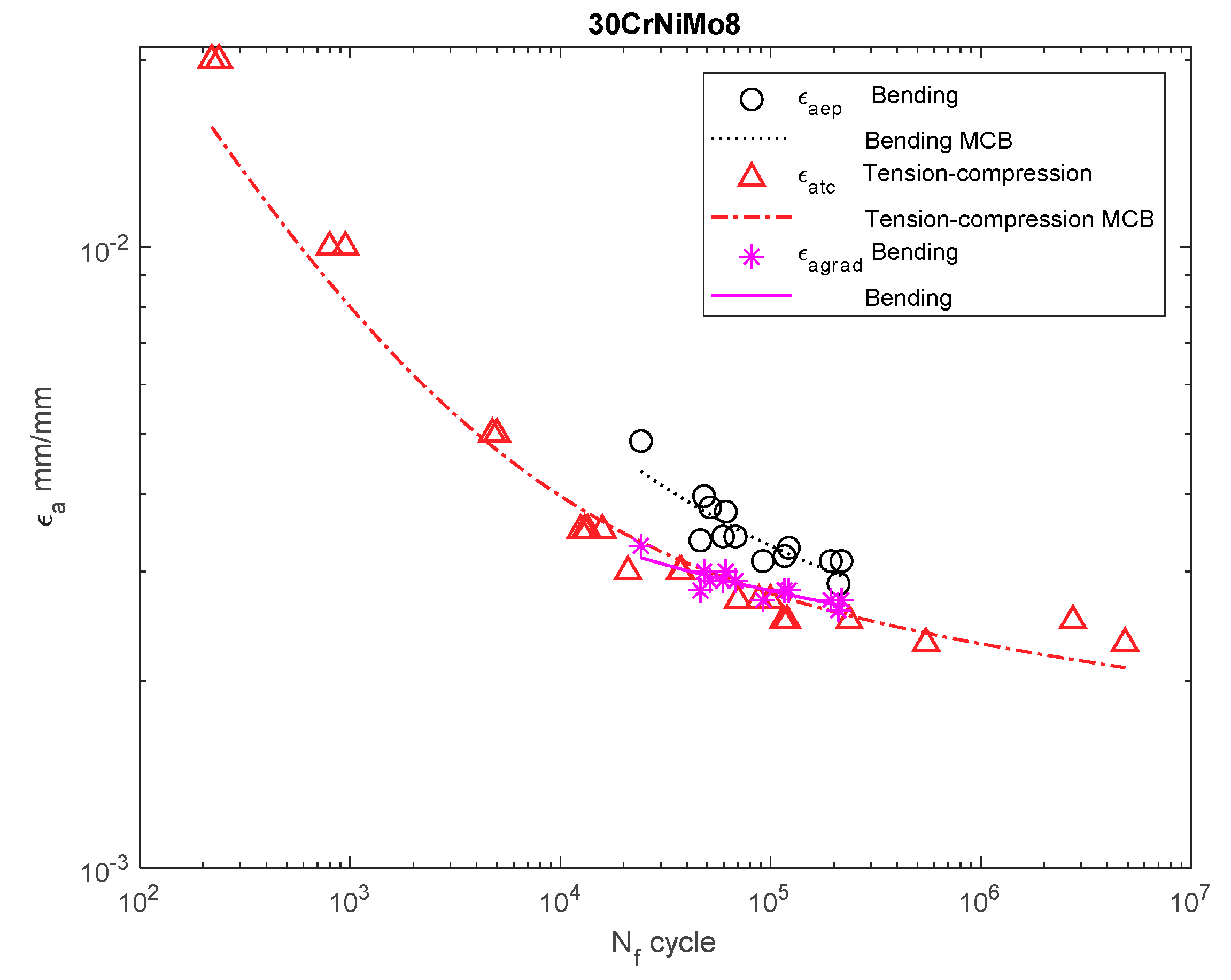
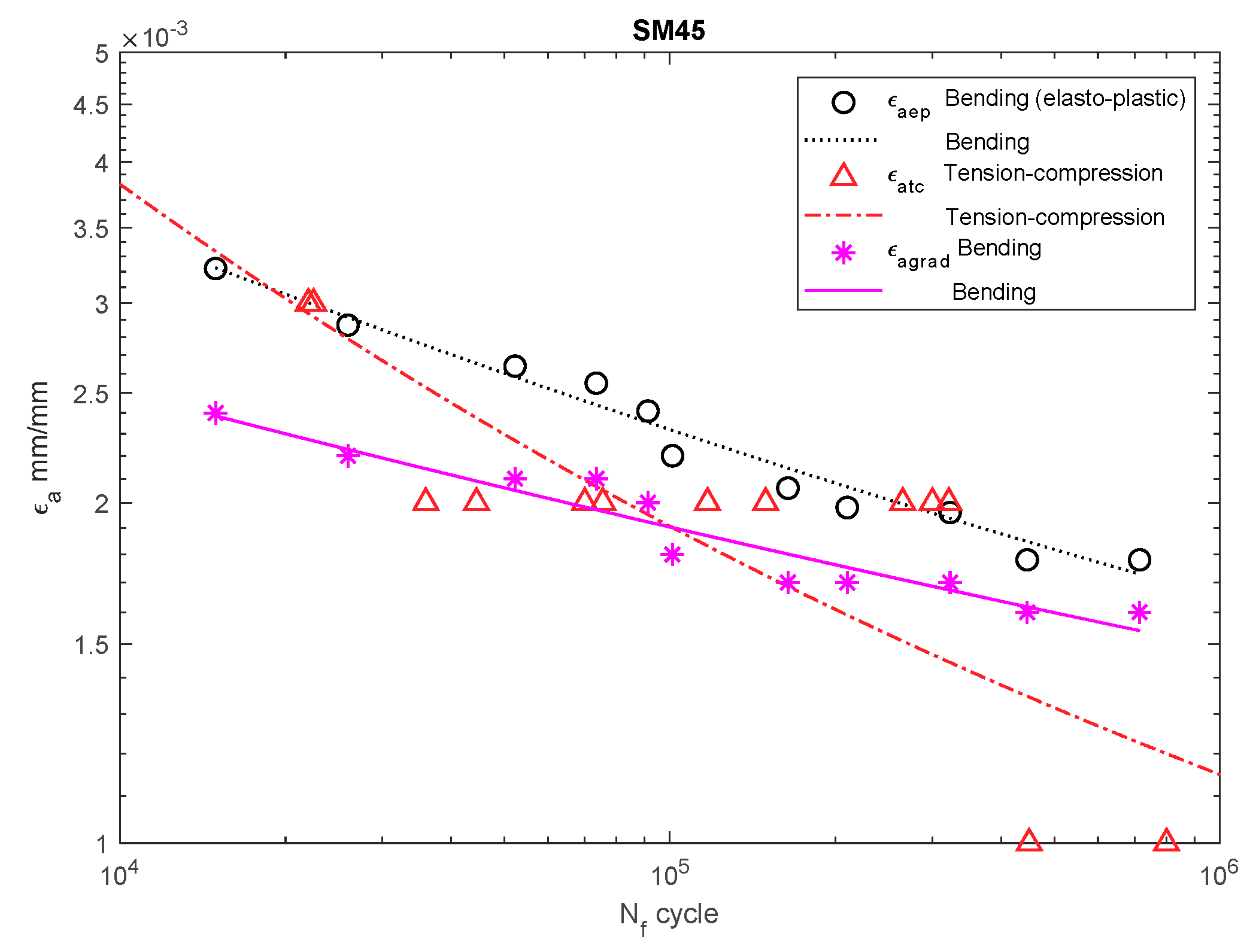
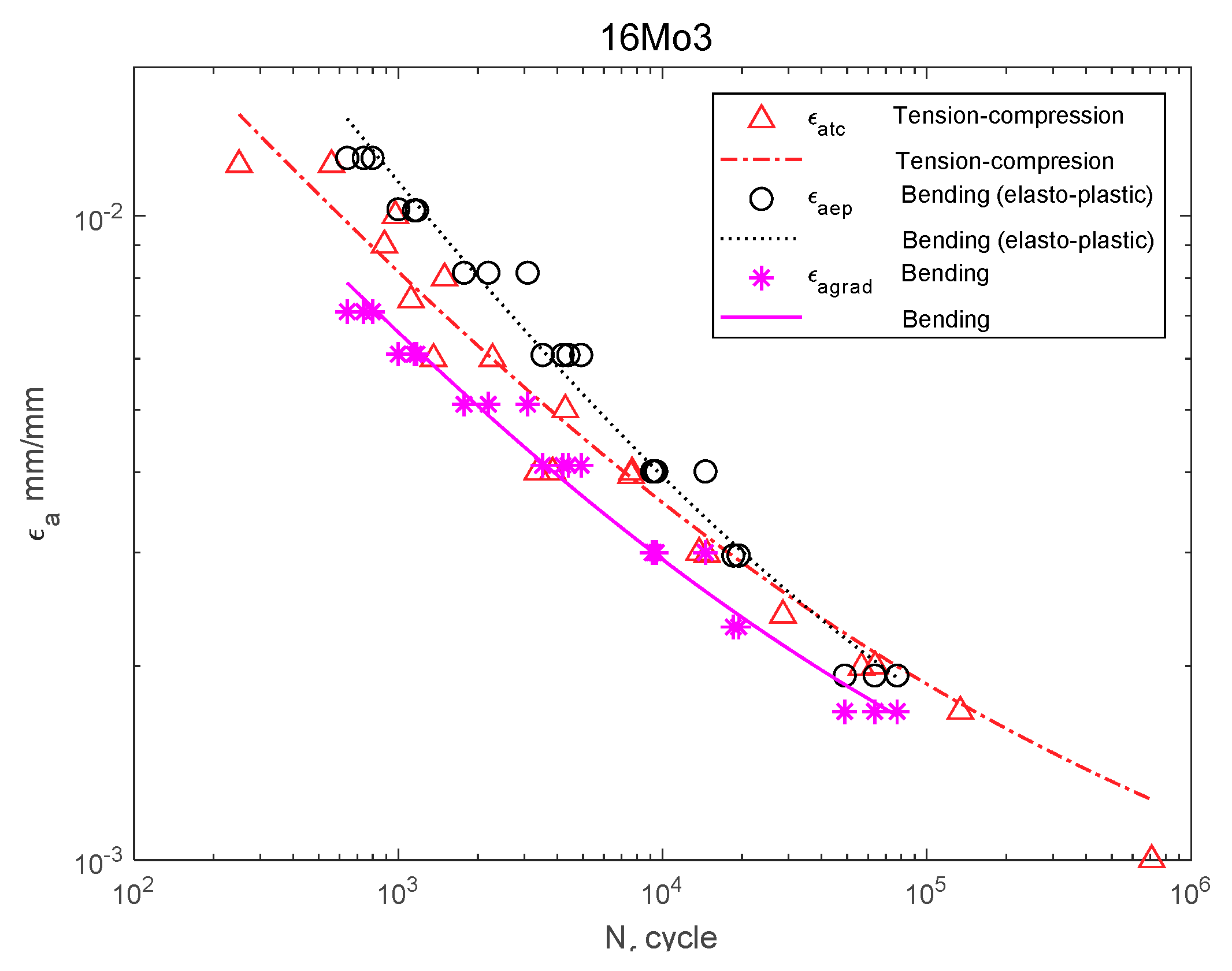
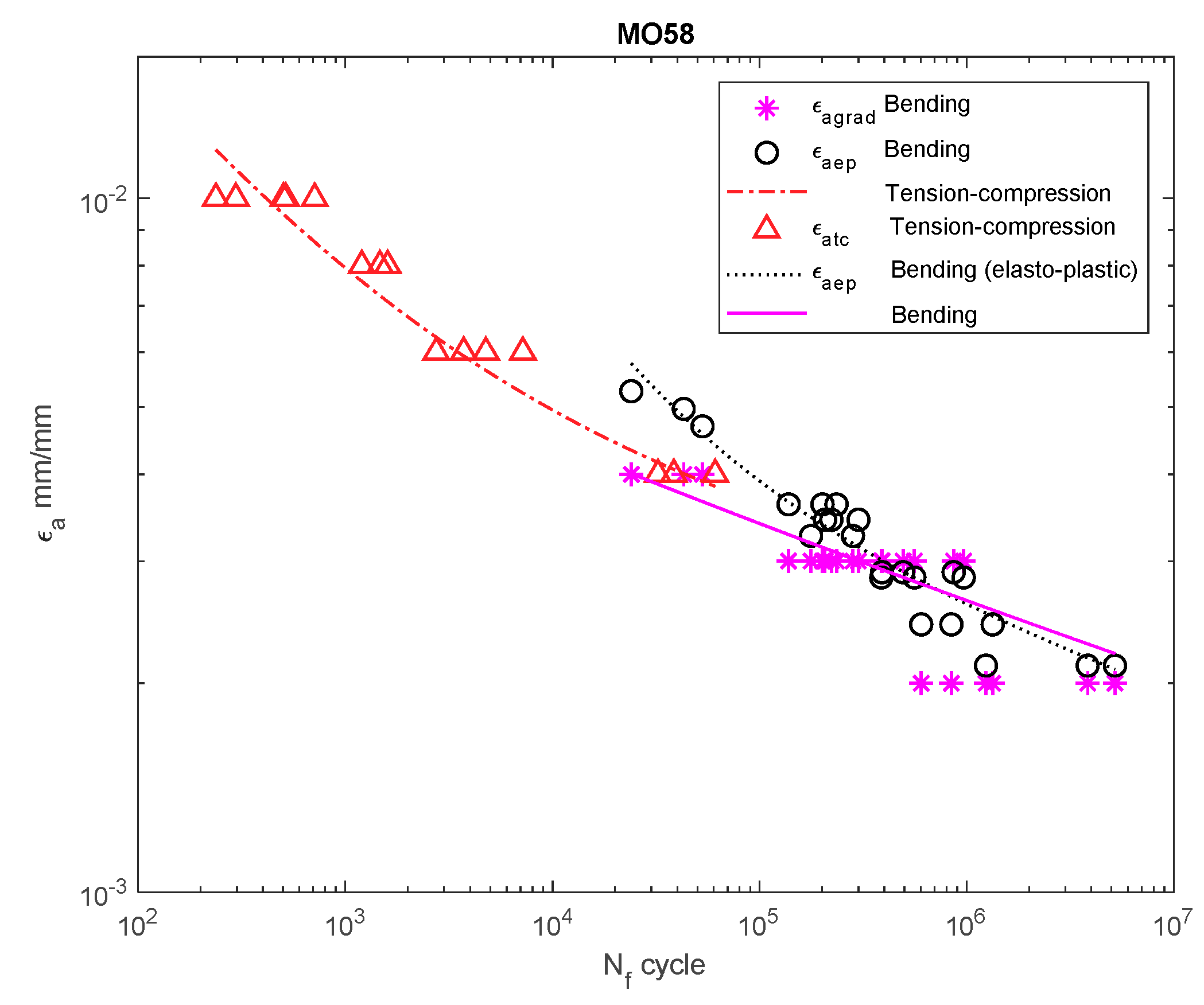
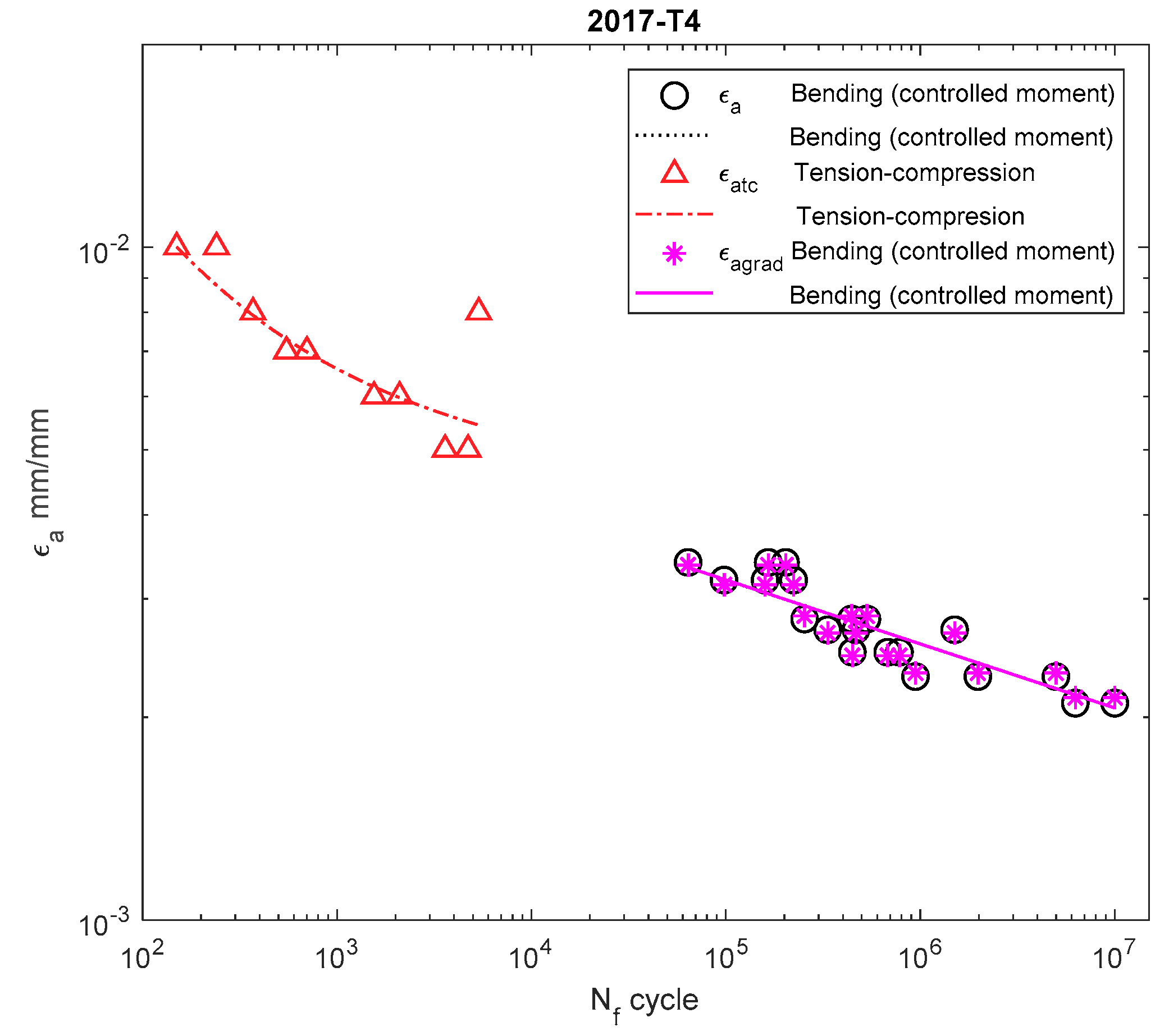
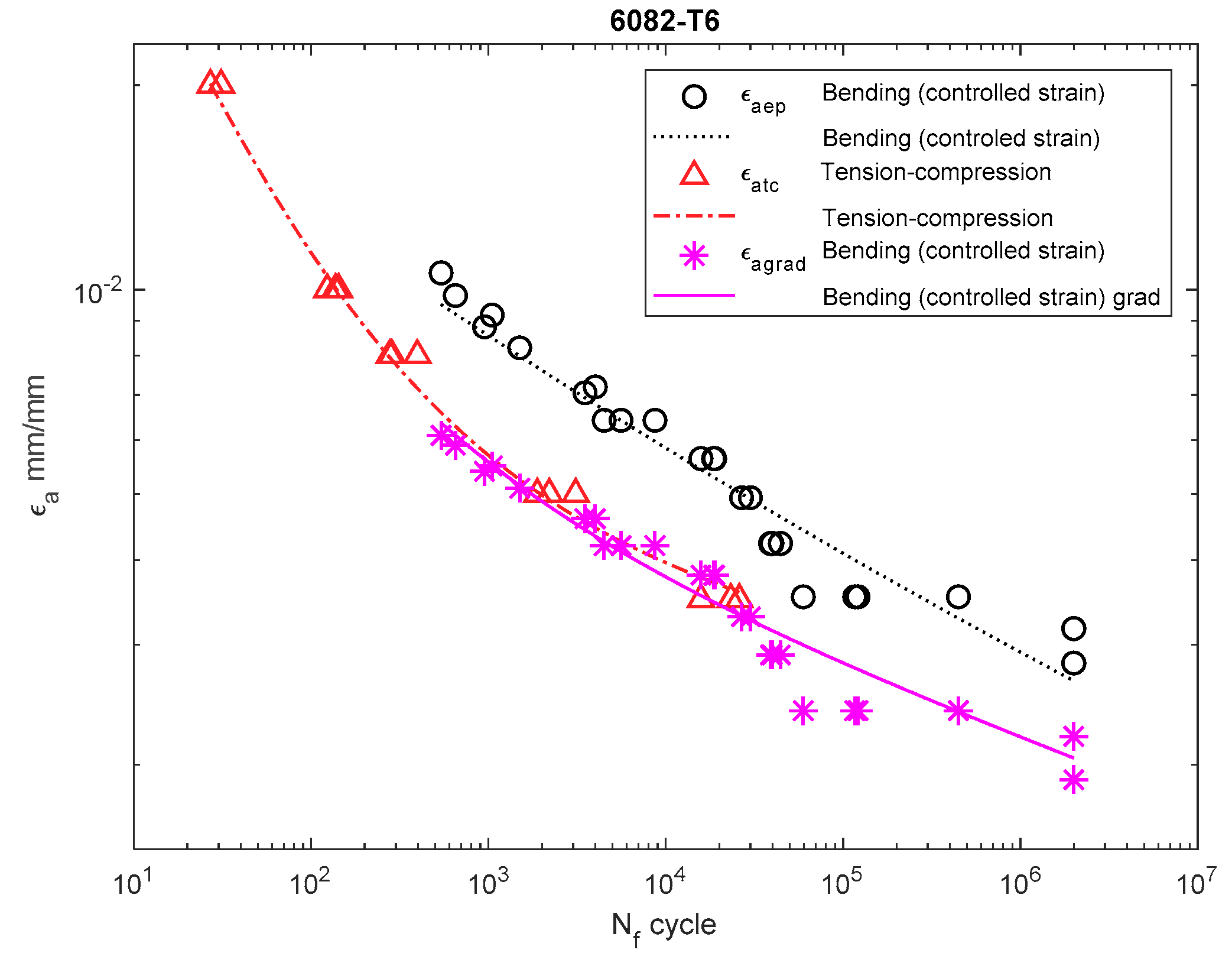
3. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Engler, O.; Tomé, C.N.; Huh, M.Y. A study of through-thickness texture gradients in rolled sheets. Metall. Mater. Trans. A 2000, 31, 2299–2315. [Google Scholar] [CrossRef]
- Aldazabal, J.; Sevillano, J.G. Hall-Petch behaviour induced by plastic strain gradients. Mater. Sci. Eng. A 2004, 365, 186–190. [Google Scholar] [CrossRef]
- Kurek, A.; Koziarska, J.; Kluger, K.; Łagoda, T. Fatigue life of 2017-T4 aluminium alloy under different types of stress. J. Mach. Constr. Maint. 2017, 4, 52–61. [Google Scholar]
- Troshchenko, V. High-cycle fatigue and inelasticity of metals. In ICBMFF4. Multiaxial Fatigue Design. ESIS 21; Mechanical Engineering Publications: London, UK, 1996; pp. 335–358. [Google Scholar]
- Manson, S.S.; Muralidharan, U. Fatigue life prediction in bending from axial fatigue information. Fatigue Fract. Eng. Mater. Struct. 1987, 9, 357–372. [Google Scholar] [CrossRef]
- Hassan, T.; Liu, Z. On the difference of fatigue strengths from rotating bending, four-point bending, and cantilever bending tests. Int. J. Press. Pip. 2001, 78, 19–30. [Google Scholar] [CrossRef]
- Megahed, M.M. Prediction of bending fatigue behaviour by the reference stress approach. Fatigue Fract. Eng. Mater. Struct. 1990, 13, 361–374. [Google Scholar] [CrossRef]
- Manson, S.S. Fatigue: A complex subject—some simple approximations. Exp. Mech. 1965, 5, 193–226. [Google Scholar] [CrossRef]
- Krzyżak, D.; Kurek, M.; Łagoda, T.; Sówka, D. Influence of changes of the bending plane position on the fatigue life. Mater. Werkst. 2014, 45, 1018–1029. [Google Scholar] [CrossRef]
- Ivanov, Y.F.; Alsaraeva, K.V.; Gromov, V.E.; Popova, N.A.; Konovalov, S.V. Fatigue life of silumin treated with a high-intensity pulsed electron beam. J. Surf. Investig. 2015, 9, 1056–1059. [Google Scholar] [CrossRef]
- Ivanov, Y.F.; Koval, N.N.; Gorbunov, S.V.; Vorobyov, S.V.; Konovalov, S.V.; Gromov, V.E. Multicyclic fatigue of stainless steel treated by a high-intensity electron beam: Surface layer structure. Russ. Phys. J. 2011, 54, 575–583. [Google Scholar] [CrossRef]
- Dorr, T.; Wagner, L. Influence of stress gradient on fatigue behavior of shot pending timetal 1100. In The Sixth International Conference on Shot Peening; Jack, C., Ed.; ICSP6: San Francisco, CA, USA, 1996; pp. 223–232. [Google Scholar]
- Gil Sevillano, J.; de las Cuevas, F. A comparison of the internal stresses in a transformation-induced plasticity-assisted steel and a twinning-induced plasticity steel. Mater. Sci. Technol. 2019, 35, 409–419. [Google Scholar] [CrossRef]
- Norberg, S.; Olsson, M. The effect of loaded volume and stress gradient on the fatigue limit. Int. J. Fatigue 2007, 29, 2259–2272. [Google Scholar] [CrossRef]
- Ashton, P.J.; Harte, A.M.; Leen, S.B. A strain gradient, crystal plasticity model for microstruktore-sensitive fretting crack initiation in ferritic-pearlitic steel for flexible marine risers. Int. J. Fatigue 2018, 111, 81–92. [Google Scholar] [CrossRef]
- Kadi, N.; Pluvinage, G. Effective stress range in fatigue initiation emanating from notch, Fatigue ’99. Beijing Inst. Aeronaut. Mater. 1999, 2, 1175–1179. [Google Scholar]
- Adib, R.; Schmitt, C.; Pluvinage, G. Application of volumetric method to the assessment of damage inducted by action of foreign object on gas pipes. Strength Mater. 2006, 38, 409–416. [Google Scholar] [CrossRef][Green Version]
- Filippini, M. Stress gradient calculations at notches. Int. J. Fatigue 2000, 22, 397–409. [Google Scholar] [CrossRef]
- Milosevic, I.; Gerhard, W.; Grun, F.; Kober, M. Influence of size effect and stress gradient on the high-cycle fatigue strength of a 1.4542 steel. Procedia Eng. 2016, 160, 61–68. [Google Scholar] [CrossRef]
- Kurek, A.; Koziarska, J.; Łagoda, T. Wytrzymałość zmęczeniowa materiałów konstrukcyjnych na zginanie wahadłowe i rozciąganie-ściskanie. In Proceedings of the 9-th International Symposium Mechanics of Materials and Structures, Augustów, Poland, 2–6 June 2017. [Google Scholar]
- Kurek, A.; Koziarska, J.; Kurek, M.; Kulesa, A.; Łagoda, T. Porównanie charakterystyk wytrzymałości zmęczeniowej wybranych stali dla rozciągania-ściskania i zginania wahadłowego. Transp. Przemysłowy I Masz. Rob. 2017, 3, 54–61. [Google Scholar]
- Niesłony, A.; Kurek, A. Influence of the selected fatigue characteristics of the material on calculated fatigue life under variable amplitude loading. In Applied Mechanics and Materials; Trans Tech Publications: Stafa-Zurich, Switzerland, 2012; Volume 104, pp. 197–205. [Google Scholar]
- Niesłony, A.; Kurek, A.; El Dsoki, C.; Kaufmann, H. A study of compatibility between two classical fatigue curve models based on some selected structural materials. Int. J. Fatigue 2012, 39, 88–94. [Google Scholar] [CrossRef]
- Basquin, O.H. The exponential law of endurance tests. Am. Soc. Test. Mater. Proc. 1910, 10, 625–630. [Google Scholar]
- Coffin, L.F. A study of the effect of cyclic thermal stresses on a ductile metal. Trans. ASME 1954, 76, 931–950. [Google Scholar]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; University of Washington Libraries: Washington, WA, USA, 1943. [Google Scholar]
- Lachowicz, C.; Łagoda, T.; Macha, E.; Dragon, A.; Petit, J. Selections of algorithms for fatigue life calculation of elements made of 10HNAP steel under uniaxial random loadings. Studia Geotech. Mech. 1996, 18, 19–43. [Google Scholar]
- Łagoda, T.; Macha, E. Energy approach to fatigue under combined cyclic bending with torsion of smooth and notched specimens. Mater. Sci. 1998, 34, 630–639. [Google Scholar] [CrossRef]
- Boller, C.; Seeger, T. Materials Data for Cyclic Loading. In Parts AE; Elsevier Science Publishers: Amsterdam, The Netherlands, 1987; pp. 205–225. [Google Scholar]
- Kulesa, A.; Kurek, A.; Łagoda, T.; Achtelik, H.; Kluger, K. Low cycle fatigue of steel in strain controlled cyclic bending. Acta Mech. Autom. 2016, 10, 62–65. [Google Scholar]
- Sanetra, C. Untersuchungen zum Festigkeitsverhalten bei mehrachsiger Randombeans–pruchung unter Biegung und Torsion. Ph.D. Thesis, Universitat Clausthal, Clausthal, Germany, 1991. [Google Scholar]
- Kohut, M.; Łagoda, T. Badania zmęczeniowe mosiądzu MO58 w warunkach proporcjonalnego cyklicznego zginania ze skręcaniem. In Proceedings of the III Sympozjum Mechaniki Zniszczenia Materiałów i Konstrukcji, Augustów, Poland, 1–4 June 2005; pp. 159–162. [Google Scholar]
- Kohut, M.; Słowik, J. Badania zmęczeniowe mosiądzu Mo58 (B124, C38000 wg ASTM) przy kontrolowanym odkształceniu w jednoosiowym cyklicznym stanie obciążenia. Zeszyty Naukowe. Mechanika/Politechnika Opolska 2005, 85, 31–38. [Google Scholar]
- Lee, S.B. A criterion for fully reversed out of phase torsion and bending. In Multiaxial Fatigue; Miller, K.J., Brown, M.W., Eds.; ASTM International: Washington, DC, USA, 1985; pp. 553–568. [Google Scholar]
- Kardas, D.; Kluger, K.; Łagoda, T.; Ogonowski, P. Fatigue life under proportional constant amplitude bending with torsion in energy approach basic on aluminium alloy. Mater. Sci. 2017, 44, 541–549. [Google Scholar] [CrossRef]
- Będkowski, W.; Łagoda, T.; Słowik, J. Strain controlled tests for determining the change of the material fatigue parameters. Mater. Sci. 2007, 43, 492–498. [Google Scholar] [CrossRef]
- Niesłony, A.; Łagoda, T.; Walat, K.; Kurek, M. Multiaxial fatigue behaviour of AA6068 and AA2017A aluminium alloys under in-phase bending with torsion loading condition. Mater. Werkst. 2014, 45, 947–952. [Google Scholar] [CrossRef]
- Mroziński, St. Wyznaczanie własności niskocyklowych stopu aluminium PA4 w temperaturze otoczenia. Raport z badań. Ph.D. Thesis, UTP w Bydgoszczy, Bydgoszcz, Poland, 2012. (in Polish). [Google Scholar]
- Walat, K.; Łagoda, T. Trwałość zmęczeniowa elementów maszyn w płaszczyźnie krytycznej wyznaczonej przez ekstremum kowariancji naprężeń. In Studia i monografie. Z.294 Politechnika Opolska; Ofic. Wydaw. PO: Opole, Poland, 2011; pp. 91–105. [Google Scholar]




| Material | Chemical Composition | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | Si | Mn | P | S | Cr | Ni | Mo | Cu | Fe | Mg | Zn | Zr + Ti | Pb | Sn | Al | |
| 10HNAP | 0.115 | 0.41 | 0.71 | 0.082 | 0.028 | 0.81 | 1.90 | 0.30 | - | The rest | - | - | - | - | - | - |
| 30CrNiMo8 | 0.3 | 0.27 | 0.49 | 0.019 | 0.009 | 3.89 | 1.90 | 0.30 | - | The rest | - | - | - | - | - | - |
| SM45C | 0.45 | 0.35 | 0.64 | 0.011 | 0.012 | - | - | - | - | The rest | - | - | - | - | - | - |
| 16Mo3 | 0.19 | 0.28 | 0.69 | 0.019 | 0.024 | - | - | 0.33 | - | The rest | - | - | - | - | - | - |
| MO58 | - | - | - | - | - | - | Max 0.2 | - | 56–60 | Max 0.5 | - | The rest | - | 1–3.5 | Max 0.5 | Max 1 |
| 2017(A) | - | 0.2–0.8 | 0.4–1.0 | - | - | <0.10 | - | - | 3.5–4.5 | <0.7 | 0.4–1.0 | <0.25 | <0.25 | - | - | The rest |
| 6082 | - | 0.7–1.3 | 0.4–1.0 | - | - | <0.25 | - | - | <0.1 | <0.5 | 0.6–1.2 | <0.2 | <0.1 | - | - | The rest |
| Material | Rp0.2 (MPa) | Rm (MPa) | A5 (%) | ν |
|---|---|---|---|---|
| 10HNAP | 464 | 566 | 32 | 0.29 |
| 30CrNiMo8 | 795 | 1014 | 6.3 | 0.29 |
| SM45C | 430 | 680 | 15 | 0.29 |
| 16Mo3 | 335 | 481 | 24 | 0.30 |
| MO58 | 399 | 484 | - | 0.32 |
| 2017-T6 | 395 | 545 | 21 | 0.32 |
| 6082-T4 | 365 | 385 | 27.2 | 0.32 |
| 10HNAP | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Testing Conditions | Material Constant | |||||||||
| E (GPa) | Ramberg–Osgood | Basquin | Manson–Coffin–Basquin (MCB) | TRMS | ||||||
| K’ (MPa) | n’ | A | m | σ’f (MPa) | ε’f | b | c | |||
| Bending | 205 | - | - | 35.96 | 11.39 | - | - | - | - | - |
| Bending (e–p) | - | - | 46.64 | 16.24 | 675 | 0.239 | −0.052 | −0.340 | 1.616 | |
| Tension–compression | 853 | 0.156 | 29.07 | 9.57 | 685 | 0.245 | −0.063 | −0.399 | 1.114 | |
| Bending (grad) | 58.51 | 21.41 | 501 | 0.0349 | −0.039 | −2569 | 1.152 | |||
| 30CrNiMo8 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Testing Conditions | Material Constant | |||||||||
| E (GPa) | Ramberg–Osgood | Basquin | MCB | TRMS | ||||||
| K’ (MPa) | n’ | A | m | σ’f (MPa) | ε’f | b | c | |||
| Bending | 206 | - | - | 25.57 | 7.35 | - | - | - | - | |
| Bending (e–p) | - | - | 52.07 | 17.30 | 911 | 0.602 | −0.045 | −0.548 | 1.229 | |
| Tension–compression | 972 | 0.085 | 49.79 | 16.64 | 851 | 0.471 | −0.043 | −0.597 | 1.123 | |
| Bending (grad) | - | - | 84.25 | 29.38 | 693 | 0.041 | −0.027 | −0.384 | 1.159 | |
| SM45C | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Testing Conditions | Material Constant | |||||||||
| E (GPa) | Ramberg–Osgood | Basquin | MCB | TRMS | ||||||
| K’ (MPa) | n’ | A | m | σ’f (MPa) | ε’f | b | c | |||
| Bending | 201.5 | - | - | 31.13 | 10.29 | - | - | - | - | |
| Bending (e–p) | - | - | 37.78 | 13.38 | 671 | 0.035 | −0.071 | −0.298 | 1.246 | |
| Tension–compression | 1414 | 0.231 | 23.69 | 7.76 | 1140 | 0.406 | −0.122 | −0.53 | 1.067 | |
| Bending (grad) | 44.02 | 16.18 | 527 | 0.009 | −0.058 | −0.224 | 1.168 | |||
| 16Mo3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Testing Conditions | Material Constant | |||||||||
| E (GPa) | Ramberg–Osgood | Basquin | MCB | TRMS | ||||||
| K’ (MPa) | n’ | A | m | σ’f (MPa) | ε’f | b | c | |||
| Bending | 210 | - | - | 21.07 | 6.80 | - | - | - | - | |
| Bending (e–p) | - | - | 24.91 | 8.40 | 980 | 0.769 | −0.116 | −0.580 | 1.250 | |
| Tension–compression | 1038 | 0.133 | 27.94 | 9.67 | 780 | 0.233 | −0.096 | −0.473 | 1.106 | |
| Bending (grad) | 26.47 | 9.05 | 884 | 0.071 | −0.107 | −0.635 | 1.244 | |||
| MO58 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Testing Conditions | Material Constant | |||||||||
| E (GPa) | Ramberg–Osgood | Basquin | MCB | TRMS | ||||||
| K’ (MPa) | n’ | A | m | σ’f (MPa) | ε’f | b | c | |||
| Bending | 96.9 | - | - | 19.98 | 5.86 | - | - | - | - | |
| Bending (e–p) | - | - | 25.06 | 8.04 | 1175 | 4.71 | −0.110 | −0.717 | 1.169 | |
| Tension–compression | 723.3 | 0.121 | 50.92 | 18.59 | 549 | 0.11 | −0.049 | −0.434 | 1.091 | |
| Bending (grad) | - | - | 25.76 | 8.3380 | 936 | 0.01 | −0.095 | −0.265 | 1.155 | |
| 2017A-T4 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Testing Conditions | Material Constant | |||||||||
| E (GPa) | Ramberg–Osgood | Basquin | MCB | TRMS | ||||||
| K’ (MPa) | n’ | A | m | σ’f (MPa) | ε’f | b | c | |||
| Bending at the controlled moment | 72 | - | - | 25.59 | 8.65 | 738 | 1 | −0.095 | 0 | 1.498 |
| Tension–compression | 617 | 0.066 | 35.55 | 12.54 | 553 | 0.193 | −0.044 | −0.678 | 1.158 | |
| Bending (grad) | - | - | 25.59 | 8.65 | 738 | 1 | −0.095 | 0 | 1.498 | |
| 6082-T6 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Testing Conditions | Material Constant | |||||||||
| E (MPa) | Ramberg–Osgood | Basquin | MCB | TRMS | ||||||
| K’ (MPa) | n’ | A | m | σ’f (MPa) | ε’f | b | c | |||
| Bending at the controlled moment | 76.998 | - | - | 23.7053 | 7.9930 | 905 | 0.0530 | −0.116 | −0.610 | 1.179 |
| Bending at the controlled moment (grad) | - | - | - | - | 687 | 0.0419 | −0.096 | −0.516 | 1.183 | |
| Bending at the controlled strain | - | - | 25.1731 | 8.6950 | 768 | 0.2836 | −0.105 | 0.649 | 1.150 | |
| Bending at the controlled strain (grad) | - | - | 26.47 | 9.28 | 696 | 0.0835 | −0.098 | −0.548 | 1.153 | |
| Tension–compression | 616 | 0.099 | 37.5945 | 13.7902 | 533 | 0.185 | −0.065 | −0.634 | 1.050 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurek, A.; Koziarska, J.; Łagoda, T. The Influence of the Strain and Stress Gradient in Determining Strain Fatigue Characteristics for Oscillatory Bending. Materials 2020, 13, 173. https://doi.org/10.3390/ma13010173
Kurek A, Koziarska J, Łagoda T. The Influence of the Strain and Stress Gradient in Determining Strain Fatigue Characteristics for Oscillatory Bending. Materials. 2020; 13(1):173. https://doi.org/10.3390/ma13010173
Chicago/Turabian StyleKurek, Andrzej, Justyna Koziarska, and Tadeusz Łagoda. 2020. "The Influence of the Strain and Stress Gradient in Determining Strain Fatigue Characteristics for Oscillatory Bending" Materials 13, no. 1: 173. https://doi.org/10.3390/ma13010173
APA StyleKurek, A., Koziarska, J., & Łagoda, T. (2020). The Influence of the Strain and Stress Gradient in Determining Strain Fatigue Characteristics for Oscillatory Bending. Materials, 13(1), 173. https://doi.org/10.3390/ma13010173





