Double- and Multi-Femtosecond Pulses Produced by Birefringent Crystals for the Generation of 2D Laser-Induced Structures on a Stainless Steel Surface
Abstract
:1. Introduction
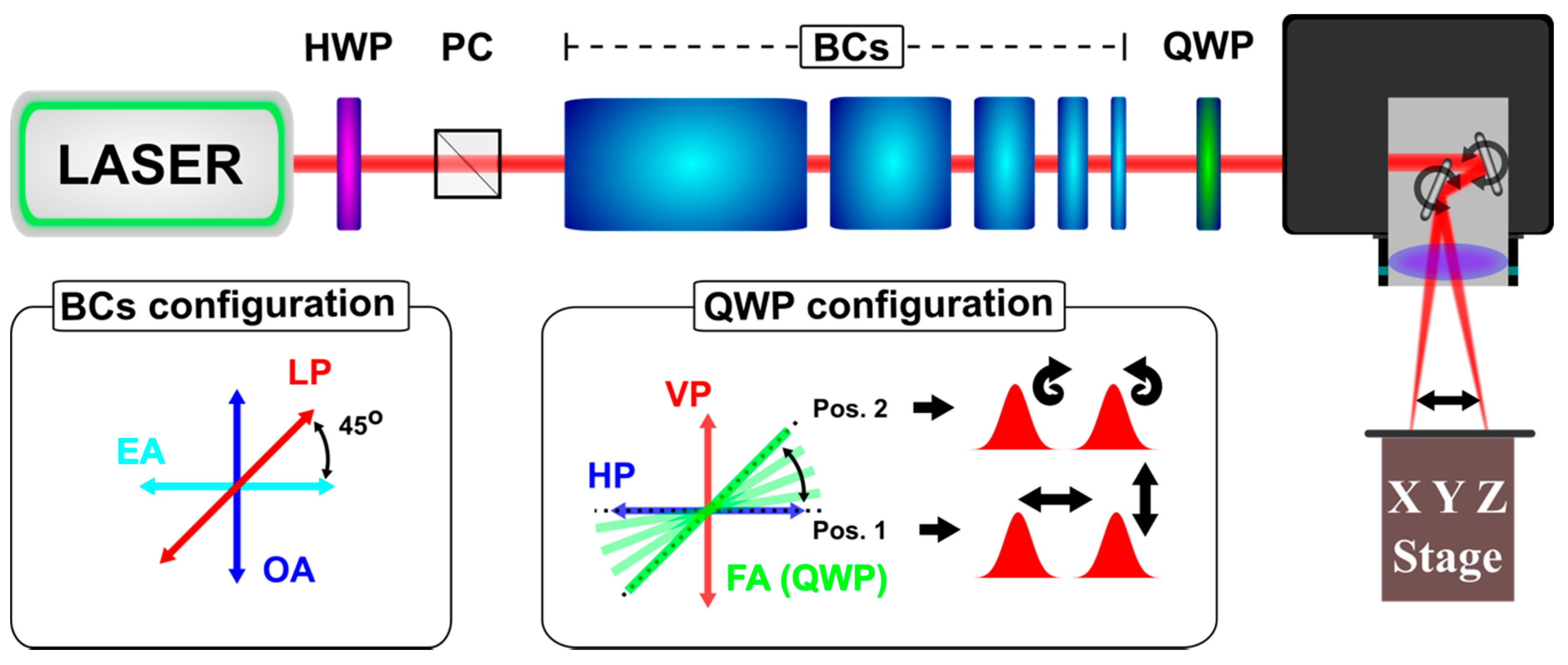
2. Materials and Methods
3. Results and Discussion
3.1. The Effect of Delay and Polarization
3.2. The Effect of Dose
3.3. Structure Optimization for Double Pulses
3.4. Structures Obtained with Bursts of Pulses
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zorba, V.; Stratakis, E.; Barberoglou, M.; Spanakis, E.; Tzanetakis, P.; Anastasiadis, S.H.; Fotakis, C. Biomimetic artificial surfaces quantitatively reproduce the water repellency of a lotus leaf. Adv. Mater. 2008, 20, 4049–4054. [Google Scholar] [CrossRef]
- Vorobyev, A.Y.; Guo, C. Colorizing metals with femtosecond laser pulses. Appl. Phys. Lett. 2008, 92, 041914. [Google Scholar] [CrossRef]
- Guay, J.-M.; Calà Lesina, A.; Côté, G.; Charron, M.; Poitras, D.; Ramunno, L.; Berini, P.; Weck, A. Laser-induced plasmonic colours on metals. Nat. Commun. 2017, 8, 16095. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bonse, J.; Koter, R.; Hartelt, M.; Spaltmann, D.; Pentzien, S.; Höhm, S.; Rosenfeld, A.; Krüger, J. Tribological performance of femtosecond laser-induced periodic surface structures on titanium and a high toughness bearing steel. Appl. Surf. Sci. 2015, 336, 21–27. [Google Scholar] [CrossRef]
- Epperlein, N.; Menzel, F.; Schwibbert, K.; Koter, R.; Bonse, J.; Sameith, J.; Krüger, J.; Toepel, J. Influence of femtosecond laser produced nanostructures on biofilm growth on steel. Appl. Surf. Sci. 2017, 418, 420–424. [Google Scholar] [CrossRef]
- Simitzi, C.; Efstathopoulos, P.; Kourgiantaki, A.; Ranella, A.; Charalampopoulos, I.; Fotakis, C.; Athanassakis, I.; Stratakis, E.; Gravanis, A. Laser fabricated discontinuous anisotropic microconical substrates as a new model scaffold to control the directionality of neuronal network outgrowth. Biomaterials 2015, 67, 115–128. [Google Scholar] [CrossRef]
- Xia, F.; Jiang, L. Bio-Inspired, Smart, Multiscale Interfacial Materials. Adv. Mater. 2008, 20, 2842–2858. [Google Scholar] [CrossRef] [Green Version]
- Elbourne, A.; Crawford, R.J.; Ivanova, E.P. Nano-structured antimicrobial surfaces: From nature to synthetic analogues. J. Colloid Interface Sci. 2017, 508, 603–616. [Google Scholar] [CrossRef]
- Siddique, R.H.; Gomard, G.; Hölscher, H. The role of random nanostructures for the omnidirectional anti-reflection properties of the glasswing butterfly. Nat. Commun. 2015, 6, 6909. [Google Scholar] [CrossRef] [Green Version]
- Bonse, J.; Hohm, S.; Kirner, S.V.; Rosenfeld, A.; Kruger, J. Laser-Induced Periodic Surface Structures—A Scientific Evergreen. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 9000615. [Google Scholar] [CrossRef]
- Romano, J.; Helbig, R.; Fraggelakis, F.; Garcia-Giron, A.; Werner, C.; Kling, R.; Dimov, S. Springtail-inspired triangular laser-induced surface textures on metals using MHz ultrashort pulses. Accept. ASME J. Micro Nano Manuf. 2019. [Google Scholar] [CrossRef]
- Skoulas, E.; Manousaki, A.; Fotakis, C.; Stratakis, E. Biomimetic surface structuring using cylindrical vector femtosecond laser beams. Sci. Rep. 2017, 7, 45114. [Google Scholar] [CrossRef] [Green Version]
- Romano, J.-M.; Garcia-Giron, A.; Penchev, P.; Dimov, S. Triangular laser-induced submicron textures for functionalising stainless steel surfaces. Appl. Surf. Sci. 2018, 440, 162–169. [Google Scholar] [CrossRef]
- Gregorčič, P.; Sedlaček, M.; Podgornik, B.; Reif, J. Formation of laser-induced periodic surface structures (LIPSS) on tool steel by multiple picosecond laser pulses of different polarizations. Appl. Surf. Sci. 2016, 387, 698–706. [Google Scholar] [CrossRef]
- Cong, J.; Yang, J.; Zhao, B.; Xu, X. Fabricating subwavelength dot-matrix surface structures of Molybdenum by transient correlated actions of two-color femtosecond laser beams. Opt. Express 2015, 23, 5357. [Google Scholar] [CrossRef]
- Fraggelakis, F.; Mincuzzi, G.; Lopez, J.; Manek-Hönninger, I.; Kling, R. 2D laser induced periodic surface structures with double cross-polarized pulses. Laser-Based Micro-Nanoprocessing XII 2018. [Google Scholar]
- Fraggelakis, F.; Mincuzzi, G.; Lopez, J.; Manek-Hönninger, I.; Kling, R. Controlling 2D laser nano structuring over large area with double femtosecond pulses. Appl. Surf. Sci. 2019, 470, 677–686. [Google Scholar] [CrossRef]
- Fraggelakis, F.; Mincuzzi, G.; Lopez, J.; Kling, R.; Manek-Hönninger, I. Controlling Micron and Submicron Scale Laser Induced Surface Structures on Stainless Steel with Industrial Femtosecond Lasers. J. Laser Micro/Nanoeng. 2018, 13, 206–210. [Google Scholar]
- Derrien, T.J.-Y.J.Y.; Krüger, J.; Itina, T.E.; Höhm, S.; Rosenfeld, A.; Bonse, J. Rippled area formed by surface plasmon polaritons upon femtosecond laser double-pulse irradiation of silicon: the role of carrier generation and relaxation processes. Appl. Phys. A Mater. Sci. Process. 2013, 117, 77–81. [Google Scholar] [CrossRef] [Green Version]
- Giannuzzi, G.; Gaudiuso, C.; Di Franco, C.; Scamarcio, G.; Lugarà, P.M.; Ancona, A. Large area laser-induced periodic surface structures on steel by bursts of femtosecond pulses with picosecond delays. Opt. Lasers Eng. 2019, 114, 15–21. [Google Scholar] [CrossRef]
- Höhm, S.; Herzlieb, M.; Rosenfeld, A.; Krüger, J.; Bonse, J. Dynamics of the formation of laser-induced periodic surface structures (LIPSS) upon femtosecond two-color double-pulse irradiation of metals, semiconductors, and dielectrics. Appl. Surf. Sci. 2015, 374, 331–338. [Google Scholar] [CrossRef]
- Fraggelakis, F.; Stratakis, E.; Loukakos, P.A. Control of periodic surface structures on silicon by combined temporal and polarization shaping of femtosecond laser pulses. Appl. Surf. Sci. 2018, 444, 154–160. [Google Scholar] [CrossRef]
- Sundaram, S.K.; Mazur, E. Inducing and probing non-thermal transitions in semiconductors using femtosecond laser pulses. Nat. Mater. 2002, 1, 217–224. [Google Scholar] [CrossRef]
- Tsibidis, G.D.; Barberoglou, M.; Loukakos, P.A.; Stratakis, E.; Fotakis, C. Dynamics of ripple formation on silicon surfaces by ultrashort laser pulses in subablation conditions. Phys. Rev. B 2012, 86, 115316. [Google Scholar] [CrossRef]
- Déziel, J.-L.; Dumont, J.; Gagnon, D.; Dubé, L.J.; Messaddeq, S.H.; Messaddeq, Y. Toward the formation of crossed laser-induced periodic surface structures. J. Opt. 2015, 17, 075405. [Google Scholar] [CrossRef] [Green Version]
- Tsibidis, G.D.; Mimidis, A.; Skoulas, E.; Kirner, S.V.; Krüger, J.; Bonse, J.; Stratakis, E. Modelling periodic structure formation on 100Cr6 steel after irradiation with femtosecond-pulsed laser beams. Appl. Phys. A 2018, 124, 27. [Google Scholar] [CrossRef]
- Garcia-Lechuga, M.; Puerto, D.; Fuentes-Edfuf, Y.; Solis, J.; Siegel, J. Ultrafast Moving-Spot Microscopy: Birth and Growth of Laser-Induced Periodic Surface Structures. ACS Photonics 2016, 3, 1961–1967. [Google Scholar] [CrossRef] [Green Version]
- Zhigilei, L.V.; Lin, Z.; Ivanov, D.S. Atomistic modeling of short pulse laser ablation of metals: Connections between melting, spallation, and phase explosion. J. Phys. Chem. C 2009, 113, 11892–11906. [Google Scholar] [CrossRef]
- Fang, R.; Vorobyev, A.; Guo, C. Direct visualization of the complete evolution of femtosecond laser-induced surface structural dynamics of metals. Light Sci. Appl. 2017, 6, e16256-7. [Google Scholar] [CrossRef]
- Tsibidis, G.D.; Skoulas, E.; Papadopoulos, A.; Stratakis, E. Convection roll-driven generation of supra-wavelength periodic surface structures on dielectrics upon irradiation with femtosecond pulsed lasers. Phys. Rev. B 2016, 94, 1–18. [Google Scholar] [CrossRef]
- Kirichenko, N.A.; Barmina, E.V.; Shafeev, G.A. Theoretical and Experimental Investigation of the Formation of High Spatial Frequency Periodic Structures on Metal Surfaces Irradiated by Ultrashort Laser Pulses. Phys. Wave Phenom. 2018, 26, 264–273. [Google Scholar] [CrossRef]
- Zhou, S.; Ouzounov, D.; Li, H.; Bazarov, I.; Dunham, B.; Sinclair, C.; Wise, F. Efficient temporal shaping of ultrashort pulses with birefringent crystals. Appl. Opt. 2007, 46, 8488–8492. [Google Scholar] [CrossRef]
- Rapp, S.; Kaiser, M.; Schmidt, M.; Huber, H.P. Ultrafast pump-probe ellipsometry setup for the measurement of transient optical properties during laser ablation. Opt. Express 2016, 24, 17572–17592. [Google Scholar] [CrossRef]
- Barberoglou, M.; Tsibidis, G.D.; Gray, D.; Magoulakis, E.; Fotakis, C.; Stratakis, E.; Loukakos, P.A. The influence of ultra-fast temporal energy regulation on the morphology of Si surfaces through femtosecond double pulse laser irradiation. Appl. Phys. A Mater. Sci. Process. 2013, 113, 273–283. [Google Scholar] [CrossRef]
- Hoöhm, S.; Rohloff, M.; Rosenfeld, A.; Kruger, J.; Bonse, J. Dynamics of the formation of laser-induced periodic surface structures on dielectrics and semiconductors upon femtosecond laser pulse irradiation sequences. Appl. Phys. A Mater. Sci. Process. 2013, 110, 553–557. [Google Scholar] [CrossRef]
- Höhm, S.; Rosenfeld, A.; Krüger, J.; Bonse, J. Area dependence of femtosecond laser-induced periodic surface structures for varying band gap materials after double pulse excitation. Appl. Surf. Sci. 2013, 278, 7–12. [Google Scholar] [CrossRef]
- Sedao, X.; Maurice, C.; Garrelie, F.; Colombier, J.P.; Reynaud, S.; Quey, R.; Pigeon, F. Influence of crystal orientation on the formation of femtosecond laser-induced periodic surface structures and lattice defects accumulation. Appl. Phys. Lett. 2014, 104, 171605. [Google Scholar] [CrossRef]
- Bonse, J.; Rosenfeld, A.; Krüger, J. On the role of surface plasmon polaritons in the formation of laser-induced periodic surface structures upon irradiation of silicon by femtosecond-laser pulses. J. Appl. Phys. 2009, 106, 104910. [Google Scholar] [CrossRef]
- Sipe, J.E.; Young, J.F.; Preston, J.S.; Van Driel, H.M. Laser-induced periodic surface structure. I. Theory. Phys. Rev. B 1983, 27, 1141–1154. [Google Scholar] [CrossRef]
- Tsibidis, G.D.; Fotakis, C.; Stratakis, E. From ripples to spikes: A hydrodynamical mechanism to interpret femtosecond laser-induced self-assembled structures. Phys. Rev. B 2015, 92, 041405. [Google Scholar] [CrossRef]
- Koschmieder, E.L.; Pallas, S.G. Heat transfer through a shallow, horizontal convecting fluid layer. Int. J. Heat Mass Transf. 1974, 17, 991–1002. [Google Scholar] [CrossRef]
- Busse, F.H. Non-linear properties of thermal convection. Reports Prog. Phys. 1978, 41, 1929. [Google Scholar] [CrossRef]
- Cross, M.C.; Hohenberg, P.C. Pattern formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 851–1112. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Zhang, N.; Yang, J.; Qiao, H.; Guo, C. Direct fabricating large-area nanotriangle structure arrays on tungsten surface by nonlinear lithography of two femtosecond laser beams. Opt. Express 2018, 26, 11718–11727. [Google Scholar] [CrossRef]
- Alamri, S.; Fraggelakis, F.; Kunze, T.; Krupop, B.; Mincuzzi, G.; Kling, R.; Lasagni, A.F. On the Interplay of DLIP and LIPSS Upon Ultra-Short Laser Pulse Irradiation. Materials 2019, 12, 1018. [Google Scholar] [CrossRef]
- Dromey, B.; Zepf, M.; Landreman, M.; O’Keeffe, K.; Robinson, T.; Hooker, S.M. Generation of a train of ultrashort pulses from a compact birefringent crystal array. Appl. Opt. 2007, 46, 5142. [Google Scholar] [CrossRef]
- Skolski, J.Z.P.; Römer, G.R.B.E.; Obona, J.V.; Ocelik, V.; Huis In ’t Veld, A.J.; De Hosson, J.T.M. Laser-induced periodic surface structures: Fingerprints of light localization. Phys. Rev. B 2012, 85, 075320. [Google Scholar] [CrossRef]
- Skolski, J.Z.P.; Römer, G.R.B.E.; Vincenc Obona, J.; Huis in ’T Veld, A.J. Modeling laser-induced periodic surface structures: Finite-difference time-domain feedback simulations. J. Appl. Phys. 2014, 115, 103102. [Google Scholar] [CrossRef]
- Bonse, J.; Hoöhm, S.; Rosenfeld, A.; Kruger, J. Sub-100-nm laser-induced periodic surface structures upon irradiation of titanium by Ti:sapphire femtosecond laser pulses in air. Appl. Phys. A Mater. Sci. Process. 2013, 110, 547–551. [Google Scholar] [CrossRef]
- Gaudiuso, C.; Giannuzzi, G.; Volpe, A.; Lugarà, P.M.; Choquet, I.; Ancona, A. Incubation during laser ablation with bursts of femtosecond pulses with picosecond delays. Opt. Express 2018, 26, 3801. [Google Scholar] [CrossRef]






| Setup | Delay | Overlap (pps) | Hatch (H) | Fluence (Φ) | Dose (ppstot) | Source |
|---|---|---|---|---|---|---|
| Delay line | |1 ps|≤ Δτ<|10 ps| | 10 | 1 μm | 0.1 J/cm2 | 250 | [17] |
| BCs | 1.5 ps, 3 ps | 20 | 2 μm | 0.1 J/cm2 | 240 | Figure 2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fraggelakis, F.; Giannuzzi, G.; Gaudiuso, C.; Manek-Hönninger, I.; Mincuzzi, G.; Ancona, A.; Kling, R. Double- and Multi-Femtosecond Pulses Produced by Birefringent Crystals for the Generation of 2D Laser-Induced Structures on a Stainless Steel Surface. Materials 2019, 12, 1257. https://doi.org/10.3390/ma12081257
Fraggelakis F, Giannuzzi G, Gaudiuso C, Manek-Hönninger I, Mincuzzi G, Ancona A, Kling R. Double- and Multi-Femtosecond Pulses Produced by Birefringent Crystals for the Generation of 2D Laser-Induced Structures on a Stainless Steel Surface. Materials. 2019; 12(8):1257. https://doi.org/10.3390/ma12081257
Chicago/Turabian StyleFraggelakis, Fotis, Giuseppe Giannuzzi, Caterina Gaudiuso, Inka Manek-Hönninger, Girolamo Mincuzzi, Antonio Ancona, and Rainer Kling. 2019. "Double- and Multi-Femtosecond Pulses Produced by Birefringent Crystals for the Generation of 2D Laser-Induced Structures on a Stainless Steel Surface" Materials 12, no. 8: 1257. https://doi.org/10.3390/ma12081257
APA StyleFraggelakis, F., Giannuzzi, G., Gaudiuso, C., Manek-Hönninger, I., Mincuzzi, G., Ancona, A., & Kling, R. (2019). Double- and Multi-Femtosecond Pulses Produced by Birefringent Crystals for the Generation of 2D Laser-Induced Structures on a Stainless Steel Surface. Materials, 12(8), 1257. https://doi.org/10.3390/ma12081257








