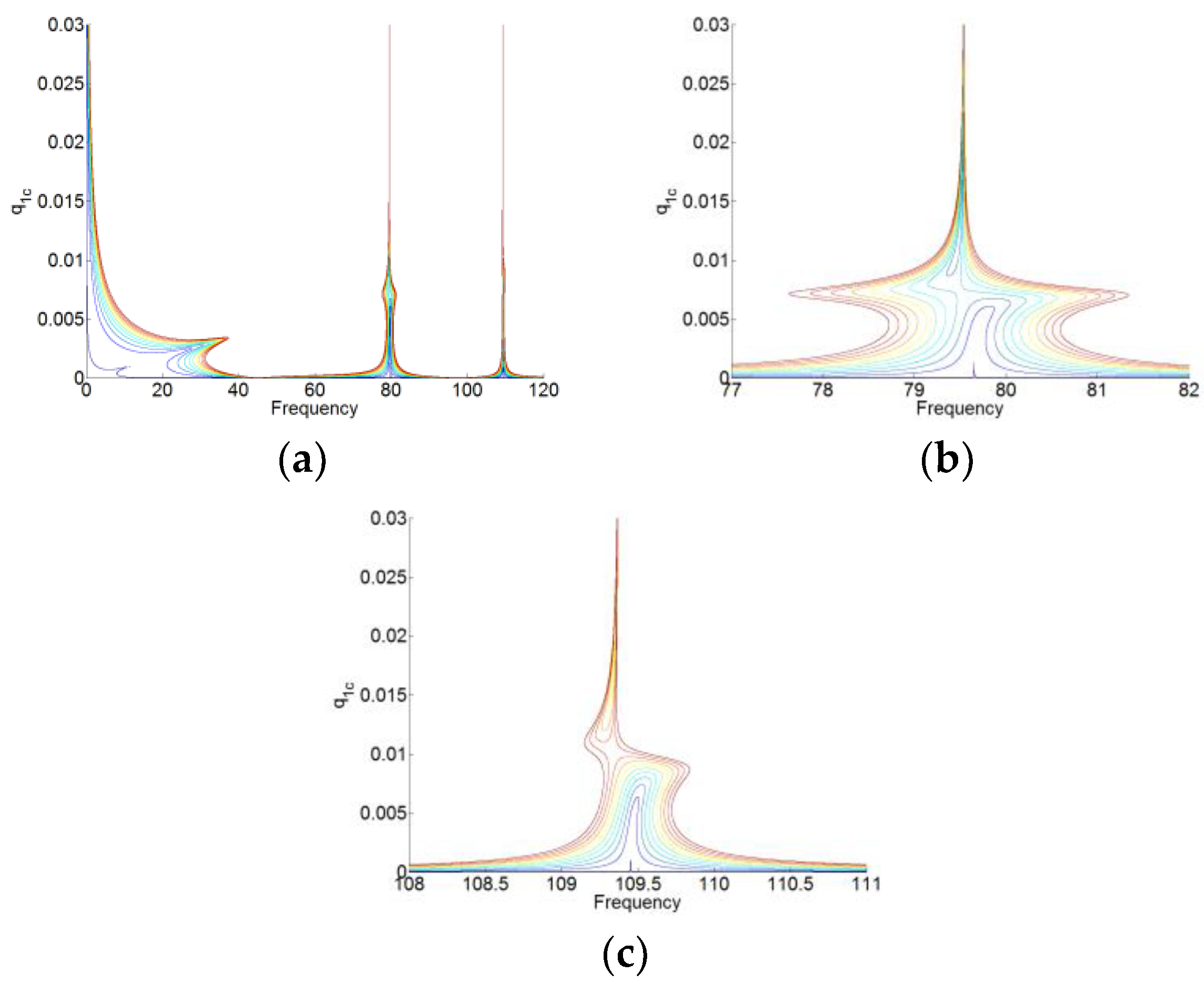
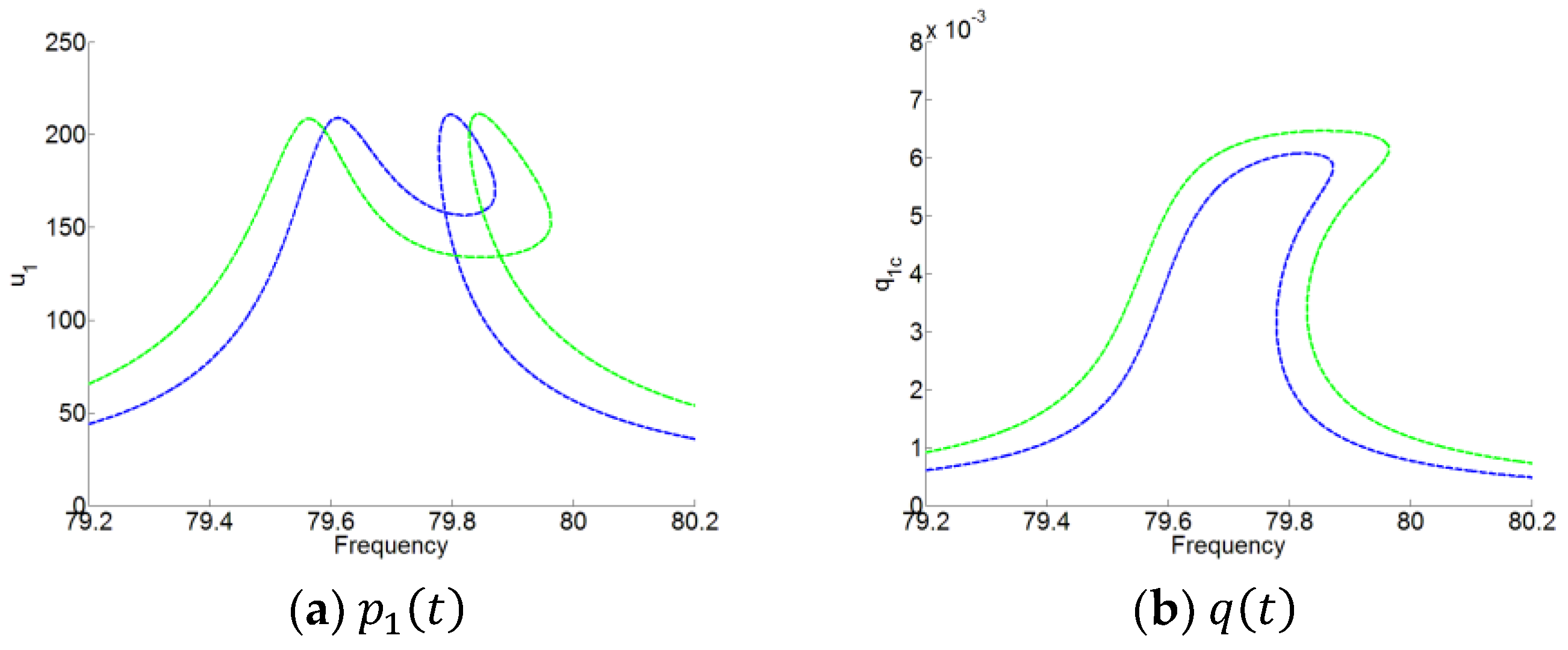
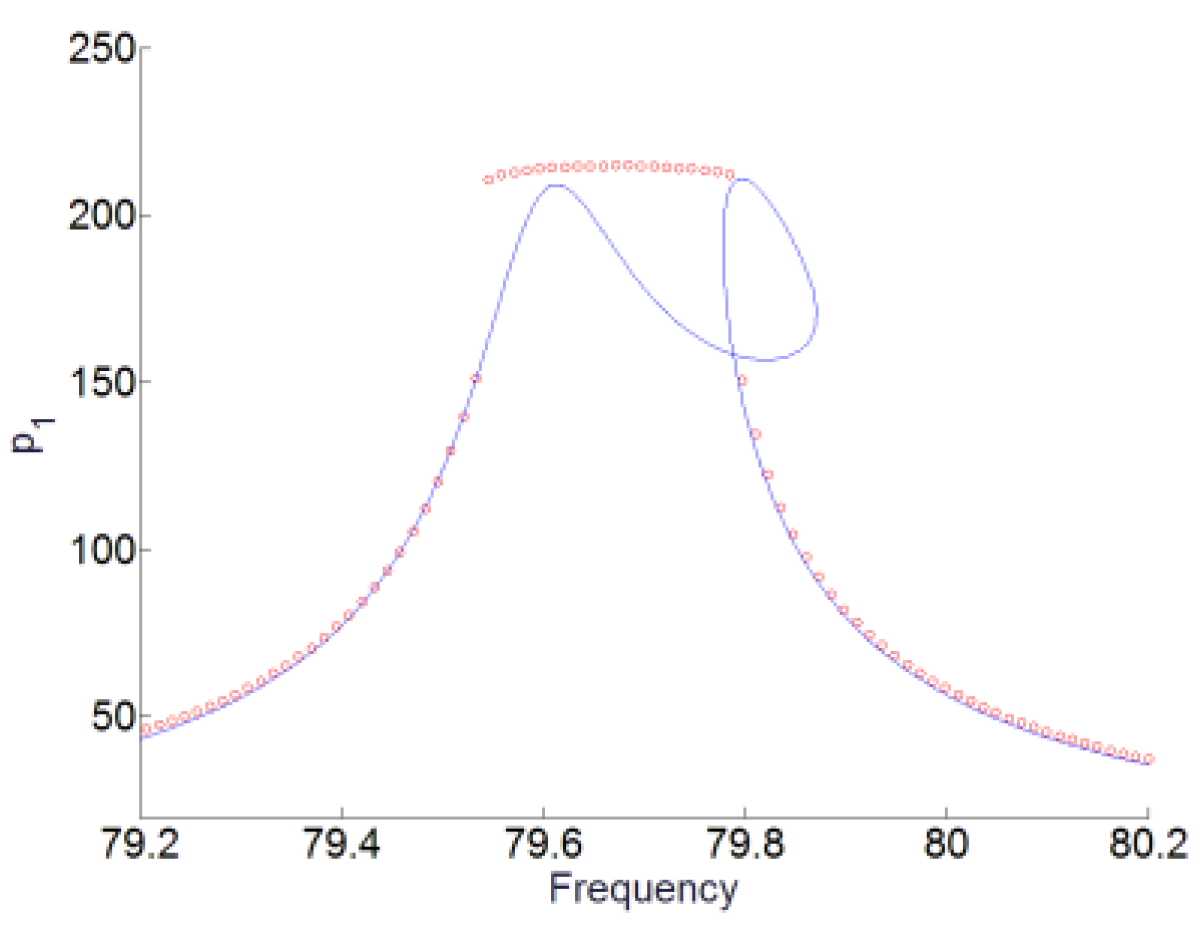
1. Introduction
Many techniques, which include active noise control method [
1] and vibration damping materials [
2], are used to control noise inside a 3D enclosed cavity. The computer aided engineering (CAE) methods are applied to easily treat with interior acoustic problems, such as finite element method (FEM), boundary element method (BEM), and extended methods based on above CAE methods [
3,
4,
5]. Recently, acoustic metamaterials are studied by the researchers to control sound waves, where a lot of progress has been made [
6,
7]. Meanwhile, there are many challenges in the practical implementation of acoustic metamaterials [
8].
Since the concept of targeted energy transfer (TET) was proposed by Vakakis and Gendelman [
9,
10] in 2001, many studies have been made in view of application in the field of mechanical vibrations [
11,
12,
13,
14,
15] by a purely nonlinear absorber called as nonlinear energy sink (NES). Meanwhile, in acoustic field, the TET phenomenon was firstly demonstrated inside one tube (1D acoustic system) by a nonlinear membrane NES [
16]. The TET between the membrane and the tube for both free and forced oscillations was investigated [
17,
18]. Moreover, a loudspeaker working outside its linear regime was demonstrated that it could also be an efficient NES [
19]. In these studies [
16,
17,
18], the nonlinear membrane NES was used to reduce one acoustic mode of the tube standing for the linear system. Cote et al. [
20] analyzed the TET phenomenon between the nonlinear membrane NES and two acoustic modes of the tube and observed the membrane could reduce the two resonance peaks, simultaneously.
In view of extending the application of the membrane NES in acoustic field, an acoustic cavity (3D acoustic system) was considered and the TET phenomenon was observed inside the acoustic cavity by the nonlinear membrane NES without considering the pre-stress of the membrane [
21,
22,
23]. By analyzing the nonlinear normal modes (NNM) and the periodic forced responses of a two degrees-of-freedom (DOF) system comprised of one acoustic mode of cavity and a nonlinear membrane NES, the desired working zone for the membrane NES was defined and the two thresholds of the zone were also determined analytically and semi-analytically, respectively [
21]. Based on these analytical results, the parametric analysis of the membrane was studied to reveal that the radius of the membrane affected mainly the desired working zone [
22]. To extending the results obtained by the 2DOFs, the 3DOFs system with two nonlinear membranes and one acoustic mode was also investigated [
23,
24]. Two nonlinear membranes could enlarge the desired working zone of the NES.
In this paper, in order to control the low frequency broadband noise (20–200 Hz) inside 3D acoustic cavity and consider the influence of the pre-stress for the TET, a general model of the system with several acoustic modes of 3D acoustic cavity and one nonlinear membrane is firstly built. The influence of the pre-stress of the membrane for the TET is investigated. A multi-DOFs system comprised by a nonlinear membrane absorber and two acoustic modes or multi-acoustic modes are studied. The forced responses of the system are analyzed. The desired working zone and the value of the plateau for low frequency broadband noise of the nonlinear membrane absorber are investigated. Numerical simulations are finally preformed to validate the TET phenomenon of the system and the analytical results.
2. Description of the System
2.1. The Acoustic Cavity and the Membrane
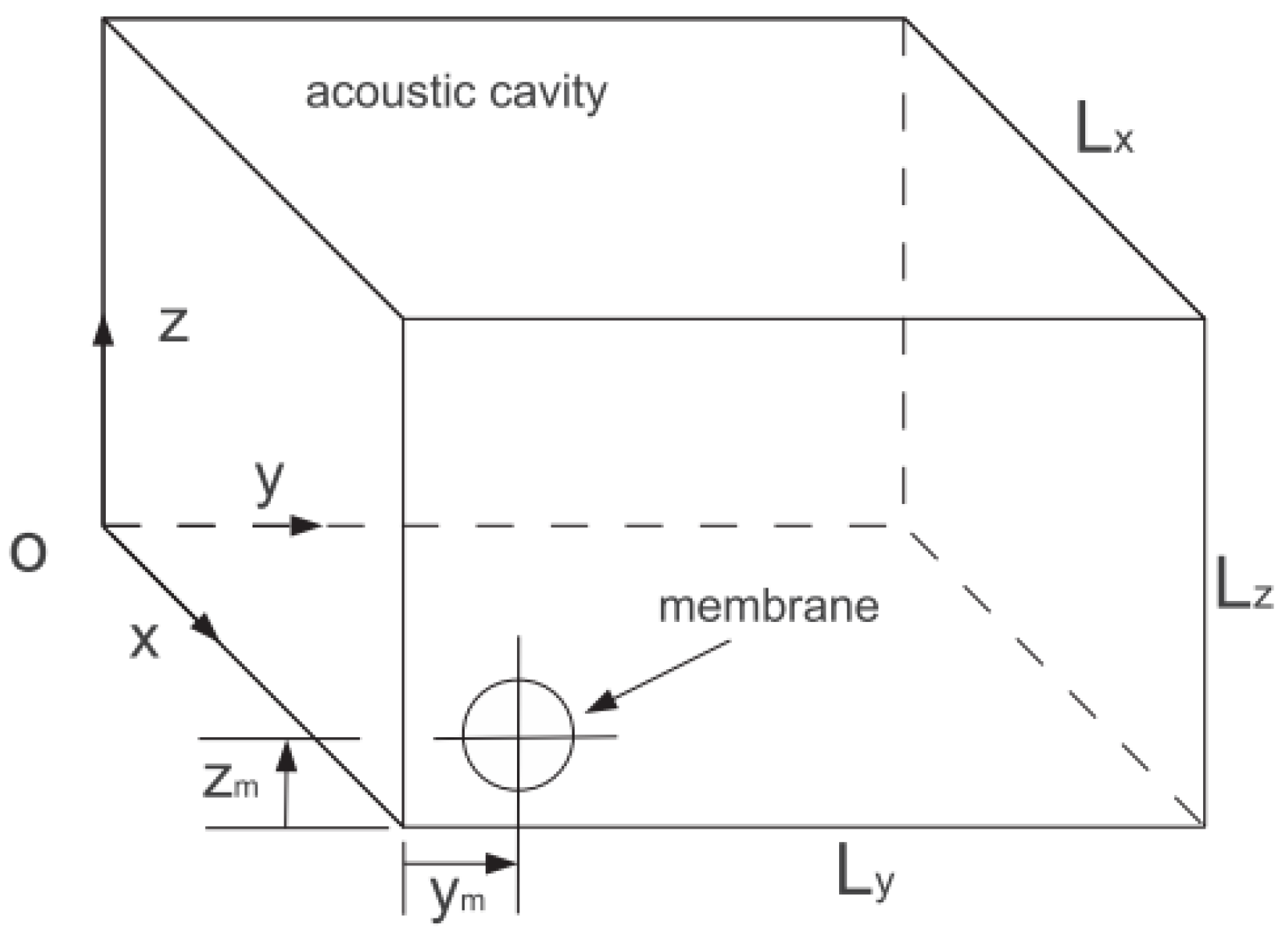
The schema of the system in this paper is shown in
Figure 1, which is comprised of an acoustic medium inside a parallelepiped cavity and a thin viscoelastic membrane that is mounted on one wall of the cavity. The dimensions of the acoustic cavity are
,
and
and the position of the membrane is marked as (
,
,
) (
).
In order to build a general model, the modes of 3D acoustic cavity between the frequency band 20–200 Hz and one nonlinear membrane are, respectively, considered as the linear system with multi-DOFs and the NES. We assume that six walls of the acoustic cavity shown in
Figure 1 are rigid. Thus, the mode shape of the cavity
is defined as following:
In this paper, we assume that the modes between the frequency band 20–200 Hz of the cavity are separated in frequency, and we focus on the interaction between the modes of the cavity and the membrane with the pre-stress. Here, in order to consider several modes of the acoustic cavity, we use the marks
and
to respectively represent each mode shape and its corresponding acoustic pressure
. Thus, the acoustic pressure inside the acoustic cavity is represented in the following form:
For the membrane, in this paper, one DOF model based on the membrane in Reference [
17] is taken into account. In References [
21,
22,
23], the membrane was mounted on one wall of the cavity and analyzed for the TET without the pre-stress. Here, the influence of the pre-stress of the membrane for the TET is analyzed, where the term of linear stiffness is used to present the pre-stress. We assume if the size of the membrane on the wall is small by comparing to the size of the acoustic cavity and the several low frequency modes are considered, the acoustic pressure in contact with the membrane is uniform and defined to equal to the value at the center of the membrane. Thus, the equation of the membrane is as follows:
where,
is the transversal displacement of the membrane center (direction
in
Figure 1) and
is the acoustic pressure amplitude inside the cavity. The coefficients
and
are the linear and nonlinear stiffness, respectively.
and
are, respectively, the first resonance frequency of the membrane with and without the pre-stress.
, and
are the radius, the thickness, Young’s modulus, Poisson’s ratio, the viscous parameter, and the density of the membrane, respectively.
2.2. Coupling Between Several Acoustic Modes and a Nonlinear Membrane
The membrane is mounted on the wall of the cavity by the clamped boundary condition. Thus, the equations that govern the acoustic pressure inside the acoustic cavity are as follows:
where
is the source of force inside the cavity and
is the position of the source.
and
are the internal volume of the cavity, the surface of the cavity and the surface of the membrane, respectively.
is the surface of the cavity without the surface of the membrane.
and
are the density of the air and the sound velocity, respectively.
The system is performed a Rayleigh–Ritz reduction by using the mode shape
as a single shape function for
and for the test function
[
22,
23]:
Then, the following equations are obtained:
where,
and equal to and , respectively.
For
,
Finally, the general model of the system with several acoustic modes of 3D acoustic cavity and one nonlinear membrane is obtained by dividing the corresponding mass of each equation of Equations (3) and (7), replacing the pressure amplitude by the displacement amplitude
and introducing a coefficient
for the acoustic damping:
where,
For the parameters, we choose the dimensions of the cavity are m, m, m. The position of the membrane is and the position of the source of forcing is . The values of the membrane and air parameters are:
m, m, s−1, MPa, , kg m−3, kg m−3, and m s−1. And they are fixed along the paper. The units of , , and are Pa, m/s2, Hz and s, respectively and the unit of the amplitude of and is m.
3. Influence of the Pre-Stress of the Membrane for the TET
In Reference [
21], the TET phenomenon of the system with one mode of the acoustic cavity and one membrane without the pre-stress was observed according to the strongly modulated response (SMR) [
25,
26]. And the desired working zone for the membrane NES as the forcing level interval was defined based on the first destabilization of the resonance peak and the appearance of an additional branch of periodic regimes. In order to analyze the influence of the pre-stress of the membrane for the TET, a system comprised by the first mode of the acoustic cavity and one membrane with the pre-stress is considered in the following form:
where,
Here,
represents the term of the pre-stress of the membrane. For different pre-stress, the different
values are taken into account based on the test results in Reference [
17]. However,
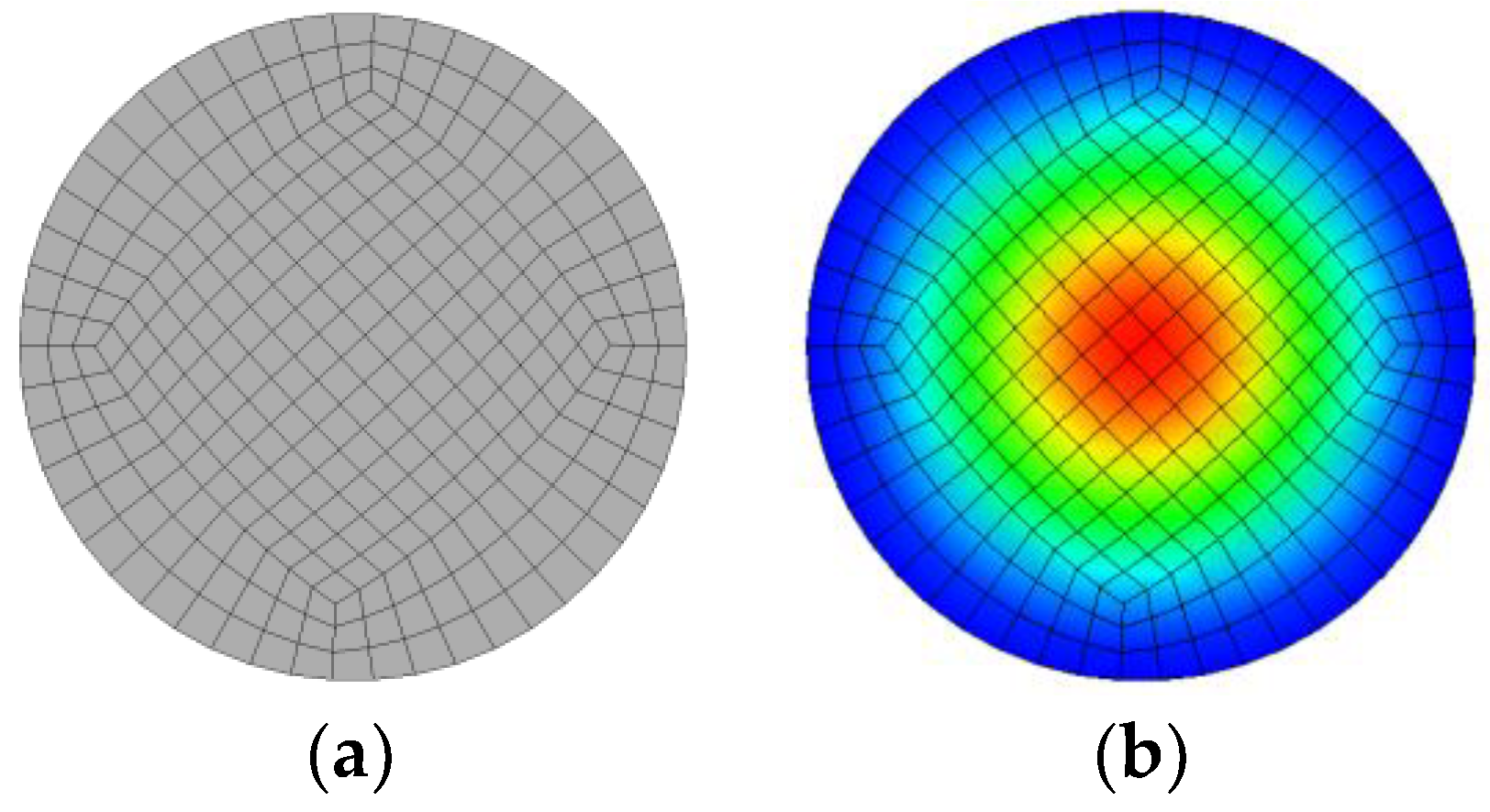
is a constant for the membrane without the pre-stress. In this paper, the FEA method is used to calculate the value of
to validate the formulae of
. The FE model of the membrane is built and the first mode of the membrane is obtained, as shown in
Figure 2. We can see that the values obtained by FEA and the theoretical formulae are same as
.
The term of
is just added in the system (12) with the pre-stress of the membrane compared with the system without the pre-stress of the membrane in Reference [
21]. Here, by using the harmonic balance method (HBM) with a single harmonic term, the periodic forced responses of the system are investigated. In Equation (12), the nonlinear terms are
and
. Thus, in order to get the easy calculation, we set
and take the force
and the displacements
and
as follows:
By substituting the solutions in Equation (14) into Equation (12) and neglecting the higher harmonic in
, the following algebraic equations are obtained:
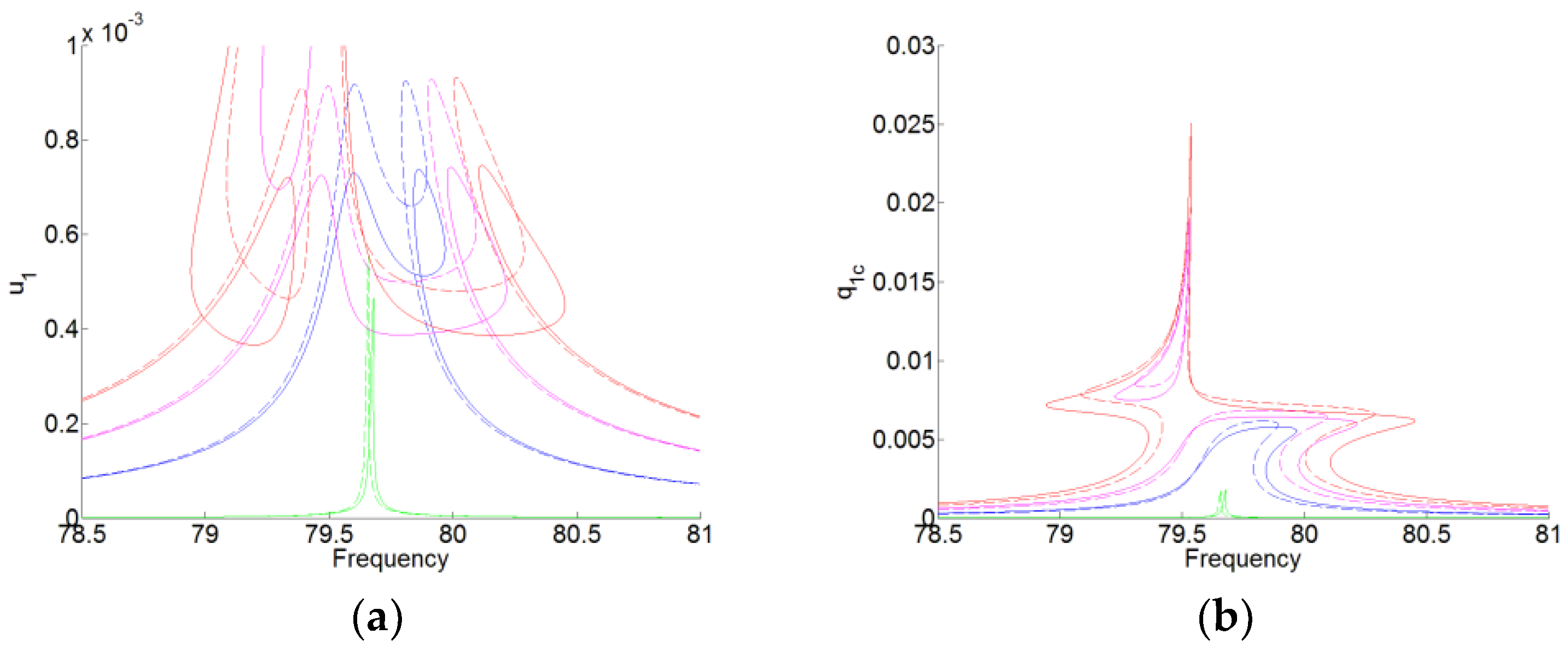
For Equation (15), there are eight unknown parameters. We take the amplitude of the membrane
and the angular frequency of the force
as the master parameters. Thus, the response surfaces are obtained with the pre-stress of the membrane (
), as shown in
Figure 3. In
Figure 3, the dashed lines represent the responses without the pre-stress of the membrane, which are the same results in Reference [
21]. The solid lines represent the responses with the pre-stress of the membrane. We can see that according to the form of the responses, the TET phenomenon can occur for the system with the membrane with the pre-stress. And the membrane with the pre-stress can reduce the amplitude of the acoustic displacement, which is the plateau of the amplitude of
.
In Reference [
21], the desired working zone for the membrane NES without the pre-stress as the forcing level interval was defined based on the first destabilization of the resonance peak and the appearance of an additional branch of periodic regimes. The analytical formula of the two thresholds
and
are defined. In order to analyze the influence of the pre-stress of the membrane for the TET of the system, three configurations for the pre-stress of the membrane are chosen, which are
,
and
, respectively.
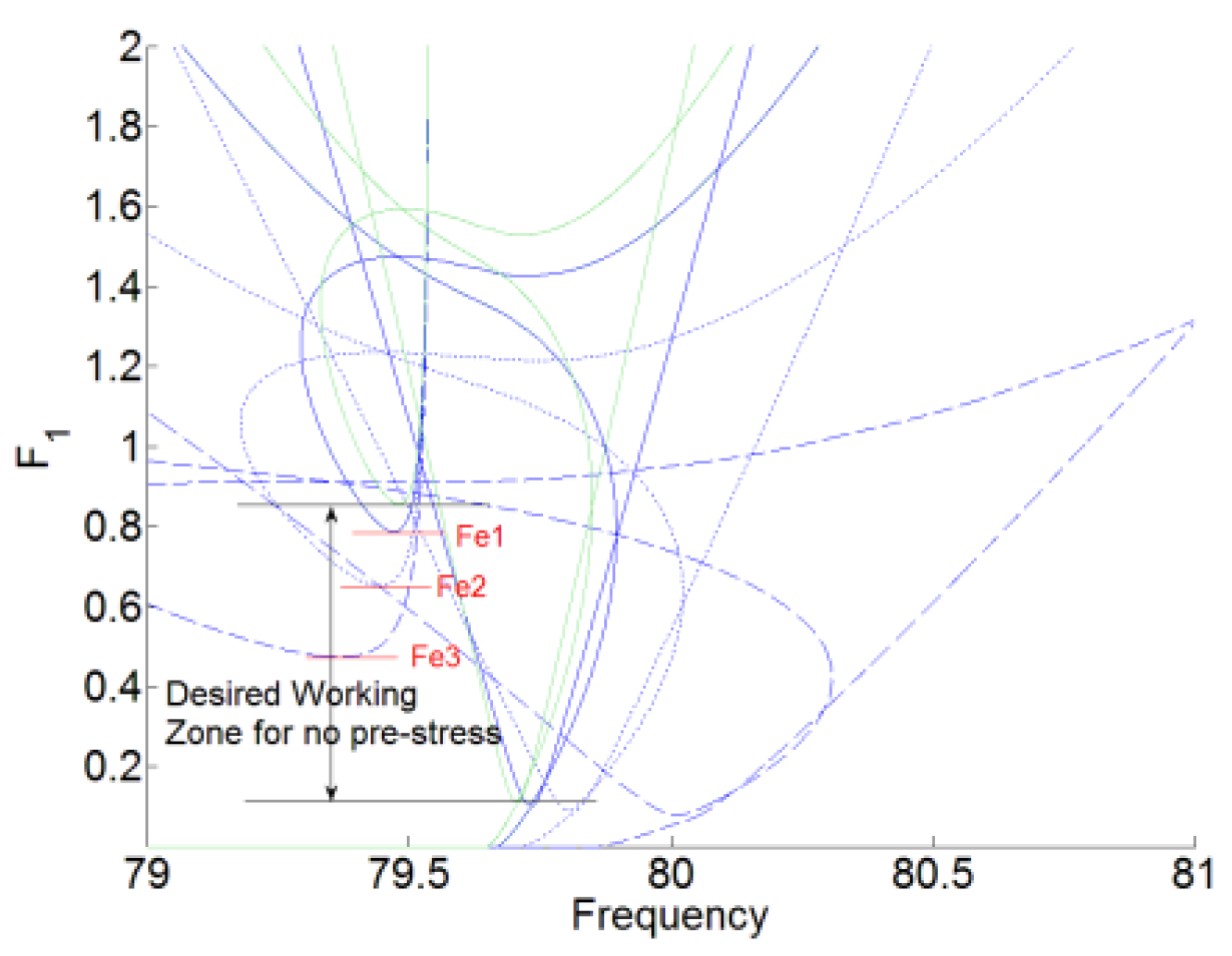
Figure 4 and
Figure 5 show the desired working zone for the membrane NES and the plateau of the amplitude
for the acoustic displacement with three different pre-stress, which are represented by
,
, and
.
,
, and
represent the ending thresholds for
,
, and
, respectively.
,
,
, and
represent the plateau of the amplitude of for the acoustic displacement for no pre-stress,
,
, and
, respectively. By comparing with no pre-stress of the membrane, which is represented by the green and solid lines, the higher of the first resonance frequency
, the narrower desired working zone for the membrane NES. And the beginning threshold
is nearly unchanged, while the ending threshold
decreases with the increase of the resonance frequency
. But, with the higher pre-stress, we also can obtain the lower value for the plateau of the amplitude of
(the value of the response suppression) and the larger bandwidth of frequency for the noise suppression.
The numerical simulations of the system (12) are performed by using the 4th and 5th order Runge–Kutta method to validate the TET phenomenon of the system with the pre-stress of the membrane. Here, we only take an example
to analyze the numerical results.
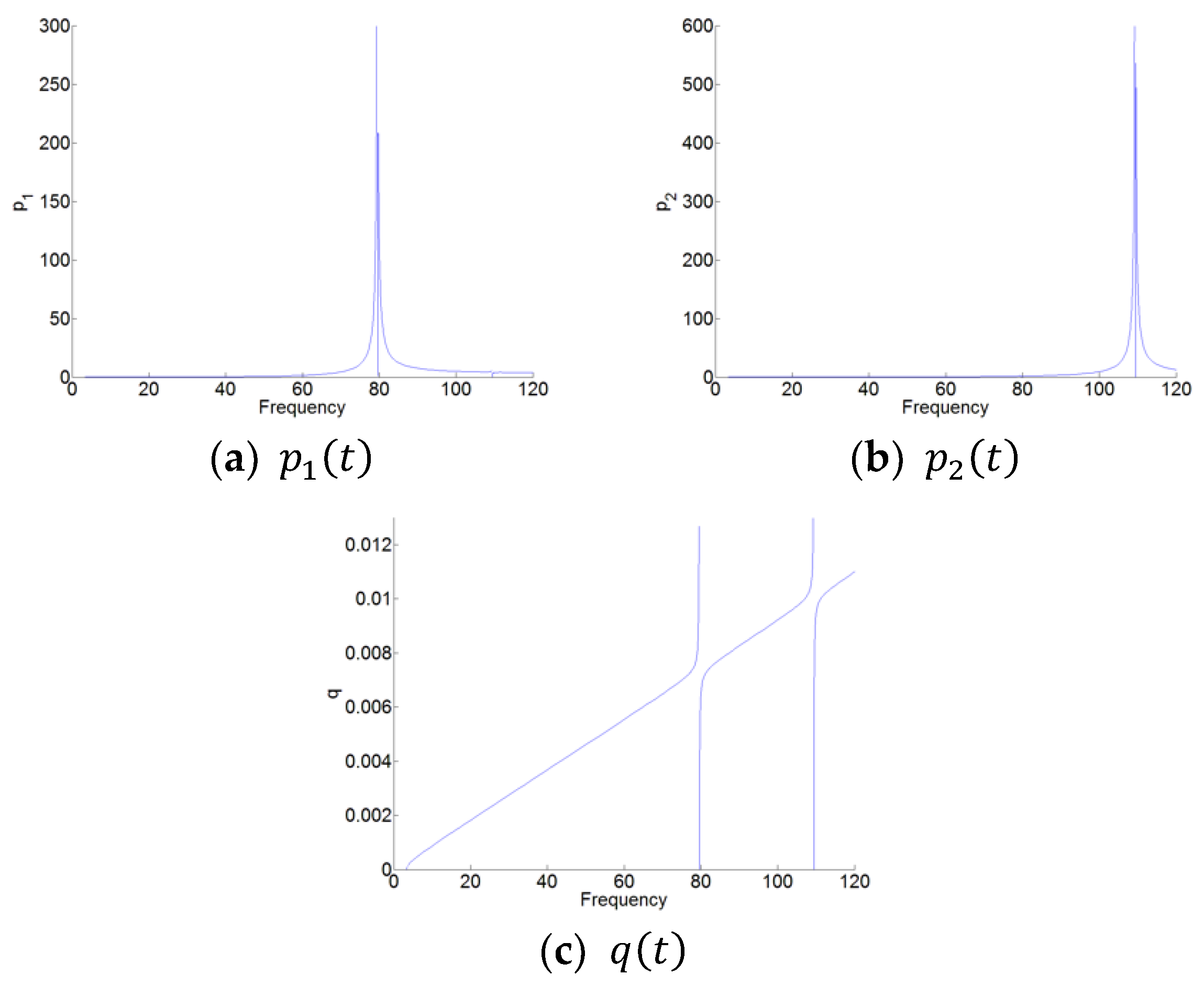
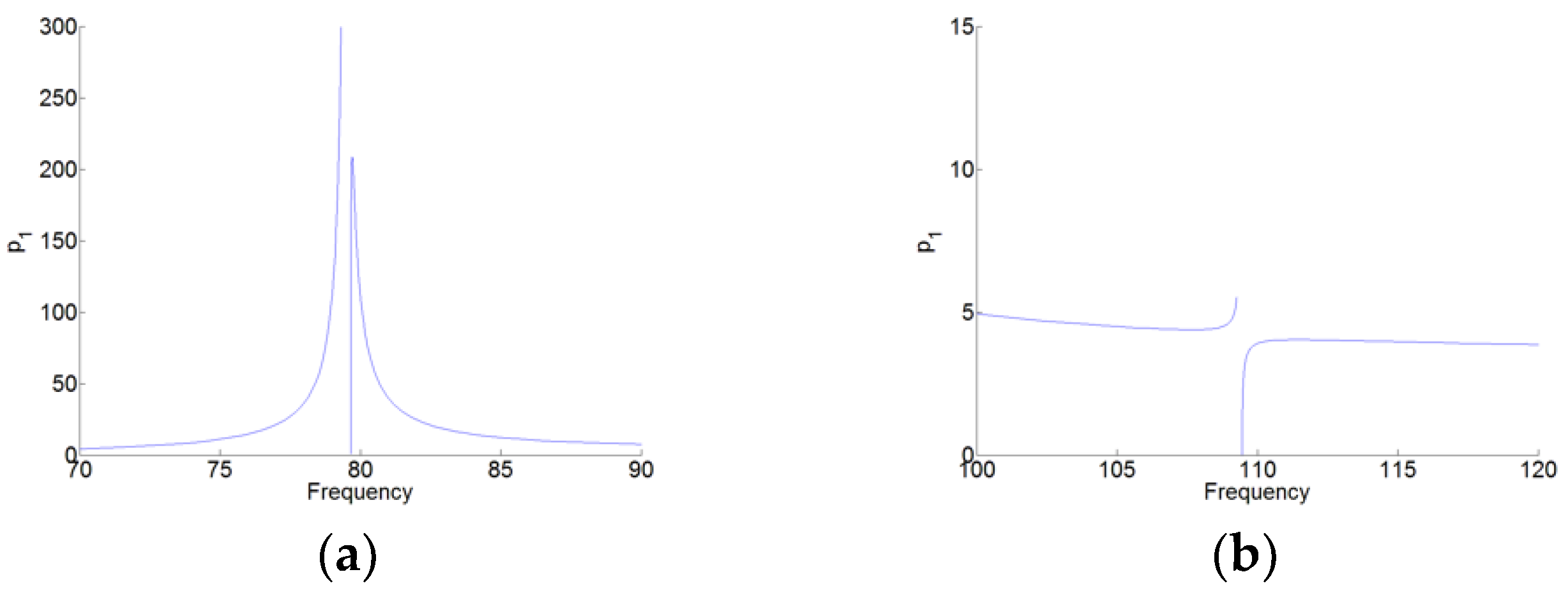
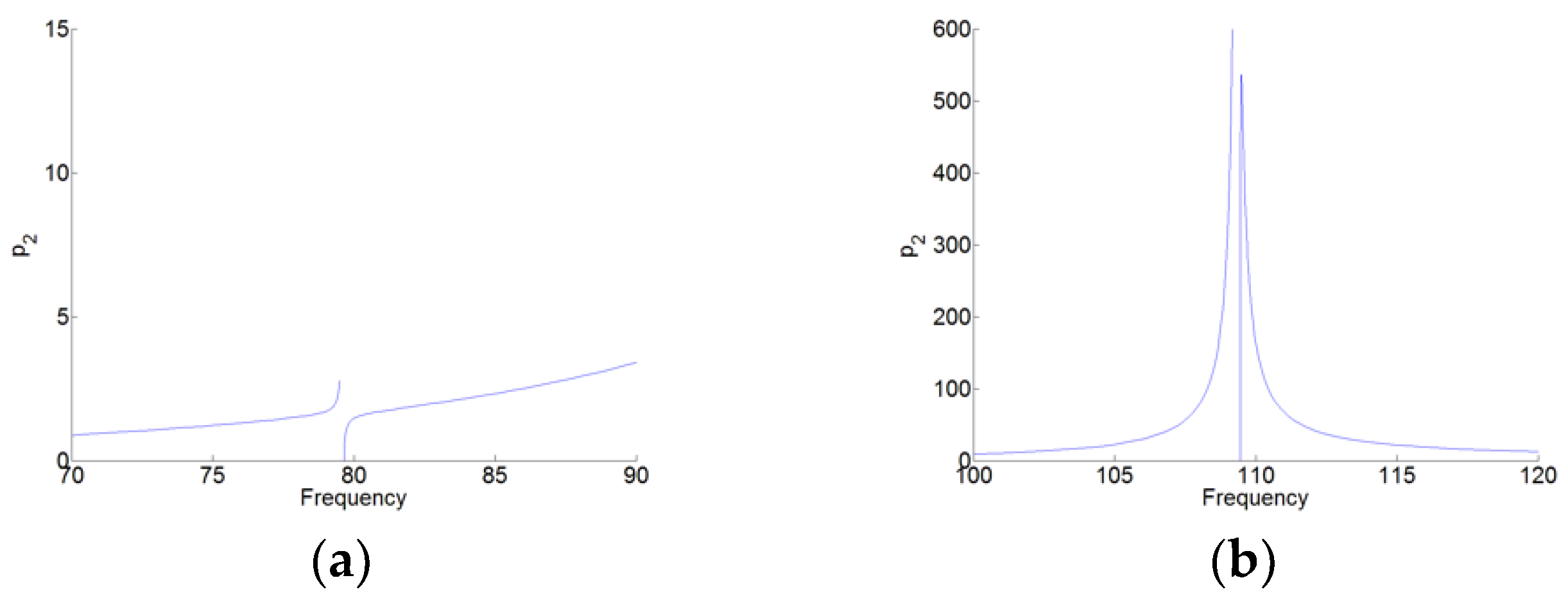
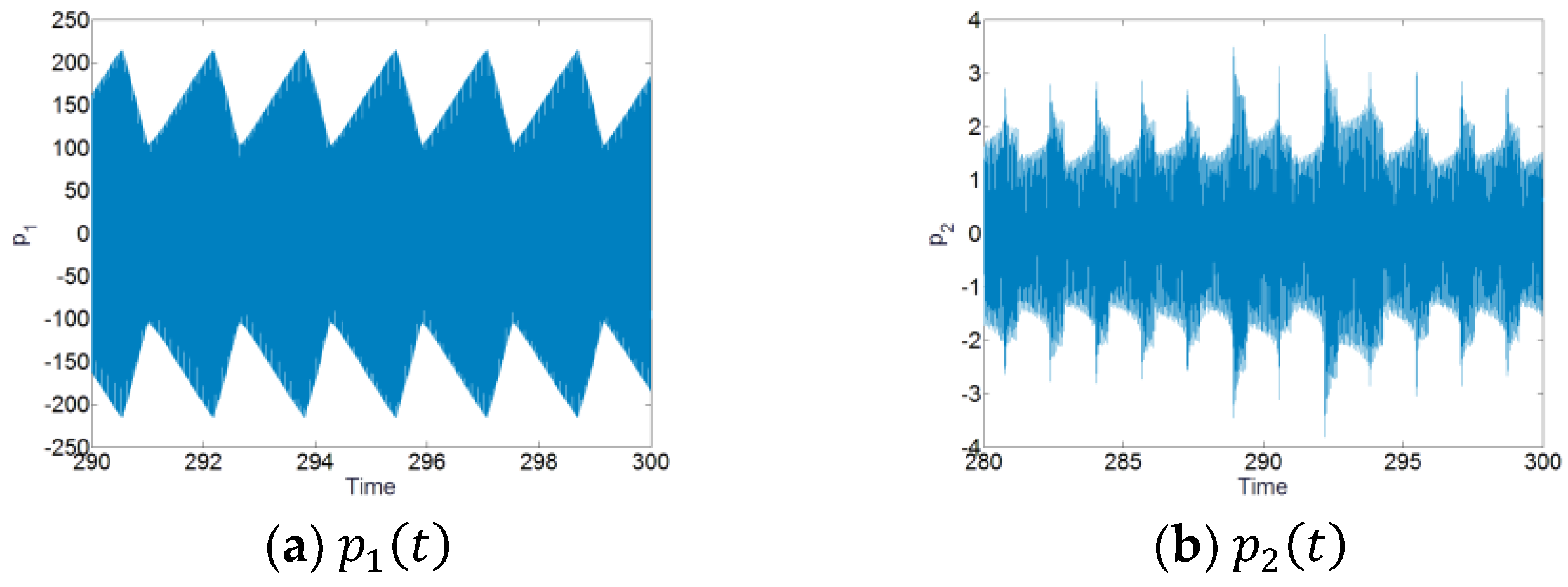
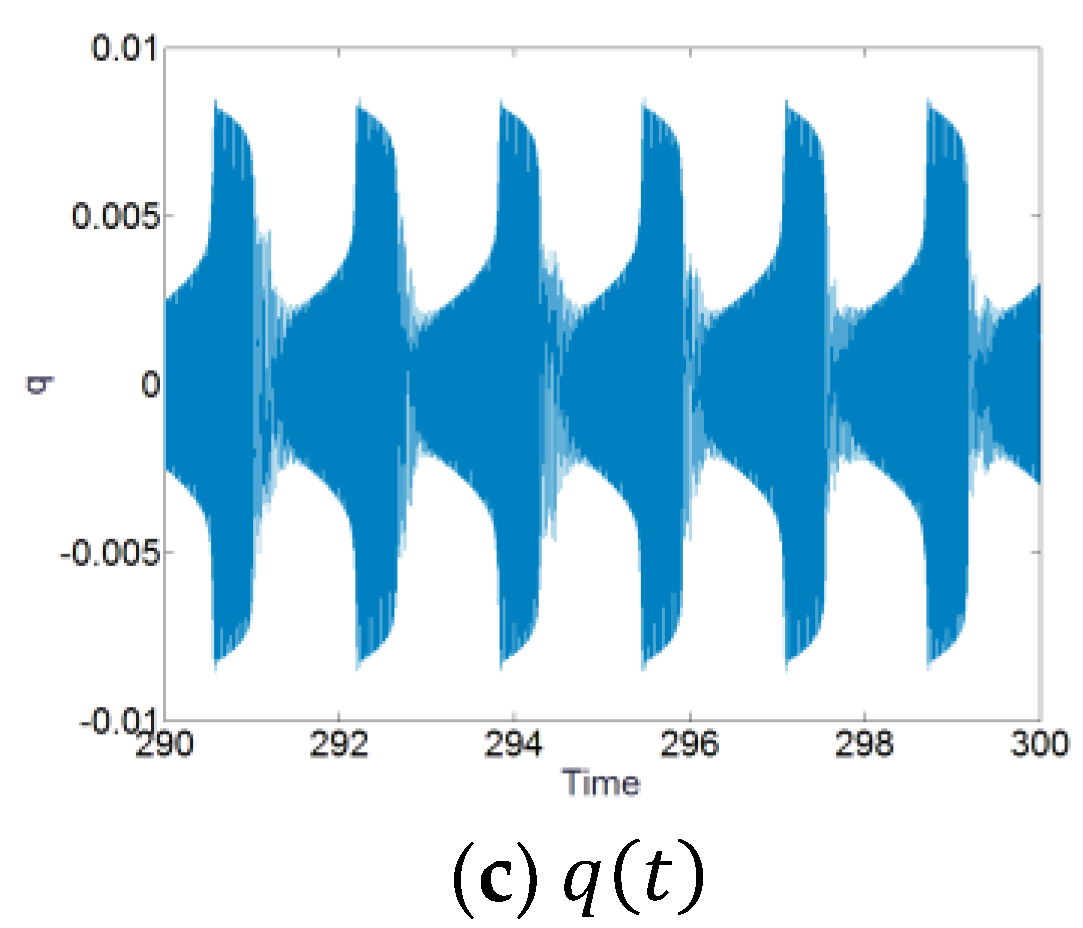
Figure 6 shows the time series for the displacements
and
with the forcing level
and the excitation frequency 79.9 Hz. We can see that the responses of the system show the SMR. Thus, the TET phenomenon occurs for the system with the pre-stress of the membrane. Meanwhile, the value of the plateau for
in
Figure 6a by the dashed and black line show a good correspondence with the value of the plateau in
Figure 5 by ‘Plateau2’.
6. Discussion and Conclusions
In order to control the low frequency broadband noise (20–200 Hz) inside 3D acoustic cavity and consider the influence of the pre-stress for the TET, a general model of the system with several acoustic modes of 3D acoustic cavity and one nonlinear membrane is built. The analytical formula of the first resonance frequency for the membrane without the pre-stress is validated by the FEA method. For the results of the influence of the pre-stress of the membrane NES, if the membrane has the higher pre-stress (represented by the first resonance frequency with the pre-stress ), the narrower desired working zone for the membrane NES is obtained with no change for the beginning threshold and decrease for the ending threshold . However, the lower value of the plateau of the amplitude of and the larger bandwidth of frequency for the noise suppression could be got. The results for the membrane with the pre-stress are validated by the numerical simulations.
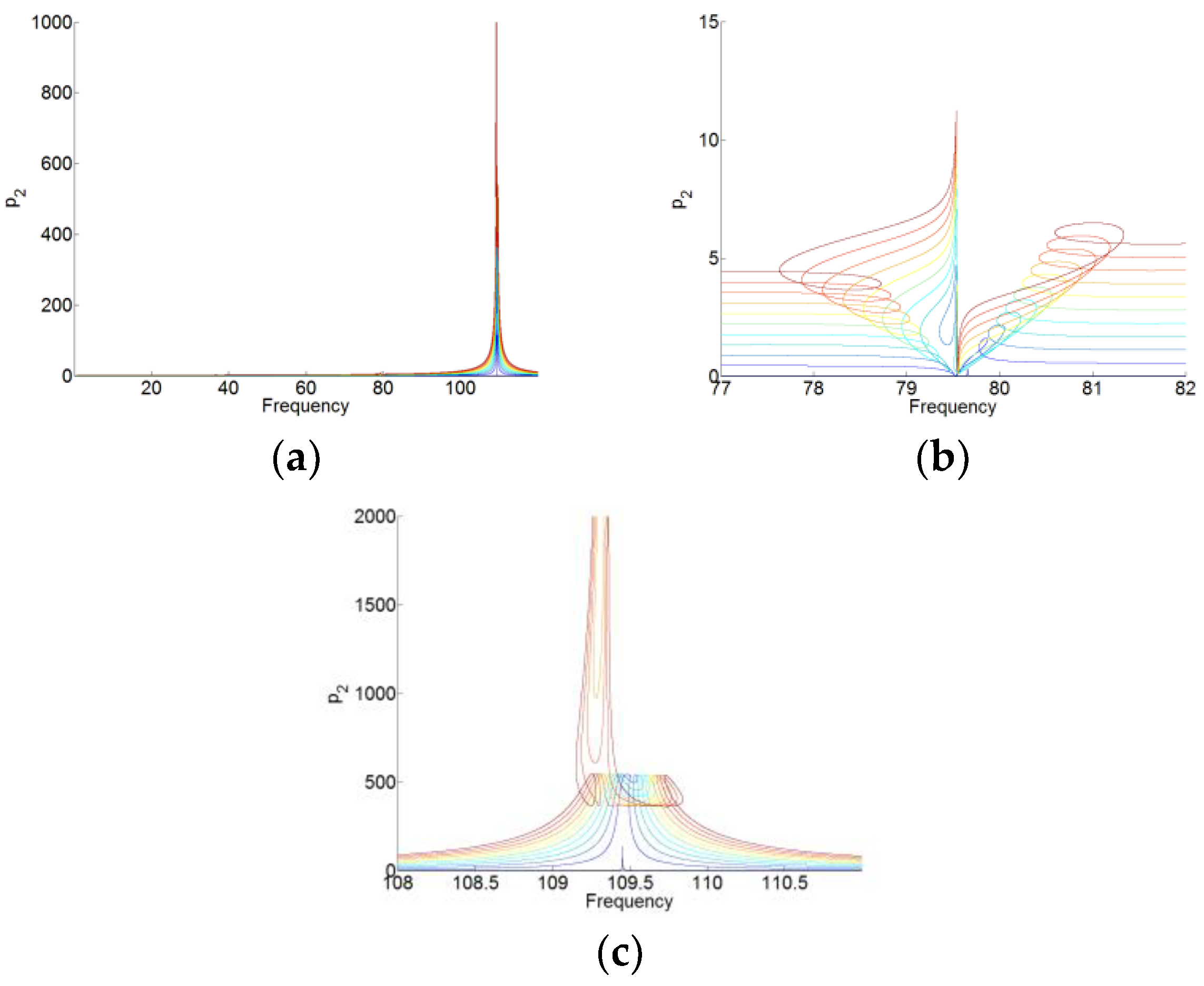
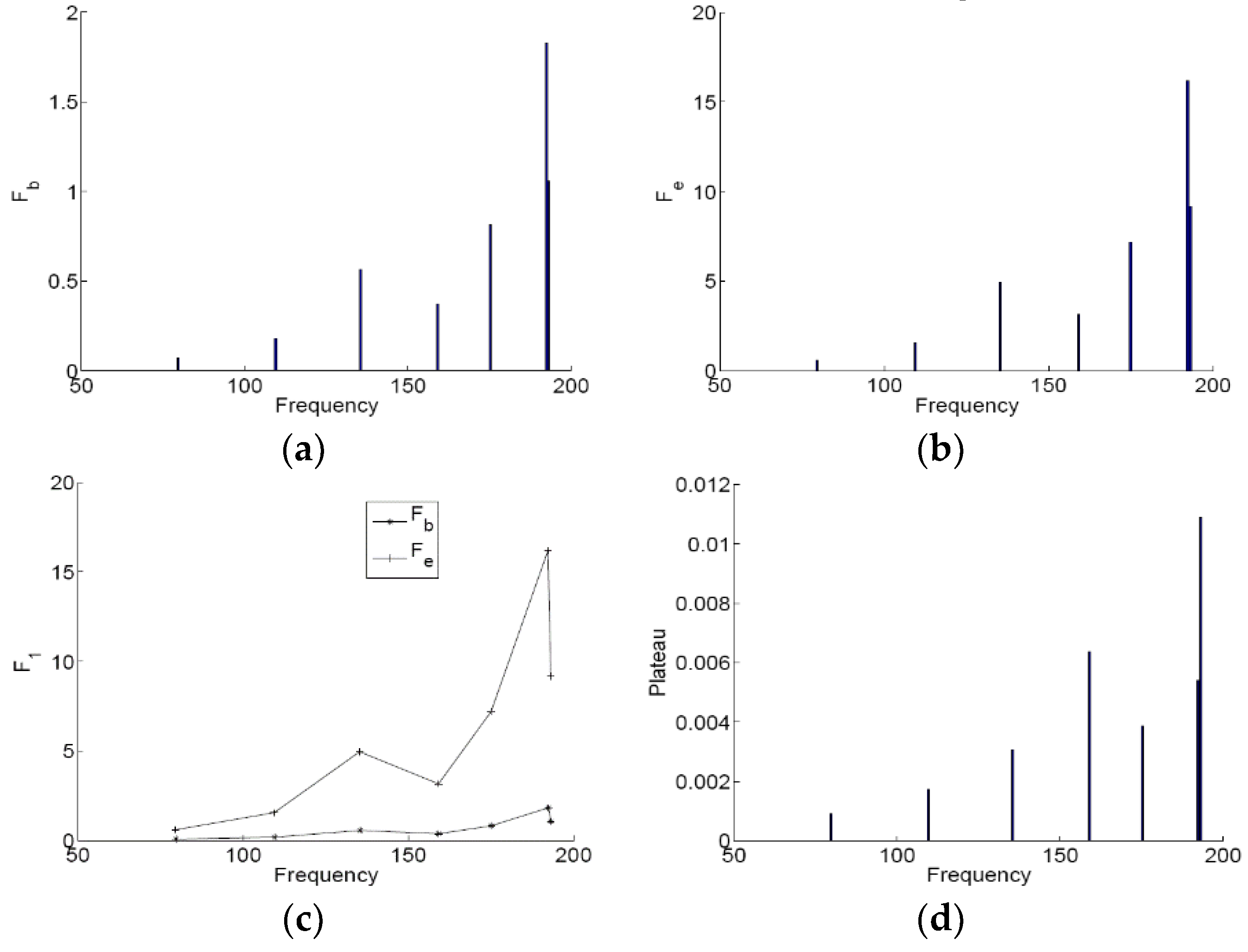
A three DOFs system comprised by the membrane and two acoustic modes is then studied to demonstrate the membrane could work for the two acoustic modes. We can separate the two modes of the cavity to couple the membrane for looking for the solutions of the system according to the analytical results. Moreover, the numerical simulations are performed to validate the analytical predictions and the TET phenomenon. Finally, the multi-DOFs system with seven modes and the membrane is analyzed to get the desired working zone and the value of the plateau of the nonlinear membrane absorber for low frequency broadband noise. It will be helpful to design the nonlinear membrane NES according the dimension of a given 3D acoustic cavity to reduce the low frequency noise. It provides us a new treatment to control passively the low frequency broadband noise.
In this paper, for 3D acoustic cavity, the irregular acoustic cavity and the acoustic damping modes are not considered. For the nonlinear membrane, the membrane is not considered to be mounted on the flexible plate. Because these will cause a coupling between the acoustic cavity modes and also affect the forced responses inside 3D acoustic cavity. In future, different above conditions will be analyzed for the practical applications of the membrane. And the analytical and numerical results of the system will be also validated by the experimental methods. For other applications of the nonlinear membrane, the acoustic metamaterials based on the membrane will be taken in account and the sound energy harvesting based on TET by using the designed structures including the nonlinear membrane will be investigated. It may provide novel applications for the membrane and the secondary energy utilization of noise inside 3D acoustic cavity.