Design of Polarization-Independent and Wide-Angle Broadband Absorbers for Highly Efficient Reflective Structural Color Filters
Abstract
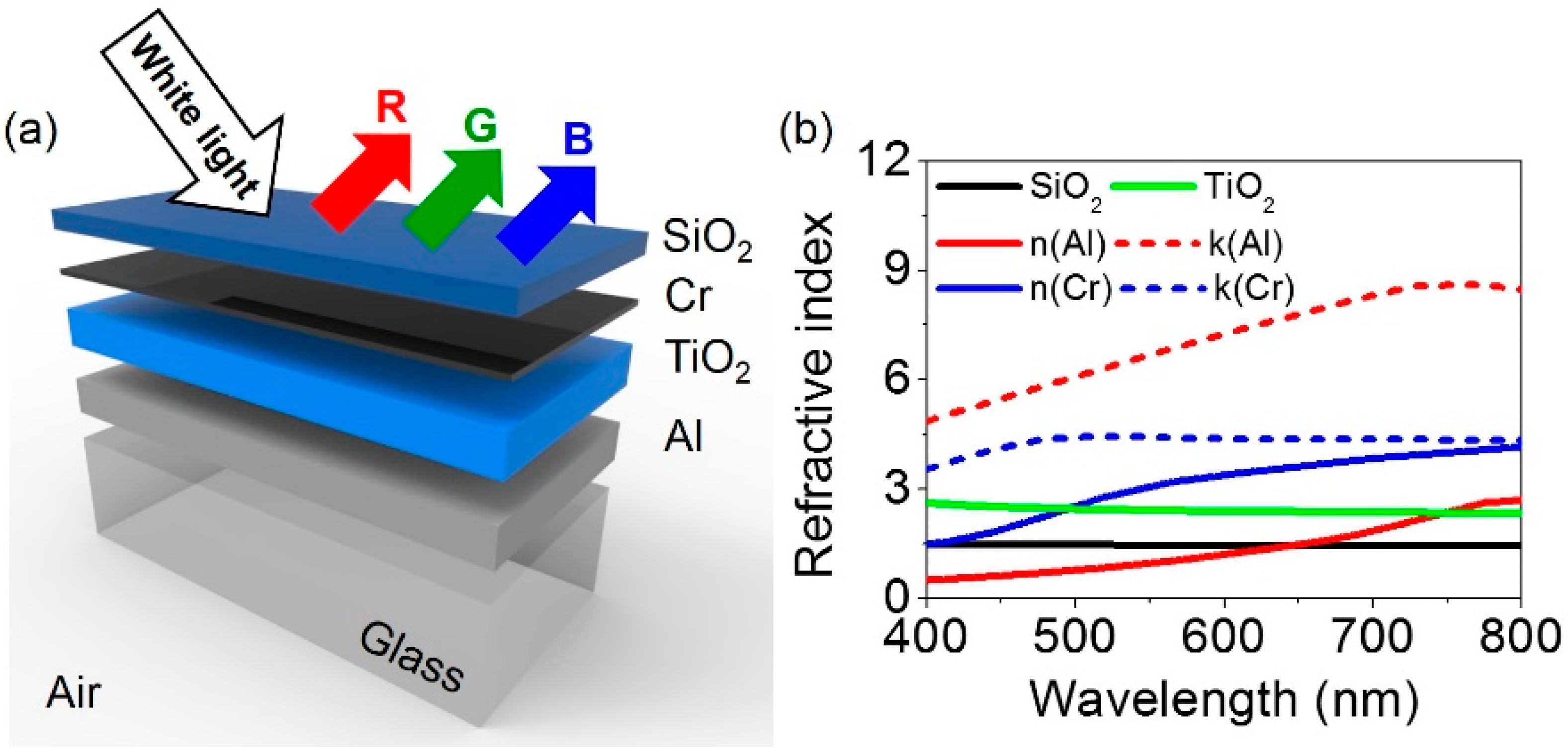
1. Introduction
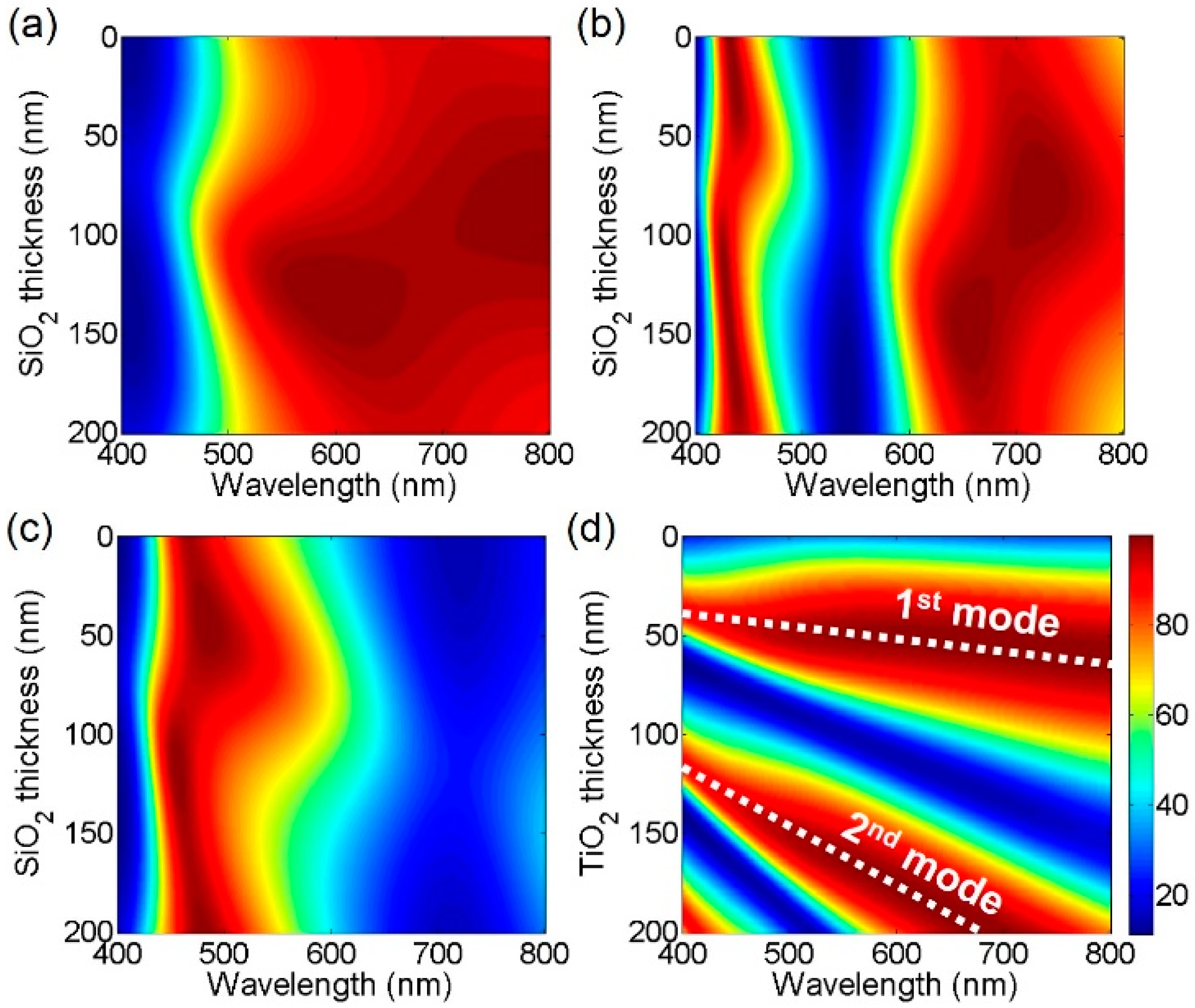
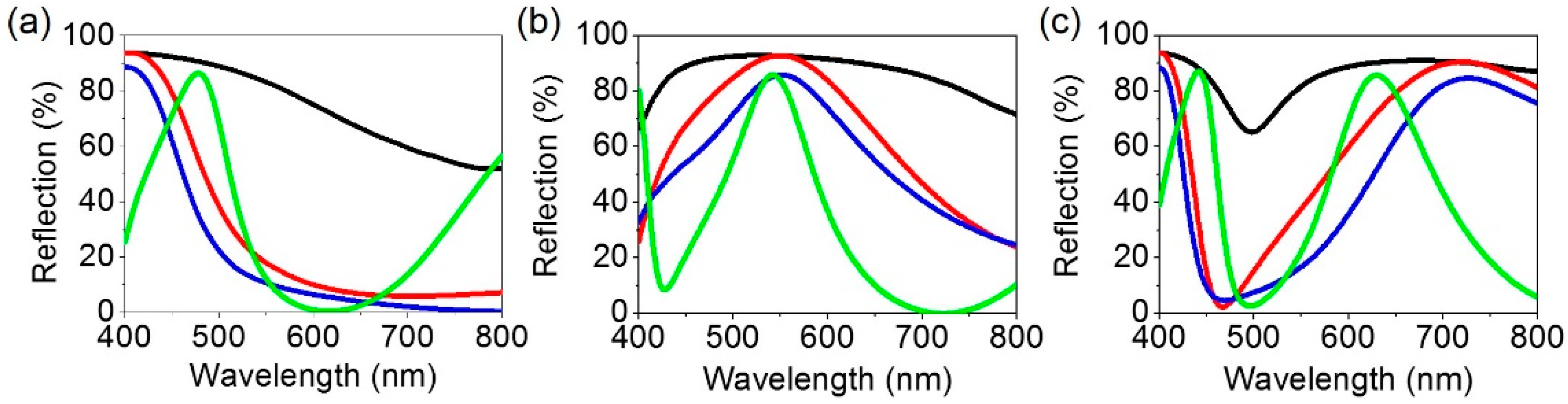
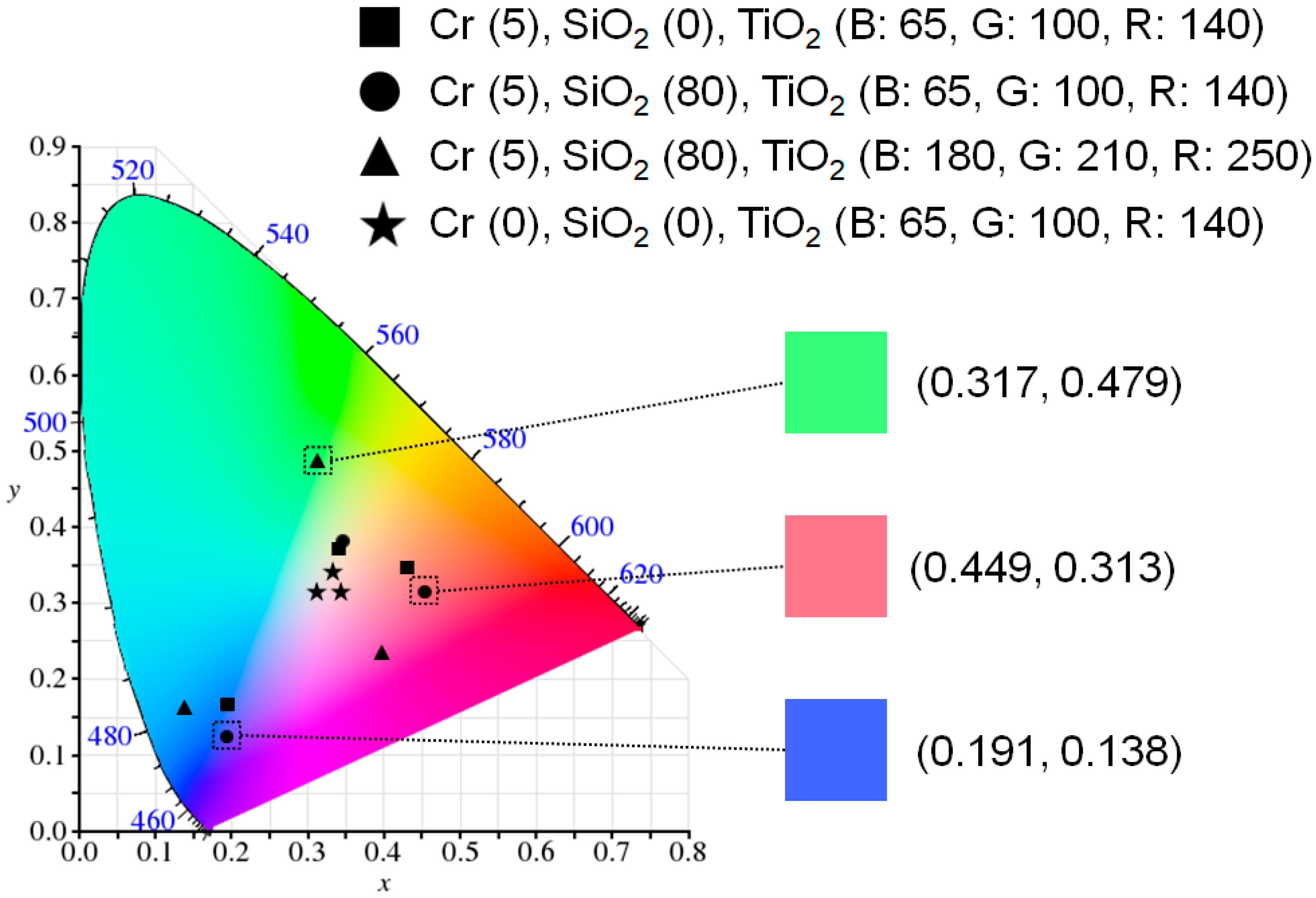
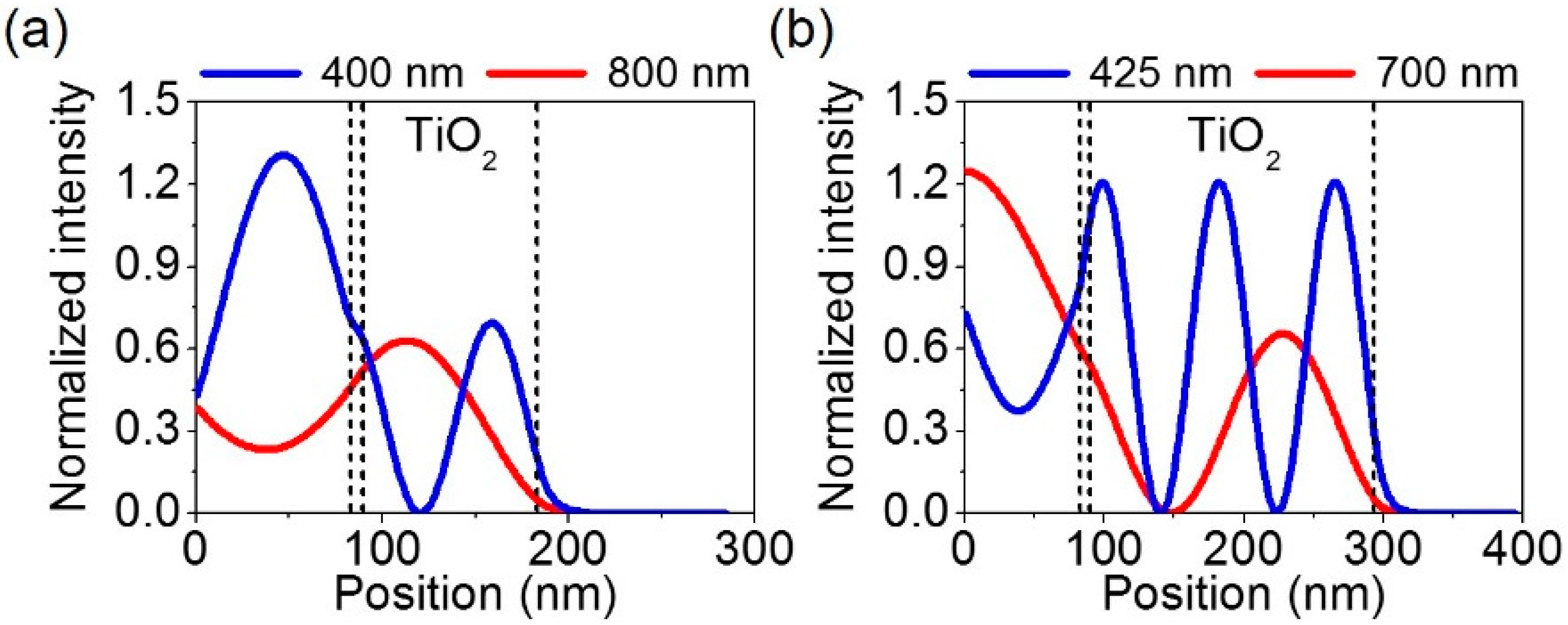
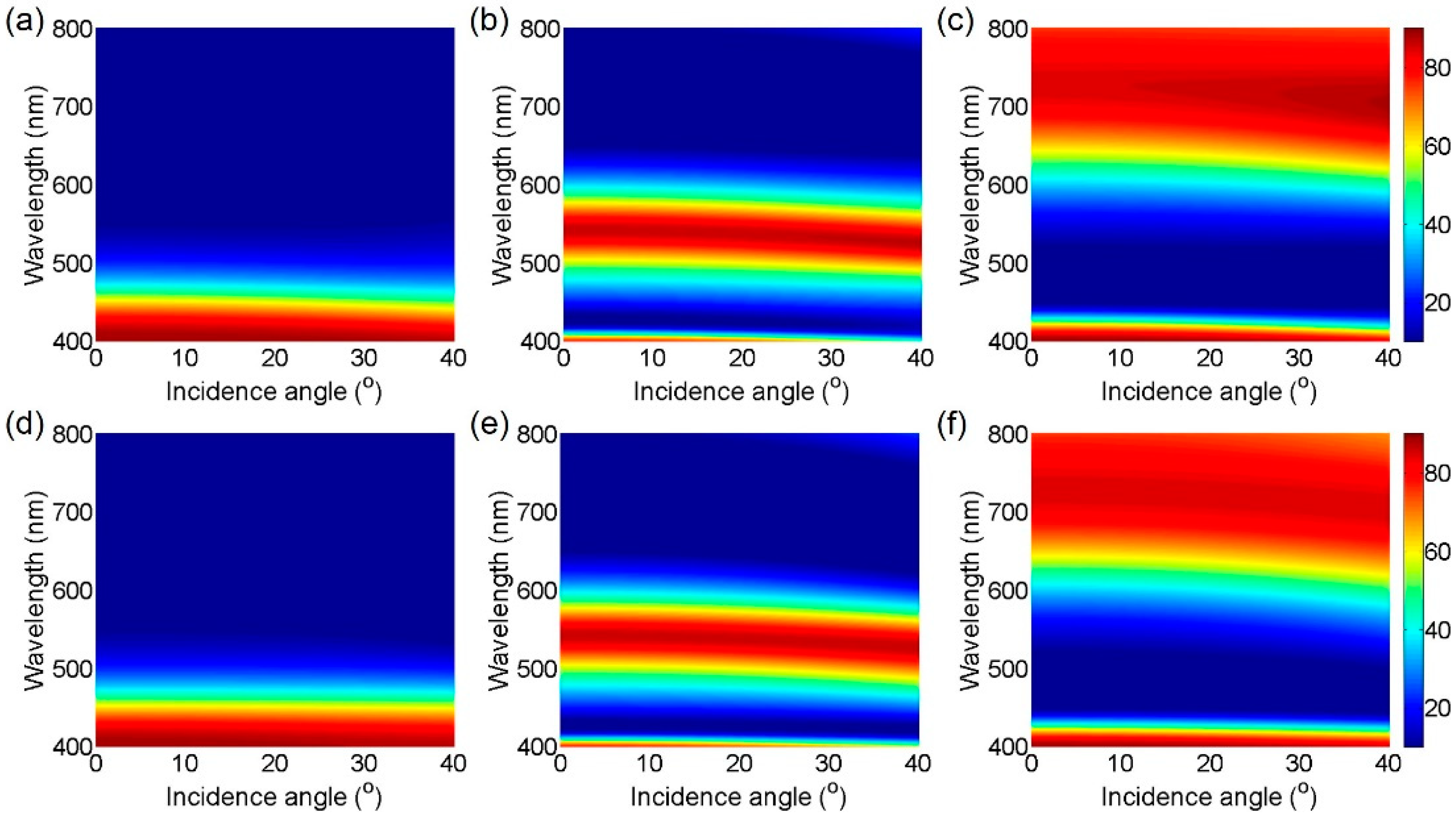
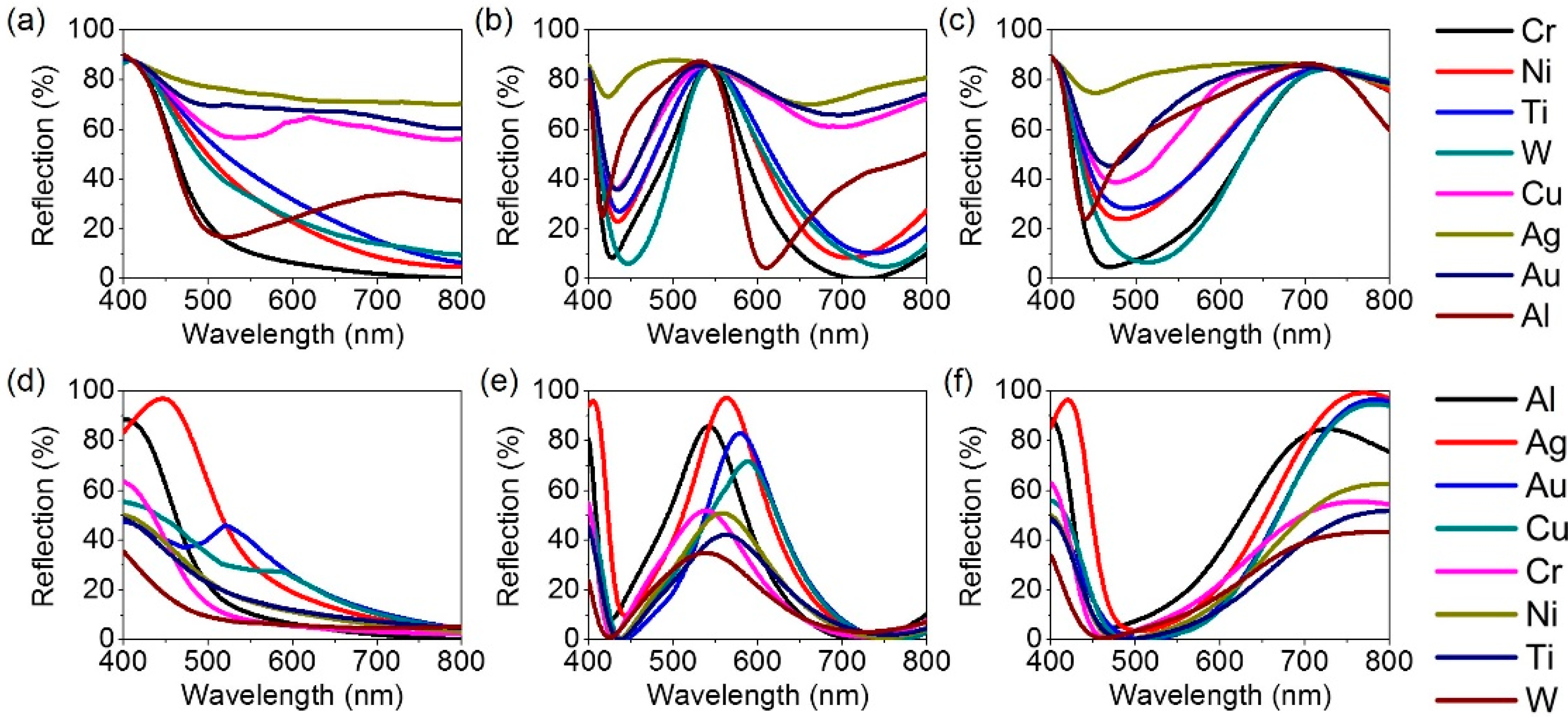
2. Results and Discussion
3. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Sabnis, R.W. Color filter technology for liquid crystal displays. Displays 1999, 20, 119–129. [Google Scholar] [CrossRef]
- Guo, J.; Huard, C.M.; Yang, Y.; Shin, Y.J.; Lee, K.-T.; Guo, L.J. Ito-free, compact, color liquid crystal devices using integrated structural color filters and graphene electrodes. Adv. Opt. Mater. 2014, 2, 435–441. [Google Scholar] [CrossRef]
- Yoon, Y.-T.; Lee, S.-S. Transmission type color filter incorporating a silver film based etalon. Opt. Express 2010, 18, 5344–5349. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.-T.; Seo, S.; Yong Lee, J.; Jay Guo, L. Ultrathin metal-semiconductor-metal resonator for angle invariant visible band transmission filters. Appl. Phys. Lett. 2014, 104, 231112. [Google Scholar] [CrossRef]
- Li, Z.; Butun, S.; Aydin, K. Large-area, lithography-free super absorbers and color filters at visible frequencies using ultrathin metallic films. ACS Photonics 2015, 2, 183–188. [Google Scholar] [CrossRef]
- Ji, C.; Lee, K.-T.; Xu, T.; Zhou, J.; Park, H.J.; Guo, L.J. Engineering light at the nanoscale: Structural color filters and broadband perfect absorbers. Adv. Opt. Mater. 2017, 5, 1700368. [Google Scholar] [CrossRef]
- Cho, E.-H.; Kim, H.-S.; Cheong, B.-H.; Oleg, P.; Xianyua, W.; Sohn, J.-S.; Ma, D.-J.; Choi, H.-Y.; Park, N.-C.; Park, Y.-P. Two-dimensional photonic crystal color filter development. Opt. Express 2009, 17, 8621–8629. [Google Scholar] [CrossRef]
- Cho, E.-H.; Kim, H.-S.; Sohn, J.-S.; Moon, C.-Y.; Park, N.-C.; Park, Y.-P. Nanoimprinted photonic crystal color filters for solar-powered reflective displays. Opt. Express 2010, 18, 27712–27722. [Google Scholar] [CrossRef]
- Kanamori, Y.; Ozaki, T.; Hane, K. Reflection color filters of the three primary colors with wide viewing angles using common-thickness silicon subwavelength gratings. Opt. Express 2014, 22, 25663–25672. [Google Scholar] [CrossRef] [PubMed]
- Yoon, Y.-T.; Lee, H.-S.; Lee, S.-S.; Kim, S.H.; Park, J.-D.; Lee, K.-D. Color filter incorporating a subwavelength patterned grating in poly silicon. Opt. Express 2008, 16, 2374–2380. [Google Scholar] [CrossRef]
- Kaplan, A.F.; Xu, T.; Guo, L.J. High efficiency resonance-based spectrum filters with tunable transmission bandwidth fabricated using nanoimprint lithography. Appl. Phys. Lett. 2011, 99, 143111. [Google Scholar] [CrossRef]
- Uddin, M.J.; Magnusson, R. Highly efficient color filter array using resonant si3n4 gratings. Opt. Express 2013, 21, 12495–12506. [Google Scholar] [CrossRef]
- Wang, C.-T.; Hou, H.-H.; Chang, P.-C.; Li, C.-C.; Jau, H.-C.; Hung, Y., Jr.; Lin, T.-H. Full-color reflectance-tunable filter based on liquid crystal cladded guided-mode resonant grating. Opt. Express 2016, 24, 22892–22898. [Google Scholar] [CrossRef]
- Xu, T.; Wu, Y.-K.; Luo, X.; Guo, L.J. Plasmonic nanoresonators for high-resolution colour filtering and spectral imaging. Nat. Commun. 2010, 1, 59. [Google Scholar] [CrossRef]
- Wang, J.; Fan, Q.; Zhang, S.; Zhang, Z.; Zhang, H.; Liang, Y.; Cao, X.; Xu, T. Ultra-thin plasmonic color filters incorporating free-standing resonant membrane waveguides with high transmission efficiency. Appl. Phys. Lett. 2017, 110, 031110. [Google Scholar] [CrossRef]
- Chen, T.; Reinhard, B.M. Assembling color on the nanoscale: Multichromatic switchable pixels from plasmonic atoms and molecules. Adv. Mater. 2016, 28, 3522–3527. [Google Scholar] [CrossRef] [PubMed]
- Cheng, F.; Gao, J.; Luk, T.S.; Yang, X. Structural color printing based on plasmonic metasurfaces of perfect light absorption. Sci. Rep. 2015, 5, 11045. [Google Scholar] [CrossRef] [PubMed]
- Zeng, B.; Gao, Y.; Bartoli, F.J. Ultrathin nanostructured metals for highly transmissive plasmonic subtractive color filters. Sci. Rep. 2013, 3, 2840. [Google Scholar] [CrossRef]
- Do, Y.S.; Park, J.H.; Hwang, B.Y.; Lee, S.-M.; Ju, B.-K.; Choi, K.C. Plasmonic color filter and its fabrication for large-area applications. Adv. Opt. Mater. 2013, 1, 133–138. [Google Scholar] [CrossRef]
- Miyamichi, A.; Ono, A.; Kamehama, H.; Kagawa, K.; Yasutomi, K.; Kawahito, S. Multi-band plasmonic color filters for visible-to-near-infrared image sensors. Opt. Express 2018, 26, 25178–25187. [Google Scholar] [CrossRef]
- Si, G.; Zhao, Y.; Lv, J.; Lu, M.; Wang, F.; Liu, H.; Xiang, N.; Huang, T.J.; Danner, A.J.; Teng, J.; et al. Reflective plasmonic color filters based on lithographically patterned silver nanorod arrays. Nanoscale 2013, 5, 6243–6248. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.J.; Si, G.Y.; Leong, E.S.P.; Xiang, N.; Danner, A.J.; Teng, J.H. Light-driven plasmonic color filters by overlaying photoresponsive liquid crystals on gold annular aperture arrays. Adv. Mater. 2012, 24, OP131–OP135. [Google Scholar] [CrossRef] [PubMed]
- Si, G.; Zhao, Y.; Liu, H.; Teo, S.; Zhang, M.; Huang, T.J.; Danner, A.J.; Teng, J. Annular aperture array based color filter. Appl. Phys. Lett. 2011, 99, 033105. [Google Scholar] [CrossRef]
- Liu, Y.J.; Si, G.Y.; Leong, E.S.P.; Wang, B.; Danner, A.J.; Yuan, X.C.; Teng, J.H. Optically tunable plasmonic color filters. Appl. Phys. A 2012, 107, 49–54. [Google Scholar] [CrossRef]
- Si, G.; Zhao, Y.; Leong, E.S.P.; Lv, J.; Jun Liu, Y. Incident-angle dependent color tuning from a single plasmonic chip. Nanotechnology 2014, 25, 455203. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, Y.; Hu, S.; Lv, J.; Ying, Y.; Gervinskas, G.; Si, G. Artificial structural color pixels: A review. Materials 2017, 10, 944. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Leong, E.S.P.; Liu, Y.J.; Si, G. Tuning plasmon resonance in depth-variant plasmonic nanostructures. Mater. Des. 2016, 96, 64–67. [Google Scholar] [CrossRef]
- Wu, Y.-K.R.; Hollowell, A.E.; Zhang, C.; Guo, L.J. Angle-insensitive structural colours based on metallic nanocavities and coloured pixels beyond the diffraction limit. Sci. Rep. 2013, 3, 1194. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Shen, W.; Zhang, Y.; Peng, H.; Zhang, X.; Liu, X. Design and simulation of omnidirectional reflective color filters based on metal-dielectric-metal structure. Opt. Express 2014, 22, 11384–11391. [Google Scholar] [CrossRef]
- Lee, K.-T.; Seo, S.; Guo, L.J. High-color-purity subtractive color filters with a wide viewing angle based on plasmonic perfect absorbers. Adv. Opt. Mater. 2015, 3, 347–352. [Google Scholar] [CrossRef]
- Park, C.-S.; Shrestha, V.R.; Lee, S.-S.; Kim, E.-S.; Choi, D.-Y. Omnidirectional color filters capitalizing on a nano-resonator of ag-tio2-ag integrated with a phase compensating dielectric overlay. Sci. Rep. 2015, 5, 8467. [Google Scholar] [CrossRef] [PubMed]
- Park, C.-S.; Shrestha, V.R.; Lee, S.-S.; Choi, D.-Y. Trans-reflective color filters based on a phase compensated etalon enabling adjustable color saturation. Sci. Rep. 2016, 6, 25496. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.-T.; Ji, C.; Banerjee, D.; Guo, L.J. Angular- and polarization-independent structural colors based on 1d photonic crystals. Laser Photon. Rev. 2015, 9, 354–362. [Google Scholar] [CrossRef]
- Shrestha, V.R.; Lee, S.-S.; Kim, E.-S.; Choi, D.-Y. Non-iridescent transmissive structural color filter featuring highly efficient transmission and high excitation purity. Sci. Rep. 2014, 4, 4921. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.-T.; Jang, J.-Y.; Park, S.J.; Ji, C.; Guo, L.J.; Park, H.J. Subwavelength nanocavity for flexible structural transmissive color generation with a wide viewing angle. Optica 2016, 3, 1489–1495. [Google Scholar] [CrossRef]
- Kats, M.A.; Blanchard, R.; Genevet, P.; Capasso, F. Nanometre optical coatings based on strong interference effects in highly absorbing media. Nat. Mater. 2013, 12, 20–24. [Google Scholar] [CrossRef]
- Lee, K.-T.; Seo, S.; Lee, J.Y.; Guo, L.J. Strong resonance effect in a lossy medium-based optical cavity for angle robust spectrum filters. Adv. Mater. 2014, 26, 6324–6328. [Google Scholar] [CrossRef]
- Kats, M.A.; Capasso, F. Optical absorbers based on strong interference in ultra-thin films (laser photonics rev. 10(5)/2016). Laser Photon. Rev. 2016, 10, 699. [Google Scholar] [CrossRef]
- Lee, K.-T.; Jang, J.-Y.; Park, S.J.; Ji, C.; Yang, S.-M.; Guo, L.J.; Park, H.J. Angle-insensitive and cmos-compatible subwavelength color printing. Adv. Opt. Mater. 2016, 4, 1696–1702. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
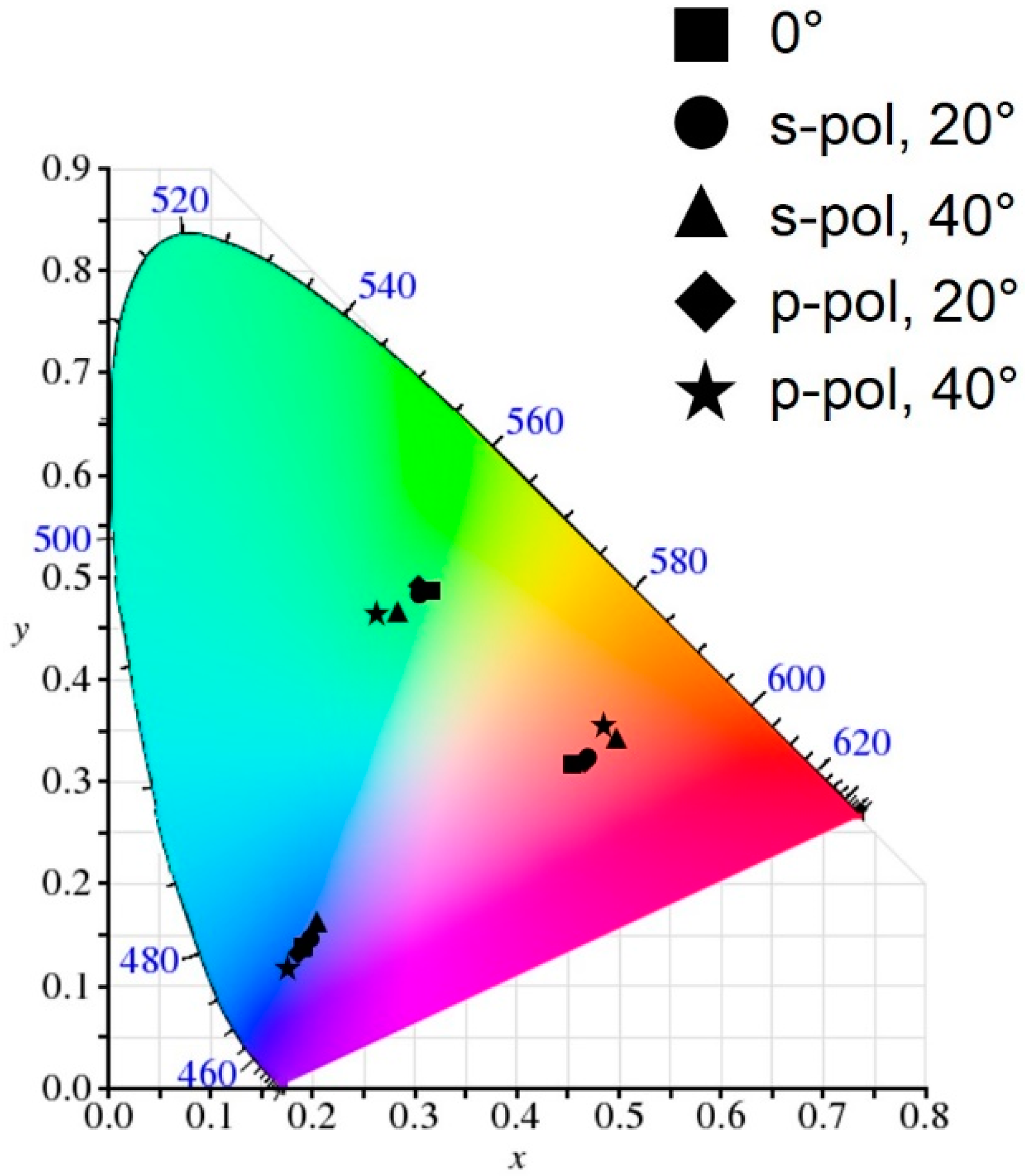
| Polarization | s-Polarization | p-Polarization | |||
|---|---|---|---|---|---|
| Angle of Incidence | 0° | 20° | 40° | 20° | 40° |
| Blue | (0.191, 0.138) | (0.194, 0.141) | (0.206, 0.158) | (0.189, 0.137) | (0.176, 0.121) |
| Green | (0.317, 0.479) | (0.304, 0.475) | (0.276, 0.460) | (0.303, 0.477) | (0.259, 0.461) |
| Red | (0.449, 0.313) | (0.463, 0.326) | (0.491, 0.346) | (0.459, 0.327) | (0.478, 0.366) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, K.-T.; Kang, D.; Park, H.J.; Park, D.H.; Han, S. Design of Polarization-Independent and Wide-Angle Broadband Absorbers for Highly Efficient Reflective Structural Color Filters. Materials 2019, 12, 1050. https://doi.org/10.3390/ma12071050
Lee K-T, Kang D, Park HJ, Park DH, Han S. Design of Polarization-Independent and Wide-Angle Broadband Absorbers for Highly Efficient Reflective Structural Color Filters. Materials. 2019; 12(7):1050. https://doi.org/10.3390/ma12071050
Chicago/Turabian StyleLee, Kyu-Tae, Daeshik Kang, Hui Joon Park, Dong Hyuk Park, and Seungyong Han. 2019. "Design of Polarization-Independent and Wide-Angle Broadband Absorbers for Highly Efficient Reflective Structural Color Filters" Materials 12, no. 7: 1050. https://doi.org/10.3390/ma12071050
APA StyleLee, K.-T., Kang, D., Park, H. J., Park, D. H., & Han, S. (2019). Design of Polarization-Independent and Wide-Angle Broadband Absorbers for Highly Efficient Reflective Structural Color Filters. Materials, 12(7), 1050. https://doi.org/10.3390/ma12071050





