Finite Element Model Updating Combined with Multi-Response Optimization for Hyper-Elastic Materials Characterization
Abstract
1. Introduction
2. Testing Process
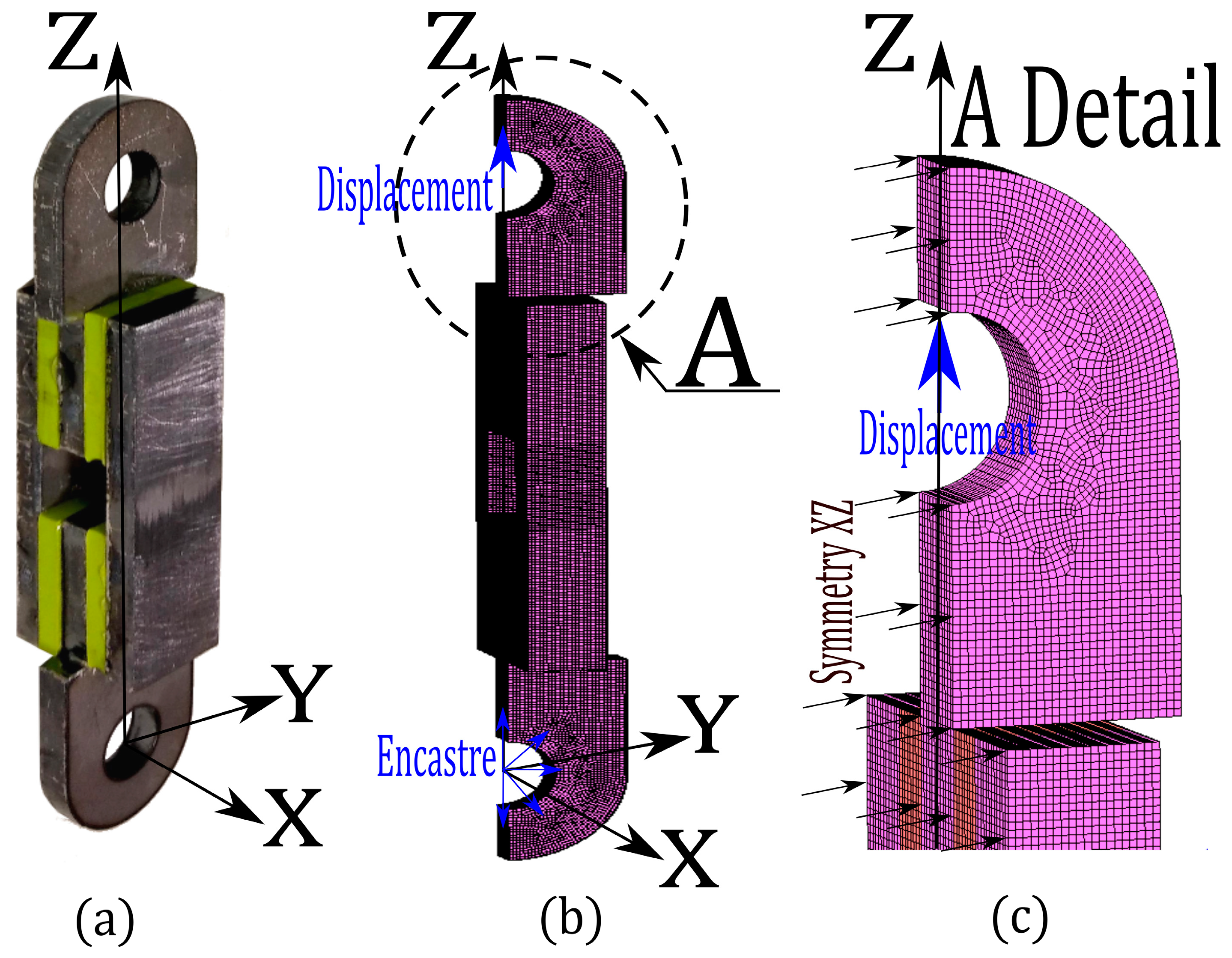
3. Finite Element Models Proposed
Mesh Sensitivity Analysis
4. Modeling with the RSM
5. Combining FEM and MRS to Optimize Mechanical Problems
6. Case Study
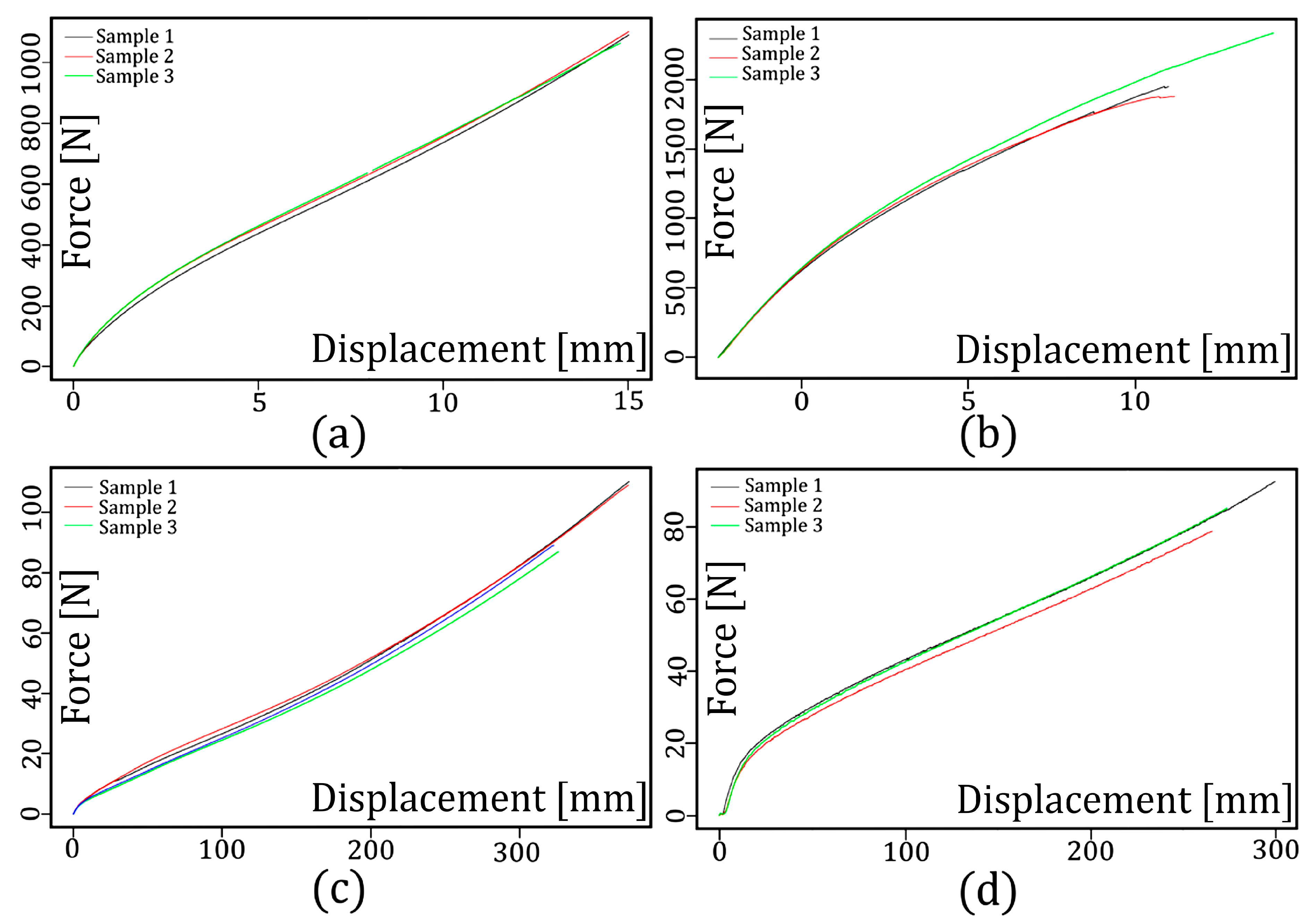
6.1. Experimental Results
6.2. Design of Experiments
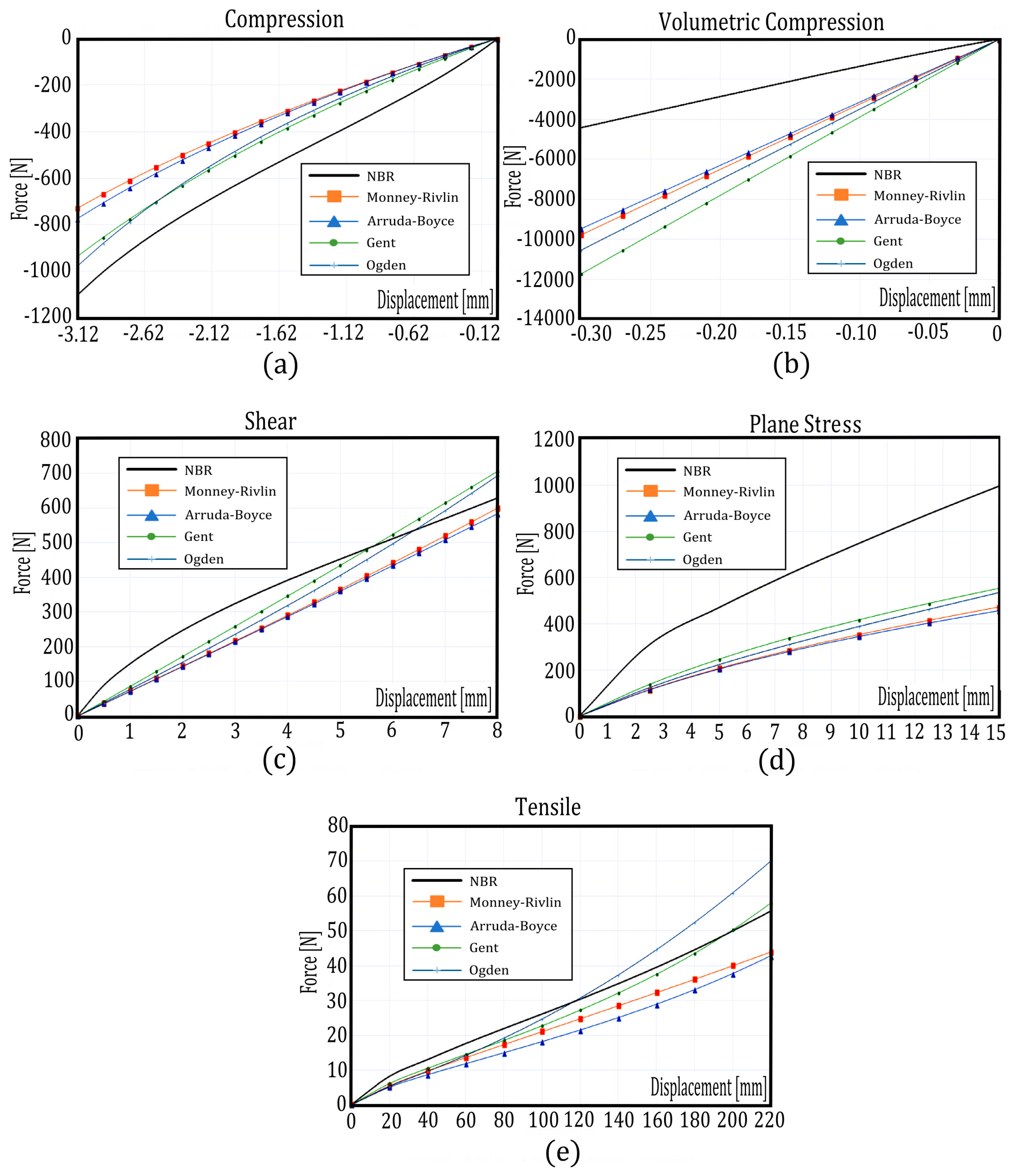
6.3. Modeling the EF for the Materials Studied According to the Standardized Tests
6.4. Multi-Response Optimization
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
List of Symbols/Nomenclature
| Symbol | Nomenclature |
| λi | Invariant |
| ANOVA | Analysis of the variance |
| C10, C01, C11 | Mooney–Rivlin material constants |
| Chain | Arruda–Boyce material constant max length of a chain |
| Ci | Constants of material |
| DIC | Digital image correlation method |
| DoE | Design of experiments |
| E | Young’s Modulus; Gent material constant |
| ER | Error function |
| EVA | Ethylene-vinyl acetate |
| FE | Finite element |
| FEM | Finite element method |
| Inv | Gent material constant, invariant |
| K1, K2 | Ogden material constants |
| MAE | Mean absolute error |
| MRS | Multi-response surface method |
| Nkt | Arruda–Boyce material constant, Number of chains in a material network |
| NBR | Nitrile butadiene rubber |
| PUR | Polyurethane |
| RAM | Random access memory |
| RMSE | Root mean square error |
| SBR | Styrene butadiene rubber |
References
- Treloar, L.R.G. The Physics of Rubber Elasticity; Oxford University Press: New York, NY, USA, 1975. [Google Scholar]
- Ghosh, S.K. Engineering Materials: Properties and Selection; Prentice Hall: Reston, VA, USA, 1983. [Google Scholar]
- Mooney, M. A theory of large elastic deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Rivlin, R.S. Large elastic deformations of isotropic materials IV. Further developments of the general theory. Philos. Trans. R. Soc. Lond. A 1948, 241, 379–397. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Gent, A.N. A new constitutive relation for rubber. Rubber Chem. Technol. 1996, 69, 59–61. [Google Scholar] [CrossRef]
- Ogden, R.W. Large deformation isotropic elasticity–on the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. Lond. A 1972, 326, 565–584. [Google Scholar] [CrossRef]
- Ogden, R.W. Non-Linear Elastic Deformations; Dover Publications Inc.: Mineola, NY, USA, 1997. [Google Scholar]
- ISO 37:2017. Rubber, Vulcanized or Thermoplastic—Determination of Tensile Stress-Strain Properties; ISO: Geneva, Switzerland, 2017.
- ISO 7743:2017. Rubber, Vulcanized or Thermoplastic—Determination of Compression Stress-Strain Properties; ISO: Geneva, Switzerland, 2017.
- ISO 1827:2007. Rubber, Vulcanized or Thermoplastic—Determination of Shear Modulus and Adhesion to Rigid Plates—Quadruple-Shear Methods; ISO: Geneva, Switzerland, 2007.
- Palmieri, G.; Sasso, M.; Chiappini, G.; Amodio, D. Virtual fields method on planar tension tests for hyperelastic materials characterisation. Strain 2011, 47, 196–209. [Google Scholar] [CrossRef]
- Sciammarella, C.A. The moire’ method—A review. Exp. Mech. 1982, 22, 418–433. [Google Scholar] [CrossRef]
- Genovese, K.; Lamberti, L.; Pappalettere, C. Mechanical characterization of hyperelastic materials with fringe projection and optimization techniques. Opt. Lasers Eng. 2006, 44, 423–442. [Google Scholar] [CrossRef]
- Erf, R. Speckle Metrology; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Sasso, M.; Palmieri, G.; Chiappini, G.; Amodio, D. Characterization of hyperelastic rubber-like materials by biaxial and uniaxial stretching tests based on optical methods. Polym. Test. 2008, 27, 995–1004. [Google Scholar] [CrossRef]
- Sutton, M.A.; Wolters, W.J.; Peters, W.H.; Ranson, W.F.; McNeil, S.R. Determination of displacements using an improved digital correlation method. Image Vis. Comput. 1983, 1, 133–139. [Google Scholar] [CrossRef]
- Hild, F.; Roux, S. Digital image correlation: From displacement measurement to identification of elastic properties—A review. Strain 2006, 42, 69–80. [Google Scholar] [CrossRef]
- Sasso, M.; Newaz, G.; Amodio, D. Material characterization at high strain rate by Hopkinson bar tests and finite element optimization. Mater. Sci. Eng. A 2008, 487, 289–300. [Google Scholar] [CrossRef]
- Grédiac, M. Principe des travaux virtuels et identification. Comptes Rendus de l’Académie des Sciences 1989, 309, 1–5. [Google Scholar]
- Grédiac, M.; Pierron, F.; Avril, S.; Toussaint, E. The virtual fields method for extracting constitutive parameters from full-field measurements: A review. Strain 2006, 42, 233–253. [Google Scholar] [CrossRef]
- Shahzad, M.; Kamran, A.; Siddiqui, M.Z.; Farhan, M. Mechanical characterization and FE modelling of a hyperelastic material. Mater. Res. 2015, 18, 918–924. [Google Scholar] [CrossRef]
- Promma, N.; Raka, B.; Grediac, M.; Toussaint, E.; Le Cam, J.B.; Balandraud, X.; Hild, F. Application of the virtual fields method to mechanical characterization of elastomeric materials. Int. J. Solids Struct. 2009, 46, 698–715. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, H.; Li, A. Parameter identification methods for hyperelastic and hyper-viscoelastic models. Appl. Sci. 2016, 6, 386. [Google Scholar] [CrossRef]
- Lostado, R.; Martinez, R.F.; Mac Donald, B.J.; Villanueva, P.M. Combining soft computing techniques and the finite element method to design and optimize complex welded products. Integr. Comput-Aid. Eng. 2015, 22, 153–170. [Google Scholar] [CrossRef]
- Lostado Lorza, R.; Escribano García, R.; Fernandez Martinez, R.; Martínez Calvo, M.Á. Using Genetic Algorithms with Multi-Objective Optimization to Adjust Finite Element Models of Welded Joints. Metals 2018, 8, 230. [Google Scholar] [CrossRef]
- Gómez, F.S.; Lorza, R.L.; Bobadilla, M.C.; García, R.E. Improving the Process of Adjusting the Parameters of Finite Element Models of Healthy Human Intervertebral Discs by the Multi-Response Surface Method. Materials 2017, 10, 1116. [Google Scholar] [CrossRef] [PubMed]
- Lostado, R.; Martínez-de-Pisón, F.J.; Fernández, R.; Fernández, J. Using genetic algorithms to optimize the material behaviour model in finite element models of processes with cyclic loads. J. Strain Anal. Eng. Des. 2011, 46, 143–159. [Google Scholar] [CrossRef]
- Amin, A.F.; Wiraguna, S.I.; Bhuiyan, A.R.; Okui, Y. Hyperelasticity model for finite element analysis of natural and high damping rubbers in compression and shear. J. Eng. Mech. 2006, 132, 54–64. [Google Scholar] [CrossRef]
- Connolly, S.J.; MacKenzie, D.; Comlekci, T. Multi-objective optimization of hyperelastic material constants: A feasibility study. In Proceedings of the 10th European Conference on Constitutive Models for Rubbers, Munich, Germany, 28–31 August 2017. [Google Scholar]
- ISO 471:1995. Rubber—Temperatures, Humidities and Times for Conditioning and Testing; ISO: Geneva, Switzerland, 1995.
- MSC Mentat Marc. MSC MARC User Guide, Version 2016; MSC Software Corporation: Santa Ana, CA, USA, 2016. [Google Scholar]
- Box, G.; Wilson, K. On the Experimental Attainment of Optimum Conditions. J. R. Stat. Soc. Ser. B 1951, 13, 1–45. [Google Scholar] [CrossRef]
- Marwala, T. Finite-Element-Model Updating Using Computional Intelligence Techniques; Springer: London, UK, 2010. [Google Scholar]
- Lostado, R.; Escribano García, R.; Fernández Martínez, R. Optimization of operating conditions for a double-row tapered roller bearing. Int. J. Mech. Mater. Des. 2015, 12, 353–373. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Anderson, V.L.; McLean, R.A. Design of Experiments: A Realistic Approach; CRC Press: Boca Raton, FL, USA, 1974. [Google Scholar]
- RC Team R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 23 February 2016).
- Kuhn, M. Desirability: Desirabiliy Function Optimization and Ranking. R Package V.1.6. Available online: http://CRAN.R-project.org/package=desirability (accessed on 23 February 2019).
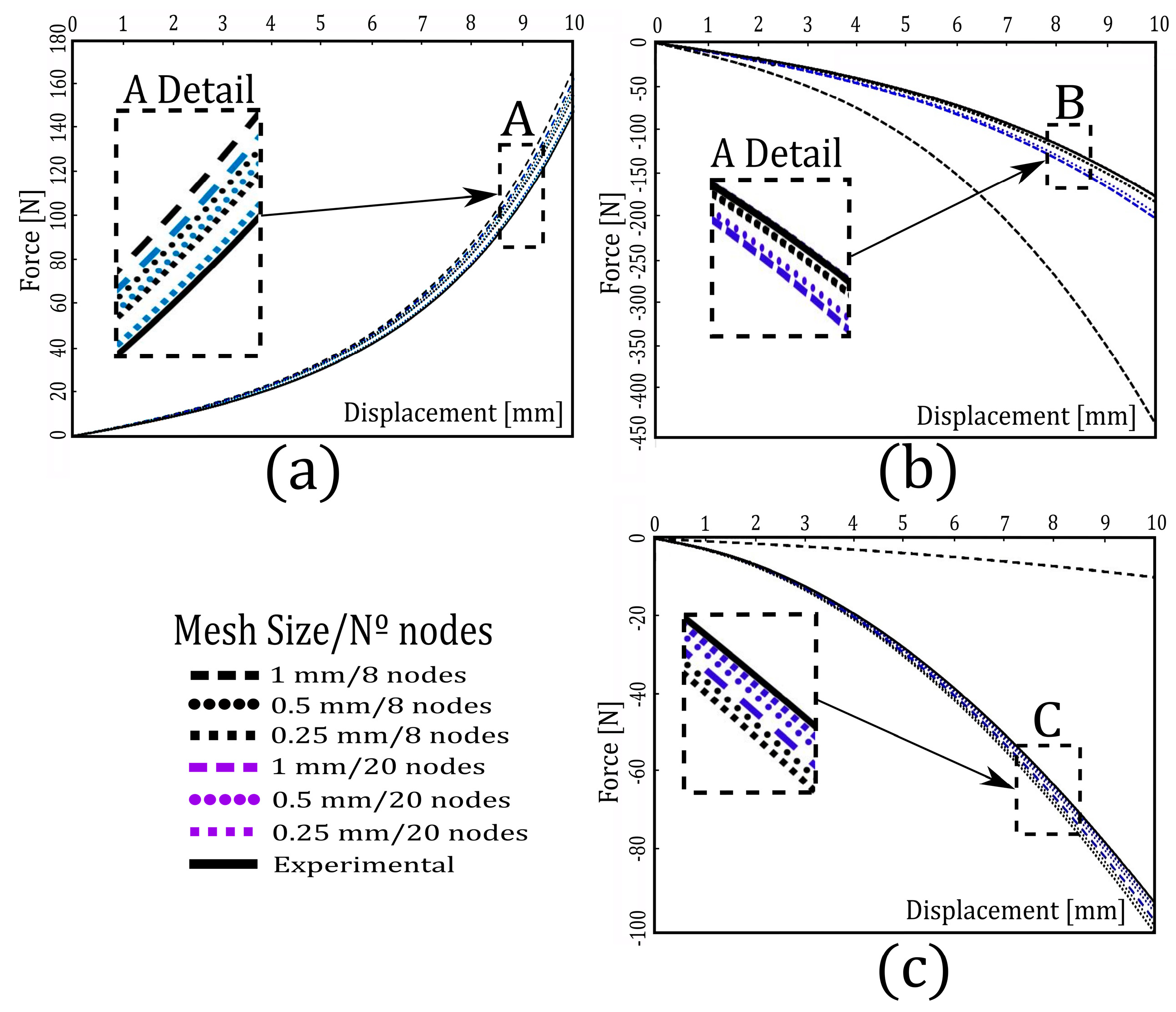
| Test | Size [mm] | Nº Elements | N° Nodes | Time [min] | MAE |
|---|---|---|---|---|---|
| (Linear/ Quadratic) | (Linear/ Quadratic) | (Linear/ Quadratic) | |||
| Tensile | 1 | 1568 | 1950/5850 | 1/5 | 65.05/3.54 |
| 0.5 | 11440 | 7190/21570 | 6/180 | 5.94/1.96 | |
| 0.25 | 91520 | 28762/86290 | 76/1728 | 4.71/0.90 | |
| Planar Stress | 1 | 10150 | 10872/32612 | 16/106 | 12.66/8.57 |
| 0.5 | 81200 | 43482/130442 | 143/1232 | 8.62/2.08 | |
| 0.25 | 649600 | 173922/521762 | 1980/12000 | 3.35/1.81 | |
| Compression | 1 | 4866 | 2223/6668 | 13/493 | 11.95/9.61 |
| 0.5 | 35904 | 8480/25438 | 201/1952 | 8.45/6.49 | |
| 0.25 | 281424 | 33544/100628 | 1598/9000 | 6.04/1.44 | |
| Volumetric Compression | 1 | 2958 | 1371/3746 | 6/28 | 1968.48/35.14 |
| 0.5 | 22156 | 5361/15241 | 52/474 | 3.36/8.97 | |
| 0.25 | 165416 | 19441/58320 | 740/14000 | 2.98/2.55 | |
| Shear test | 1 | 20560 | 8264/24792 | 36/280 | 174.20/20.33 |
| 0.5 | 163928 | 59496/179328 | 400/4833 | 5.17/15.47 | |
| 0.25 | 1308160 | 329702/992708 | 10163/ | 5.01/0.38 |
| Hyper-Elastic Model | DoE | Input Constant | Magnitude | Levels | ||||
|---|---|---|---|---|---|---|---|---|
| −1 | −0.5 | 0 | 0.5 | 1 | ||||
| Mooney–Rivlin | 5k | C10 | MPa | −0.25 | 0.13 | 0.5 | 0.88 | 1.25 |
| C01 | MPa | −0.3 | 0.03 | 0.35 | 0.68 | 1 | ||
| C11 | MPa | 0 | 0.13 | 0.25 | 0.38 | 0.5 | ||
| Arruda–Boyce | 3k | Nkt | - | 0.26 | -- | 0.58 | -- | 0.9 |
| Chain | - | 2 | -- | 13.5 | -- | 25 | ||
| Gent | 5k | E | MPa | 0.6 | 1.375 | 2.15 | 2.925 | 3.7 |
| inv | 63 | 67.125 | 71.25 | 75.375 | 79.5 | |||
| Ogden | 5k | K1 | - | 0 | 0.125 | 0.25 | 0.375 | 0.5 |
| K2 | - | −0.5 | −0.3125 | −0.125 | 0.062 | 0.25 | ||
| Inputs | Output | ||||
|---|---|---|---|---|---|
| Sample | C10 | C01 | C11 | Displacement | Force |
| (MPa) | (MPa) | (MPa) | (mm) | (N) | |
| 1 | −0.25 | 0.35 | 0.125 | 0.00 | 0.000 |
| 2 | −0.25 | 0.35 | 0.125 | 0.50 | 12.117 |
| 3 | −0.25 | 0.35 | 0.125 | 1.00 | 24.695 |
| 4 | −0.25 | 0.35 | 0.125 | 1.50 | 38.228 |
| 5 | −0.25 | 0.35 | 0.125 | 2.00 | 53.264 |
| 6 | −0.25 | 0.35 | 0.125 | 2.50 | 70.419 |
| 7 | −0.25 | 0.35 | 0.125 | 3.00 | 90.374 |
| 8 | −0.25 | 0.35 | 0.125 | 3.50 | 113.829 |
| 9 | −0.25 | 0.35 | 0.125 | 4.00 | 141.470 |
| 10 | −0.25 | 0.35 | 0.125 | 4.50 | 173.949 |
| 11 | −0.25 | 0.35 | 0.125 | 5.00 | 211.880 |
| … | … | … | … | … | … |
| 2623 | 1.25 | 1.00 | 0.500 | 9.00 | 7288.559 |
| 2624 | 1.25 | 1.00 | 0.500 | 9.50 | 7975.014 |
| 2625 | 1.25 | 1.00 | 0.500 | 10.00 | 8703.273 |
| Hyper-Elastic Models | Ci | NBR | PUR | EVA | SBR |
|---|---|---|---|---|---|
| Mooney–Rivlin | C10 (MPa) | 0.367 | 0.982 | 0.572 | 0.112 |
| C01 (MPa) | −0.069 | −0.056 | −0.292 | 0.152 | |
| C11 (MPa) | 0.005 | 0.005 | 0.002 | 0.005 | |
| Arruda–Boyce | Nkt | 0.578 | 0.643 | 0.567 | 0.579 |
| Chain | 24.644 | 3.75 | 15.054 | 17.354 | |
| Gent | E (MPa) | 2.144 | 2.982 | 2.237 | 1.899 |
| inv1 | 76.465 | 70.645 | 63.1 | 79.46 | |
| Ogden | k1 | 0.254 | 0.329 | 0.361 | 0.124 |
| k2 | −0.261 | −0.499 | −0.119 | −0.426 |
| Hyper-Elastic Models | NBR | PUR | EVA | SBR | ||||
|---|---|---|---|---|---|---|---|---|
| MAEnorm | Time (min.) | MAEnorm | Time (min.) | MAEnorm | Time (min.) | MAEnorm | Time (min.) | |
| Mooney–Rivlin | 0.054 | 802 | 0.127 | 840 | 0.116 | 720 | 0.061 | 870 |
| Arruda–Boyce | 0.194 | 668 | 0.536 | 715 | 0.246 | 621 | 0.225 | 742 |
| Gent | 0.282 | 725 | 0.916 | 767 | 0.426 | 708 | 0.361 | 737 |
| Ogden | 0.054 | 905 | 0.736 | 963 | 0.381 | 893 | 0.287 | 926 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Íñiguez-Macedo, S.; Lostado-Lorza, R.; Escribano-García, R.; Martínez-Calvo, M.Á. Finite Element Model Updating Combined with Multi-Response Optimization for Hyper-Elastic Materials Characterization. Materials 2019, 12, 1019. https://doi.org/10.3390/ma12071019
Íñiguez-Macedo S, Lostado-Lorza R, Escribano-García R, Martínez-Calvo MÁ. Finite Element Model Updating Combined with Multi-Response Optimization for Hyper-Elastic Materials Characterization. Materials. 2019; 12(7):1019. https://doi.org/10.3390/ma12071019
Chicago/Turabian StyleÍñiguez-Macedo, Saúl, Rubén Lostado-Lorza, Rubén Escribano-García, and María Ángeles Martínez-Calvo. 2019. "Finite Element Model Updating Combined with Multi-Response Optimization for Hyper-Elastic Materials Characterization" Materials 12, no. 7: 1019. https://doi.org/10.3390/ma12071019
APA StyleÍñiguez-Macedo, S., Lostado-Lorza, R., Escribano-García, R., & Martínez-Calvo, M. Á. (2019). Finite Element Model Updating Combined with Multi-Response Optimization for Hyper-Elastic Materials Characterization. Materials, 12(7), 1019. https://doi.org/10.3390/ma12071019







