Superconducting YBCO Foams as Trapped Field Magnets
Abstract
:1. Introduction
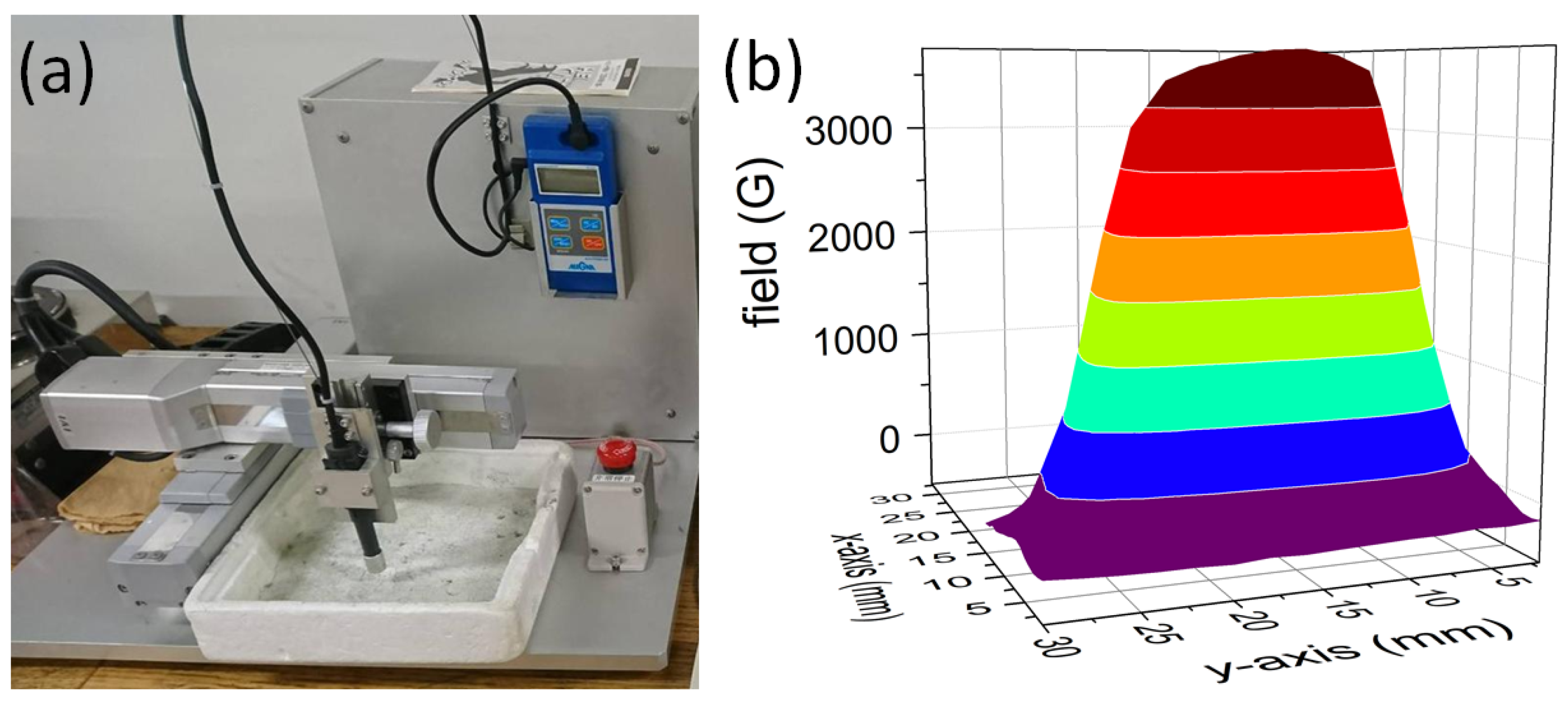
2. Experimental Procedures
2.1. Sample Preparation
2.2. Magnetic Measurements
3. Results and Discussion
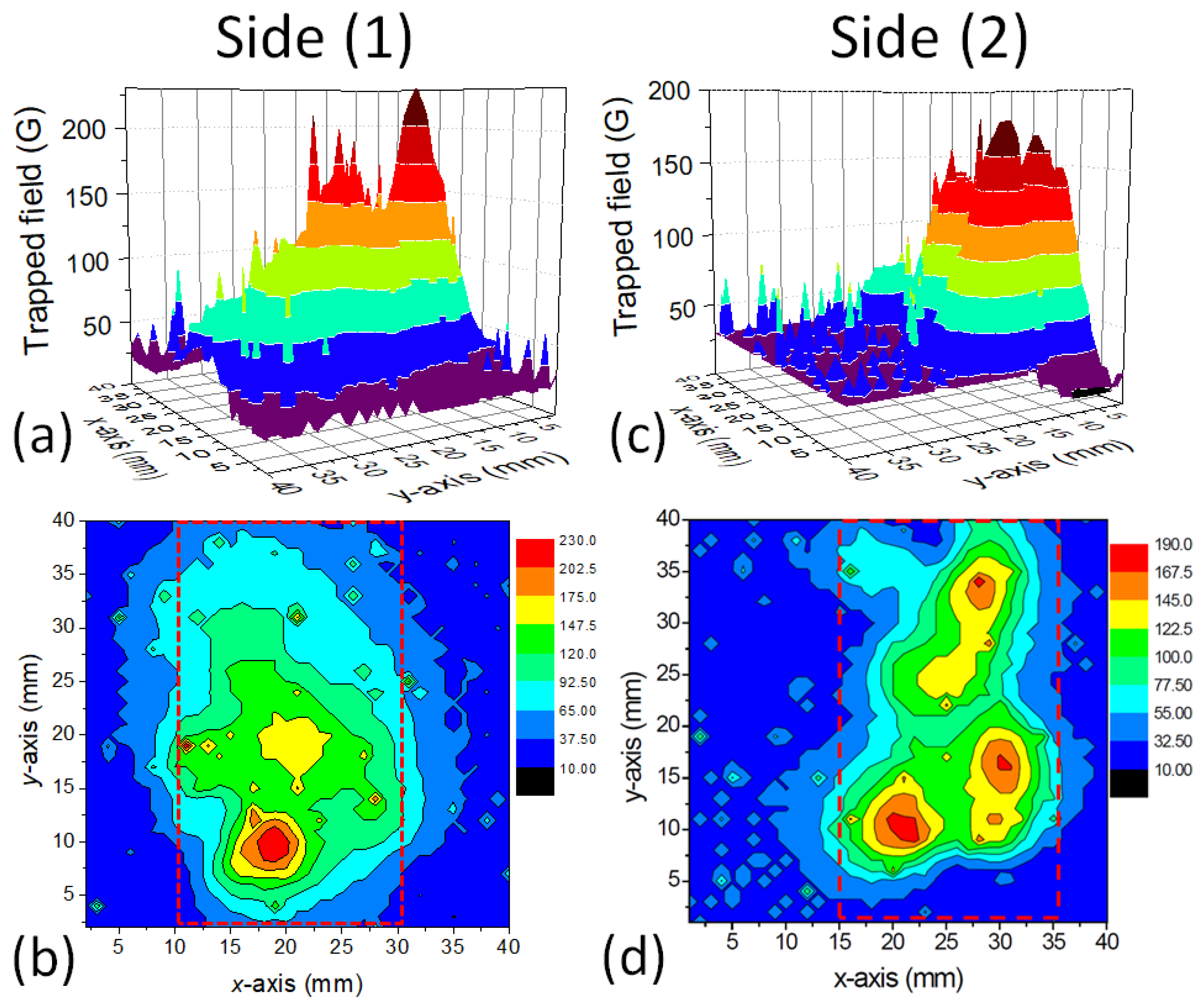
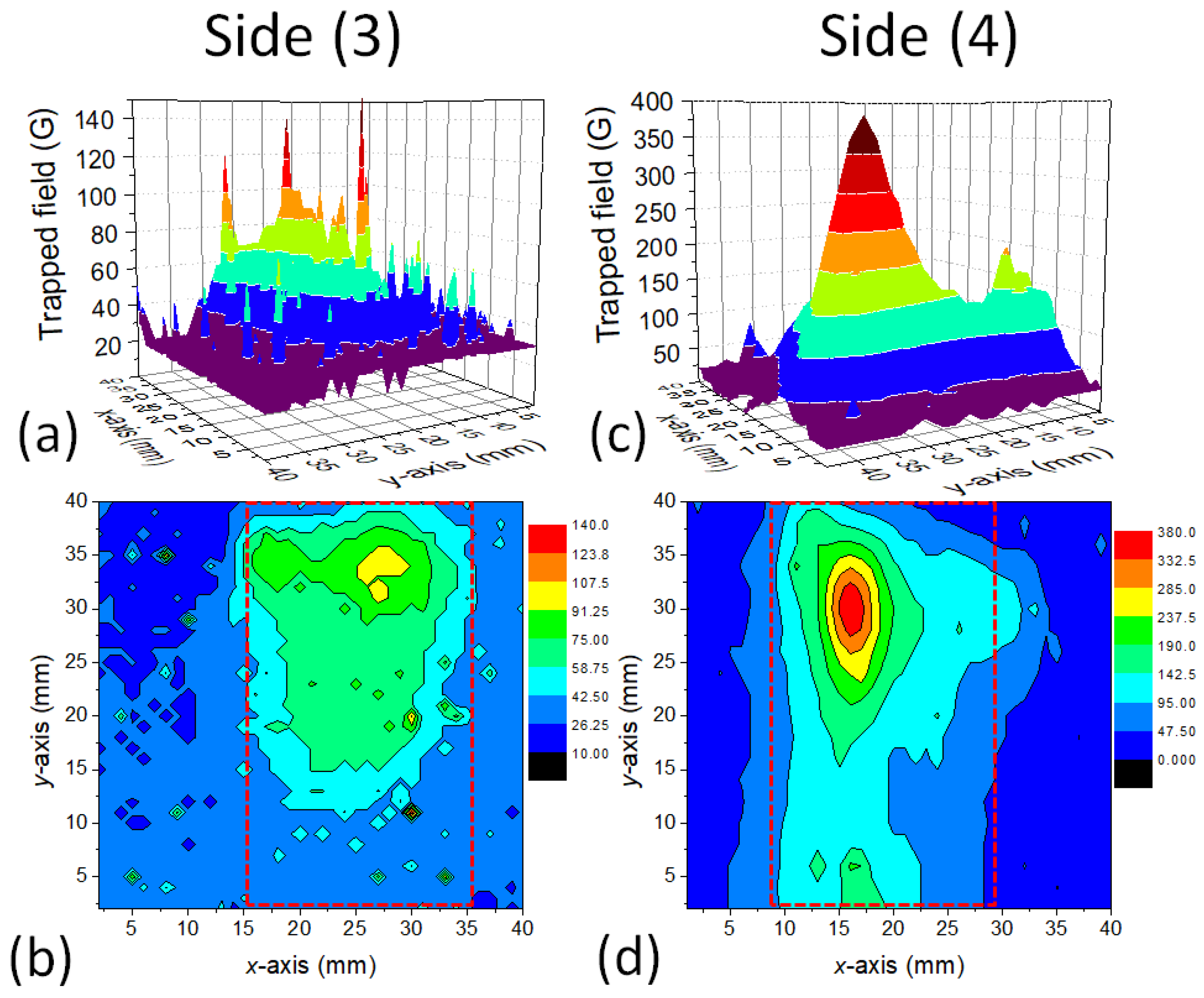
3.1. Trapped Fields
- The large sample size of the foam piece employed in the present paper did not allow the use of an electromagnet due to the limited space between the pole shoes.
- The present foam sample was pure YBCO with no extra flux-pinning sites.
- The current shape of the foams was never optimized to reach large trapped fields, nor was the texture of the sample fully optimized.
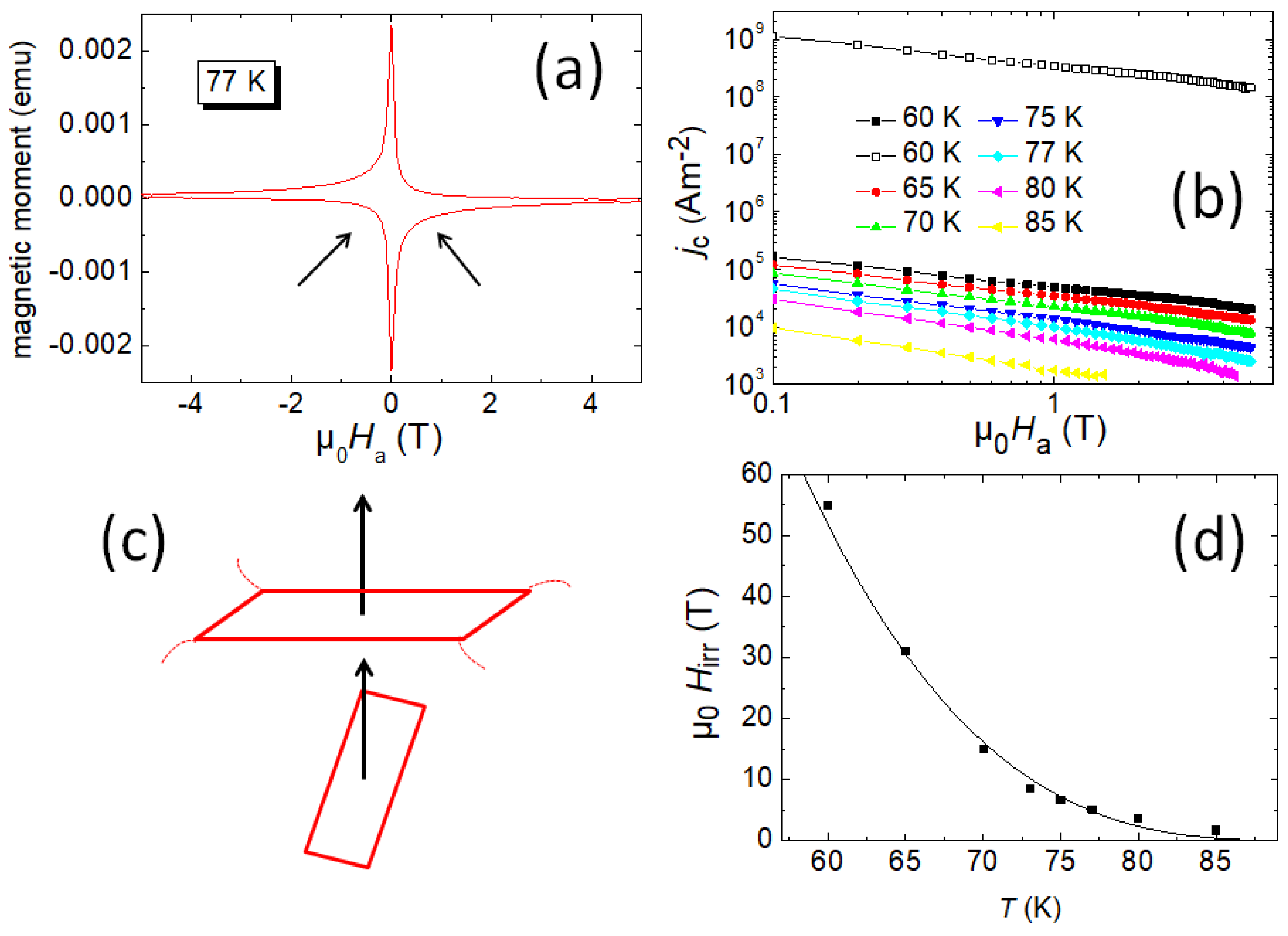
3.2. Current Flow in Foam Samples
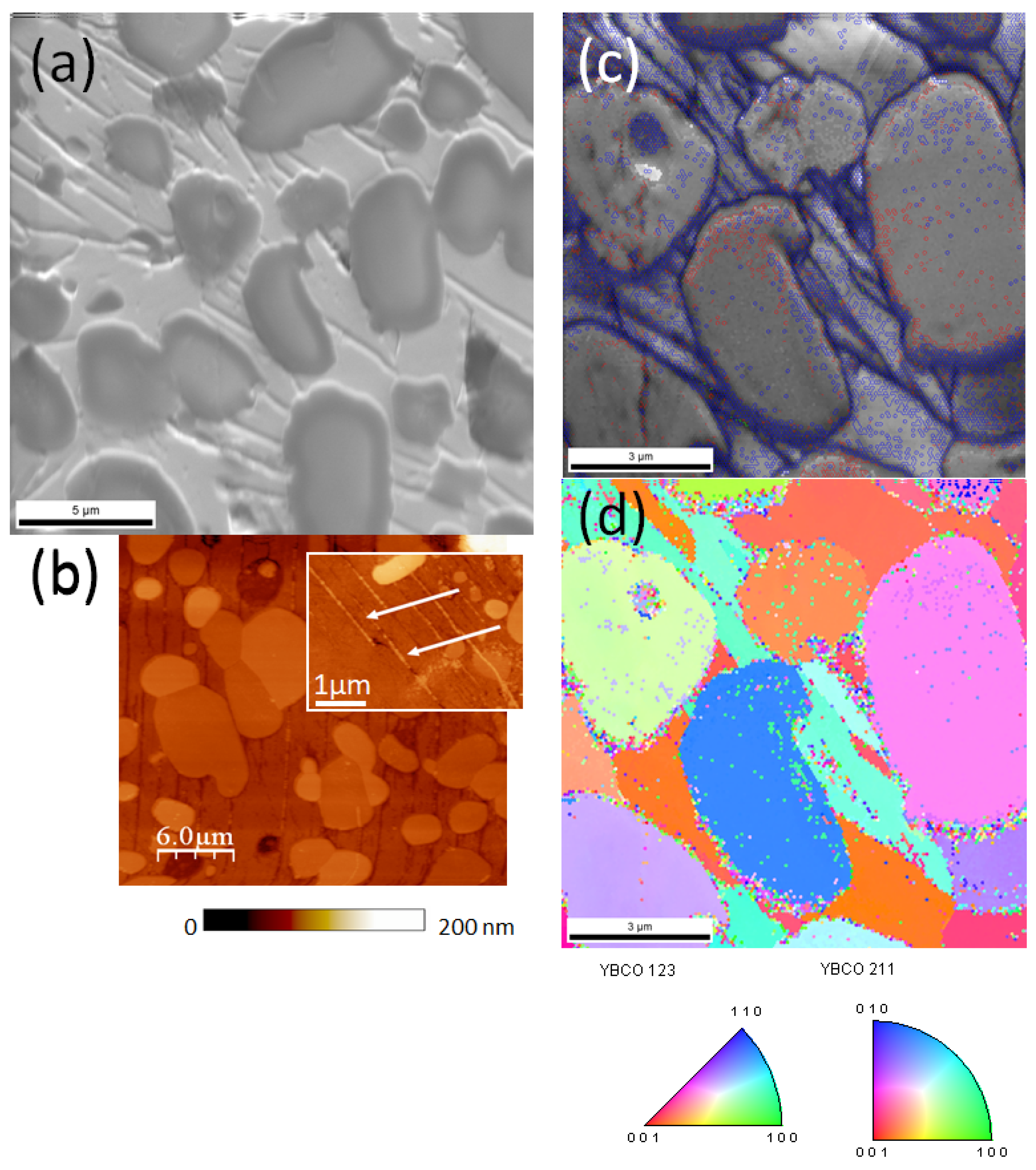
3.3. Microstructure
4. Applications of Superconducting Foam Samples
- TF magnets can be applied as static or rotating elements in electric motors and generators (see, e.g., the review in Reference [58]). Here, the reduced weight of the foam samples is very promising. This also applies to magnetic coupling elements in the power line, which is employed to transmit power into a container with different atmospheric conditions. Such lightweight machinery and coupling elements may be useful for space applications.
- TF magnets are portable systems. As long as the system is kept below superconducting transition temperature , the magnetic field stays in the sample. Using persistent current mode, there is no need for any power supply.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Larbalestier, D.C.; Gurevich, A.; Feldmann, D.M.; Polyanskii, A. High-Tc superconducting materials for electric power applications. Nature 2001, 414, 368–377. [Google Scholar] [CrossRef] [PubMed]
- Eisterer, M.; Moon, S.H.; Freyhardt, H.C. Current developments in HTSC coated conductors for applications. Supercond. Sci. Technol. 2016, 29, 060301. [Google Scholar] [CrossRef]
- Durrell, J.H.; Ainslie, M.D.; Zhou, D.; Vanderbemden, P.; Bradshaw, T.; Speller, S.; Filipenko, M.; Cardwell, D.A. Bulk superconductors: A roadmap to applications. Supercond. Sci. Technol. 2018, 31, 103501. [Google Scholar] [CrossRef]
- Gurevich, A. To use or not to use cool superconductors. Nat. Mater. 2011, 10, 255–259. [Google Scholar] [CrossRef] [PubMed]
- Tournier, R.; Beaugnon, E.; Belmont, O. Processing of large Y1Ba2Cu3O7−x single domains for current-limiting applications. Supercond. Sci. Technol. 2000, 13, 886–896. [Google Scholar] [CrossRef]
- Johansen, T.H. Flux-pinning-induced stress and magnetostriction in bulk superconductors. Supercond. Sci. Technol. 2000, 13, R121–R137. [Google Scholar] [CrossRef]
- Diko, P. Cracking in melt-grown RE-Ba-Cu-O single-grain bulk superconductors. Supercond. Sci. Technol. 2004, 17, R45–R58. [Google Scholar] [CrossRef]
- Tomita, M.; Murakami, M. High-temperature superconductor bulk magnets that can trap magnetic fields above 17 tesla at 29 K. Nature 2003, 421, 517–520. [Google Scholar] [CrossRef] [PubMed]
- Durrell, J.H.; Dennis, A.R.; Jaroszynski, J.; Ainslie, M.D.; Palmer, K.G.B.; Shi, Y.-H.; Campbell, A.M.; Hull, J.; Strasik, M.; Hellstrom, E.E.; et al. A trapped field of 17.6 T in melt-processed bulk Gd–Ba–Cu–O reinforced with shrink-fit steel. Supercond. Sci. Technol. 2014, 27, 082001. [Google Scholar] [CrossRef]
- Vakaliuk, O.I.; Ainslie, M.D.; Halbedel, B. Lorentz force velocimetry using a bulk HTS magnet system: Proof-of-Concept. Supercond. Sci. Technol. 2018, 31, 084003. [Google Scholar] [CrossRef]
- Nettleship, I. Applications of porous ceramics. Key Eng. Mater. 1996, 122, 305–324. [Google Scholar] [CrossRef]
- Colombo, P. Ceramic foams: Fabrication, properties and applications. Key Eng. Mater. 2002, 206–213, 1913–1918. [Google Scholar] [CrossRef]
- Hill, C.; Eastoe, J. Foams: From nature to industry. Adv. Colloid Interface Sci. 2017, 247, 496–513. [Google Scholar] [CrossRef]
- Jung, A.; Diebels, S.; Koblischka-Veneva, A.; Schmauch, J.; Barnoush, A.; Koblischka, M.R. Microstructural analysis of electrochemical coated open-cell metal foams by EBSD and nanoindentation. Adv. Eng. Mater. 2013, 16, 15–20. [Google Scholar] [CrossRef]
- Noudem, J.G. Developing of shaping textured superconductors. J. Supercond. 2011, 24, 105–110. [Google Scholar] [CrossRef]
- Reddy, E.S.; Schmitz, G.J. Superconducting foams. Supercond. Sci. Technol. 2002, 15, L21–L24. [Google Scholar] [CrossRef]
- Reddy, E.S.; Schmitz, G.J. Ceramic foams. Am. Ceram. Soc. Bull. 2002, 81, 35–37. [Google Scholar]
- Shoer, J.; Wilson, W.; Jones, L.; Knobel, M.; Peck, M. Microgravity Demonstrations of Flux Pinning for Station-Keeping and Reconfiguration of CubeSat-Sized Spacecraft. J. Spacecr. Rockets 2010, 47, 1066–1069. [Google Scholar] [CrossRef]
- Yang, W.; Liao, D.; Yao, L. Effects of magnetization conditions on dynamic characteristics of spacecrafts with superconducting flux pinning docking interfaces. J. Appl. Phys. 2018, 124, 213901. [Google Scholar] [CrossRef]
- Nicholas, L.; Johnson, E.; Stansbery, J.-C.; Liou, M.; Horstman, C.; Stokely, D. Whitlock The characteristics and consequences of the break-up of the Fengyun-1C spacecraft. Acta Astronaut. 2008, 63, 128–135. [Google Scholar]
- Giffin, A.; Shneider, M.N.; Miles, R.B. Potential micrometeoroid and orbital debris protection system using a gradient magnetic field and magnetic flux compression. Appl. Phys. Lett. 2010, 97, 054102. [Google Scholar] [CrossRef]
- Zheng, F. Model for Choosing Best Alternative to Remove Space Junk. Adv. Eng. Res. (AER) 2017, 130, 1067–1070. [Google Scholar]
- Bartolomé, E.; Granados, X.; Puig, T.; Obradors, X.; Reddy, E.S.; Schmitz, G.J. Critical state in superconducting single-crystalline YBa2Cu3O7 foams: Local versus long-range currents. Phys. Rev. B 2004, 70, 144514. [Google Scholar] [CrossRef]
- Noudem, R.E.S.; Tarka, M.; Goodilin, E.A.; Noe, M.; Zeisberger, M.; Schmitz, G.J. Electrical performance of single domain YBa2Cu3Oy fabrics. Physica C 2002, 366, 93–101. [Google Scholar] [CrossRef]
- Noudem, J.G.; Guilmeau, E.; Chateigner, D.; Lambert, S.; Reddy, E.S.; Ouladdiaf, B.; Schmitz, G.J. Properties of YBa2Cu3Oy-textured superconductor foams. Physica C 2003, 408–410, 655–656. [Google Scholar] [CrossRef]
- Bean, C.P. Magnetization of hard superconductors. Phys. Rev. Lett. 1962, 8, 250–253. [Google Scholar] [CrossRef]
- Chen, I.-G.; Liu, J.; Weinstein, R.; Lau, K. Characterization of YBa2Cu3O7, including critical current density Jc, by trapped magnetic field. J. Appl. Phys. 1992, 72, 1013–1020. [Google Scholar] [CrossRef]
- Koblischka, M.R.; Koblischka-Veneva, A.; Reddy, E.S.; Schmitz, G.J. Analysis of the microstructure of superconducting YBCO foams by means of AFM and EBSD. J. Adv. Ceram. 2014, 3, 317–325. [Google Scholar] [CrossRef]
- Koblischka-Veneva, A.; Koblischka, M.R.; Ide, N.; Inoue, K.; Muralidhar, M.; Hauet, T.; Murakami, M. Microstructural and magnetic analysis of a superconducting foam and comparison with IG-processed bulk samples. J. Phys. Conf. Ser. 2016, 695, 012002. [Google Scholar] [CrossRef]
- Koblischka, M.R.; Koblischka-Veneva, A.; Berger, K.; Nouailhetas, Q.; Douine, B.; Reddy, E.S.; Schmitz, G.J. Current flow and flux pinning properties of YBCO foam struts. IEEE Trans. Appl. Supercond. 2019, 29, 8001405. [Google Scholar] [CrossRef]
- Shi, Y.; Dennis, A.R.; Durrell, J.H.; Cardwell, D.A. The effect of size and aspect ratio on the trapped field properties of single grain, Y–Ba–Cu–O bulk superconductors. Supercond. Sci. Technol. 2019, 32, 025005. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, W.; Yang, P.; Zhang, C.; Chen, J.; Zhang, L.; Chen, L. Influence of trapped field on the levitation force of SmBCO bulk superconductor. Physica C 2017, 542, 28–33. [Google Scholar] [CrossRef]
- Zhou, D.; Shi, Y.; Zhao, W.; Dennis, A.R.; Beck, M.; Ainslie, M.D.; Palmer, K.G.B.; Cardwell, D.A.; Durrell, J.H. Full Magnetization of Bulk (RE)Ba2Cu3O7−δ Magnets With Various Rare-Earth Elements Using Pulsed Fields at 77 K. IEEE Trans. Appl. Supercond. 2017, 27, 6800704. [Google Scholar] [CrossRef]
- Hari Babu, N.; Kambara, M.; Smith, P.J.; Cardwell, D.A.; Shi, Y. Fabrication of large single-grain Y–Ba–Cu–O through nfiltration and seeded growth processing. J. Mater. Res. 2000, 15, 1235–1238. [Google Scholar] [CrossRef]
- Liu, Y.; Pan, B.; Li, Z.; Xiang, H.; Qian, J.; Du, G.; Huang, S.; Yao, X.; Izumi, M.; Wang, Y. YBa2Cu3O7−δ superconductor bulks composited by Y2BaCuO5 nanoparticles derived from homogeneous nucleation catastrophe. J. Am. Ceram. Soc. 2017, 100, 3858–3864. [Google Scholar] [CrossRef]
- Koblischka, M.R.; Koblischka-Veneva, A.; Chang, C.; Hauet, T.; Reddy, E.S.; Schmitz, G.J. Flux pinning analysis of superconducting YBCO foam struts. IEEE Trans. Appl. Supercond. 2018. [Google Scholar] [CrossRef]
- Namburi, D.K.; Durrell, J.H.; Jaroszynski, J.; Shi, Y.; Ainslie, M.D.; Huang, K.; Dennis, A.R.; Hellstrom, E.E.; Cardwell, D.A. A trapped field of 14.3 T in Y-Ba-Cu-O bulk superconductors fabricated by buffer-assisted seeded infiltration and growth. Supercond. Sci. Technol. 2018, 31, 125004. [Google Scholar] [CrossRef]
- Gokhfeld, D.M. The circulation radius and critical current density in type-II superconductors. Tech. Phys. Lett. 2019, 45, 1–3. [Google Scholar]
- Noudem, J.G.; Reddy, E.S.; Schmitz, G.J. Magnetic and transport properties of YBa2Cu3Oy superconductor foams. Physica C 2002, 390, 286–290. [Google Scholar] [CrossRef]
- Petrov, M.I.; Tetyueva, T.N.; Kveglis, L.I.; Efremov, A.A.; Zeer, G.M.; Shaikhutdinov, K.A.; Balaev, D.A.; Popkov, S.I.; Ovchinnikov, S.G. Synthesis, microstructure, and the transport and magnetic properties of Bi-containing high-temperature superconductors with a porous structure. Tech. Phys. Lett. 2003, 29, 986–988. [Google Scholar] [CrossRef]
- Fiertek, P.; Sadowski, W. Processing of porous structures of YBa2Cu3O7−δ high-temperature superconductor. Mater. Sci. Pol. 2006, 24, 1103–1108. [Google Scholar]
- Fiertek, P.; Andrzejewski, B.; Sadowski, W. Synthesis and transport properties of porous superconducting ceramics of YBa2Cu3O7−δ. Rev. Adv. Mater. Sci. 2010, 23, 52–56. [Google Scholar]
- Koblischka, M.R.; Koblischka-Veneva, A. Porous high-Tc superconductors and their applications. AIMS Mater. Sci. 2018, 5, 1199–1213. [Google Scholar] [CrossRef]
- Jirsa, M.; Půst, L.; Dlouhý, D.; Koblischka, M.R. Fishtail shape in the magnetic hysteresis loop for superconductors: Interplay between different pinning mechanisms. Phys. Rev. B 1997, 55, 3276–3284. [Google Scholar] [CrossRef]
- Polat, Ö.; Sinclair, J.W.; Zuev, Y.L.; Thompson, J.R.; Christen, D.K.; Cook, S.W.; Kumar, D.; Chen, Y.; Selvamanickam, V. Thickness dependence of magnetic relaxation and E − J characteristics in superconducting Gd-Y-Ba-Cu-O films with strong vortex pinning. Phys. Rev. B 2011, 84, 024519. [Google Scholar] [CrossRef]
- Roas, B.; Saemann-Ischenko, G.; Schultz, L. Anisotropy of the critical current density in epitaxial YBa2Cu3Ox thin films. Phys. Rev. Lett. 1990, 64, 479–482. [Google Scholar] [CrossRef]
- Altin, E.; Gokhfeld, D.M.; Demirel, S.; Oz, E.; Kurt, F.; Altin, S.; Yakinci, M.E. Vortex pinning and magnetic peak effect in Eu(Eu,Ba)2.125Cu3Ox. J. Mater. Sci.: Mater. Electron. 2014, 25, 1466–1473. [Google Scholar] [CrossRef]
- Iida, K.; Babu, N.H.; Shi, Y.; Cardwell, D.A. Seeded infiltration and growth of large, single domain Y–Ba–Cu–O bulk superconductors with very high critical current densities. Supercond. Sci. Technol. 2005, 18, 1421–1427. [Google Scholar] [CrossRef]
- Kumar, N.D.; Rajasekharan, T.; Muraleedharan, K.; Banerjee, A.; Seshubai, V. Unprecedented current density to high fields in YBa2Cu3O7−δ superconductor through nano-defects generated by preform optimization in infiltration growth process. Supercond. Sci. Technol. 2010, 23, 105020. [Google Scholar] [CrossRef]
- Ihara, N.; Matsushita, T. Effect of flux creep on irreversibility lines in superconductors. Physica C 1996, 257, 223–231. [Google Scholar] [CrossRef]
- Matsushita, T.; Otabe, E.S.; Wada, H.; Takahama, Y.; Yamauchi, H. Size dependencies of the peak effect and irreversibility field in superconducting Sm-123 powders. Physica C 2003, 397, 38–46. [Google Scholar] [CrossRef]
- Hari Babu, N.; Shi, Y.; Iida, K.; Cardwell, D.A. A practical route for the fabrication of large single-crystal (RE)–Ba–Cu–O superconductors. Nat. Mater. 2005, 4, 476–480. [Google Scholar] [CrossRef]
- Rotta, M.; Namburi, D.K.; Shi, Y.; Pessoa, A.L.; Carvalho, C.L.; Durrell, J.H.; Cardwell, D.A.; Zadorosny, R. Synthesis of Y2BaCuO5 nano-whiskers by a solution blow spinning technique and their successful introduction into single-grain, YBCO bulk superconductors. Ceram. Int. 2019, 45, 3948–3953. [Google Scholar] [CrossRef]
- Pavan Kumar Naik, S.; Muralidhar, M.; Koblischka, M.R.; Koblischka-Veneva, A.; Oka, T.; Murakami, M. Novel method of tuning the size of Y2BaCuO5 particles and their influence on the physical properties of bulk YBa2Cu3O7−δ superconductor. APEX 2019. submitted for publication. [Google Scholar]
- Veneva, A.; Iordanov, I.; Toshev, L.; Stoyanova-Ivanova, A.; Gogova, D. A study of the effect of KClO3 addition on the AC susceptibility and microstructure of high-temperature (T-c(onset) at 105 K) YBCO ceramic superconductors. Physica C 1998, 308, 175–184. [Google Scholar] [CrossRef]
- Orlova, T.S.; Laval, J.Y. Microstructure and Superconducting Properties of the DyBaCuO Ceramic Doped with Na2CO3, NaCl, and KClO3. Phys. Solid State 2007, 49, 2058–2064. [Google Scholar] [CrossRef]
- Santosh, M.; Koblischka, M.R. Experimenting with a superconducting levitation train. Eur. J. Phys. Educ. 2014, 5, 1–9. [Google Scholar]
- Lévêque, J.; Berger, K.; Douine, B. Superconducting Motors and Generators. In High Temperature Superconductors: Synthesis, Occurence and Applications; Muralidhar, M., Koblischka, M.R., Eds.; NOVA Science Publishers: Commack, NY, USA, 2018; pp. 263–290. [Google Scholar]
- Fujishiro, H.; Tateiwa, T.; Fujiwara, A.; Oka, T.; Hayashi, H. Higher trapped field over 5 T on HTSC bulk by modified pulsed field magnetizing. Physica C 2006, 445–448, 334–338. [Google Scholar] [CrossRef]
- Ainslie, M.D.; Mochizuki, H.; Fujishiro, H.; Zhai, W.; Namburi, D.K.; Shi, Y.; Zou, J.; Dennis, A.R.; Cardwell, D.A. Pulsed Field Magnetization of Single-Grain Bulk YBCO Processed From Graded Precursor Powders. IEEE Trans. Appl. Supercond. 2016, 26, 6800104. [Google Scholar] [CrossRef]
- Montminy, M.D.; Tannenbaum, A.R.; Macosko, C.W. The 3D structure of real polymer foams. J. Colloid Interface Sci. 2004, 280, 202–211. [Google Scholar] [CrossRef]
- Nie, Z.; Lin, Y.; Tong, Q. Modeling structures of open cell foams. Comput. Mater. Sci. 2017, 131, 160–169. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koblischka, M.R.; Naik, S.P.K.; Koblischka-Veneva, A.; Murakami, M.; Gokhfeld, D.; Reddy, E.S.; Schmitz, G.J. Superconducting YBCO Foams as Trapped Field Magnets. Materials 2019, 12, 853. https://doi.org/10.3390/ma12060853
Koblischka MR, Naik SPK, Koblischka-Veneva A, Murakami M, Gokhfeld D, Reddy ES, Schmitz GJ. Superconducting YBCO Foams as Trapped Field Magnets. Materials. 2019; 12(6):853. https://doi.org/10.3390/ma12060853
Chicago/Turabian StyleKoblischka, Michael R., Sugali Pavan Kumar Naik, Anjela Koblischka-Veneva, Masato Murakami, Denis Gokhfeld, Eddula Sudhakar Reddy, and Georg J. Schmitz. 2019. "Superconducting YBCO Foams as Trapped Field Magnets" Materials 12, no. 6: 853. https://doi.org/10.3390/ma12060853
APA StyleKoblischka, M. R., Naik, S. P. K., Koblischka-Veneva, A., Murakami, M., Gokhfeld, D., Reddy, E. S., & Schmitz, G. J. (2019). Superconducting YBCO Foams as Trapped Field Magnets. Materials, 12(6), 853. https://doi.org/10.3390/ma12060853




