Computational Multiscale Solvers for Continuum Approaches
Abstract
1. Introduction
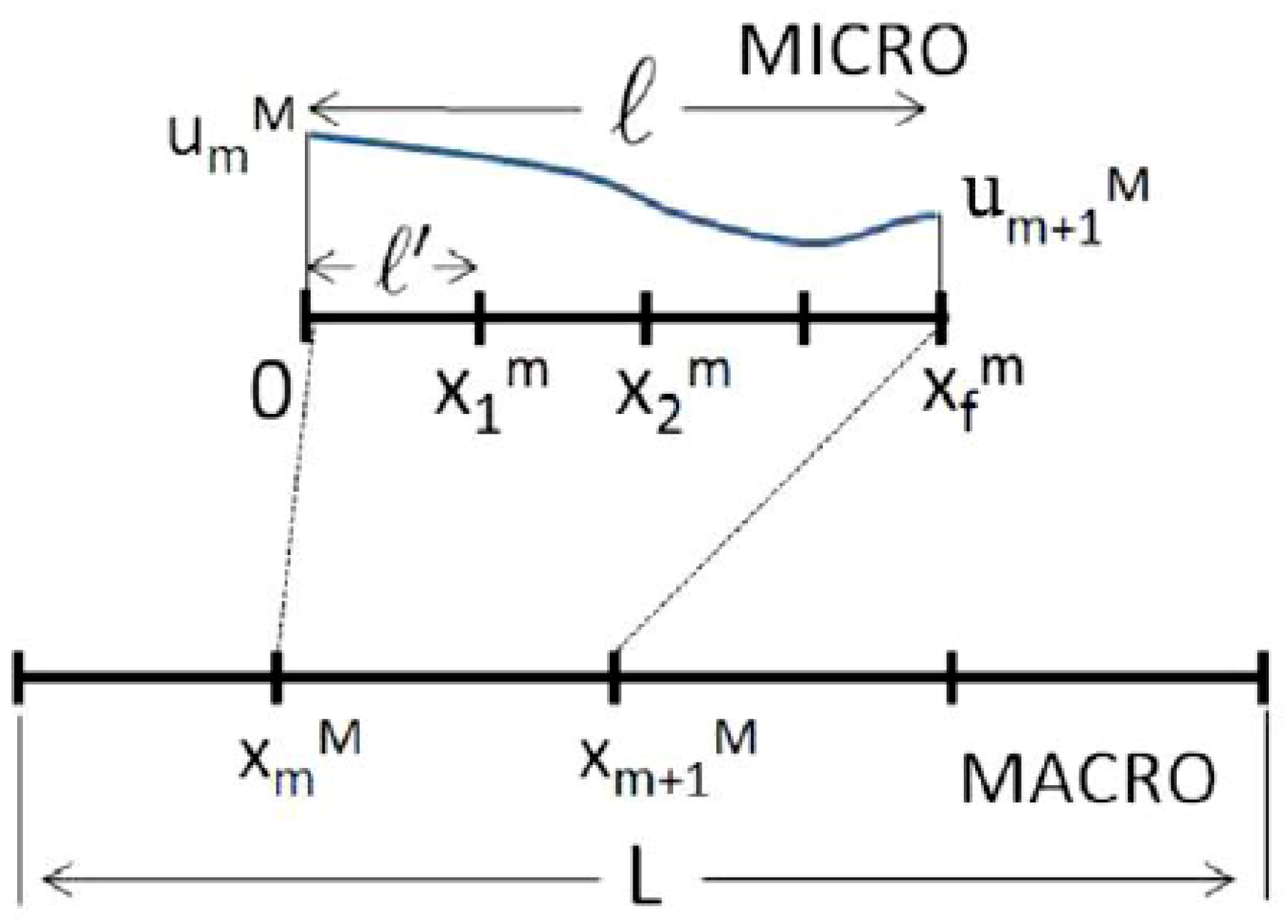
1.1. Temporal Scales
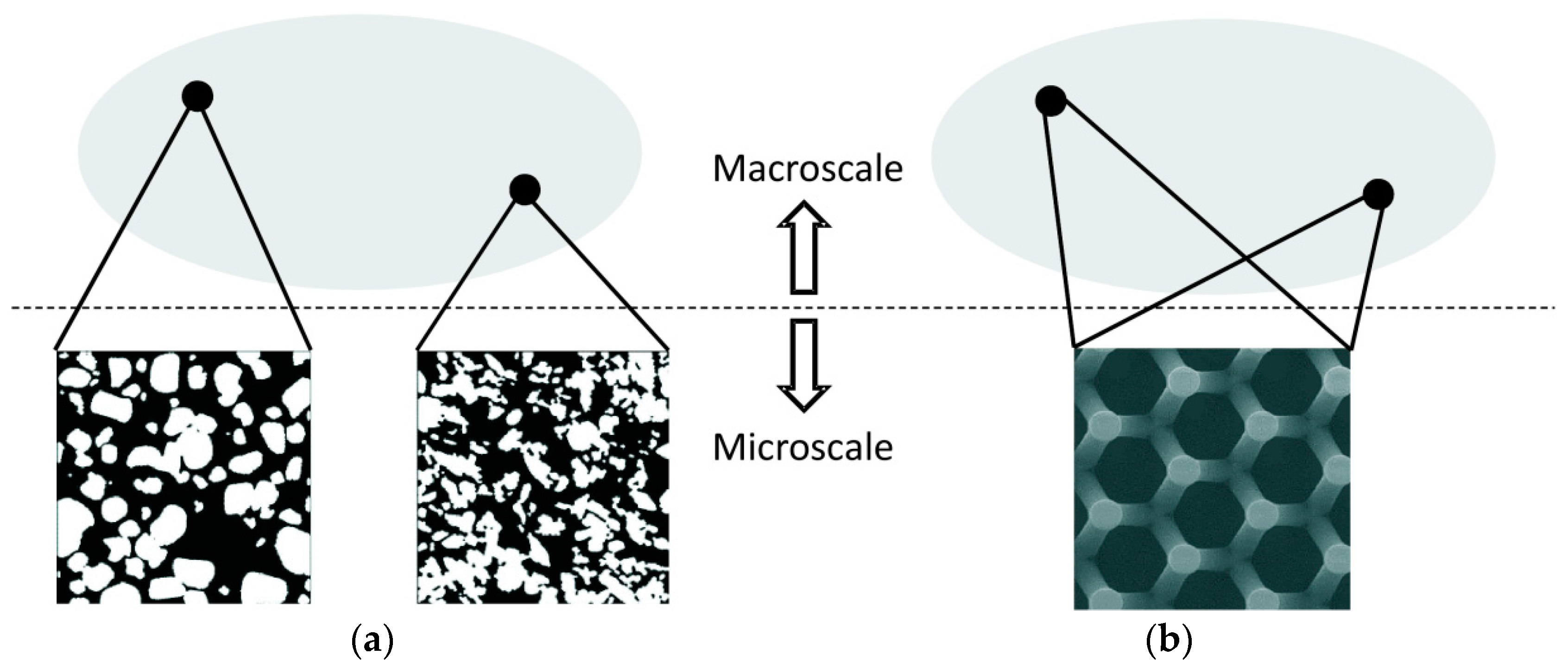
1.2. Spatial Scales
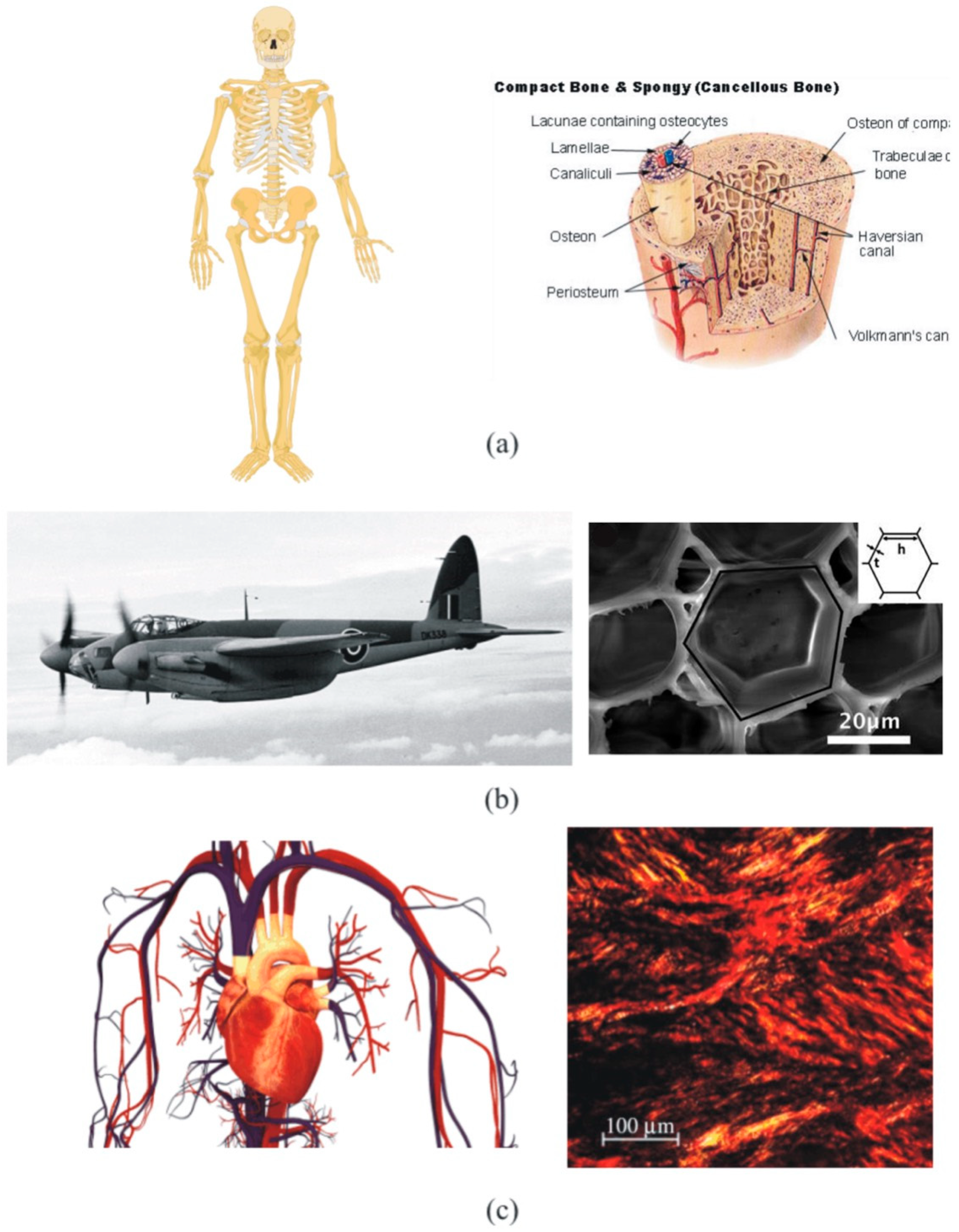
- Bone: Bone microstructure exhibits a certain degree of porosity ranging from 5% in cortical bone to 90% in cancellous or trabecular bone (see Figure 2a). Bones are part of the structural support of animals, i.e., the skeleton, so the criterion followed by evolution and natural selection in the design of such a microstructure is to economize the resistance/weight ratio. Man-made structures inspired by this criterion include the sandwich and foam structures. The associated multiscale problems in bone tissue are both mechanical and fluidics, since it is important to know the stress distribution and velocity of the fluid within the microstructure as well as the skeleton response to loads [9,10,11,12,13].
- Wood: This class of natural lightweight structures found in trees [14], see Figure 2b, is associated with structural problems with application in primitive handmade structures as well as light but stiff constructions, such as the World War II combat aircraft de Havilland Mosquito [15]. The microarchitectural arrangement of wood panels make them a lightweight stiff structure.
- Fibered tissues: Soft tissues are usually “reinforced” by collagen fibers (see Figure 2c). Examples of these tissues are blood vessels and arteries and the cardiac tissue, which is also embedded with cardiomyocytes. Collagen remodels in the microscopic scale during life tuning the mechanical properties of the macroscopic tissue, which influences the development of certain vascular disorders such as hypertension [16]. Even though the associated mechanical problem has been established macroscopically with success in the case of blood vessels [17,18,19,20,21], it is necessary to account for the fiber scale to include the mechanoelectrical activity of cardiomyocytes, as pointed out above, for the case of the cardiac tissue [22].
- Concrete: It has been widely used as a building material since the mid-18th century. It is microstructurally made through a mixture of water, cement, aggregates, and reinforcement. The result is a cheap, easy, and resistant macroscopic material (see Figure 3a). The overall mechanical and thermal behavior can be obtained by an analysis of its microstructure. Regarding its mechanical behavior, it is well known that, microscopically, the progression of cracks in the cement is stopped by the aggregates, whereas the reinforcement provides tension stiffness. Recently, engineered cementitious composites (ECC) have emerged as a class of ultra-ductile fiber-reinforced cementitious composites, whose better mechanical properties were the result of years of study to develop a material microstructurally designed using micromechanics concepts [23].
- Metal matrix composites (MMC): They belong to the class of composite materials with different phases being one of them at least a metal. A two-phase MMC contains a matrix and a reinforcement. The idea is to obtain a hybrid material with excellent properties such as wear resistance, friction coefficient, mechanical resistance, or thermal conductivity (see Figure 3b). All these properties can be derived from an analysis of its associated structure at the microstructural level.
- Composite materials: These are fibered materials usually composed of a polymeric or resin matrix phase and a fiber reinforcement (see Figure 3c). They have excellent resistance/weight ratio as well as electrical, thermal and acoustic isolating properties. All these properties derive from the microscopic orientation and density of fibers within the matrix.
- Biomaterials: The current generation of biomaterials includes self-active materials which interact with the human body with improved regeneration and healing capabilities. An example is the scaffolds used in tissue engineering. Here scaffolds are used as a temporary porous structural support to attach cells and to segregate new matrix tissue. After the regeneration process is complete the structure naturally degrades (see Figure 3d). The associated analysis of this problem is both multiscale and multiphysical in nature. A summary of it may be found in [24].
1.3. Scope and Outline
2. Homogenization-Based Multiscale Approaches
- Neumann:
- Dirichlet:
- Periodic:
2.1. Linear Elasticity
2.1.1. Localization
- The stress vectors are opposite on opposite sides of the boundary .
- The local strain is split into its average and fluctuating terms such that,thus, the periodicity boundary conditions yield
2.1.2. Homogenization
2.1.3. Variational Formulation
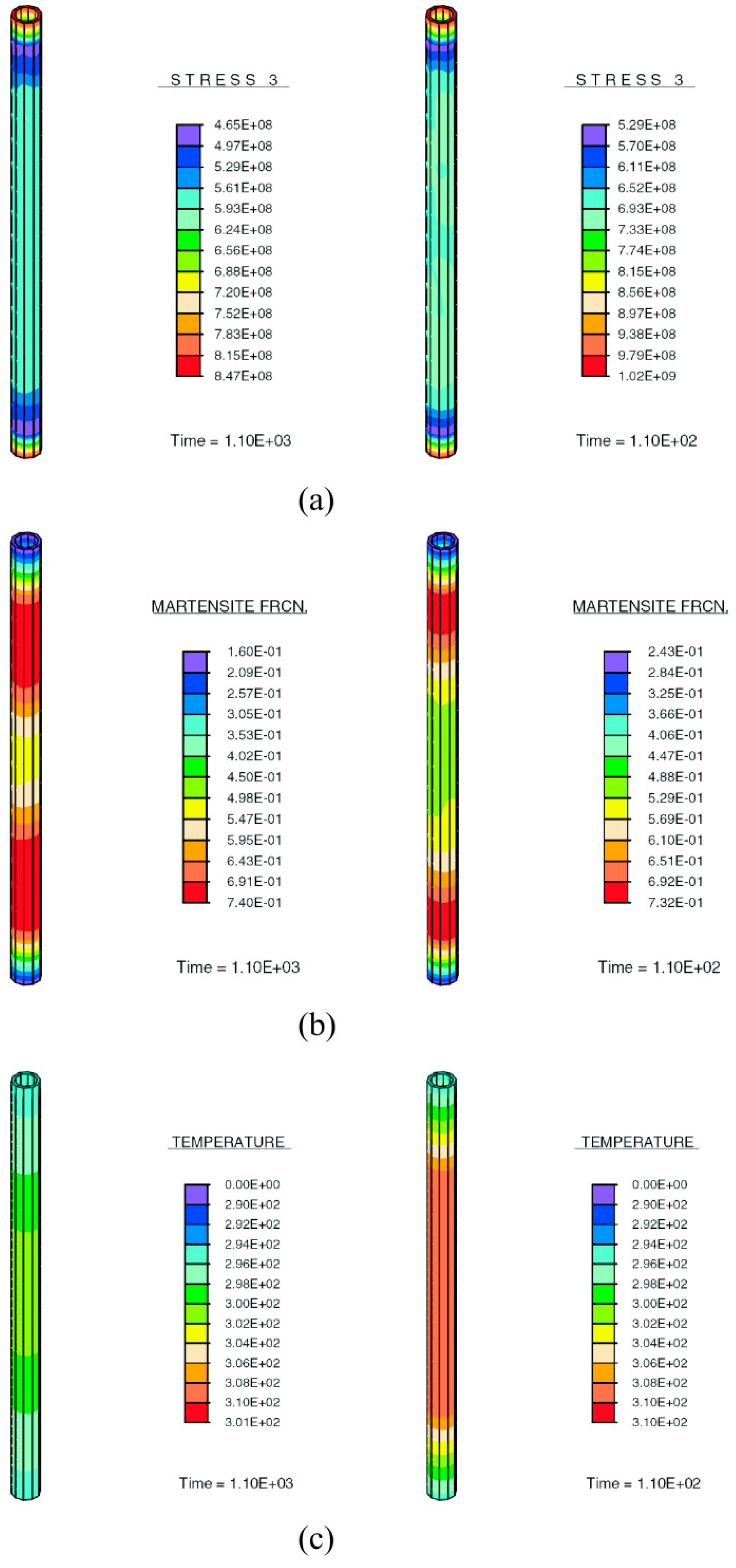
2.1.4. Illustrative Example
2.2. Nonlinear Mechanics
2.3. Darcy and Fick Problems
2.3.1. Localization
2.3.2. Homogenization
2.3.3. Variational Formulation
2.3.4. Illustrative Example
2.4. Heat Transfer
2.5. Multiphysics: Thermomechanics, Poroelasticity, and Others
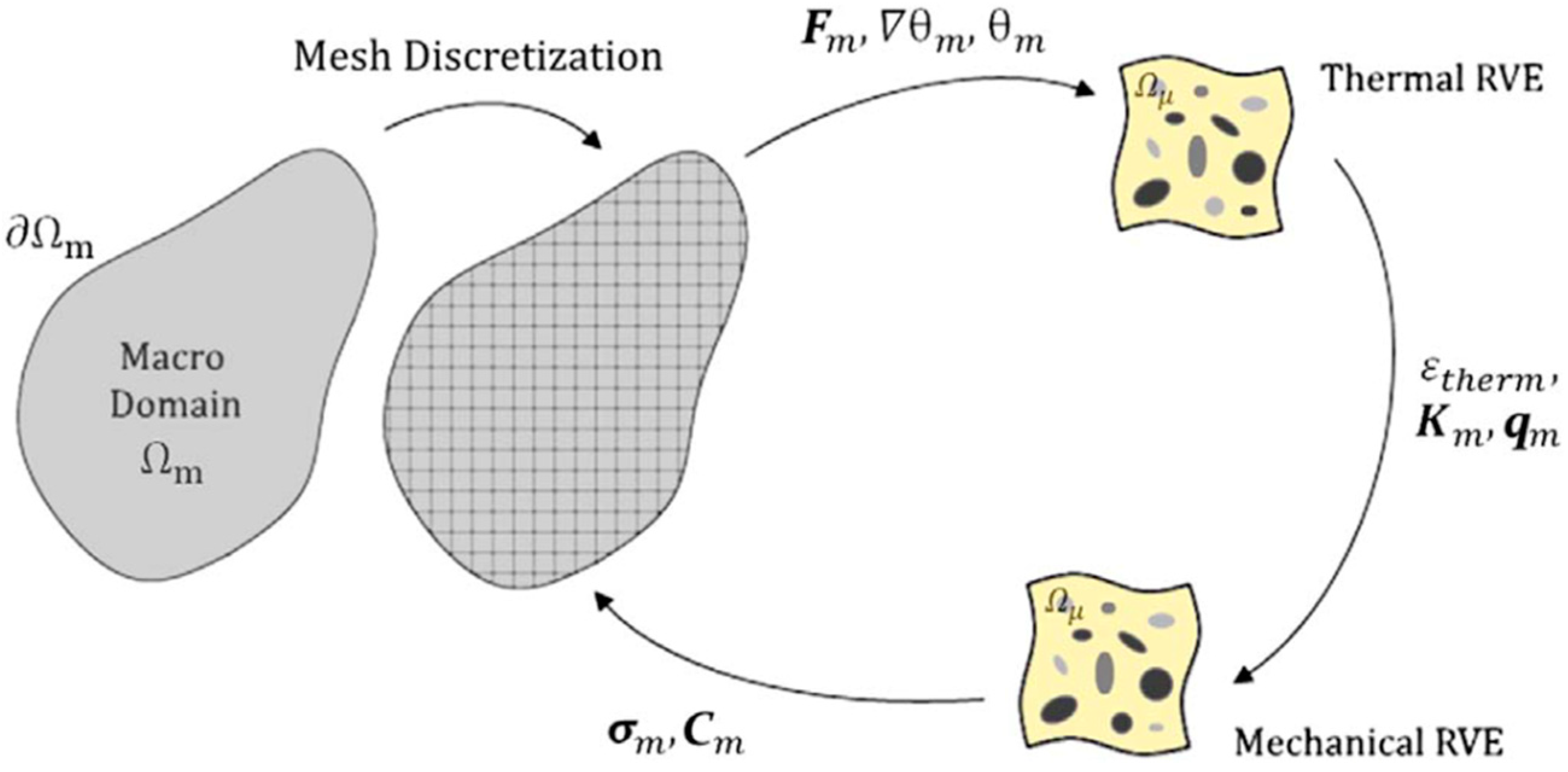
2.5.1. Thermomechanics
2.5.2. Poroelasticity
2.5.3. Others
3. Non-Homogenization-Based Multiscale Approaches
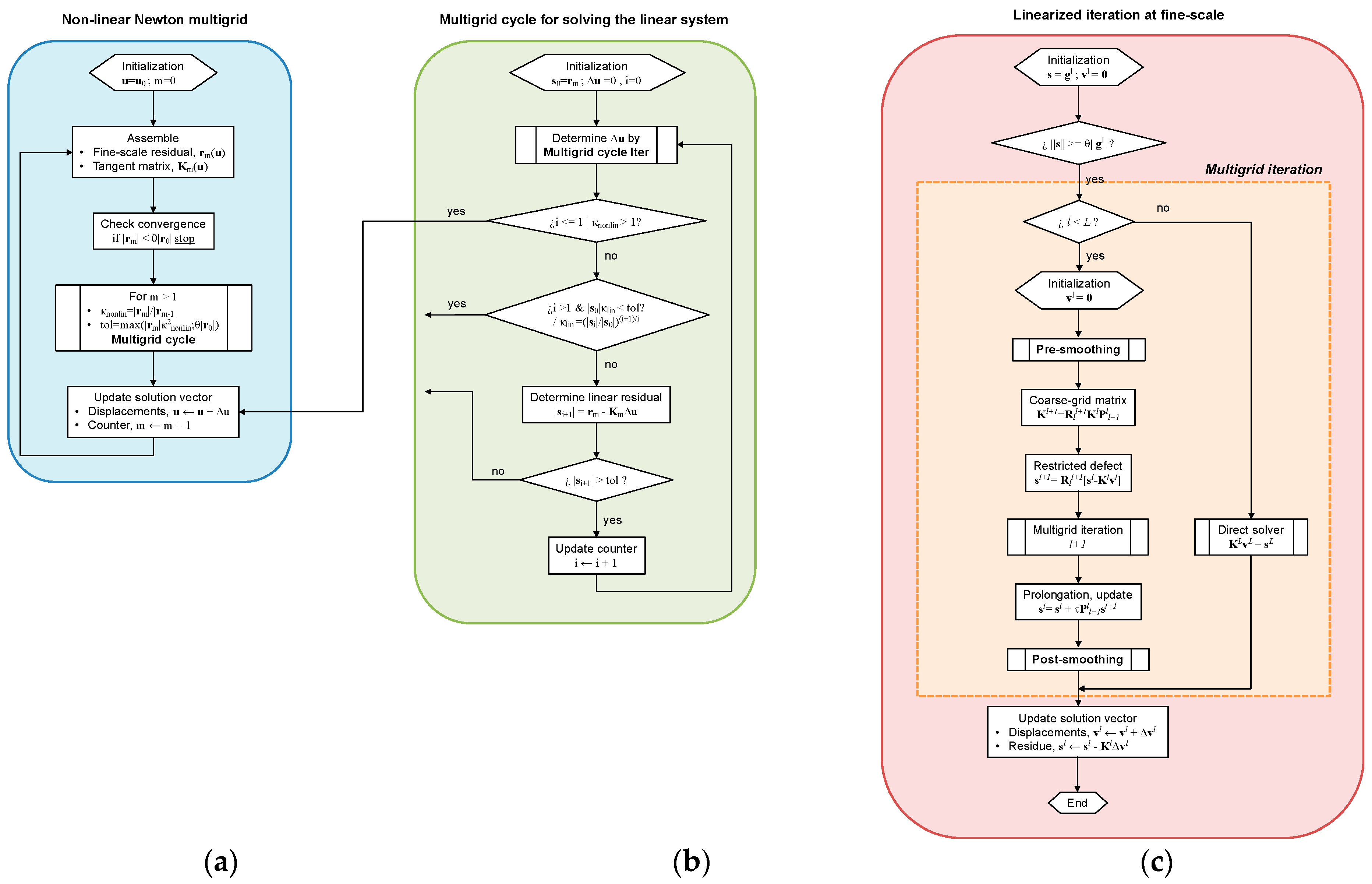
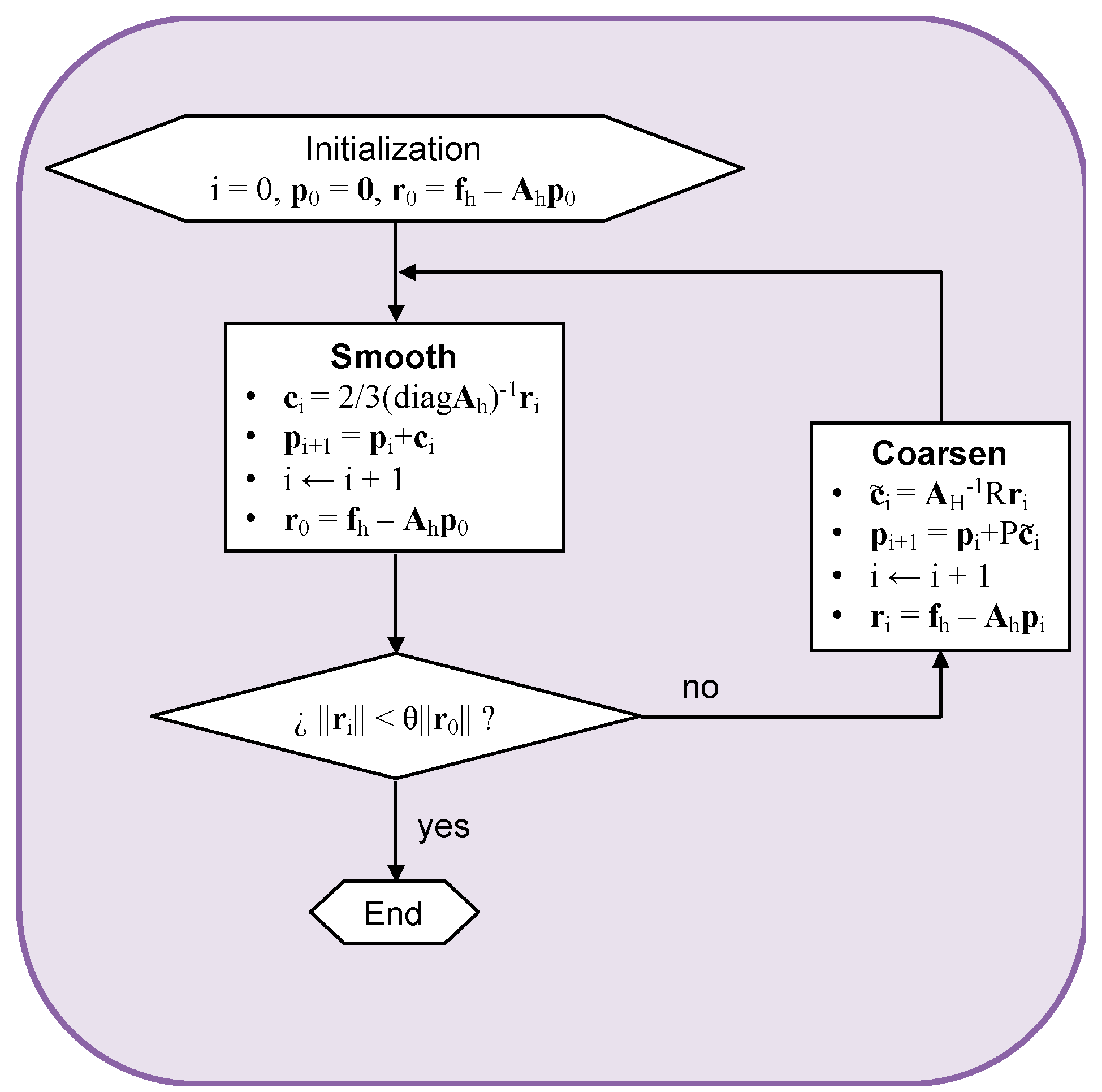
3.1. Multigrid
3.1.1. Non-Linear Mechanics
3.1.2. Darcy Flow
3.1.3. Heat Transfer
3.2. Domain Decomposition
3.2.1. Linear Elasticity
- Dirichlet boundary conditions: on
- Neumann boundary conditions: on
3.2.2. Non-Linear Mechanics
- Dirichlet boundary conditions: on
- Neumann boundary conditions: on
3.2.3. The Finite Element Tearing and Interconnecting (FETI) Method
3.2.4. Darcy and Fick Problems
- Conservation of mass: on
- Balance of normal forces: on
- Beavers-Joseph-Saffman condition: on
- Flux continuity: on
- Balance of neutron current: on
3.2.5. Heat Transfer
- Flux continuity: on
- Temperature continuity: on
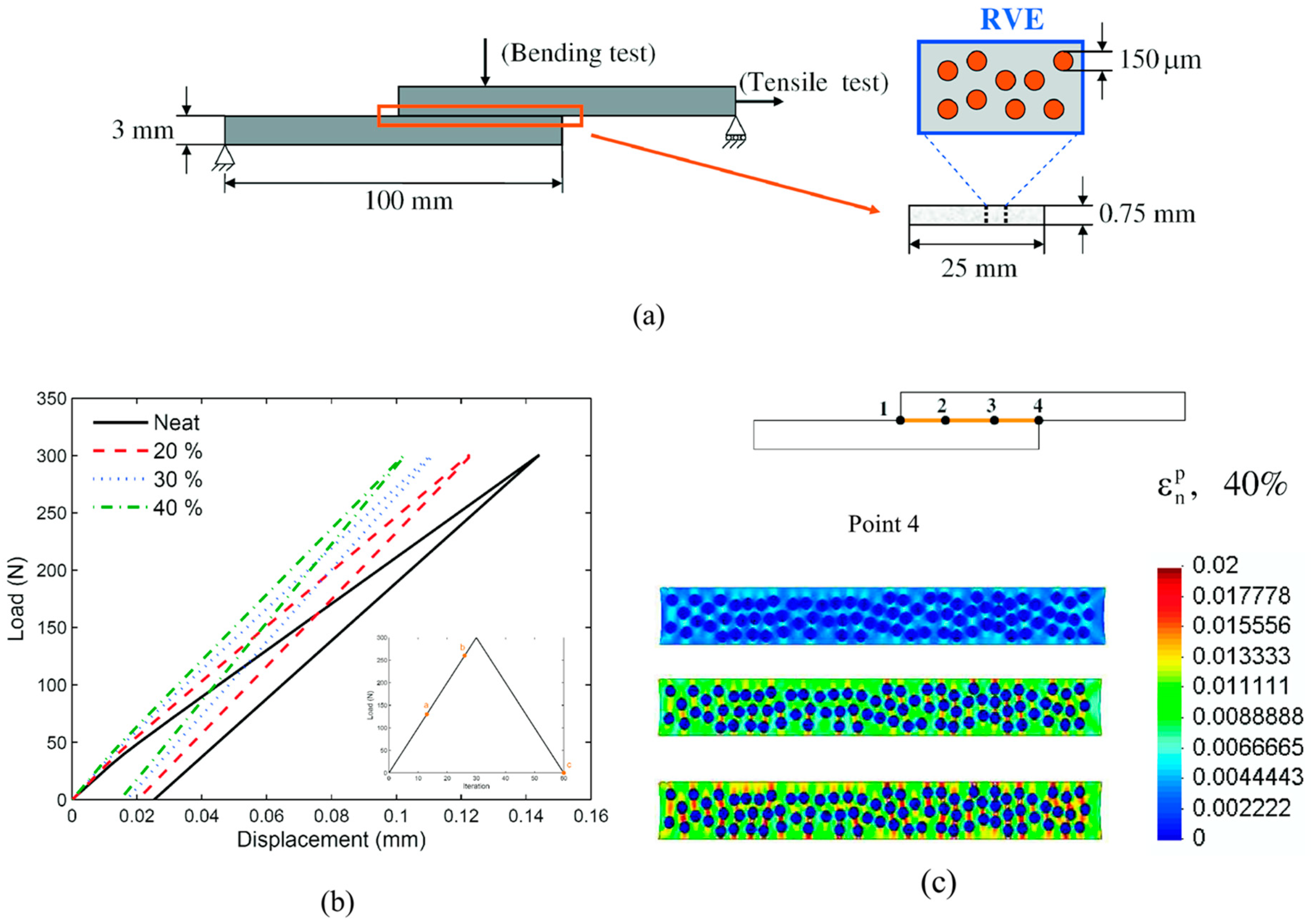
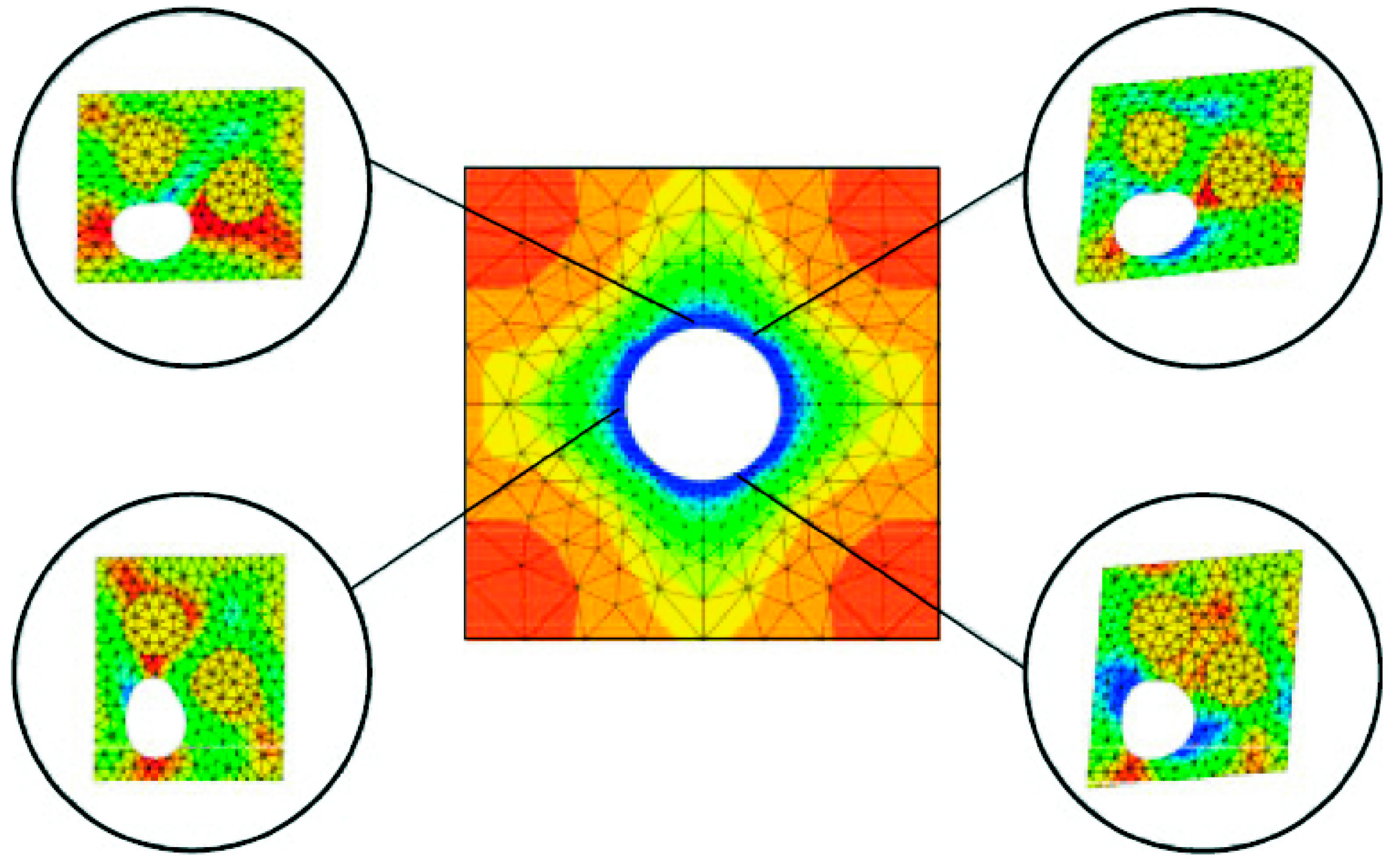
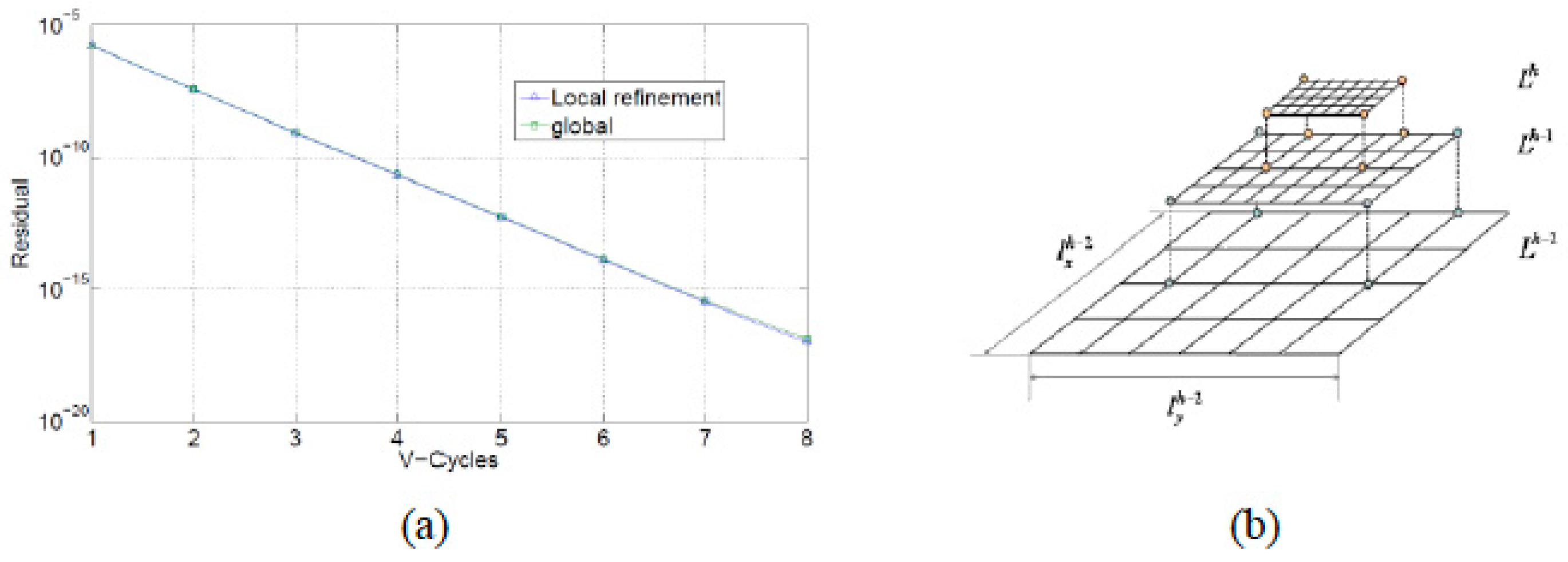
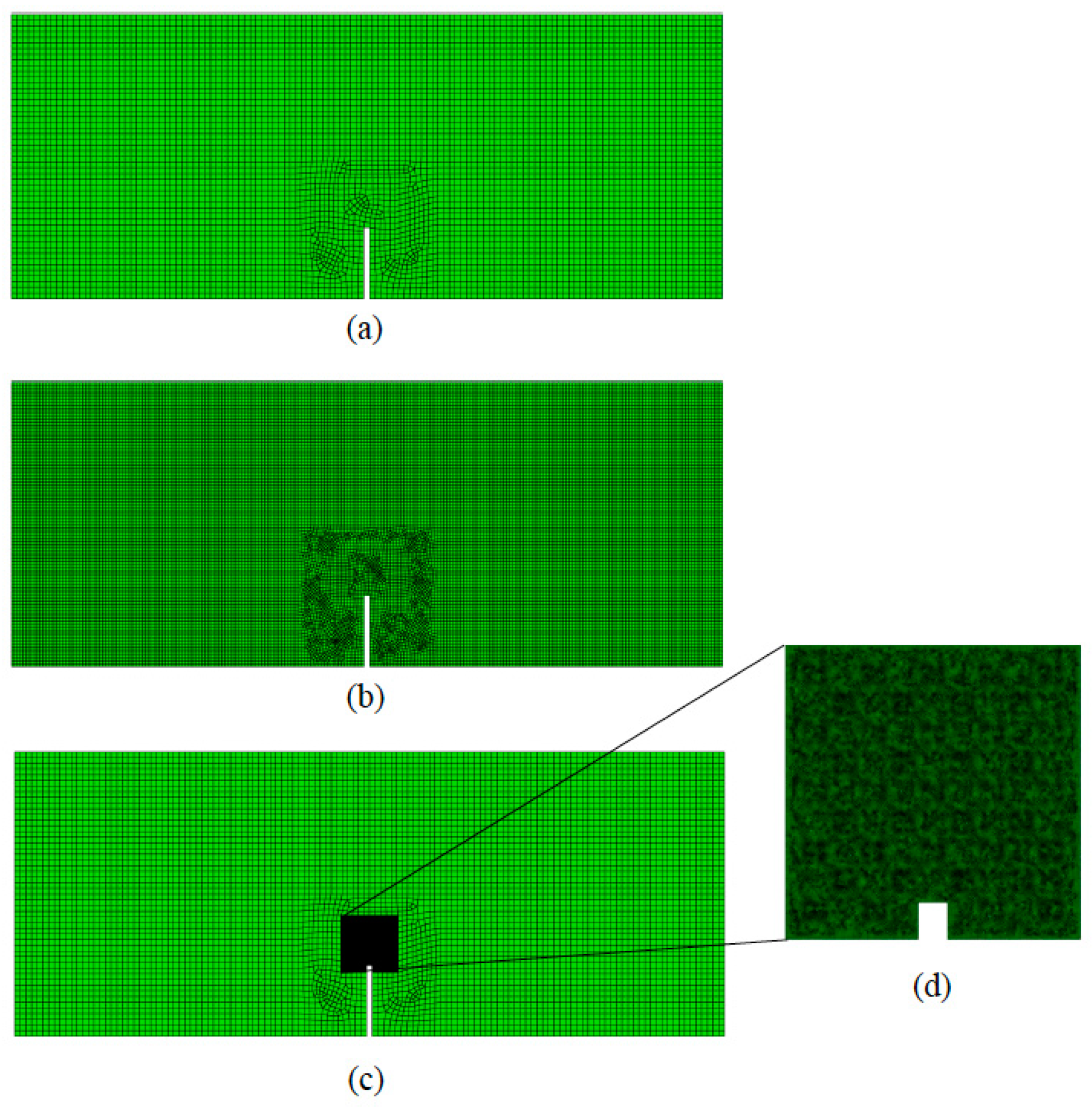
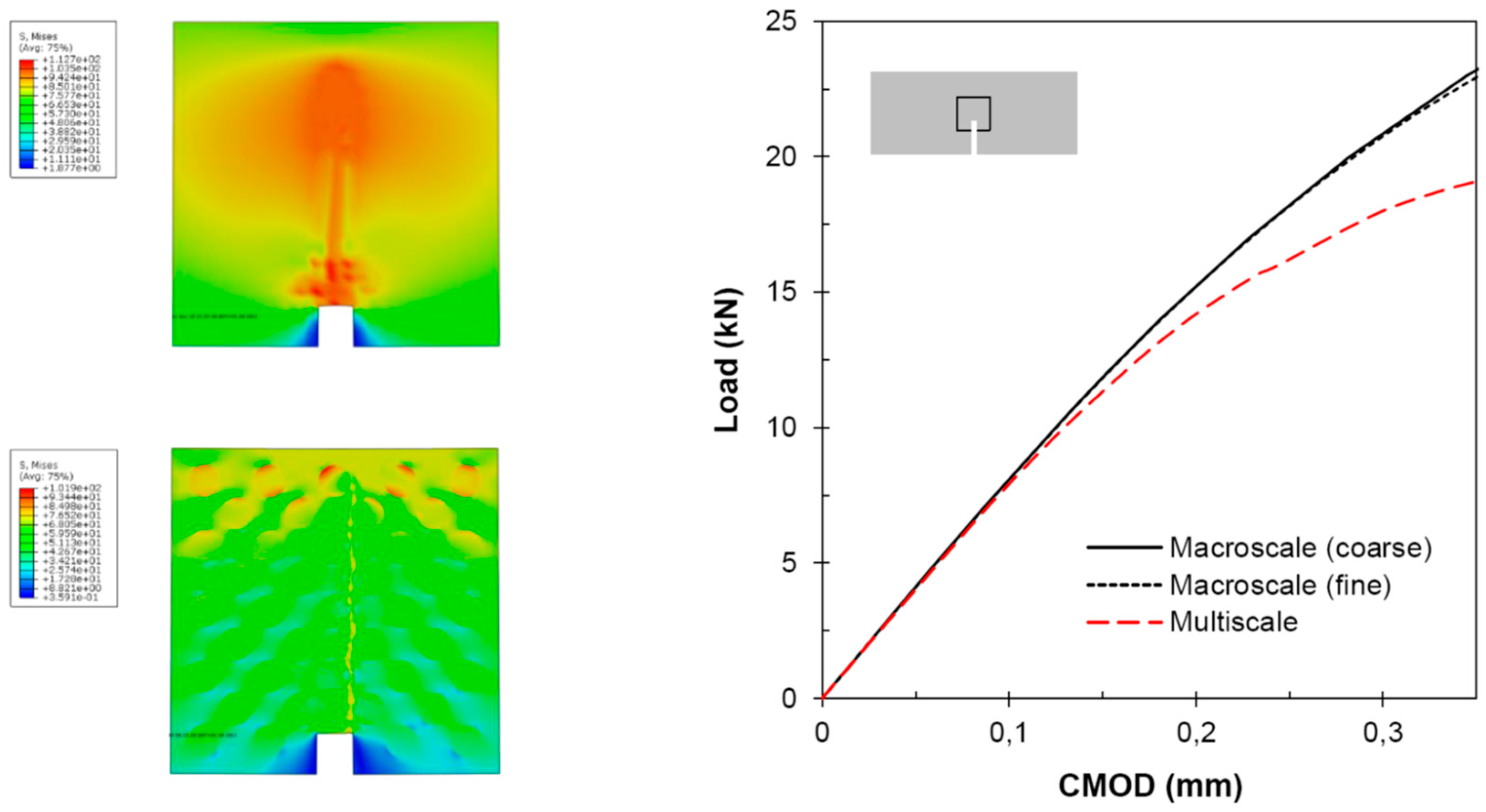
3.2.6. Illustrative Example
4. Proper Generalized Decomposition Multiscale Approaches
4.1. PGD in HM Methods
4.2. PGD in NHM Methods
- Dirichlet: on
- Neumann: on
5. Multiscale Multiphysical Software
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- National Research Council. Integrated Computational Materials Engineering: A Transformational Discipline for Improved Competitiveness and National Security; The National Academies Press: Washington, DC, USA, 2008. [Google Scholar]
- Curtin, W.A.; Needleman, A.; Ortiz, M.; Phillips, R.; Kaxiras, E.; Cedar, G.; Farkas, D. Virtual Design and Testing of Materials: A Multiscale Approach; Brown University: Providence, RI, USA, 2006. [Google Scholar]
- Horstemeyer, M.F. Integrated Computational Materials Engineering (ICME) for Metals: Using Multiscale Modeling to Invigorate Engineering Design with Science; Wiley: New York, NY, USA, 2012. [Google Scholar]
- Clayton, R.; Bernus, O.; Cherry, E.; Dierckx, H.; Fenton, F.; Mirabella, L.; Panfilov, A.; Sachse, F.; Seemann, G.; Zhang, H. Models of cardiac tissue electrophisiology: Progress, challenges and open questions. Prog. Biophys. Mol. Biol. 2011, 104, 22–48. [Google Scholar] [CrossRef] [PubMed]
- Heidenreich, E.A.; Ferrero, J.M.; Doblaré, M.; Rodríguez, J.F. Adaptive macro finite elements for the numerical solution of monodomain equations in cardiac electrophysiology. Ann. Biomed. Eng. 2010, 38, 2331–2345. [Google Scholar] [CrossRef] [PubMed]
- Wong, J.; Göktepe, S.; Kuhl, E. Computational modeling of electrochemical coupling: A novel finite element approach towards ionic models for cardiac electrophysiology. Comput. Methods Appl. Mech. Eng. 2011, 200, 3139–3158. [Google Scholar] [CrossRef]
- Wong, J.; Göktepe, S.; Kuhl, E. Computational modeling of chemo-electro-mechanical coupling: A novel implicit monolithic finite element approach. Int. J. Numer. Method Biomed. Eng. 2013, 29, 1104–1133. [Google Scholar] [CrossRef] [PubMed]
- Hunter, P.J.; Crampin, E.J.; Nielsen, P.M. Bioinformatics, multiscale modeling and the IUPS Physiome Project. Brief. Bioinform. 2008, 9, 333–343. [Google Scholar] [CrossRef] [PubMed]
- Hamed, E.; Jasiuk, I. Multiscale damage and strength of lamellar bone modeled by cohesive finite elements. J. Mech. Behav. Biomed. Mater. 2013, 28C, 94–110. [Google Scholar] [CrossRef] [PubMed]
- Paoletti, N.; Liò, P.; Merelli, E.; Viceconti, M. Multilevel computational modeling and quantitative analysis of bone remodeling. IEEE/ACM Trans. Comput. Biol. Bioinform. 2012, 9, 1366–1378. [Google Scholar] [CrossRef] [PubMed]
- Podshivalov, L.; Fischer, A.; Bar-Yoseph, P.Z. 3D hierarchical geometric modeling and multiscale FE analysis as a base for individualized medical diagnosis of bone structure. Bone 2011, 48, 693–703. [Google Scholar] [CrossRef] [PubMed]
- Gonçalves-Coelho, P.; Rui Fernandes, P.; Carrio-Rodrigues, H. Multiscale modeling of bone tissue with surface and permeability control. J. Biomech. 2011, 44, 321–329. [Google Scholar]
- Ilic, S.; Hackl, K.; Gilbert, R. Application of the multiscale FEM to the modeling of cancellous bone. Biomech. Model. Mechanobiol. 2010, 9, 87–102. [Google Scholar] [CrossRef] [PubMed]
- Borrega, M.; Ahvenainen, P.; Serimaa, R.; Gibson, L.J. Composition and structure of balsa (Ochroma pyramidale) wood. Wood Sci. Technol. 2015, 49, 403–420. [Google Scholar] [CrossRef]
- Howe, S. De Havilland Mosquito: An Illustrated History; Crécy Publishing Limited: Manchester, UK, 1999. [Google Scholar]
- Sáez, P. Theoretical and Computational Study of the Mechano-Biology in Hypertension Disease; Servicio de Publicaciones de la Universidad de Zaragoza: Zaragoza, Spain, 2013. [Google Scholar]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. 2000, 61, 1–48. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Gasser, T.C.; Stadler, M. A structural model for the viscoelastic behavior of arterial walls: Continuum formulation and finite element analysis. Eur. J. Mech. A-Solids 2002, 21, 441–463. [Google Scholar] [CrossRef]
- Gasser, T.C.; Holzapfel, G.A. A rate-independent elastoplastic constitutive model for (biological) fiber-reinforced composites at finite strains: Continuum basis, algorithmic formulation and finite element implementation. Comput. Mech. 2002, 29, 340–360. [Google Scholar] [CrossRef]
- Pena, E.; Calvo, B.; Martínez, M.A.; Doblaré, M. On finite-strain damage of viscoelastic-fibred materials. Application to soft biological tissues. Int. J. Numer. Methods Eng. 2008, 74, 1198–1218. [Google Scholar] [CrossRef]
- Pena, E.; Alastrué, V.; Laborda, A.; Martínez, M.A.; Doblaré, M. A constitutive formulation of vascular tissue mechanics including viscoelasticity and softening behaviour. J. Biomech. 2010, 43, 984–989. [Google Scholar] [CrossRef] [PubMed]
- Murtada, S.C.; Arner, A.; Holzapfel, G.A. Experiments and mechanochemical modeling of smooth muscle contraction: Significance of filament overlap. J. Theor. Biol. 2012, 297, 176–186. [Google Scholar] [CrossRef] [PubMed]
- Li, V.C. ECC-Tailored Composites through Micromechanical Modeling. Fiber Reinforced Concrete: Present and the Future; CSCE: Montreal, QC, Canada, 1998. [Google Scholar]
- Sanz-Herrera, J.A.; García-Aznar, J.M.; Doblaré, M. A mathematical approach to bone tissue engineering. Philos. Trans. A Math. Phys. Eng. Sci. 2009, 367, 2055–2078. [Google Scholar] [CrossRef] [PubMed]
- Terada, K.; Kikuchi, N. A class of general algorithms for multi-scale analyses of heterogeneous media. Comput. Methods Appl. Mech. Eng. 2001, 190, 5427–5464. [Google Scholar] [CrossRef]
- Miehe, C.; Bayreuther, C.G. On multiscale FE analyses of heterogeneous structures: From homogenization to multigrid solvers. Int. J. Numer. Methods Eng. 2007, 71, 1135–1180. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Stroeven, M.; Sluys, L.J. Multiscale continuous and discontinuous modeling of heterogeneous materials: A review on recent developments. J. Multiscale Model. 2011, 3, 1–42. [Google Scholar] [CrossRef]
- Schmidt, T.; Lothenbach, B.; Romer, M.; Neuenschwander, J.; Scrivener, K. Physical and microstructural aspects of sulfate attack on ordinary and limestone blended Portland cements. Cement. Conc. Res. 2009, 39, 1111–1121. [Google Scholar] [CrossRef]
- Broughton, J.Q.; Abraham, F.F.; Bernstein, N.; Kaxiras, E. Concurrent coupling of length scales: Methodology and application. Phys. Rev. B 1999, 60, 2391–2403. [Google Scholar] [CrossRef]
- Belytschko, T.; Xiao, S.P. Coupling methods for continuum model with molecular model. Int. J. Multiscale Comput. Eng. 2003, 1, 115–126. [Google Scholar] [CrossRef]
- Curtin, W.A.; Miller, R.E. Atomistic/continuum coupling in computational materials science. Model. Simul. Mater. Sci. Eng. 2003, 11, R33–R68. [Google Scholar] [CrossRef]
- Li, X.; Weinan, E. Multiscale modeling of the dynamics of solids at finite temperature. J. Mech. Phys. Solids 2005, 53, 1650–1685. [Google Scholar] [CrossRef]
- Khare, R.; Mielke, S.L.; Schatz, G.C.; Belytschko, T. Multiscale coupling schemes spanning the quantum mechanical, atomistic forcefield, and continuum regimes. Comput. Methods Appl. Mech. Eng. 2008, 197, 3190–3202. [Google Scholar] [CrossRef]
- Botelhoa, E.C.; Figiela, L.; Rezendeb, M.C.; Laukea, B. Mechanical behavior of carbon fiber reinforced polyamide composites. Compos. Sci. Technol. 2003, 63, 1843–1855. [Google Scholar] [CrossRef]
- Okuda, T.; Ioku, K.; Yonezawa, I.; Minagi, H.; Kawachi, G.; Gonda, Y.; Murayama, H.; Shibata, Y.; Minami, S.; Kamihira, S.; et al. The effect of microstructure of β-tricalcium phosphate on the metabolism of subsequently formed bone tissue. Biomaterials 2007, 28, 2612–2621. [Google Scholar] [CrossRef] [PubMed]
- Diego, R.B.; Mas-Estelles, J.; Sanz, J.A.; Garcia-Aznar, J.M.; Salmeron-Sanchez, M. Polymer scaffolds with interconnected spherical pores and controlled architecture for tissue engineering. Fabrication, mechanical properties and finite element modeling. J. Biomed. Mater. Res. B 2007, 81, 448–455. [Google Scholar] [CrossRef] [PubMed]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Cailletaud, G.; Forest, S.; Jeulin, D.; Feyel, F.; Galliet, I.; Mounoury, V.; Quilici, S. Some elements of microstructural mechanics. Comput. Mater. Sci. 2003, 27, 351–374. [Google Scholar] [CrossRef]
- Jiang, G.; Shen, K.; Wang, M.R. Nanotechnology and Nanomaterials: Updates in Advanced Lithography. Fabrication of 3D Micro- and Nano-Structures by Prism-Assisted UV and Holographic Lithography; IntechOpen: London, UK, 2013. [Google Scholar]
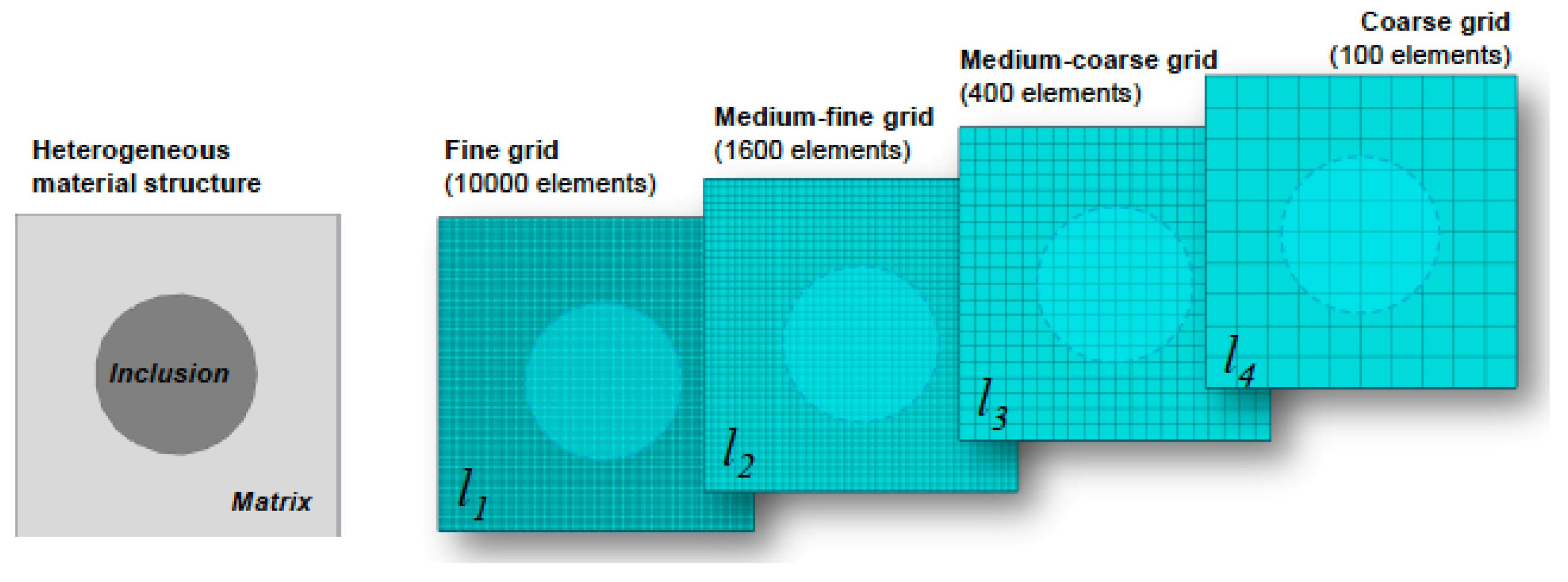
- Gitman, I.M.; Askes, H.; Sluys, L.J. Representative volume: Existence and size determination. Eng. Fract. Mech. 2007, 74, 2518–2534. [Google Scholar] [CrossRef]
- Suquet, P.M. Elements of Homogenization for Inelastic Solid Mechanics. Trends and Applications of Pure Mathematics to Mechanics. Homogenization Techniques for Composite Media; Lecture Notes in Physics; Springer: Berlin, Germany, 1987; pp. 193–278. [Google Scholar]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A 1957, 241, 376. [Google Scholar]
- Nemat-Nasser, S.; Hori, M. Micromechanics: Overall Properties of Heterogeneous Materials; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Hashin, Z. The elastic moduli of heterogeneous materials. J. Appl. Mech. 1962, 29, 143. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Iwakuma, T.; Hejazi, M. On composites with a periodic structure. Mech. Mater. 1982, 1, 239–267. [Google Scholar] [CrossRef]
- Kachanov, M.; Tsukrov, I.; Shafiro, B. Effective moduli of solids with cavities of various shapes. Appl. Mech. Rev. 1994, 47, S151–S174. [Google Scholar] [CrossRef]
- Zohdi, T.I.; Feucht, M.; Gross, D.; Wriggers, P. A description of macroscopic damage through microstructural relaxation. Int. J. Numer. Methods Eng. 1998, 43, 493–506. [Google Scholar] [CrossRef]
- Bernard, O.; Ulm, F.J.; Lemarchand, E. A multiscale mictomechanics-hydration model for the early-age elastic properties of cement-based materials. Cem. Concr. Res. 2003, 33, 1293–1309. [Google Scholar] [CrossRef]
- Wriggers, P.; Moftah, S.O. Mesoscale models for concrete: Homogenisation and damage behaviour. Finite Elem. Anal. Des. 2006, 42, 623–636. [Google Scholar] [CrossRef]
- Takano, N.; Zako, M.; Kubo, F.; Kimura, K. Microstructure-based stress analysis and evaluation for porous ceramics by homogenization method with digital image-based modeling. Int. J. Solids Struct. 2003, 40, 1225–1242. [Google Scholar] [CrossRef]
- Fish, J.; Yu, Q.; Shek, K. Computational damage mechanics for composite materials based on mathematical homogenization. Int. J. Numer. Methods Eng. 1999, 45, 1657–1679. [Google Scholar] [CrossRef]
- Takano, N.; Uetsuji, Y.; Kashiwagi, Y.; Zako, M. Hierarchical modelling of textile composite materials and structures by the homogenization method. Model. Simul. Mater. Sci. Eng. 1999, 7, 207–231. [Google Scholar] [CrossRef]
- Peng, X.; Cao, J. A dual homogenization and finite element approach for material characterization of textile composites. Compos. B Eng. 2002, 33, 45–56. [Google Scholar] [CrossRef]
- Matsuda, T.; Nimiya, Y.; Ohno, N.; Tokuda, M. Analysis of in-plane elastic-viscoplastic behavior of plain-woven GFRP composites based on a homogenization theory. Key Eng. Mater. 2004, 274, 919–924. [Google Scholar] [CrossRef]
- Challagulla, K.S.; Georgiades, A.V.; Kalamkarov, A.L. Asymptotic homogenization modeling of thin composite network structures. Compos. Struct. 2007, 79, 432–444. [Google Scholar] [CrossRef]
- Nakata, K.; Matsuda, T.; Kawai, M. Multi-scale creep analysis of plain-woven laminates using time-dependent homogenization theory: Effects of laminate configuration. Int. J. Mod. Phys. B 2008, 22, 6173–6178. [Google Scholar] [CrossRef]
- Feyel, F. Multiscale FE2 elastoviscoplastic analysis of composite structures. Comput. Mater. Sci. 1999, 16, 344–354. [Google Scholar] [CrossRef]
- Yuan, Z.; Fish, J. Toward realization of computational homogenization in practice. Int. J. Numer. Methods Eng. 2007, 73, 361–380. [Google Scholar] [CrossRef]
- Matous, K.; Kulkarni, M.G.; Geubelle, P.H. Multiscale cohesive failure modeling of heterogeneous adhesives. J. Mech. Phys. Solids 2008, 56, 1511–1533. [Google Scholar] [CrossRef]
- Kulkarni, M.G.; Matous, K.; Geubelle, P.H. Coupled multi-scale cohesive modeling of failure in heterogeneous adhesives. Int. J. Numer. Methods Eng. 2010, 84, 916–946. [Google Scholar] [CrossRef]
- Reina-Romo, E.; Sanz-Herrera, J.A. Multiscale simulation of particle-reinforced elastic-plastic adhesives at small strains. Comput. Methods Appl. Mech. Eng. 2011, 200, 2211–2222. [Google Scholar] [CrossRef]
- Gitman, I.M.; Askes, H.; Sluys, L.J. Coupled-volume multi-scale modelling of quasi-brittle material. Eur. J. Mech. A-Solids 2007, 27, 302–327. [Google Scholar] [CrossRef]
- Bazant, Z.P. Can multiscale-multiphysics methods predict softening damage and structural failure? Int. J. Multiscale Comput. Eng. 2010, 8, 61–67. [Google Scholar] [CrossRef]
- Kouznetsova, V.; Geers, M.G.D.; Brekelmans, W.A.M. Multi-scale constitu- tive modelling of heterogeneous materials with a gradient-enhanced computational homogenization scheme. Int. J. Numer. Meth. Eng. 2002, 54, 1235–1260. [Google Scholar] [CrossRef]
- Saiki, I.; Terada, K.; Ikeda, K.; Hori, M. Appropriate number of unit cells in a representative volume element for micro-structural bifurcation encountered in a multi-scale modeling. Comput. Methods Appl. Mech. Eng. 2002, 191, 2561–2585. [Google Scholar] [CrossRef]
- Belytschko, T.; Loehnert, S.; Song, J.H. Multiscale aggregating discontinuities: A method for circumventing loss of material stability. Int. J. Numer. Methods Eng. 2008, 73, 869–894. [Google Scholar] [CrossRef]
- Belytschko, T.; Song, J.H. Coarse-graining of multiscale crack propagation. Int. J. Numer. Methods Eng. 2010, 81, 537–563. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Lloberas-Valls, O.; Stroeven, M.; Sluys, L.J. Homogenization-based multiscale crack modelling: From micro-diffusive damage to macro-cracks. Comput. Methods Appl. Mech. Eng. 2011, 200, 1220–1236. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Lloberas-Valls, O.; Stroeven, M.; Sluys, L.J. Computational homogenization for multiscale crack modelling, implementational and computational aspects. Int. J. Numer. Meth. Eng. 2012, 89, 192–226. [Google Scholar] [CrossRef]
- Terada, K.; Ito, T.; Kikuchi, N. Characterization of the mechanical behaviours of solid-fluid mixture by the homogenization method. Comput. Methods Appl. Mech. Eng. 1998, 153, 223–257. [Google Scholar] [CrossRef]
- Kuentzer, N.; Simacek, P.; Advani, S.G.; Walsh, S. Permeability characterization of dual scale fibrous porous media. Compos. A Appl. Sci. Manuf. 2006, 37, 2057–2068. [Google Scholar] [CrossRef]
- Zhou, F.P.; Kuentzer, N.; Simacek, P.; Advani, S.G.; Walsh, S. Analytic characterization of the permeability of dual-scale fibrous porous media. Compos. Sci. Technol. 2006, 66, 2795–2803. [Google Scholar] [CrossRef]
- Hamila, N.; Boisse, P. A meso-macro three node finite element for draping of textile composite preforms. Appl. Compos. Sci. 2007, 14, 235–250. [Google Scholar] [CrossRef]
- Zhou, F.; Alms, J.; Advani, S.G. A closed form solution for flow in dual scale fibrous porous media under constant injection pressure conditions. Compos. Sci. Technol. 2008, 68, 699–708. [Google Scholar] [CrossRef]
- Wang, J.F.; Hwang, W.R. Permeability prediction of fibrous porous media in a bi-periodic domain. J. Compos. Mater. 2008, 42, 909–929. [Google Scholar] [CrossRef]
- Loix, F.; Badel, P.; Orgeas, L.; Geindreau, C.; Boisse, P. Woven fabric permeability: From textile deformation to fluid flow mesoscale simulations. Compos. Sci. Technol. 2008, 68, 1624–1630. [Google Scholar] [CrossRef]
- Verleye, B.; Croce, R.; Griebel, M.; Klitz, M.; Lomov, S.V.; Morren, G.; Sol, H.; Verpoest, I.; Roose, D. Permeability of textile reinforcements: Simulation, influence of shear and validation. Compos. Sci. Technol. 2008, 68, 2804–2810. [Google Scholar] [CrossRef]
- Chen, Z.-R.; Lu, M.; Ye, L. A dual-permeability network model for multilayer woven fabrics. Int. J. Appl. Mech. 2009, 1, 709–736. [Google Scholar] [CrossRef]
- Chen, Z.-R.; Ye, L.; Lu, M. Permeability predictions for woven fabric preforms. J. Compos. Mater. 2010, 44, 1569–1586. [Google Scholar] [CrossRef]
- Yazdchi, K.; Srivastava, S.; Luding, S. Micro-macro relations for flow through random arrays of cylinders. Compos. A Appl. Sci. Manuf. 2012, 43, 2007–2020. [Google Scholar] [CrossRef]
- Rouhi, M.S.; Wysocki, M.; Larsson, R. Modeling of coupled dual-scale flow-deformation processes in composites manufacturing. Compos. A Appl. Sci. Manuf. 2013, 46, 108–116. [Google Scholar] [CrossRef]
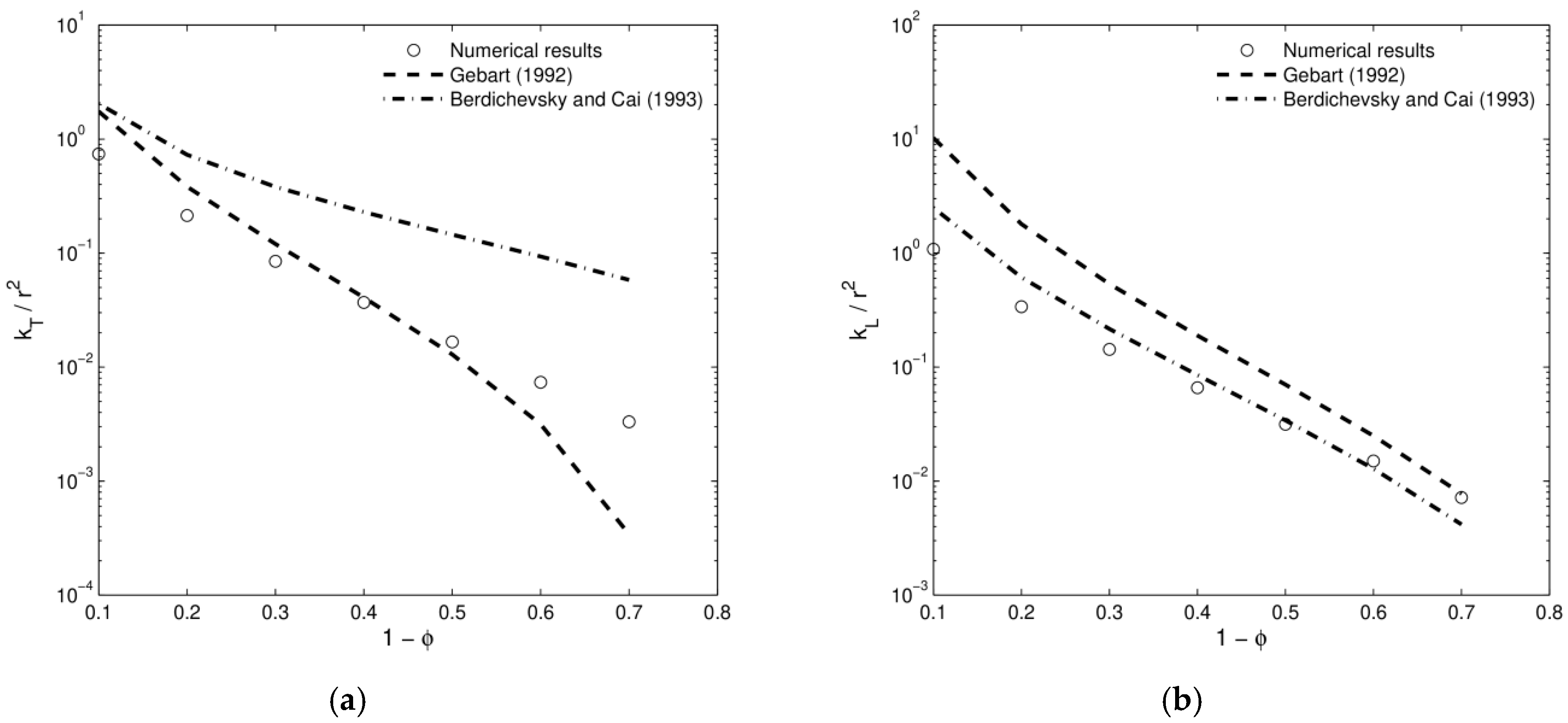
- Gebart, B. Permeability of unidirectional reinforcements for RTM. J. Compos. Mater. 1992, 8, 1100–1133. [Google Scholar] [CrossRef]
- Berdichevsky, A.; Cai, Z. Preform permeability predictions by self-consistent methods and finite element simulation. Polym. Compos. 1993, 14, 132–143. [Google Scholar] [CrossRef]
- Takano, N.; Zako, M.; Okazaki, T.; Terada, K. Microstructure-based evaluation of the influence of woven architecture on permeability by asymptotic homogenization theory. Compos. Sci. Technol. 2002, 62, 1347–1356. [Google Scholar] [CrossRef]
- Song, Y.S.; Youn, J.R. Asymptotic expansion homogenization of permeability tensor for plain woven fabrics. Compos. A Appl. Sci. Manuf. 2006, 37, 2080–2087. [Google Scholar] [CrossRef]
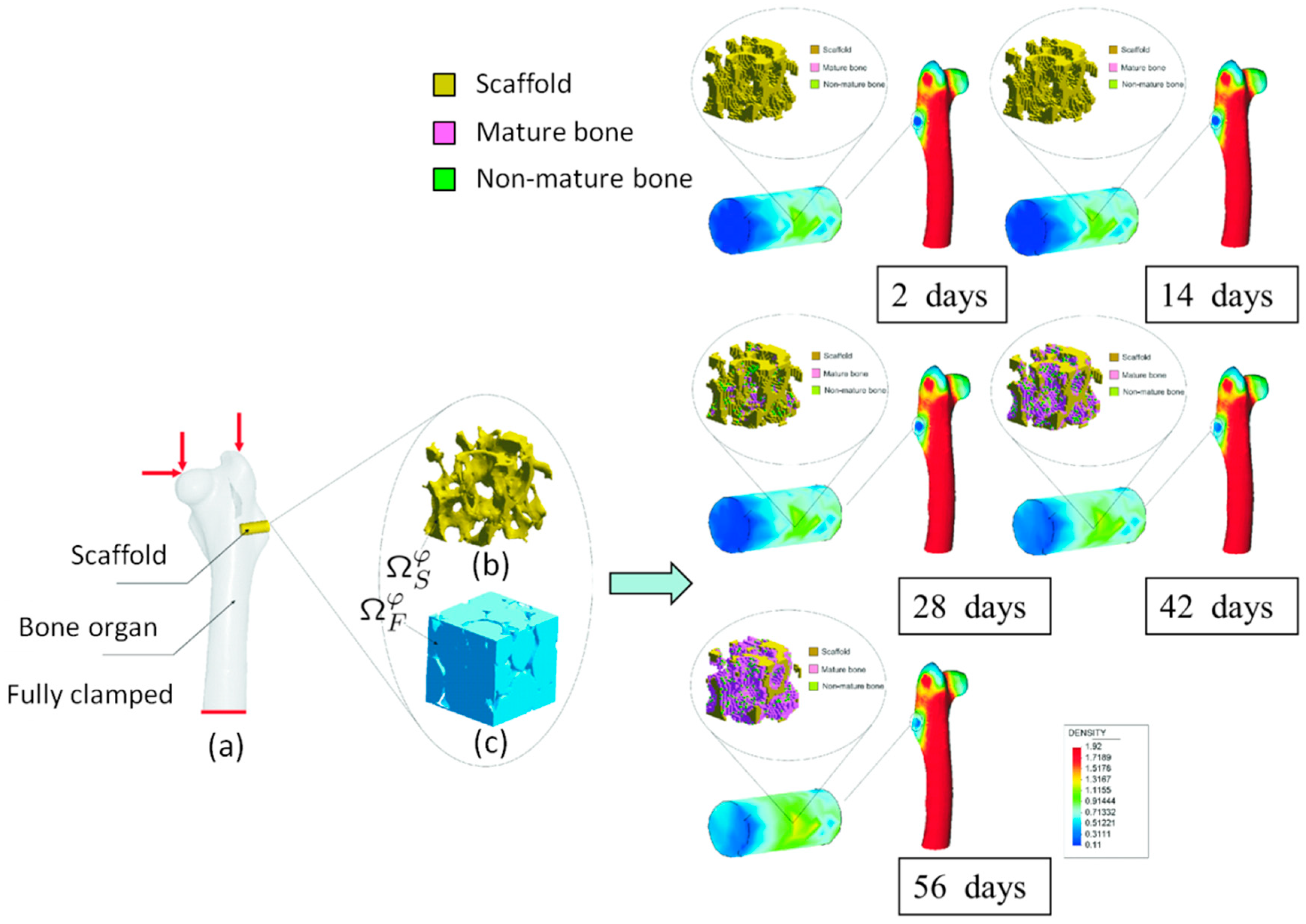
- Sanz-Herrera, J.A.; García-Aznar, J.M.; Doblaré, M. A mathematical model for bone tissue regeneration inside a specific type of scaffold. Biomech. Model. Mechanobiol. 2008, 7, 355–366. [Google Scholar] [CrossRef] [PubMed]
- Sanz-Herrera, J.A.; Kasper, C.; van Griensven, M.; Garcí-Aznar, J.M.; Ochoa, I.; Doblaré, M. Mechanical and flow characterization of Sponceram carriers: Evaluation by homogenization theory and experimental validation. J. Biomed. Mater. Res. B-Appl. Biomater. 2008, 87, 42–48. [Google Scholar] [CrossRef] [PubMed]
- Sanz-Herrera, J.A.; García-Aznar, J.M.; Doblaré, M. Micro-macro numerical modelling of bone regeneration in tissue engineering. Comput. Methods Appl. Mech. Eng. 2008, 197, 3092–3107. [Google Scholar] [CrossRef]
- Takano, N.; Zako, M.; Okuno, Y. Multi-scale finite element analysis of porous materials and components by asymptotic homogenization theory and enhanced mesh superposition method. Model. Simul. Mater. Sci. Eng. 2003, 11, 137–156. [Google Scholar] [CrossRef]
- Rosen, B.W.; Hashin, Z. Effective thermal expansion coefficients and specific heats of composite materials. Int. J. Eng. Sci. 1970, 8, 157–173. [Google Scholar] [CrossRef]
- Auriault, J.L. Effective macroscopic description of heat conduction in periodic composites. Int. J. Heat Mass Transf. 1983, 26, 861–869. [Google Scholar] [CrossRef]
- Ostoja-Starzewski, M.; Schulte, J. Bounding of effective thermal conductivities of multiscale materials by essential and natural boundary conditions. Phys. Rev. B 1996, 54, 278–285. [Google Scholar] [CrossRef]
- Jiang, M.; Jasiuk, I.; Ostoja-Starzewski, M. Apparent thermal conductivity of periodic two-dimensional composites. Compos. Mater. Sci. 2002, 25, 329–338. [Google Scholar] [CrossRef]
- Alzina, A.; Toussaint, E.; Beakou, A.; Beakou, A.; Skoczen, B. Multiscale modelling of thermal conductivity in composite materials for cryogenic structures. Compos. Struct. 2006, 74, 175–185. [Google Scholar] [CrossRef]
- Özdemir, I.; Brekelmans, W.A.M.; Geers, M.G.D. Computational homogenization for heat conduction in heterogeneous solids. Int. J. Numer. Methods Eng. 2008, 73, 185–204. [Google Scholar] [CrossRef]
- Springer, G.S.; Tsai, S.W. Thermal conductivities of unidirectional materials. J. Compos. Mater. 1967, 1, 166–173. [Google Scholar] [CrossRef]
- Hashin, Z. Assessment of the self consistent scheme approximation: Conductivity of particulate composites. J. Compos. Mater. 1968, 2, 284–300. [Google Scholar] [CrossRef]
- Lewis, T.; Nielsen, L. Dynamic mechanical properties of particulate-filled polymers. J. Appl. Polym. Sci. 1970, 14, 1449–1471. [Google Scholar] [CrossRef]
- Chung, P.W.; Tamma, K.K.; Namburu, R.R. Homogenization of temperature-dependent thermal conductivity in composite materials. J. Thermophys. Heat Transf. 2001, 15, 10–17. [Google Scholar] [CrossRef]
- Monteiro, E.; Yvonnet, J.; He, Q.C. Computational homogenization for nonlinear conduction in heterogeneous materials using model reduction. Comput. Mater. Sci. 2008, 42, 704–712. [Google Scholar] [CrossRef]
- Muliana, A.H.; Kim, J.S. A two-scale homogenization framework for nonlinear effective thermal conductivity of laminated composites. Acta Mech. 2010, 212, 319–347. [Google Scholar] [CrossRef]
- Sengupta, A.; Papadopoulos, P.; Taylor, R.L. A multiscale finite element method for modeling fully coupled thermomechanical problems in solids. Int. J. Numer. Methods Eng. 2012, 91, 1386–1405. [Google Scholar] [CrossRef]
- Francfort, G.A.; Suquet, P.M. Homogenization and mechanical dissipation in thermo-viscoelasticity. Arch. Ration. Mech. Anal. 1986, 96, 265–293. [Google Scholar] [CrossRef]
- Yu, Q.; Fish, J. Multiscale asymptotic homogenization for multiphysics problems with multiple spatial and temporal scales: A coupled thermo-viscoelastic example problem. Int. J. Solids Struct. 2002, 39, 6429–6452. [Google Scholar] [CrossRef]
- Montero-Chacón, F.; Zaghi, S.; Rossi, R.; García-Pérez, E.; Heras-Pérez, I.; Martínez, X.; Oller, S.; Doblaré, M. Multiscale thermo-mechanical analysis of multi-layered coatings in solar thermal applications. Finite Elem. Anal. Des. 2017, 127, 31–43. [Google Scholar] [CrossRef]
- Moyne, C.; Murad, M. Macroscopic behavior of swelling porous media derived from micromechanical analysis. Trans. Porous Media 2003, 50, 127–151. [Google Scholar] [CrossRef]
- Bouhlel, M.; Jamei, M.; Geindreau, C. Microstructural effects on the overall poroelastic properties of saturated porous media. Model. Simul. Mater. Sci. Eng. 2010, 18, 045009. [Google Scholar] [CrossRef]
- Hollister, S.J. Porous scaffold design for tissue engineering. Nat. Mater. 2005, 4, 518–524. [Google Scholar] [CrossRef] [PubMed]
- Hollister, S.J.; Lin, C.Y. Computational design of tissue engineering scaffolds. Comput. Methods Appl. Mech. Eng. 2007, 196, 2991–2998. [Google Scholar] [CrossRef]
- Luizar-Obregon, J.A.; Murad, M.A.; Rochinha, F.A. Computational homogenization of nonlinear hydromechanical coupling in poroplasticity. Int. J. Multiscale Compos. Eng. 2006, 4, 693–732. [Google Scholar] [CrossRef]
- Brandt, A. Multi-level adaptive solutions to boundary-value problems. Math. Comput. 1977, 31, 137–180. [Google Scholar] [CrossRef]
- Quarteroni, A.; Valli, A. Domain Decomposition Methods for Partial Differential Equations; Oxford Science Publications: Oxford, UK, 1999. [Google Scholar]
- Wilson, E.L. The static condensation algorithm. Int. J. Numer. Methods Eng. 1974, 8, 198–203. [Google Scholar] [CrossRef]
- Dahmen, W.; Kurdila, A.; Oswald, P. Multiscale Wavelet Methods for Partial Differential Equations, 1st ed.; Academic Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Nielsen, S.O.; Lopez, C.F.; Srinivas, G.; Klein, M.L. Coarse grain models and the computer simulation of soft materials. J. Phys. Condens. Matter 2004, 16, 481–512. [Google Scholar] [CrossRef]
- Tadmor, E.B.; Ortiz, M.; Phillips, R. Quasicontinuum analysis of defects in solids. Philos. Mag. A 1996, 73, 1529–1563. [Google Scholar] [CrossRef]
- Xiao, S.P.; Belytschko, T. A bridging domain method for coupling continua with molecular dynamics. Comput. Methods Appl. Mech. Eng. 2004, 193, 1645–1669. [Google Scholar] [CrossRef]
- Weinan, E.; Engquist, B.; Li, X.; Ren, W.; Vanden-Eijnden, E. Heterogeneous multiscale methods: A review. Commun. Comput. Phys. 2007, 2, 367–450. [Google Scholar]
- Weinan, E.; Engquist, B. The heterogeneous multi-scale methods. Commun. Math. Sci. 2003, 1, 87–133. [Google Scholar]
- Rath, J.M. Darcy Flow, Multigrid, and Upscaling. Multiscale Optimization Methods and Applications; Springer: Berlin, Germany, 2006; pp. 337–366. [Google Scholar]
- Boffy, H.; Baietto, M.C.; Sainsot, P.; Lubrecht, A.A. Detailed modelling of a moving heat source using multigrid methods. Tribol. Int. 2012, 46, 279–287. [Google Scholar] [CrossRef]
- Venner, C.; Lubrecht, A.A. Multilevel Methods in Lubrication; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Douglas, J., Jr.; Paes-Leme, P.J.; Roberts, J.E.; Wang, J. A parallel iterative procedure applicable to the approximate bsolution of second order partial differential equations by mixed finite element methods. Numer. Math. 1993, 65, 95–108. [Google Scholar] [CrossRef]
- Ganis, B.; Yotov, I. Implementation of a mortar mixed finite element method using a multiscale flux basis. Comput. Methods Appl. Mech. Eng. 2009, 198, 3989–3998. [Google Scholar] [CrossRef]
- Unger, J.F.; Eckardt, S. Multiscale Modeling of Concrete. Arch. Compos. Meth. Eng. 2011, 18, 341–393. [Google Scholar] [CrossRef]
- Lloberas-Valls, O.; Rixen, D.J.; Simone, A.; Sluys, L.J. Domain decomposition techniques for the efficient modeling of brittle heterogeneous materials. Comput. Methods Appl. Mech. Eng. 2011, 200, 1577–1590. [Google Scholar] [CrossRef]
- Galvis, J.; Sarkis, M. Balancing Domain Decomposition Methods for Mortar Coupling Stokes-Darcy Systems. In Domain Decomposition Methods in Science and Engineering XVI; Springer: Berlin/Heidelberg, Germany, 2007; pp. 373–380. [Google Scholar]
- Discacciati, M.; Quarteroni, A. Convergence analysis of a subdomain iterative method for the finite element approximation of the coupling of Stokes and Darcy equations. Comput. Vis. Sci. 2004, 6, 93–103. [Google Scholar] [CrossRef]
- Jamelot, E.; Ciarlet, P., Jr. Fast non-overlapping Schwarz domain decomposition methods for solving the neutron diffusion equation. J. Compos. Phys. 2013, 241, 445–463. [Google Scholar] [CrossRef]
- Aarnes, J.; Hou, T.Y. Multiscale domain decomposition methods for elliptic problems with high aspect ratios. AMAS 2002, 18, 63–76. [Google Scholar] [CrossRef]
- Ladevèze, P. The large time increment method for the analysis of structures with nonlinear constitutive relation described by internal variables. C. R. Acad. Sci. 1989, 309, 1095–1099. [Google Scholar]
- Nèron, D.; Ladevèze, P. Proper generalized decomposition for multiscale and multiphysics problems. Arch. Comput. Methods Eng. 2010, 17, 351–372. [Google Scholar] [CrossRef]
- Lamari, H.; Ammar, A.; Cartraud, P.; Legrain, G.; Chinesta, F.; Jacquemin, F. Routes for efficient computational homogenization of nonlinear materials using the proper generalized decomposition. Arch. Comput. Methods Eng. 2010, 17, 373–391. [Google Scholar] [CrossRef]
- Chinesta, F.; Ladevèze, P.; Cueto, E. A short review on model order reduction based on proper generalized decomposition. Arch. Comput. Methods Eng. 2011, 18, 395–404. [Google Scholar] [CrossRef]
- El Halabi, F.; Gonzalez, D.; Chico, A.; Doblaré, M. FE2 multiscale in linear elasticity based on parametrized microscale models using proper generalized decomposition. Comput. Methods Appl. Mech. Eng. 2013, 257, 183–202. [Google Scholar] [CrossRef]
- Leuschner, M.; Fritzen, F. Reduced order homogenization for viscoplastic composite materials including dissipative imperfect interfaces. Mech. Mater. 2017, 104, 121–138. [Google Scholar] [CrossRef]
- Bhattacharyya, M.; Fau, A.; Nackenhorst, U.; Néron, D.; Ladevèze, P. A LATIN-based model reduction approach for the simulation of cycling damage. Comput. Mech. 2018, 62, 725–743. [Google Scholar] [CrossRef]
- Vitse, M.; Néron, D.; Boucard, P.-A. Dealing with a nonlinear material behavior and its variability through PGD models: Application to reinforced concrete structures. Finite Elem. Anal. Des. 2019, 153, 22–37. [Google Scholar] [CrossRef]
- Ladevèze, P.; Chamoin, L. On the verification of model reduction methods based on the proper generalized decomposition. Comput. Methods Appl. Mech. Eng. 2011, 200, 2032–2047. [Google Scholar] [CrossRef]
- Chinesta, F.; Leygue, A.; Bordeu, F.; Aguado, J.; Cueto, E.; González, D.; Alfaro, I.; Ammar, A.; Huerta, A. PGD-based computational vademecum for efficient design, optimization and control. Arch. Comput. Methods Eng. 2013, 20, 31–59. [Google Scholar] [CrossRef]
- Ammar, A.; Chinesta, F.; Cueto, E.; Doblaré, M. Proper Generalized Decomposition of time-multiscale models. Int. J. Numer. Methods Eng. 2012, 90, 569–596. [Google Scholar] [CrossRef]
- El Halabi, F.; González, D.; Sanz-Herrera, J.A.; Doblaré, M. A PGD-based multiscale formulation for non-linear solid mechanics under small deformations. Comput. Methods Appl. Mech. Eng. 2016, 305, 806–826. [Google Scholar] [CrossRef]
- Allison, J.; Backman, D.; Christodoulou, L. Integrated computational materials engineering: A new paradigm for the global materials profession. JOM 2006, 58, 25–27. [Google Scholar] [CrossRef]
- Llorca, J.; González, C.; Molina-Aldareguía, J.M.; Segurado, J.; Seltzer, R.; Sket, F.; Rodríguez, M.; Sádaba, S.; Muñoz, R.; Canal, L.P. Multiscale modeling of composite materials: A roadmap towards virtual testing. Adv. Mater. 2011, 23, 5130–5147. [Google Scholar] [CrossRef] [PubMed]
- Montero-Chacón, F.; Chiumenti, M.; Segurado, J.; Doblaré, M. Integrated computational materials engineering in solar plants: The virtual materials design project. JOM 2018, 70, 1659–1669. [Google Scholar] [CrossRef]
- ANSYS® Academic Research Mechanical, Release 18.1; Release 18.1; Ansys Inc.: Canonsburg, PA, USA, 2018.
- Simulia, ABAQUS 6.13 User’s Manual; Dassault Systems: Providence, RI, USA, 2013.
- COMSOL Multiphysics® v. 5.4; COMSOL AB: Stockholm, Sweden; Available online: www.comsol.com (accessed on 23 February 2019).
- Van Rossum, G. Python Tutorial; Technical Report CS-R9526; Centrum voor Wiskunde en Informatica (CWI): Amsterdam, The Netherlands, 1995. [Google Scholar]
- Dadvand, P.; Mora, J.; González, C.; Arraez, A.; Ubach, P.; Oñate, E. Kratos: An object-oriented environment for development of multi-physics analysis software. In Proceedings of the WCCMV Fifth World Congress on Computational Mechanics, Vienna, Austria, 7–12 July 2002. [Google Scholar]
- Alnaes, M.S.; Blechta, J.; Hake, J.; Johansson, A.; Kehlet, B.; Logg, A.; Richardson, C.; Ring, J.; Rognes, M.E.; Wells, G.N. The FEniCS Project Version 1.5. Arch. Numer. Softw. 2015, 3, 9–23. [Google Scholar]
- Dhondt, G.; Wittig, K. CalculiX—A Free Software Three-Dimensional Structural Finite Element Program; MTU Aero Engines GmbH: Munich, Germany, 2007. [Google Scholar]
- Taylor, R.L. FEAP—Finite Element Analysis Program. University of California: Berkeley, CA, USA, 2014. Available online: http://www.ce.berkeley/feap (accessed on 23 February 2019).
- EDF R&D. Modèle d’endommagement de Mazars. Code_Aster documentation, Clé: R7.01.08. 2012. Available online: https://www.code-aster.org/V2/doc/v11/fr/man_r/r7/r7.01.08.pdf (accessed on 23 February 2019).
- MSC. Patran User’s Guide; MSC Software Corporation: Newport Beach, CA, USA, 2018. [Google Scholar]
- Ribó, R.; Pasenau, M.; Escolano, E.; Pérez, J.; Coll, A.; Melendo, A. GiD The Personal Pre and Postprocessor; Reference Manual; CIMNE: Barcelona, Spain, 2006; unpublised research. [Google Scholar]
- Robert McNeel & Associates, Rhinoceros 3d. (n.d.) Available online: https://www.rhino3d.com/ (accessed on 12 February 2019).
- Geuzaine, C.; Remacle, J.-F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]


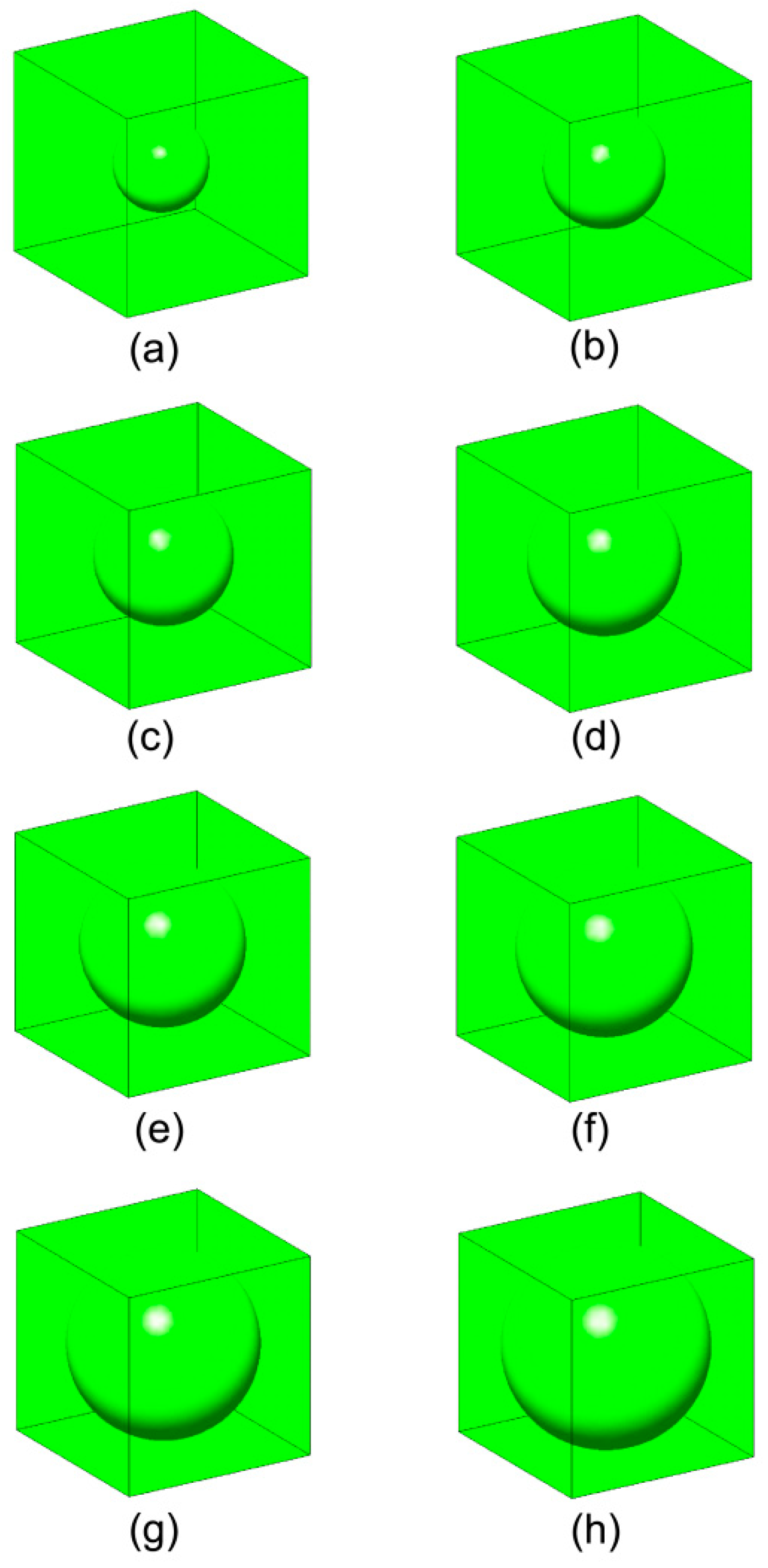
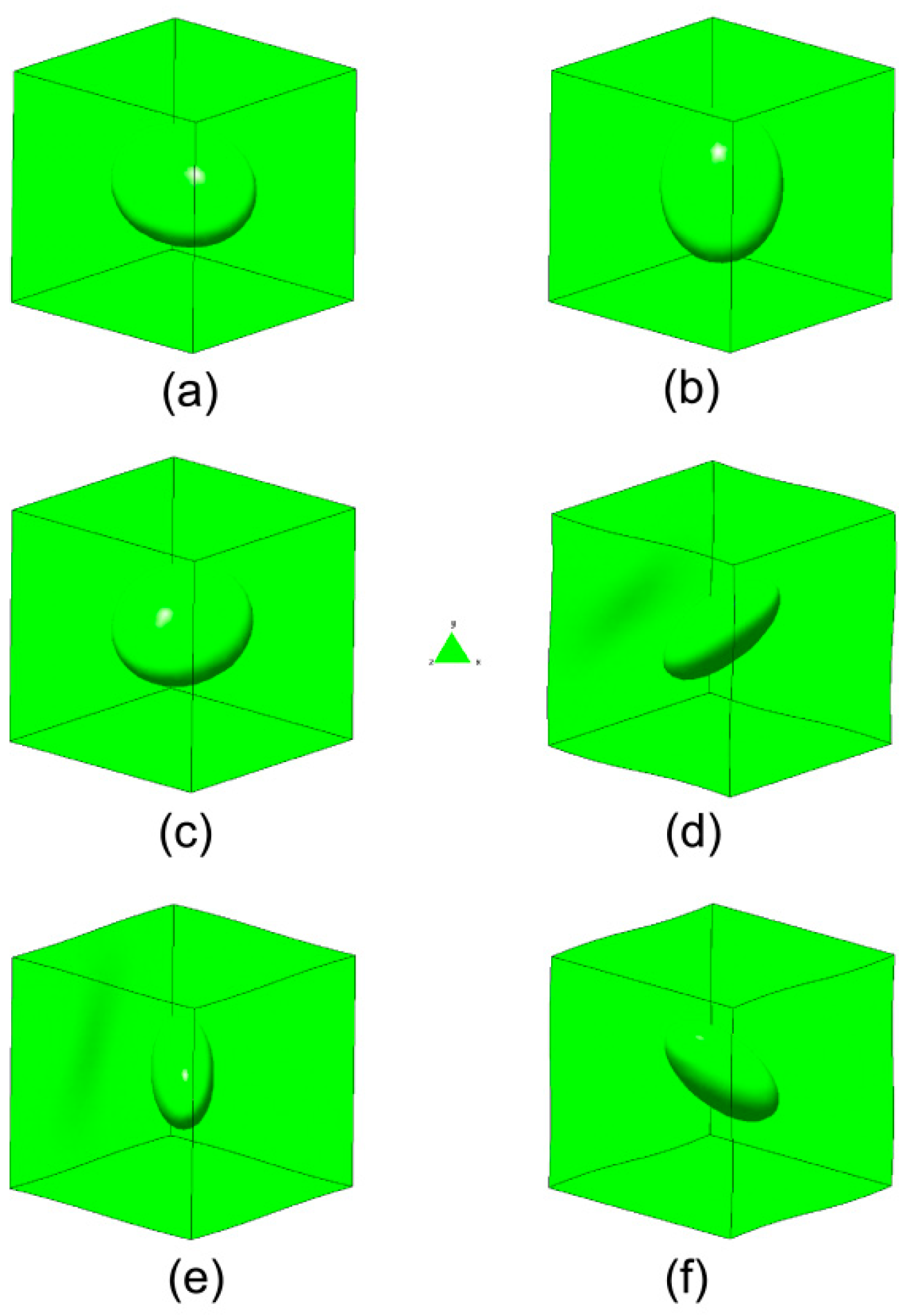
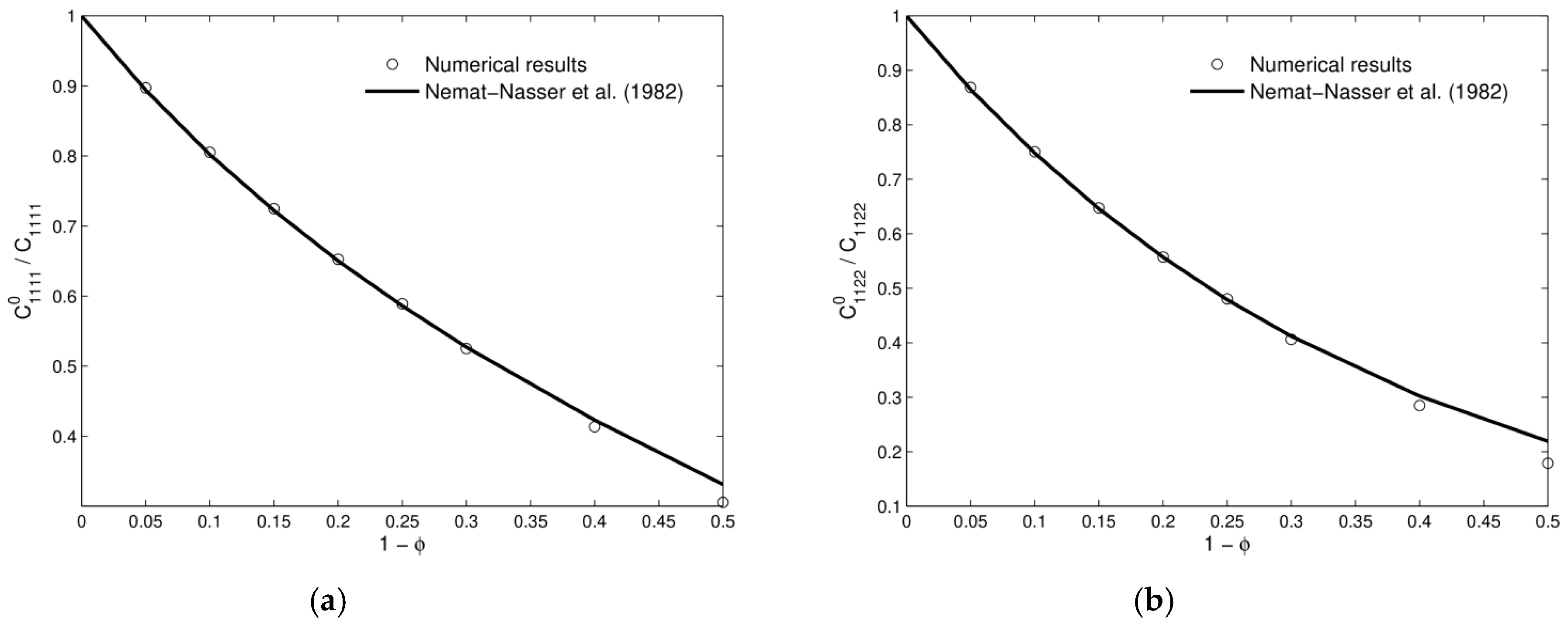
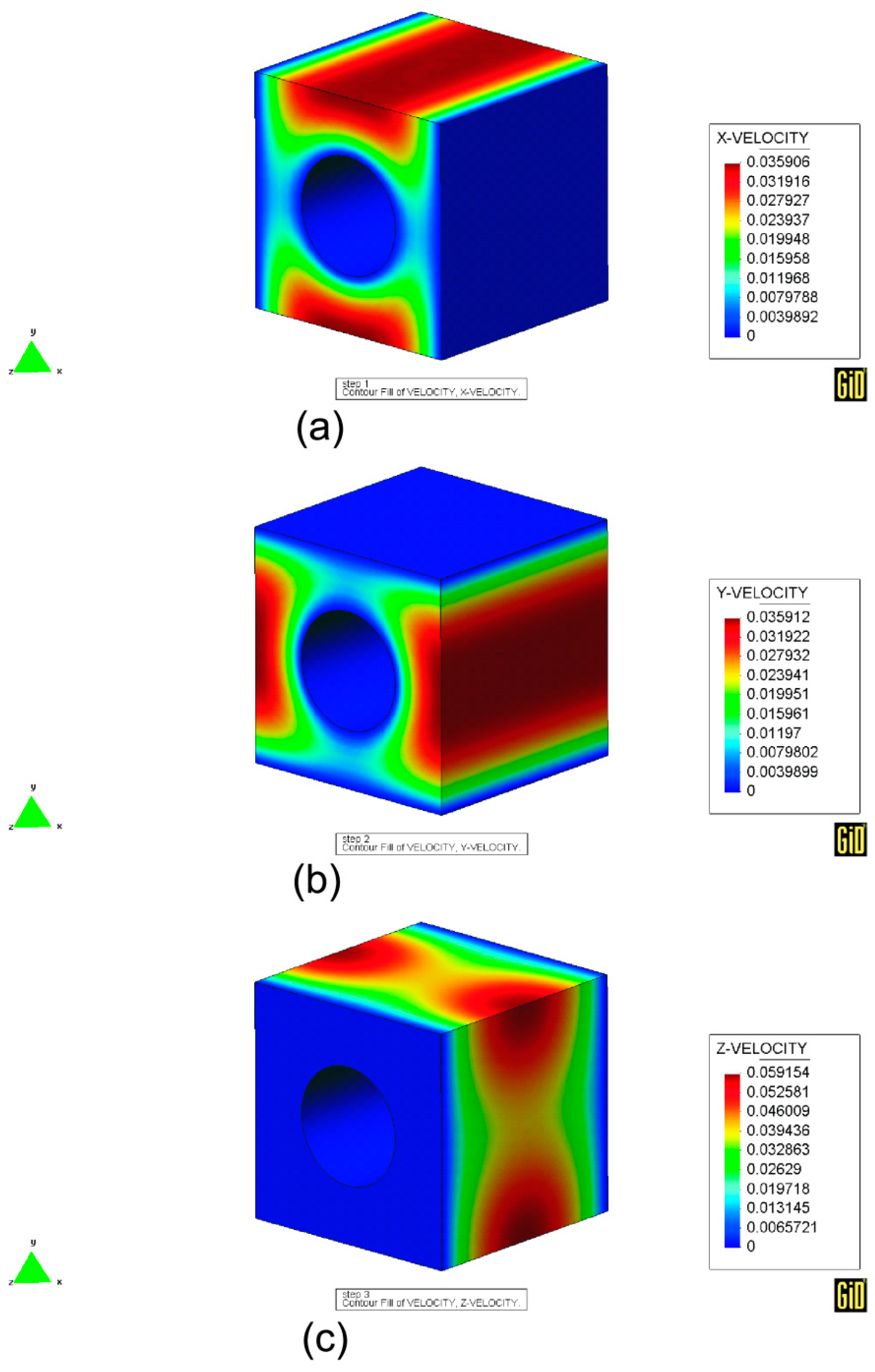

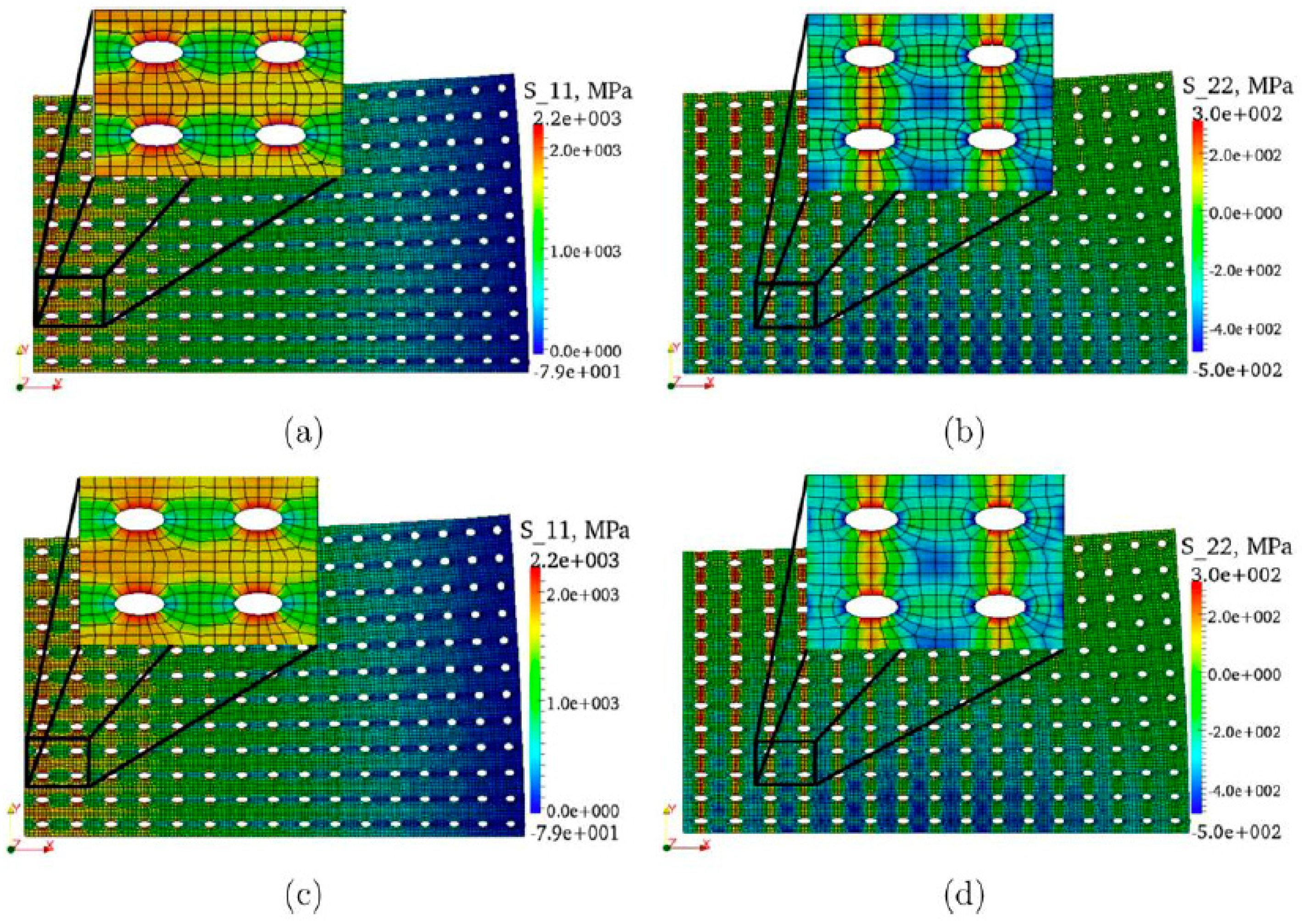
| Void Fraction | (Theoretical) | (Numerical) | (Theoretical) | (Numerical) |
|---|---|---|---|---|
| 0.05 | 0.894 | 0.897 | 0.865 | 0.868 |
| 0.1 | 0.802 | 0.805 | 0.748 | 0.750 |
| 0.15 | 0.722 | 0.725 | 0.646 | 0.648 |
| 0.2 | 0.650 | 0.652 | 0.557 | 0.557 |
| 0.25 | 0.586 | 0.589 | 0.479 | 0.480 |
| 0.3 | 0.527 | 0.525 | 0.412 | 0.406 |
| 0.4 | 0.423 | 0.413 | 0.302 | 0.285 |
| 0.5 | 0.331 | 0.305 | 0.219 | 0.179 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montero-Chacón, F.; Sanz-Herrera, J.A.; Doblaré, M. Computational Multiscale Solvers for Continuum Approaches. Materials 2019, 12, 691. https://doi.org/10.3390/ma12050691
Montero-Chacón F, Sanz-Herrera JA, Doblaré M. Computational Multiscale Solvers for Continuum Approaches. Materials. 2019; 12(5):691. https://doi.org/10.3390/ma12050691
Chicago/Turabian StyleMontero-Chacón, Francisco, José A. Sanz-Herrera, and Manuel Doblaré. 2019. "Computational Multiscale Solvers for Continuum Approaches" Materials 12, no. 5: 691. https://doi.org/10.3390/ma12050691
APA StyleMontero-Chacón, F., Sanz-Herrera, J. A., & Doblaré, M. (2019). Computational Multiscale Solvers for Continuum Approaches. Materials, 12(5), 691. https://doi.org/10.3390/ma12050691






