First-Principles Investigation of Adsorption of Ag on Defected and Ce-doped Graphene
Abstract
1. Introduction
2. Theoretical Method
3. Results and Discussion
3.1. Adsorption Energy and Charge Transfer
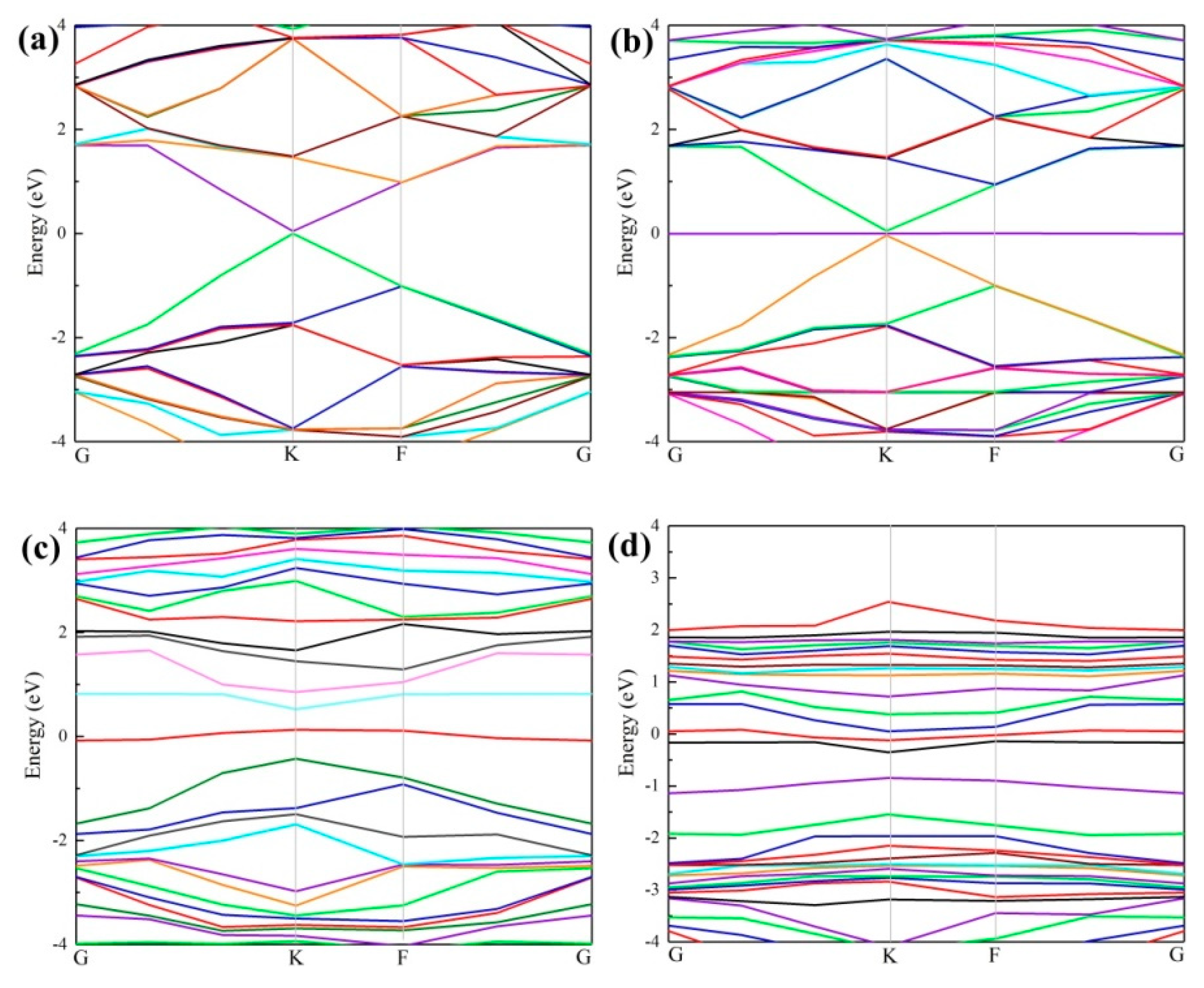
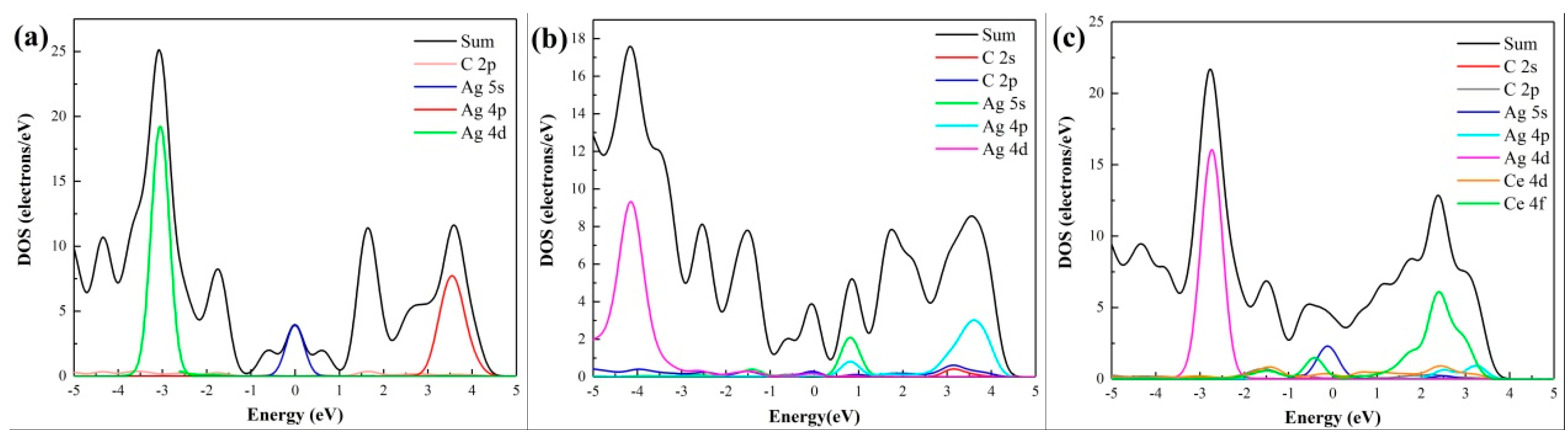
3.2. Density of States
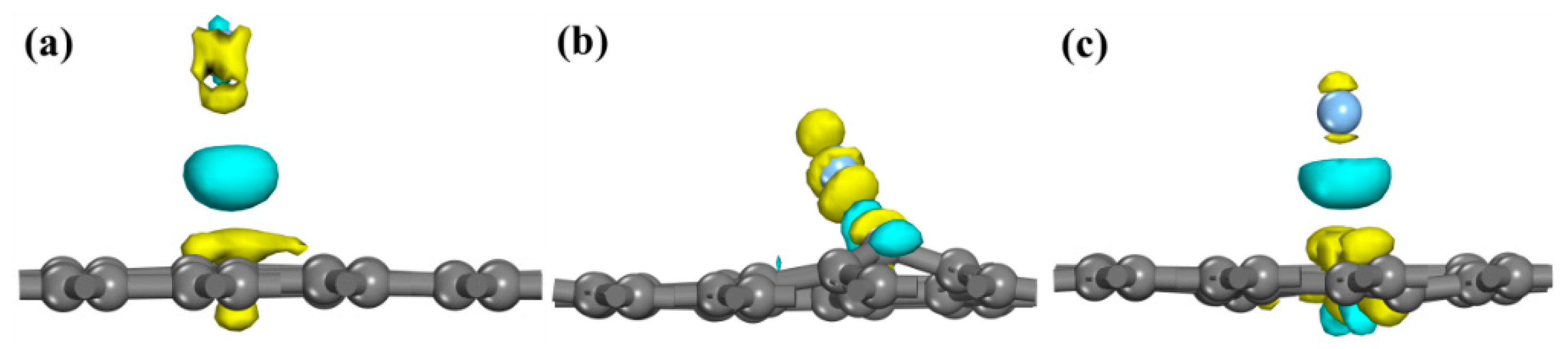
3.3. Population Analysis
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Lai, Z.; Xue, S.; Han, X.; Gu, L.; Gu, W. Study on Microstructure and Property of Brazed Joint of AgCuZn-X(Ga, Sn, In, Ni) Brazing Alloy. Rare Metal Mater. Eng. 2010, 39, 397–400. [Google Scholar]
- Zhang, L.; Feng, J.; Zhang, B.; Jing, X. Ag–Cu–Zn alloy for brazing TiC cermet/steel. Mater. Lett. 2005, 59, 110–113. [Google Scholar] [CrossRef]
- Wang, H.; Xue, S.-B. Effect of Ag on the properties of solders and brazing filler metals. J. Mater. Sci. Mater. Electron. 2015, 27, 1–13. [Google Scholar] [CrossRef]
- Khorram, A.; Ghoreishi, M. Comparative study on laser brazing and furnace brazing of Inconel 718 alloys with silver based filler metal. Opt. Laser Technol. 2015, 68, 165–174. [Google Scholar] [CrossRef]
- Chen, Y.; Yun, D.; Sui, F.; Long, W.; Zhang, G.; Liu, S. Influence of sulphur on the microstructure and properties of Ag–Cu–Zn brazing filler metal. Mater. Sci. Technol. 2013, 29, 1267–1271. [Google Scholar] [CrossRef]
- Sui, F.; Long, W.; Liu, S.; Zhang, G.; Bao, L.; Li, H.; Chen, Y. Effect of calcium on the microstructure and mechanical properties of brazed joint using Ag–Cu–Zn brazing filler metal. Mater. Des. 2013, 46, 605–608. [Google Scholar] [CrossRef]
- Demianová, K.; Behúlová, M.; Milan, O.; Turňa, M.; Sahul, M. Brazing of Aluminum Tubes Using Induction Heating. Adv. Mater. Res. 2012, 1405–1409. [Google Scholar] [CrossRef]
- Shao, L.; Chen, G.; Ye, H.; Wu, Y.; Qiao, Z.; Zhu, Y.; Niu, H. Sulfur dioxide adsorbed on graphene and heteroatom-doped graphene: A first-principles study. Eur. Phys. J. B 2013, 86, 54. [Google Scholar] [CrossRef]
- He, Y.L.; Liu, D.X.; Qu, Y.; Yao, Z. Adsorption of Hydrogen Molecule on the Intrinsic and Al-Doped Graphene: A First Principle Study. Adv. Mater. Res. 2012, 507, 61–64. [Google Scholar] [CrossRef]
- Sen, D.; Thapa, R.; Chattopadhyay, K. Small Pd cluster adsorbed double vacancy defect graphene sheet for hydrogen storage: A first-principles study. Int. J. Hydrog. Energy 2013, 38, 3041–3049. [Google Scholar] [CrossRef]
- Thirumal, V.; Pandurangan, A.; Jayavel, R.; Ilangovan, R. Synthesis and characterization of boron doped graphene nanosheets for supercapacitor applications. Synth. Metals 2016, 220, 524–532. [Google Scholar] [CrossRef]
- Cai, Z.; Xiong, H.; Zhu, Z.; Huang, H.; Li, L.; Huang, Y.; Yu, X. Electrochemical synthesis of graphene/polypyrrole nanotube composites for multifunctional applications. Synth. Metals 2017, 227, 100–105. [Google Scholar] [CrossRef]
- Song, X.-R.; Li, H.-J.; Zeng, X. Brazing of C/C composites to Ti6Al4V using multiwall carbon nanotubes reinforced TiCuZrNi brazing alloy. J. Alloys Compd. 2016, 664, 175–180. [Google Scholar] [CrossRef]
- Wang, X.; Xing, W.; Zhang, P.; Song, L.; Yang, H.; Hu, Y. Covalent functionalization of graphene with organosilane and its use as a reinforcement in epoxy composites. Compos. Sci. Technol. 2012, 72, 737–743. [Google Scholar] [CrossRef]
- Qi, J.L.; Wang, Z.Y.; Lin, J.H.; Zhang, T.Q.; Zhang, A.T.; Cao, J.; Zhang, L.X.; Feng, J.C. Graphene-enhanced Cu composite interlayer for contact reaction brazing aluminum alloy 6061. Vacuum 2017, 136, 142–145. [Google Scholar] [CrossRef]
- Chang, K.; Chen, W. L-cysteine-assisted synthesis of layered MoS2/graphene composites with excellent electrochemical performances for lithium ion batteries. ACS Nano 2011, 5, 4720–4728. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Guqiao, D. Research progress in graphene reinforced metal matrix composites. Electron. Compon. Mater. 2017, 36, 78. [Google Scholar]
- Ma, D.; Wu, P. Improved microstructure and mechanical properties for Sn58Bi0.7Zn solder joint by addition of graphene nanosheets. J. Alloys Compd. 2016, 671, 127–136. [Google Scholar] [CrossRef]
- Huang, Y.; Xiu, Z.; Wu, G.; Tian, Y.; He, P. Sn–3.0Ag–0.5Cu nanocomposite solders reinforced by graphene nanosheets. J. Mater. Sci. Mater. Electron. 2016, 27, 6809–6815. [Google Scholar] [CrossRef]
- Huang, Y.; Xiu, Z.; Wu, G.; Tian, Y.; He, P.; Gu, X.; Long, W. Improving shear strength of Sn-3.0Ag-0.5Cu/Cu joints and suppressing intermetallic compounds layer growth by adding graphene nanosheets. Mater. Lett. 2016, 169, 262–264. [Google Scholar] [CrossRef]
- Hu, X.; Chan, Y.; Zhang, K.; Yung, W.K.C. Effect of graphene doping on microstructural and mechanical properties of Sn–8Zn–3Bi solder joints together with electromigration analysis. J. Alloys Compd. 2013, 580, 162–171. [Google Scholar] [CrossRef]
- Liu, X.; Han, Y.; Jing, H.; Wei, J.; Xu, L. Effect of graphene nanosheets reinforcement on the performance of Sn-Ag-Cu lead-free solder. Mater. Sci. Eng. A 2013, 562, 25–32. [Google Scholar] [CrossRef]
- Chen, F.; Gupta, N.; Behera, R.K.; Rohatgi, P.K. Graphene-Reinforced Aluminum Matrix Composites: A Review of Synthesis Methods and Properties. JOM 2018, 70, 837–845. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Abidi, N.; Cabrales, L. Wettability and Surface Free Energy of Graphene Films. Langmuir 2009, 25, 11078–11081. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Michaelides, A.; Alfè, D.; Schimka, L.; Kresse, G.; Wang, E. Adsorption and diffusion of water on graphene from first principles. Phys. Rev. B 2011, 84, 033402. [Google Scholar] [CrossRef]
- Kysilka, J.; Rubes, M.; Grajciar, L.; Nachtigall, P.; Bludsky, O. Accurate Description of Argon and Water Adsorption on Surfaces of Graphene-Based Carbon Allotropes. J. Phys. Chem. A 2011, 115, 11387–11393. [Google Scholar] [CrossRef] [PubMed]
- Błoński, P.; Otyepka, M. First-principles study of the mechanism of wettability transition of defective graphene. Nanotechnology 2017, 28, 64003. [Google Scholar] [CrossRef]
- Ashraf, A.; Wu, Y.; Wang, M.C.; Yong, K.; Sun, T.; Jing, Y.; Haasch, R.T.; Aluru, N.R.; Nam, S. Doping-Induced Tunable Wettability and Adhesion of Graphene. Nano Lett. 2016, 16, 4708–4712. [Google Scholar] [CrossRef]
- Dazhi, F.; Guili, L.; Shuang, Z. Effects of vacancy and deformation on an Al atom adsorbed on graphene. Chin. J. Phys. 2018, 56, 689–695. [Google Scholar] [CrossRef]
- Liu, Y.; An, L.; Gong, L. First-principles study of Cu adsorption on vacancy-defected/Au-doped graphene. Mod. Phys. Lett. B 2018, 32, 1850139. [Google Scholar] [CrossRef]
- Wu, C.M.L.; Yu, D.Q.; Law, C.M.T.; Wang, L. Properties of lead-free filler alloys with rare earth element additions. Mater. Sci. Eng. R 2004, 44, 1–44. [Google Scholar] [CrossRef]
- Yang, C.; Xu, J.; Ding, W.; Chen, Z.; Fu, Y. Effect of cerium on microstructure, wetting and mechanical properties of Ag-Cu-Ti filler alloy. J. Rare Earths 2009, 27, 1051–1055. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Payne, M.C. First principles methods using castep. Z. Kristallogr. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Milman, V.; Refson, K.; Clark, S.; Pickard, C.; Yates, J.; Gao, S.-P.; Hasnip, P.; Probert, M.; Perlov, A.; Segall, M.; et al. Electron and vibrational spectroscopies using DFT, plane waves and pseudopotentials: CASTEP implementation. J. Mol. Struct. THEOCHEM 2010, 954, 22–35. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Car, R.; Parrinello, M. Unified Approach for Molecular Dynamics and Density-Functional Theory. Phys. Rev. Lett. 1985, 55, 2471–2474. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Erratum: Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1993, 48, 4978. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Wan, W.; Wang, H. First-Principles Investigation of Adsorption and Diffusion of Ions on Pristine, Defective and B-doped Graphene. Materials 2015, 8, 6163–6178. [Google Scholar] [CrossRef] [PubMed]
- Granatier, J.; Lazar, P.; Prucek, R.; Šafářová, K.; Zbořil, R.; Otyepka, M.; Hobza, P. Interaction of Graphene and Arenes with Noble Metals. J. Phys. Chem. C 2012, 116, 14151–14162. [Google Scholar] [CrossRef]
- Del Castillo, R.M.; Sansores, L.E. Study of the electronic structure of Ag, Au, Pt and Pd clusters adsorption on graphene and their effect on conductivity. Eur. Phys. J. B 2015, 88, 248. [Google Scholar] [CrossRef]
- Amft, M.; Lebègue, S.; Eriksson, O.; Skorodumova, N.V. Adsorption of Cu, Ag, and Au atoms on graphene including van der Waals interactions. J. Phys. Condens. Matter 2011, 23, 395001. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; He, C.; Li, T.; Gong, S.; Zhao, L.; Tao, J. First-principles study on the electronic and magnetic properties of armchair graphane/graphene heterostructure nanoribbons. Solid State Commun. 2015, 211, 23–28. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhang, Y.; Störmer, H.L.; Kim, P. Quantum Hall States near the Charge-Neutral Dirac Point in Graphene. Phys. Rev. Lett. 2007, 99, 106802. [Google Scholar] [CrossRef]
- Yu, W.J.; Liao, L.; Chae, S.H.; Lee, Y.H.; Duan, X. Toward Tunable Band Gap and Tunable Dirac Point in Bilayer Graphene with Molecular Doping. Nano Lett. 2011, 11, 4759–4763. [Google Scholar] [CrossRef]
- De Lara-Castells, M.P.; Mitrushchenkov, A.O.; Stoll, H. Combining density functional and incremental post-Hartree-Fock approaches for van der Waals dominated adsorbate-surface interactions: Ag2/graphene. J. Chem. Phys. 2015, 143, 102804. [Google Scholar] [CrossRef]
- Ashrafian, S.; Jahanshahi, M.; Ganji, M.D.; Agheb, R. Greatly enhanced adsorption of platinum on periodic graphene nanobuds: A first-principles study. Appl. Surf. Sci. 2015, 351, 1105–1115. [Google Scholar] [CrossRef]
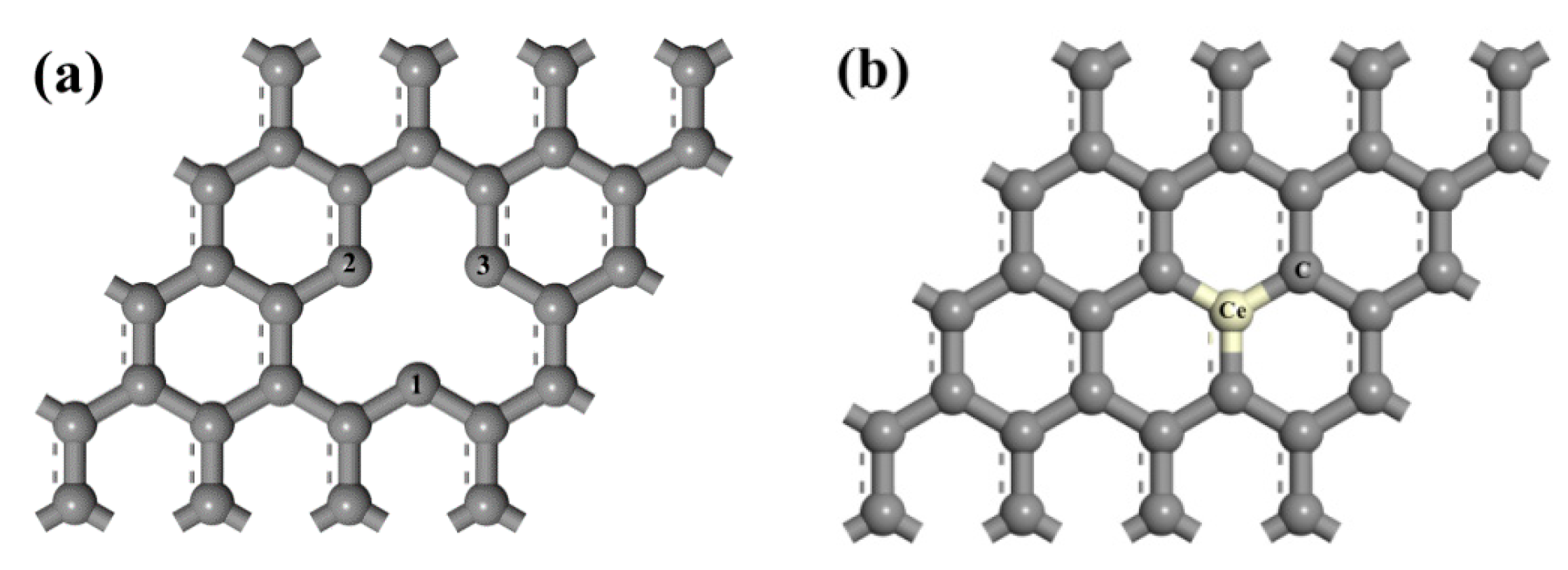
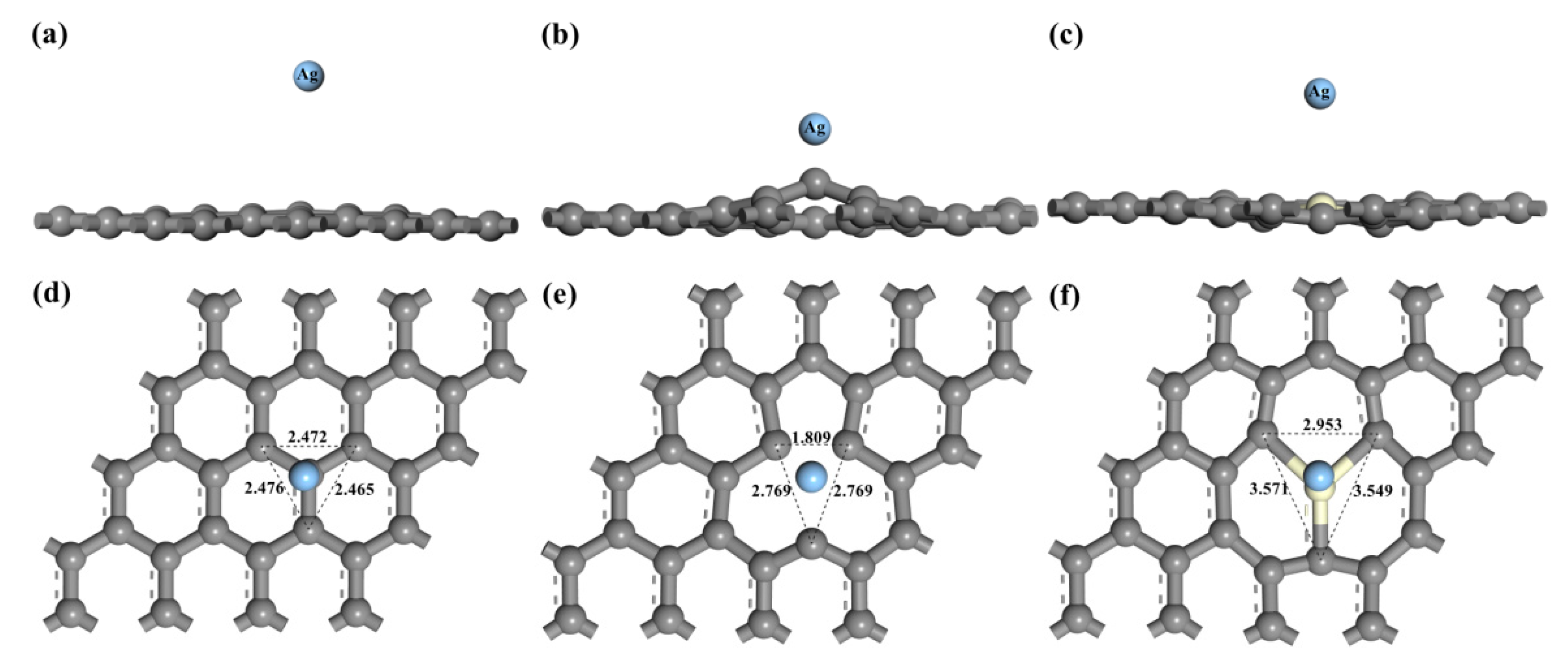
| Type of Graphene | D/Å | Ead/eV | Q/e | ∆h/Å | |||
|---|---|---|---|---|---|---|---|
| T | B | H | |||||
| Intrinsic graphene | 1.564 | −0.011 | −0.009 | −0.010 | 0.09 | 0.055 | |
| VG | 1.025 | −2.358 | −2.226 | −2.439 | 0.78 | 0.380 | |
| Ce-doped graphene | 1.530 | TCe: −2.241 | TC: −2.230 | −2.226 | −2.218 | Ce: 1.96 | 0.147 |
| Ag: −0.17 | |||||||
| Adsorption System | Bond | Population | Length/10−1 nm | P/charge·nm−1 |
|---|---|---|---|---|
| VG | Ag–C1 | 0.54 | 2.14657 | 2.516 |
| Ag–C2 | −0.06 | 2.51845 | −0.238 | |
| Ag–C2 | −0.06 | 2.52454 | −0.238 | |
| Ce-G | Ag–Ce | 0.28 | 2.99968 | 0.933 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Z.; Hu, M.; Liu, J.; Luo, X.; Zhang, K.; Tang, Z. First-Principles Investigation of Adsorption of Ag on Defected and Ce-doped Graphene. Materials 2019, 12, 649. https://doi.org/10.3390/ma12040649
Fan Z, Hu M, Liu J, Luo X, Zhang K, Tang Z. First-Principles Investigation of Adsorption of Ag on Defected and Ce-doped Graphene. Materials. 2019; 12(4):649. https://doi.org/10.3390/ma12040649
Chicago/Turabian StyleFan, Zhou, Min Hu, Jianyi Liu, Xia Luo, Kun Zhang, and Zhengchao Tang. 2019. "First-Principles Investigation of Adsorption of Ag on Defected and Ce-doped Graphene" Materials 12, no. 4: 649. https://doi.org/10.3390/ma12040649
APA StyleFan, Z., Hu, M., Liu, J., Luo, X., Zhang, K., & Tang, Z. (2019). First-Principles Investigation of Adsorption of Ag on Defected and Ce-doped Graphene. Materials, 12(4), 649. https://doi.org/10.3390/ma12040649




