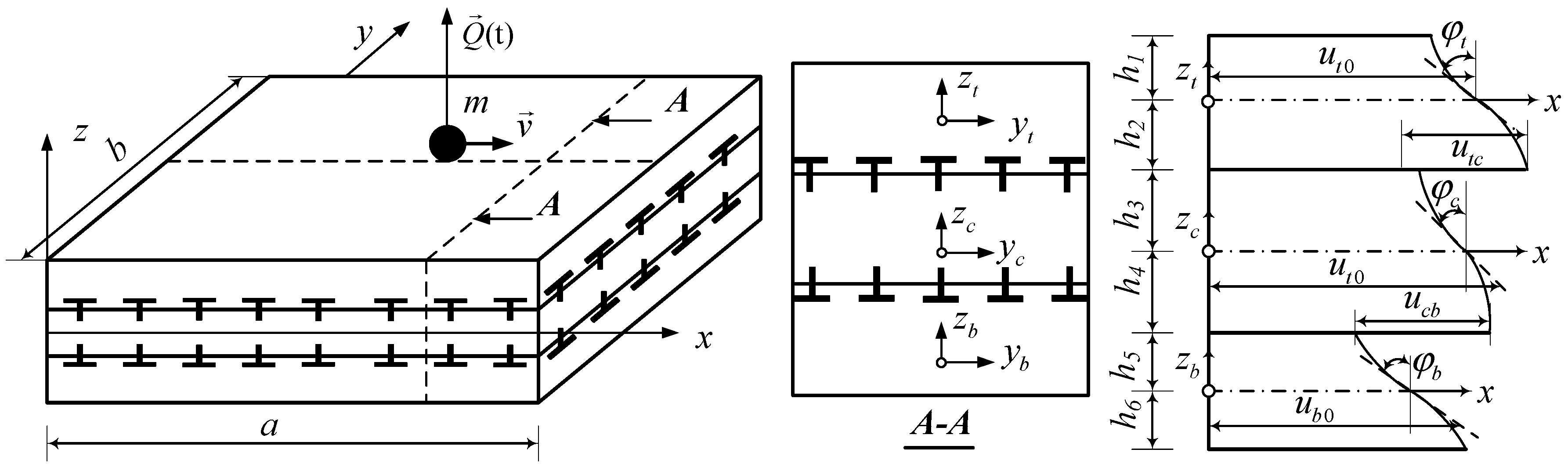
1. Introduction
In recent years, composite layered systems have attracted a great of interest from many researchers due to their optimized material configuration, such as their high strength-to-weight ratio and stiffness-to-weight ratio. For a multi-layer composite beam, all of its layers are connected by shear connectors, which play a very crucial role in the mechanical behavior of the beam. Newmark et al. [
1] proposed the governing differential equations for elastically connected steel-concrete beams, based on the linear elastic Euler–Bernoulli beam theory. Various later works [
2,
3,
4] improved the shear effect of Newmark’s model by using Timoshenko composite beam theory. Silva et al. [
5] and Nguyen et al. [
6,
7] utilize the finite element method (FEM) to analyze the linear static properties of multi-layered composite beams. Later on, Newmark’s model was developed for dynamic and non-linear problems [
8,
9,
10,
11,
12].
In addition, for the Timoshenko beam theory (TBT), Chakrabarti et al. [
13,
14] introduced static analysis of two-layer composite beams by using higher order beam theory (HBT). The dynamic response of composite beams with shear connectors was computed using the finite element method (FEM) and higher-order beam theory [
15]. HBT has partially overcome the side effect of shear correction factor. Additionally, Subramanian [
16] used HBT and FEM for dynamic analysis of laminated composite beams. Li et al. [
17] studied the free vibration of axially loaded composite beams with general boundary conditions using hyperbolic shear deformation theory. Vo and Thai [
18] presented the static behavior of composite beams using various refined shear deformation theories [
19].
Most of the higher order theories, including Reddy’s higher order beam theory (RHBT) [
20], tend to ignore the transverse deformation of multi-layer beams. Manjunatha and Kant [
21] proposed to use C
0 finite element [
22,
23] and a set of higher order theories for the analysis of composite and sandwich beams. Kant’s theories incorporate the non-linear variation of displacement through beam thickness to eliminate the use of shear correction coefficients. Yan et al. [
24] developed a three-dimensional damage plasticity based on the finite element model (FEM) to simulate the ultimate strength behavior of the SCS sandwich structure under concentrated loads.
Carrena [
25] worked on the assumption that the displacement field is expanded in terms of generic functions, which is the unified formulation by Carrera (CUF) [
26], to examine the static response of beams with different cross sections, such as square, C-shaped and bridge-like sections. Based on the mentioned approach, Cinefra et al. [
27] employed MITC9 (Mixed Interpolated of Tensorial Components using 9 nodes) shell elements to analyze the mechanical behavior of laminated composite plates and shells. Muresan et al. [
28] carried out research on the stability of the thin walled prismatic bars based in the generalized beam theory (GBT), which is an efficient approach developed by Schardt [
29]. Yu et al. [
30] used the variational asymptotic beam section analysis (VABS) for mechanical behavior of various cross sections, such as the elliptic and triangular sections.
The dynamic behaviors of plates under moving loads are also interesting problems in engineering such as bridges and roads, space vehicles, submarines and mechanical engineering and so on. So many scholars have studied on this aspect in past decades. Ouyang [
31] briefly reviewed a variety of moving-load problems and several analytical solution methods. Fryba [
32] has summarized a variety of engineering problems that analyzed the dynamics of structures under moving loads. Song et al. [
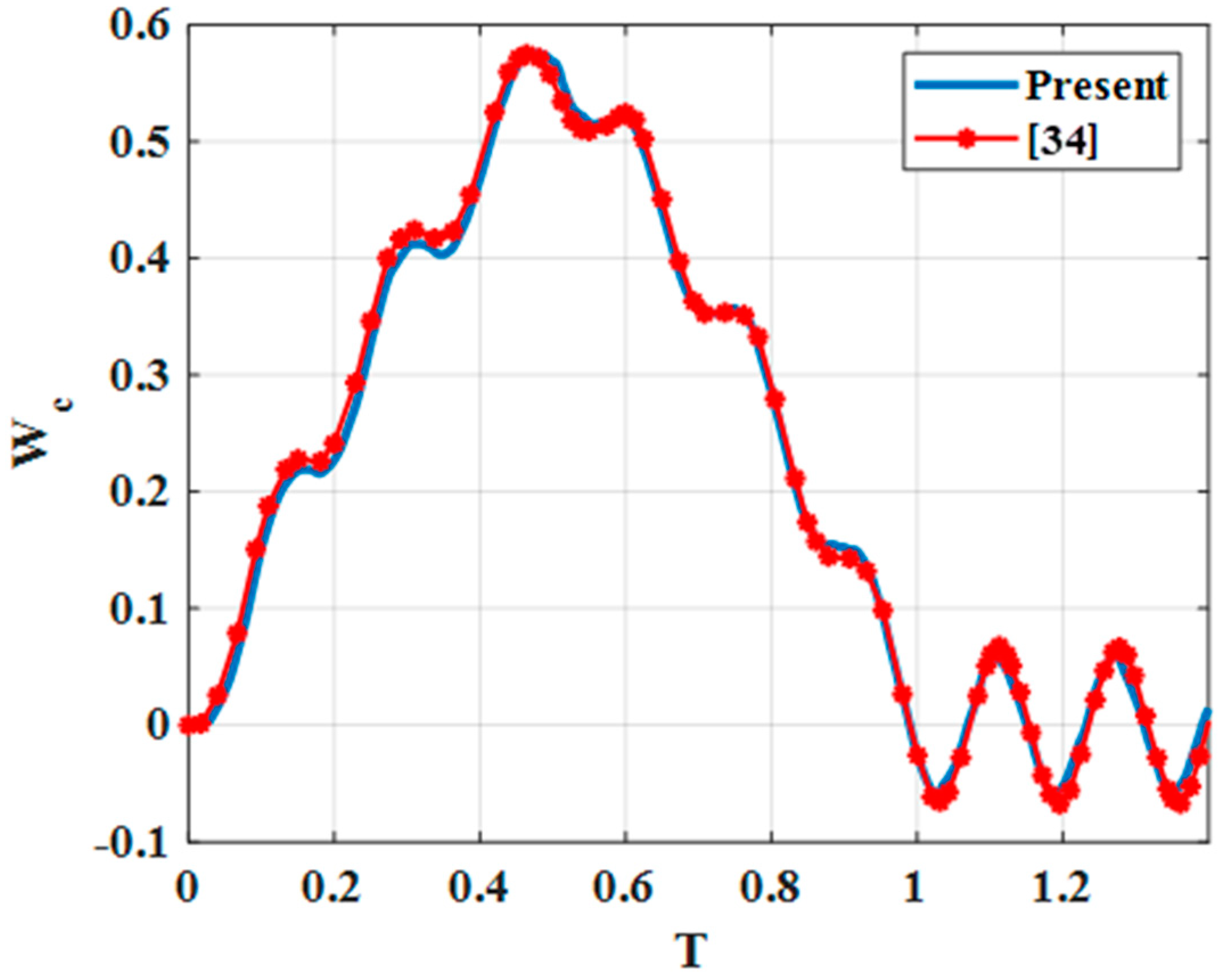
33] proposed a novel method to predict the dynamic behaviors of flat plate of arbitrary boundary conditions subjected to moving loads, based on the Kirchhoff plate theory.
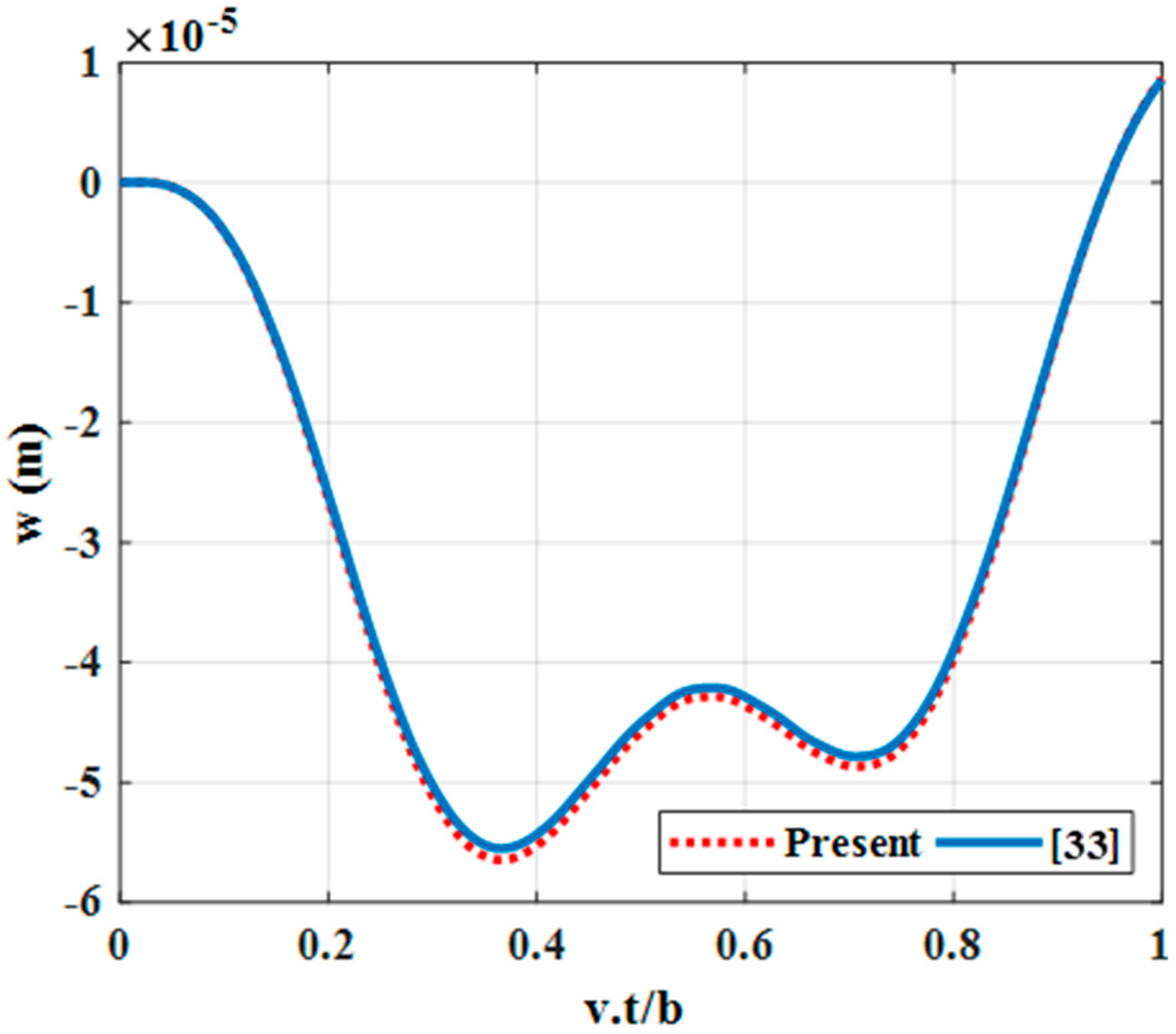
Although there are plenty of published works dealing with the non-linear, linear, static and dynamic problems of composite and sandwich beams using shear connectors, to our knowledge, there seems to be no analysis regarding the calculation of triple-layer composite plate with layers connected by shear connectors subjected to moving load. In this paper, we combined the published theories on multi-layered beams, Mindlin’s plate theory, and finite element modelling to simulate the oscillation of triple-layer plates with layers connected by shear connectors subjected to moving loads. We also built the mechanical properties and established equations describing the dynamic response of the plates. Additionally, we studied the influence of geometric parameters, material, load, etc., on the dynamic response of the referred plate under the influence of a moving load.
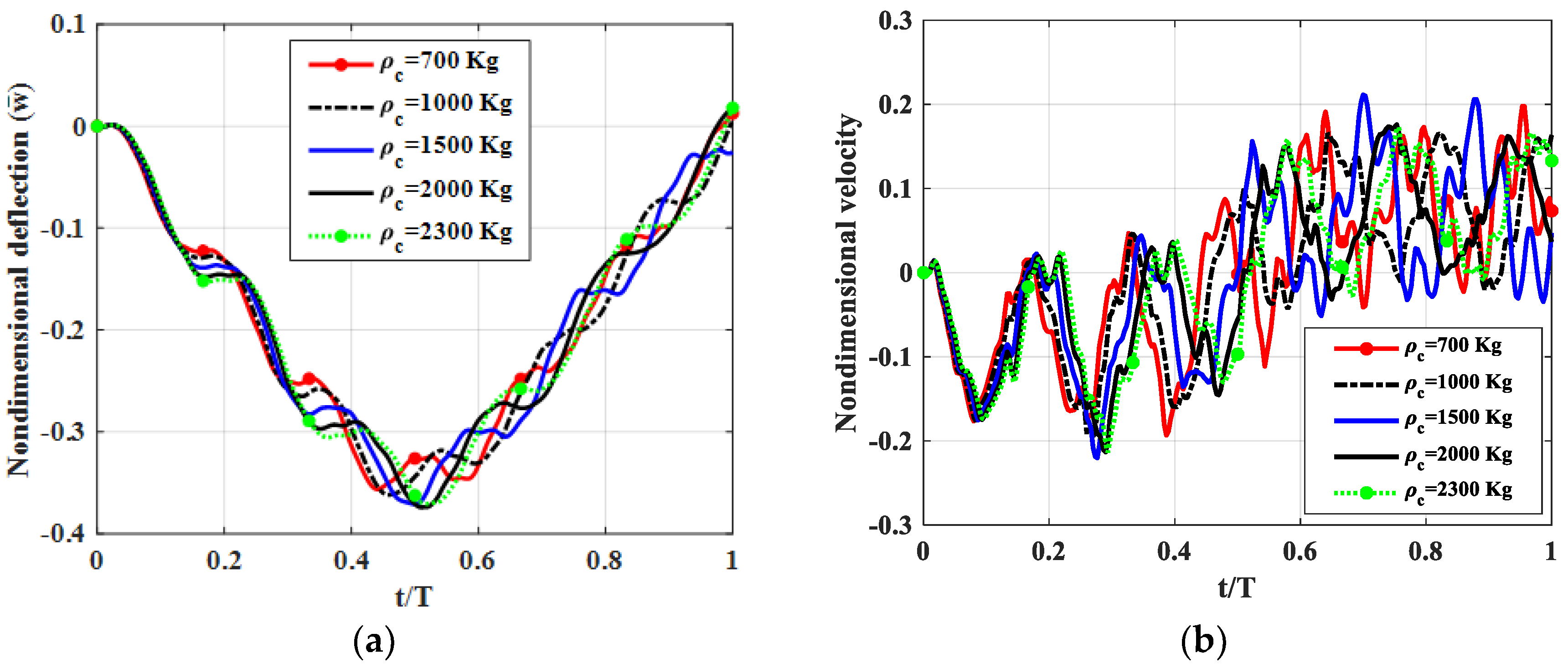
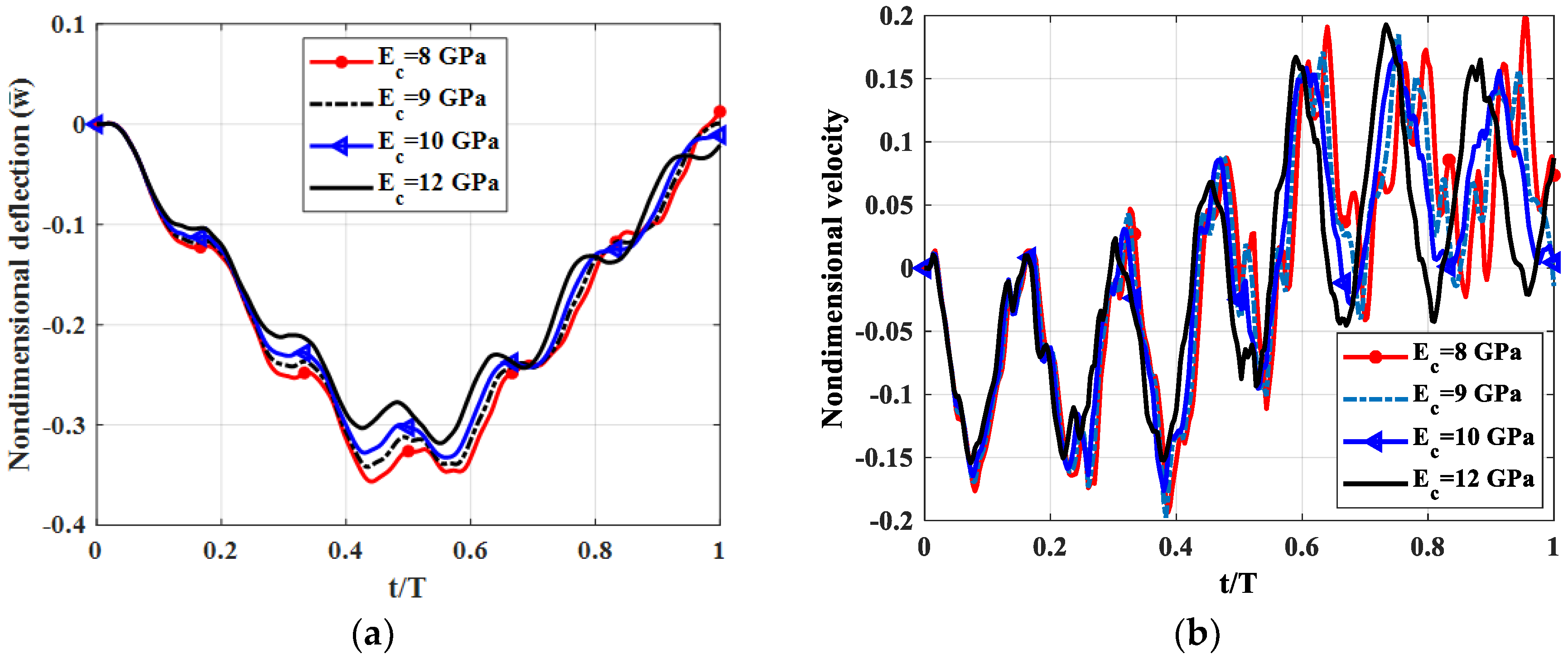
5. Conclusions
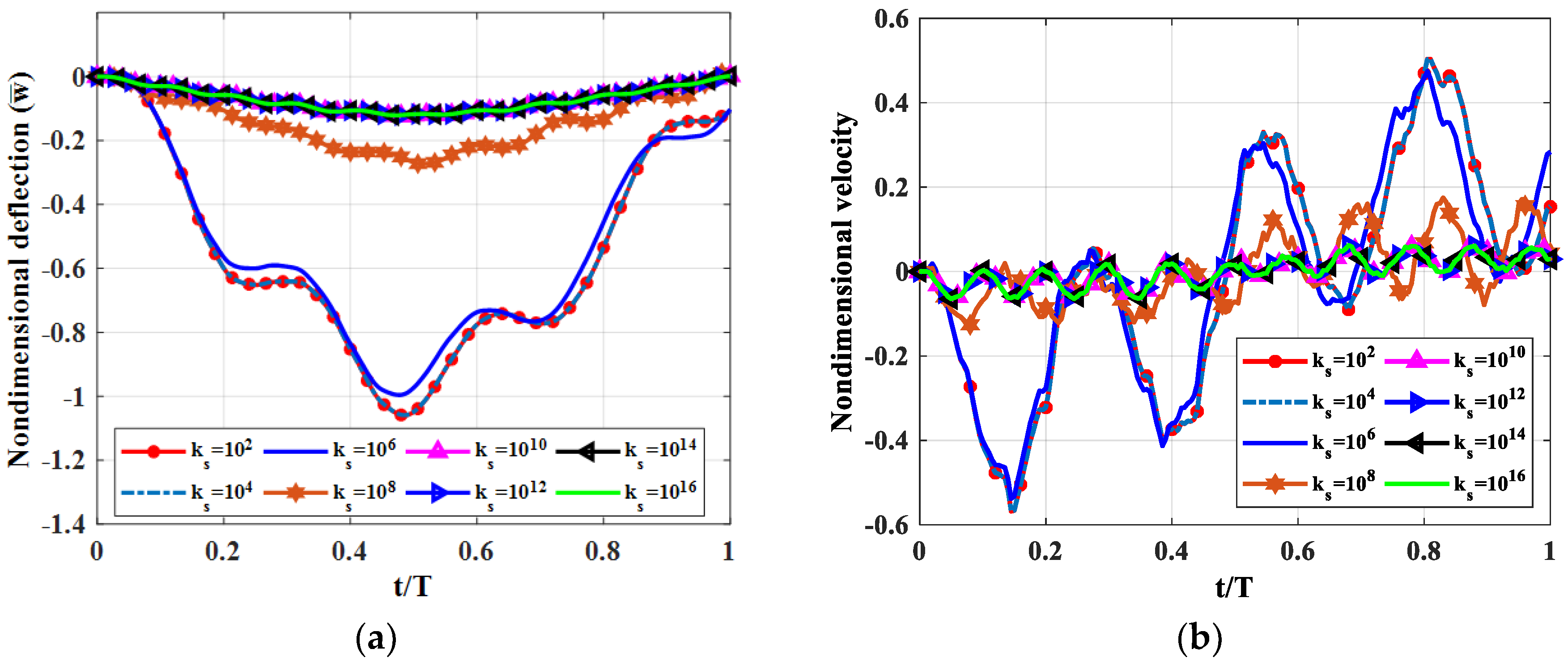
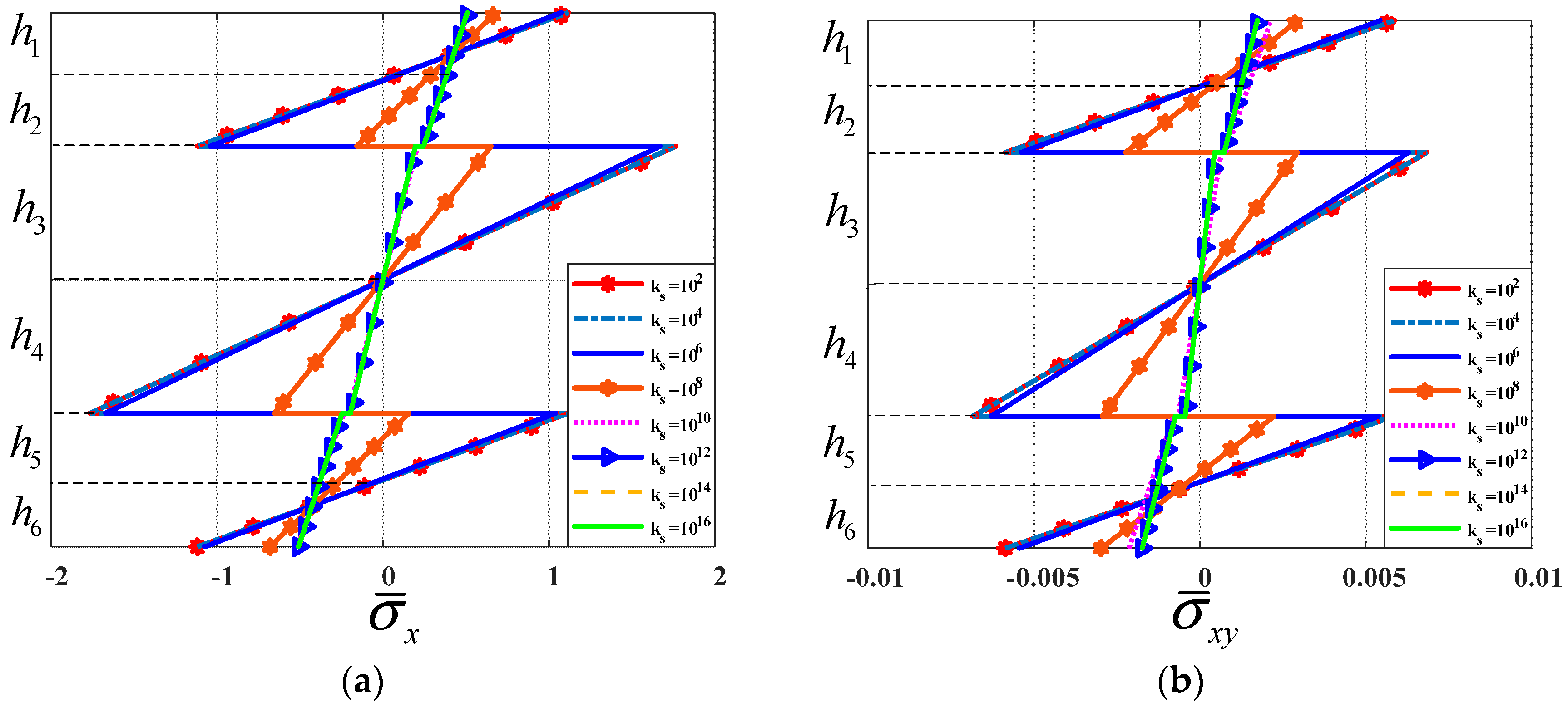
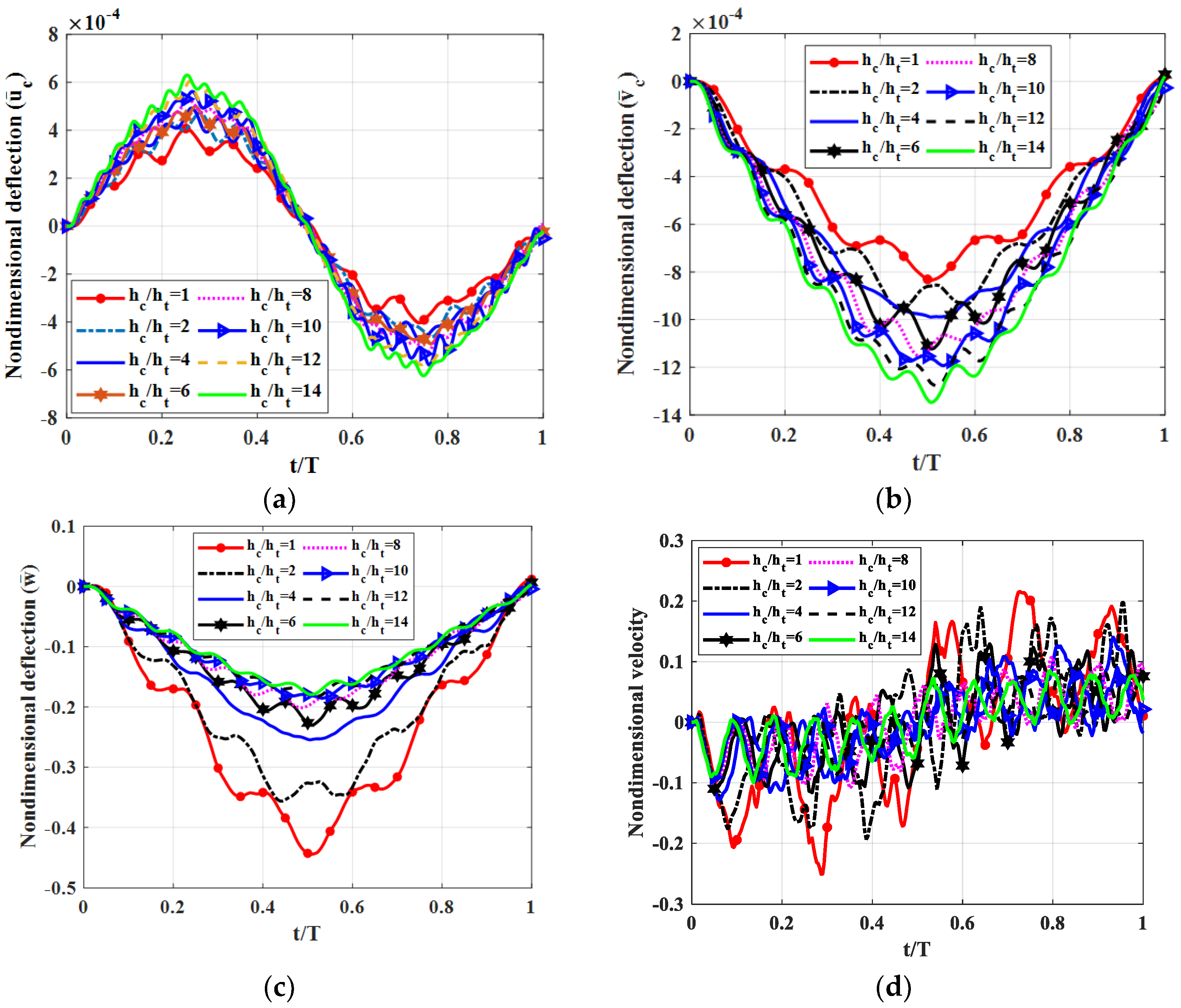
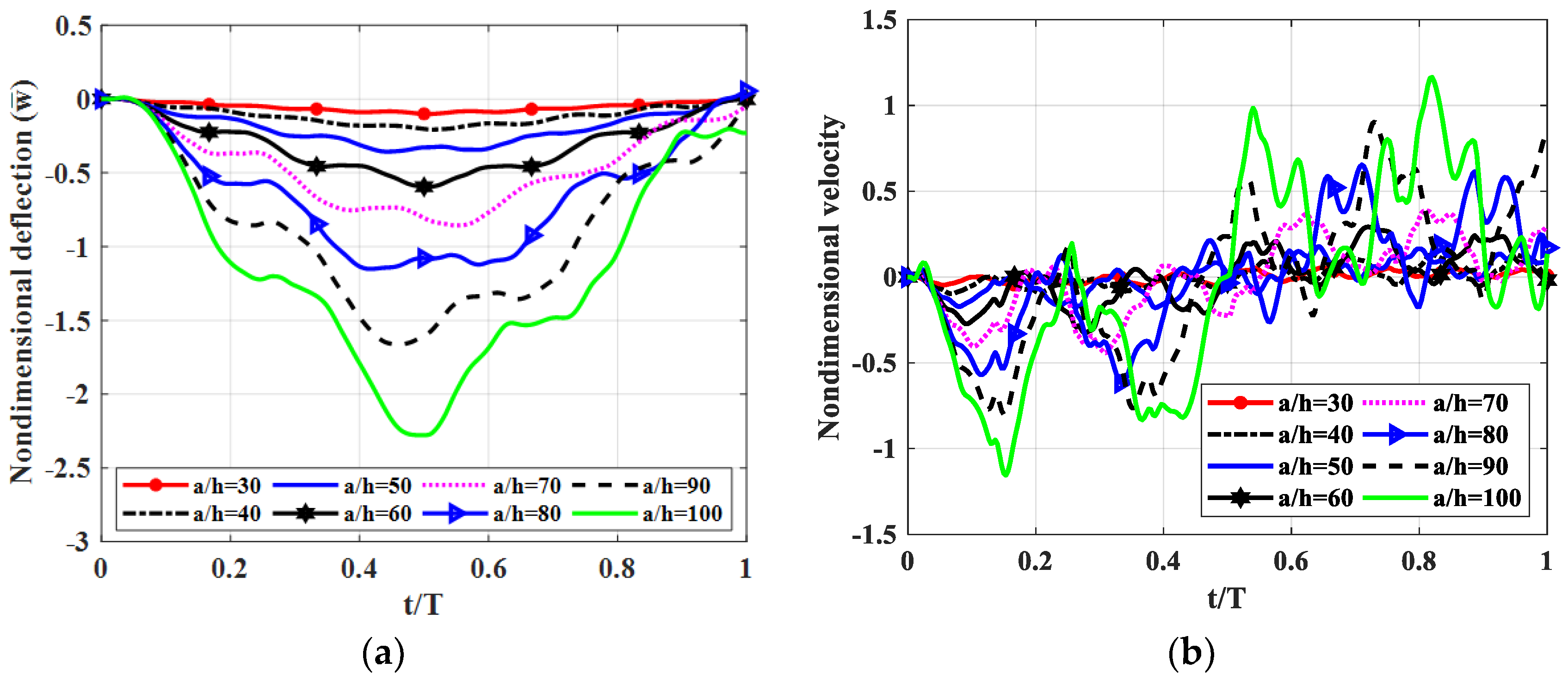
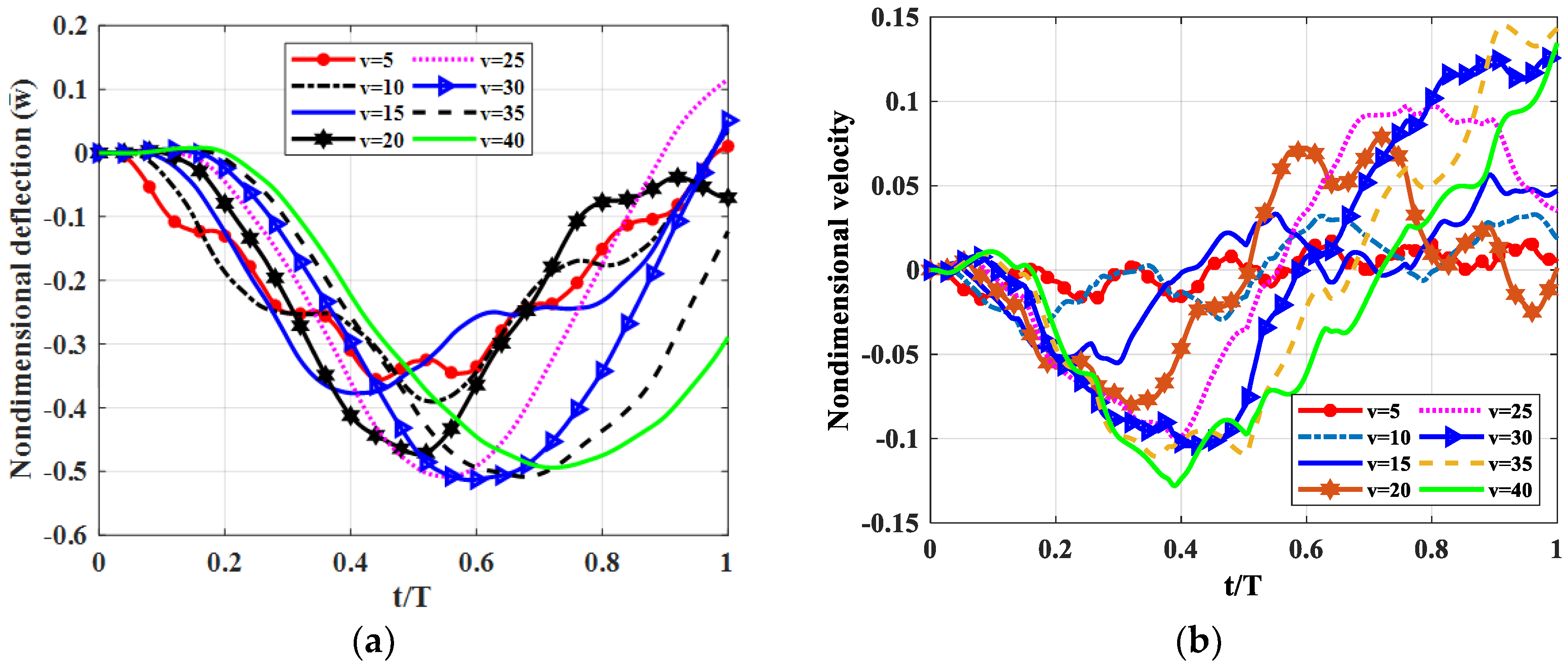
By using published theories of multi-layered beams, Mindlin’s plate theory and finite element modelling, we simulated the forced vibration of a triple-layer plate with layers connected by shear connectors subjected to a moving load. The influences of some structural parameters on the dynamic response of the plate were also examined in the paper. We found that, in the regarded plate, the shear coefficient of the shear connector played a crucial role. Specifically, when the shear coefficient was sufficiently large, the plate could be considered a sandwich plate. The flexibility of the shear coefficient helped engineer a plate with the desired mechanical properties. From the results of numerical tests, we proposed that to reduce plate vibration, the elastic modulus of the middle layer should be smaller than the outside two layers, and the thickness of the middle layers should be 20–30 times larger than the two outside layers.