Fatigue Life Assessment of Rolling Bearings Made from AISI 52100 Bearing Steel
Abstract
1. Introduction
- The procedure does not require time-consuming and expensive experimental tests,
- The calculation can be quickly and easily made using theoretical or FE models,
- It allows for the optimization of shapes of rolling elements and raceways.
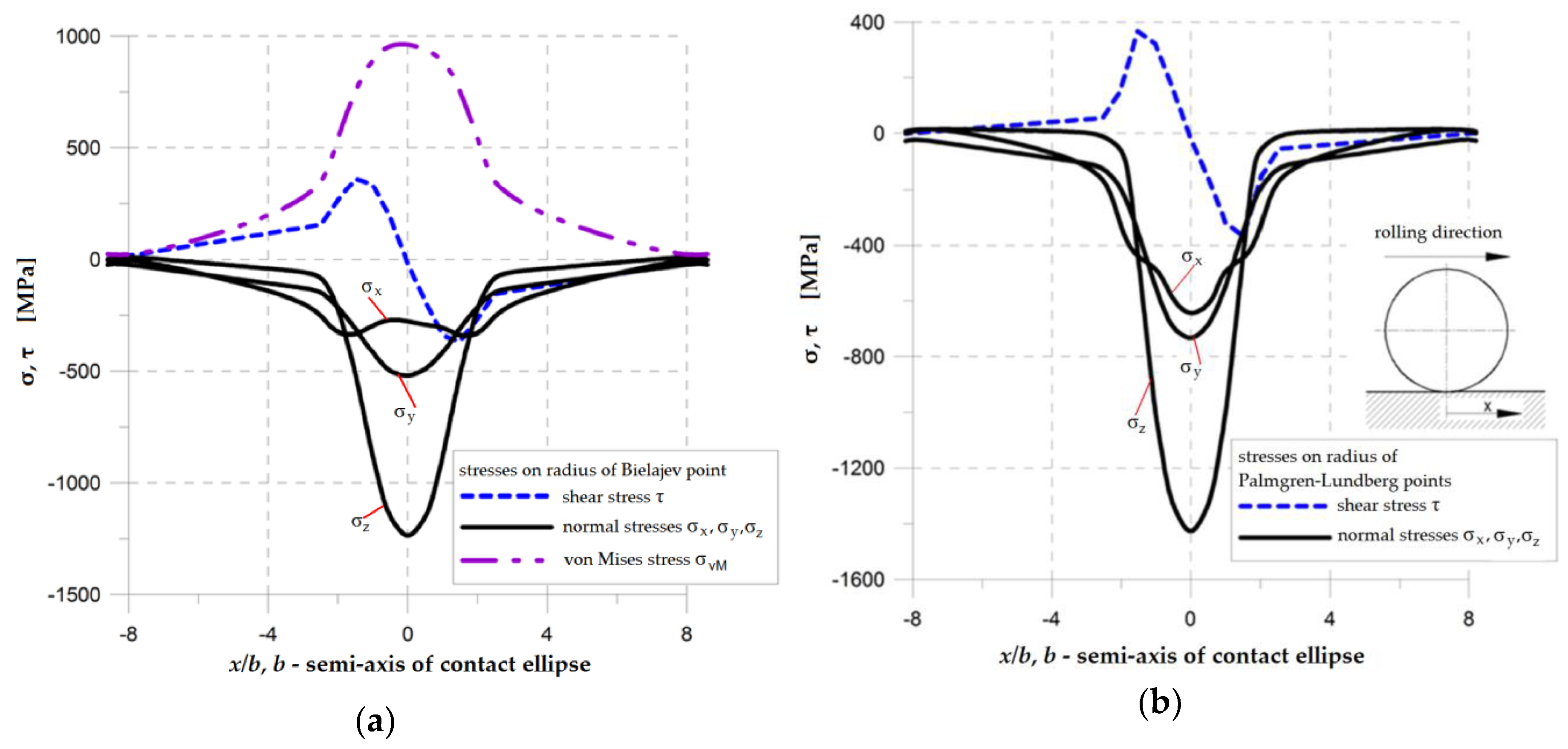
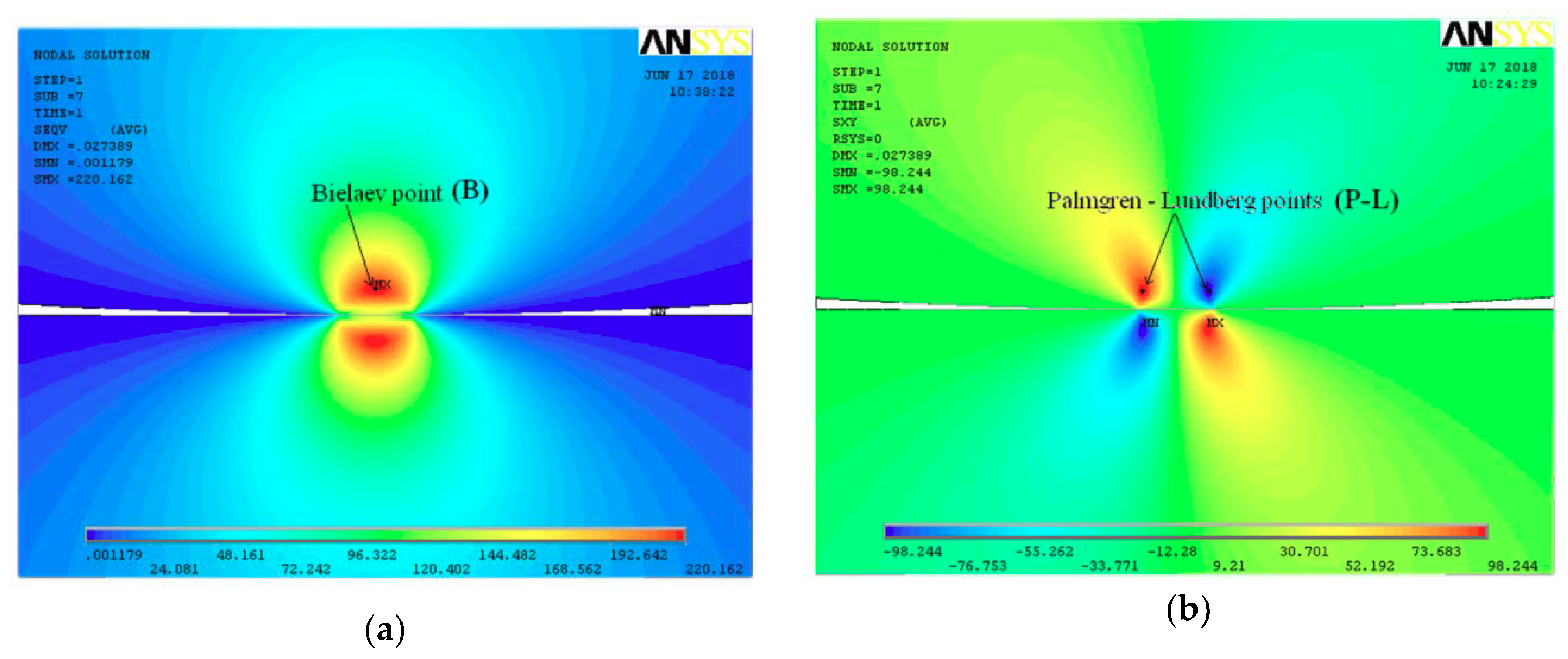
2. Fatigue in Rolling Bearings
- surface cracks (pitting)—triggered by surface defects or roughness and the presence of micro-notches, through which further crack growth can be accelerated by grease penetration [40],
- subsurface cracks (spalling)—caused by the alternate shear stresses, the presence of inclusions, etc., which originate cracks near the surface of rolling [3],
- cracks originated at deep defects also appearing in the low-stress zone.
- steady-state contact (lack of rolling or rolling with low velocity) under various loading, and
- rolling contact (RC).
3. Material
- -
- for median life (50% of failure life):
- -
- for 10% failure life (90% rating life for material):
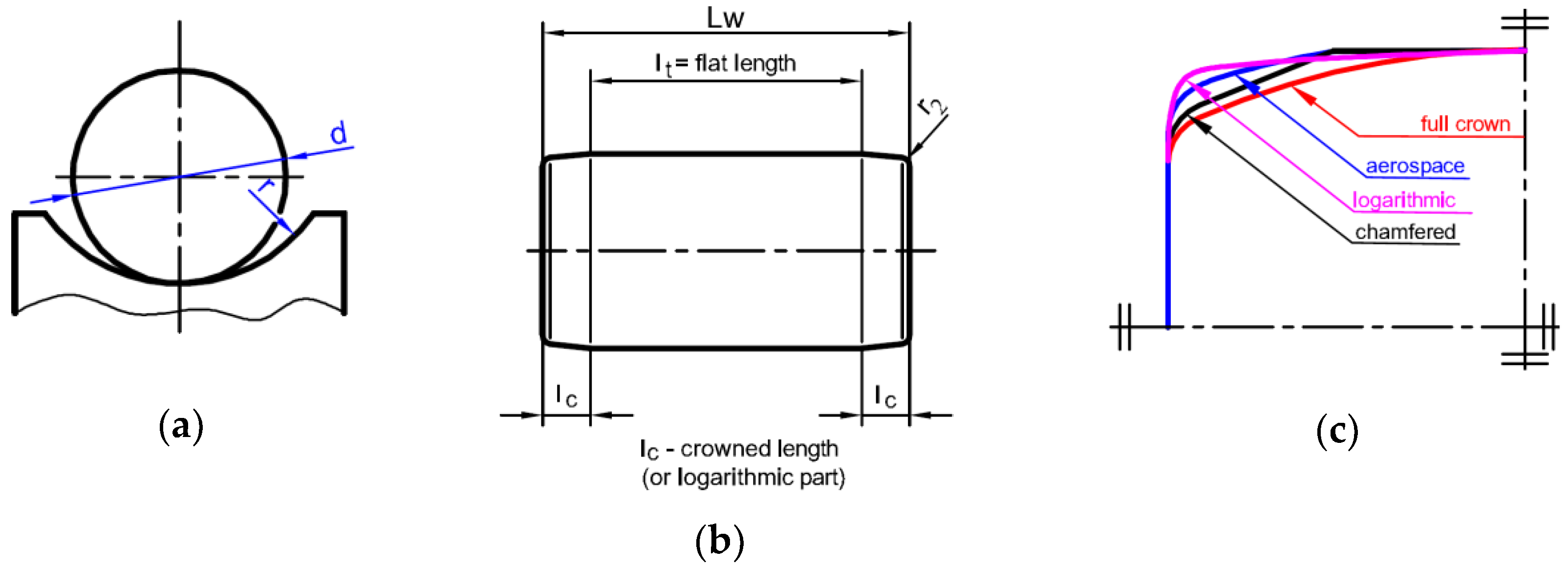
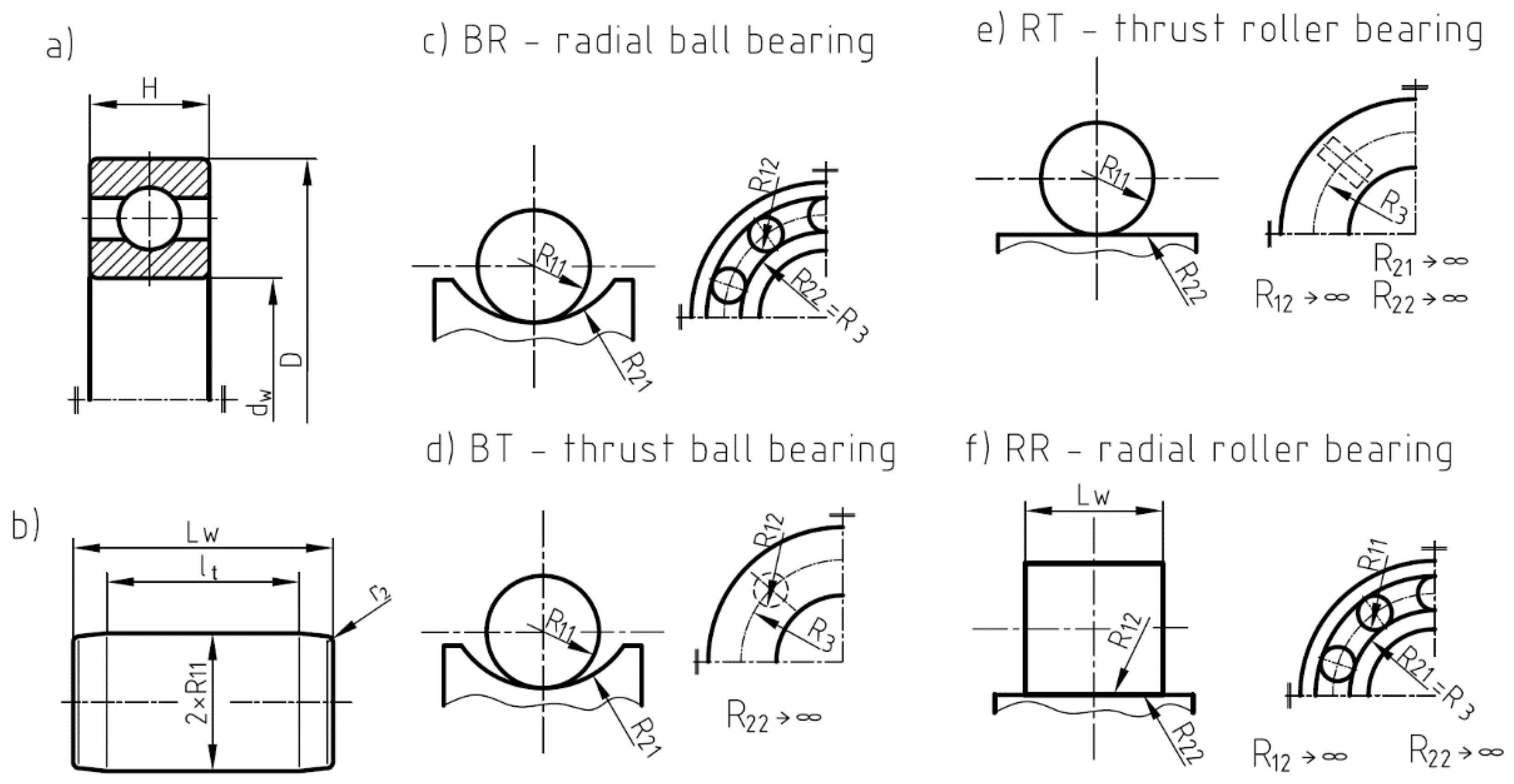
4. Rolling Bearing Geometry
5. Analytical Procedure for the Fatigue Life Assessment of Rolling Bearings
- determination of the geometries of the rolling elements (the radii of curvatures, the contact length, etc.) and loading conditions,
- determination of the material properties (static: the Young modulus—E, the Poisson’s ratio—ν; fatigue: the Wöhler diagrams for alternate bending and alternate torsion fatigue strength), which are discussed in chapter 3,
- calculation of the loading acting on rolling elements—see Section 5.1,
- calculation of the maximal contact stress po and dimensions of the contact area (elliptical: semi-axes of the contact area; line: contact length)—see Section 5.2,
- calculation of subsurface stresses using analytical formula—see Section 5.2,
- estimation of fatigue loading or fatigue life (in cycles)—see Section 5.3.
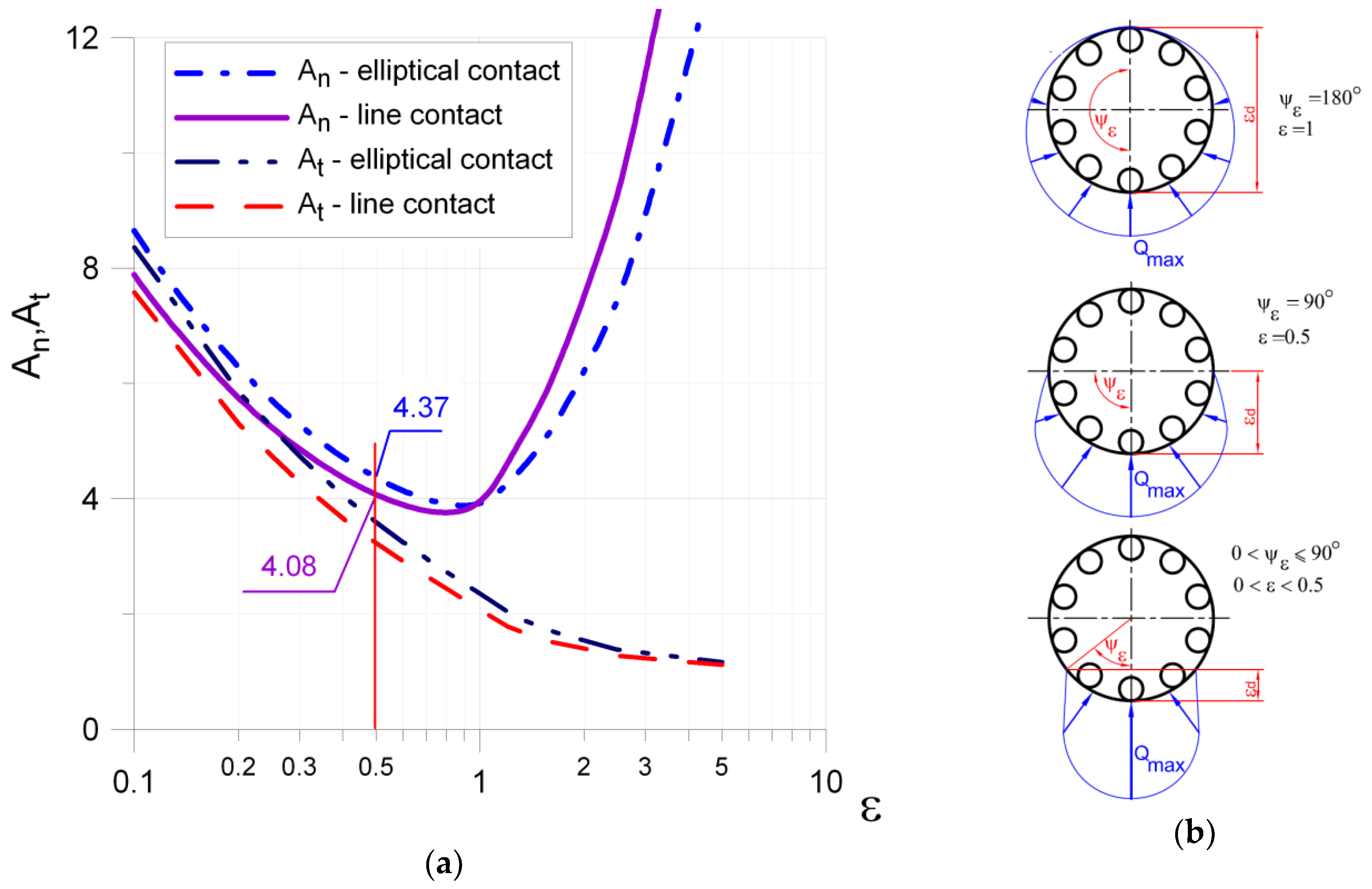
5.1. Determination of Loading in Rolling Elements
- -
- thrust roller bearing and thrust ball bearing subjected to axial loading:
- -
- thrust roller bearing subjected to eccentric axial loading:
- -
- thrust ball bearing subjected to eccentric axial loading:
- -
- one-row radial/angular roller bearing subjected to radial loading:
- -
- one-row radial/angular roller bearing subjected to radial and axial loadings:
- -
- one-row radial/angular ball bearing subjected to radial loading:
- -
- one-row radial/angular ball bearing subjected to radial and axial loadings:
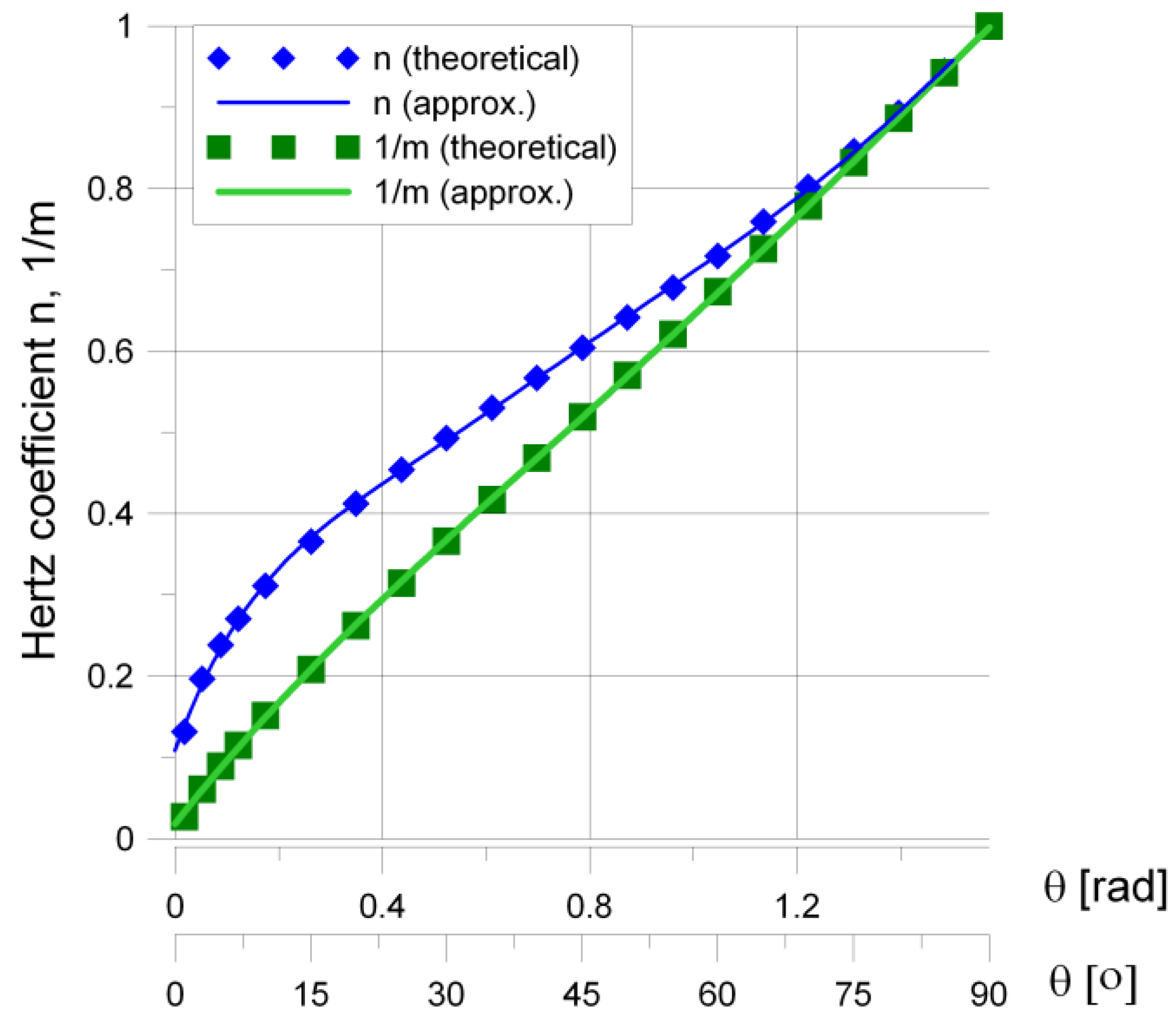
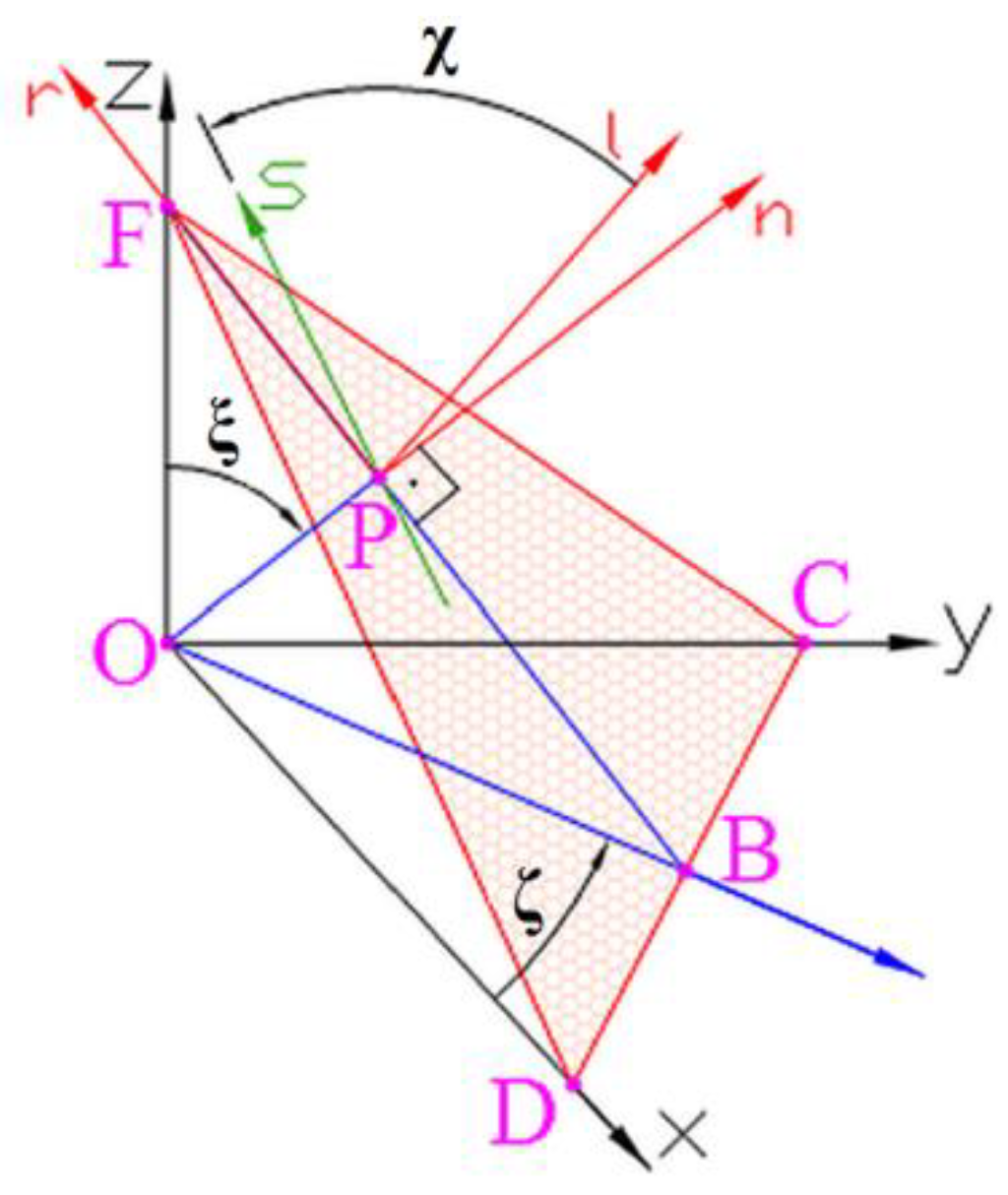
5.2. Determination of Contact Parameters
5.3. Application of Fatigue Life Model
- -
- Juvinall proposal
- -
- Heywood model
- -
- Moore model
- -
- Shighley and Mitschke model
- -
- Roark model
6. Results and Discussion
- -
- for the thrust ball and roller bearing:
- -
- for the radial ball and roller bearing:
7. Conclusions
- Only the geometries of bearing and rolling elements and two Wöhler curves for the material (τ−1 and σ−1) are necessary for the analysis,
- The method does not need the additional data from experimental tests for an investigated rolling bearing,
- The calculations can be made quickly (using analytical solutions), including real multiaxial stress state in elements,
- The obtained results are consistent with the data given in catalogues.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| a1—modification factor for reliability |
| a2—material and processing factor |
| a3—application factor |
| An, At—coefficient of the maximal loading for line and point contact |
| a, b—semi-axes of contact area or contact length of rectangular contact area |
| C—basic dynamic load rating [N] |
| d—diameter of rolling element |
| dw—bore diameter of bearing |
| D—outside diameter of bearing |
| E*—equivalent Young’s modulus |
| f—race conformity ratio |
| fL—coefficient which defines the effective length of roller |
| Fa—applied axial loading |
| Fr—applied radial loading |
| FuCAT—catalogue fatigue load |
| FuP1—calculated fatigue load |
| H—bearing width |
| i—number of rows of rolling elements |
| k—exponent of bearing type |
| ks—size factor |
| Kj—generalized stiffness |
| L—rated service life (in millions of revolutions) for 10% probability of failure |
| Lw—roller length |
| lc—crowned length of roller |
| lt—flat length of roller |
| m, n, A, B—coefficients of elliptical contact |
| N—number of cycles to failure |
| N1—number of cycles per one full turn of bearing |
| P—external equivalent load [N] |
| P*—radial loading per unit length |
| po—maximal contact pressure |
| Qmax—maximal load of the most strenuous rolling element |
| R*—equivalent radius |
| R11,R12—minimum and the maximum principal radii of curvatures of the first body at the initial contact point, respectively |
| R21, R22—minimum and the maximum principal radii for the second body at the initial contact point, respectively |
| R3—radius on which the rolling elements are rolling |
| r2—fillet radius of the edges of roller |
| t—time |
| T—time of one cycle |
| Z—number of rolling elements in one row |
| α—angle of bearing operation |
| ε — coefficient of loading distribution on rolling element |
| δ—difference between the calculated and catalogue fatigue load |
| δdefl—total deflection in rolling bearing |
| τ—shear stress |
| τa—amplitude of shear stress |
| ζ, ξ, χ—angles defining material plane and direction of shear stress on material plane |
| φ—angle between the planes of principal curvatures of the two surfaces |
| θ—auxiliary angle |
| σ—normal stress |
| σH,MAX—maximal hydrostatic stress |
| σVM—Von Mises stress |
| σ−1—alternate bending fatigue strength |
| τ−1—alternate torsion fatigue strength |
| τP1—equivalent fatigue stress |
| ν—Poisson’s ratio |
| ψ—location angle |
| ψε—angle corresponding to the effectively loaded part of the bearing raceway circumference |
References
- Demirhan, N.; Kanber, B. Stress and displacement distributions on cylindrical roller bearing rings using FEM. Mech. Based Des. Struct. Mach. 2008, 36, 86–102. [Google Scholar] [CrossRef]
- Li, S.-X.; Su, Y.-S.; Shu, X.-D.; Chen, J.-J. Microstructural evolution in bearing steel under rolling contact fatigue. Wear 2017, 380–381, 146–153. [Google Scholar] [CrossRef]
- Ebert, F.J. Fundamentals of Design and Technology of Rolling Element Bearings. Chin. J. Aeronaut. 2010, 23, 123–136. [Google Scholar] [CrossRef]
- Sadeghi, F.; Jalalahmadi, B.; Slack, T.S.; Raje, N.; Arakere, N.K. A Review of Rolling Contact Fatigue. J. Tribol. 2009, 131, 041403. [Google Scholar] [CrossRef]
- Zaretsky, E.V. Selection of rolling-element bearing steels for long-life applications. In Effect of Steel Manufacturing Processes on the Quality of Bearing Steels; Hoo, J.J.C., Ed.; ASTM STP 987; American Society for Testing and Materials: Philadelphia, PA, USA, 1988; pp. 5–43. [Google Scholar]
- Vlcek, B.L.; Zaretsky, E.V. Rolling-element fatigue testing and data analysis—A tutorial. Tribol. Trans. 2011, 54, 523–541. [Google Scholar] [CrossRef]
- Guzmán, F.G.; Oezel, M.; Jacobs, G.; Burghardt, G.; Broeckmann, C.; Janitzky, T. Reproduction of white etching cracks under rolling contact loading on thrust bearing and two-disc test rigs. Wear 2017, 390–391, 23–32. [Google Scholar]
- Upadhyay, R.K.; Kumaraswamidhas, L.A.; Azam, M.S. Rolling element bearing failure analysis: A case study. Case Stud. Eng. Fail. Anal. 2013, 1, 15–17. [Google Scholar] [CrossRef]
- Evans, M.-H.; Walker, J.C.; Ma, C.; Wang, L.; Wood, R.J.K. A FIB/TEM study of butterfly crack formation and white etching area (WEA) microstructural changes under rolling contact fatigue in 100Cr6 bearing steel. Mater. Sci. Eng. A 2013, 570, 127–134. [Google Scholar] [CrossRef]
- Harada, H.; Mikami, T.; Shibata, M.; Sokai, D.; Yamamoto, A.; Tsubakino, H. Microstructural changes and crack initiation with white etching area formation under rolling/sliding contact in bearing steel. ISIJ Int. 2005, 45, 1897–1902. [Google Scholar] [CrossRef]
- Hansen, K.T.; Fæster, S.; Natarajan, A.; Mishin, O.V.; Danielsen, H.K.; Jensen, D.J.; Klit, P. Analysis of bearing steel exposed to rolling contact fatigue. IOP Conf. Ser. Mater. Sci. Eng. 2017, 219, 012024. [Google Scholar] [CrossRef]
- Rycerz, P.; Olver, A.; Kadiric, A. Propagation of surface initiated rolling contact fatigue cracks in bearing steel. Int. J. Fatigue 2017, 97, 29–38. [Google Scholar] [CrossRef]
- Gong, Y.; Fei, J.-L.; Tang, J.; Yang, Z.-G.; Han, Y.-M.; Li, X. Failure analysis on abnormal wear of roller bearings in gearbox for wind turbine. Eng. Fail. Anal. 2017, 82, 26–38. [Google Scholar] [CrossRef]
- Mughrabi, H.; Christ, H.-J. Cyclic deformation and fatigue of selected ferritic and austenitic steels: Specific aspects. ISIJ Int. 1997, 37, 1154–1169. [Google Scholar] [CrossRef]
- Warda, B.; Chudzik, A. Fatigue life prediction of the radial roller bearing with the correction of roller generators. Int. J. Mech. Sci. 2014, 89, 299–310. [Google Scholar] [CrossRef]
- Poplawski, J.V.; Peters, S.M.; Zaretsky, E.V. Effect of roller profile on cylindrical roller bearing life prediction—Part II comparison of roller profiles. Tribol. Trans. 2001, 44, 417–427. [Google Scholar] [CrossRef]
- Oswald, F.B.; Zaretsky, E.V. Effect of Roller Geometry on Roller Bearing Load-Life Relation; NASA/TM—2015-218895; NASA: Greenbelt, MD, USA, 2015.
- Romanowicz, P.; Szybiński, B. Estimation of maximum fatigue loads and bearing life in ball bearings using multi-axial high-cycle fatigue criterion. Appl. Mech. Mater. 2014, 621, 95–100. [Google Scholar] [CrossRef]
- Tong, V.-C.; Hong, S.-W. Modeling and analysis of double-row cylindrical roller bearings. J. Mech. Sci. Technol. 2017, 31, 3379–3388. [Google Scholar] [CrossRef]
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Lv, Y.; Yuan, R.; Wang, T.; Li, H.; Song, G. Health Degradation Monitoring and Early Fault Diagnosis of a Rolling Bearing Based on CEEMDAN and Improved MMSE. Materials 2018, 11, 1009. [Google Scholar] [CrossRef]
- Gao, Z.; Lin, J.; Wang, X.; Xu, X. Bearing Fault Detection Based on Empirical Wavelet Transform and Correlated Kurtosis by Acoustic Emission. Materials 2017, 10, 571. [Google Scholar] [CrossRef]
- Romanowicz, P.; Szybiński, B. Analytical estimation of maximal fatigue loads in cylindrical roller bearings. Appl. Mech. Mater. 2014, 477–478, 54–57. [Google Scholar] [CrossRef]
- Poplawski, J.V.; Peters, S.M.; Zaretsky, E.V. Effect of roller profile on cylindrical roller bearing life prediction—Part I: Comparison of bearing life theories. Tribol. Trans. 2001, 44, 339–350. [Google Scholar] [CrossRef]
- ISO 281:2007 Rolling Bearings—Dynamic Load Ratings and Rating Life; International Organization for Standardization: Geneva, Switzerland, 2007.
- Shimizu, S.; Tosha, K.; Tsuchiya, K. New data analysis of probabilistic stress-life (P_S_N) curve and its application for structural materials. Int. J. Fatigue 2010, 32, 565–575. [Google Scholar] [CrossRef]
- Saki, T. Review and Prospects for Current Studies on Very High Cycle Fatigue of Metallic Materials for Machine Structure Use. In Proceedings of the 4th International Conference on Very High Cycle Fatigue (VHCF-4), AnnArbor, MI, USA, 19–22 August 2007; pp. 3–12. [Google Scholar]
- Romanowicz, P. Numerical assessment of fatigue load capacity of cylindrical crane wheel using multiaxial high-cycle fatigue criteria. Arch. Appl. Mech. 2017, 87, 1707–1726. [Google Scholar] [CrossRef]
- Romanowicz, P. Application of selected multiaxial high-cycle fatigue criteria to rolling contact problems. Key Eng. Mater. 2013, 542, 157–170. [Google Scholar] [CrossRef]
- Papadopoulos, I.V.; Davoli, P.; Gorla, C.; Filippini, M.; Bernasconi, A. A comparative study of multi-axial high-cycle fatigue criteria for metals. Int. J. Fatigue 1997, 19, 219–235. [Google Scholar] [CrossRef]
- Bernasconi, A.; Filippini, M.; Foletti, S.; Vaudo, D. Multiaxial fatigue of a railway steel under nonproportional loading. Int. J. Fatigue 2006, 28, 663–672. [Google Scholar] [CrossRef]
- Sackfield, A.; Hills, D.A. Some useful results in the classical Hertz contact problem. J. Strain Anal. 1983, 18, 101–105. [Google Scholar] [CrossRef]
- Radzimovsky, E.I. Stress distribution and strength condition of two rolling cylinders pressed together. Univ. Ill. Bull. 1953, 50, 1–40. [Google Scholar]
- Romanowicz, P.; Szybiński, B. Analytical and numerical assessment of fatigue properties in rolling bearings. In Proceedings of the Integrity, Reliability and Failure of Mechanical Systems (IRF’2013), Madeira, Portugal, 23–27 June 2013. [Google Scholar]
- Guo, Y.B.; Barkey, M.E. Modeling of rolling contact fatigue for hard machined components with process-induced residual stress. Int. J. Fatigue 2004, 26, 605–613. [Google Scholar] [CrossRef]
- Govindarajan, N.; Gnanamoorthy, R. Rolling/sliding contact fatigue life prediction of sintered and hardened steels. Wear 2007, 262, 70–78. [Google Scholar] [CrossRef]
- Vrbka, M.; Šamánek, O.; Šperka, P.; Návrat, T.; Křupka, I.; Hartl, M. Effect of surface texturing on rolling contact fatigue within mixed lubricated non-conformal rolling/sliding contacts. Tribol. Int. 2010, 43, 1457–1465. [Google Scholar] [CrossRef]
- Bhadeshia, H. Steels for bearings. Prog. Mater. Sci. 2011, 57, 268–435. [Google Scholar] [CrossRef]
- Walker, P.F.F. Improving the reliability of highly loaded rolling bearings: The effect of upstream processing on inclusions. Mater. Sci. Technol. 2014, 30, 385–410. [Google Scholar] [CrossRef]
- Fajdiga, G.; Glodez, S.; Kramar, J. Pitting formation due to surface and subsurface initiated fatigue crack growth in contacting mechanical elements. Wear 2007, 262, 1217–1224. [Google Scholar] [CrossRef]
- Auclair, G.; Ruby-Meyer, F.; Meilland, R.; Rocabois, P. Cleanliness assessment: A critical review and a real need to predict rolling contact fatigue behaviour. In Bearing Steels: Into the 21st Century’; Hoo, J.J.C., Green, W.B., Eds.; ASTM STP 1327; American Society for Testing and Materials: Philadelphia, PA, USA, 1998; pp. 39–54. [Google Scholar]
- Tian, C.; Liu, J.H.; Lu, H.C.; Dong, H. Estimation of maximum inclusion by statistics of extreme values method in bearing steel. J. Iron Steel Res. Int. 2017, 24, 1131–1136. [Google Scholar] [CrossRef]
- Deng, S.; Hua, L.; Han, X.; Huang, S. Investigation of rolling contact fatigue cracks in ball bearings. Int. J. Fract. 2014, 188, 71–78. [Google Scholar] [CrossRef]
- Sakai, T.; Sato, Y.; Oguma, N. Characteristic S-N properties of high-carbon-chromium-bearing steel under axial loading in long-life fatigue. Fatigue Fract. Eng. Mater. Struct. 2002, 25, 765–773. [Google Scholar] [CrossRef]
- Pandkar, A.S.; Arakere, N.; Subhash, G. Microstructure-sensitive accumulation of plastic strain due to ratcheting in bearing steels subject to rolling contact fatigue. Int. J. Fatigue 2014, 63, 191–202. [Google Scholar] [CrossRef]
- Zenner, H.; Simbürger, A.; Liu, J. On the fatigue limit of ductile metals under complex multiaxial loading. Int. J. Fatigue 2000, 22, 137–145. [Google Scholar] [CrossRef]
- Liu, J.; Zenner, H. Fatigue limit of ductile metals under multiaxial loading. Eur. Struct. Integr. Soc. 2003, 31, 147–164. [Google Scholar]
- DIN 5402-1 Rolling Bearings—Parts of Rolling Bearings—Part 1: Cylindrical Rollers; Standard by Deutsches Institut Fur Normung E.V. (German National Standard): Berlin, Germany, 2014.
- Hertz, H. On the contact of elastic solids. J. Reine Angew. Math. 1882, 92, 156–171. [Google Scholar]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Hamrock, B.J.; Anderson, W.J. Rolling-Element Bearings; NASA Reference Publication 1105; NASA: Greenbelt, MD, USA, 1983.
- Timoshenko, S.; Goodier, J.N. Theory of Elasticity, 2nd ed.; McGraw-Hill Book Co.: New York, NY, USA, 1951. [Google Scholar]
- Cooper, D.H. Tables of Hertzian Contact-Stress Coefficients; Report R-387; University of Illinois: Urbana, IL, USA, 1968. [Google Scholar]
- Shigley, J.E.; Mischke, C.R.; Brown, T.H., Jr. Standard Handbook of Machine Design, 3rd ed.; McGraw-Hill: New York, NY, USA, 2004. [Google Scholar]
- Catalogue of Rolling Bearings. Available online: www.skf.com (accessed on 10 November 2018).



| Chemical Composition (wts) [%] | C | Cr | Si | Mn | P | S |
|---|---|---|---|---|---|---|
| AISI 52100 | 0.95–1.05 | 1.30–1.65 | 0.15–0.35 | 0.25–0.45 | ≤0.027 | ≤0.025 |
| Designation and Type 1 and An and fL | Principal Dimensions, Rollers Dimensions, Principal Radii of Curvatures, Number of Rolling Elements, Catalogue Fatigue Load [55] | Calculated Maximal Fatigue Loading | Difference | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| dw/D/H mm | R11 mm | lt (Lw) mm | 2*R3 mm | Z | FuCAT kN | FuP1 kN | δ % | |||
| Roller | Ring | Roller | Ring | |||||||
| K81102TN, RT, fL = 80% | 15/28/9 | 1.75 | 1.9 (3.5) | 21.5 | 12 | 2.45 | 2.48 | 2.49 | 1.2 | 1.6 |
| 81104TN, RT, fL = 80% | 20/35/10 | 2.25 | 2.7 (4.5) | 27.87 | 13 | 4.65 | 4.9 | 4.84 | 5.4 | 4.1 |
| K81206TN, RT, fL = 80% | 30/52/16 | 3.75 | 5.1 (7.5) | 41.5 | 12 | 13.4 | 14.54 | 14.28 | 8.5 | 6.6 |
| 81106TN, RT, fL = 80% | 30/47/11 | 2.5 | 3.1 (5) | 38.82 | 17 | 7.65 | 7.82 | 7.65 | 2.2 | 0 |
| K81110TN, RT, fL = 90% | 50/70/14 | 3 | 4.5 (6.0) | 59.5 | 24 | 16.6 | 18.19 | 17.52 | 9.6 | 5.5 |
| K81113TN, RT, fL = 90% | 65/90/18 | 3.75 | 5.85 (7.5) | 78 | 29 | 32.5 | 35.53 | 33.21 | 9.3 | 2.2 |
| K89413TN, RT, fL = 100% | 65/140/15 | 7.5 | 28.4 (30) | 103 | 15 | 143 | 162.5 | 144.5 | 13.6 | 1.0 |
| K81224TN, RT, fL = 100% | 120/170/39 | 7.5 | 13.4 (15) | 145 | 24 | 104 | 114 | 109.1 | 9.6 | 4.9 |
| 81240M, RT, fL = 90% | 200/280/62 | 13 | 21.6 (26) | 246.5 | 22 | 255 | 262.2 | 255.2 | 2.8 | 0.1 |
| 891/710M, RT, fL = 80% | 710/850/85 | 18 | 26.4 (36) | 780 | 56 | 900 | 918.4 | 868 | 2.04 | −3.6 |
| NU2304ECP, RR, An = 4.08, fL = 80% | 20/52/21 | 4.5 | 9.9 (14) | 27.5 | 10 | 4.8 | 6.3 (N1 = 3.1) | (a) 4.9 (N1 = 10) (b) 5.69 (N1 = 5) | 31.3 | (a) 2.1 (b) 18.5 |
| NU410, RR, An = 4.08, fL = 100% | 50/130/31 | 10 | 18.8 (20) | 70.8 | 10 | 16.6 | - | 17.94 | - | 8.1 |
| NJ220ECP, RR, An = 4.08, fL = 100% | 100/180/34 | 11 | 22.2 (24) | 119 | 17 | 36.5 | - | 38.54 | - | 5.6 |
| NJ340ECML, RR, An = 4.08, fL = 90% | 200/420/80 | 28 | 47.4 (56) | 258 | 15 | 150 | - | 157.7 | - | 5.1 |
| NUP19/600ECMA/HA1, RR, An = 4.08, fL = 80% | 600/800/90 | 27 | 40.2 (54) | 649 | 35 | 275 | - | 280.5 | - | 2 |
| Designation and Type 2 and An and f | Principal Dimensions, Rolling Element Dimensions, Principal Radii of Curvatures, Number of Rolling Elements, Catalogue Fatigue Load [55] | Calculated Maximal Fatigue Loading | Difference | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| dw/D/H mm | R11 = R12 mm | R21 mm | 2*R3 mm | Z | FuCAT kN | FuP1 kN | δ % | |||
| r.e. 2 | Ring | r.e. 2 | Ring | |||||||
| 53204, BT, f = 0.57 | 20/40/14.7 | 3.57 | −4.07 | 32 | 12 | 1.4 | 1.6 | 1.45 | 14.3 | 3.6 |
| 53307, BT, f = 0.55 | 35/68/25.6 | 6 | −6.6 | 52 | 10 | 3.55 | 3.73 | 3.60 | 5.1 | 1.4 |
| 53310, BT, f = 0.55 | 50/95/34.3 | 7.94 | −8.734 | 72 | 11 | 6.3 | 6.54 | 6.22 | 3.81 | −1.3 |
| 53316, BT, f = 0.54 | 80/140/47.6 | 11 | −11.88 | 110 | 12 | 13.7 | 13.8 | 13.1 | 0.73 | −4.4 |
| 53228, BT, f = 0.54 | 140/200/48.6 | 11 | −11.88 | 170 | 19 | 17.6 | 19.0 | 18.0 | 8.0 | 2.3 |
| 6304, BR, An = 4.37, f = 0.54 | 20/52/15 | 4.765 | −5.146 | 26.43 | 7 | 0.34 | - | 0.33 | - | −2.0 |
| 6310, BR, An = 4.37, f = 0.53 | 50/110/27 | 9.53 | −10.102 | 60.95 | 8 | 1.6 | - | 1.48 | - | −7.5 |
| 6320, BR, An = 4.37, f = 0.53 | 100/215/47 | 18.26 | −19.356 | 121.0 | 8 | 4.75 | - | 4.49 | - | −5.5 |
| 6040, BR, An = 4.37, f = 0.53 | 200/3310/51 | 16.67 | −17.67 | 221.7 | 14 | 6.4 | - | 6.7 | - | 4.7 |
| 6080M, BR, An = 4.37, f = 0.54 | 400/600/90 | 30.16 | −32.573 | 439.7 | 15 | 16.3 | - | 16.1 | - | −1.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romanowicz, P.J.; Szybiński, B. Fatigue Life Assessment of Rolling Bearings Made from AISI 52100 Bearing Steel. Materials 2019, 12, 371. https://doi.org/10.3390/ma12030371
Romanowicz PJ, Szybiński B. Fatigue Life Assessment of Rolling Bearings Made from AISI 52100 Bearing Steel. Materials. 2019; 12(3):371. https://doi.org/10.3390/ma12030371
Chicago/Turabian StyleRomanowicz, Paweł J., and Bogdan Szybiński. 2019. "Fatigue Life Assessment of Rolling Bearings Made from AISI 52100 Bearing Steel" Materials 12, no. 3: 371. https://doi.org/10.3390/ma12030371
APA StyleRomanowicz, P. J., & Szybiński, B. (2019). Fatigue Life Assessment of Rolling Bearings Made from AISI 52100 Bearing Steel. Materials, 12(3), 371. https://doi.org/10.3390/ma12030371





