Study of Strain-Hardening Behaviour of Fibre-Reinforced Alkali-Activated Fly Ash Cement
Abstract
:1. Introduction
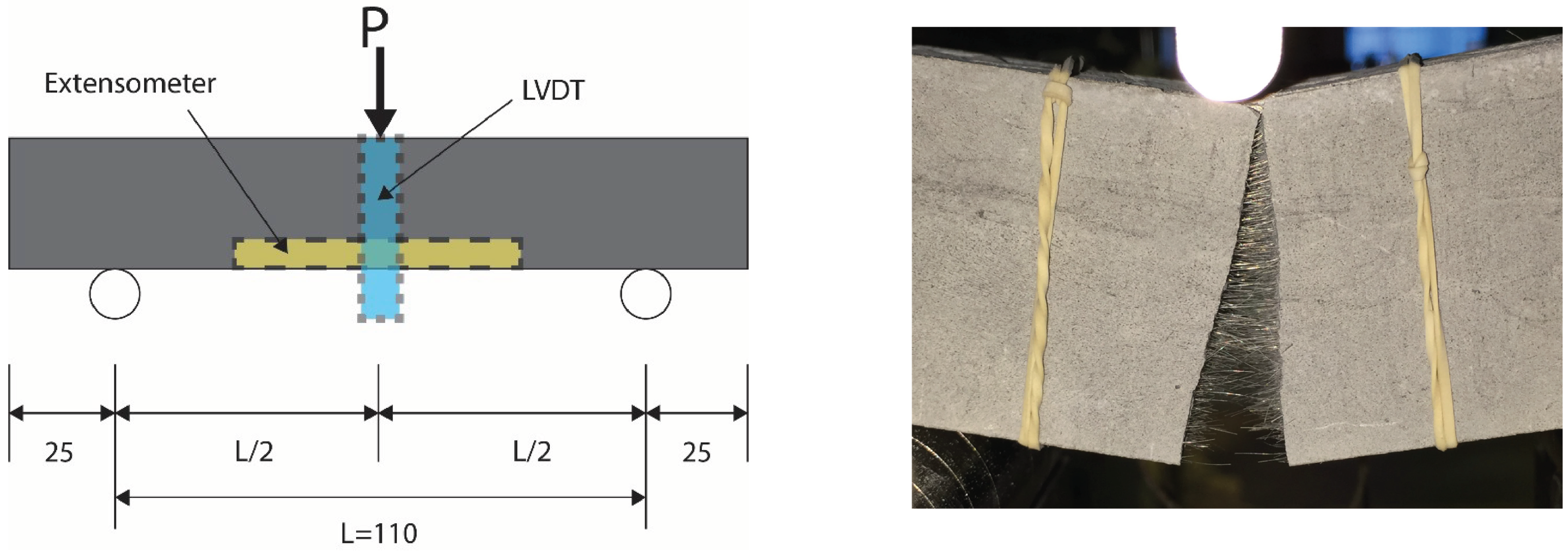
2. Materials and Methods
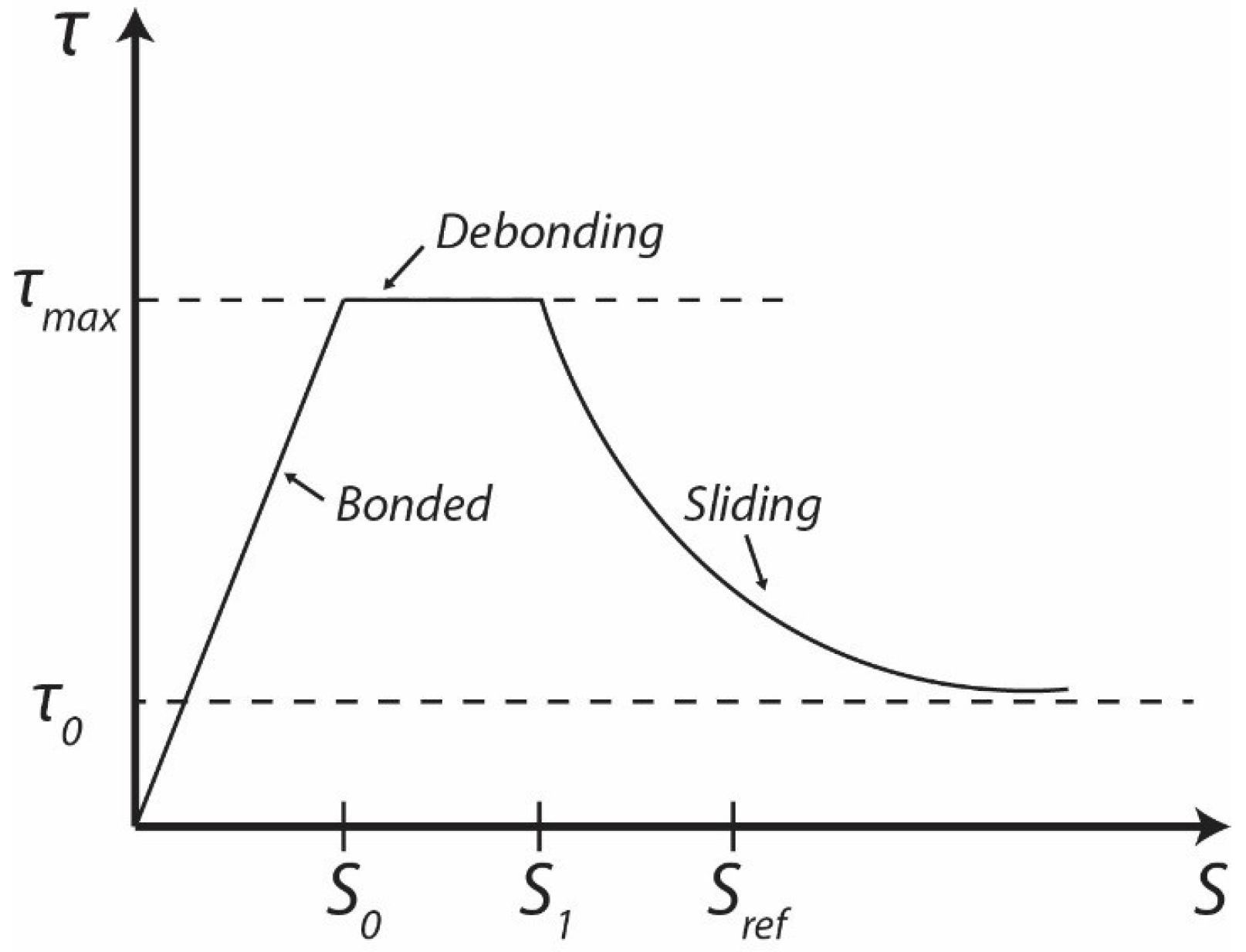
- The first stage, : the fibre and matrix is bonded until reaching the maximum interfacial bond strength ;
- The second stage, : a crack propagation could occur along the interface between the fibre and matrix which leads to complete debonding;
- The third stage, : fibre is pulled out from the matrix and starts to slip;
- Thus, the maximum pull out force is the most important parameter of HPFRCC, which can present maximum interfacial bond strength.
3. Results and Discussion
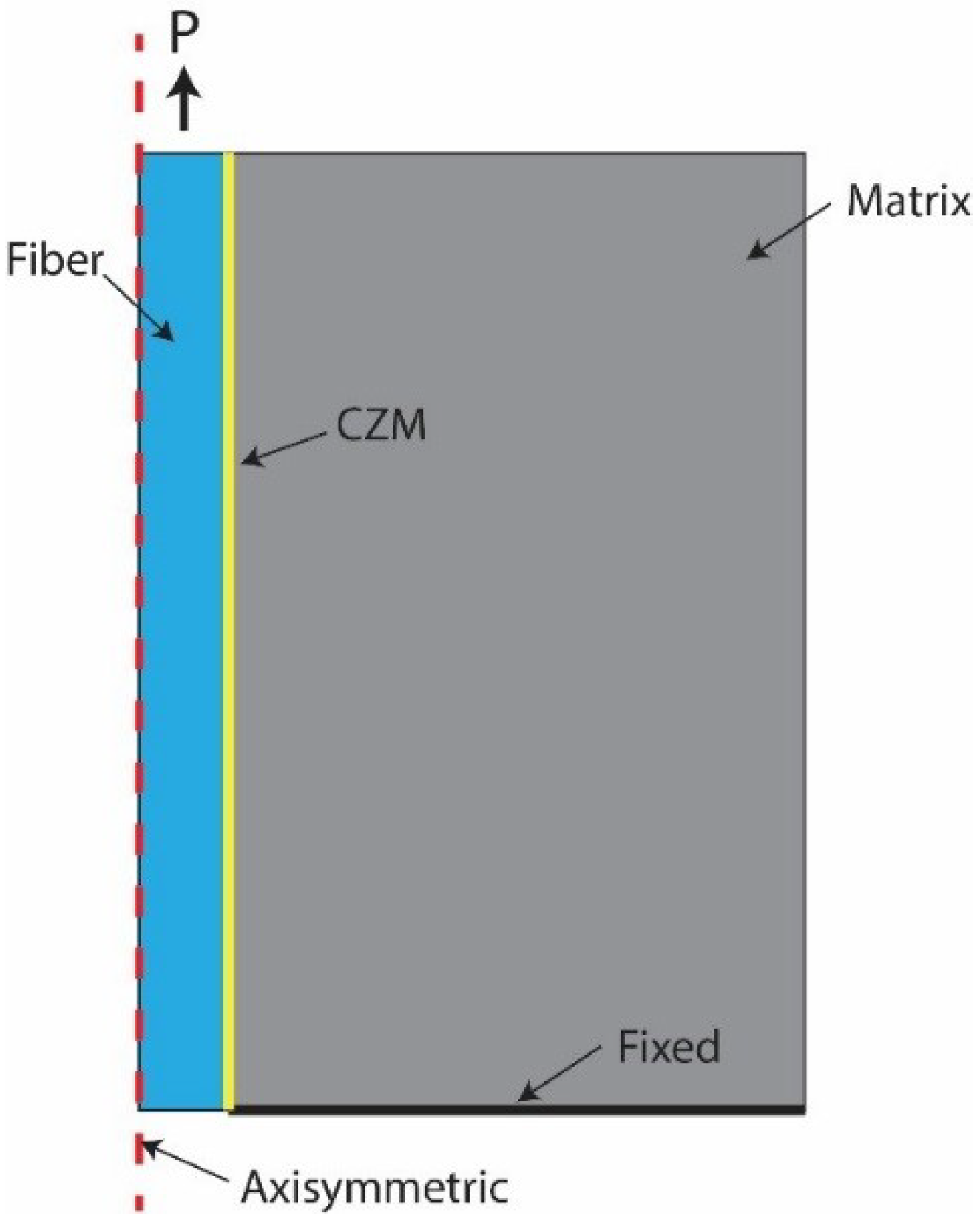
3.1. Single Fibre Pull Out
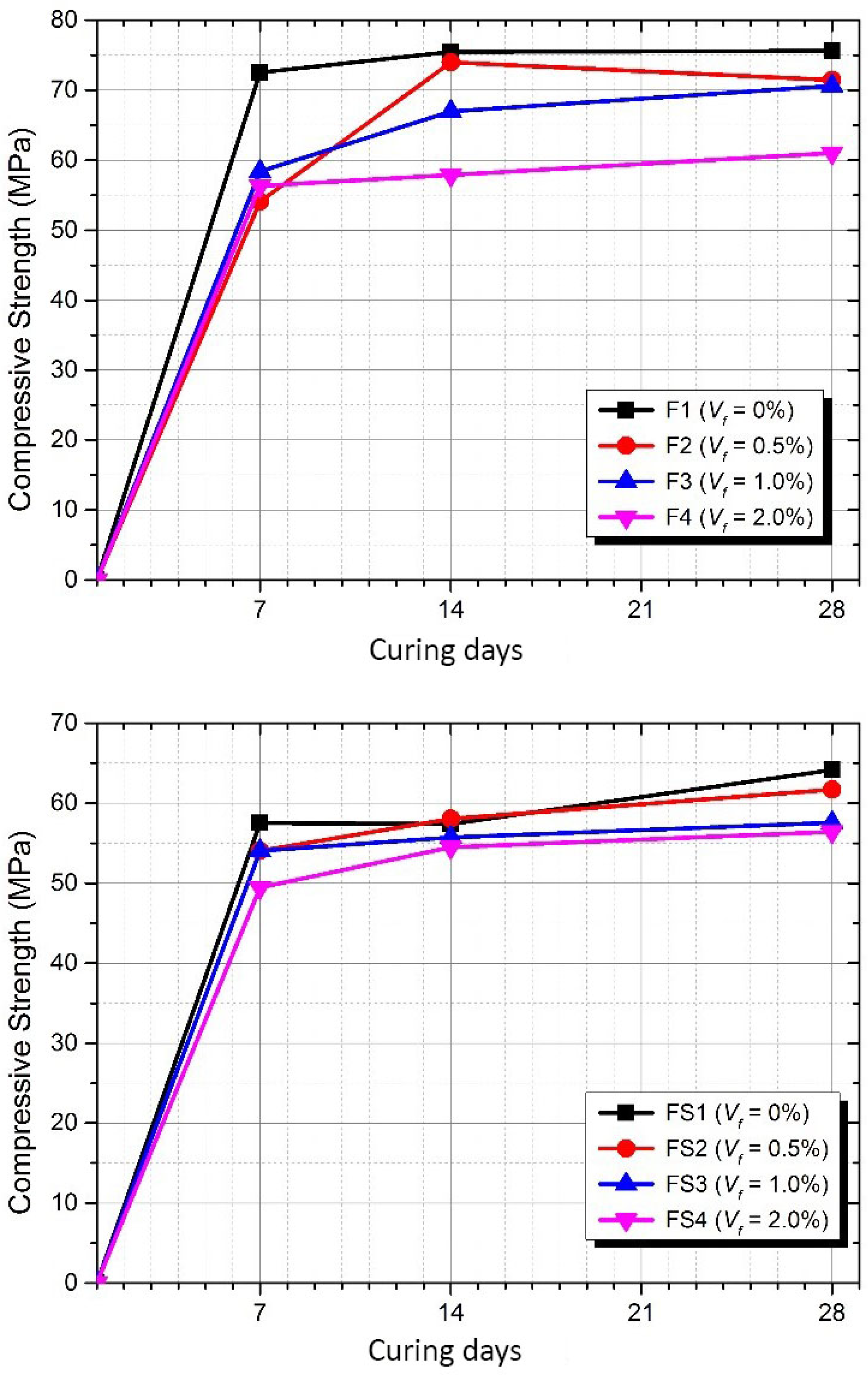
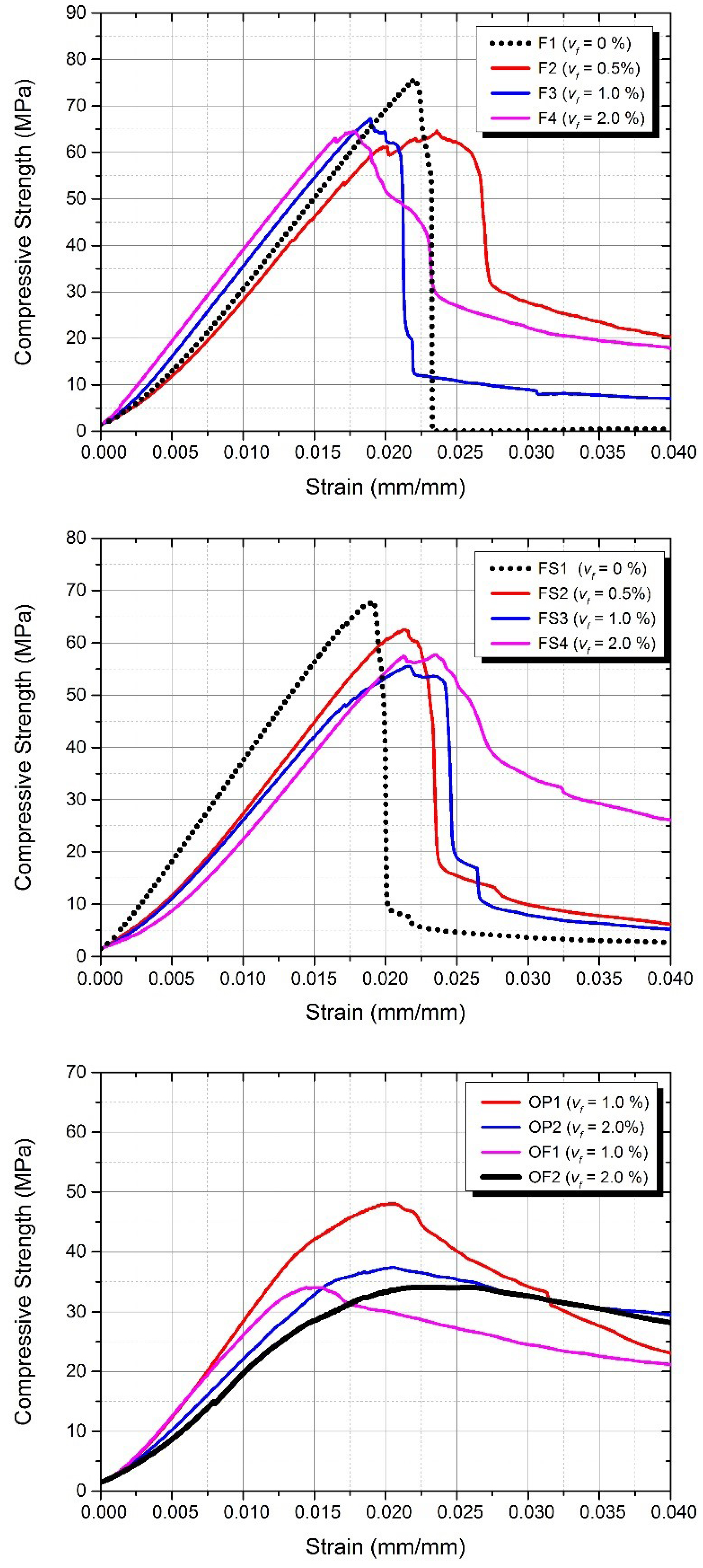
3.2. Compressive Strength
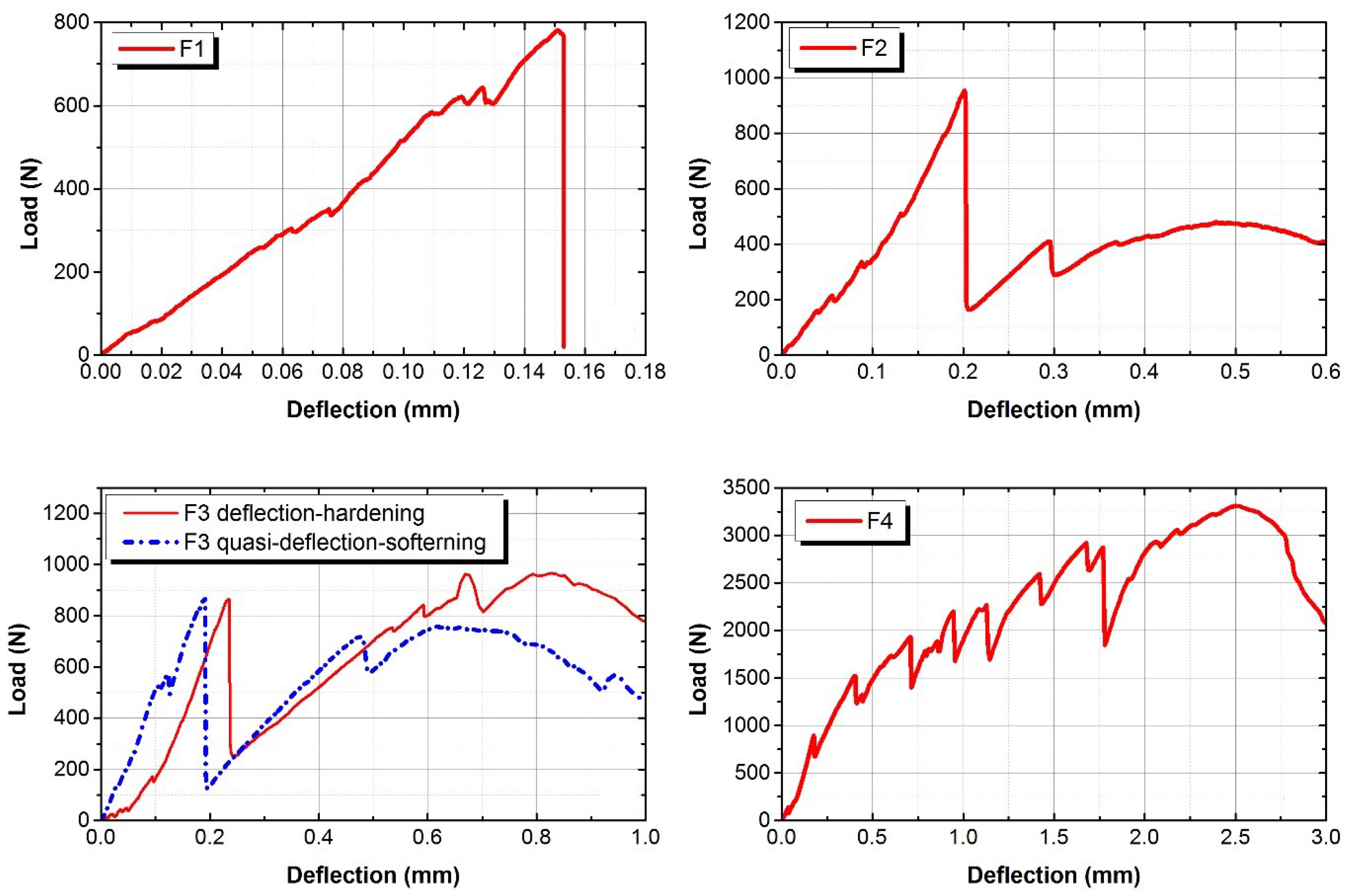
3.3. Flexural Performance
4. Conclusions
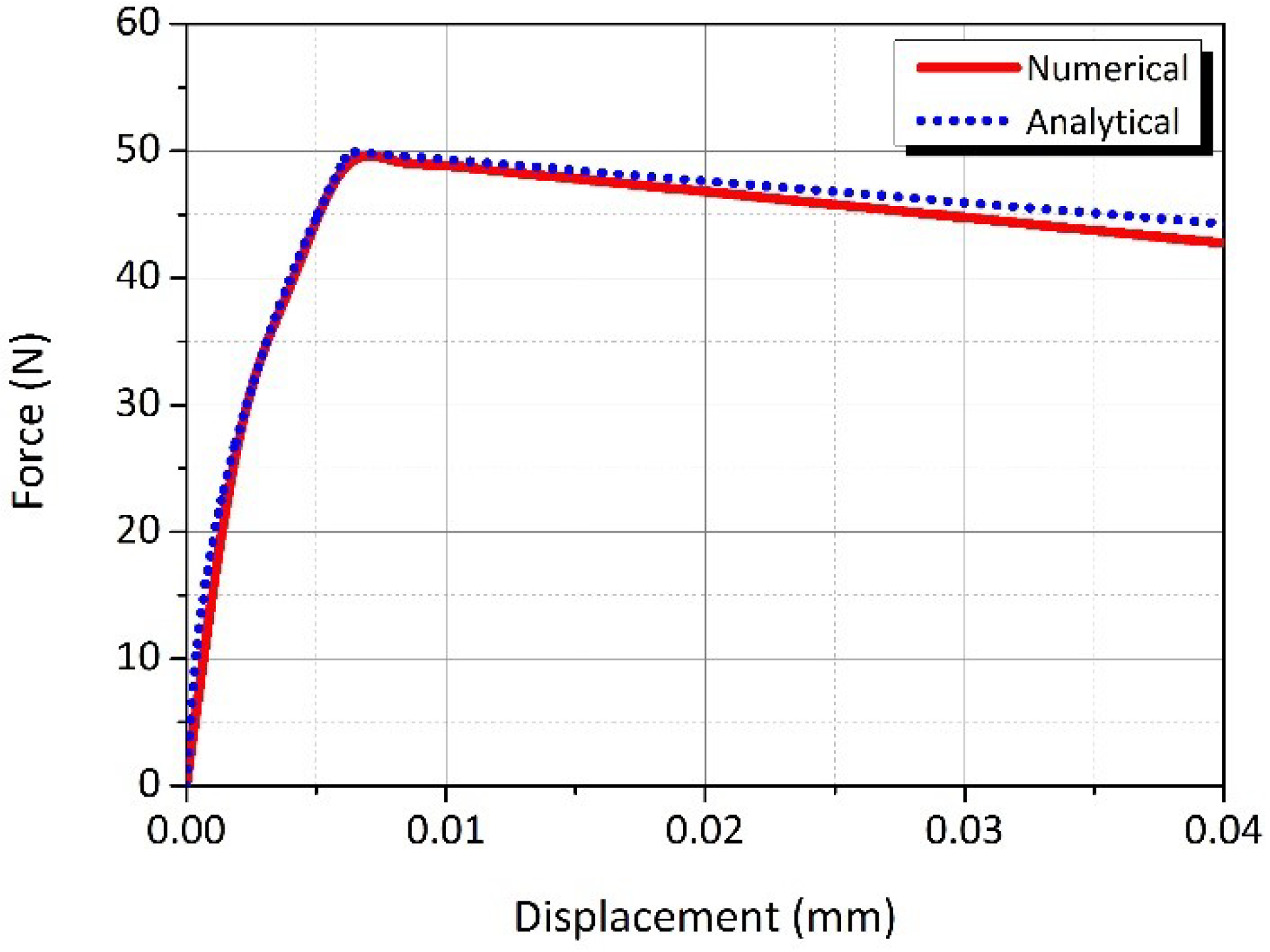
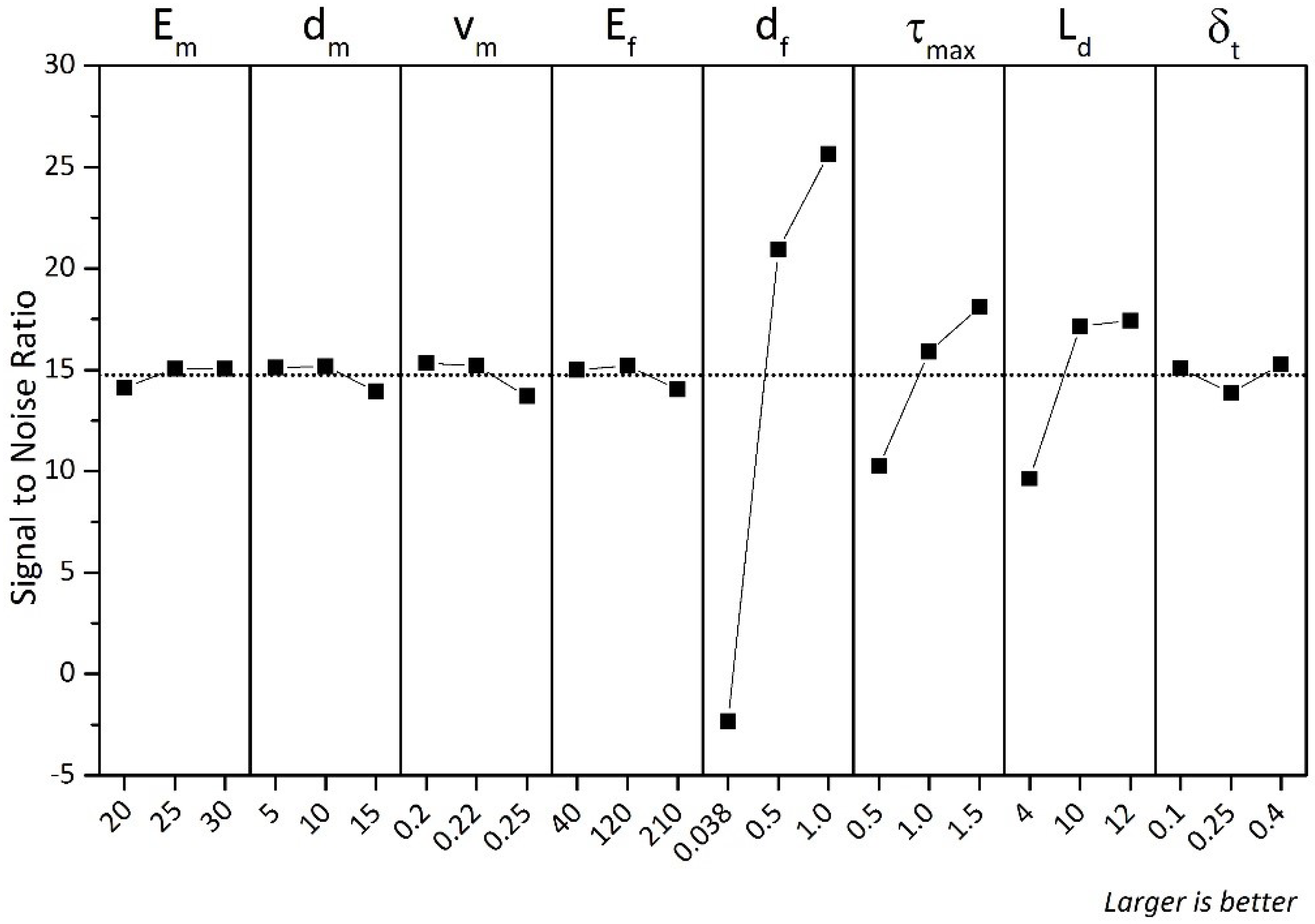
- The interfacial bond strength between the fibre and the AAFA matrix was determined to be in a range of 0.8 to 1.0 MPa. A numerical analysis coupled with a statistical analysis tool shows that an increase in the fibre diameter and embedded length would increase the interfacial bond strength.
- The strain corresponding to the compressive strength is not significantly affected by the fibre volume fraction ratio. However, while achieving the strain-hardening behaviour of the AAFA composites, the compressive strength decreased. In addition, using silica fume as a fine material in AAFA composite is not suitable as it decreases the flexural strength and strain capacity of the composite.
- The critical energy release rate of AAFA matrix determined from the indentation fracture toughness was approximately 0.01 kJ/m. The results of the flexural behaviour showed the relationship between the strain-hardening behaviour of AAFA composite and the indentation .
- For a mix design of AAFA matrix, it is recommended that should be less than 0.01 kJ/m. It is theoretically impossible to achieve the strain-hardening behaviour when is more than 0.015 kJ/m.
Author Contributions
Funding
Conflicts of Interest
References
- Shi, C.; Roy, D.; Krivenko, P. Alkali-Activated Cements and Concretes; CRC Press/Taylor and Francis: London, UK; New York, NY, USA, 2006. [Google Scholar]
- Shi, C.; Jiménez, A.F.; Palomo, A. New cements for the 21st century: The pursuit of an alternative to Portland cement. Cem. Concr. Res. 2011, 41, 750–763. [Google Scholar] [CrossRef]
- Davidovits, J. Geopolymer Chemistry and Applications; Geopolymer Institute: Saint-Quentin, France, 2008. [Google Scholar]
- Kumar, S.; Kumar, R.; Alex, T.; Bandopadhyay, A.; Mehrotra, S. Effect of mechanically activated fly ash on the properties of geopolymer cement. In Proceedings of the 4th World Congress on Geopolymer, Saint-Quentin, France, 29 June–1 July 2005; pp. 113–116. [Google Scholar]
- Naaman, A.; Reinhardt, H. High performance fiber reinforced cement composites HPFRCC-4: International RILEM Workshop. Mater. Struct. 2003, 36, 710–712. [Google Scholar] [CrossRef]
- Li, V.C. Engineered cementitious composites-tailored composites through micromechanical modeling. J. Adv. Concr. Technol. 1998. [Google Scholar] [CrossRef] [Green Version]
- Li, V.C.; Leung, C.K. Steady-state and multiple cracking of short random fiber composites. J. Eng. Mech. 1992, 118, 2246–2264. [Google Scholar] [CrossRef] [Green Version]
- Berry, E.; Hemmings, R.; Cornelius, B. Mechanisms of hydration reactions in high volume fly ash pastes and mortars. Cem. Concr. Compos. 1990, 12, 253–261. [Google Scholar] [CrossRef]
- Lee, B.Y.; Kim, J.K.; Kim, Y.Y. Prediction of ECC tensile stress-strain curves based on modified fiber bridging relations considering fiber distribution characteristics. Comput. Concr. 2010, 7, 455–468. [Google Scholar] [CrossRef] [Green Version]
- Rigaud, S.; Chanvillard, G.; Chen, J. Characterization of bending and tensile behavior of ultra-high performance concrete containing glass fibers. In High Performance Fiber Reinforced Cement Composites 6; Springer: Dordrecht, The Netherlands, 2012; pp. 373–380. [Google Scholar]
- Hardjito, D.; Rangan, B.V. Development and Properties of Low-Calcium Fly Ash-Based Geopolymer Concrete; Curtin Research Publications: Perth, Australia, 2005. [Google Scholar]
- Rangan, B.V. Fly Ash-Based Geopolymer Concrete; Curtin Research Publications: Perth, Australia, 2008. [Google Scholar]
- Chen, X.; Beyerlein, I.J.; Brinson, L.C. Curved-fiber pull-out model for nanocomposites. Part 1: Bonded stage formulation. Mech. Mater. 2009, 41, 279–292. [Google Scholar] [CrossRef]
- Chen, X.; Beyerlein, I.J.; Brinson, L.C. Curved-fiber pull-out model for nanocomposites. Part 2: Interfacial debonding and sliding. Mech. Mater. 2009, 41, 293–307. [Google Scholar] [CrossRef]
- Herrera-Franco, P.; Drzal, L. Comparison of methods for the measurement of fibre/matrix adhesion in composites. Composites 1992, 23, 2–27. [Google Scholar] [CrossRef]
- Zhan, Y.; Meschke, G. Analytical model for the pullout behavior of straight and hooked-end steel fibers. J. Eng. Mech. 2014, 140, 04014091. [Google Scholar] [CrossRef]
- ANSYS Academic Research Mechanical Release 19.2; ANSYS: Canonsburg, PA, USA, 2018.
- Kullaa, J. Dimensional analysis of bond modulus in fiber pullout. J. Struct. Eng. 1996, 122, 783–787. [Google Scholar] [CrossRef]
- Naaman, A.E.; Namur, G.G.; Alwan, J.M.; Najm, H.S. Fiber pullout and bond slip. I: Analytical study. J. Struct. Eng. 1991, 117, 2769–2790. [Google Scholar] [CrossRef]
- Budiansky, B.; Cui, Y.L. On the tensile strength of a fiberreinforced ceramic composite containing a crack-like flaw. J. Mech. Phys. Solids 1994, 42, 1–19. [Google Scholar] [CrossRef]
- Kanda, T.; Lin, Z.; Li, V.C. Tensile stress-strain modeling of pseudostrain hardening cementitious composites. J. Mater. Civ. Eng. 2000, 12, 147–156. [Google Scholar] [CrossRef] [Green Version]
- Li, V.C.; Mishra, D.K.; Wu, H.C. Matrix design for pseudo-strain-hardening fibre reinforced cementitious composites. Mater. Struct. 1995, 28, 586–595. [Google Scholar] [CrossRef]
- Li, V.C.; Wang, Y.; Backer, S. Effect of inclining angle, bundling and surface treatment on synthetic fibre pull-out from a cement matrix. Composites 1990, 21, 132–140. [Google Scholar] [CrossRef]
- Lee, H.; Vimonsatit, V.; Chindaprasirt, P. Mechanical and micromechanical properties of alkali activated fly-ash cement based on nano-indentation. Constr. Build. Mater. 2016, 107, 95–102. [Google Scholar] [CrossRef]
- Active Standard. Standard test method for flexural performance of fiber-reinforced concrete (using beam with third-point loading). ASTM-C1609 2012. [Google Scholar] [CrossRef]
- Li, V.C.; Wu, H.C.; Maalej, M.; Mishra, D.K.; Hashida, T. Tensile behavior of cement-based composites with random discontinuous steel fibers. J. Am. Ceram. Soc. 1996, 79, 74–78. [Google Scholar] [CrossRef] [Green Version]
- Soranakom, C.; Mobasher, B. Correlation of tensile and flexural responses of strain softening and strain hardening cement composites. Cem. Concr. Compos. 2008, 30, 465–477. [Google Scholar] [CrossRef]
- Ward, R.; Li, V.C. Dependence of flexural behaviour of fibre reinforced mortar on material fracture resistance and beam size. Constr. Build. Mater. 1991, 5, 151–161. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.J.; Park, S.H.; Ryu, G.S.; Koh, K.T. Comparative flexural behavior of hybrid ultra high performance fiber reinforced concrete with different macro fibers. Constr. Build. Mater. 2011, 25, 4144–4155. [Google Scholar] [CrossRef]
- Lee, B.Y.; Kim, J.K.; Kim, J.S.; Kim, Y.Y. Quantitative evaluation technique of Polyvinyl Alcohol (PVA) fiber dispersion in engineered cementitious composites. Cem. Concr. Compos. 2009, 31, 408–417. [Google Scholar] [CrossRef]
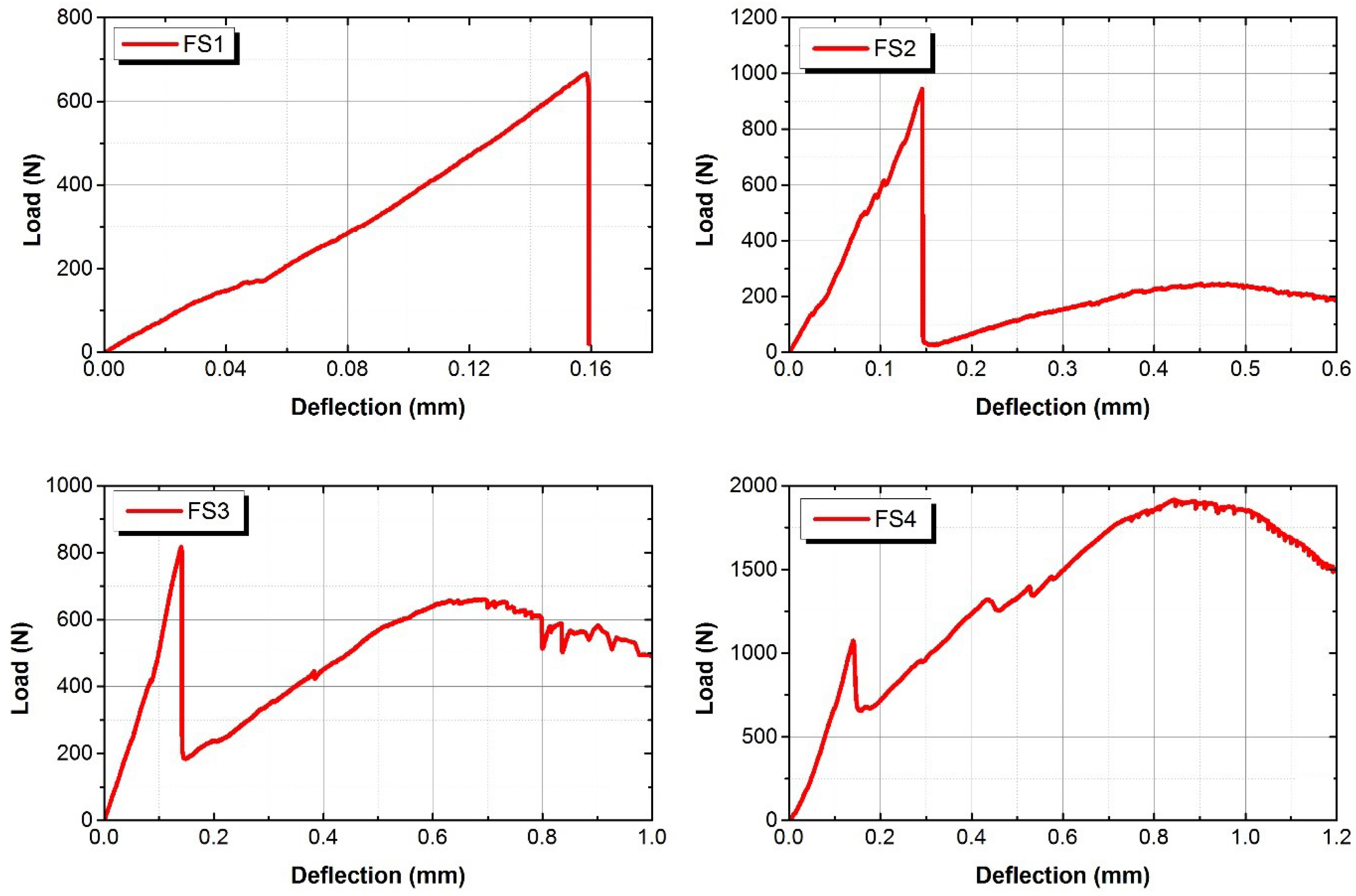
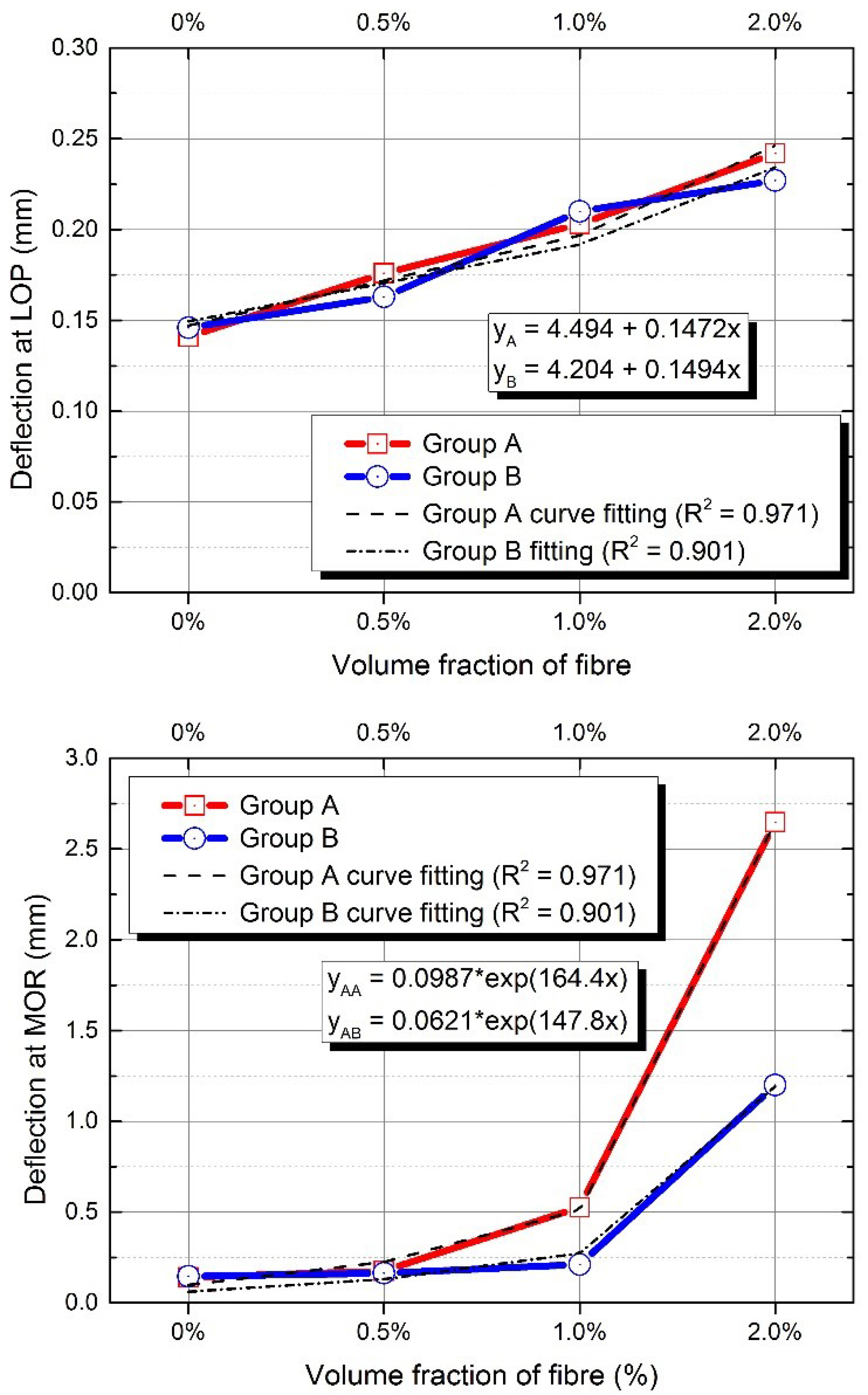
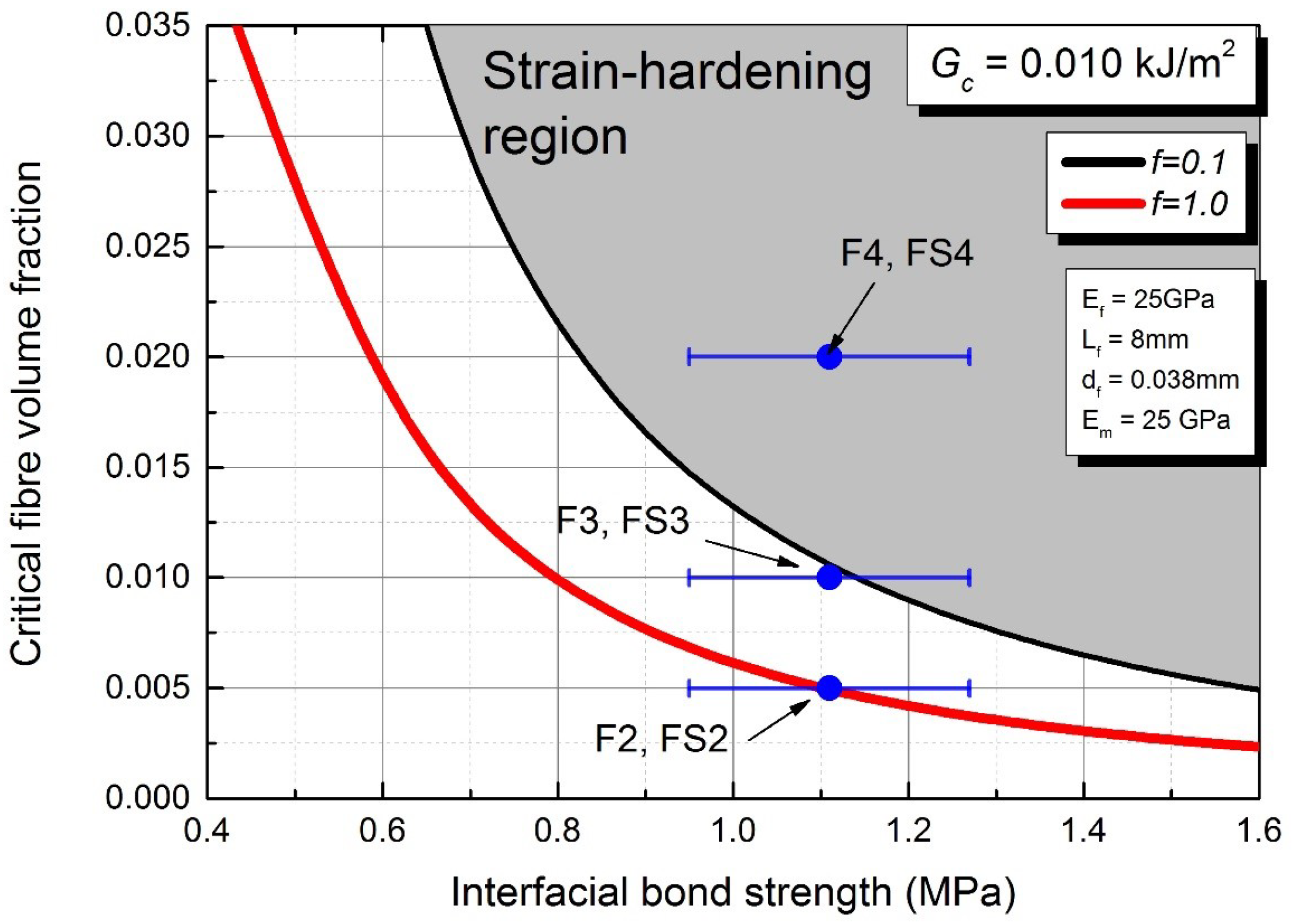
| SiO | AlO | CaO | FeO | KO |
|---|---|---|---|---|
| 65.9 | 24.0 | 1.59 | 2.87 | 1.44 |
| Group | Index | Fly Ash | Silica Fume | PVA Fiber * |
|---|---|---|---|---|
| A | F1 | 1 | - | - |
| F2 | 1 | - | 0.5% | |
| F3 | 1 | - | 1.0% | |
| F4 | 1 | - | 2.0% | |
| B | FS1 | 1 | 0.2% | - |
| FS2 | 1 | 0.2% | 0.5% | |
| FS3 | 1 | 0.2% | 1.0% | |
| FS4 | 1 | 0.2% | 2.0% |
| Parameter | Level 1 | Level 2 | Level 3 |
|---|---|---|---|
| Elastic modulus of matrix, (GPa) | 20 | 25 | 30 |
| Diameter of matrix, (mm) | 5 | 10 | 15 |
| Poisson’s ratio of matrix | 0.2 | 0.22 | 0.25 |
| Elastic modulus of fibre (GPa) | 40 | 120 | 210 |
| Diameter of fibre, (mm) | 0.038 | 0.5 | 1 |
| Fibre embedded length, (mm) | 4 | 10 | 12 |
| Maximum tangential traction, (MPa) | 0.5 | 1 | 1.5 |
| Complete tangential displacement, (mm) | 0.1 | 0.25 | 0.4 |
| No. | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 |
| 3 | 1 | 1 | 1 | 1 | 3 | 3 | 3 | 3 |
| 4 | 1 | 2 | 2 | 2 | 1 | 1 | 1 | 2 |
| 5 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 3 |
| 6 | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 1 |
| 7 | 1 | 3 | 3 | 3 | 1 | 1 | 1 | 3 |
| 8 | 1 | 3 | 3 | 3 | 2 | 2 | 2 | 1 |
| 9 | 1 | 3 | 3 | 3 | 3 | 3 | 3 | 2 |
| 10 | 2 | 1 | 2 | 3 | 1 | 2 | 3 | 1 |
| 11 | 2 | 1 | 2 | 3 | 2 | 3 | 1 | 2 |
| 12 | 2 | 1 | 2 | 3 | 3 | 1 | 2 | 3 |
| 13 | 2 | 2 | 2 | 3 | 1 | 1 | 3 | 2 |
| 14 | 2 | 2 | 3 | 1 | 2 | 3 | 1 | 3 |
| 15 | 2 | 2 | 3 | 1 | 3 | 1 | 2 | 1 |
| 16 | 2 | 3 | 1 | 2 | 1 | 2 | 3 | 3 |
| 17 | 2 | 3 | 1 | 2 | 1 | 2 | 3 | 3 |
| 18 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 2 |
| 19 | 3 | 1 | 3 | 2 | 1 | 3 | 2 | 1 |
| 20 | 3 | 1 | 3 | 2 | 1 | 3 | 3 | 2 |
| 21 | 3 | 1 | 3 | 2 | 3 | 2 | 1 | 3 |
| 22 | 3 | 2 | 1 | 3 | 1 | 3 | 2 | 2 |
| 23 | 3 | 2 | 1 | 3 | 2 | 1 | 3 | 3 |
| 24 | 3 | 2 | 1 | 3 | 3 | 2 | 1 | 1 |
| 25 | 3 | 3 | 2 | 1 | 1 | 3 | 2 | 3 |
| 26 | 3 | 3 | 2 | 1 | 2 | 1 | 3 | 1 |
| 27 | 3 | 3 | 2 | 1 | 3 | 2 | 1 | 2 |
| No. | (N) | No. | (N) | No. | (N) |
|---|---|---|---|---|---|
| 1 | 0.23 | 10 | 1.27 | 19 | 1.43 |
| 2 | 15.51 | 11 | 9.42 | 20 | 9.41 |
| 3 | 56.09 | 12 | 15.71 | 21 | 12.57 |
| 4 | 0.24 | 13 | 1.09 | 22 | 1.67 |
| 5 | 15.67 | 14 | 9.41 | 23 | 9.41 |
| 6 | 55.95 | 15 | 15.59 | 24 | 12.56 |
| 7 | 0.24 | 16 | 1.36 | 25 | 1.51 |
| 8 | 15.61 | 17 | 9.40 | 26 | 9.19 |
| 9 | 14.61 | 18 | 15.69 | 27 | 12.56 |
| Source | DF | SS | MS | Contribution % |
|---|---|---|---|---|
| 2 | 737.6 | 368.8 | 14.48 | |
| 2 | 127.2 | 63.6 | 2.50 | |
| 2 | 129.3 | 64.7 | 2.54 | |
| 2 | 124.0 | 61.9 | 2.43 | |
| 2 | 2276.5 | 1138.3 | 44.69 | |
| 2 | 454.4 | 227.2 | 8.92 | |
| 2 | 482.5 | 241.2 | 9.47 | |
| 2 | 126.7 | 63.4 | 2.49 | |
| Error | 10 | 653.8 | 63.6 | 12.48 |
| Matrix | FEM | Experimental | Ratio |
|---|---|---|---|
| OPC | 0.482 | 0.480 | 1.001 |
| AAFA | 0.530 | 0.530 | 1.000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Vimonsatit, V.; Mendis, P.; Nassif, A. Study of Strain-Hardening Behaviour of Fibre-Reinforced Alkali-Activated Fly Ash Cement. Materials 2019, 12, 4015. https://doi.org/10.3390/ma12234015
Lee H, Vimonsatit V, Mendis P, Nassif A. Study of Strain-Hardening Behaviour of Fibre-Reinforced Alkali-Activated Fly Ash Cement. Materials. 2019; 12(23):4015. https://doi.org/10.3390/ma12234015
Chicago/Turabian StyleLee, Hyuk, Vanissorn Vimonsatit, Priyan Mendis, and Ayman Nassif. 2019. "Study of Strain-Hardening Behaviour of Fibre-Reinforced Alkali-Activated Fly Ash Cement" Materials 12, no. 23: 4015. https://doi.org/10.3390/ma12234015
APA StyleLee, H., Vimonsatit, V., Mendis, P., & Nassif, A. (2019). Study of Strain-Hardening Behaviour of Fibre-Reinforced Alkali-Activated Fly Ash Cement. Materials, 12(23), 4015. https://doi.org/10.3390/ma12234015






