Author Contributions
Conceptualization, B.-f.W., H.-r.F. and D.-h.X.; methodology, D.-h.X., Z.-m.Z. and B.-f.W.; software, B.-f.W. and Z.-m.Z.; validation, B.-f.W. and Z.-m.Z.; formal analysis, Z.-m.Z.; investigation, B.-f.W., Z.-l.S. and Z.-m.Z.; resources, Z.-m.Z.; data curation, Y.-w.H. and Z.-m.Z.; writing—original draft preparation, Z.-m.Z.; writing—review and editing, D.-h.X. and Z.-m.Z.; visualization, B.-f.W. and Z.-m.Z.; supervision, D.-h.X. and B.Z.; project administration, D.-h.X. and B.Z.; funding acquisition, D.-h.X.
Figure 1.
Schematic diagram of the horn.
Figure 1.
Schematic diagram of the horn.
Figure 2.
(a) Relationship between and ; (b) Relationship between and .
Figure 2.
(a) Relationship between and ; (b) Relationship between and .
Figure 3.
Tensile specimen of the SiCp/Al composite.
Figure 3.
Tensile specimen of the SiCp/Al composite.
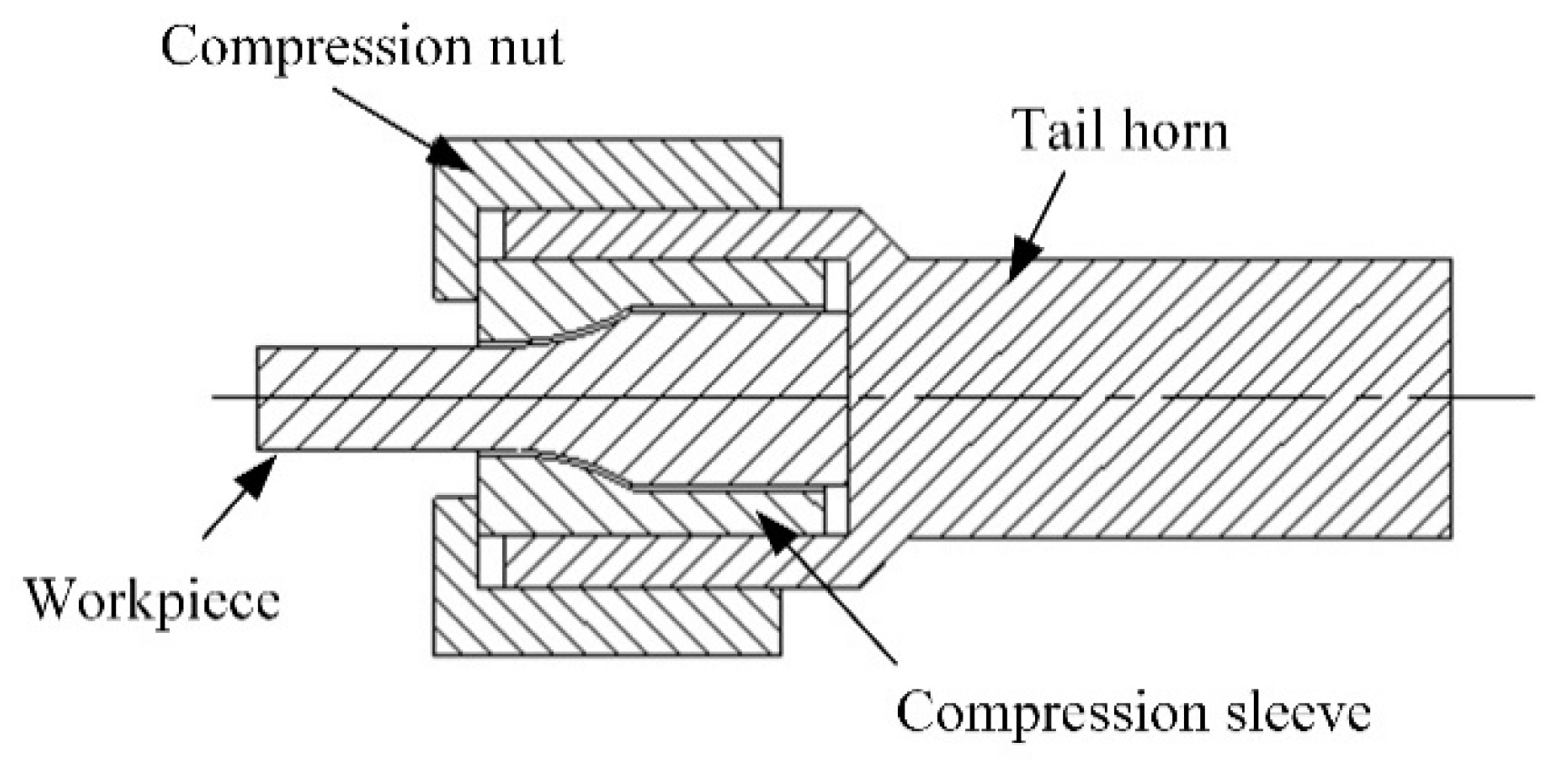
Figure 4.
Connecting structure diagram of the sample and tail horn.
Figure 4.
Connecting structure diagram of the sample and tail horn.
Figure 5.
Simulation analysis of the ultrasonic vibration tensile resonance system (a) 20 KHz; (b) 28 KHz.
Figure 5.
Simulation analysis of the ultrasonic vibration tensile resonance system (a) 20 KHz; (b) 28 KHz.
Figure 6.
The observation of the surface morphology of the SiCp/Al composite; (a) Scanning electron microscopy overall surface topography; (b) Sic particle size.
Figure 6.
The observation of the surface morphology of the SiCp/Al composite; (a) Scanning electron microscopy overall surface topography; (b) Sic particle size.
Figure 7.
The energy spectrum analysis of the SiCp/Al composites; (a) Energy spectrum analysis block diagram; (b) SiCp/Al chemical compositions.
Figure 7.
The energy spectrum analysis of the SiCp/Al composites; (a) Energy spectrum analysis block diagram; (b) SiCp/Al chemical compositions.
Figure 8.
The two-dimensional axisymmetric model and meshing.
Figure 8.
The two-dimensional axisymmetric model and meshing.
Figure 9.
The conventional tensile stage simulation cloud.
Figure 9.
The conventional tensile stage simulation cloud.
Figure 10.
The ultrasonic vibration stage stress cloud.
Figure 10.
The ultrasonic vibration stage stress cloud.
Figure 11.
The simulation stress-strain curves under different amplitudes of the ultrasonic frequency 20 kHz: (a) Amplitude 4 μm; (b) Amplitude 5.2 μm; (c) Amplitude 6 μm; and (d) Amplitude 7.3 μm.
Figure 11.
The simulation stress-strain curves under different amplitudes of the ultrasonic frequency 20 kHz: (a) Amplitude 4 μm; (b) Amplitude 5.2 μm; (c) Amplitude 6 μm; and (d) Amplitude 7.3 μm.
Figure 12.
The simulation stress-strain curves under different amplitudes of the ultrasonic frequency 28 kHz, (a) Amplitude 3 μm; (b) Amplitude 4.8 μm; (c) Amplitude 6.3 μm; and (d) Amplitude 7.8 μm.
Figure 12.
The simulation stress-strain curves under different amplitudes of the ultrasonic frequency 28 kHz, (a) Amplitude 3 μm; (b) Amplitude 4.8 μm; (c) Amplitude 6.3 μm; and (d) Amplitude 7.8 μm.
Figure 13.
Schematic of the ultrasonic vibration tensile device.
Figure 13.
Schematic of the ultrasonic vibration tensile device.
Figure 14.
The ultrasonic tensile resonance system.
Figure 14.
The ultrasonic tensile resonance system.
Figure 15.
The experimental and finite element simulation stress-strain curve during conventional tensile strength.
Figure 15.
The experimental and finite element simulation stress-strain curve during conventional tensile strength.
Figure 16.
The magnitude of the stress reduction under different amplitudes of ultrasonic vibration: (a) 20 kHz, and (b) 28 KHz.
Figure 16.
The magnitude of the stress reduction under different amplitudes of ultrasonic vibration: (a) 20 kHz, and (b) 28 KHz.
Figure 17.
The experimental stress-strain curve under different amplitude conditions: (a) 20 kHz, and (b) 28 kHz.
Figure 17.
The experimental stress-strain curve under different amplitude conditions: (a) 20 kHz, and (b) 28 kHz.
Figure 18.
A comparison of the experimental and simulated values of the stress reduction.
Figure 18.
A comparison of the experimental and simulated values of the stress reduction.
Figure 19.
The effect of the tensile rate on the magnitude of the stress reduction.
Figure 19.
The effect of the tensile rate on the magnitude of the stress reduction.
Table 1.
Material-related parameters.
Table 1.
Material-related parameters.
| Material | Density
| Elastic Modulus
| Sound Speed
| Poisson’s Ratio
|
|---|
| 45 | 7850 | 20,920 | 5170 | 0.3 |
| SiCp/Al | 3040 | 258,000 | 9212 | 0.3 |
Table 2.
1 stage horn parameters.
Table 2.
1 stage horn parameters.
| Sample Frequency | | | | | |
|---|
| f = 20 kHZ | 52 | 24 | 41 | 98 | 3.225 |
| f = 28 kHZ | 38 | 24 | 31 | 65 | 2.03 |
Table 3.
2 stage horn parameters.
Table 3.
2 stage horn parameters.
| Sample Frequency | | | | | |
|---|
| f = 20 kHZ | 24 | 16 | 64.5 | 64.5 | 2.25 |
| f = 28 kHZ | 24 | 16 | 46 | 46 | 2.25 |
Table 4.
Sample size.
| Sample Frequency | | | | | |
|---|
| f = 20 kHZ | 3 | 8 | 21.6 | 15 | 73.2 |
| f = 28 kHZ | 3 | 8 | 21.6 | 8 | 59.2 |
Table 5.
The chemical composition of the 7075Al.
Table 5.
The chemical composition of the 7075Al.
| Element | Si | Mn | Ti | Cr | Cu | Mg | Zn | Fe | Al |
|---|
| Quality score % | 0.40 | 0.30 | 0.20 | 0.21 | 1.5 | 2.3 | 5.6 | 0.50 | margin |
Table 6.
The chemical composition of the SiCp/Al composite.
Table 6.
The chemical composition of the SiCp/Al composite.
| Element | Mg | O | Si | Al | Other |
|---|
| Quality score % | 6.18 | 6.72 | 46.47 | 31.17 | margin |
Table 7.
The ultrasonic vibration tensile simulation experimental scheme.
Table 7.
The ultrasonic vibration tensile simulation experimental scheme.
| Factor | Level |
|---|
| 1 | 2 | 3 | 4 |
|---|
| f (kHz) | 20 | 24 | 28 | 32 |
| A (μm) | 4 | 5 | 6 | 7 |
| v (mm/min) | 1 | 10 | 100 | 1000 |
Table 8.
The tensile experimental design.
Table 8.
The tensile experimental design.
| Numbering | f (kHz) | A (μm) | v (mm/min) | Vibration Application Method |
|---|
| P1 | 0 | 0 | 1 | No vibration |
| U1 | 20 | 4 | 1 | 3.3–5 kN |
| U2 | 20 | 5.2 | 1 | 3.3–5 kN |
| U3 | 20 | 6 | 1 | 3.3–5 kN |
| U4 | 20 | 7.3 | 1 | 3.3–5 kN |
| U5 | 20 | 6 | 1 | Full vibration |
| U6 | 28 | 3 | 1 | 3.3–5 kN |
| U7 | 28 | 4.8 | 1 | 3.3–5 kN |
| U8 | 28 | 6.3 | 1 | 3.3–5 kN |
| U9 | 28 | 7.8 | 1 | 3.3–5 kN |
| U10 | 28 | 6.3 | 1 | Full vibration |
Table 9.
The orthogonal simulation results of the stress reduction amplitude.
Table 9.
The orthogonal simulation results of the stress reduction amplitude.
| Numbering | Frequency f (kHz) | Amplitude A (μm) | Tensile Rate
v (mm/min) | Stress Reduction
Δσ (MPa) |
|---|
| 1 | 20 | 4 | 1 | 30.75 |
| 2 | 20 | 5 | 10 | 36.51 |
| 3 | 20 | 6 | 100 | 42.33 |
| 4 | 20 | 7 | 1000 | 44.24 |
| 5 | 24 | 4 | 10 | 32.08 |
| 6 | 24 | 5 | 1 | 40.73 |
| 7 | 24 | 6 | 1000 | 39.27 |
| 8 | 24 | 7 | 100 | 53.19 |
| 9 | 28 | 4 | 100 | 31.63 |
| 10 | 28 | 5 | 1000 | 35.51 |
| 11 | 28 | 6 | 1 | 50.9 |
| 12 | 28 | 7 | 10 | 59.14 |
| 13 | 32 | 4 | 1000 | 25.53 |
| 14 | 32 | 5 | 100 | 38.37 |
| 15 | 32 | 6 | 10 | 52.17 |
| 16 | 32 | 7 | 1 | 61.13 |
Table 10.
The intuitive analysis table of the stress reduction.
Table 10.
The intuitive analysis table of the stress reduction.
| Numbering | Frequency f (kHz) | Amplitude A (μm) | tensile Rate v (mm/min) |
|---|
| k1 | 38.46 | 30 | 45.88 |
| k2 | 41.32 | 37.78 | 44.98 |
| k3 | 44.3 | 46.17 | 41.38 |
| k4 | 44.3 | 54.25 | 36.14 |
| Range | 5.84 | 24.25 | 9.74 |