ANN-Based Fatigue Strength of Concrete under Compression
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Gathering
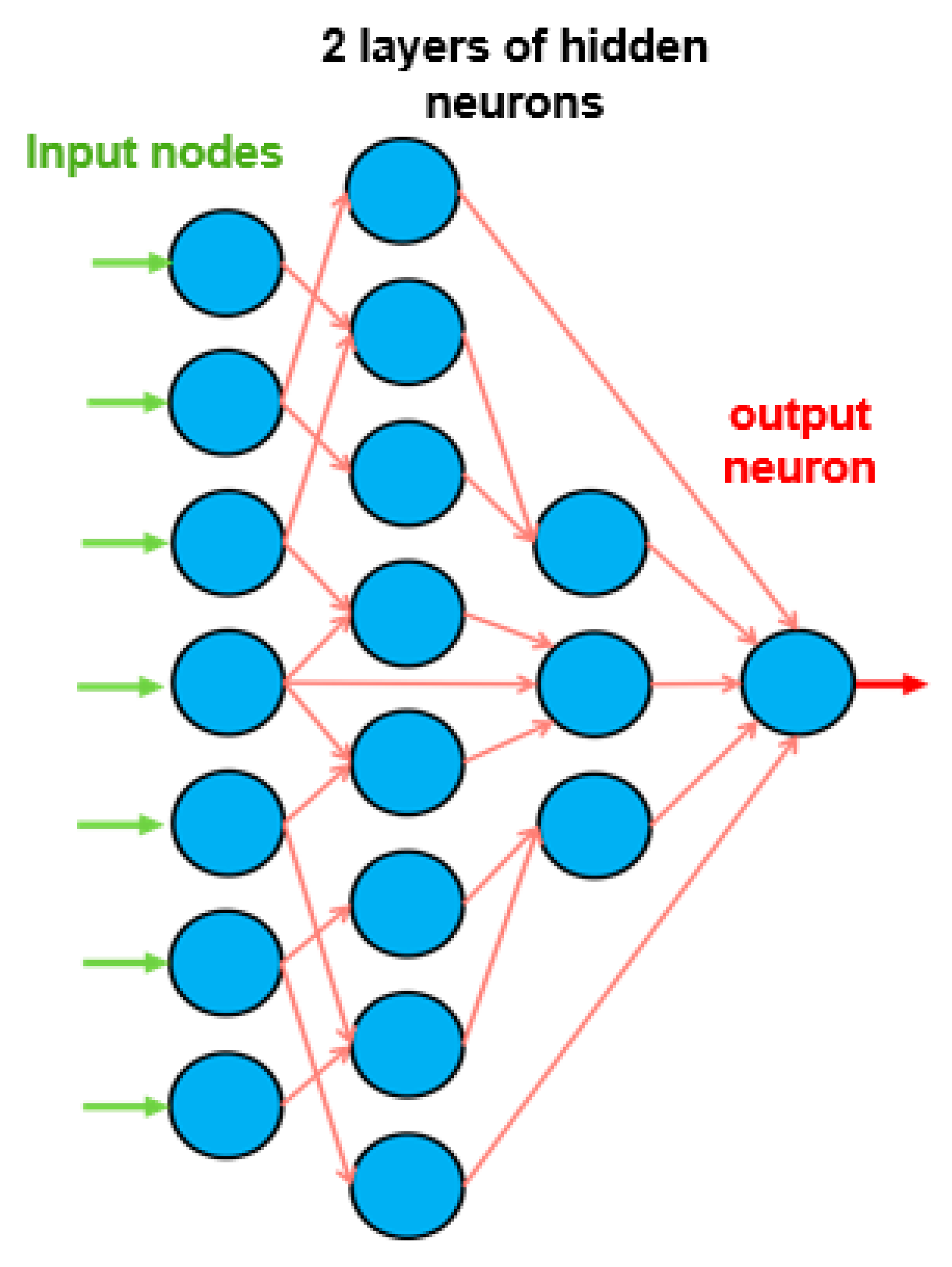
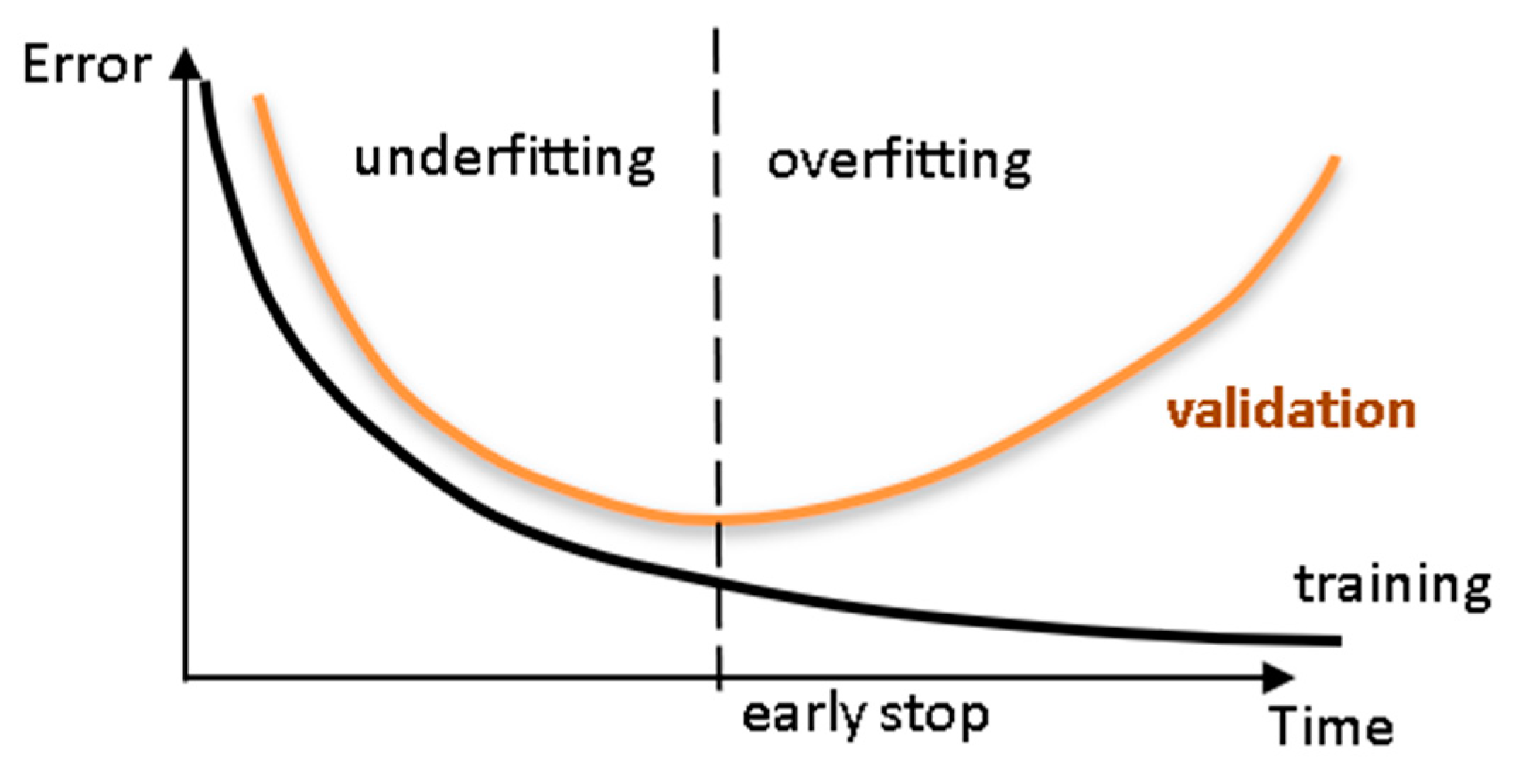
2.2. Characteristics of Artificial Neural Networks in This Study
3. Results
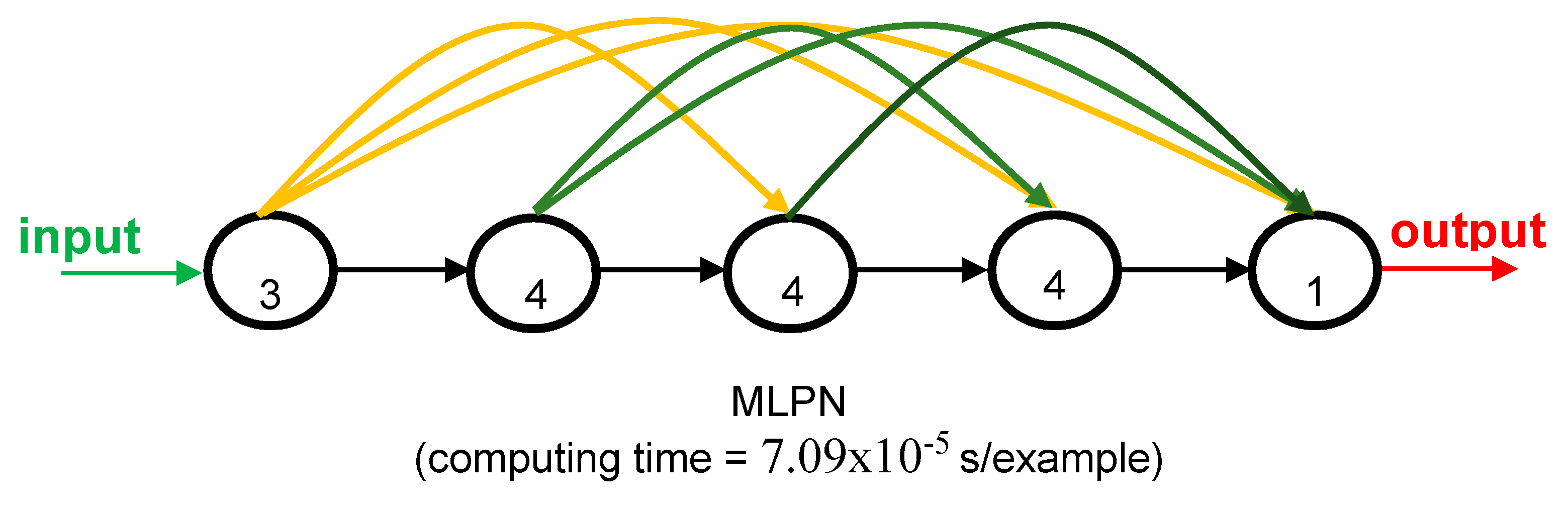
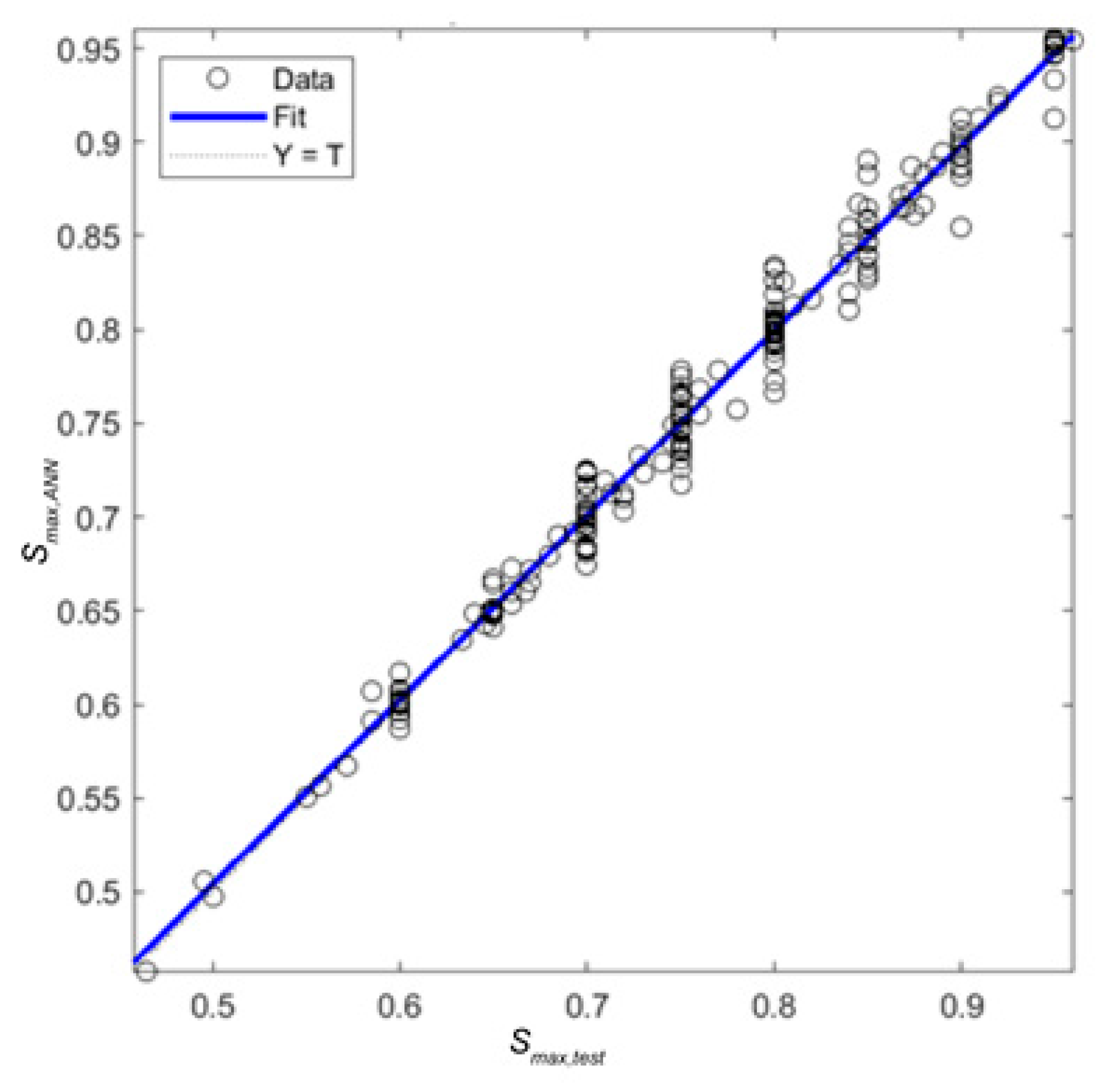
3.1. Proposed ANN-Based Model
3.2. Performance Indicators of Results
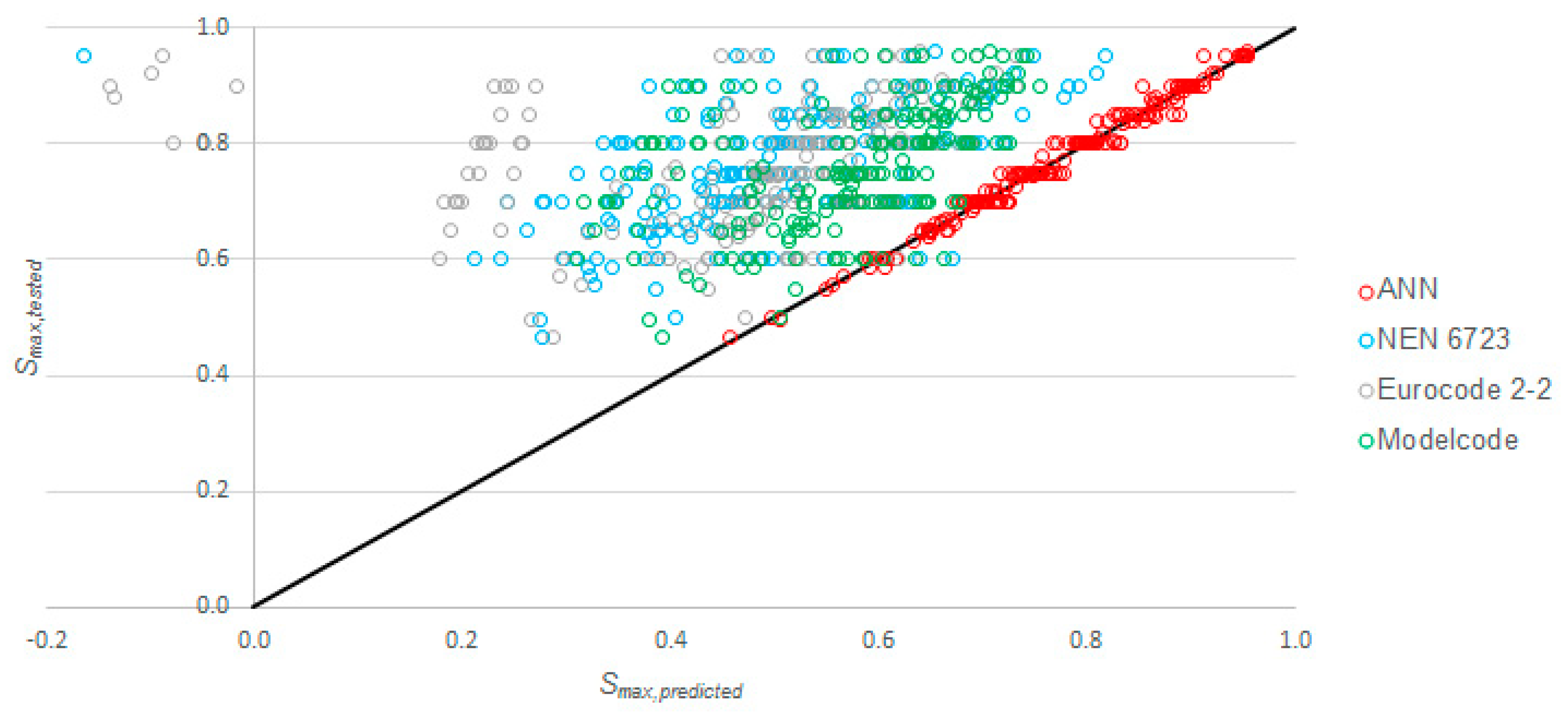
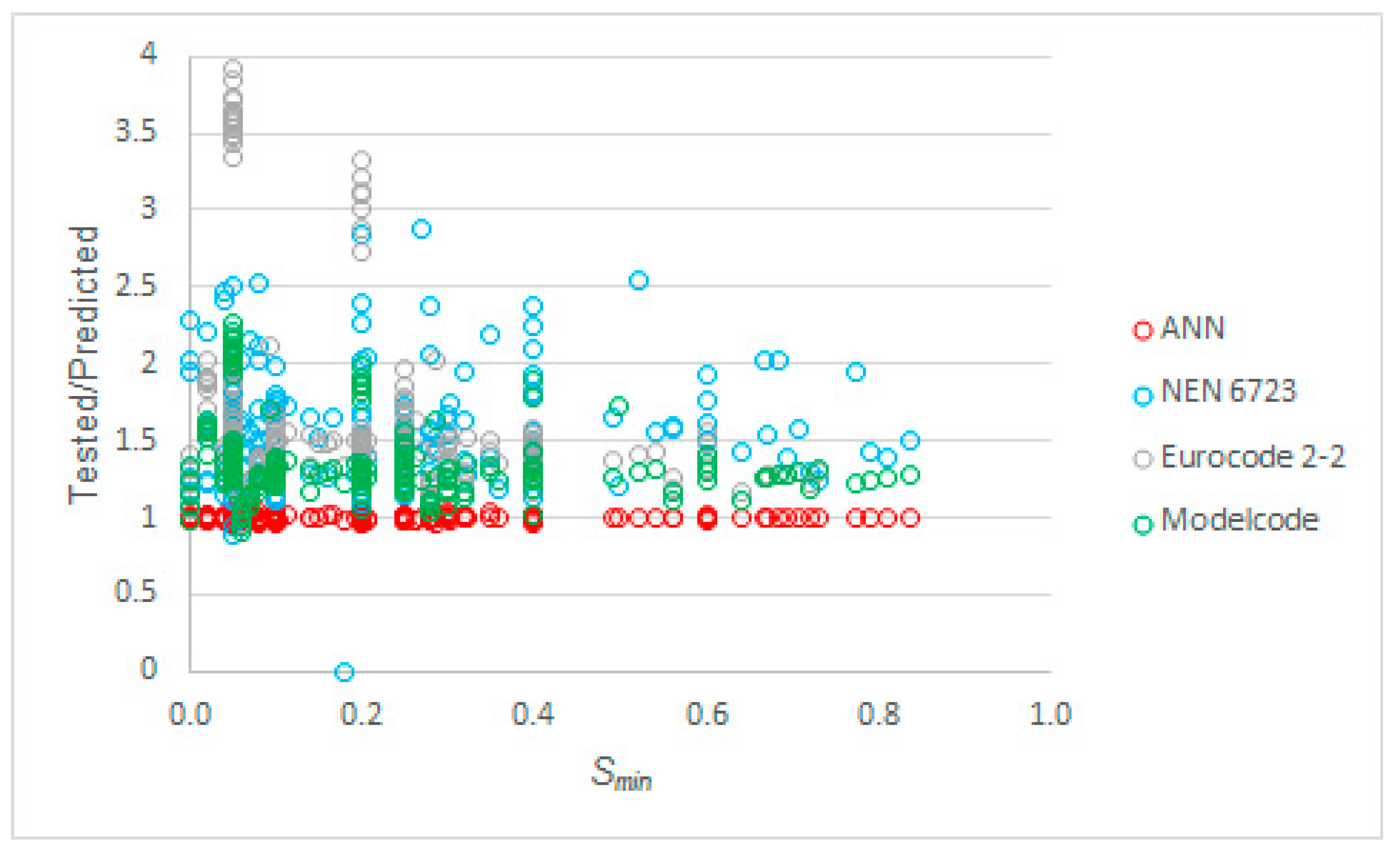
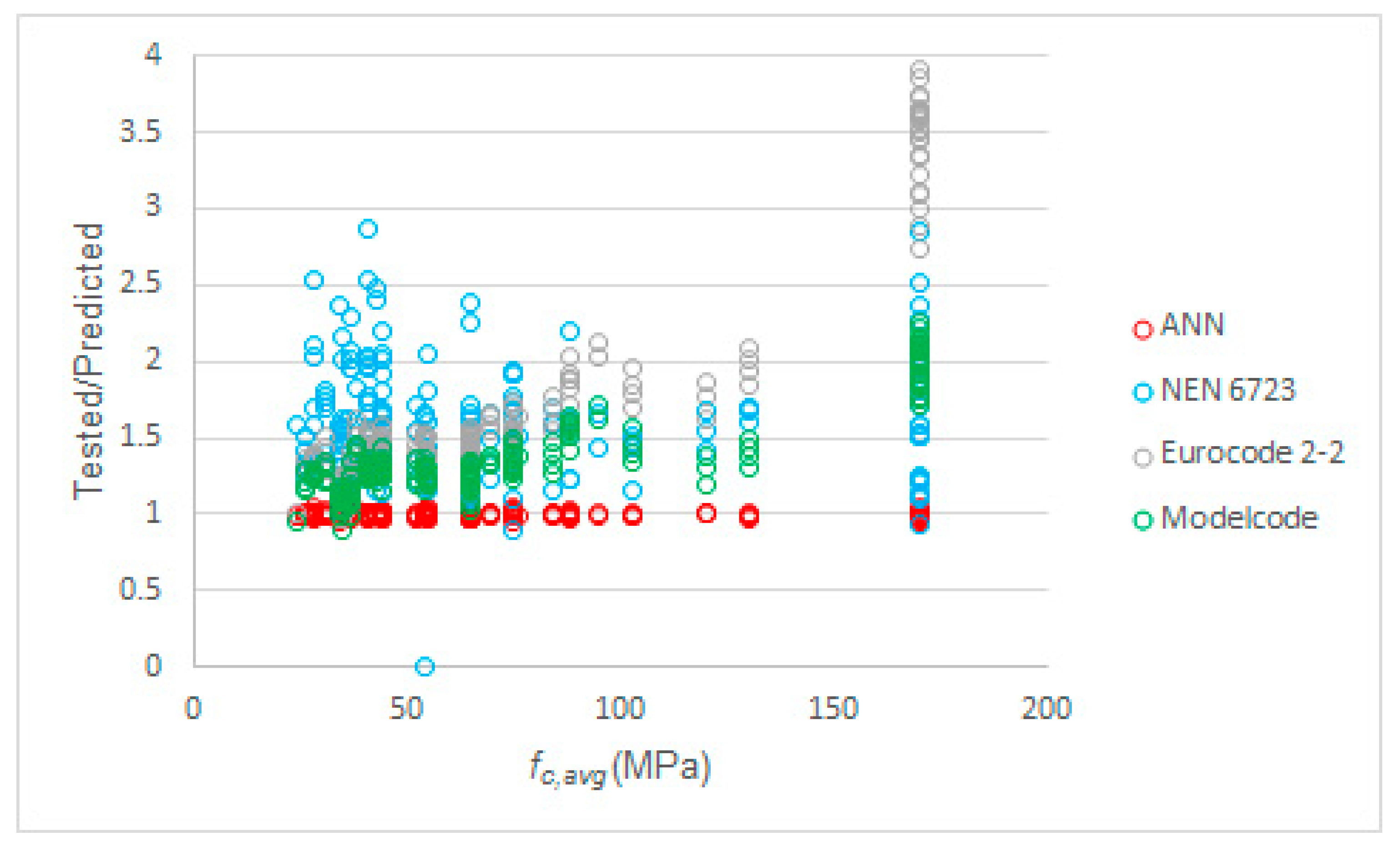
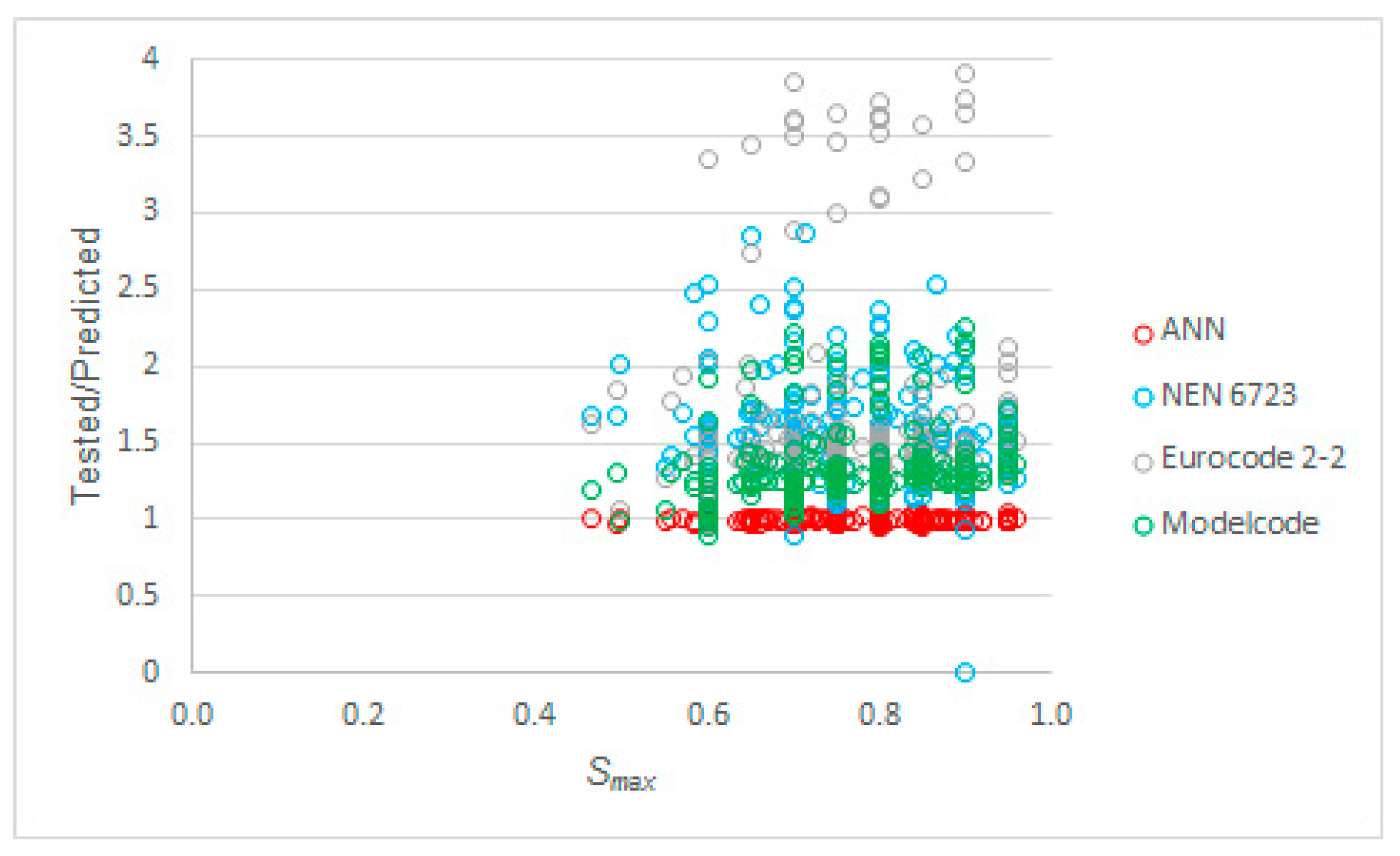
3.3. Comparison between ANN-Based and Existing Methods
4. Discussion
5. Summary and Conclusions
- We derived an input dataset with 203 datapoints obtained from experiments reported in the literature. Each datapoint was unique. Where necessary, the geometric average of number of cycles to failure of repeat tests was determined;
- We selected three input parameters for the input dataset (concrete compressive strength, lower bound of the stress ratio, and number of cycles to failure) and one output parameter (upper bound of the stress ratio) in line with the parameters used in the currently used code expressions;
- We used different methods for 14 features of the ANN models to find the most suitable features. We looked at 219 combinations of features and selected the neural net with the best performance.
- Of the studied methods in the current codes, we found that the expression from the fib model code performed best when compared to the experimental results gathered in the dataset. The average value of tested to predicted upper bound of the stress ratio was 1.37 with a coefficient of variation of 20.5%;
- We can see that our proposed model outperformed the code equations for the prediction of the upper bound of the stress ratio, since the average value of tested to predicted upper bound of the stress ratio was 1.00 with a coefficient of variation of 1.7%;
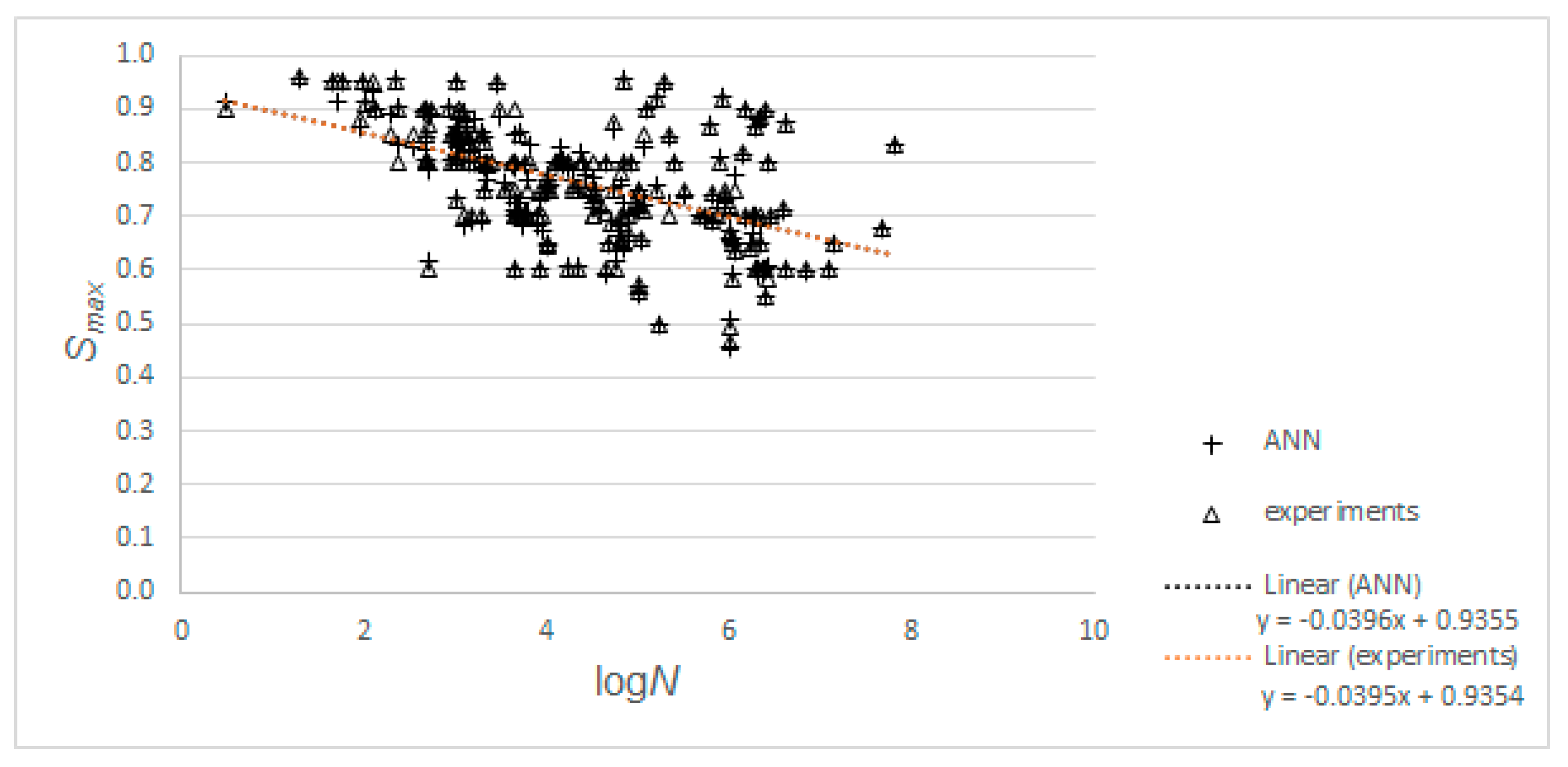
- The tested to predicted values obtained with our proposed model did not show any dependence on any of the input or the output parameters, i.e., our model performed consistently well over the full range of the parameters. In contrast, plotting the tested to predicted ratios obtained with the code equations showed that these depended on the input and the output parameters. In particular, the predicted values for the upper bound of the stress ratio with the code equations became overly conservative as the concrete compressive strength increased;
- The computational time of our proposed neural net is small (0.07 milliseconds per datapoint).
- Experiments on high-cycle fatigue are necessary. Given the required time for such experiments, however, it is unlikely that such experiments can be carried out. Perhaps, numerical analyses can be used to generate datapoints for N > 64 million cycles;
- The proposed method was derived from test results and aims at average values. Further studies are necessary to define the safety factors for design and assessment based on our proposed method;
- The proposed ANN-based model is only valid for the parameter ranges in the input dataset. However, these ranges cover most practical cases, except, as mentioned earlier, N > 64 million cycles. In practice, we need 250 or 500 million cycles for design and assessment;
- The mechanics of the problem and the reasons for the large scatter in fatigue tests were not addressed in this study. The parameter studies presented here, however, give insight in the governing parameters and can be used in the future for comparison to expressions that are derived based on mechanics.
- Regardless the high quality of the predictions yielded by the proposed model for the used data, the reader should not blindly accept that model as accurate for any other instances falling inside the input domain of the design dataset. Any analytical approximation model must undergo extensive validation before it can be taken as reliable (the more inputs, the larger the validation process). Models proposed until that stage are part of a learning process towards excellence.
Author Contributions
Funding
Conflicts of Interest
Preprint
Notations
| b | bias of neuron |
| e | relative error |
| f | frequency |
| f’b,rep,k | characteristic value of the uniaxial short term concrete compressive strength |
| f’b,rep,v | characteristic value of the concrete compressive strength in the limit state of fatigue |
| f’b,v | fatigue reference strength |
| fc | concrete compressive strength |
| fc,cyl,mean | average measured value of the concrete cylinder compressive strength |
| fcd | design concrete compressive strength |
| fcd,fat | design fatigue strength |
| fck | characteristic concrete compressive strength |
| fck,fat | characteristic concrete compressive strength for the limit state of fatigue |
| fc,mean,max | maximum measured concrete compressive strength |
| k1 | a factor from the Eurocode expression for fatigue |
| m | the number of cycles of constant amplitude |
| ni | the number of cycles with a constant amplitude at interval i |
| s | a factor that depends on the strength class of the cement |
| t | the concrete age in days |
| t0 | the time of the start of the cyclic loading on the concrete |
| tT | the concrete age in days, corrected for temperature |
| AVG | average value |
| CHAR | characteristic value based on a normal distribution |
| COV | coefficient of variation |
| Ecd,max,equ | the maximum compressive stress level |
| Ecd,min,equ | the minimum compressive stress level |
| Ecd,max,i | the maximum compressive stress level for the considered interval |
| Ecd,min,i | the minimum compressive stress level for the considered interval |
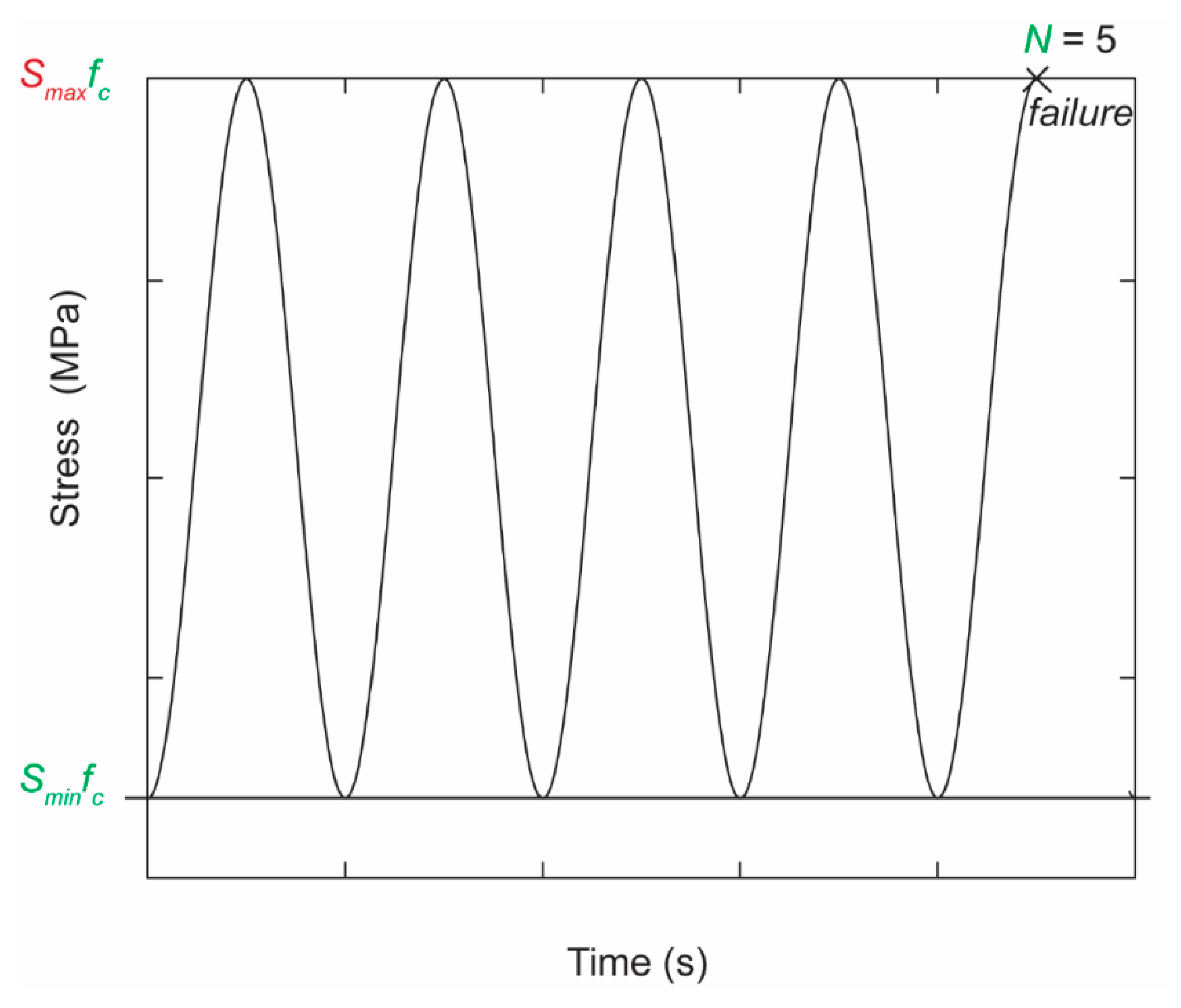
| N | number of load cycles |
| N1 | first part of the S-N curve in the fib Model Code |
| N2 | second part of the S-N curve in the fib Model Code |
| Ni | the number of cycles to failure with a constant amplitude at interval i |
| R | stress ratio |
| Requ | stress ratio |
| Ri | stress ratio of the considered interval |
| Ri* | the stress ratio for Smax,EC |
| S | fraction of compressive strength applied in load cycle |
| Sc,max | maximum fraction of compressive strength applied in load cycles |
| Sc,min | minimum fraction of compressive strength applied in load cycles |
| Smax | maximum fraction of strength applied in load cycles |
| Smax,ANN | the predicted value based on the neural network. |
| Smax,EC | the value of Smax associated with 106 cycles |
| Smax,pred | the value of Smax from the proposed methods for a given number of cycles N |
| Smax,test | the value for Smax in the experiments for a given number of cycles N |
| Smin | minimum fraction of strength applied in load cycles |
| STD | standard deviation |
| T(Δti) | temperature during time period Δti |
| W | weight of connection between neurons |
| Y | expression used in the fatigue formula of the fib Model Code |
| βcc(t0) | coefficient for the concrete strength at first load application |
| βcc(t) | describes the strength development with time |
| βc,sus(t,t0) | factor for sustained loading |
| γm | partial factor for the material |
| γc | partial factor for concrete |
| γc,fat | partial factor for concrete in the limit state of fatigue |
| σ’b,d,max | design value of the maximum compressive stress in the concrete |
| σ’b,d,min | design value of the minimum compressive stress in the concrete |
| σcd,max,equ | upper stress of the ultimate amplitude for N cycles |
| σcd,min,equ | lower stress of the ultimate amplitude for N cycles |
| σc,max | upper compressive stress of the ultimate amplitude for N cycles |
| σc,min, | lower compressive stress of the ultimate amplitude for N cycles |
| Δti | number of days with temperature T |
References
- CEB Committee GTG 15. Fatigue of Concrete Structures, CEB Bulletin d’information No 188; Comité Européen du Béton: Lausanne, Switzerland, 1988; p. 262. [Google Scholar]
- Suzuki, T.; Ohtsu, M.; Shigeishi, M. Relative damage evaluation of concrete in a road bridge by AE rate-process analysis. Mater. Struct. 2007, 40, 221–227. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L.; Koekkoek, R.; van der Veen, C.; Sliedrecht, H. Fatigue Assessment of Prestressed Concrete Slab-Between-Girder Bridges. Appl. Sci. 2019, 9, 2312. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L.; Van der Veen, C.; Koekkoek, R.T.; Sliedrecht, H. Fatigue testing of transversely prestressed concrete decks. ACI Struct. J. 2019, 116, 143–154. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L.; Van der Veen, C.; Koekkoek, R.T.; Sliedrecht, H. Punching capacity of prestressed concrete bridge decks under fatigue. ACI Struct. J. 2019, 116, 209–2018. [Google Scholar] [CrossRef]
- Foraboschi, P. Analytical model to predict the lifetime of concrete members externally reinforced with FRP. Theor. Appl. Fract. Mech. 2015, 75, 137–145. [Google Scholar] [CrossRef]
- Foraboschi, P. Shear strength computation of reinforced concrete beams strengthened with composite materials. Compos. Mech. Comput. Appl. Int. J. 2012, 3, 227–252. [Google Scholar] [CrossRef]
- Blasón, S.; Poveda, E.; Ruiz, G.; Cifuentes, H.; Fernández Canteli, A. Twofold normalization of the cyclic creep curve of plain and steel-fiber reinforced concrete and its application to predict fatigue failure. Intern. J. Fatigue 2019, 120, 215–227. [Google Scholar] [CrossRef]
- Tilly, G.P. Fatigue of steel reinforcement bars in concrete: a review. Fatigue Fract. Eng. Mater. Struct. 1979, 2, 251–268. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Hubler, M.H. Theory of cyclic creep of concrete based on Paris law for fatigue growth of subcritical microcracks. J. Mech. Phys. Solids 2014, 63, 187–200. [Google Scholar] [CrossRef]
- Bennett, E.W.; Muir, S.E.S.J. Some fatigue tests of high-strength concrete in axial compression. Mag. Concr. Res. 1967, 19, 113–117. [Google Scholar] [CrossRef]
- Hordijk, D.A.; Wolsink, G.M.; Vries, J.d. Fracture and fatigue behaviour of a high strength limestone concrete as compared to gravel concrete. Heron. 1995, 40, 125–146. [Google Scholar]
- Hsu, T.T.C. Fatigue of plain concrete. J. Am. Concr. Inst. 1981, 78, 292–305. [Google Scholar]
- Wang, H.L.; Song, Y.P. Fatigue capacity of plain concrete under fatigue loading with constant confined stress. Mater. Struct. 2011, 44, 253–262. [Google Scholar] [CrossRef]
- Yu, R.C.; Saucedo, L.; Ruiz, G. A porbabilistisc fatigue model for quasi-brittle materials. Adv. Mater. Res. 2014, 875–877, 1239–1242. [Google Scholar] [CrossRef]
- Mander, J.B.; Panthaki, F.D.; Kasalanati, A. Low-Cycle Fatigue Behavior of Reinforcing Steel. J. Mater. Civ. Eng. 1994, 6, 453–468. [Google Scholar] [CrossRef]
- Tilly, G.P. Fatigue testing and performance of steel reinforcement bars. Matér. Constr. 1984, 17, 43–49. [Google Scholar] [CrossRef]
- Teworte, F.; Herbrand, M.; Hegger, J. Structural Assessment of Concrete Bridges in Germany—Shear Resistance under Static and Fatigue Loading. Struct. Eng. Intern. 2015, 25, 266–274. [Google Scholar] [CrossRef]
- Muller, J.F.; Dux, P.F. Fatigue of Prestressed Concrete Beams with Inclined Strands. J. Struct. Eng. 1994, 120, 1122–1139. [Google Scholar] [CrossRef]
- Naaman, A.E.; Founas, M. Partially Prestressed Beams under Random-Amplitude Fatigue Loading. J. Struct. Eng. 1991, 117, 3742–3761. [Google Scholar] [CrossRef]
- Oudah, F.; El-Hacha, R. Research progress on the fatigue performance of RC beams strengthened in flexure using Fiber Reinforced Polymers. Compos. Part B-Eng. 2013, 47, 82–95. [Google Scholar] [CrossRef]
- Isojeh, B.; El-Zeghayar, M.; Vecchio, F.J. High-cycle fatigue life prediction of reinforced concrete deep beams. Eng. Struct. 2017, 150, 12–24. [Google Scholar] [CrossRef]
- Isojeh, B.; El-Zeghayar, M.; Vecchio, F.J. Fatigue Resistance of Steel Fiber-Reinforced Concrete Deep Beams. ACI Struct. J. 2017, 114. [Google Scholar] [CrossRef]
- Teng, S.; Kong, F.K.; Poh, S.P. Shear strength of reinforced and prestressed concrete deep beams. Part 1: current design methods and a proposed equation. Proc. Inst. Civ. Eng. Struct. Build. 1998, 128, 112–123. [Google Scholar] [CrossRef]
- Teng, S.; Kong, F.K.; Poh, S.P. Shear strength of reinforced and prestressed concrete deep beams. Part 2: the supporting evidence. Proc. Inst. Civ. Eng. Struct. Build. 1998, 128, 124–143. [Google Scholar] [CrossRef]
- Gallego, J.M.; Zanuy, C.; Albajar, L. Shear fatigue behaviour of reinforced concrete elements without shear reinforcement. Eng. Struct. 2014, 79, 45–57. [Google Scholar] [CrossRef]
- Hawkins, N.M. Fatigue Characteristics in Bond and Shear of Reinforced Concrete Beams. Spec. Publ. 1974, 41, 203–236. [Google Scholar]
- Hegger, J.; Marzahn, G.; Teworte, F.; Herbrand, M. Principal tensile stress criterion for the shear assessment of existing concrete bridges. Beton- und Stahlbetonbau 2015, 110, 82–95. [Google Scholar] [CrossRef]
- Liu, F.; Zhou, J.; Yan, L. Study of stiffness and bearing capacity degradation of reinforced concrete beams under constant-amplitude fatigue. PLoS ONE 2018, 13, e0192797. [Google Scholar] [CrossRef]
- Bachman, P.M.; Kreger, M.E.; Breen, J.E. An Exploratory Investigation of Shear Fatigue Behavior of Prestressed Concrete Girders; The University of Texas at Austin: Austin, TX, USA, 1987; p. 198. [Google Scholar]
- Teworte, F.; Hegger, J. Shear Fatigue of Prestressed Concrete Beams. In Proceedings of the IABSE, London, UK, 20–23 September 2011; p. 8. [Google Scholar]
- Tien, S.C.; Clyde, E.K. Static and Fatigue Strength in Shear of Beams with Tensile Reinforcement. ACI J. Proc. 1958, 54, 1033–1057. [Google Scholar] [CrossRef]
- Ueda, T. Behavior in Shear of Reinforced Concrete Beams under Fatigue Loading; University of Tokyo: Toyko, Japan, 1983; p. 124. [Google Scholar]
- Yuan, M.; Yan, D.; Zhong, H.; Liu, Y. Experimental investigation of high-cycle fatigue behavior for prestressed concrete box-girders. Constr. Build. Mater. 2017, 157, 424–437. [Google Scholar] [CrossRef]
- Fujiyama, C.; Gebreyouhannes, E.; Maekawa, K. Present Achievement and Future Possibility of Fatigue Life Simulation Technology for RC Bridge Deck Slabs. Internet J. Soc. Soc. Manag Syst. 2008, 4, 8. [Google Scholar]
- Sonoda, K.; Horikawa, T. Fatigue Strength of Reinforced Concrete Slabs under Moving Loads; IABSE Reports; IABSE: Zürich, Switzerland, 1982. [Google Scholar]
- Harajli, M.H.; Naaman, A.E. Static and Fatigue Tests on Partially Prestressed Beams. J. Struct. Eng. 1985, 111, 1602–1618. [Google Scholar] [CrossRef]
- Shahawi, M.E.; Batchelor, B.D. Fatigue of Partially Prestressed Concrete. J. Struct. Eng. 1986, 112, 524–537. [Google Scholar] [CrossRef]
- Xin, Q.; Dou, Y.; Chen, W. Load Spectrum and Fatigue Life Computer Analysis of Prestressed Concrete Bridges. Int. J. Secur. Appl. 2015, 9, 247–266. [Google Scholar] [CrossRef]
- Xin, Q.; Dou, Y.; Li, S. Fatigue Behavior of Prestressed Concrete Beams under Overload. Int. J. Secur. Appl. 2017, 10, 124–131. [Google Scholar] [CrossRef]
- Zeng, D.; Wang, G.-l.; Xie, J.; Zheng, X.-h. Exploratory Experimental Study on Fatigue Prestress Loss of Prestressed Concrete Beams. J. Highw. Transp. Res. Dev. (Engl. Ed.) 2014, 8, 37–41. [Google Scholar] [CrossRef]
- Foraboschi, P. Structural layout that takes full advantage of the capabilities and opportunities afforded by two-way RC floors, coupled with the selection of the best technique, to avoid serviceability failures. Eng. Fail. Anal. 2016, 70, 387–418. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, X.; Bu, J. Nonlinear damage accumulation of concrete subjected to variable amplitude fatigue loading. Bull. Pol. Acad. Sci.-Tech. 2018, 66, 157–163. [Google Scholar]
- Holmen, J.O. Fatigue of concrete by constant and variable amplitude loading. ACI SP-75: Fatigue Concr. Struct. 1982, 75, 71–110. [Google Scholar]
- Keerthana, K.; Chandra Kishen, J.M. An experimental and analytical study on fatigue damage in concrete under variable amplitude loading. Intern. J. Fatigue 2018, 111, 278–288. [Google Scholar] [CrossRef]
- Lohaus, L.; Anders, S. High-cycle Fatigue of Ultra-high Performance Concrete – Fatigue Strength and Damage Development. In Proceedings of the 2nd International Congress, Naples, Italy, 5–8 June 2006; p. 10. [Google Scholar]
- Petkovic, G.; Lenschow, R.; Stemland, H.; Rosseland, S. Fatigue of high-strength concrete. ACI SP-121: High-Strength Concr. 1990, 121, 505–525. [Google Scholar]
- Kim, J.K.; Kim, Y.Y. Experimental study of the fatigue behavior of high strength concrete. Cem. Concr. Res. 1996, 26, 1513–1523. [Google Scholar] [CrossRef]
- Lohaus, L.; Wefer, M.; Oneschkow, N. Ermüdungsbemessungsmodell für normal-, hoch- und ultrahochfeste Betone. Beton- und Stahlbetonbau 2011, 106, 836–846. [Google Scholar] [CrossRef]
- Code Committee 351 001. Technical Foundations for Structures. In Regulations for Concrete - Bridges - Structural Requirements and Calculation Methods, NEN 6723:2009; Nederlands Normalisatie Instituut: Gouda, The Netherlands, 2009; p. 72. [Google Scholar]
- CEN. Eurocode 2: Design of Concrete Structures - General Rules and Rules for Buildings. NEN-EN 1992-1-1+C2:2011; Comité Européen de Normalisation: Brussels, Belgium, 2011; p. 246. [Google Scholar]
- CEN. Eurocode 2: Design of Concrete Structures - Concrete Bridges - Design and Detailing Rules. NEN-EN 1992-2+C1:2011; Comité Européen de Normalisation: Brussels, Belgium, 2011; p. 113. [Google Scholar]
- Fédération Internationale du Béton. Model Code 2010: Final Draft; International Federation for Structural Concrete: Lausanne, Switzerland, 2012; p. 676. [Google Scholar]
- Hertzmann, A.; Fleet, D. Machine Learning and Data Mining, Lecture Notes CSC 411/D11; University of Toronto: Toronto, ON, Canada, 2012. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Hern, A. Google Says Machine Learning Is the Future. So I Tried It Myself. Available online: https://www.theguardian.com/technology/2016/jun/28/google-says-machine-learning-is-the-future-so-i-tried-it-myself (accessed on 14 November 2019).
- Wilamowski, B.M.; Irwin, J.D. The Industrial Electronics Handbook, 2nd ed.; CRC; Taylor & Francis Distributor: Boca Raton, FL, USA, 2011; p. 4052. [Google Scholar]
- Prieto, A.; Prieto, B.; Ortigosa, E.M.; Ros, E.; Pelayo, F.; Ortega, J.; Rojas, I. Neural networks: An overview of early research, current frameworks and new challenges. Neurocomputing 2016, 214, 242–268. [Google Scholar] [CrossRef]
- Abambres, M.; Lantsoght, E. Neural Network-Based Formula for Shear Capacity Prediction of One-Way Slabs under Concentrated Loads, HAL. 2018. Available online: https://hal.archives-ouvertes.fr/hal-02074675 (accessed on 14 November 2019). [CrossRef]
- Adhikary, B.B.; Mutsuyoshi, H. Prediction of shear strength of steel fiber RC beams using neural networks. Constr. Build. Mater. 2006, 20, 801–811. [Google Scholar] [CrossRef]
- Al-Musawi, A.A. Determination of shear strength of steel fiber RC beams: application of data-intelligence models. Front. Struct. Civ. Eng. 2019, 13, 667–673. [Google Scholar] [CrossRef]
- Aymerich, F.; Serra, M. Prediction of fatigue strength of composite laminates by means of neural networks. Key Eng. Mater. 1998, 144, 231–240. [Google Scholar] [CrossRef]
- Flood, I. Towards the next generation of artificial neural networks for civil engineering. Adv. Eng. Inform. 2008, 22, 4–14. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yun, G.J.; Alavi, A.H. An evolutionary approach for modeling of shear strength of RC deep beams. Mater. Struct. 2013, 46, 2109–2119. [Google Scholar] [CrossRef]
- Gholizadeh, S.; Pirmoz, A.; Attarnejad, R. Assessment of load carrying capacity of castellated steel beams by neural networks. J. Constr. Steel Res. 2011, 67, 770–779. [Google Scholar] [CrossRef]
- Gunaratnam, D.J.; Gero, J.S. Effect of Representation on the Performance of Neural Networks in Structural Engineering Applications. Comput. -Aided Civ. Infrastruct. Eng. 1994, 9, 97–108. [Google Scholar] [CrossRef]
- Hossain, K.M.A.; Gladson, L.R.; Anwar, M.S. Modeling shear strength of medium- to ultra-high-strength steel fiber-reinforced concrete beams using artificial neural network. Neural Comput. Appl. 2016. [Google Scholar] [CrossRef]
- Min, J.; Park, S.; Yun, C.-B.; Lee, C.-G.; Lee, C. Impedance-based structural health monitoring incorporating neural network technique for identification of damage type and severity. Eng. Struct. 2012, 39, 210–220. [Google Scholar] [CrossRef]
- Mukherjee, A.; Deshpande, J.M.; Anmala, J. Prediction of Buckling Load of Columns Using Artificial Neural Networks. J. Struct. Eng. 1996, 122, 1385–1387. [Google Scholar] [CrossRef]
- Naderpour, H.; Kheyroddin, A.; Amiri, G.G. Prediction of FRP-confined compressive strength of concrete using artificial neural networks. Compos. Struct. 2010, 92, 2817–2829. [Google Scholar] [CrossRef]
- Naderpour, H.; Nagai, K.; Fakharian, P.; Haji, M. Innovative models for prediction of compressive strength of FRP-confined circular reinforced concrete columns using soft computing methods. Compos. Struct. 2019, 215, 69–84. [Google Scholar] [CrossRef]
- Haykin, S.S. Neural Networks and Learning Machines, 3rd ed.; Prentice Hall/Pearson: New York, NY, USA, 2009; p. 906. [Google Scholar]
- Lantsoght, E.O.L.; van der Veen, C.; de Boer, A. Proposal for the fatigue strength of concrete under cycles of compression. Constr. Build. Mater. 2016, 107, 138–156. [Google Scholar] [CrossRef]
- Hordijk, D.A. Vergelijkend onderzoek naar een aantal materiaaleigenschappen van grindbeton en kalksteenbeton. In Fase II: Vermoeiing; TNO: Delft, The Netherlands, 1994; p. 59. [Google Scholar]
- Hohberg, R. Zum Ermüdungsverhal-ten von Beton. Ph.D. Thesis, TU Berlin, Berlin, Germany, 2004. [Google Scholar]
- CUR-onderzoekcommissie C 33 “Wisselbelasting”. Vermoeiing van beton, deel 4: drukspanningen (2); Technical Report; CUR-VB: Gouda, The Netherlands, April 1993. [Google Scholar]
- CUR-onderzoekcommissie C 33 "Wisselbelasting". Vermoeiing van beton, deel 1: drukspanningen; Technical CUR-VB: Gouda, The Netherlands, December 1983. [Google Scholar]
- Klausen, D. Festigkeit und Schädigung von Beton bei häufig wiederholter Beanspruchung. Ph.D. Thesis, Technische Hochschule Darmstadt, Darmstadt, Germany, 1978. [Google Scholar]
- Tepfers, R.; Kutti, T. Fatigue strength of plain, ordinary and lightweight concrete. ACI J. Proc. 1979, 76, 635–652. [Google Scholar]
- Tue, N.V.; Mucha, S. Ermüdungsfestigkeit von hochfestem Beton unter Druckbeanspruchung. Bautech. 2006, 83, 497–504. [Google Scholar] [CrossRef]
- Saucedo, L.; Yu, R.C.; Medeiros, A.; Zhang, X.; Ruiz, G. A probabilistic fatigue model based on the initial distribution to consider frequency effect in plain and fiber reinforced concrete. Intern. J. Fatigue 2013, 48, 308–318. [Google Scholar] [CrossRef]
- Zhao, Z.; Haldar, A. Bridge fatigue damage evaluation and updating using non-destructive inspections. Eng. Fract. Mech. 1996, 53, 775–788. [Google Scholar] [CrossRef]
- Developer. dataset + tabled results Zenodo, Num3ros: Lisbon, Portugal. Available online: https://zenodo.org/record/3385103#.XdA7o_57mpo (accessed on 3 September 2019). [CrossRef]
- Abambres, M.; Lantsoght, E.O.L. ANN-Based Shear Capacity of Steel Fiber-Reinforced Concrete Beams without Stirrups. Fibers 2019, 7, 88. [Google Scholar] [CrossRef]
- The Mathworks Inc. Matlab R2017a, User’s Guide; The Mathworks Inc.: Natick, MA, USA, 2017. [Google Scholar]
- Abambres, M. ANN Software Validation Report; Figshare. 2018. Available online: https://figshare.com/articles/ANNSoftwareValidation-Report_pdf/6962873 (accessed on 30 October 2019).
- Abambres, M.; Marcy, M.; Doz, G. Potential of Neural Networks for Structural Damage Localization. ACI Av. en Cienc. e Ing. 2019, 11. [Google Scholar] [CrossRef]
- Developer. W and b arrays [Data set] (fatigue). Zenodo, Num3ros: Lisbon, Portugal, September 4th 2019. Available online: https://zenodo.org/record/3385133#.Xc-O-WYRVPZ (accessed on 16 November 2019). [CrossRef]
- PTC Inc. MathCad 15.0 User Manual; PTC: Needham, MA, USA, 2015. [Google Scholar]
- Fehling, E.; Schmidt, M.; Teichmann, T.; Bunje, K.; Bornemann, R.; Middendorf, B. Entwicklung, Dauerhaftigkeit und Berechnung Ultrahochfester Betone (UHPC); Universitat Kassel: Kassel, Germany, 2005; p. 132. [Google Scholar]
- Forrest, R.W.B.; Higgins, C.; Senturk, A.E. Experimental and Analytical Evaluation of Reinforced Concrete Girders under Low-Cycle Shear Fatigue. Aci. Struct. J. 2010, 107, 199–207. [Google Scholar]
- Amiri, M.; Droguett, E.L.; Iyyer, N.; Naderi, M. The second law of thermodynamics and degradation of materials. In Proceedings of the Safety and Reliability of Complex Engineered Systems, Zurich, Switzerland, 7–10 September 2015; pp. 4101–4105. [Google Scholar]
- CEN. General Rules and Rules for Buildings. Eurocode 2: Design of Concrete Structures. NEN-EN 1992-1-1:2005; Comité Européen de Normalisation: Brussels, Belgium, 2005; p. 229. [Google Scholar]

| Code | Ref | Equations | Nr |
|---|---|---|---|
| NEN 6723:2009 | [50] | with γm = 1.2 | (1) |
| (2) | |||
| (3) | |||
| (4) | |||
| NEN-EN 1992-1-1+C2:2011 | [51] | with fck in MPa and k1 = 0.85 | (5) |
| (6) | |||
| (7) | |||
| (8) | |||
| (9) | |||
| (10) | |||
| NEN-EN 1992-2+C1:2011 | [52] | (11) | |
| (12) | |||
| fib model code 2010 | [53] | with fck in MPa, βc,sus(t, t0) = 0.85 and s = 0.25 for cement class 42.5 N | (13) |
| (14) | |||
| (15) | |||
| (16) | |||
| (17) | |||
| (18) | |||
| (19) | |||
| (20) | |||
| (21) | |||
| (22) |
| Input Parameters | Input Number | Min | Max | ||
|---|---|---|---|---|---|
| Concrete properties | fc,cyl (MPa) | average concrete compressive strength | 1 | 24 | 170 |
| Loading | Smin (-) | lower limit of stress range | 2 | 0 | 0.836 |
| N (-) | number of cycles to failure | 3 | 3 | 63,841,046 | |
| Output | Smax (-) | upper limit of stress range | 1 | 0.465 | 0.960 |
| F1 | F2 | F3 | F4 | F5 | F6 | F7 |
|---|---|---|---|---|---|---|
| Qualitative Var Represent | Dimensional Analysis | Input Dimensionality Reduction | % Train-Valid-Test | Input Normalization | Output Transfer | Output Normalization |
| Boolean Vectors | Yes | Linear Correlation | 80-10-10 | Linear Max Abs | Logistic | Lin [a, b] = 0.7[φmin, φmax] |
| Eq Spaced in ]0,1] | No | Auto-Encoder | 70-15-15 | Linear [0, 1] | - | Lin [a, b] = 0.6[φmin, φmax] |
| - | - | - | 60-20-20 | Linear [−1, 1] | Hyperbolic Tang | Lin [a, b] = 0.5[φmin, φmax] |
| - | - | Ortho Rand Proj | 50-25-25 | Nonlinear | - | Linear Mean Std |
| - | - | Sparse Rand Proj | - | Lin Mean Std | Bilinear | No |
| - | - | No | - | No | Compet | - |
| Identity |
| F8 | F9 | F10 | F11 | F12 | F13 | F14 |
|---|---|---|---|---|---|---|
| Net Architectue | Hidden Layers | Connectivity | Hidden Transfer | Parameter Initialization | Learning Algorithm | Training Mode |
| MLPN | 1 HL | Adjacent Layers | Logistic | Midpoint (W) + Rands (b) | BP | Batch |
| RBFN | 2 HL | Adj Layers + In-Out | Identity-Logistic | Rands | BPA | Mini-Batch |
| - | 3 HL | Fully-Connected | Hyperbolic Tang | Randnc (W) + Rands (b) | LM | Online |
| - | - | - | Bipolar | Randnr (W) + Rands (b) | ELM | - |
| - | - | - | Bilinear | Randsmall | mb ELM | - |
| - | - | - | Positive Sat Linear | Rand [−Δ, Δ] | I-ELM | - |
| - | - | - | Sinusoid | SVD | CI-ELM | - |
| Thin-Plate Spline | MB SVD | - | ||||
| Gaussian | - | - | ||||
| Multiquadratic | - | - | ||||
| Radbas | - | - | ||||
| Thin-Plate Spline | MB SVD | - |
| Model | AVG | STD | COV | Min | Max | |
|---|---|---|---|---|---|---|
| Proposed model | 1.00 | 0.02 | 1.69% | 0.955 | 1.053 | |
| NEN 6723:2009 | [50] | 1.55 | 0.63 | 40.53% | −5.828 | 2.869 |
| 1.59 | 0.35 | 22.27% | 0.893 | 2.869 | ||
| NEN-EN 1992-2+C1:2011 | [52] | 1.07 | 4.59 | 430.61% | −56.25 | 3.913 |
| 1.70 | 0.69 | 40.90% | 0.971 | 3.913 | ||
| fib model code 2010 | [53] | 1.37 | 0.28 | 20.46% | 0.906 | 2.261 |
| 1.37 | 0.28 | 20.68% | 0.906 | 2.261 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abambres, M.; Lantsoght, E.O.L. ANN-Based Fatigue Strength of Concrete under Compression. Materials 2019, 12, 3787. https://doi.org/10.3390/ma12223787
Abambres M, Lantsoght EOL. ANN-Based Fatigue Strength of Concrete under Compression. Materials. 2019; 12(22):3787. https://doi.org/10.3390/ma12223787
Chicago/Turabian StyleAbambres, Miguel, and Eva O.L. Lantsoght. 2019. "ANN-Based Fatigue Strength of Concrete under Compression" Materials 12, no. 22: 3787. https://doi.org/10.3390/ma12223787
APA StyleAbambres, M., & Lantsoght, E. O. L. (2019). ANN-Based Fatigue Strength of Concrete under Compression. Materials, 12(22), 3787. https://doi.org/10.3390/ma12223787






