Comprehensive Modelling of the Hysteresis Loops and Strain–Energy Density for Low-Cycle Fatigue-Life Predictions of the AZ31 Magnesium Alloy
Abstract
1. Introduction
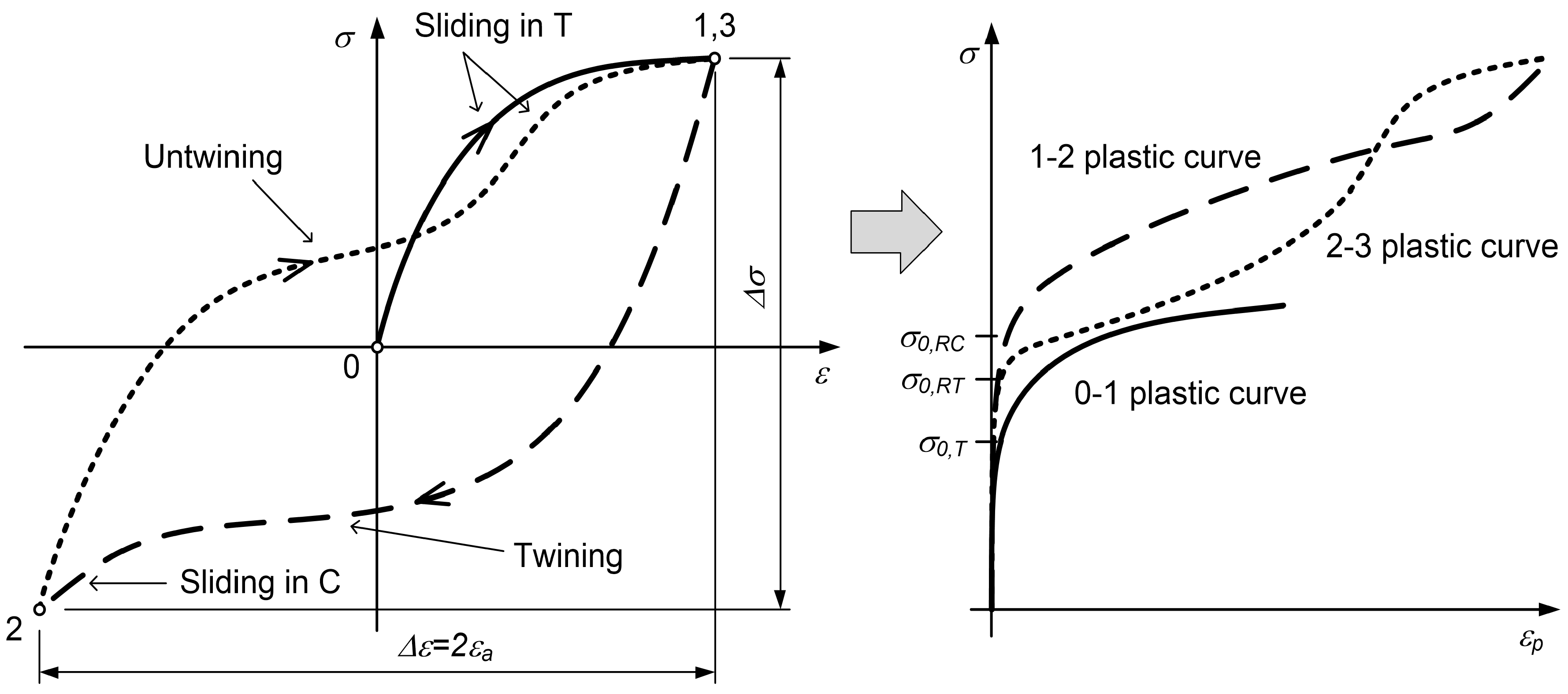
- A monotonic tensile curve (0–1) is a sum of the constant monotonic tensile yield stress and the exponential curve with the generic form .
- A compressive reverse loading path (1–2) is a combination of the constant monotonic compressive yield stress , the exponential curve for modelling the twinning process and the sigmoidal function for modelling the sliding plasticity during the compression.
- A tensile reverse loading path (2–3) is a combination of the constant monotonic tensile yield stress , the exponential curve for modelling the untwining process and the sigmoidal function for modelling the sliding plasticity during the compression. The parameters for this model are different from the parameters of the second model.
2. Theoretical Background
2.1. Strain–Energy Density of a Closed Hysteresis Loop
2.2. Calculating Fatigue-Life with an Energy Approach
2.3. Modelling the Energy Density of Closed Hysteresis Loops for Variable–Strain Time Series
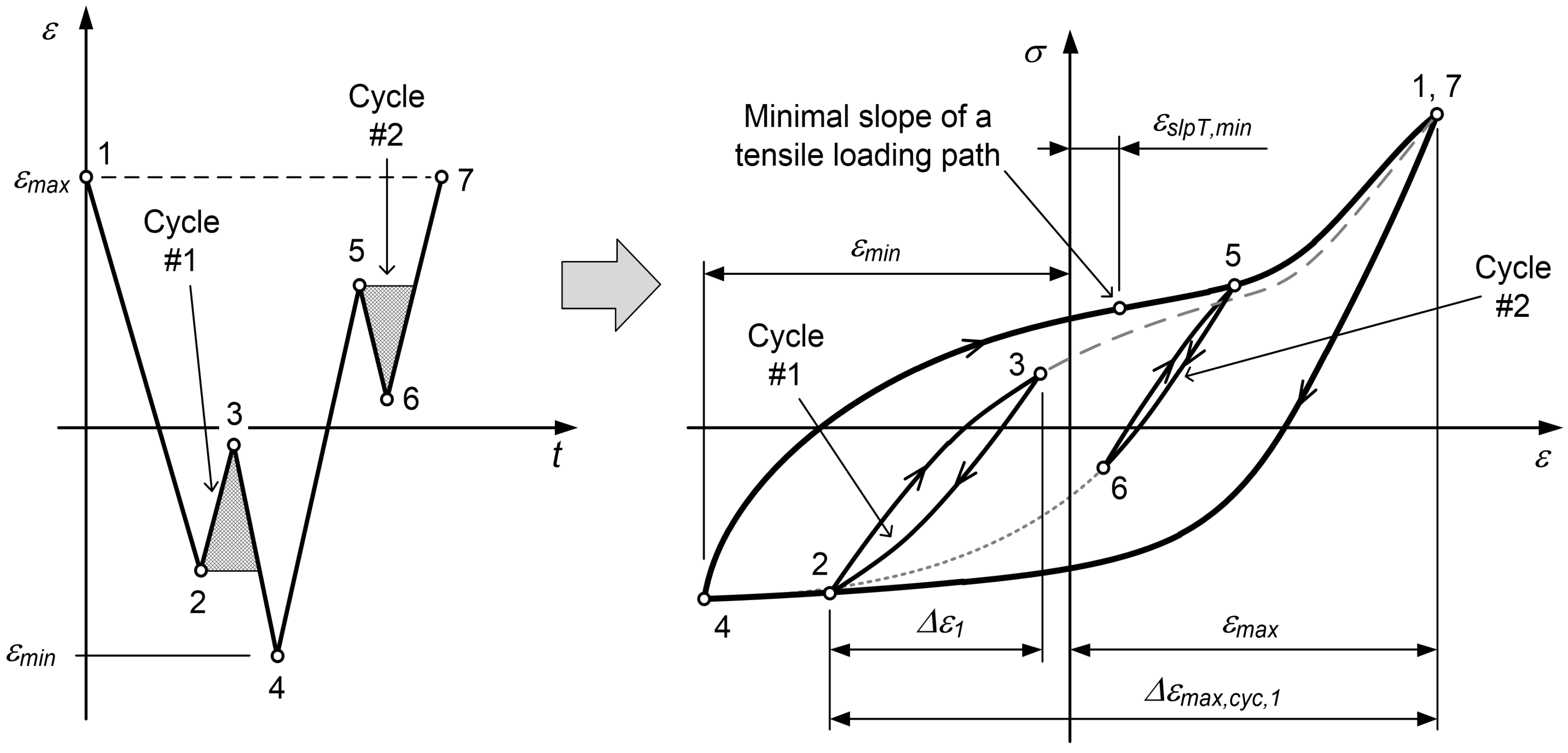
2.3.1. Extracting Closed Hysteresis Loops of Loading Cycles
2.3.2. Modelling the Tensile Loading Paths
- If the tensile loading path originates from the outermost compressive loading path, but not from (as is the case for the segment 2–3 in Figure 3), its tensile loading path is modelled with Equation (4) and the parameter is calculated as follows:According to the case in Figure 3, for the first loading cycle is .
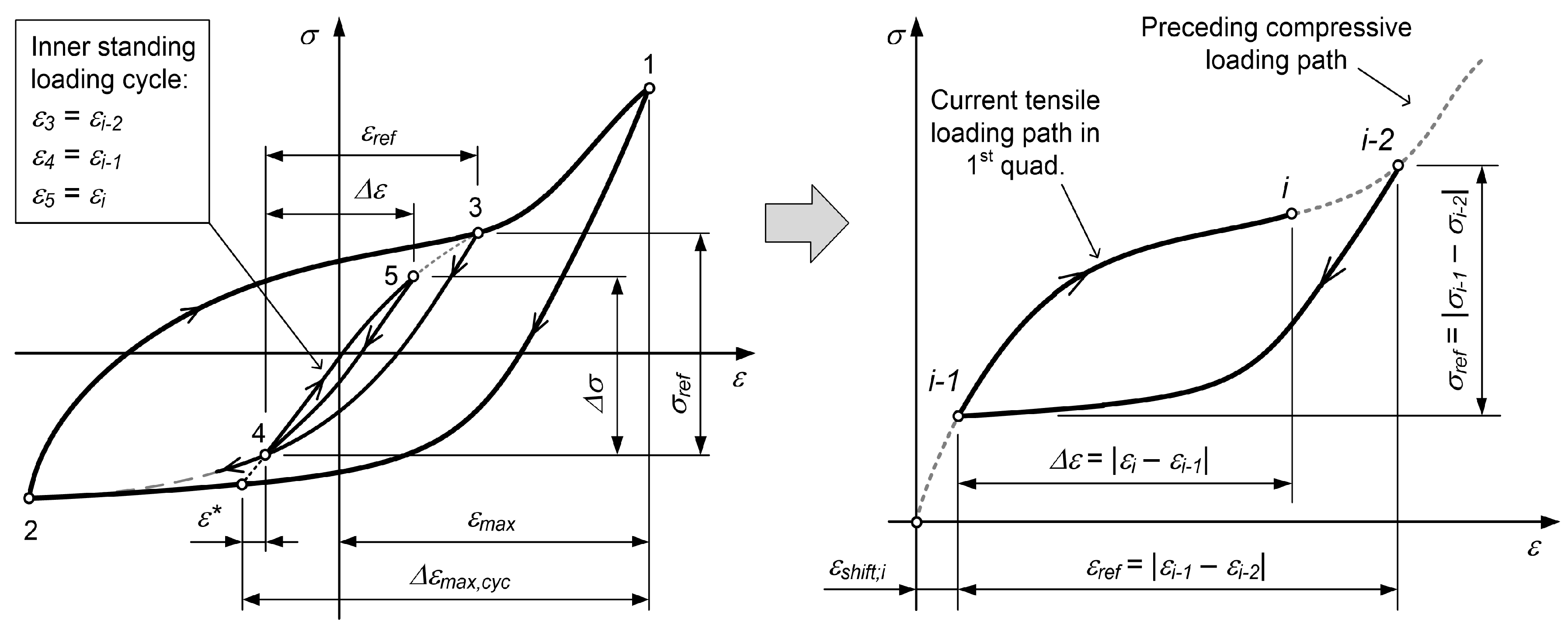
- If the tensile loading path originates from the inner compressive loading path, the corresponding parameter is determined first by extending the line with a slope of the elastic modulus E from the point to the outermost compressive loading path (see the left diagram in Figure 4):where connects the reversal point with the intersection of the tangent to the tensile loading path and the outermost compressive loading path, as shown in Figure 5. The tensile loading path of the loading cycle (e.g., the segment 4–5 in Figure 4) is then modelled as a linear combination of the tensile loading path from Equation (4) with the corresponding parameter from Equation (18) and the compressive loading path of the previous strain range (the segment 3–4 in Figure 4) with both of the curves modelled in the first quadrant of the – space:The model for the compressive loading path is described below. The mixing weight is defined as follows (see also Figure 4):
- For the inner loading cycles, part of which is also the tensile loading path, the rule of closed hysteresis loops must hold, as defined by Jayakumar [34]. In our case, this means that a strain shift must be determined for the inner tensile loading path to ensure that its model, which starts at the point , reaches exactly the point of the preceding compressive loading path . To calculate the strain shift , the tensile loading path is modelled in the first quadrant of the – space (see the right-hand diagram in Figure 4 (In general, the quantity is not equal to the quantity in Figure 4)).
- Given that the time series of the previous stresses to corresponding to the strain values to are known, the highest stress in the current tensile loading path that corresponds to the strain is calculated as follows:
2.3.3. Modelling the Tensile Loading Paths
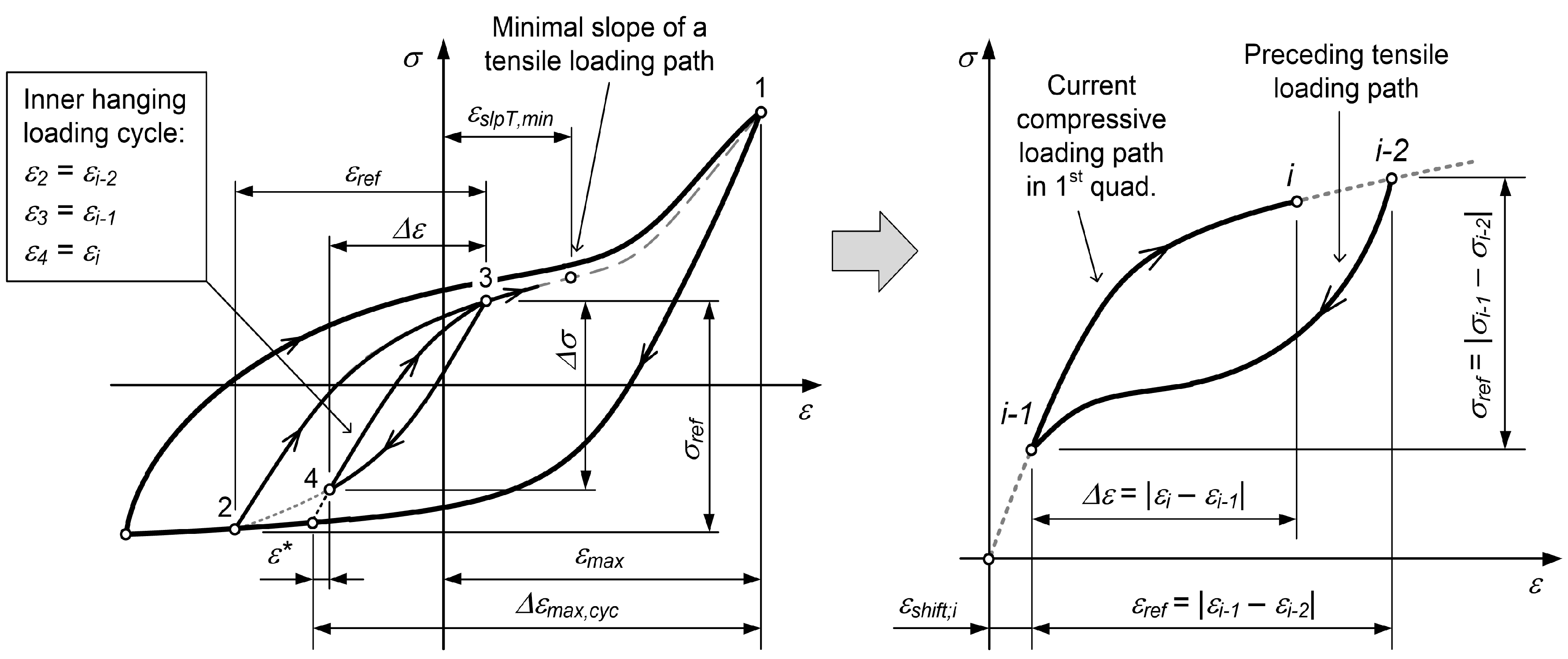
- If the compressive loading path does not originate from the strain , regardless of its basic tensile loading path, its model depends on the value of the reference strain . If the reference strain is smaller than the value from the preceding tensile loading path (e.g., the – curve segment 2–3 in Figure 5), the model of the compressive loading path is equal to the model of the preceding tensile loading path, , but in the opposite direction.represents the strain that corresponds to the minimum slope of the preceding tensile loading path . If the reference strain is larger than the value from the preceding tensile loading path (e.g., the segment 4–5 in Figure 3), the compressive loading path is a linear combination of the outermost compressive loading path from Equation (3) (the segment 1–2 in Figure 3 or Figure 5) and the Ramberg–Osgood term from Equation (4):The mixing weight is defined as follows (see also Figure 3 and Figure 5):
- As with the tensile loading path model, the strain shift must also be determined for the compressive loading path in order for its extension to reach exactly the point of the preceding tensile loading path (see Figure 5).
- Given that the time series of the previous stresses to corresponding to the strain values to are known, the lowest stress in the current compressive loading path that corresponds to the strain is calculated as follows:In Equation (25), the compressive loading path must be modelled in the first quadrant of the – space.
2.3.4. Strain–Energy Density Calculation
3. Experimental Data
- Static tensile tests were performed up to the rupture of the specimen with an on-line measurement of the engineering stress and strain during the experiment (four specimens). One specimen was used for metallographic experiments in the zone of maximum strain.
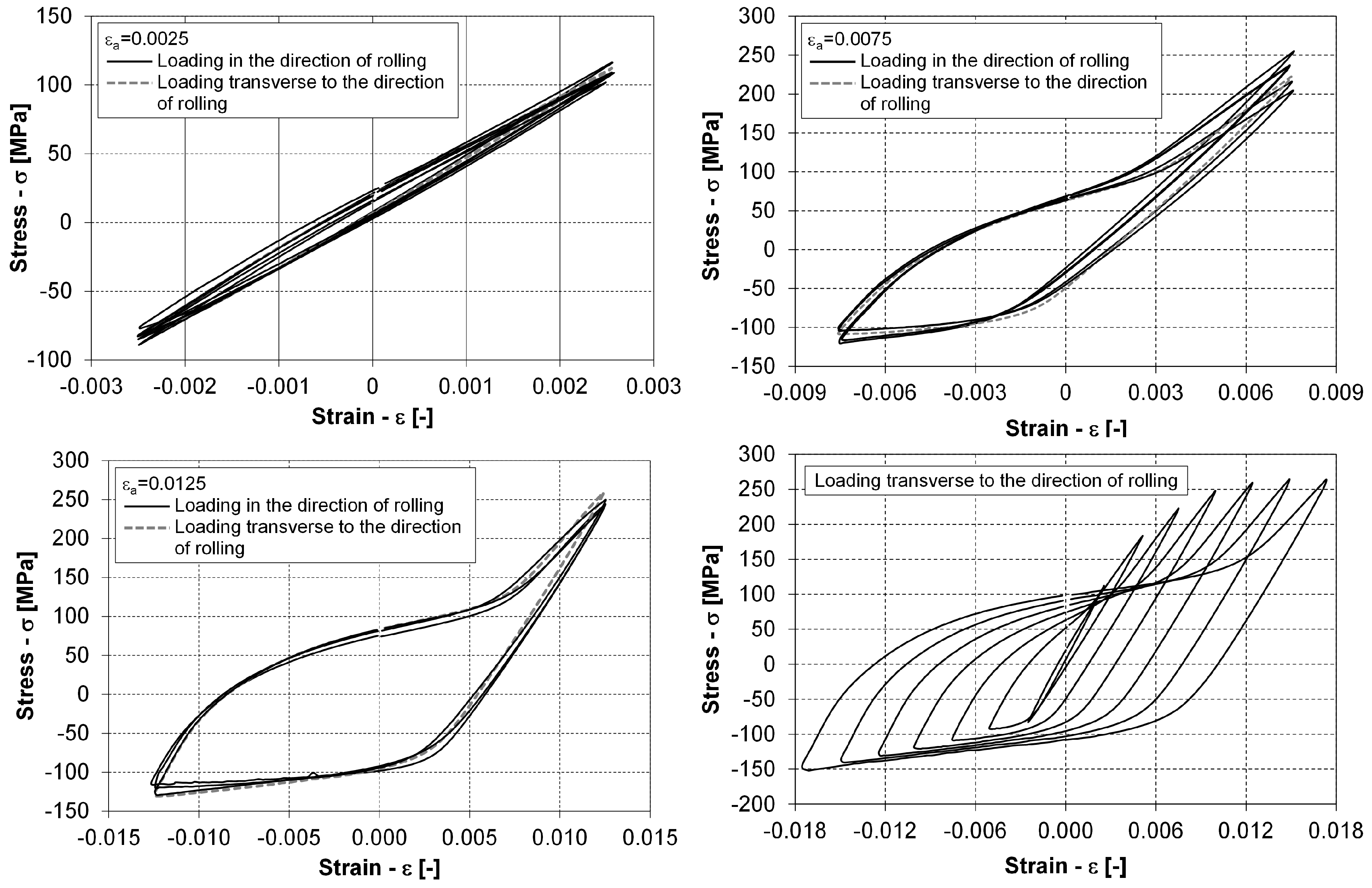
- Strain-controlled fully reversal () low-cycle fatigue experiments with constant strain amplitudes were performed to determine the shape of the closed hysteresis loops at different loading levels and the energy fatigue-life curve: (four specimens), (three specimens), (one specimen), (three specimens), (one specimen) and (one specimen). In each experiment, the number of loading cycles to a break N was acquired. One specimen was also used for the metallographic experiments.
- Strain-controlled, fully reversal (), step-wise, low-cycle fatigue experiments with increasing strain amplitudes were performed until failure. At each strain amplitude level, 20 loading cycles were completed to stabilise the hysteresis loops. The initial strain amplitude was and the second strain amplitude level was . After that loading block, the strain–amplitude level was increased by in each of the next loading blocks. The step-wise test was terminated after the rupture of the specimen. The purpose of this test was to determine the shape of the closed hysteresis loops and the hardening rule (isotropic or kinematic). Altogether, five step-wise experiments were performed.
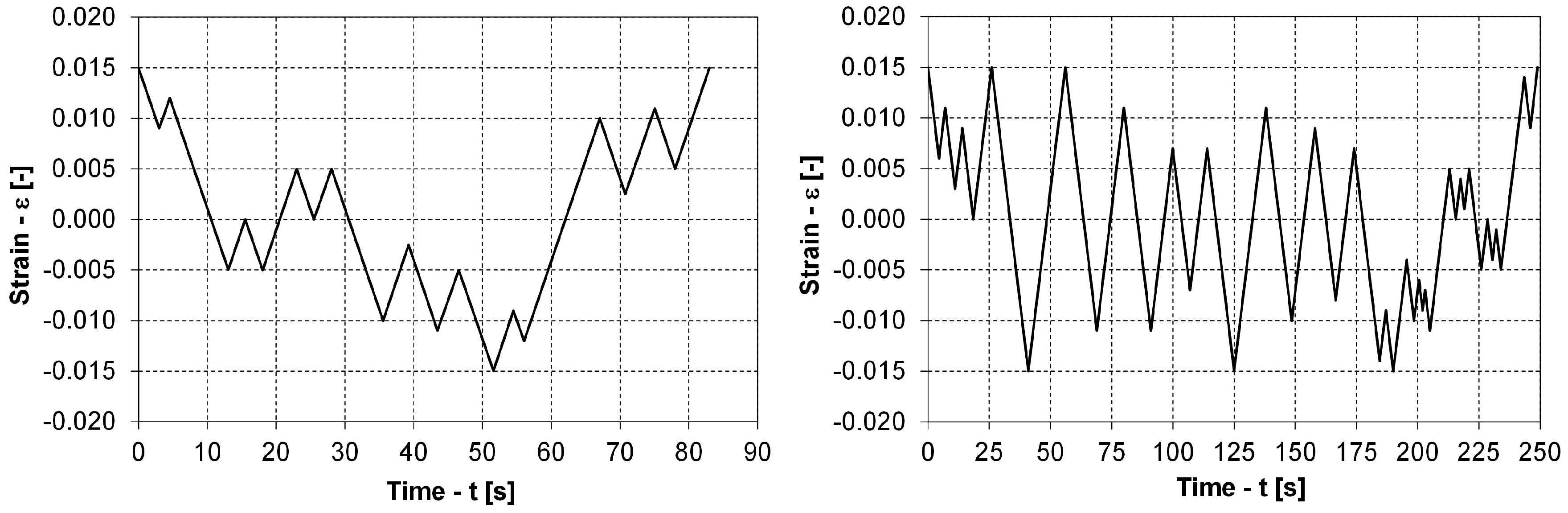
- Strain-controlled, variable, low-cycle fatigue experiments for two different strain time histories were performed, as presented in Figure 6. Altogether, two variable-load, low-cycle fatigue experiments were performed between the limit strains of and to validate the proposed model for predicting the low-cycle fatigue life of the magnesium alloy AZ31.
4. Results and Discussion
4.1. Experimental Results and Their Modelling
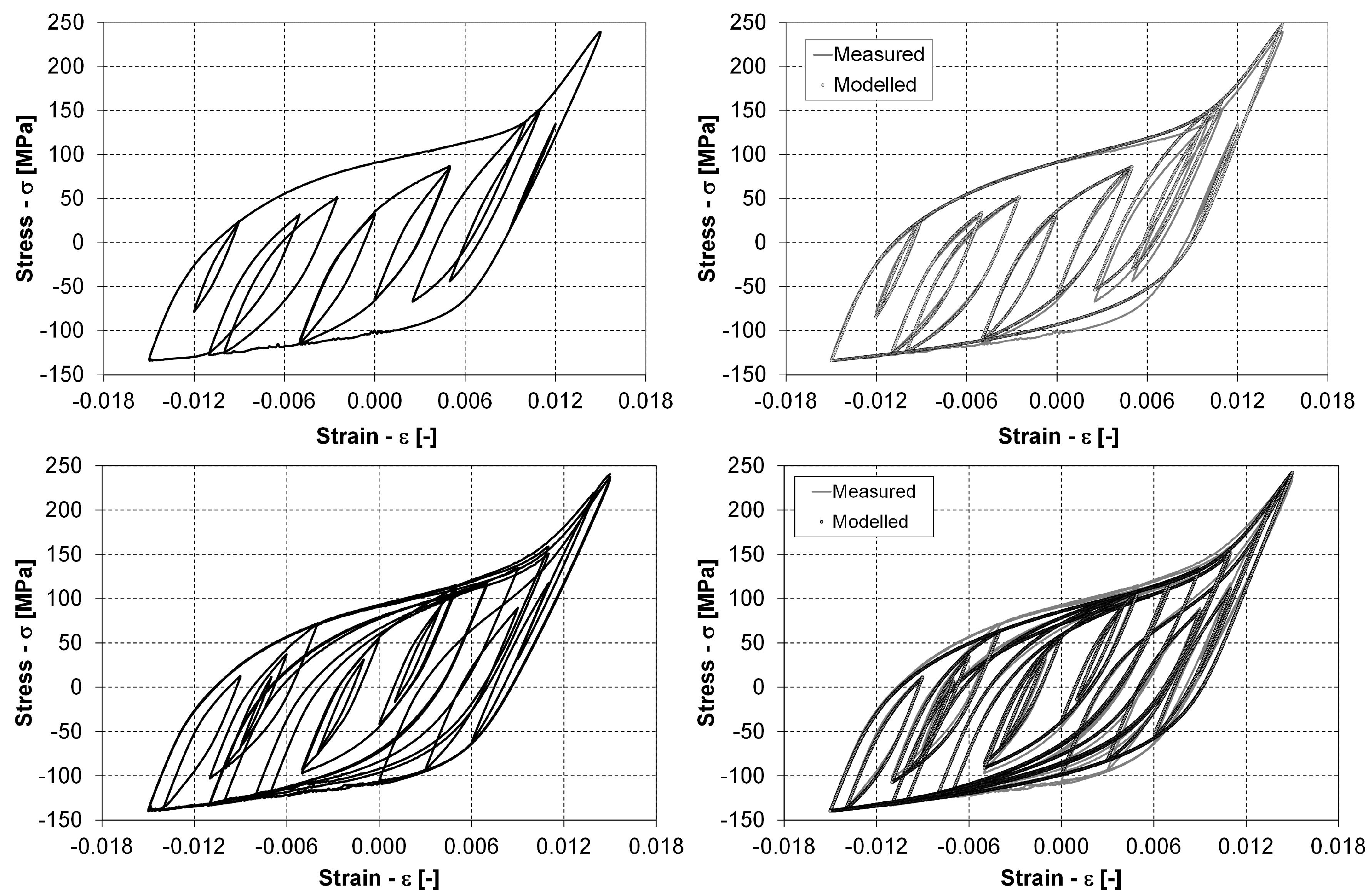
- The stabilised hysteresis loops only (up to the outermost hysteresis–loop envelope) should be considered for predicting the number of loading cycles to failure.
- After a certain strain–amplitude level is reached during the cyclic loading, it is its (the outermost) hysteresis loop that governs the stress–strain behaviour, also for the smaller strain–amplitude loading cycles.
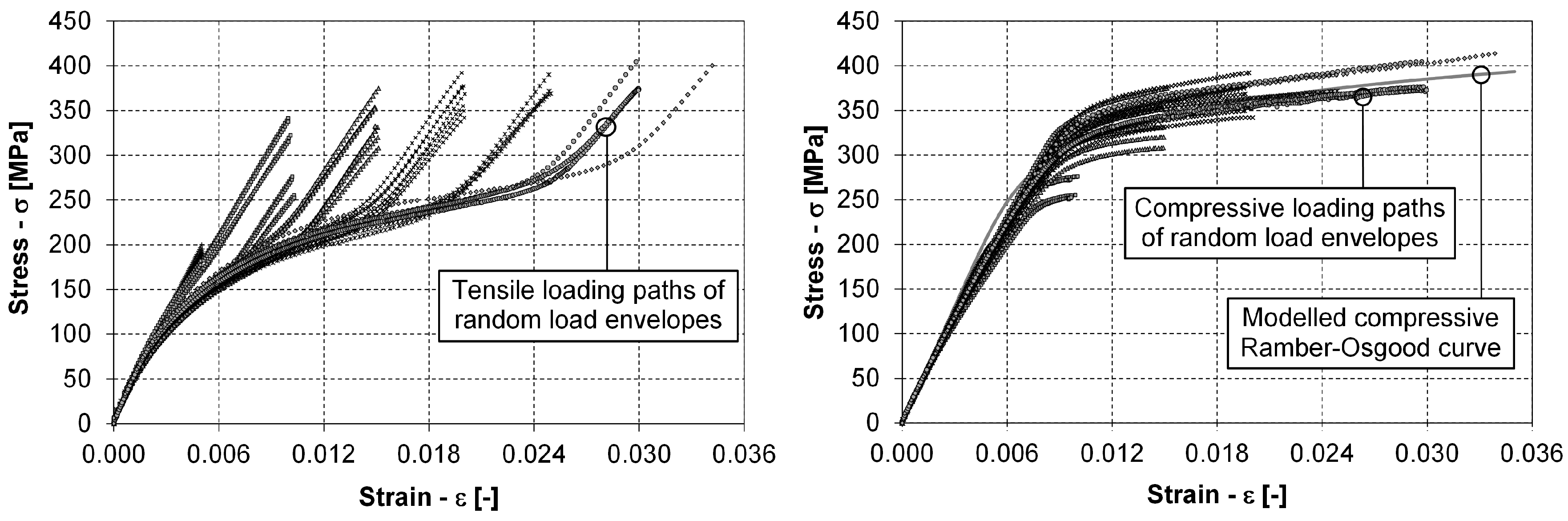
- The parameters of the Ramberg–Osgood relationship for the outermost compressive loading path that is modelled with Equation (3) should be determined either just for the highest strain amplitude loading level or for all the compressive loading paths from the domain of the kinematic hardening, i.e., in our case.
- To build a general model for the tensile loading paths from Equation (4) by considering all the experimental data, the tensile loading paths as presented in the left-hand diagram of Figure 11 must first be extended to the outer-most compressive loading path. Only after this transformation can the parameters of Equation (4) be determined.
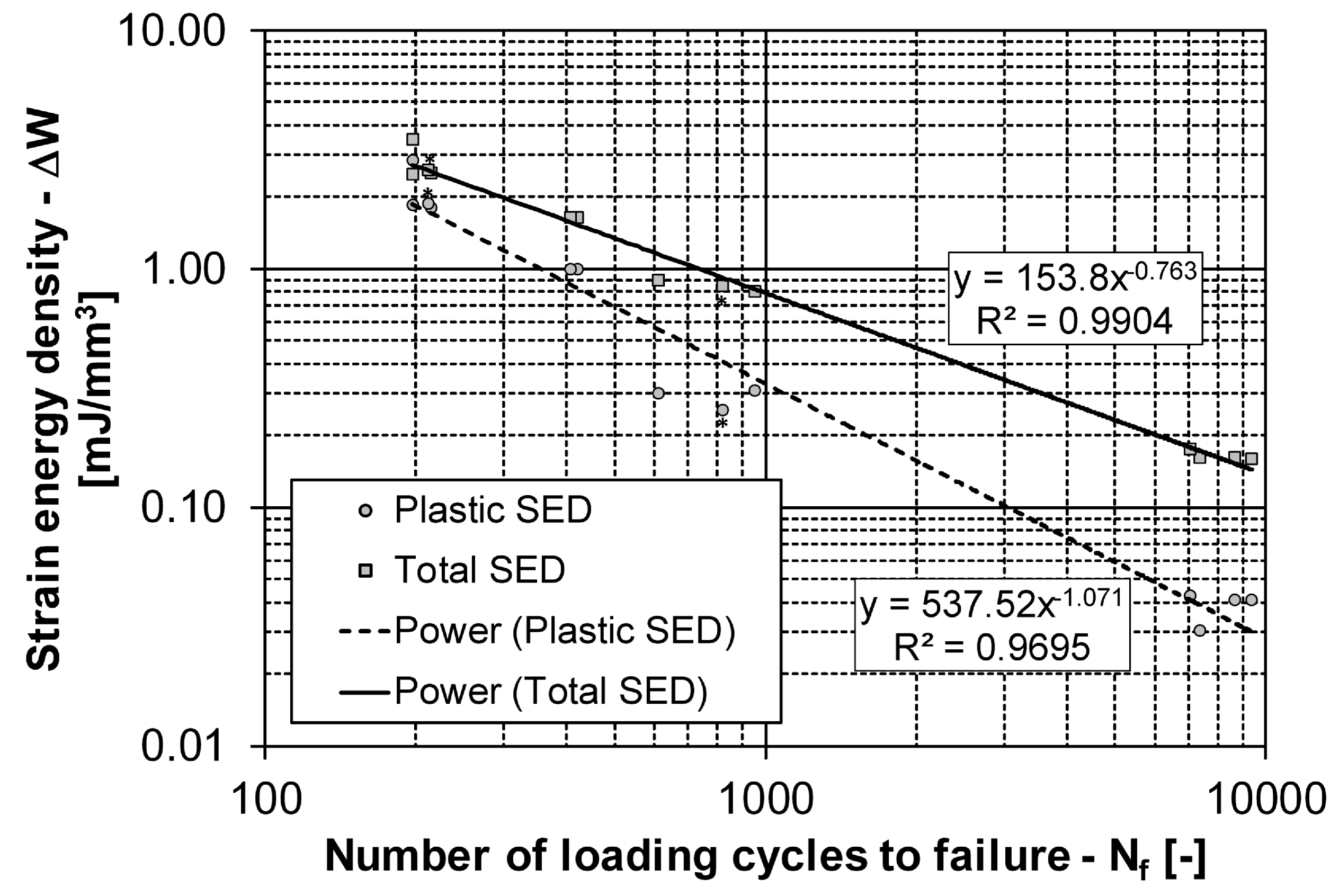
4.2. Prediction of Fatigue Life Using the Strain–Energy Density
- plastic strain–energy density : , ; and
- total strain–energy density curve : , .
5. Conclusions
- A new model for tensile and compressive elastic–plastic hysteresis loops is presented, which enables the modelling of an arbitrary hysteresis loop in the low-cycle fatigue domain with only 10 parameters.
- Static, dynamic and metallographic experiments were carried out to determine the elastic–plastic response of the AZ31 alloy and to estimate the influence of the loading direction on the microstructure of thin AZ31 sheets.
- The presented hysteresis-loop model was validated against experimental fatigue-life data that emerge from different tests: constant strain–amplitude testing, step-wise variation of the strain–amplitude levels and the arbitrary variation of strain amplitudes in a variable signal.
- An energy fatigue-life curve was determined on the basis of the experimental data that were applied for predicting the fatigue life in the low-cycle fatigue domain.
- It was proven that the fatigue lives that are predicted on the basis of the modelled hysteresis loops are equivalent to the fatigue lives that are predicted on the basis of the measured stress–strain response.
- It was shown that better fatigue-life predictions were obtained on the basis of the plastic strain–energy densities than the total strain–energy densities.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| First parameter of the scaling term in the sigmoid function | |
| Second parameter of the scaling term in the sigmoid function | |
| First parameter of the shifting term in the sigmoid function | |
| Second parameter of the shifting term in the sigmoid function | |
| k | Number of levels or data points |
| n | Hardening exponent in the Ramberg–Osgood equation |
| Number of repetitions | |
| w | Weighting factor |
| A | Scaling parameter for the exponential function |
| B | Scaling parameter for the strain in the exponential function, scaling term in the sigmoid function |
| D | Scaling parameter for the strain in the sigmoid function |
| Fatigue damage | |
| Critical fatigue damage | |
| E | Young’s modulus |
| F | Shifting term in the sigmoid function |
| K | Parameter of the Ramberg–Osgood equation related to the yield strength |
| Number of loading cycles to failure | |
| R | Load ratio |
| Sum of squared distances | |
| e | Strain |
| Extension of the partial tensile loading path to the outer-most compressive loading path along the strain axis | |
| Strain shift for the tensile/compressive loading path to ensure closing of the hysteresis loop | |
| s | Stress |
| D | Increment or interval width |
| Strain–energy density related to one hysteresis loop | |
| Strain range | |
| Strain range for the complete tensile loading path | |
| Stress range | |
| a | Index related to the amplitude quantity |
| Index related to the elastic strain–energy density | |
| Running indices | |
| Maximum value of the quantity | |
| Minimum value of the quantity | |
| p | Index related to the plastic strain–energy density |
| t | Index related to the total strain–energy density |
| C | Index related to the compressive loading path |
| DP | Index related to the data point |
| T | Index related to the tensile loading path |
References
- Demir, A.G.; Previtali, B.; Ge, Q.; Vedani, M.; Wu, W.; Migliavacca, F.; Petrini, L.; Biffi, C.A.; Bestetti, M. Biodegradable magnesium coronary stents: Material, design and fabrication. Int. J. Comput. Integr. Manuf. 2014, 27, 936–945. [Google Scholar] [CrossRef]
- Vidyasagar, A.; Tutcuoglu, A.D.; Kochmann, D.M. Deformation patterning in finite-strain crystal plasticity by spectral homogenization with application to magnesium. Comput. Method Appl. Mech. Eng. 2018, 335, 584–609. [Google Scholar] [CrossRef]
- Abdollahzadeh, A.; Shokuhfar, A.; Omidvar, H.; Cabrera, J.; Solonin, A.; Ostovari, A.; Abbasi, M. Structural evaluation and mechanical properties of AZ31/SiC nano-composite produced by friction stir welding process at various welding speeds. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 831–841. [Google Scholar] [CrossRef]
- Cauthen, C.; Daniewicz, S.R.; Shamsaei, N. Modeling fatigue crack growth behavior in rolled AZ31 magnesium alloy using CTOD based strip yield modeling. Int. J. Fatigue 2017, 96, 196–207. [Google Scholar] [CrossRef]
- Lv, F.; Yang, F.; Duan, Q.; Yang, Y.; Wu, S.; Li, S.; Zhang, Z. Fatigue properties of rolled magnesium alloy (AZ31) sheet: Influence of specimen orientation. Int. J. Fatigue 2011, 33, 672–682. [Google Scholar] [CrossRef]
- Uematsu, Y.; Kakiuchi, T.; Tamano, S.; Mizuno, S.; Tamada, K. Fatigue behavior of AZ31 magnesium alloy evaluated using single crystal micro cantilever specimen. Int. J. Fatigue 2016, 93, 30–37. [Google Scholar] [CrossRef]
- Nia, A.A.; Omidvar, H.; Nourbakhsh, S. Investigation of the effects of thread pitch and water cooling action on the mechanical strength and microstructure of friction stir processed AZ31. Mater. Des. (1980–2015) 2013, 52, 615–620. [Google Scholar]
- Sajuri, Z.B.; Miyashita, Y.; Hosokai, Y.; Mutoh, Y. Effects of Mn content and texture on fatigue properties of as-cast and extruded AZ61 magnesium alloys. Int. J. Mech. Sci. 2006, 48, 198–209. [Google Scholar] [CrossRef]
- Klemenc, J.; Šeruga, D.; Nagode, M. A Durability Prediction for the Magnesium Alloy AZ31 based on Plastic and Total Energy. Metals 2019, 9, 973. [Google Scholar] [CrossRef]
- Hasegawa, S.; Tsuchida, Y.; Yano, H.; Matsui, M. Evaluation of low cycle fatigue life in AZ31 magnesium alloy. Int. J. Fatigue 2007, 29, 1839–1845. [Google Scholar] [CrossRef]
- Nervo, L.; King, A.; Fitzner, A.; Ludwig, W.; Preuss, M. A study of deformation twinning in a titanium alloy by X-ray diffraction contrast tomography. Acta Mater. 2016, 105, 417–428. [Google Scholar] [CrossRef]
- Selvarajou, B.; Kondori, B.; Benzerga, A.A.; Joshi, S.P. On plastic flow in notched hexagonal close packed single crystals. J. Mech. Phys. Solids 2016, 94, 273–297. [Google Scholar] [CrossRef]
- Wu, P.; Guo, X.; Qiao, H.; Agnew, S.; Lloyd, D.; Embury, J. On the rapid hardening and exhaustion of twinning in magnesium alloy. Acta Mater. 2017, 122, 369–377. [Google Scholar] [CrossRef]
- Xiong, Y.; Yu, Q.; Jiang, Y. An experimental study of cyclic plastic deformation of extruded ZK60 magnesium alloy under uniaxial loading at room temperature. Int. J. Plast. 2014, 53, 107–124. [Google Scholar] [CrossRef]
- Lou, X.; Li, M.; Boger, R.; Agnew, S.; Wagoner, R. Hardening evolution of AZ31B Mg sheet. Int. J. Plast. 2007, 23, 44–86. [Google Scholar] [CrossRef]
- Šeruga, D.; Nagode, M. Comparative analysis of optimisation methods for linking material parameters of exponential and power models: An application to cyclic stress–strain curves of ferritic stainless steel. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 1802–1813. [Google Scholar] [CrossRef]
- Nagode, M.; Šeruga, D. Fatigue life prediction using multiaxial energy calculations with the mean stress effect to predict failure of linear and nonlinear elastic solids. Results Phys. 2016, 6, 352–364. [Google Scholar] [CrossRef]
- Letcher, T.; Shen, M.H.H.; Scott-Emuakpor, O.; George, T.; Cross, C. An energy-based critical fatigue life prediction method for AL6061-T6. Fatigue Fract. Eng. Mater. Struct. 2012, 35, 861–870. [Google Scholar] [CrossRef]
- Ozaltun, H.; Shen, M.H.H.; George, T.; Cross, C. An Energy Based Fatigue Life Prediction Framework for In-Service Structural Components. Exp. Mech. 2011, 51, 707–718. [Google Scholar] [CrossRef]
- Park, J.; Nelson, D. Evaluation of an energy-based approach and a critical plane approach for predicting constant amplitude multiaxial fatigue life. Int. J. Fatigue 2000, 22, 23–39. [Google Scholar] [CrossRef]
- Humayun Kabir, S.M.; Yeo, T.I. Evaluation of an energy-based fatigue approach considering mean stress effects. J. Mech. Sci. Technol. 2014, 28, 1265–1275. [Google Scholar] [CrossRef]
- Jahed, H.; Varvani-Farahani, A.; Noban, M.; Khalaji, I. An energy-based fatigue life assessment model for various metallic materials under proportional and non-proportional loading conditions. Int. J. Fatigue 2007, 29, 647–655. [Google Scholar] [CrossRef]
- Jahed, H.; Albinmousa, J. Multiaxial behaviour of wrought magnesium alloys—A review and suitability of energy-based fatigue life model. Theor. Appl. Fract. Mech. 2014, 73, 97–108. [Google Scholar] [CrossRef]
- Park, S.H.; Hong, S.G.; Lee, B.H.; Bang, W.; Lee, C.S. Low-cycle fatigue characteristics of rolled Mg–3Al–1Zn alloy. Int. J. Fatigue 2010, 32, 1835–1842. [Google Scholar] [CrossRef]
- Wang, C.; Luo, T.; Zhou, J.; Yang, Y. Anisotropic cyclic deformation behavior of extruded ZA81M magnesium alloy. Int. J. Fatigue 2017, 96, 178–184. [Google Scholar] [CrossRef]
- Dallmeier, J.; Huber, O.; Saage, H.; Eigenfeld, K. Uniaxial cyclic deformation and fatigue behavior of AM50 magnesium alloy sheet metals under symmetric and asymmetric loadings. Mater. Des. 2015, 70, 10–30. [Google Scholar] [CrossRef]
- Dallmeier, J.; Denk, J.; Huber, O.; Saage, H.; Eigenfeld, K. A phenomenological stress-strain model for wrought magnesium alloys under elastoplastic strain-controlled variable amplitude loading. Int. J. Fatigue 2015, 80, 306–323. [Google Scholar] [CrossRef]
- Lee, C.A.; Lee, M.G.; Seo, O.S.; Nguyen, N.T.; Kim, J.H.; Kim, H.Y. Cyclic behavior of AZ31B Mg: Experiments and non-isothermal forming simulations. Int. J. Plast. 2015, 75, 39–62. [Google Scholar] [CrossRef]
- Muhammad, W.; Mohammadi, M.; Kang, J.; Mishra, R.K.; Inal, K. An elasto-plastic constitutive model for evolving asymmetric/anisotropic hardening behavior of AZ31B and ZEK100 magnesium alloy sheets considering monotonic and reverse loading paths. Int. J. Plast. 2015, 70, 30–59. [Google Scholar] [CrossRef]
- Roostaei, A.A.; Jahed, H. A cyclic small-strain plasticity model for wrought Mg alloys under multiaxial loading: Numerical implementation and validation. Int. J. Mech. Sci. 2018, 145, 318–329. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; Tech. Rep. NACA-TN-902; NASA: Washington, DC, USA, 1943.
- Dowling, N. Mechanical Behaviour of Materials, 3rd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 2007. [Google Scholar]
- Haibach, E. Betriebsfestigkeit: Verfahren und Daten zur Bauteilberechnung 2. Auflage; Springer: Heidelberg, Germany, 2002. [Google Scholar]
- Jayakumar, P. Modeling and Identification in Structural Dynamics; Technical Report Report no. EERL 87-01; California Institute of Technology: Pasadena, CA, USA, 1987. [Google Scholar]
- ASTM E1049 - 85(2017). Standard Practices for Cycle Counting in Fatigue Analysis; ASTM International: West Conshohocken, PA, USA, 2017. [Google Scholar]
- Amzallag, C.; Gerey, J.; Robert, J.; Bahuaud, J. Standardization of the rainflow counting method for fatigue analysis. Int. J. Fatigue 1994, 16, 287–293. [Google Scholar] [CrossRef]
- Šeruga, D.; Nagode, M.; Klemenc, J. Eliminating friction between flat specimens and an antibuckling support during cyclic tests using a simple sensor. Meas. Sci. Technol. 2019, 30, 095102. [Google Scholar] [CrossRef]
- Šeruga, D.; Nagode, M.; Klemenc, J. Stress–Strain Response Determination during Incremental Step Tests and Variable Loadings on Flat Specimens. Technologies 2019, 7, 53. [Google Scholar] [CrossRef]
- Klemenc, J.; Fajdiga, M. Estimating S–N curves and their scatter using a differential ant-stigmergy algorithm. Int. J. Fatigue 2012, 43, 90–97. [Google Scholar] [CrossRef]
- Klemenc, J. Influence of fatigue-life data modelling on the estimated reliability of a structure subjected to a constant-amplitude loading. Reliab. Eng. Syst. Saf. 2015, 142, 238–247. [Google Scholar] [CrossRef]


| Parameter Name | Compressive Loading Path | Tensile Loading Path | ||
|---|---|---|---|---|
| Elastic Modulus | E [MPa] | 43,500 | E [MPa] | 43,500 |
| Hardening Exponent | [-] | 9.5974 | [-] | 4.2376 |
| Yield-stress-dependent Parameter | [-] | [-] | ||
| Parameters of Sigmoid Function | [-] | 193.88 | ||
| [-] | 28.395 | |||
| D [-] | 523.29 | |||
| [-] | 0.95959 | |||
| [-] | (0.38102) | |||
| Strain Cycles | Measured Data | Modelled Data | Relative Error | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cycle | |||||||||||||
| [i] | [-] | [MPa] | [] | [] | [] | [MPa] | [] | [] | [] | [-] | [-] | [-] | [-] |
| 1 | 0.0150 | 239.3 | 4.101 | 0.658 | 4.760 | 247.8 | 4.055 | 0.706 | 4.761 | 0.035 | 0.011 | −0.072 | 0.000 |
| 2 | 0.0015 | 134.5 | 0.023 | 0.208 | 0.231 | 131.7 | 0.001 | 0.196 | 0.196 | −0.020 | 0.956 | 0.059 | 0.152 |
| 3 | 0.0025 | 32.6 | 0.139 | 0.012 | 0.151 | 35.5 | 0.146 | 0.014 | 0.160 | 0.090 | −0.047 | −0.188 | −0.059 |
| 4 | 0.0050 | 86.9 | 0.685 | 0.087 | 0.771 | 86.2 | 0.657 | 0.085 | 0.742 | −0.009 | 0.041 | 0.017 | 0.038 |
| 5 | 0.0025 | 86.0 | 0.128 | 0.085 | 0.213 | 86.1 | 0.145 | 0.085 | 0.230 | 0.001 | −0.135 | −0.003 | −0.082 |
| 6 | 0.0038 | 51.6 | 0.352 | 0.031 | 0.383 | 51.7 | 0.375 | 0.031 | 0.406 | 0.002 | −0.066 | −0.005 | −0.061 |
| 7 | 0.0030 | 32.1 | 0.211 | 0.012 | 0.222 | 33.8 | 0.229 | 0.013 | 0.243 | 0.053 | −0.090 | −0.109 | −0.091 |
| 8 | 0.0015 | 23.2 | 0.039 | 0.006 | 0.046 | 25.5 | 0.032 | 0.007 | 0.039 | 0.099 | 0.194 | −0.207 | 0.139 |
| 9 | 0.0037 | 136.8 | 0.311 | 0.215 | 0.526 | 148.4 | 0.315 | 0.253 | 0.568 | 0.085 | −0.015 | −0.177 | −0.081 |
| 10 | 0.0030 | 151.5 | 0.122 | 0.264 | 0.386 | 162.0 | 0.153 | 0.302 | 0.455 | 0.069 | −0.259 | −0.144 | −0.180 |
| Strain Cycles | Measured Data | Modelled Data | Relative Error | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cycle | |||||||||||||
| [i] | [-] | [MPa] | [] | [] | [] | [MPa] | [] | [] | [] | [-] | [-] | [-] | [-] |
| 1 | 0.0150 | 237.7 | 4.175 | 0.649 | 4.824 | 242.3 | 4.063 | 0.675 | 4.738 | 0.019 | 0.027 | −0.039 | 0.018 |
| 2 | 0.0025 | 117.5 | 0.069 | 0.159 | 0.228 | 111.1 | 0.122 | 0.142 | 0.264 | −0.055 | −0.771 | 0.106 | −0.160 |
| 3 | 0.0030 | 89.6 | 0.188 | 0.092 | 0.280 | 86.0 | 0.217 | 0.085 | 0.302 | −0.041 | −0.155 | 0.080 | −0.077 |
| 4 | 0.0075 | 237.2 | 1.160 | 0.647 | 1.807 | 242.3 | 1.122 | 0.675 | 1.797 | 0.021 | 0.033 | −0.043 | 0.006 |
| 5 | 0.0150 | 240.4 | 4.285 | 0.664 | 4.950 | 241.8 | 4.054 | 0.672 | 4.726 | 0.005 | 0.054 | −0.011 | 0.045 |
| 6 | 0.0110 | 150.9 | 2.751 | 0.262 | 3.013 | 151.4 | 2.532 | 0.264 | 2.795 | 0.004 | 0.080 | −0.008 | 0.072 |
| 7 | 0.0090 | 117.7 | 1.969 | 0.159 | 2.128 | 110.9 | 1.833 | 0.141 | 1.975 | −0.058 | 0.069 | 0.113 | 0.072 |
| 8 | 0.0070 | 118.8 | 1.298 | 0.162 | 1.460 | 110.8 | 1.201 | 0.141 | 1.342 | −0.067 | 0.075 | 0.129 | 0.081 |
| 9 | 0.0130 | 158.7 | 3.521 | 0.289 | 3.810 | 156.5 | 3.321 | 0.281 | 3.602 | −0.014 | 0.057 | 0.027 | 0.055 |
| 10 | 0.0095 | 135.0 | 2.174 | 0.209 | 2.383 | 134.2 | 2.089 | 0.207 | 2.296 | -0.006 | 0.039 | 0.012 | 0.037 |
| 11 | 0.0075 | 118.8 | 1.446 | 0.162 | 1.608 | 120.1 | 1.415 | 0.166 | 1.581 | 0.010 | 0.021 | −0.021 | 0.017 |
| 12 | 0.0025 | 12.6 | 0.145 | 0.002 | 0.147 | 10.8 | 0.142 | 0.001 | 0.144 | −0.139 | 0.020 | 0.259 | 0.023 |
| 13 | 0.0035 | 72.0 | 0.296 | 0.060 | 0.355 | 63.4 | 0.325 | 0.046 | 0.371 | −0.119 | −0.098 | 0.225 | −0.044 |
| 14 | 0.0020 | 41.9 | 0.084 | 0.016 | 0.100 | 34.3 | 0.080 | 0.013 | 0.094 | −0.078 | 0.042 | 0.149 | 0.059 |
| 15 | 0.0010 | 11.6 | 0.018 | 0.002 | 0.020 | 6.0 | 0.007 | 0.000 | 0.007 | −0.480 | 0.633 | 0.729 | 0.641 |
| 16 | 0.0025 | 114.4 | 0.122 | 0.150 | 0.273 | 108.0 | 0.131 | 0.134 | 0.264 | −0.056 | −0.068 | 0.109 | 0.030 |
| 17 | 0.0015 | 92.3 | 0.038 | 0.098 | 0.136 | 90.8 | 0.034 | 0.095 | 0.129 | −0.017 | 0.092 | 0.033 | 0.049 |
| 18 | 0.0050 | 113.9 | 0.686 | 0.149 | 0.836 | 108.1 | 0.646 | 0.134 | 0.780 | −0.051 | 0.060 | 0.100 | 0.067 |
| 19 | 0.0025 | 56.0 | 0.146 | 0.036 | 0.182 | 56.6 | 0.145 | 0.037 | 0.182 | 0.009 | 0.005 | −0.019 | 0.000 |
| 20 | 0.0015 | 31.1 | 0.037 | 0.011 | 0.048 | 36.4 | 0.034 | 0.015 | 0.049 | 0.169 | 0.081 | −0.366 | −0.023 |
| 21 | 0.0025 | 218.9 | 0.050 | 0.551 | 0.601 | 219.2 | 0.001 | 0.481 | 0.481 | 0.002 | 0.980 | 0.126 | 0.199 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klemenc, J.; Šeruga, D.; Nagode, A.; Nagode, M. Comprehensive Modelling of the Hysteresis Loops and Strain–Energy Density for Low-Cycle Fatigue-Life Predictions of the AZ31 Magnesium Alloy. Materials 2019, 12, 3692. https://doi.org/10.3390/ma12223692
Klemenc J, Šeruga D, Nagode A, Nagode M. Comprehensive Modelling of the Hysteresis Loops and Strain–Energy Density for Low-Cycle Fatigue-Life Predictions of the AZ31 Magnesium Alloy. Materials. 2019; 12(22):3692. https://doi.org/10.3390/ma12223692
Chicago/Turabian StyleKlemenc, Jernej, Domen Šeruga, Aleš Nagode, and Marko Nagode. 2019. "Comprehensive Modelling of the Hysteresis Loops and Strain–Energy Density for Low-Cycle Fatigue-Life Predictions of the AZ31 Magnesium Alloy" Materials 12, no. 22: 3692. https://doi.org/10.3390/ma12223692
APA StyleKlemenc, J., Šeruga, D., Nagode, A., & Nagode, M. (2019). Comprehensive Modelling of the Hysteresis Loops and Strain–Energy Density for Low-Cycle Fatigue-Life Predictions of the AZ31 Magnesium Alloy. Materials, 12(22), 3692. https://doi.org/10.3390/ma12223692








