Fatigue Life for Different Stress Concentration Factors for Stainless Steel 1.4301
Abstract
1. Introduction
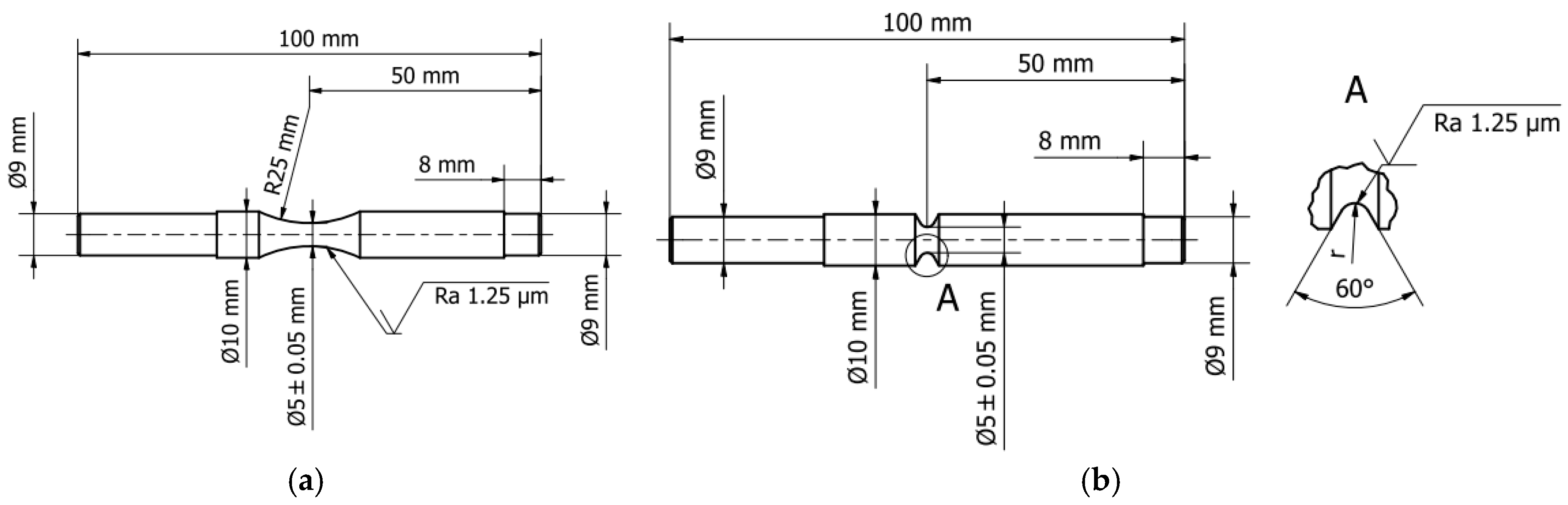
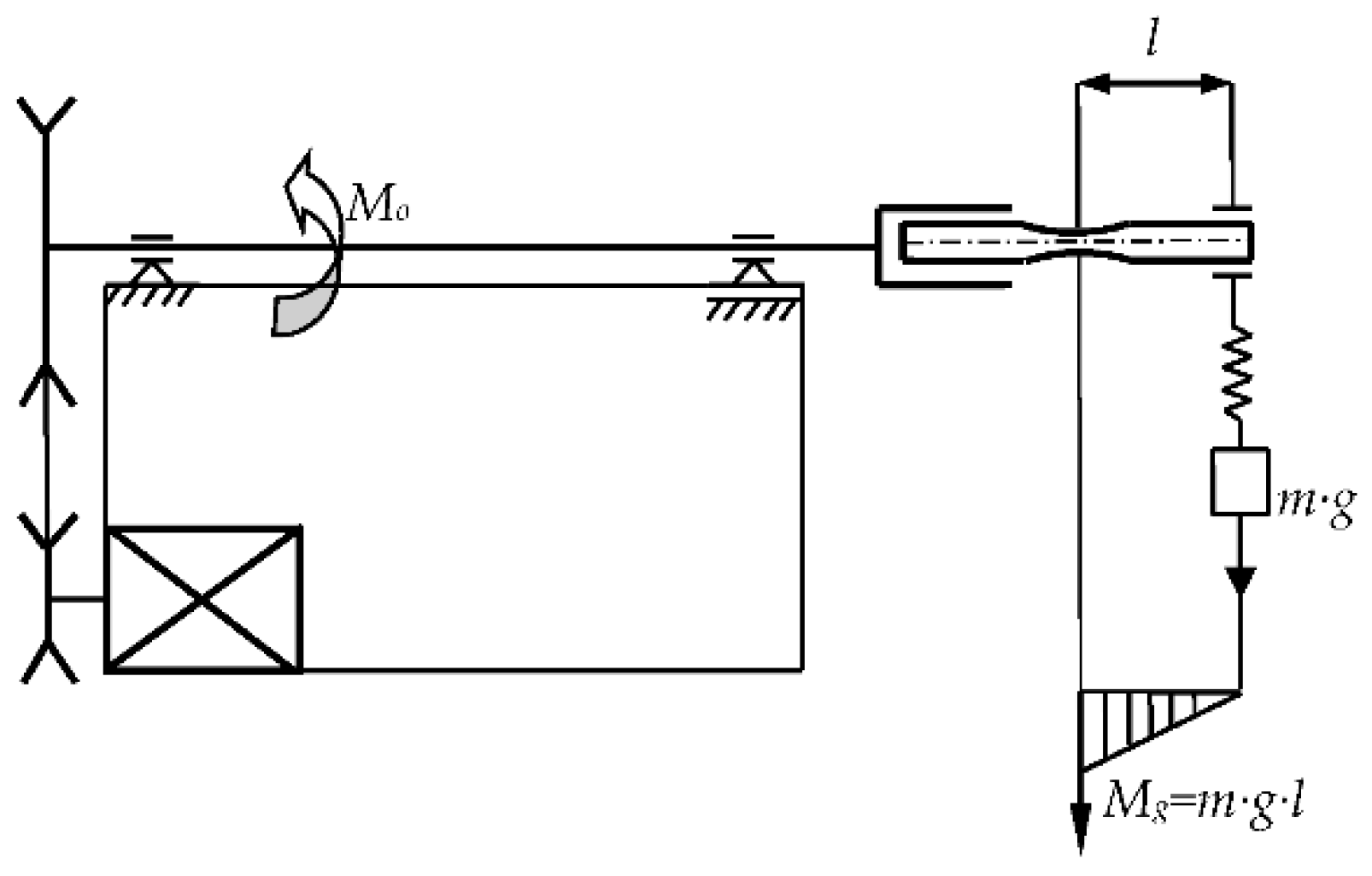
2. Materials and Methods
3. Results
- αv
- the shape parameter,
- β (Si)
- the scale parameter 10m⋅log(S)+b,
- ξ(Si)
- the location parameter 10n⋅log(S)+d,
- b
- constant term in an S–N curve equation,
- d
- constant term in an S–N curve equation in the location parameter,
- m
- scale coefficient in an S–N curve equation,
- n
- scale coefficient in an S–N curve equation in the location parameter.
- V
- the coefficient of variation
- Γ
- gamma function
- σx
- standard deviation of the 3-parameter Weibull distribution for 105 cycles
- μx
- expected value of the 3-parameter Weibull distribution for 105 cycles.
4. Discussion
5. Conclusions
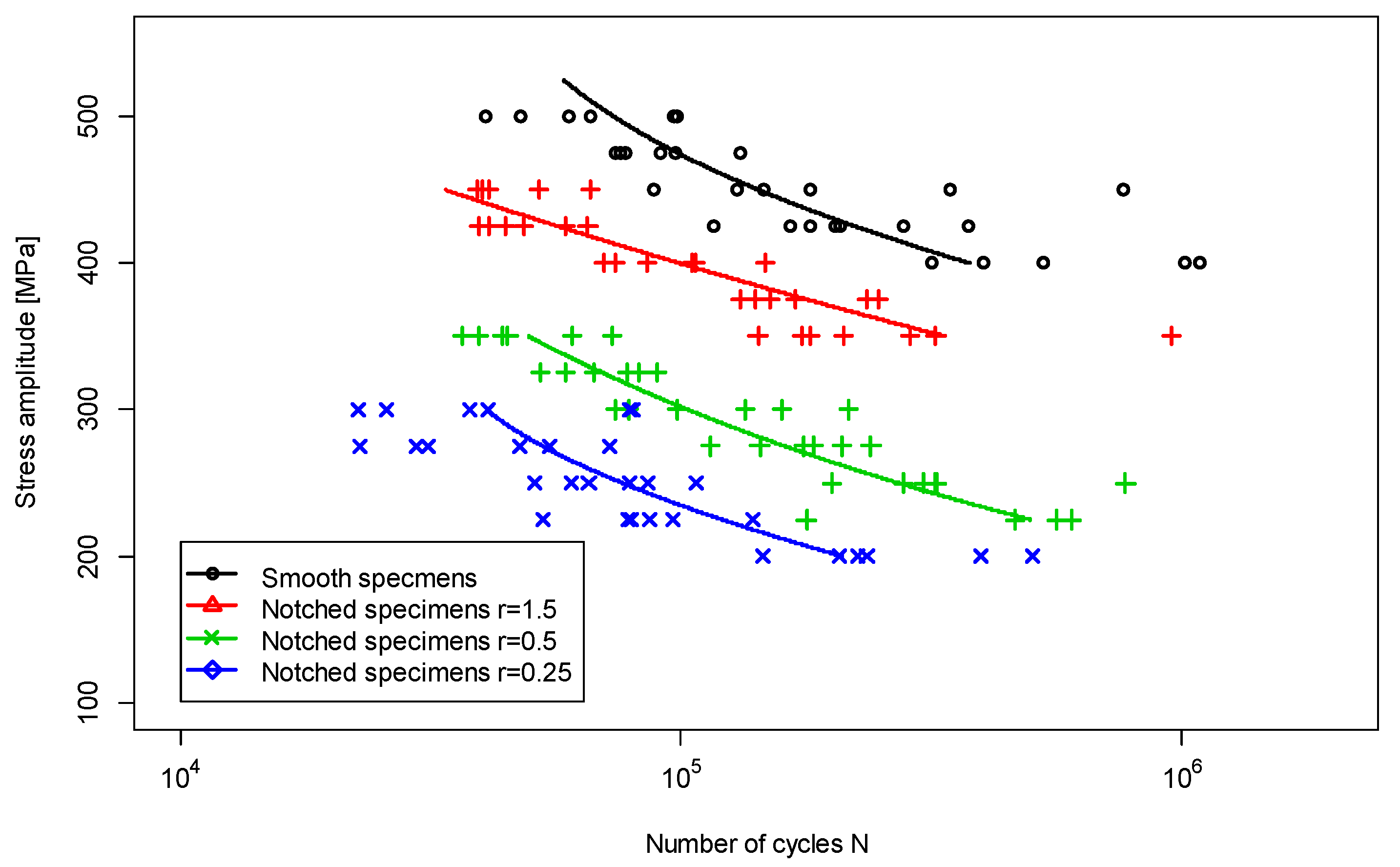
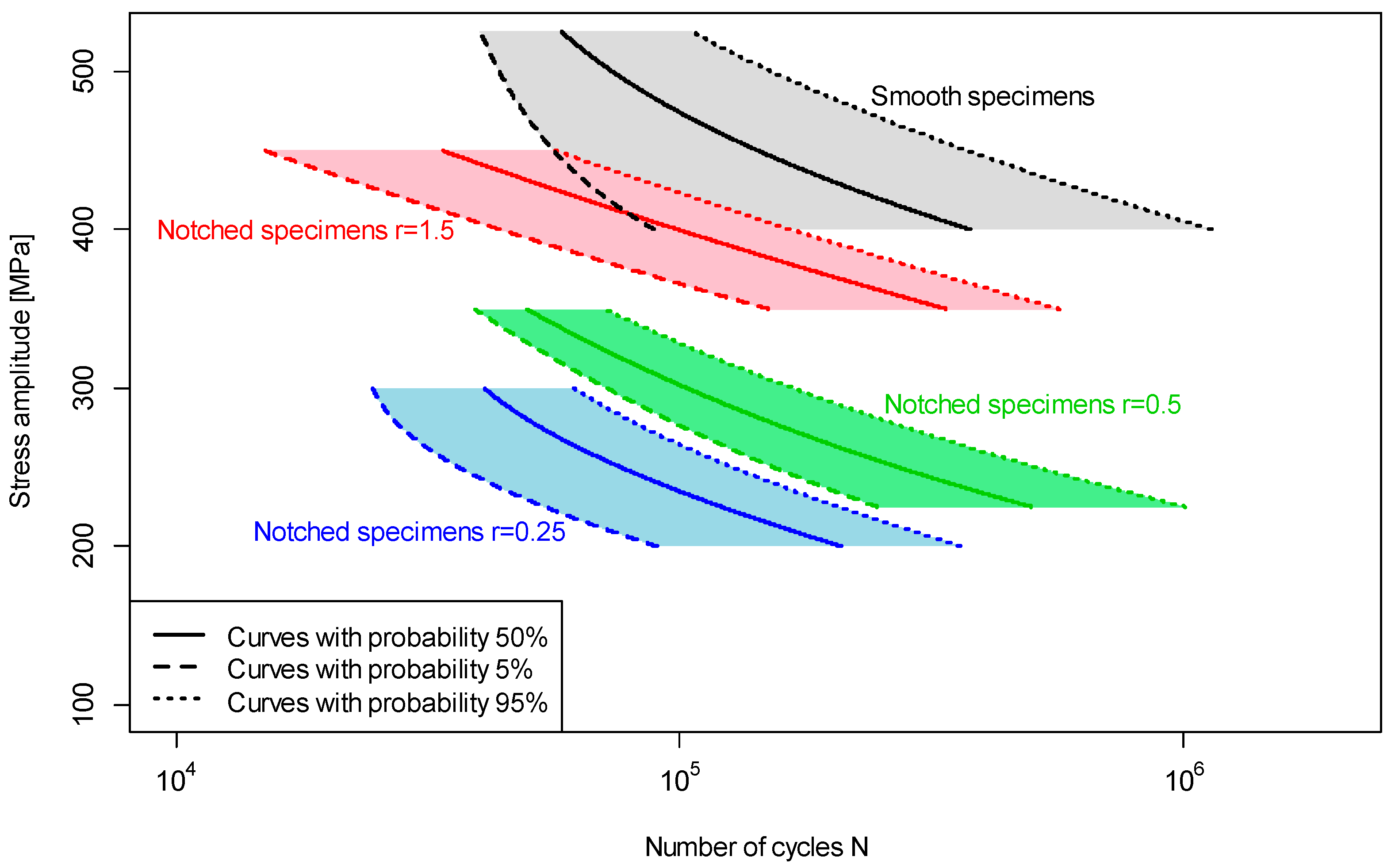
- notched samples feature lower fatigue life scatter than smooth samples,
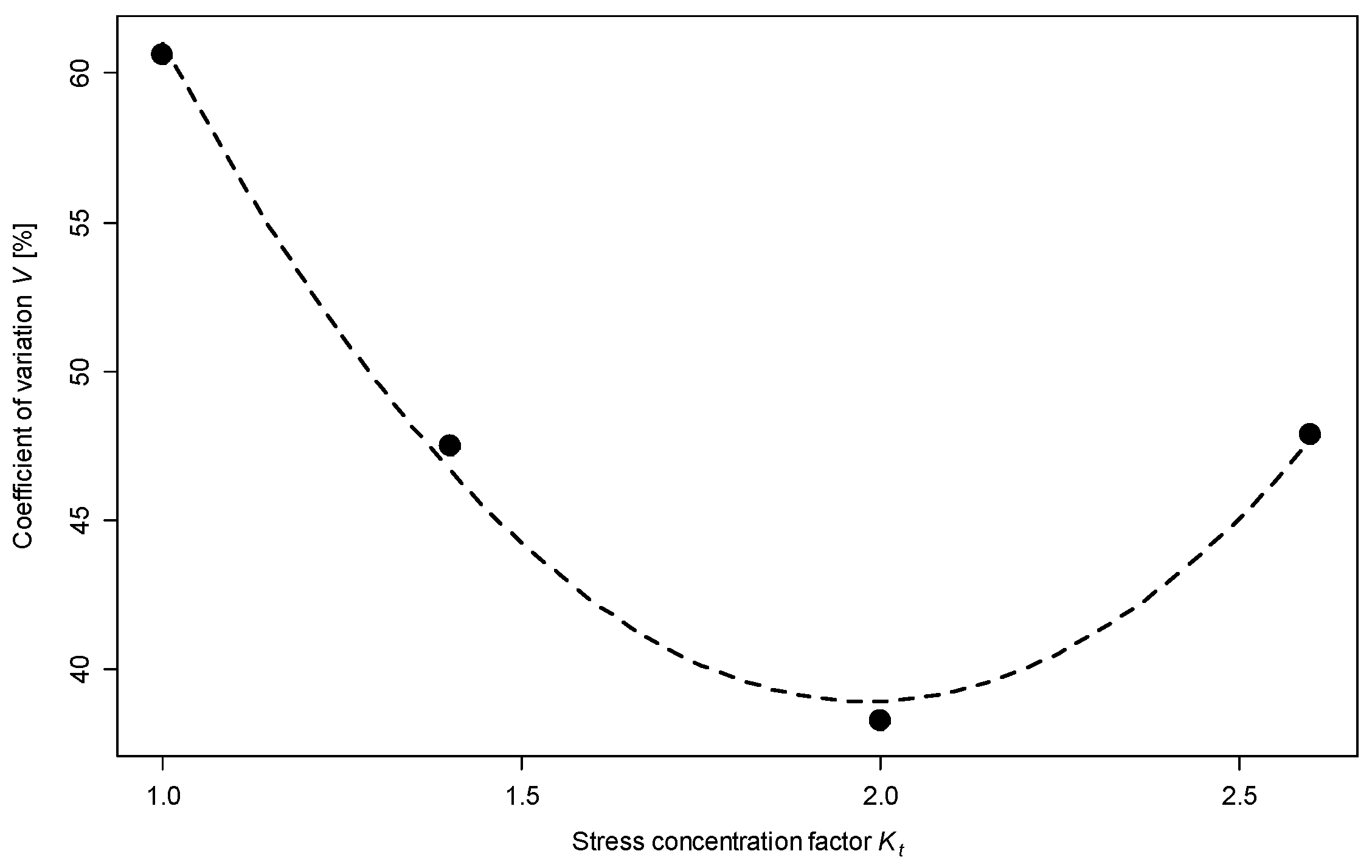
- increase in the stress concentration factor decreases the scatter of results,
- an increase in the scatter of fatigue life was observed for samples with Kt = 2.6, explained by the higher sensitivity of notched samples to the accuracy of sample preparation techniques,
- which can be further explained by a different load gradient for a specific sample geometry, which in turn should be verified in further studies.
Author Contributions
Funding
Conflicts of Interest
References
- Forum, I.S.S. Global Consolidation Stainless Steel Cold All Products Consumption Index. International Stainless Steel. Available online: http://www.worldstainless.org/Files/issf/non-image-files/PDF/statistics/190527_SCF_Public.pdf (accessed on 27 May 2019).
- International Stainless Steel Forum Stainless Steel in Figures 2019; International Stainless Steel. Available online: http://www.worldstainless.org/Files/issf/non-image-files/PDF/ISSF_Stainless_Steel_in_Figures_2019_English_public_version.pdf (accessed on 27 May 2019).
- Mohd, S.; Bhuiyan, M.S.; Nie, D.; Otsuka, Y.; Mutoh, Y. Fatigue strength scatter characteristics of JIS SUS630 stainless steel with duplex S-N curve. Int. J. Fatigue 2015, 82, 371–378. [Google Scholar] [CrossRef]
- Akita, M.; Nakajima, M.; Uematsu, Y.; Tokaji, K.; Jung, J.-W. Some factors exerting an influence on the coaxing effect of austenitic stainless steels. Fatigue Fract. Eng. Mater. Struct. 2012, 35, 1095–1104. [Google Scholar] [CrossRef]
- Brnic, J.; Turkalj, G.; Canadija, M.; Lanc, D.; Krscanski, S.; Brcic, M.; Li, Q.; Niu, J. Mechanical properties, short time creep, and fatigue of an austenitic steel. Materials 2016, 9, 298. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Han, K.; Li, D.; Cao, Z. Microstructure and Mechanical Properties Investigation of the CoCrFeNiNbx High Entropy Alloy Coatings. Crystals 2018, 8, 409. [Google Scholar] [CrossRef]
- Tomaszewski, T. Analysis of the statistical size effect model with a critical volume in the range of high-cycle fatigue. Proced. Struct. Integr. 2018, 13, 1756–1761. [Google Scholar] [CrossRef]
- Lee, Y.L.; Paw, J.; Hathaway, R.B.; Barkey, M.E. Fatigue Testing and Analysis—Theory and Practice; Elsevier Butterworth–Heinemann: Oxford, UK, 2005; ISBN 978-0-7506-7719-6. [Google Scholar]
- Ai, Y.; Zhu, S.P.; Liao, D.; Correia, J.A.F.O.; De Jesus, A.M.P.; Keshtegar, B. Probabilistic modelling of notch fatigue and size effect of components using highly stressed volume approach. Int. J. Fatigue 2019, 127, 110–119. [Google Scholar] [CrossRef]
- Strzelecki, P.; Sempruch, J.; Nowicki, K. Comparing guidelines concerning construction of the S-N curve within limited fatigue life range. Polish Marit. Res. 2015, 22, 67–74. [Google Scholar] [CrossRef]
- Kurek, M.; Lagoda, T.; Katzy, D. Comparison of Fatigue Characteristics of some Selected Materials. Mater. Test. 2014, 56, 92–95. [Google Scholar] [CrossRef]
- ASTM E-739-91. Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (S-N) and Strain-Life (ε-N) Fatigue Data; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- ISO-12107. Metallic Materials—Fatigue Testing—Statistical Planning and Analysis of Data; ISO: Geneva, Switzerland, 2012. [Google Scholar]
- Loren, S. Fatigue limit estimated using finite lives. Fatigue Fract. Eng. Mater. Struct. 2003, 26, 757–766. [Google Scholar] [CrossRef]
- Rinne, H. The Weibull Distribution; Chapman and Hall/CRC: Boca Raton, FL, USA, 2008; ISBN 9780429142574. [Google Scholar]
- Strzelecki, P.; Tomaszewski, T. Application of Weibull distribution to describe S-N curve with using small number specimens. AIP Conf. Proc. 2016, 1780, 020007. [Google Scholar]
- Klemenc, J.; Fajdiga, M. Estimating S-N curves and their scatter using a differential ant-stigmergy algorithm. Int. J. Fatigue 2012, 43, 90–97. [Google Scholar] [CrossRef]
- Topoliński, T.; Cichański, A.; Mazurkiewicz, A.; Nowicki, K. Fatigue Energy Dissipation in Trabecular Bone Samples with Stepwise-Increasing Amplitude Loading*. Mater. Test. 2011, 53, 344–350. [Google Scholar] [CrossRef]
- Strzelecki, P.; Sempruch, J. Verification of analytical models of the S-N curve within limited fatigue life. J. Theor. Appl. Mech. 2016, 54, 63. [Google Scholar] [CrossRef]
- Schijve, J. Fatigue of Structures and Materials, 2nd ed.; Springer Science+Business Media: Berlin, Germany, 2009; ISBN 978-1-4020-6807-2. [Google Scholar]
- EN 10088-1. Stainless Steels—Part 1: List of Stainless Steels Aciers; CEN: Brussels, Belgium, 2014. [Google Scholar]
- PN-EN 10278. Dimensions and Tolerances of Bright Steel Products; Polish Committee for Standardization: Warsaw, Poland, 2003. [Google Scholar]
- PN-EN ISO 6892-1:2016. Metallic Materials—Tensile Testing—Part. 1: Method of Test at Room Temperature; Polish Committee for Standardization: Warsaw, Poland, 2016. [Google Scholar]
- Boroński, D.; Kotyk, M.; Maćkowiak, P.; Śnieżek, L. Mechanical properties of explosively welded AA2519-AA1050-Ti6Al4V layered material at ambient and cryogenic conditions. Mater. Des. 2017, 133, 390–403. [Google Scholar] [CrossRef]
- Strzelecki, P.; Sempruch, J. Experimental Verification of the Analytical Method for Estimated S-N Curve in Limited Fatigue Life. Mater. Sci. Forum 2012, 726, 11–16. [Google Scholar] [CrossRef]
- ISO-1143. Metallic Materials—Rotating Bar Bending Fatigue Testing; ISO: Geneva, Switzerland, 2010. [Google Scholar]
- EN 10088-3. Stainless Steels—Part 3: Technical Delivery Conditions for Semi-Finished Products, Bars, Rods, Wire, Sections and Bright Products of Corrosion Resisting Steels for General Purposes; DIN: Berlin, Germany, 2005. [Google Scholar]
- EN 10088-4. Stainless Steels—Part 4: Technical Delivery Conditions for Sheet/Plate and Strip of Corrosion Resisting Steels for Construction Purposes; BSI: London, UK, 2010. [Google Scholar]
- ASTM E-112-12. Standard Test. Methods for Determining Average Grain Size; ASTM International: West Conshohocken, PA, USA, 2012. [Google Scholar]
- Kocańda, S.; Szala, J. Basis of Calculation of Fatigue; Wydawnictwo Naukowe PWN: Warsaw, Poland, 1997. (In Polish) [Google Scholar]
- Weibull, W. A Statistical Representation of Fatigue Failures in Solids; Elanders boktr.: Stockholm, Sweden, 1949. [Google Scholar]
- Ling, J.; Pan, J. A maximum likelihood method for estimating P_S_N curves. Int. J. Fatigue 1997, 19, 415–419. [Google Scholar] [CrossRef]
- Strzelecki, P.; Tomaszewski, T.; Sempruch, J. A method for determining a complete S-N curve using maximum likelihood. In Proceedings of the 22nd International Conference on Engineering Mechanics, Svratka, Czech Republic, 9–12 May 2016; Zolotarev, I., Radolf, V., Eds.; Institute of Thermomechanics of the Czech Academy of Sciences: Svratka, Czech Republic, 2016; pp. 530–533. [Google Scholar]
- Pollak, R.D.; Palazotto, A.N. A comparison of maximum likelihood models for fatigue strength characterization in materials exhibiting a fatigue limit. Probab. Eng. Mech. 2009, 24, 236–241. [Google Scholar] [CrossRef]
- R Core Team R: A Language and Environment for Statistical Computing; R Core Team R: Vienna, Austria, 2015.
- Strzelecki, P. Scatter of fatigue life regarding stress concentration factor. Proced. Struct. Integr. 2018, 13, 631–635. [Google Scholar] [CrossRef]
- PN-EN 13749 Railway Applications—Wheelsets and Bogies—Method of Specifying the Structural Requirements of Bogie Frames; CEN: Brussels, Belgium, 2011.
- Weibull, W. A Statistical Theory of the Strength of Materials; Generalstabens litografiska anstalts förlag: Stockholm, Sweden, 1939; p. 151. [Google Scholar]
- Gope, P.C. Scatter analysis of fatigue life and prediction of S-N curve. J. Fail. Anal. Prev. 2012, 12, 507–517. [Google Scholar] [CrossRef]
- Zheng, X.; Engler-Pinto, C.; Su, X.; Cui, H.; Wen, W. Correlation between Scatter in Fatigue Life and Fatigue Crack Initiation Sites in Cast Aluminum Alloys. SAE Int. J. Mater. Manuf. 2012, 5, 270–276. [Google Scholar] [CrossRef]
- Mohd, S.; Mutoh, Y.; Otsuka, Y.; Miyashita, Y.; Koike, T.; Suzuki, T. Scatter analysis of fatigue life and pore size data of die-cast AM60B magnesium alloy. Eng. Fail. Anal. 2012, 22, 64–72. [Google Scholar] [CrossRef]
- Siqueira, A.F.; Baptista, C.A.R.P.; Molent, L. On the determination of a scatter factor for fatigue lives based on the lead crack concept. J. Aerosp. Technol. Manag. 2013, 5, 223–230. [Google Scholar] [CrossRef]
- Ai, Y.; Zhu, S.P.; Liao, D.; Correia, J.A.F.O.; Souto, C.; De Jesus, A.M.P.; Keshtegar, B. Probabilistic modeling of fatigue life distribution and size effect of components with random defects. Int. J. Fatigue 2019, 126, 165–173. [Google Scholar] [CrossRef]
- Murakami, Y. Material defects as the basis of fatigue design. Int. J. Fatigue 2012, 41, 2–10. [Google Scholar] [CrossRef]

| % by Mass | |||||||
|---|---|---|---|---|---|---|---|
| Item | C | Si | Mn | P | S | Cr | Ni |
| Standard requirements [21] | ≤0.07 | ≤1.00 | ≤2.00 | ≤0.045 | ≤0.015 | 17.5–19.5 | 8.0–10.5 |
| Measured value | 0.05 | 0.75 | 1.56 | 0.043 | 0.010 | 18.1 | 9.7 |
| No. | r [mm] | Kt [-] |
|---|---|---|
| 1 | 1.5 | 1.4 |
| 2 | 0.5 | 2 |
| 3 | 0.25 | 2.6 |
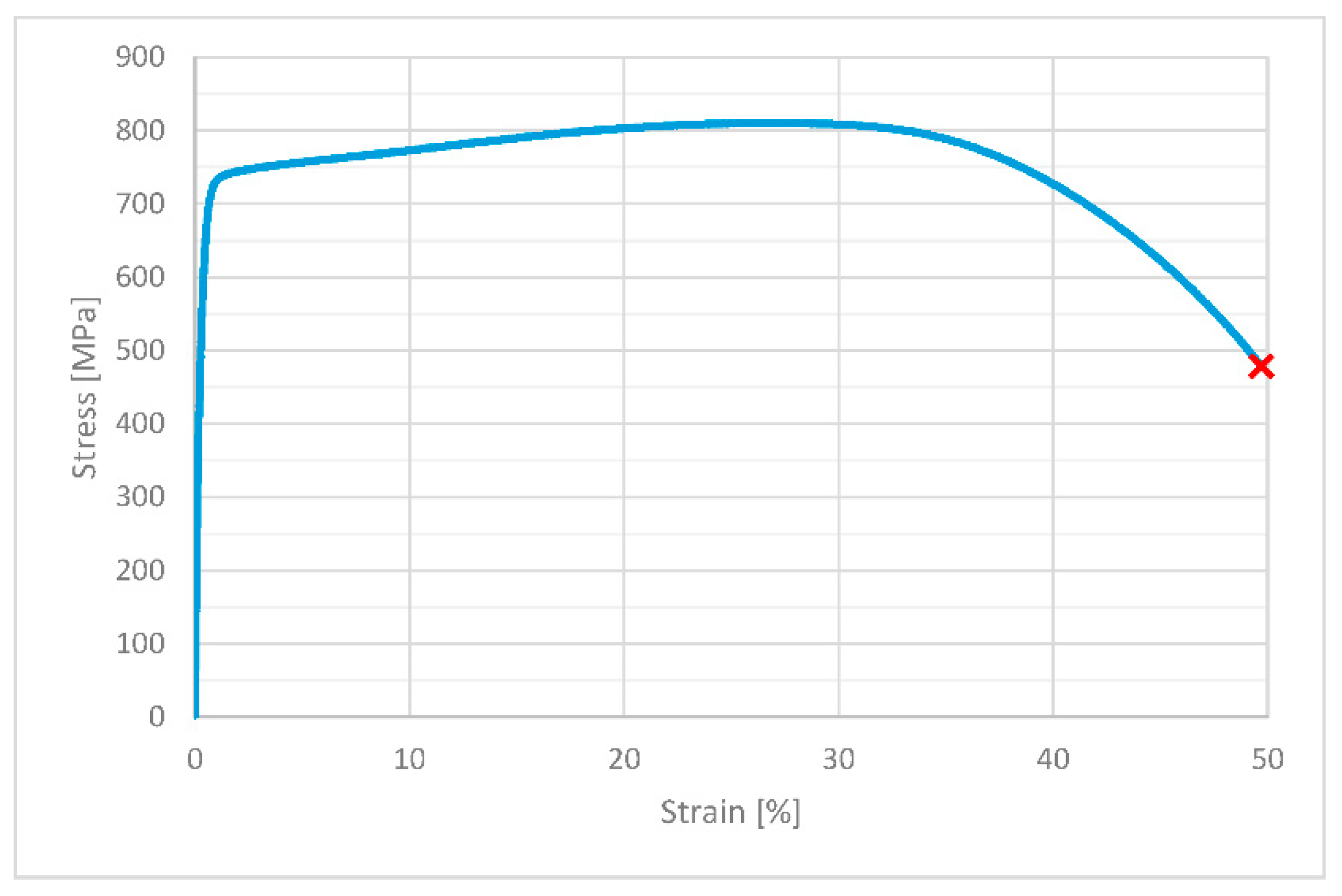
| E [MPa] | Su [MPa] | Sy [MPa] | A [%] | Z [%] |
|---|---|---|---|---|
| 206 553 | 803 | 561 | 78.3 | 43.8 |
| Geometry of Specimen | r, [mm] | αv | m | b | n | d |
|---|---|---|---|---|---|---|
| Smooth | 25 | 1.21 | −10.2 | 32.1 | −1.08 | 7.52 |
| Notched | 1.5 | 2.32 | −9.2 | 28.9 | −2.72 | 2.24 |
| 0.5 | 1.27 | −7.2 | 22.6 | −3.54 | 13.57 | |
| 0.25 | 2.16 | −4.9 | 16.7 | 2.83 | −2.89 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strzelecki, P.; Mazurkiewicz, A.; Musiał, J.; Tomaszewski, T.; Słomion, M. Fatigue Life for Different Stress Concentration Factors for Stainless Steel 1.4301. Materials 2019, 12, 3677. https://doi.org/10.3390/ma12223677
Strzelecki P, Mazurkiewicz A, Musiał J, Tomaszewski T, Słomion M. Fatigue Life for Different Stress Concentration Factors for Stainless Steel 1.4301. Materials. 2019; 12(22):3677. https://doi.org/10.3390/ma12223677
Chicago/Turabian StyleStrzelecki, Przemysław, Adam Mazurkiewicz, Janusz Musiał, Tomasz Tomaszewski, and Małgorzata Słomion. 2019. "Fatigue Life for Different Stress Concentration Factors for Stainless Steel 1.4301" Materials 12, no. 22: 3677. https://doi.org/10.3390/ma12223677
APA StyleStrzelecki, P., Mazurkiewicz, A., Musiał, J., Tomaszewski, T., & Słomion, M. (2019). Fatigue Life for Different Stress Concentration Factors for Stainless Steel 1.4301. Materials, 12(22), 3677. https://doi.org/10.3390/ma12223677






