Study on Rheological Behavior and Surface Properties of Epoxy Resin Chemical Grouting Material Considering Time Variation
Abstract
1. Introduction
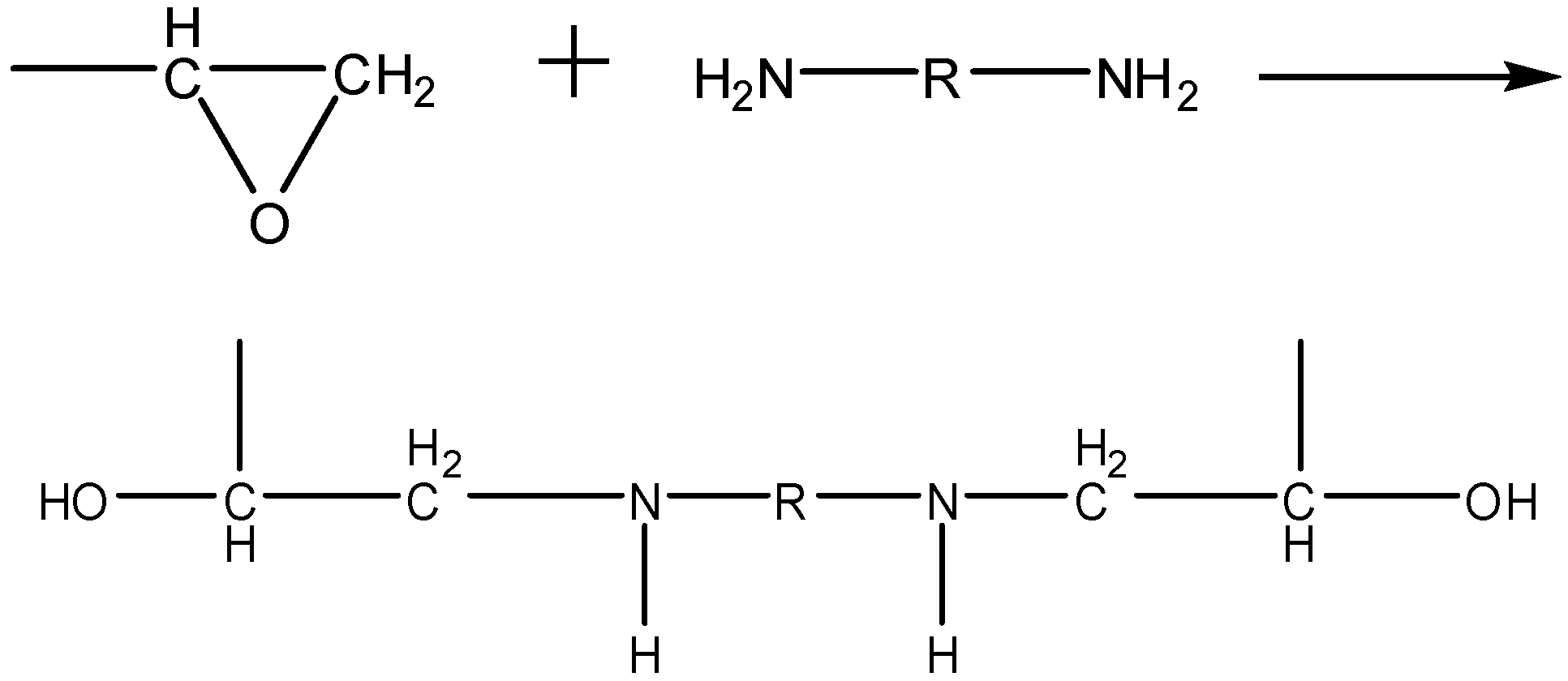
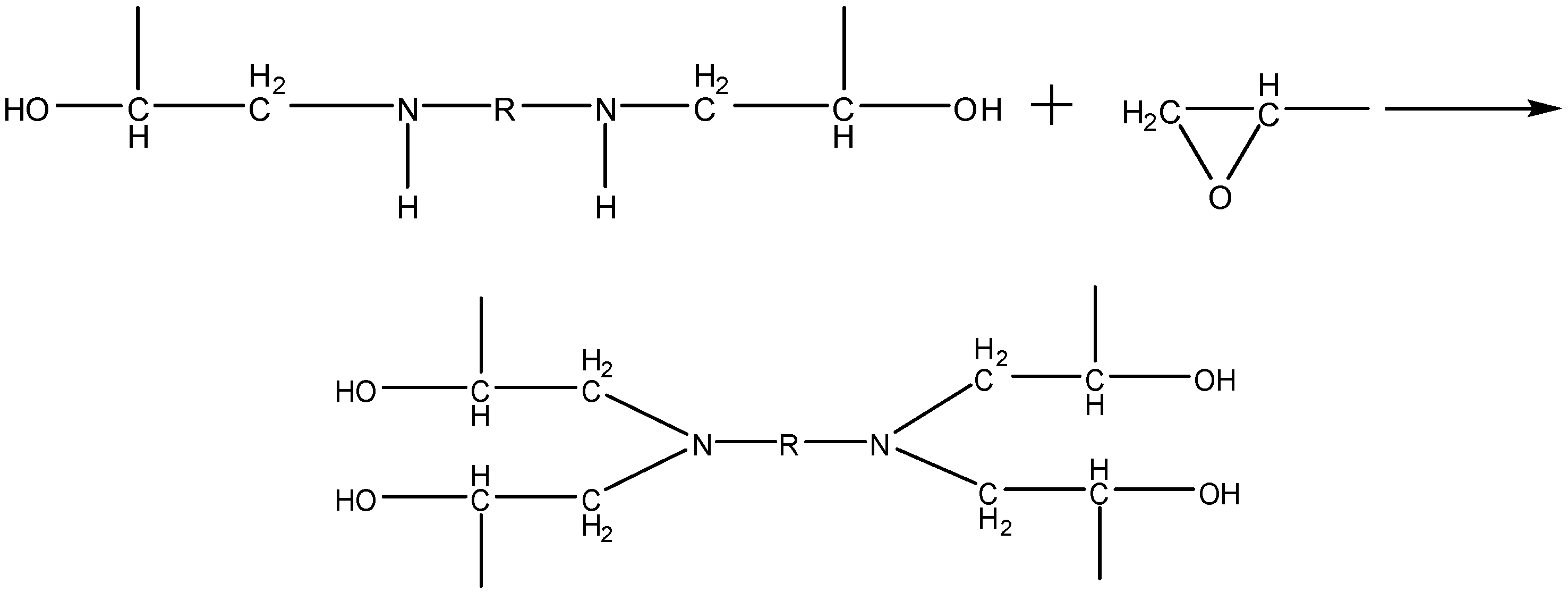
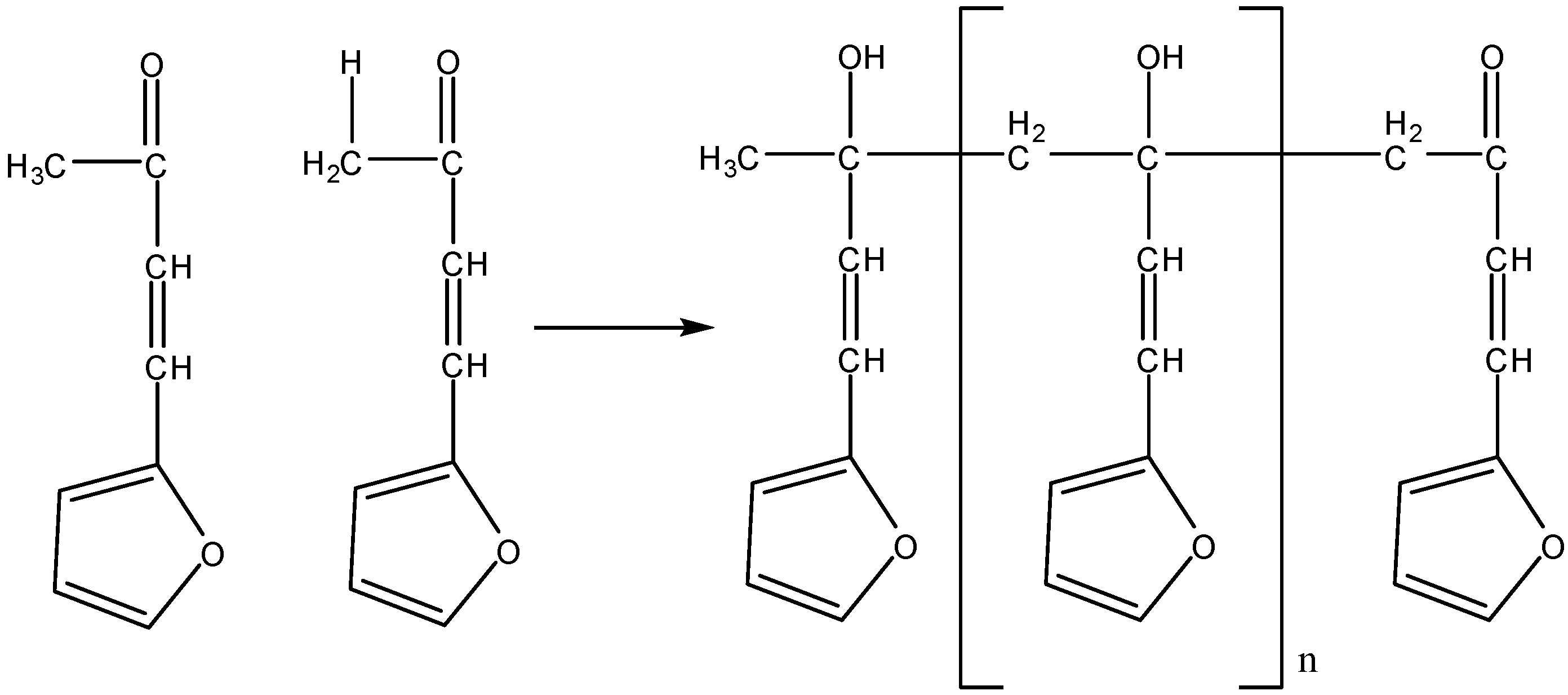
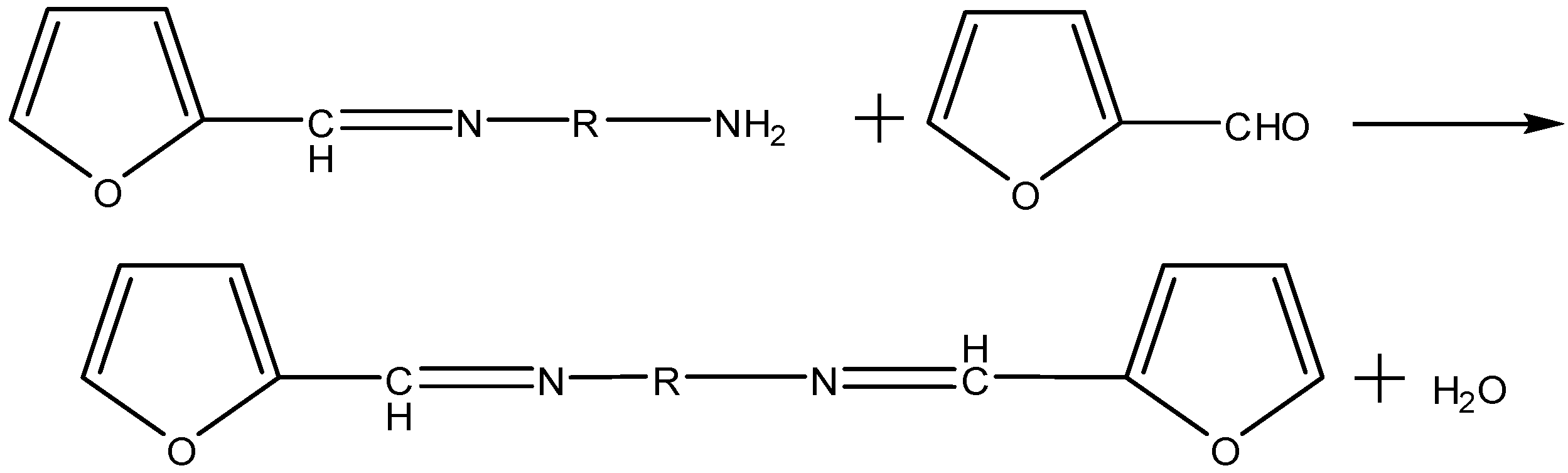
2. Characteristics of CW Epoxy Resin Grouting Material
3. Materials and Methods
3.1. Testing Materials and Preparation Methods
3.2. Testing Equipment and Methods
4. Results and Discussion
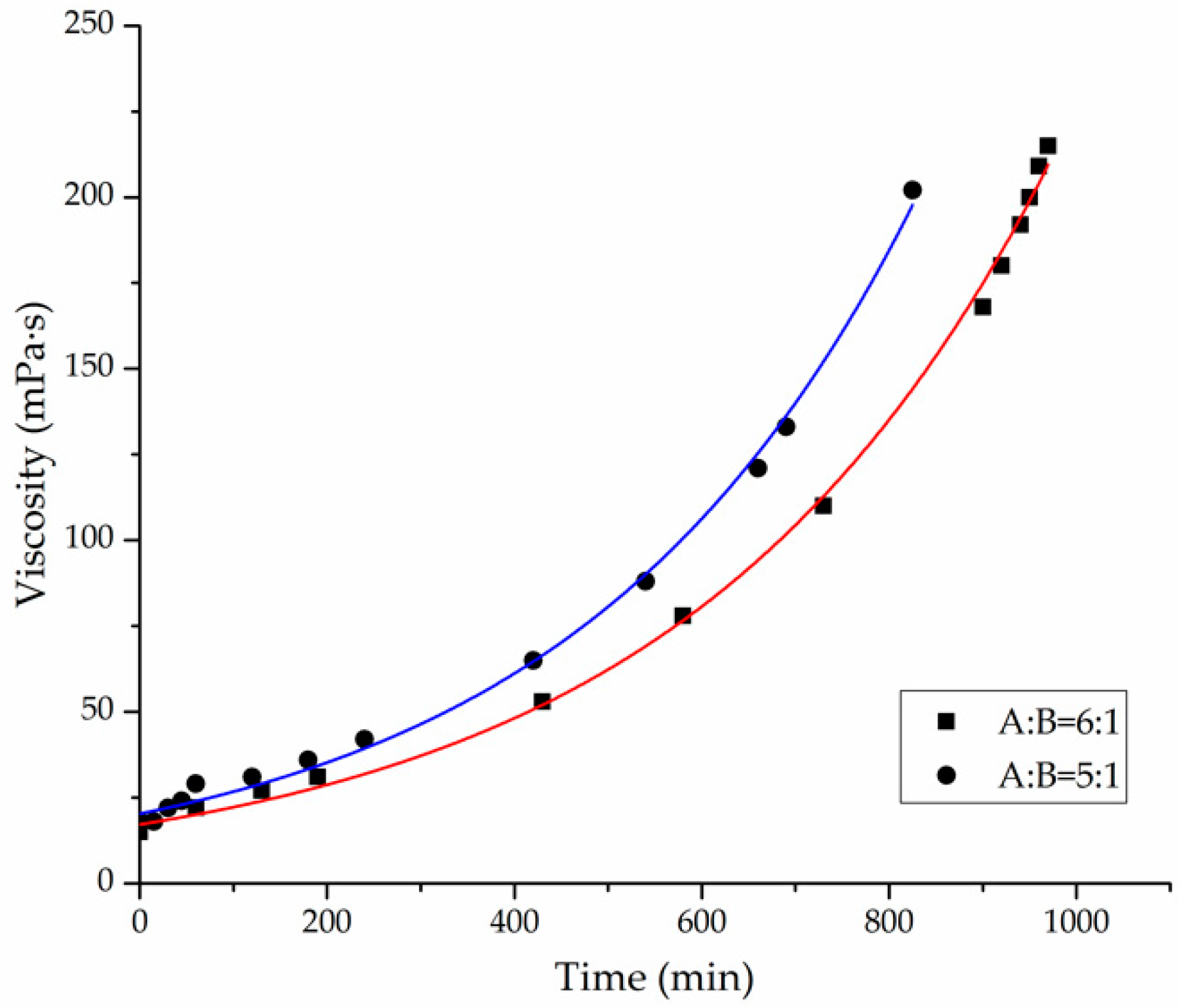
4.1. Study on Viscosity Time Denaturation of CW Epoxy Slurry at the Same Temperature
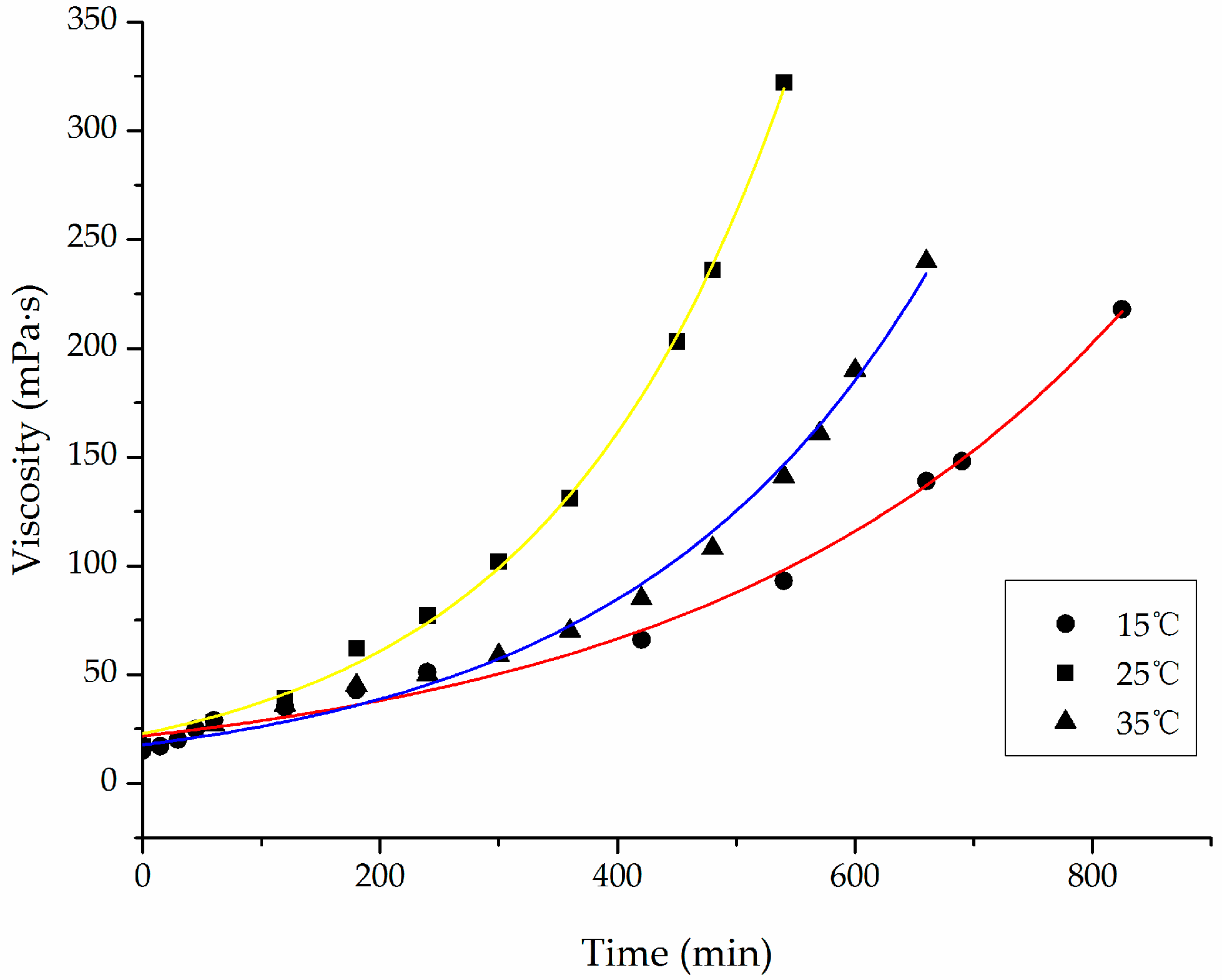
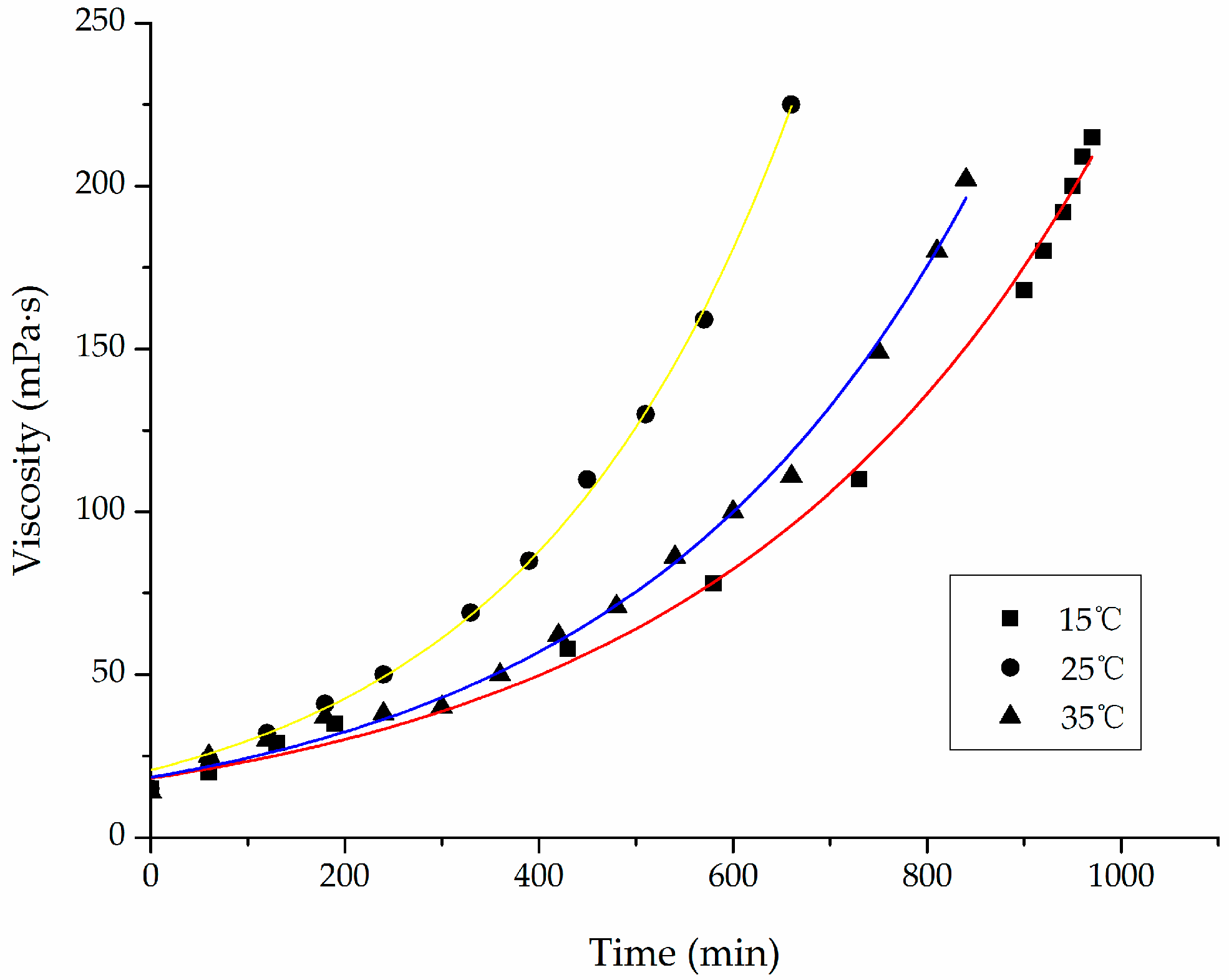
4.2. Time-Dependent Viscosity Test of CW Epoxy Slurry at Different Temperatures
4.2.1. Effect of Temperature on Rheological Characteristics of Slurry
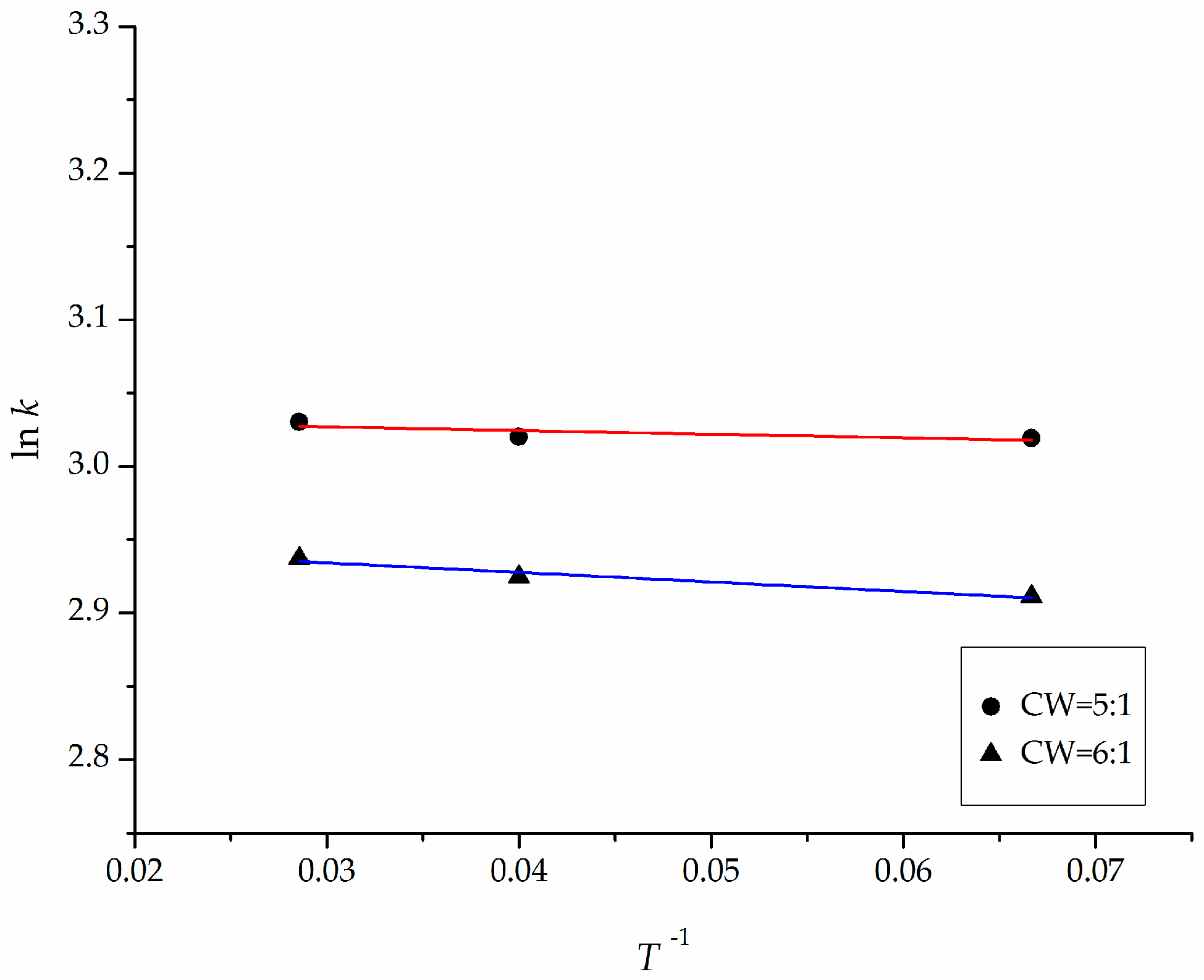
4.2.2. Discussion on the Relationship between Slurry Viscosity and Temperature-Time
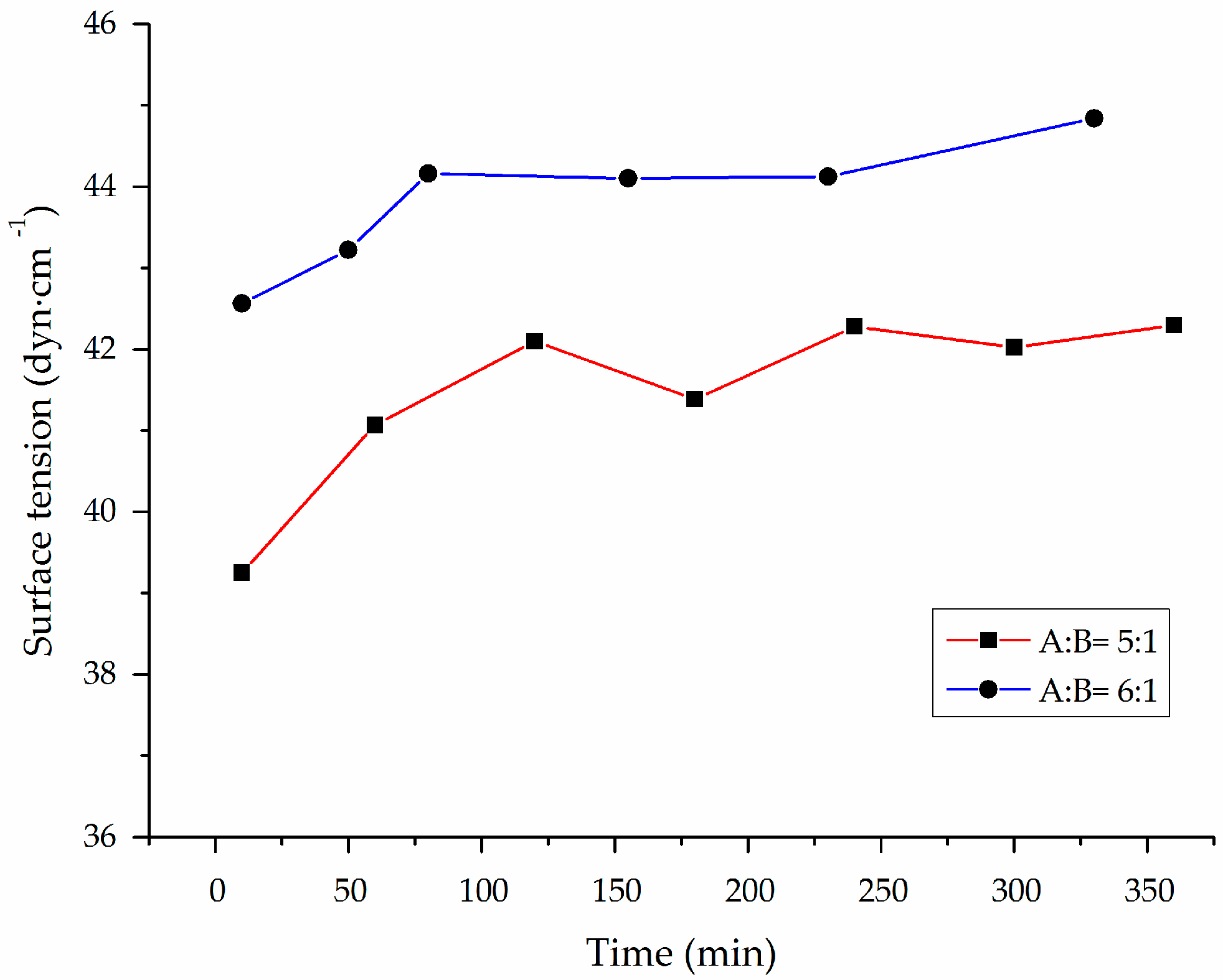
4.3. The Surface Tension of the Slurry Changes With Time
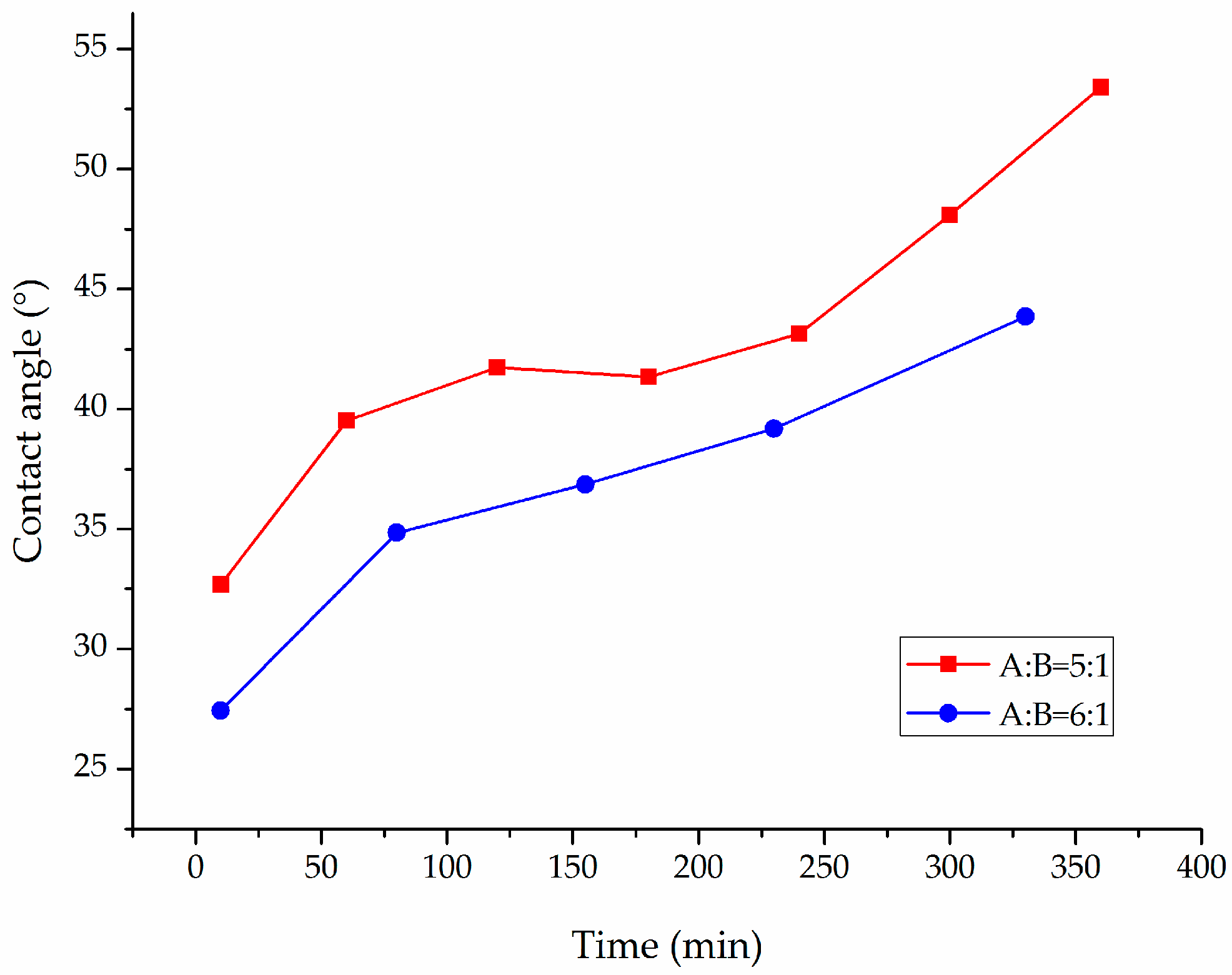
4.4. The Contact Angle of the Slurry Changes With Time
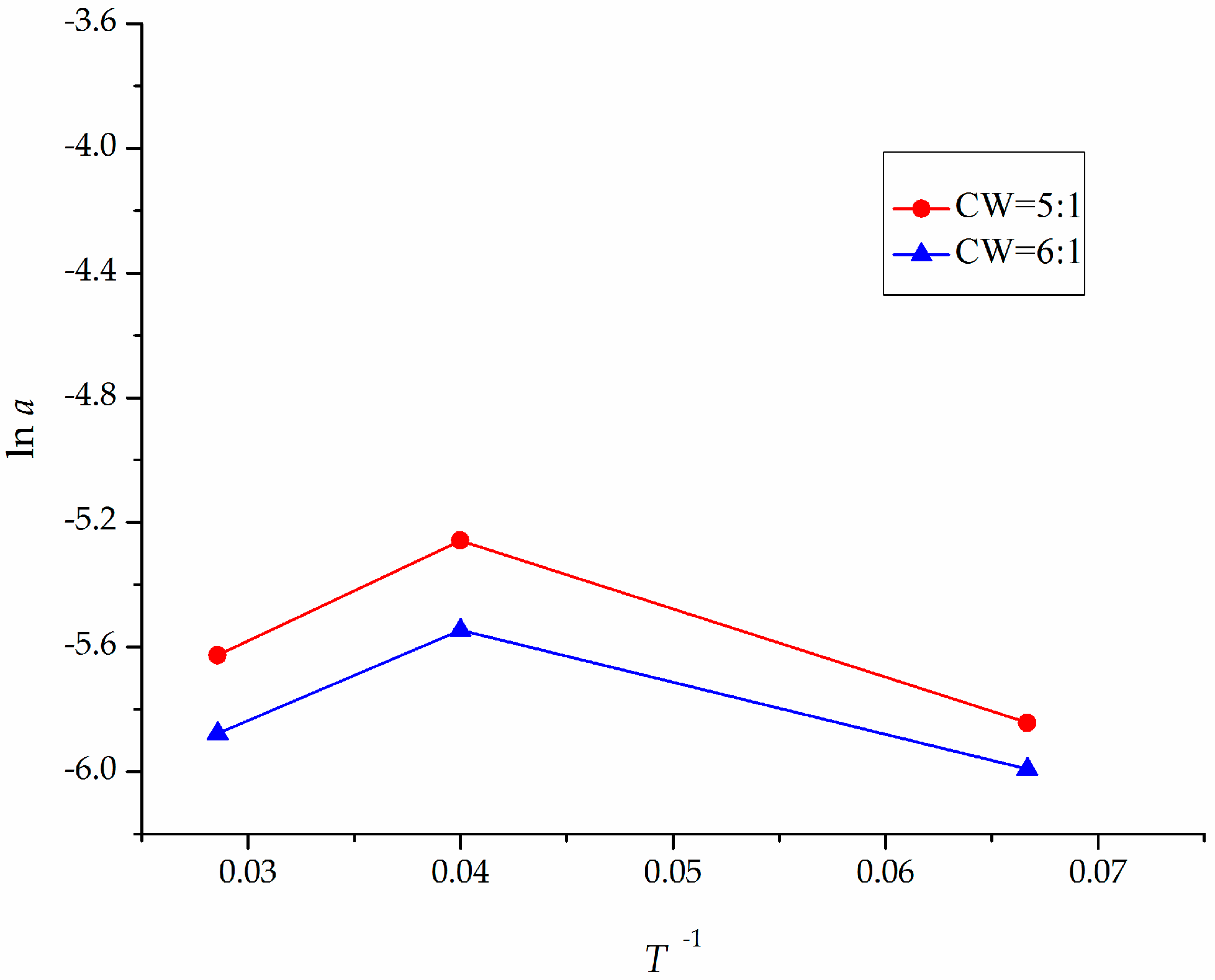
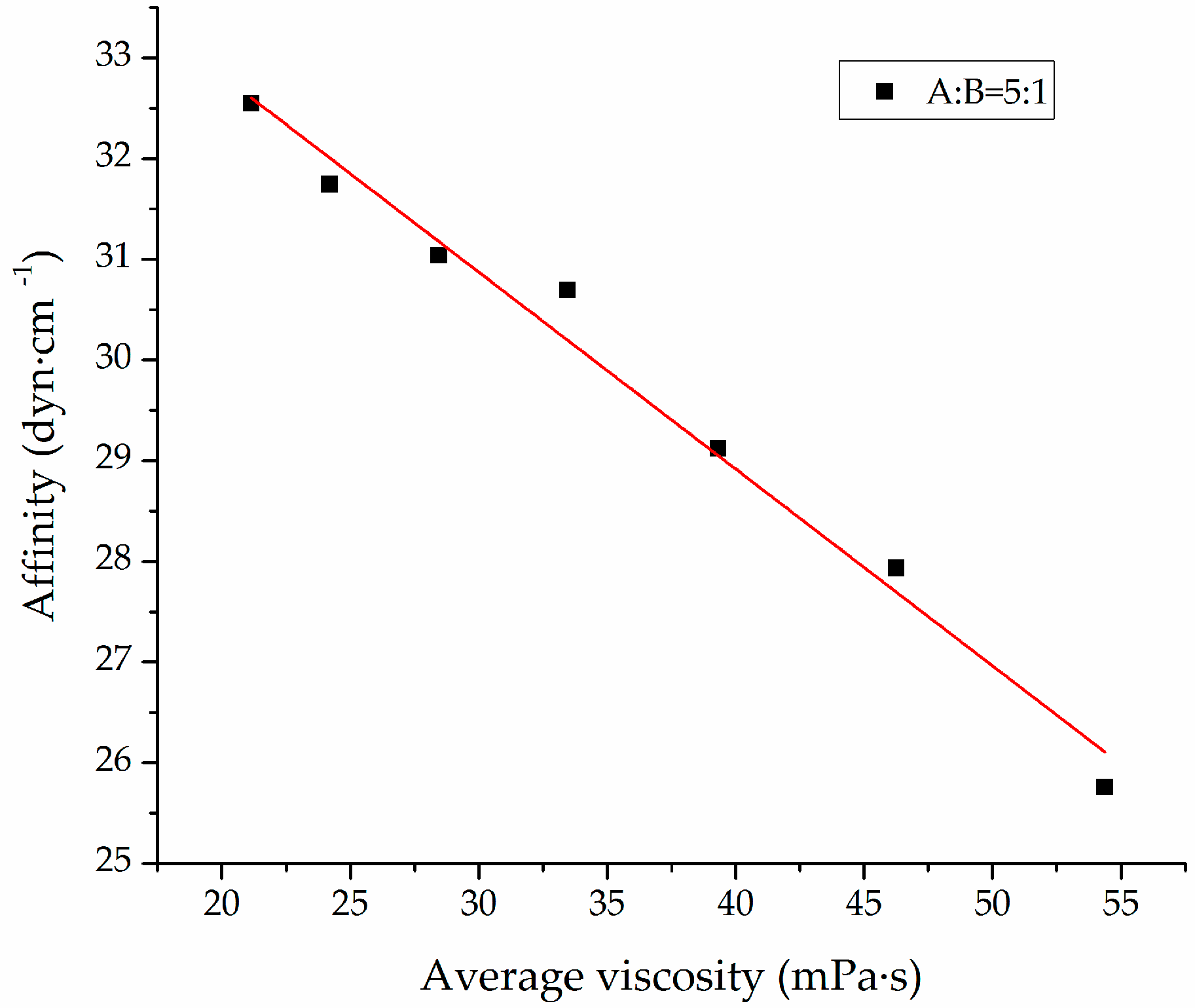
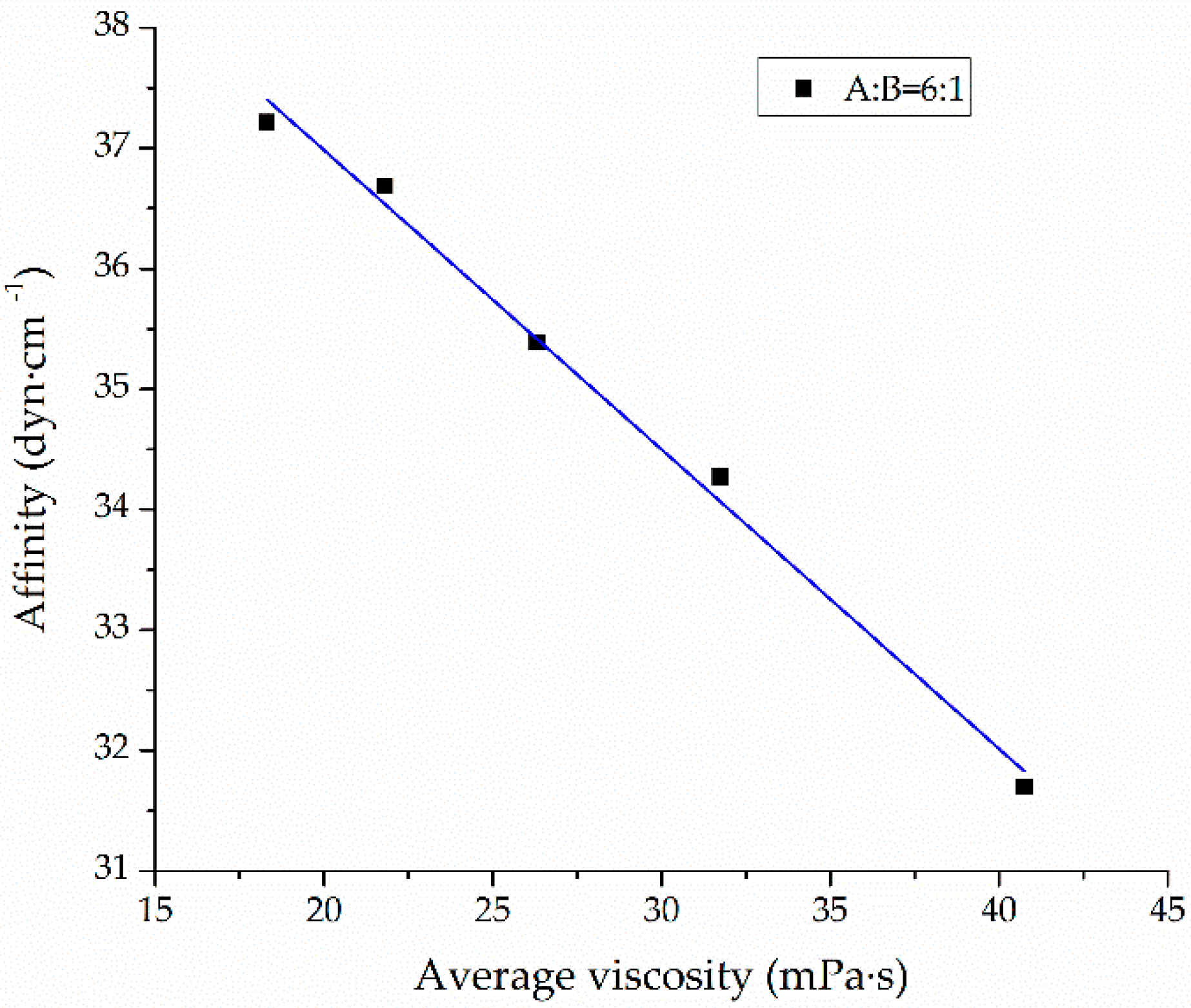
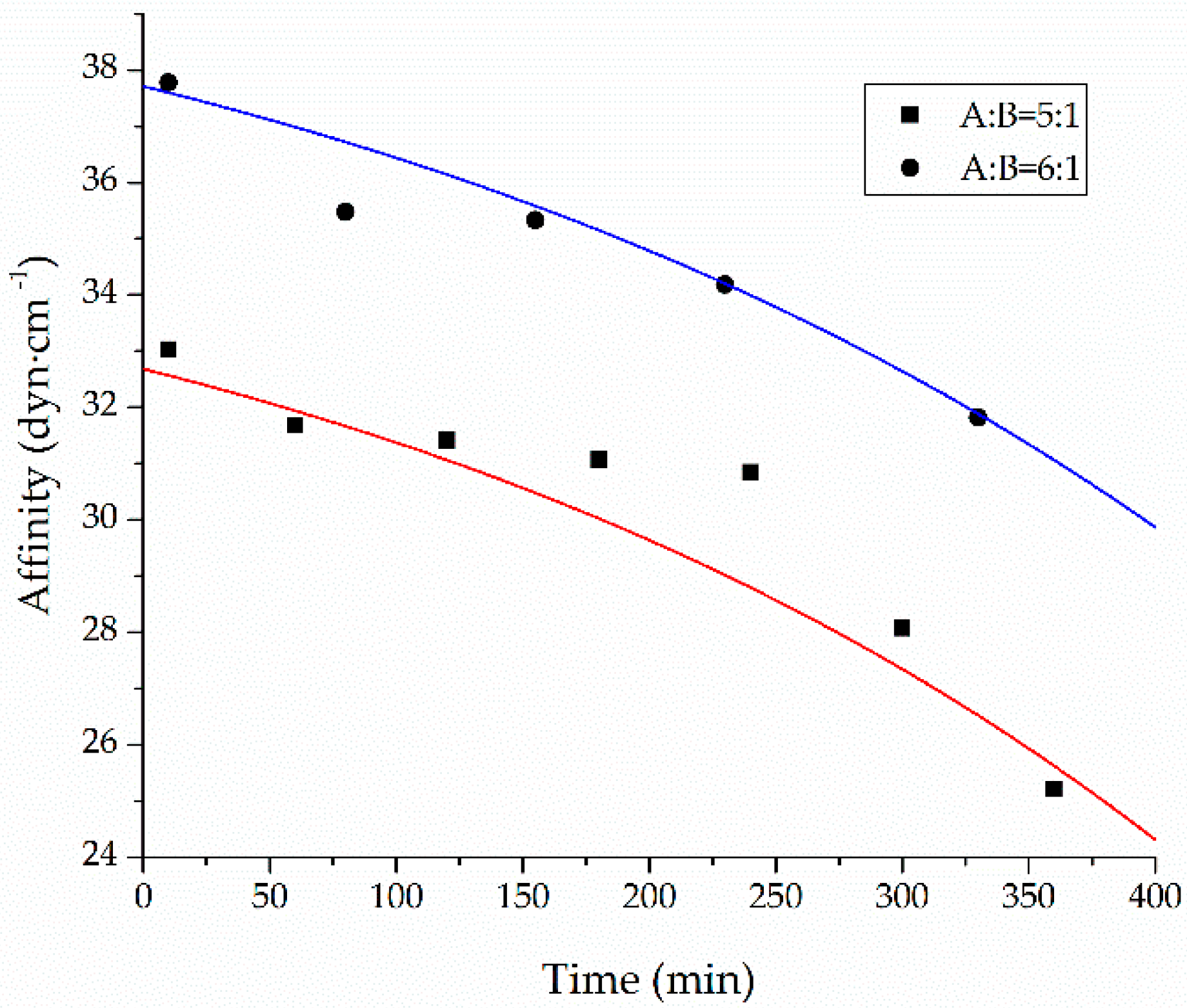
4.5. Mathematical Model Establishment of the Affinity Of Slurry With Time
5. Conclusions
- The chemical rheological characteristics of grouting material at different temperatures were discussed by using the double Arrhenius equation. The time-varying of CW epoxy grouting material’s slurry viscosity accorded with the exponential function law. The parameter A was the initial slurry viscosity, and the parameter B represented the growth rate of viscosity of slurry. The smaller the B value, the slower the slurry viscosity growth. The models of the viscosities of CW epoxy resin slurries with the changing with time at mass ratios of A:B = 5:1 and 6:1 were presented as follows, respectively: and .
- The surface tension of slurries with different mass ratios was varied and increased with the increase of reaction time until reaching equilibrium state. The initial surface tension of the slurry with a mass ratio of 5:1 was 39 dyn·cm−1, while that of the slurry with a mass ratio of 6:1 is 42 dyn·cm−1.
- The contact angle of CW epoxy resin slurry with different mass ratios increased with the increase of time. The contact angle of CW epoxy resin slurry with a mass ratio of A:B = 6:1 was lower than that of CW epoxy resin slurry with a mass ratio of 5:1 in the same time.
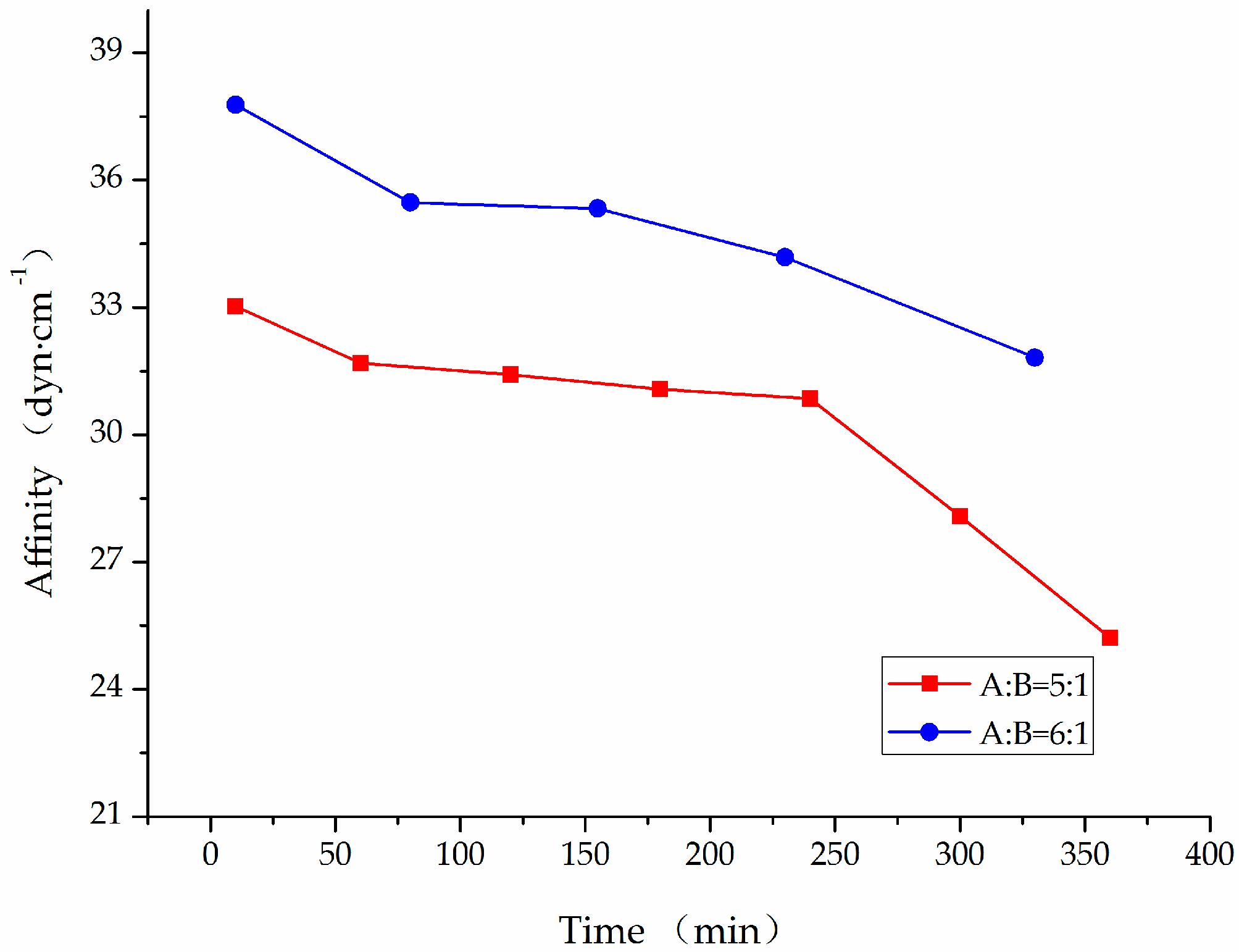
- The affinity of CW epoxy resin slurry with different mass ratios decreased with the increase of time. Because affinity reflected the infiltration and penetration ability of slurry, the infiltration and penetration ability of slurry also decreased with the increase of time. The mathematical models for the affinity of the CW epoxy resin slurry with mass ratio of A:B = 5:1 and mass ratio of A:B = 6:1 as a function of time were respectively: and . The model in this paper is mainly applicable to epoxy resin grouting materials cured at room temperature with furfural-acetone mixture diluter. The models for other resin materials and different curing conditions may be studied with reference to the method in this paper.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Crosby, A. Conservation of painted lime plaster on mud brick walls at tumacacori national monument. In Proceedings of the Third International Symposium on Mudbrick (Adobe) Preservation, Ankara, Turkey, 29 September–4 October 1980; Odtu mimarlik fakultesi: Ankara, Turkey. [Google Scholar]
- Selwitz, C. Epoxy Resins in Stone Conservation, 7th ed.; Paul Getty Trust: Los Angeles, CA, USA, 1992; p. 14. [Google Scholar]
- Wei, T.; Shao, X.M.; Zhang, J. Latest research and application of chemical grouting technology in water conservancy industry. J. Yangtze. River. Sci. Res. Inst. 2014, 31, 77–81. [Google Scholar]
- Yang, X.Z.; Wang, X.H.; Lei, J.S. Research and application of the diffusion radius of Bingham body slurry. J. Hydraul. Eng. 2004, 35, 75–79. [Google Scholar]
- Zhou, S.M.; Chen, J.J. Splitting grouting reinforcement of metro tunnels in soft-flowing silt formation. Chin. J. Geotech. Eng. 2002, 24, 222–224. [Google Scholar]
- Li, S.C.; Li, S.Z.; Zhang, Q.S. Study on advance prediction of karst fissure water and unfavorable geological conditions. Chin. J. Rock Mech. Eng. 2007, 26, 217–225. [Google Scholar]
- Zheng, D.W.; Zhang, B.; Wang, X.B. A study on calculation method of penetration theory for conforming sand layer. Chin. J. Rock Mech. Eng. 2005, 24, 5086–5089. [Google Scholar]
- Deng, H.Y.; Wang, Z.Q.; Wei, T. Study on grouting diffusion theory based on rheology of CW epoxy slurry. J. Yangtze. River. Sci. Res. Inst. 2016, 33, 121–124. [Google Scholar]
- Cheng, P.D. Study on Flow Characteristics of Viscous Time-varying Grouting Slurry in Porous Formation. Ph.D. Thesis, Shanghai University, Shanghai, China, October 2011. [Google Scholar]
- Warner, J. The Role of Surface Science in Grouting. In Proceedings of the Fourth International Conference on Grouting and Deep Mixing, New Orleans, LA, USA, 15–18 February 2012. [Google Scholar]
- Crick, C.R.; Parkin, I.P. Preparation and characterisation of superhydrophobic surface. Chem.-Eur. J. 2010, 16, 3568–3588. [Google Scholar] [CrossRef] [PubMed]
- Young, T. The Bakerian Lecture: Experiments and calculations relative to physical optics. Phil. Trans. Roy. Soc. Lond. 1804, 94, 1–16. [Google Scholar] [CrossRef][Green Version]
- Adamson, A.W.; Gast, A.P. Physical Chemistry of Surfaces, 6th ed.; John Wiley&Sons: New York, NY, USA, 1997; p. 45. [Google Scholar]
- Wu, Y.; Satio, N.; Nae, F.A. Water droplets interaction with super-hydrophobic surfaces. Surf. Sci. 2006, 600, 3710–3714. [Google Scholar] [CrossRef]
- Fürstner, R.; Barthlott, W. Wetting and self-cleaning properties of artificial superhydrophobic surfaces. Langmuir 2005, 21, 956–961. [Google Scholar] [CrossRef] [PubMed]
- Li, X.B.; Liu, Y. The mechanism and model of solid surface wettability. J. Funct. Mater. 2007, 38, 3919–3924. [Google Scholar]
- Mei, J.Y.; Ren, K.C. Research and Practice of Epoxy Grouting in Low Permeability Saturated Weak Layer Zone, 1st ed.; China Environment Press: Beijing, China, 2012; p. 55. [Google Scholar]
- Ren, K.C. Several problems in seepage calculation of chemical grouting grout. Water. Resour. Hydr. Eng. 1992, 4, 39–44. [Google Scholar]
- Rezaeidoust, A.; Puntervold, T. Smart Water as Wettability Modifier in Carbonate and Sandstone: A Discussion of Similarities/Differences in the Chemical Mechanisms. Energ. Fuel. 2009, 23, 4479–4485. [Google Scholar] [CrossRef]
- Graham, J.W.; Richrason, J.G. Theory and application of imbibition phenomena in recovery of oil. J. Pet. Technol. 1959, 11, 65–69. [Google Scholar] [CrossRef]
- Ye, L.H.; He, Y.S. Discussion on the interaction between chemical grouting fluid and grouted rock and soil. Chin. J. Geotech. Eng. 1994, 6, 47–55. [Google Scholar]
- Wang, Z.Q.; Wei, T.; Li, Z. Research and application of CW Epoxy Resin chemical grouting material. J. Yangtze. River. Sci. Res. Inst. 2011, 28, 167–170. [Google Scholar]
- Zhu, X.D.; Wang, L.J. Analysis of rheological properties and curing properties of RTM Epoxy Resin. Fiber Reinf. Plast. Compos. 2017, 8, 97–101. [Google Scholar]
- Ferry, J.D. Viscoelastic properties of polymer. J. Res. Natl. Bur. Stand. 1948, 41, 53–62. [Google Scholar] [CrossRef]
- Liu, Z.F.; Xiao, J.Y.; Zeng, J.C. Study on the process performance of low viscosity epoxy resin VIM. J. Natl. Univ. Def. Technol. 2008, 30, 20–24. [Google Scholar]
- Halley, P.J.; Mackay, M.E. Chemorheology of thermosets: An overview. Polym. Eng. Sci. 1996, 36, 593–609. [Google Scholar] [CrossRef]
- Kiuna, N.; Lawrence, C.J. A model for resin viscosity during cure in the resin transfer moulding process. Compos. Part A 2002, 33, 1497–1503. [Google Scholar] [CrossRef]
- Zhang, W.; Duan, Y.X.; Zhao, Y. Study on low viscosity epoxy resin system for resin transfer moulding process. Polym. Mater. Sci. Eng. 2000, 16, 86–88. [Google Scholar]
- Qiu, J.H.; Yi, Z.L.; Li, H.J. Study on rheological properties of epoxy resin grouting materials. New. Build. Mater. 2011, 38, 68–71. [Google Scholar]
- Wei, T.; Dong, J.J. Application of Epoxy Resin in Hydraulic Buildings, 1st ed.; Chemical Industry Press: Beijing, China, 2007; pp. 48–50. [Google Scholar]



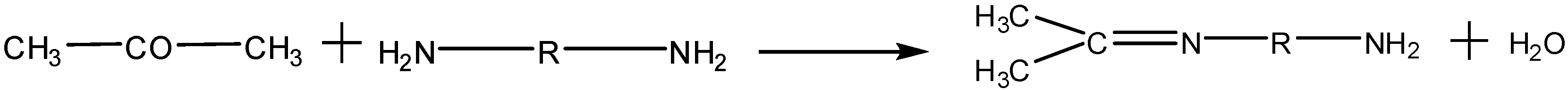
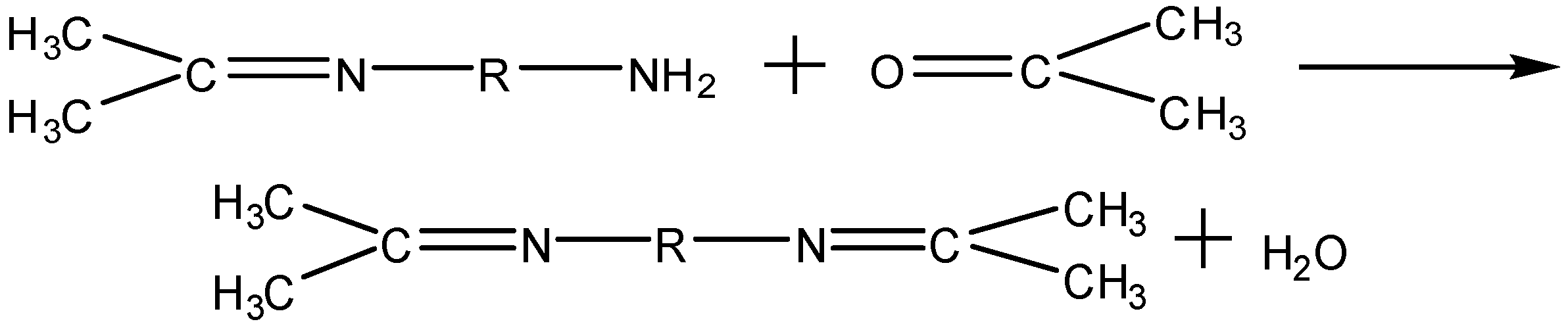
| Items | 6:1 | 5:1 | |
|---|---|---|---|
| Initial setting time (h) | 65 | 46 | |
| Slurry density (g/cm3) | 1.06 | 1.07 | |
| Compressive strength (MPa) | 62 | 68 | |
| Shear strength (MPa) | 12 | 15 | |
| Tensile strength (MPa) | 16 | 20 | |
| Bond strength (MPa) | Dry | 4.8 | 5.2 |
| Wet | 4.2 | 4.0 | |
| Temperature (°C) | Correlation Coefficient | A:B = 5:1 | A:B = 6:1 |
|---|---|---|---|
| 15 °C | k | 20.29 | 18.36 |
| a | 0.0030 | 0.0025 | |
| R2 | 0.9933 | 0.9967 | |
| 25 °C | k | 20.55 | 18.69 |
| a | 0.0049 | 0.0025 | |
| R2 | 0.9983 | 0.9981 | |
| 35 °C | k | 20.67 | 18.82 |
| a | 0.0031 | 0.0027 | |
| R2 | 0.9924 | 0.9954 |
| Slurry | Curve Equation | Fitting Coefficient |
|---|---|---|
| A:B = 5:1 | 0.9352 | |
| A:B = 6:1 | 0.9576 |
| Slurry | Initial Viscosity Model Equation |
|---|---|
| A:B = 5:1 | |
| A:B = 6:1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Z.; Wang, Z.; Zhang, D.; Wei, T. Study on Rheological Behavior and Surface Properties of Epoxy Resin Chemical Grouting Material Considering Time Variation. Materials 2019, 12, 3277. https://doi.org/10.3390/ma12203277
Su Z, Wang Z, Zhang D, Wei T. Study on Rheological Behavior and Surface Properties of Epoxy Resin Chemical Grouting Material Considering Time Variation. Materials. 2019; 12(20):3277. https://doi.org/10.3390/ma12203277
Chicago/Turabian StyleSu, Zhenhua, Zaiqin Wang, Da Zhang, and Tao Wei. 2019. "Study on Rheological Behavior and Surface Properties of Epoxy Resin Chemical Grouting Material Considering Time Variation" Materials 12, no. 20: 3277. https://doi.org/10.3390/ma12203277
APA StyleSu, Z., Wang, Z., Zhang, D., & Wei, T. (2019). Study on Rheological Behavior and Surface Properties of Epoxy Resin Chemical Grouting Material Considering Time Variation. Materials, 12(20), 3277. https://doi.org/10.3390/ma12203277




