The Use of the Kinetic Theory of Gases to Simulate the Physical Situations on the Surface of Autonomously Moving Parts During Multi-Energy Vibration Processing
Abstract
:1. Introduction
2. Basic Provisions and Approaches
2.1. Boundary Conditions
2.2. Surface of the Processed Part
2.3. Working Surface of the Vibrating Machine Reservoir
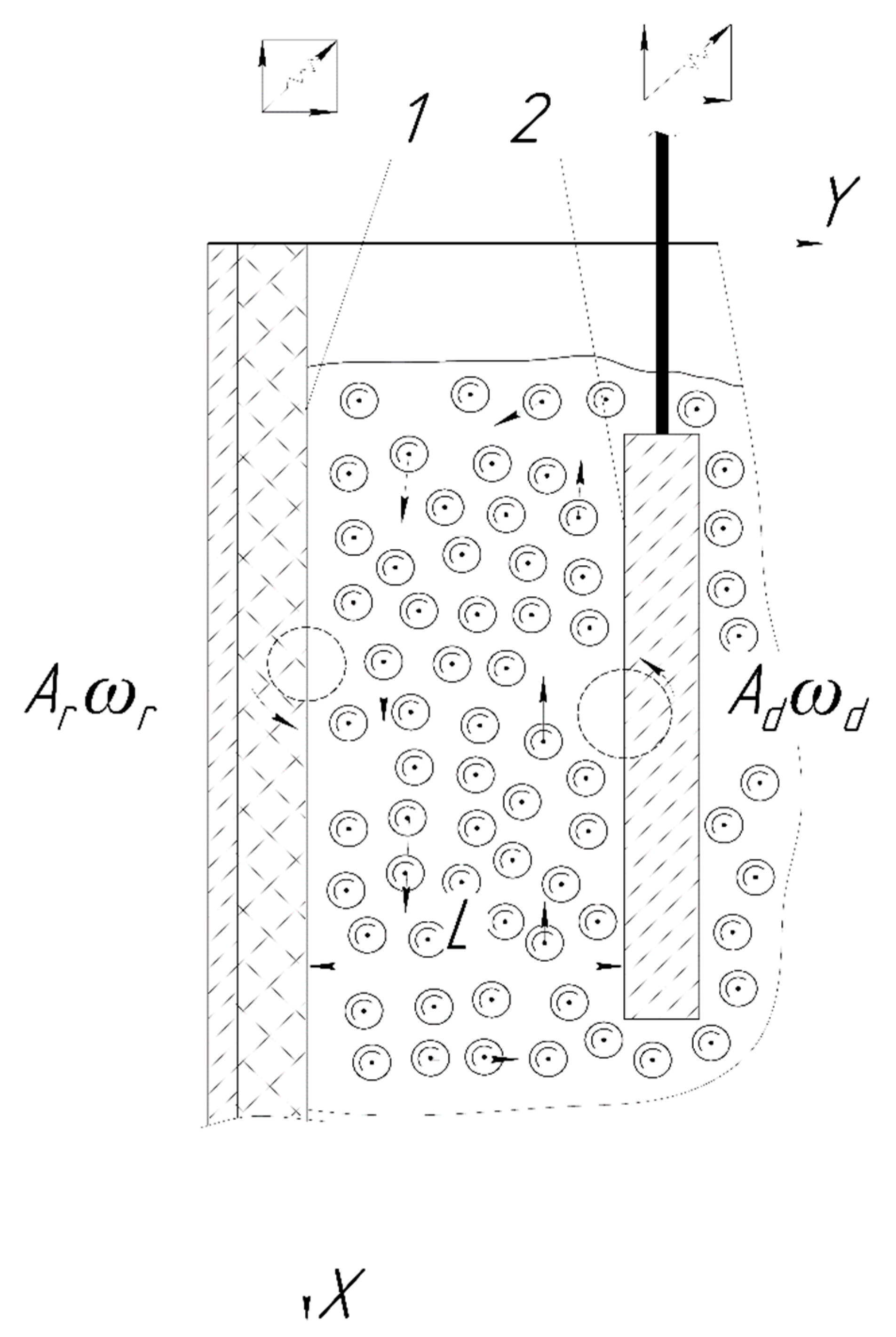
3. Collective Movement of the Abrasive Granules Between the Independently Oscillating Surfaces of the Reservoir and the Processed Part
3.1. Movement of the Collective of the Abrasive Granules Under the Action of the Working Surfaces of the Reservoir
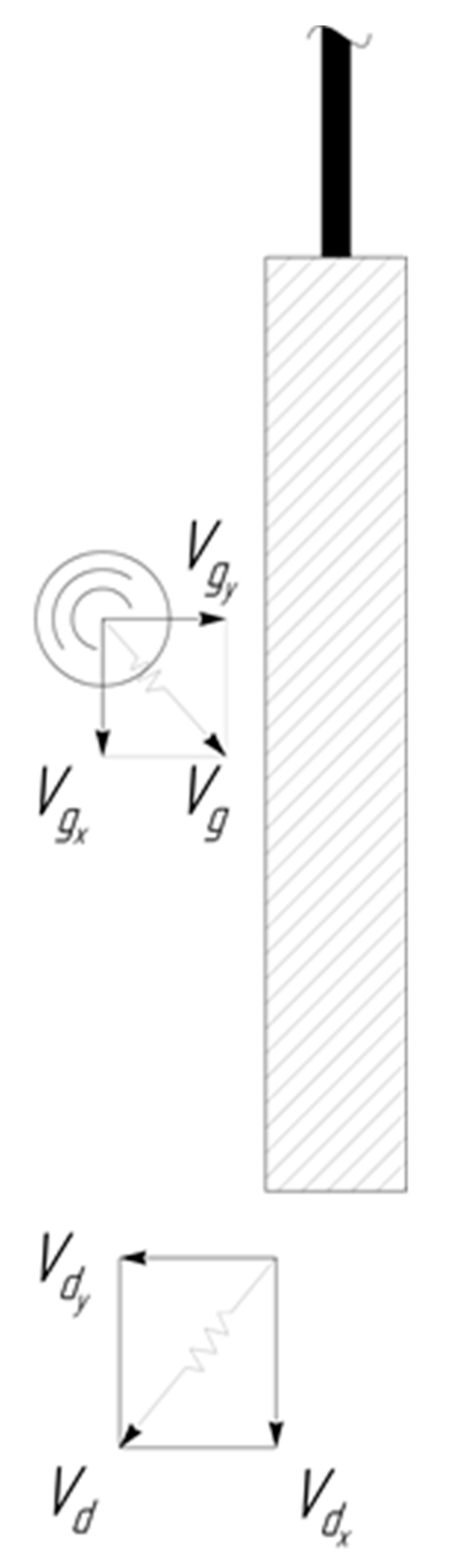
3.2. Movement of the Abrasive Granules of the Working Medium Near the Surface of the Processed Part
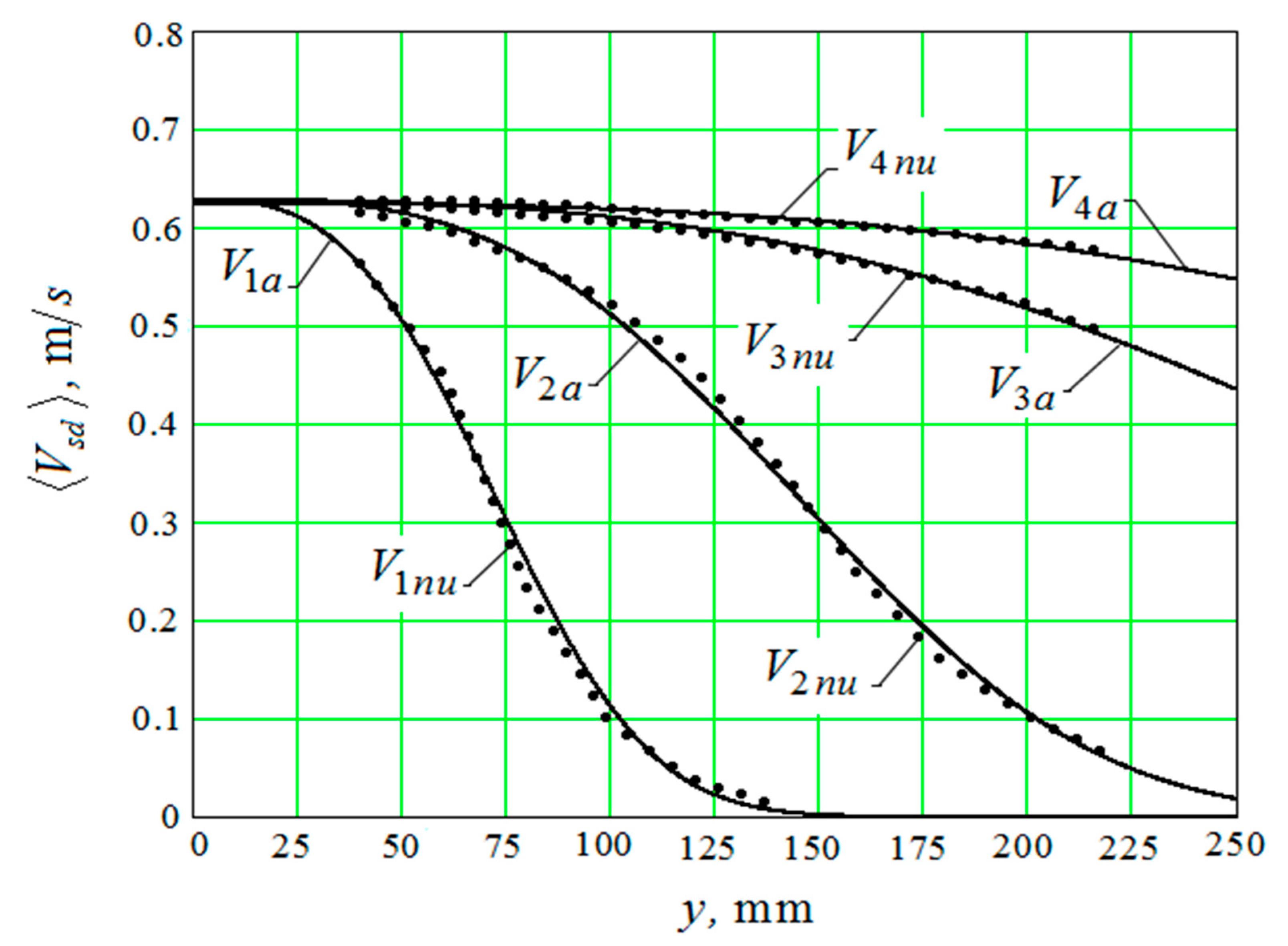
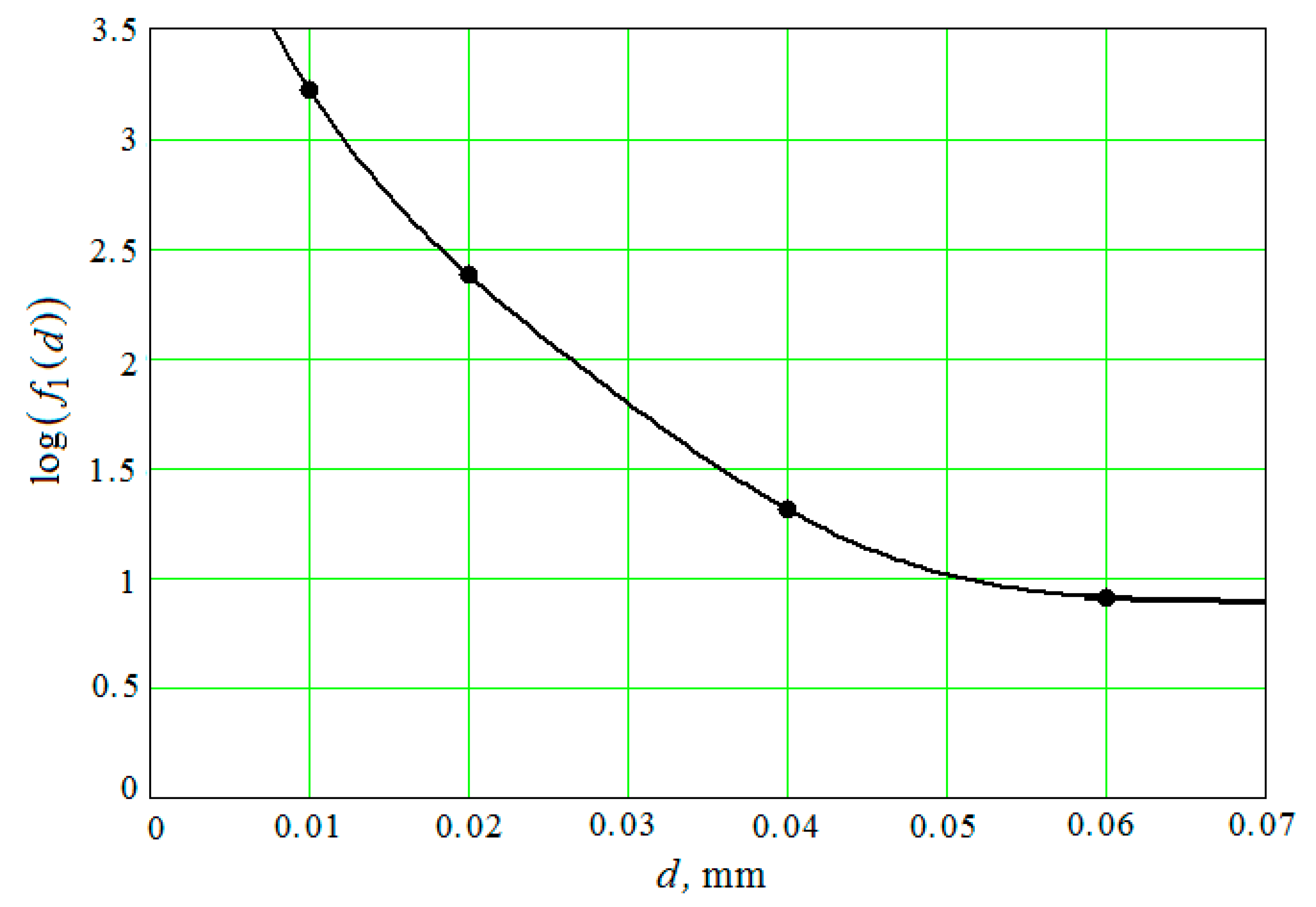
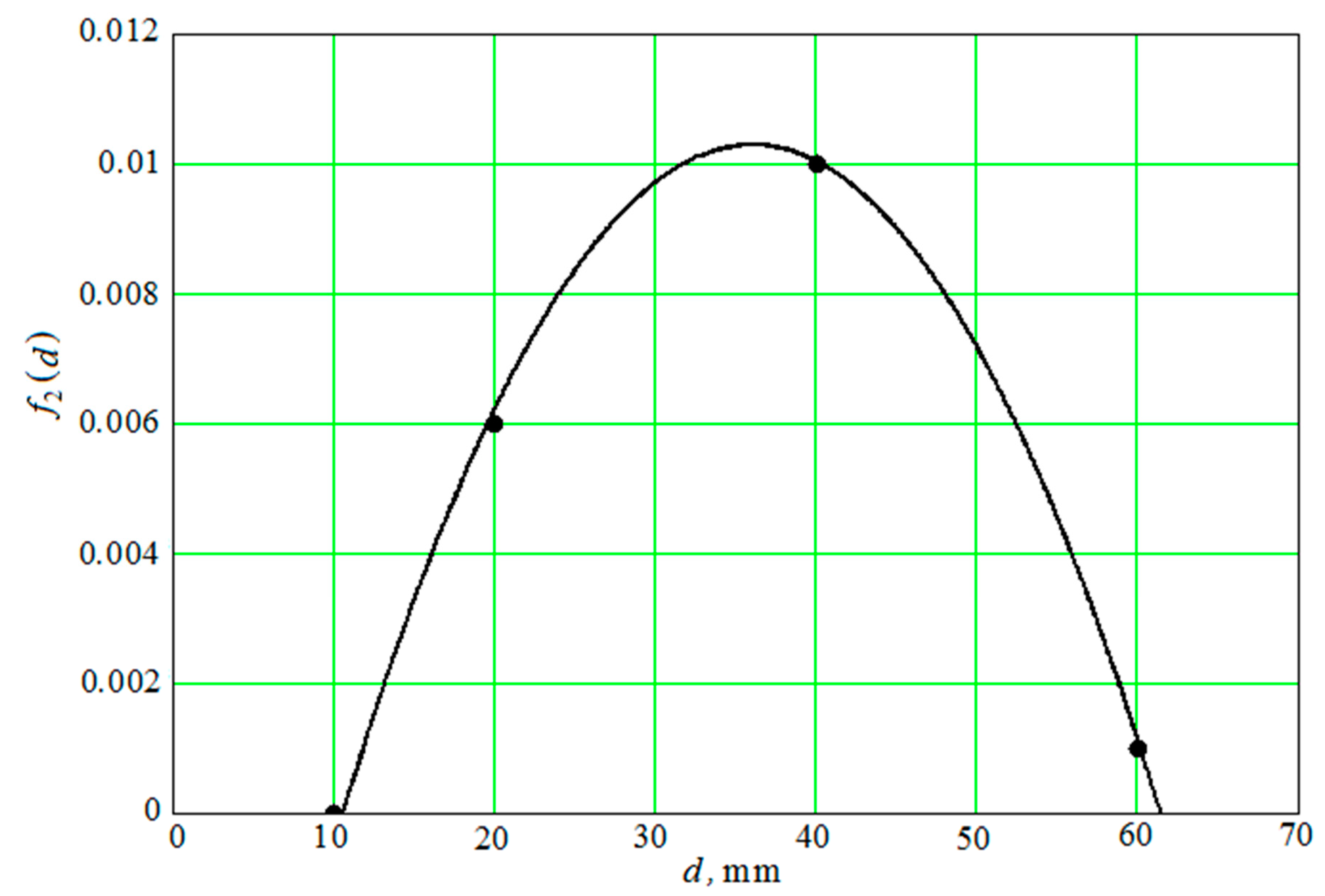
3.2.1. Dissipation of the Kinetic Energy of the Granules in the Pseudo-Gas from the Granules of the Working Medium
3.2.2. The Motion of the Medium Granules Near the Part Surface Caused by Pseudo-Waves Initiated by Oscillations of the Working Surfaces of the Vibrating Machine Reservoir
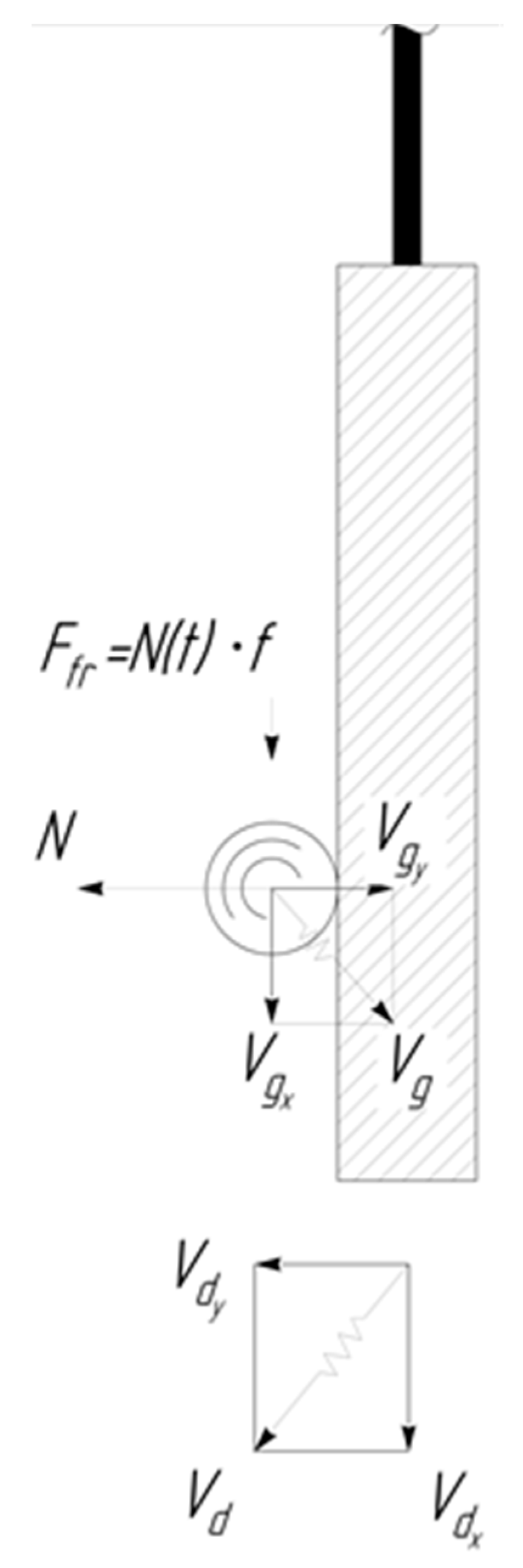
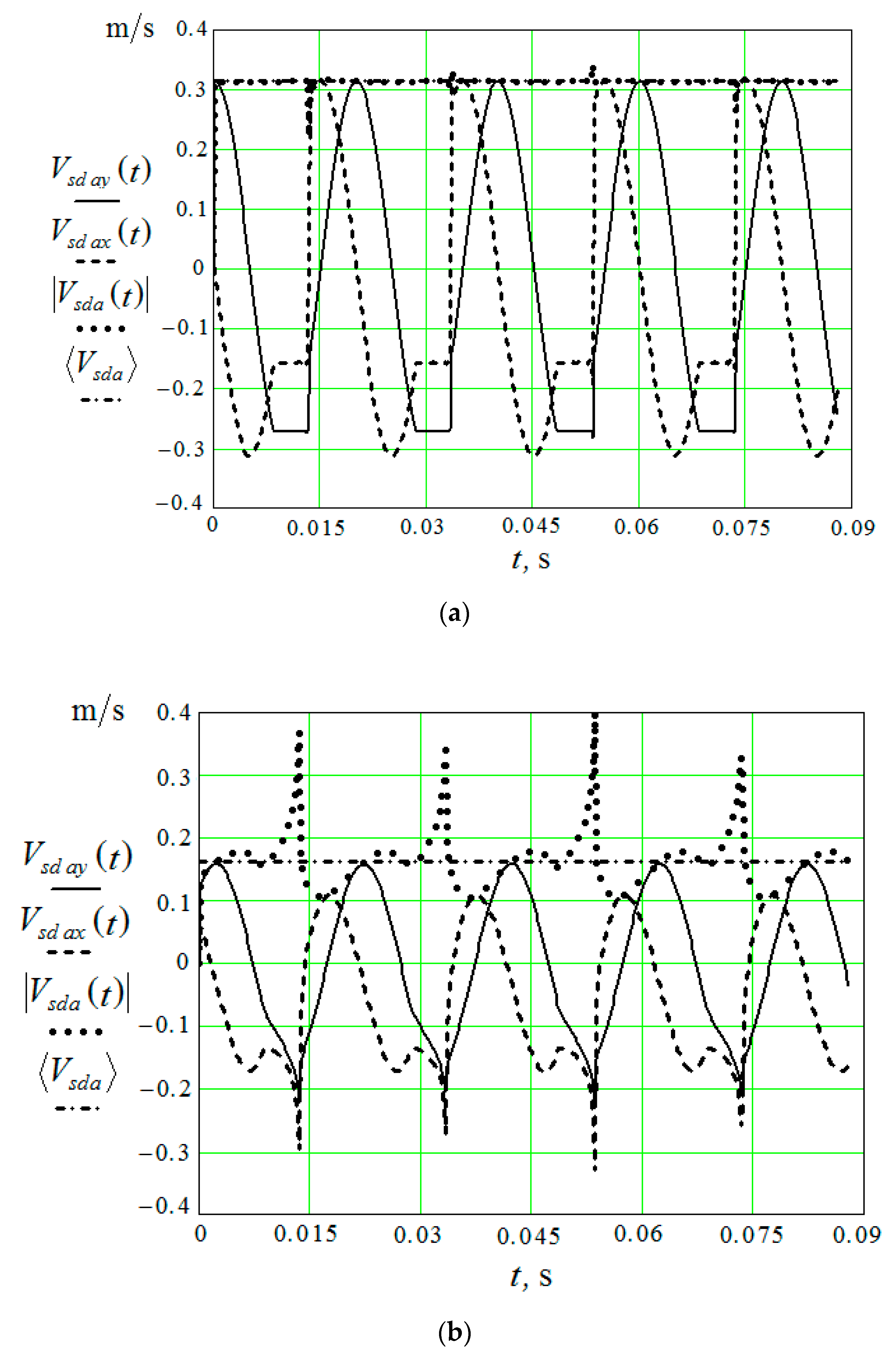
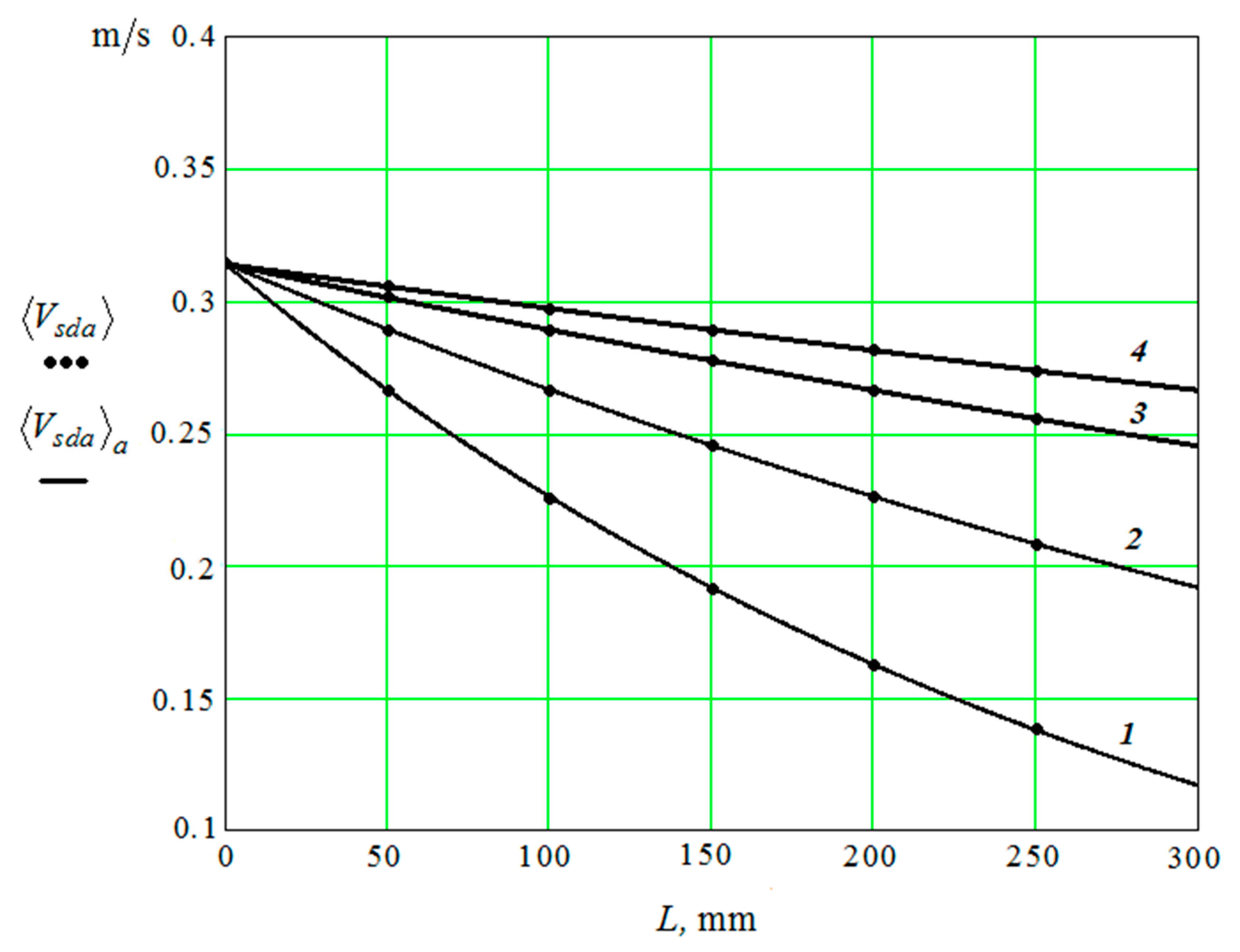
3.2.3. The Movement of the Granules Near the Surface of the Oscillating Part
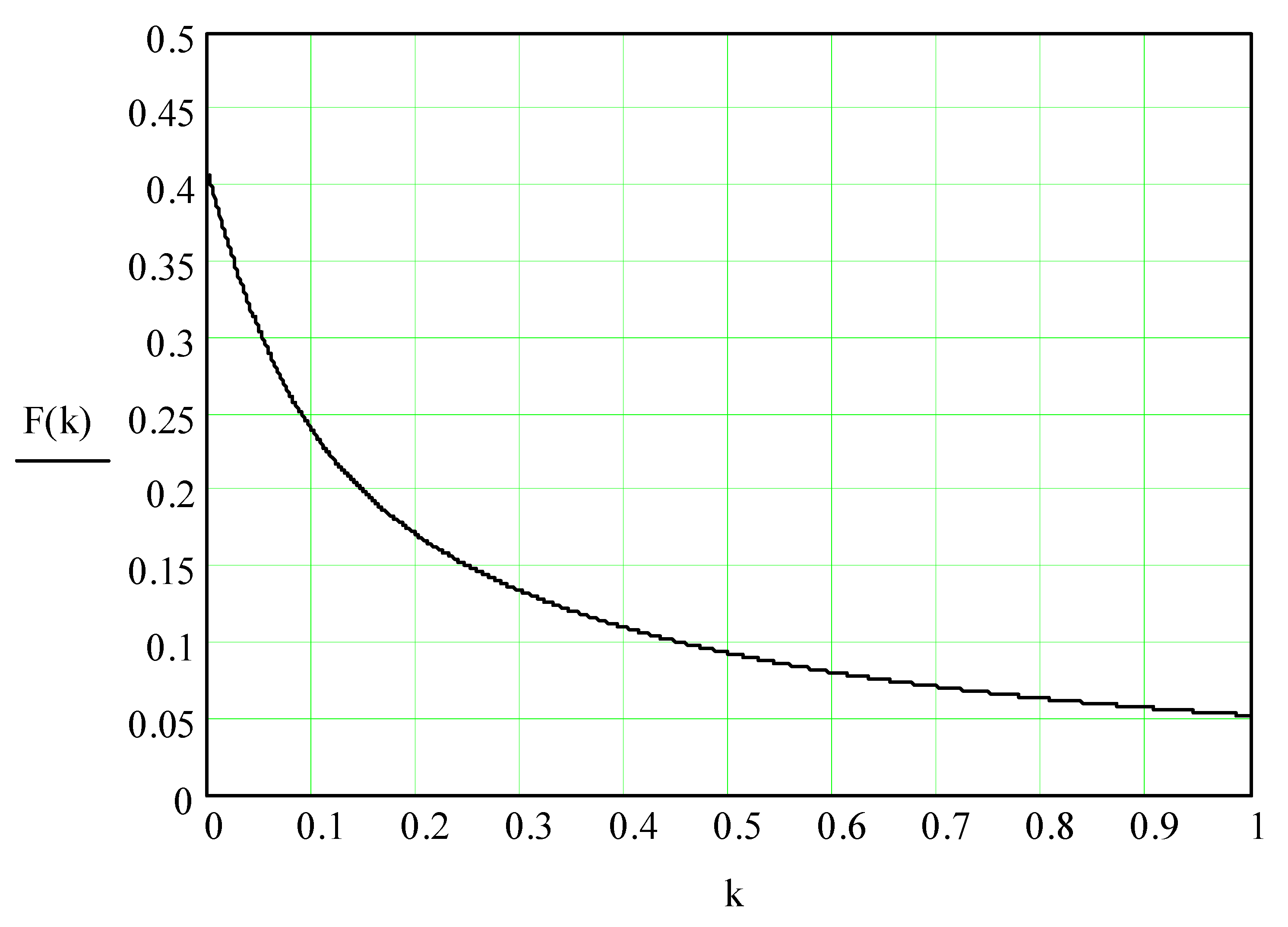
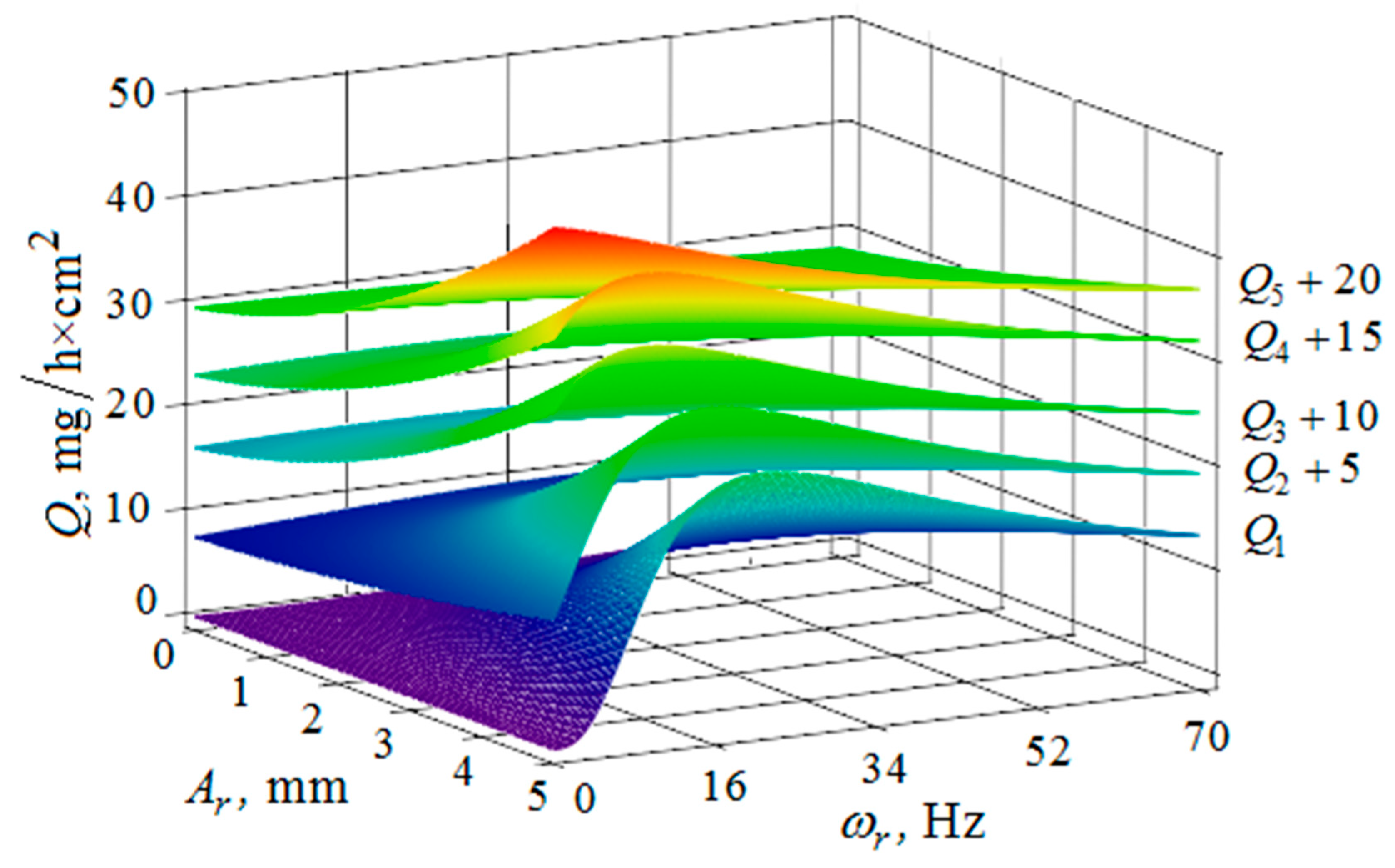
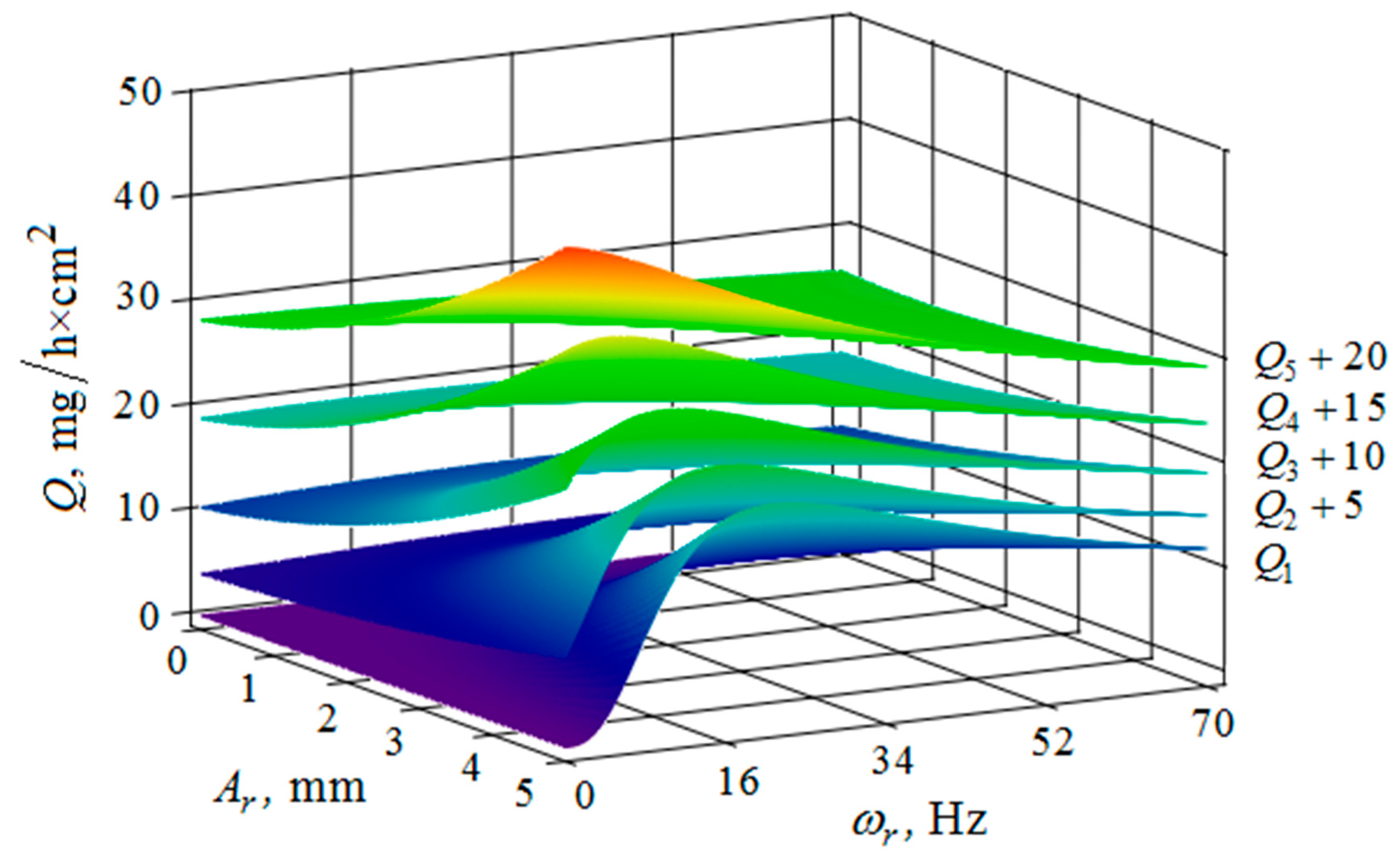
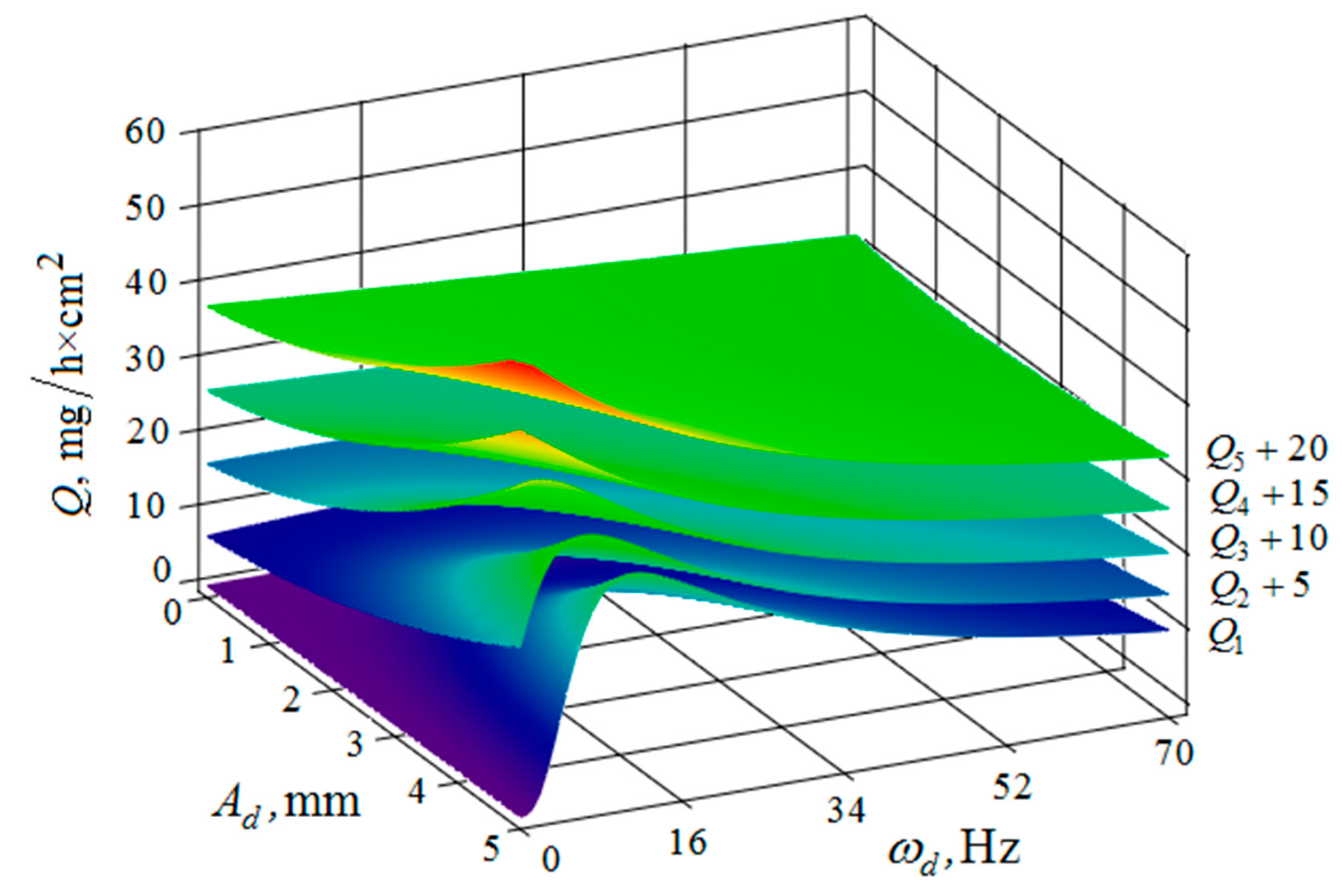
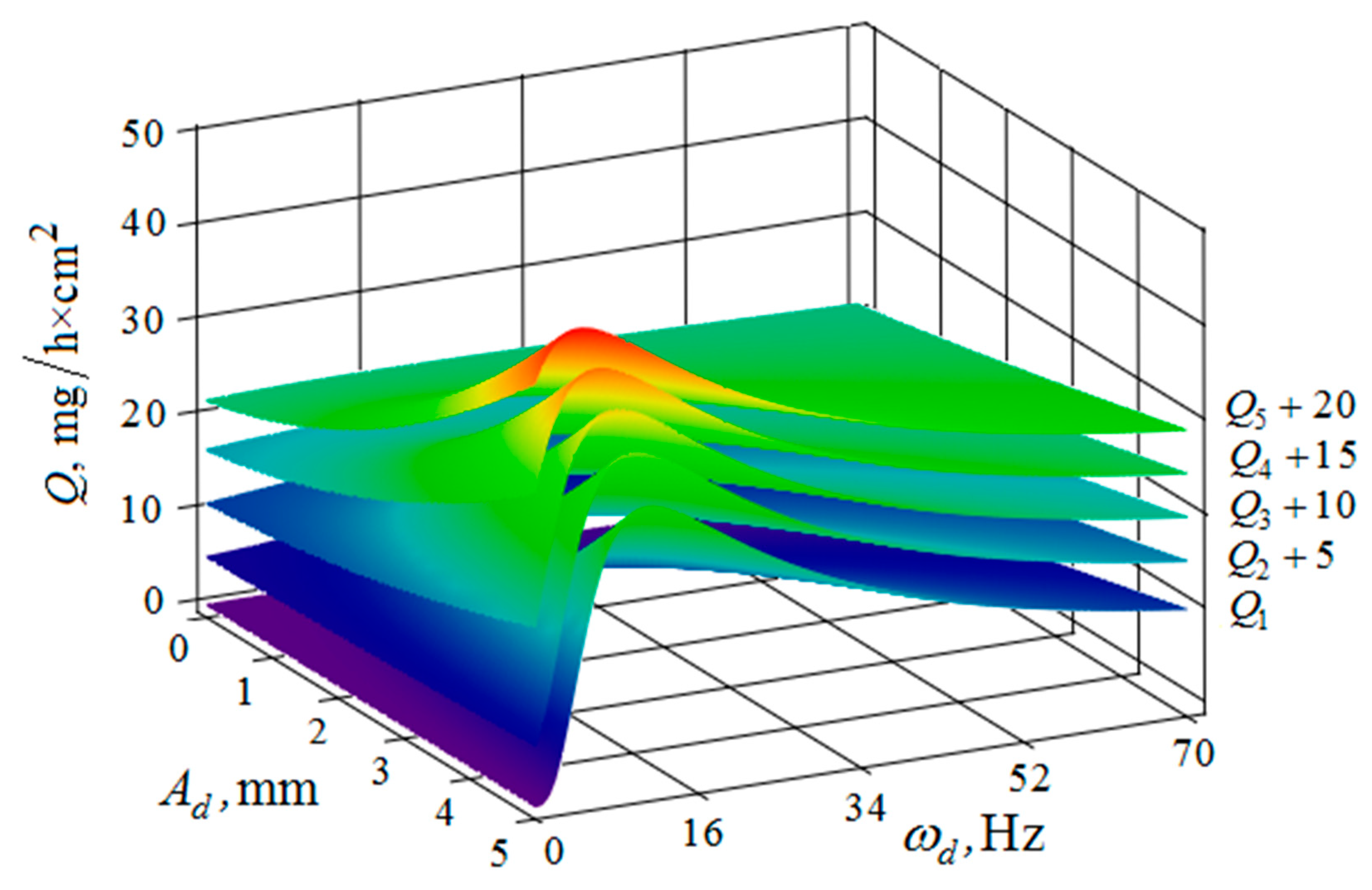
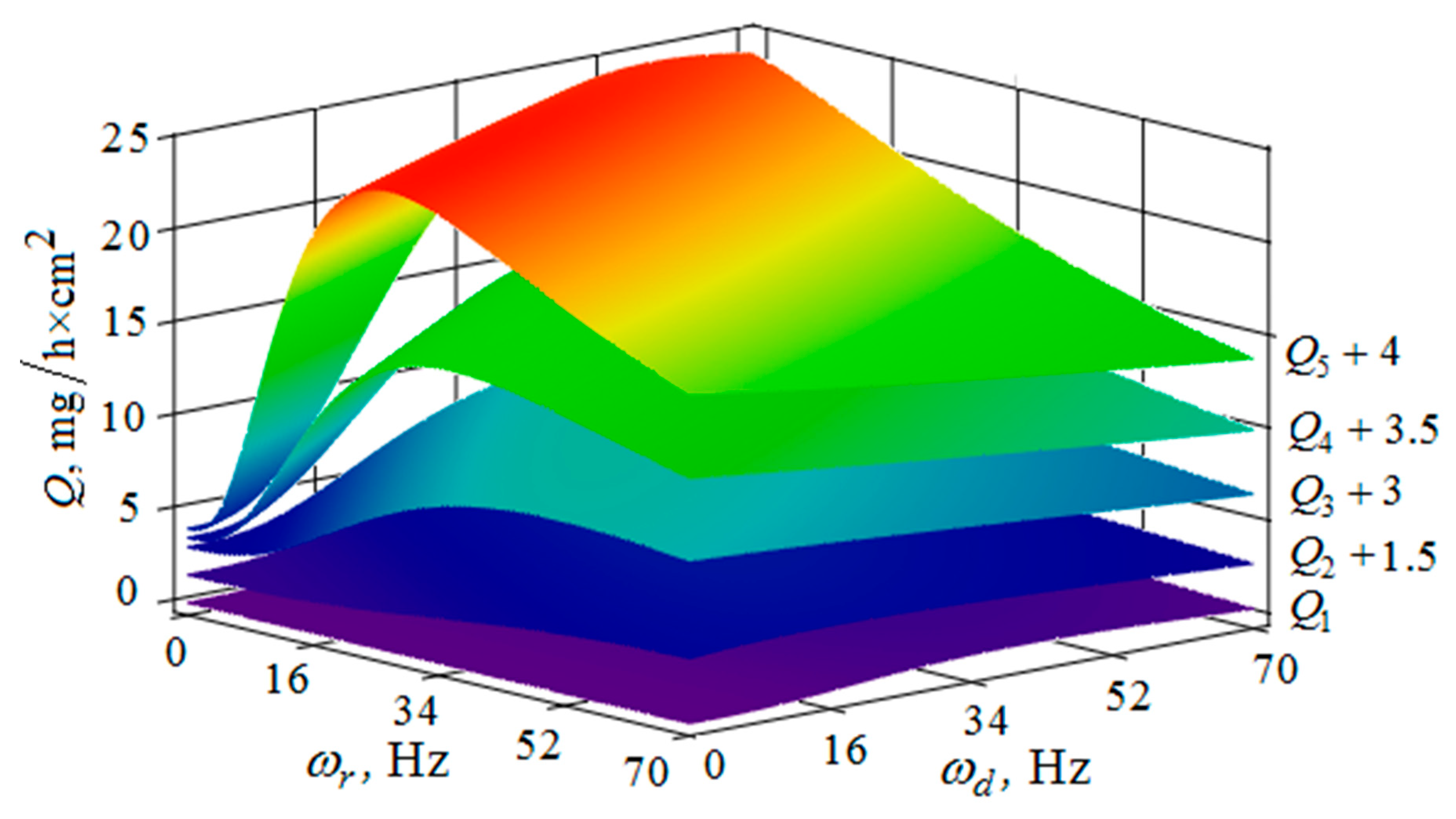
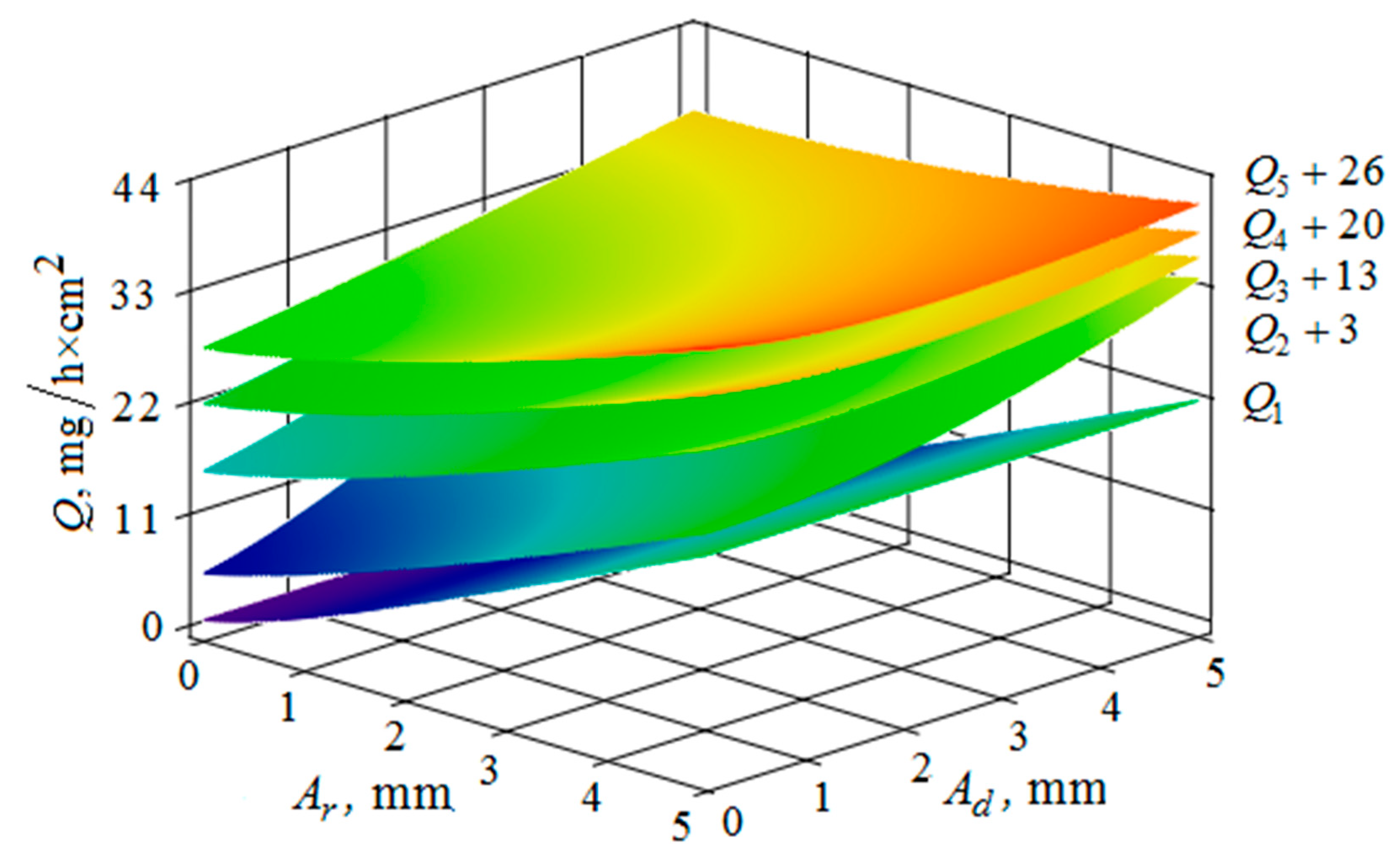
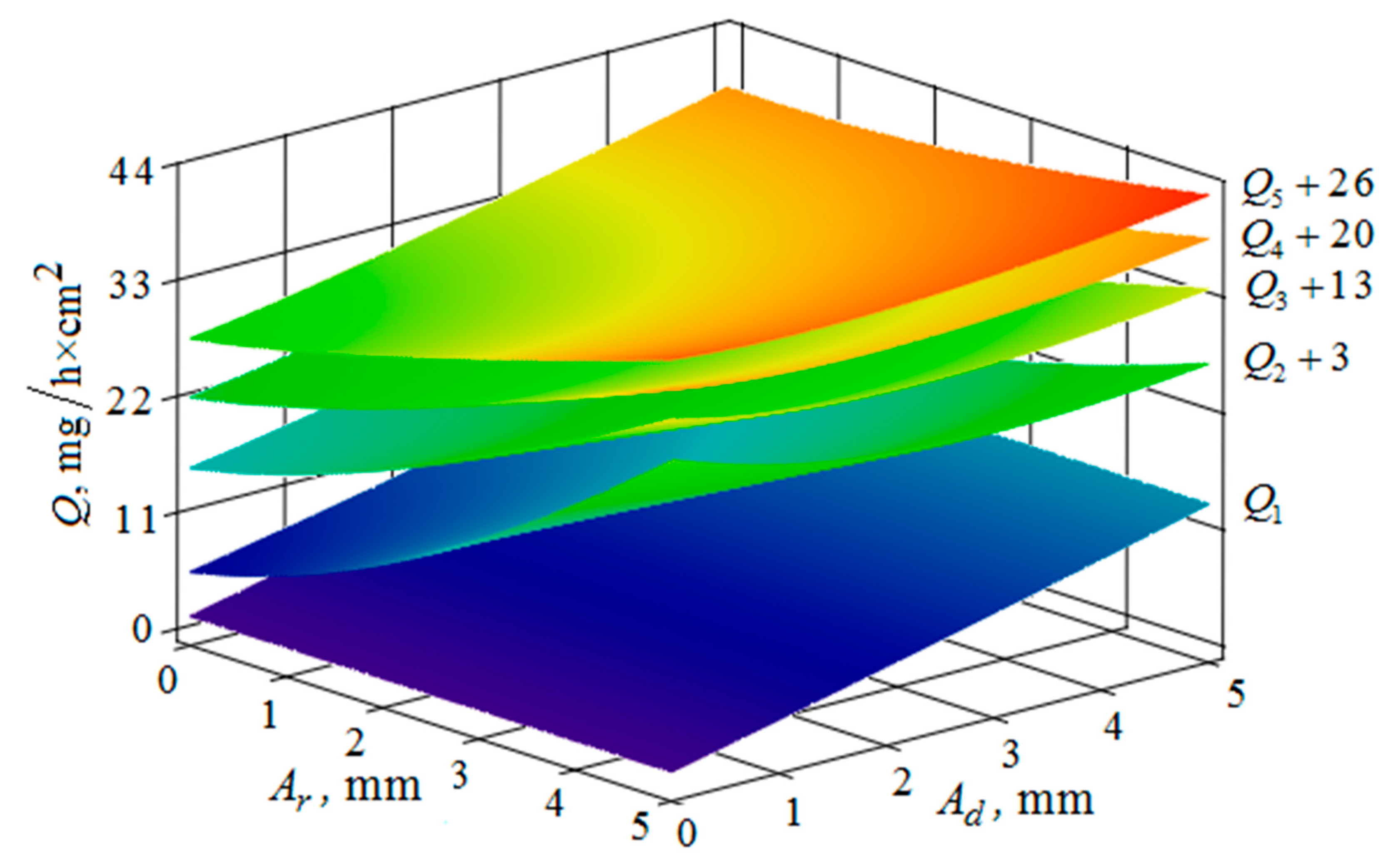
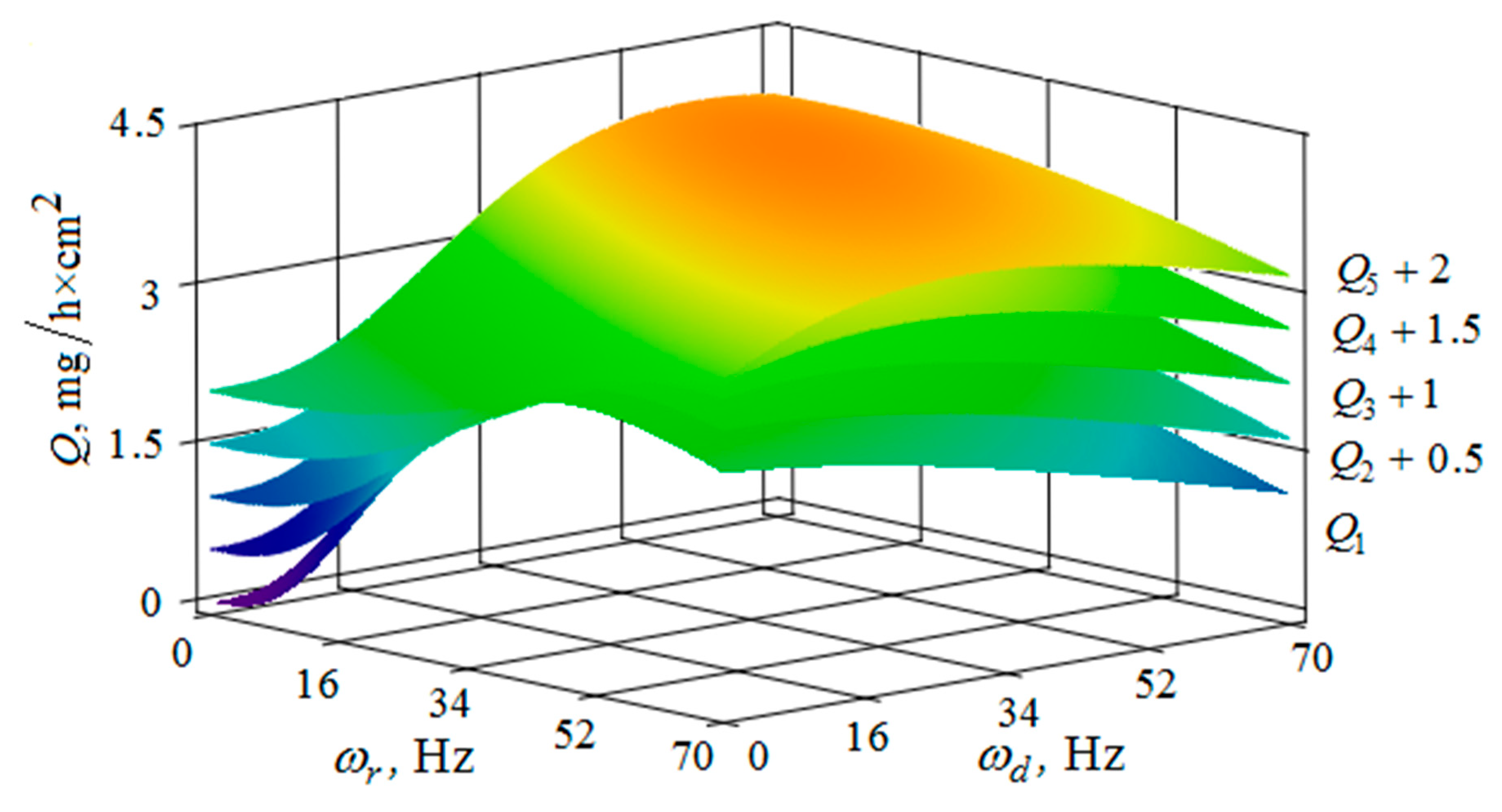
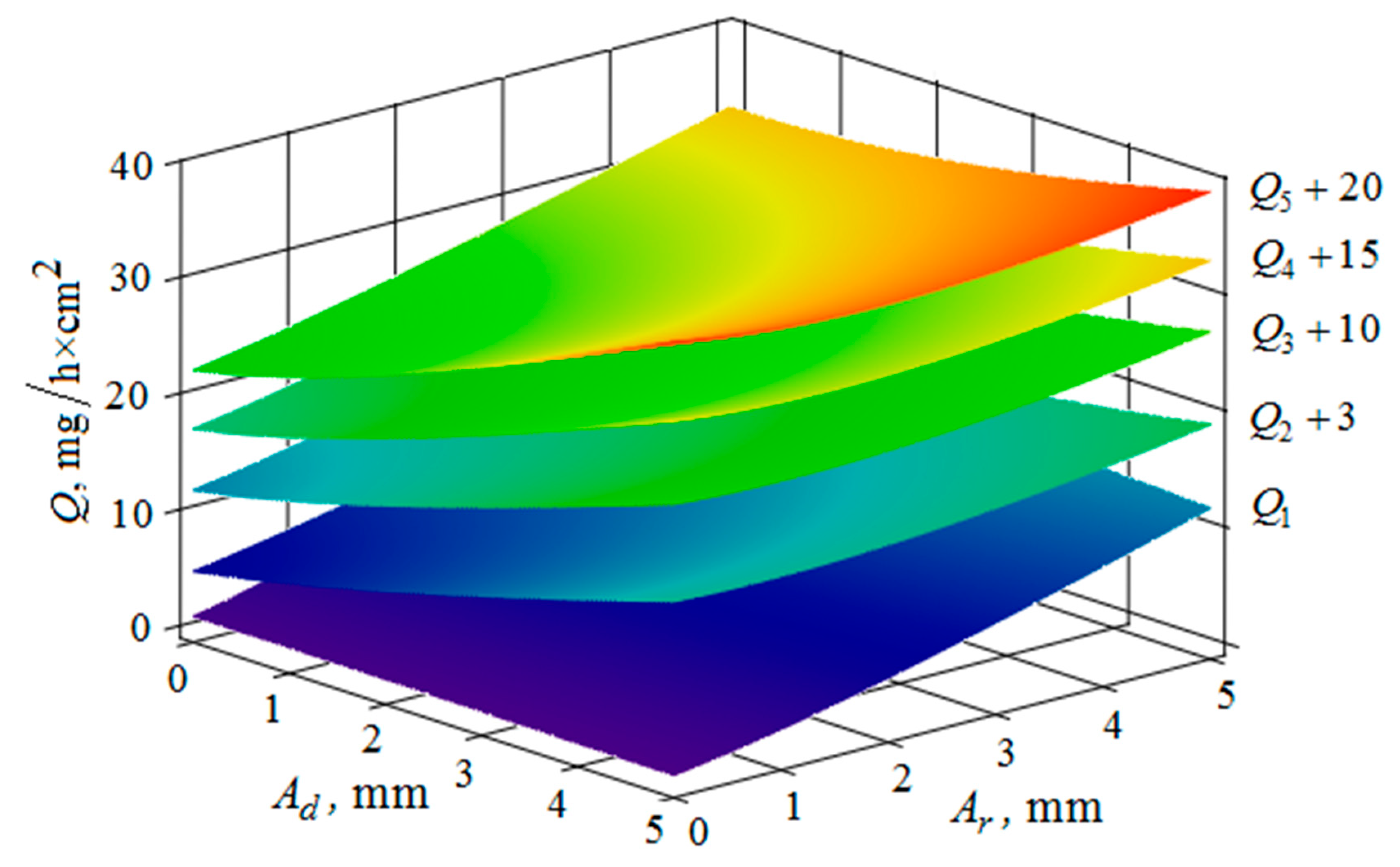
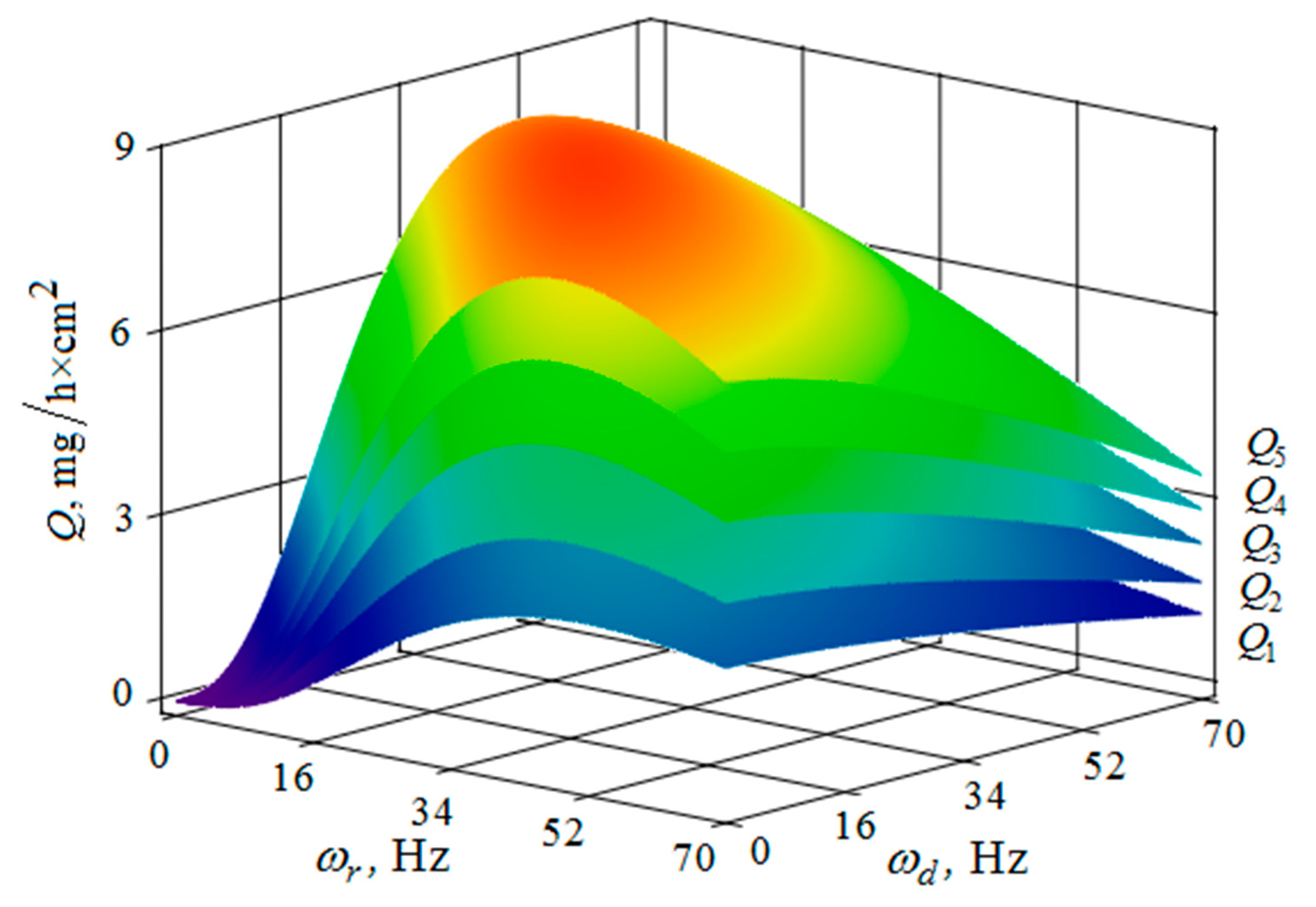
4. The Removal of Metal from the Part Surface as A Result of Multi-Agent Group Action of the Oscillating Reservoir Surface and the Part
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Babichev, A.P.; Shevtsov, S.N. Shock-wave effects involved in the process of hardening during dynamic SPD // Improvement of quality and efficiency in machine building and instrument making. In Proceedings of the Material of Anniversary Scientific and Technical Conference with Participation of Abroad, N. Novgorod, Russia, 10–13 June 1997; NNSTU, ATS: N. Novgorod, Russia, 1997. (In Russian). [Google Scholar]
- Mamalis, A.G.; Grabchenko, A.I.; Mitsyk, A.V.; Fedorovich, V.A.; Kundrak, J. Mathematical simulation of motion of working medium at finishing–grinding treatment in the oscillating reservoir. Int. J. Adv. Manuf. Technol. 2014, 70, 263–276. [Google Scholar] [CrossRef]
- Fedorovich, V.A.; Mitsyk, A.V. Mathematical Simulation of Kinematics of Vibrating Boiling Granular Medium at Treatment in the Oscillating Reservoir. Key Eng. Mater. 2014, 581, 456–461. [Google Scholar] [CrossRef]
- Mediratta, R.; Ahluwalia, K.; Yeo, S.H. State-of-the-art on vibratory finishing in the aviation industry: An industrial and academic perspective. Int. J. Adv. Manuf. Technol. 2016, 85b, 415–429. [Google Scholar] [CrossRef]
- Yang, S.; Li, W. Surface Finishing Theory and New Technology; Springer: Berlin/Heidelberg, Germany, 2018; p. 497. ISBN 978-3-662-54133-3. [Google Scholar]
- Mia, M.; Królczyk, G.; Maruda, R.; Wojciechowski, S. Intelligent optimization of hard-turning parameters using evolutionary algorithms for smart manufacturing. Materials 2019, 16, 879. [Google Scholar] [CrossRef] [PubMed]
- Nieslony, P.; Grzesik, W.; Bartoszuk, M.; Habrat, W. Analysis of mechanical characteristics of face milling process of ti6al4v alloy using experimental and simulation data. J. Mach. Eng. 2016, 16, 58–66. [Google Scholar]
- Wang, X.; Yang, S.; Li, W.; Wang, Y. Vibratory finishing co-simulation based on ADAMS-EDEM with experimental validation. Int. J. Adv. Manuf. Technol. 2018, 96, 1175–1185. [Google Scholar] [CrossRef]
- Uhlmann, E.; Dethlefs, A.; Eulitz, A. Investigation of material removal and surface topography formation in vibratory finishing. Procedia CIRP 2014, 14, 25–30. [Google Scholar] [CrossRef]
- Hashimoto, F.; Johnson, S.P. Modeling of vibratory finishing machines. CIRP Ann. Manuf. Technol. 2015, 64, 345–348. [Google Scholar] [CrossRef]
- Sokolov, V.; Krol, O. Determination of Transfer Functions for Electrohydraulic Servo Drive of Technological Equipment. In Proceedings of the Advances in Design, Simulation and Manufacturing: The Innovation Exchange, Sumy, Ukraine, 12–15 June 2018; Springer: Cham, Switzerland, 2019; pp. 364–373. [Google Scholar] [CrossRef]
- Sokolov, V.; Krol, O. Installations criterion of deceleration device in volumetric hydraulic drive. Procedia Eng. 2017, 206, 936–943. [Google Scholar] [CrossRef]
- Sokolov, V.; Rasskazova, Y. Automation of control processes of technological equipment with rotary hydraulic drive. East. Eur. J. Enterp. Technol. 2016, 2, 44–50. [Google Scholar] [CrossRef]
- Yavorsky, B.M.; Detlaf, A.A.; Lebedev, A.K. Reference Book on Physics, 8th ed.; ONIKS World and Education: Moscow, Russia, 2006. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Skudrzyk, E. The Foundations of Acoustics. Basic Mathematics and Basic Acoustics; Springer: New York, NY, USA, 1971. [Google Scholar]
- Borovin, G.K.; Lapshin, V.V.; Yurin, E.A. Nonlinear model of Collinear Collision Taking into Account Dry Friction. KIAM Preprint № 46, Moscow, 2014. Available online: http://keldysh.ru/papers/2014/prep2014_46.pdf (accessed on 19 September 2019).
- Babichev, A.P.; Babushkina, N.A.; Bratkovsky, A.M.; Grigorieva, I.S.; Meilikhov, E.Z. Physical Quantities: Handbook; Energoatomizdat: Moscow, Russia, 1991; p. 1232. [Google Scholar]
- Mitsyk, A.V. Determination of the influence of vibration treatment parameters on the pressure of granules and parts. Vib. Eng. Technol. 2010, 3, 75–79. [Google Scholar]
- Fikhtengol’ts, G.M. The Fundamentals of Mathematical Analysis; FIZMATLIT: Moscow, Russia, 2002. [Google Scholar]
- Mitsyk, A.V. Determination of the theoretical dependence of the metal removal on the main parameters of the technological process of vibration treatment. Vib. Eng. Technol. 2010, 2, 131–137. [Google Scholar]
- Matveev, A.N. Molecular Physics; Mir Publishers: Moscow, Russia, 1985; p. 450. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kundrák, J.; Mitsyk, A.V.; Fedorovich, V.A.; Morgan, M.; Markopoulos, A.P. The Use of the Kinetic Theory of Gases to Simulate the Physical Situations on the Surface of Autonomously Moving Parts During Multi-Energy Vibration Processing. Materials 2019, 12, 3054. https://doi.org/10.3390/ma12193054
Kundrák J, Mitsyk AV, Fedorovich VA, Morgan M, Markopoulos AP. The Use of the Kinetic Theory of Gases to Simulate the Physical Situations on the Surface of Autonomously Moving Parts During Multi-Energy Vibration Processing. Materials. 2019; 12(19):3054. https://doi.org/10.3390/ma12193054
Chicago/Turabian StyleKundrák, János, Andrey V. Mitsyk, Vladimir A. Fedorovich, Michael Morgan, and Angelos P. Markopoulos. 2019. "The Use of the Kinetic Theory of Gases to Simulate the Physical Situations on the Surface of Autonomously Moving Parts During Multi-Energy Vibration Processing" Materials 12, no. 19: 3054. https://doi.org/10.3390/ma12193054
APA StyleKundrák, J., Mitsyk, A. V., Fedorovich, V. A., Morgan, M., & Markopoulos, A. P. (2019). The Use of the Kinetic Theory of Gases to Simulate the Physical Situations on the Surface of Autonomously Moving Parts During Multi-Energy Vibration Processing. Materials, 12(19), 3054. https://doi.org/10.3390/ma12193054







