Electronic Transport Properties of Silicane Determined from First Principles
Abstract
1. Introduction
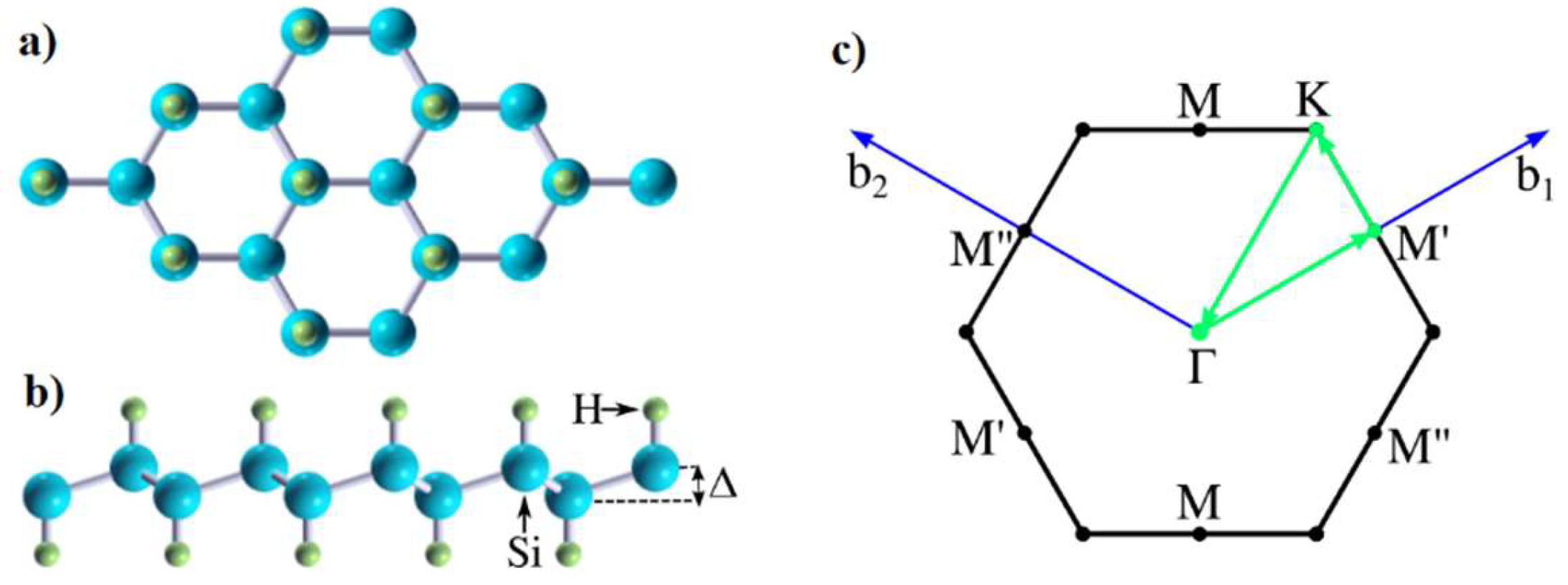
2. Computational Methodology and Silicane Structure
2.1. Methodology
2.2. Structure
3. Results and Discussions
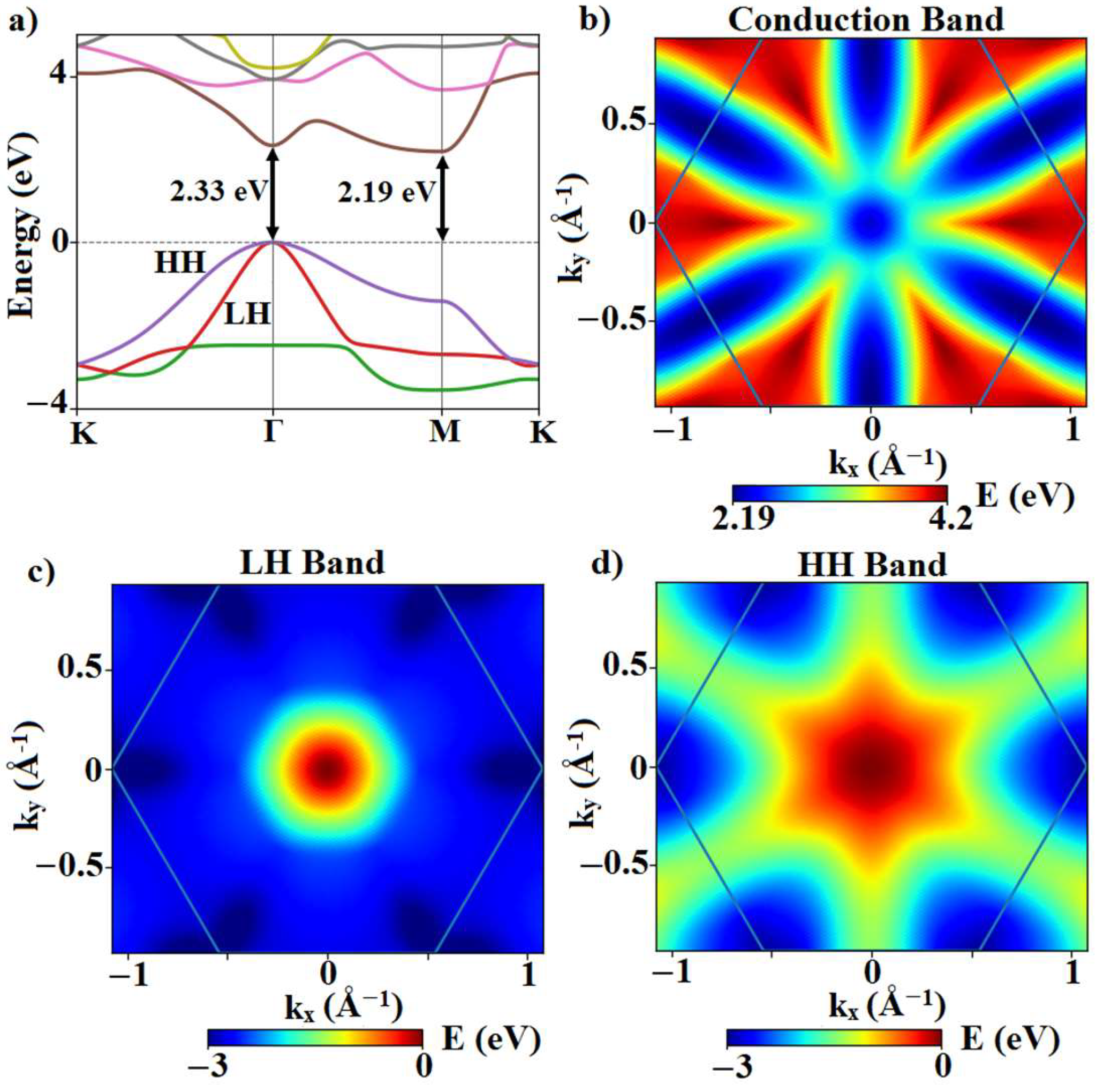
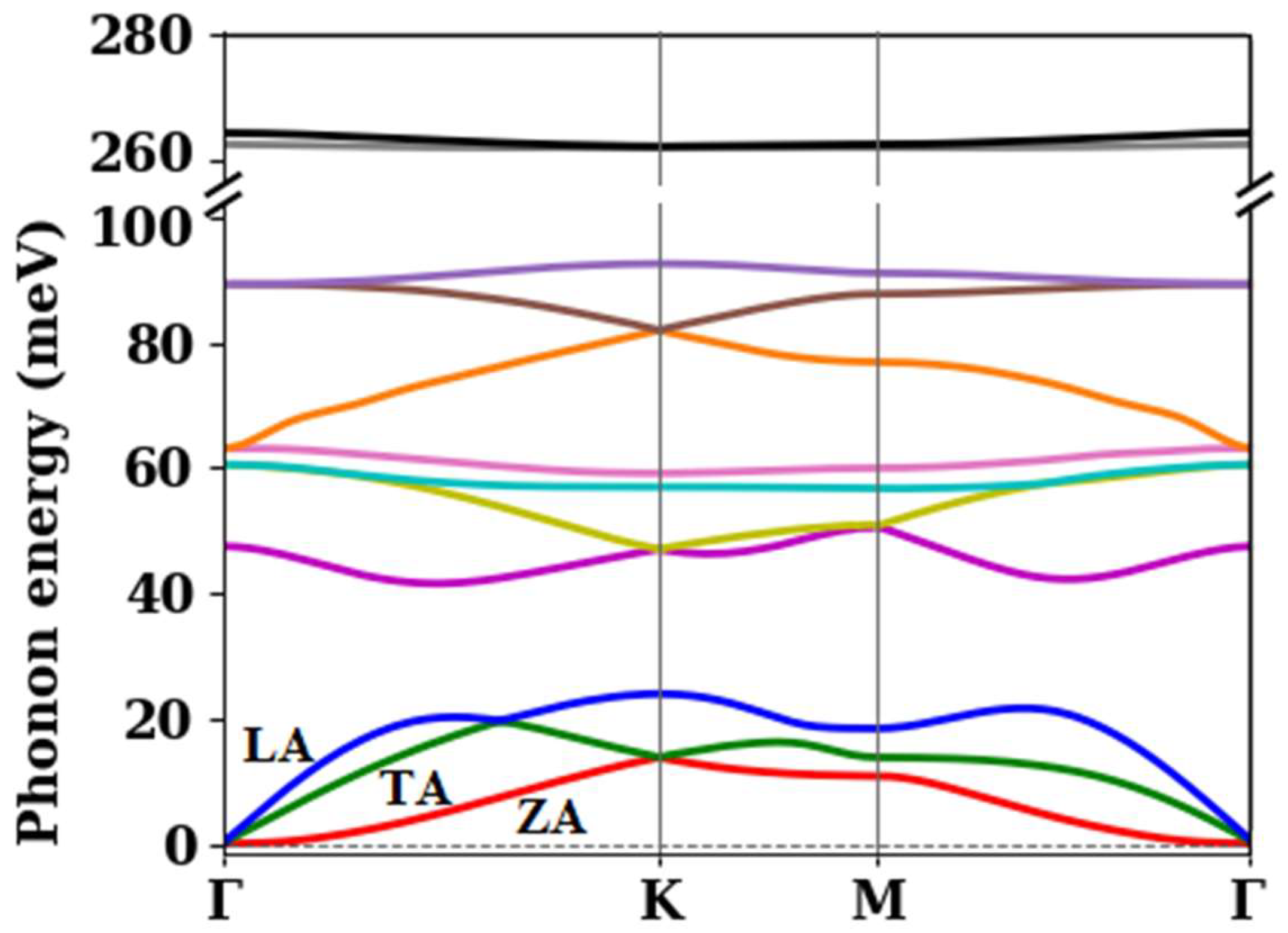
3.1. Electronic Band Structure and Phonon Dispersion
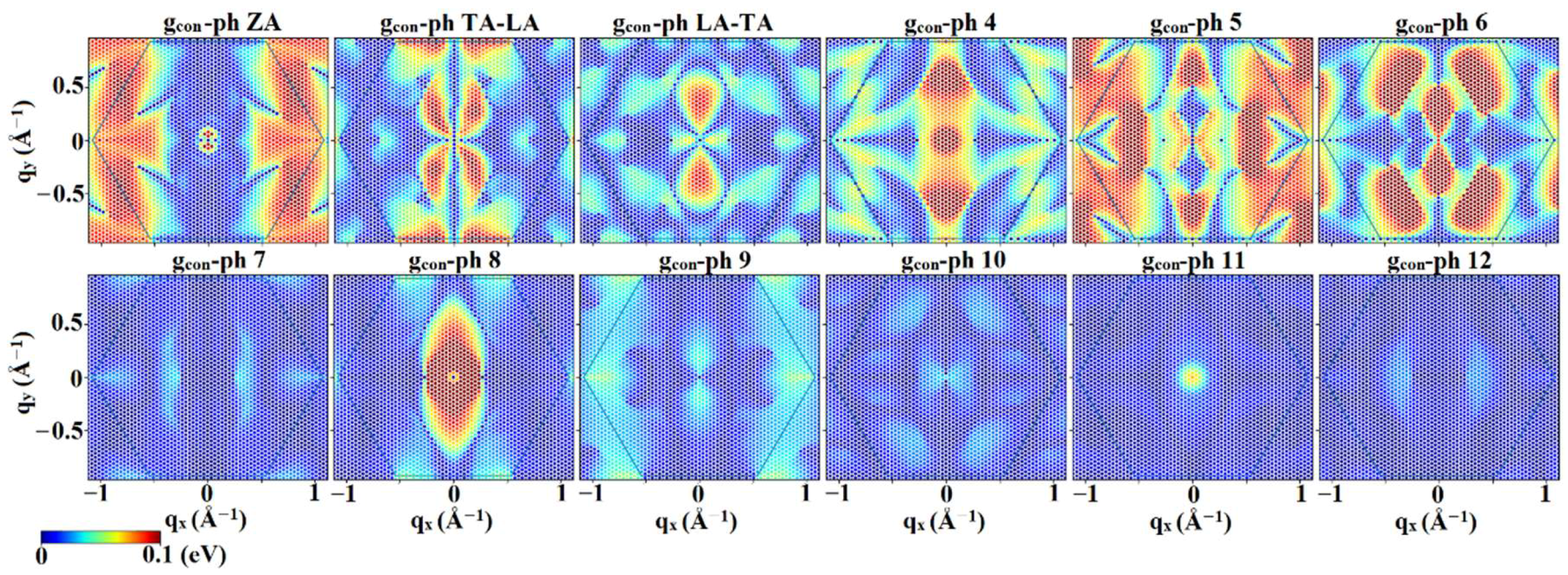
3.2. Interaction Matrix Elements
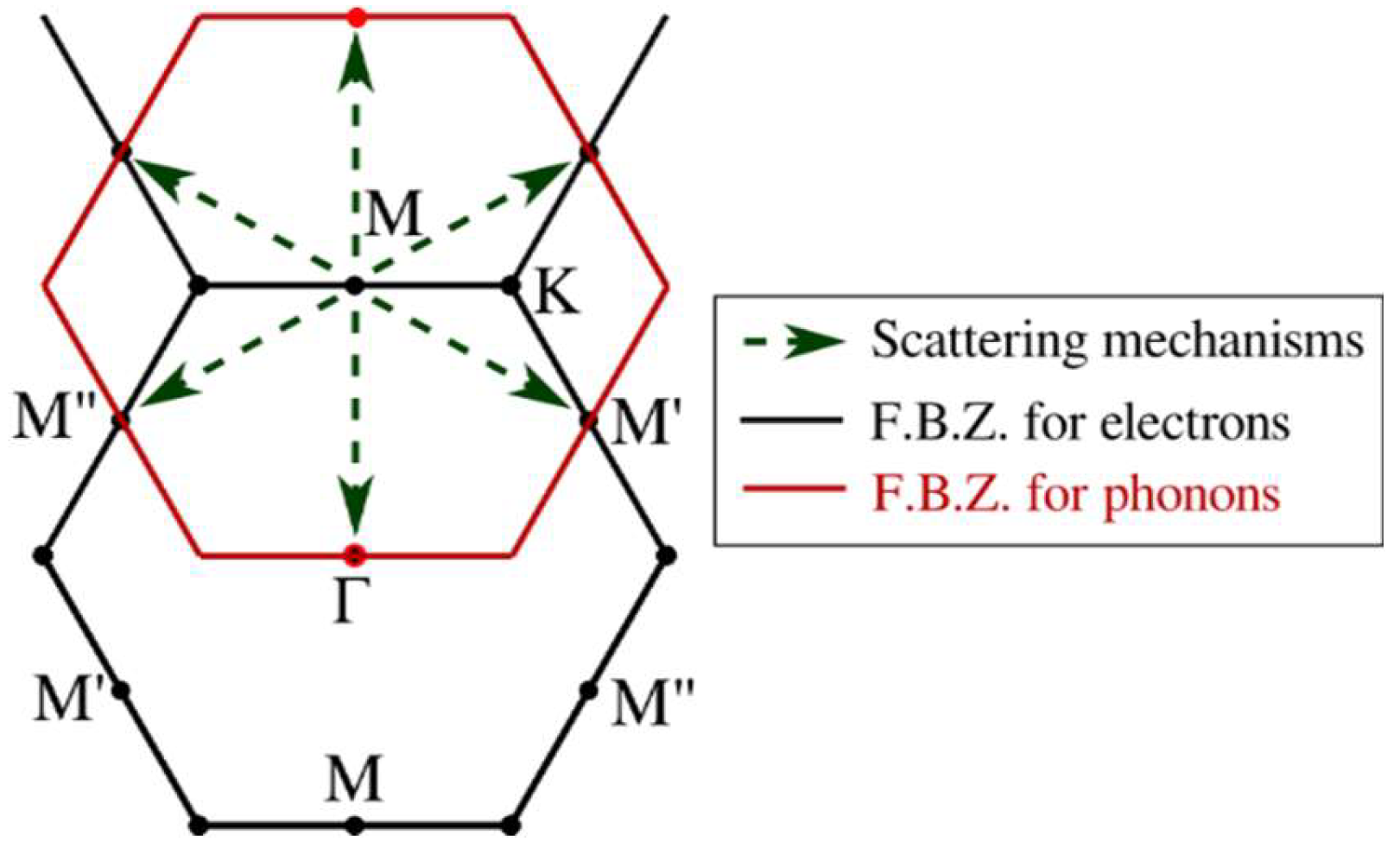
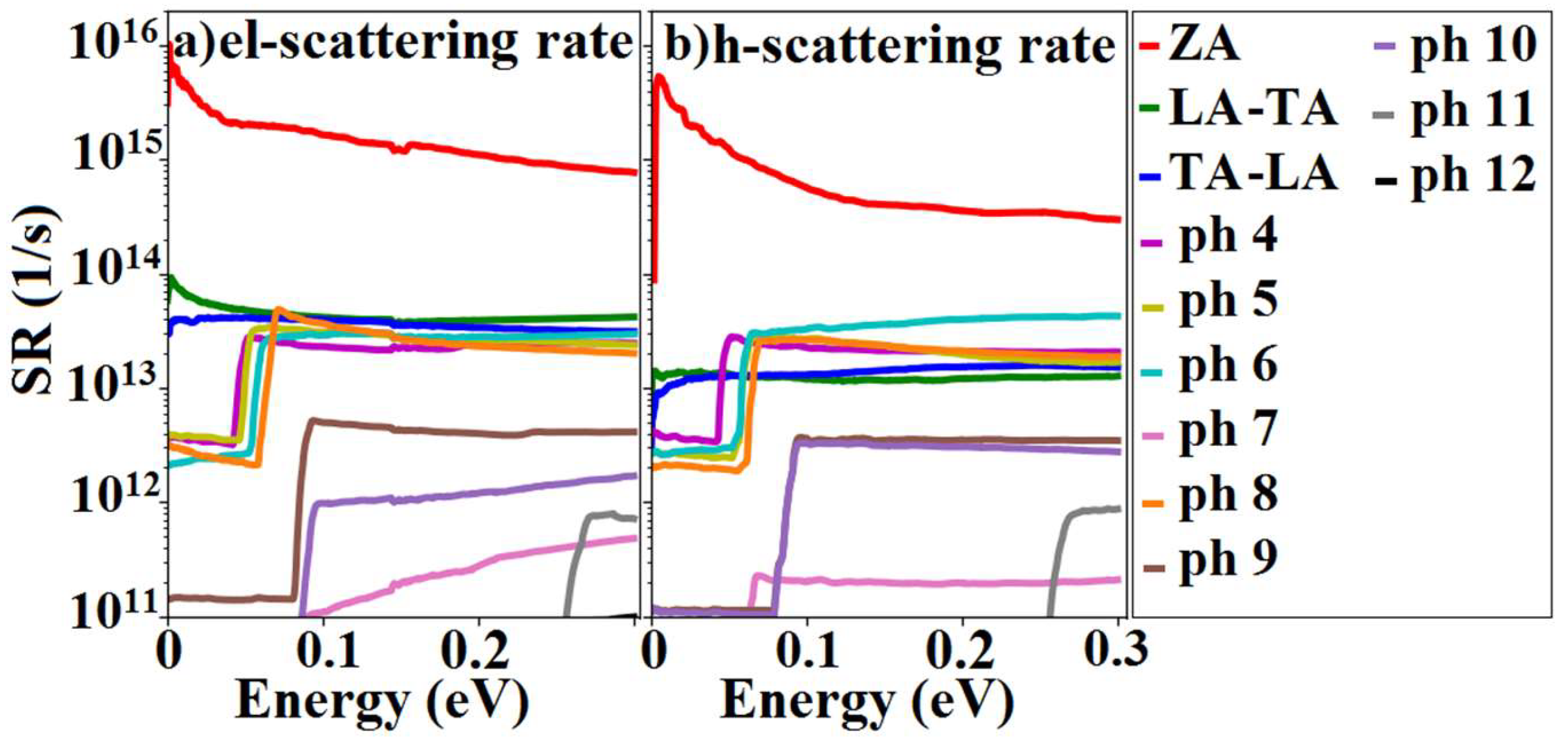
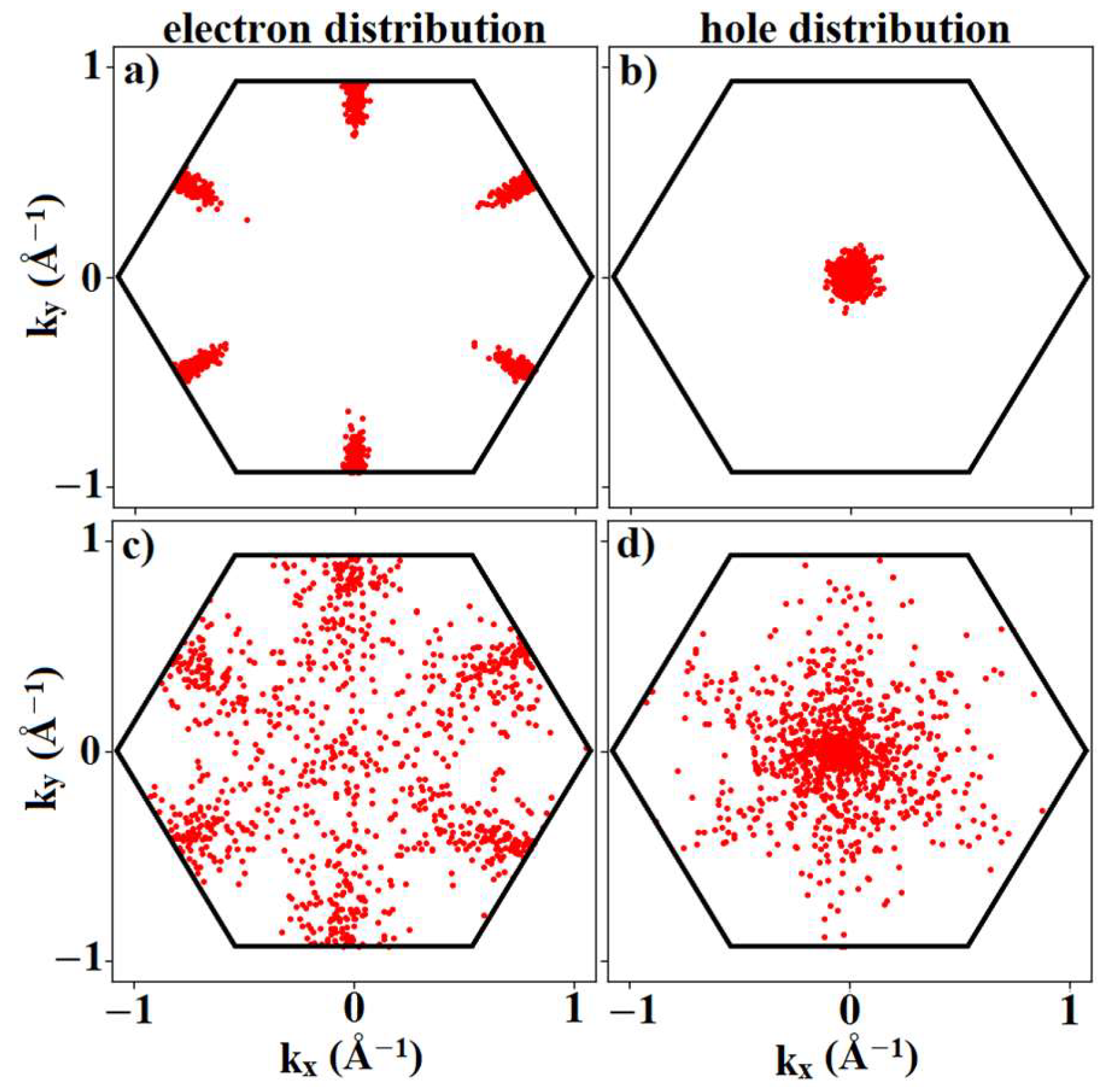
3.3. Scattering Rates
3.4. Mobility Calculations
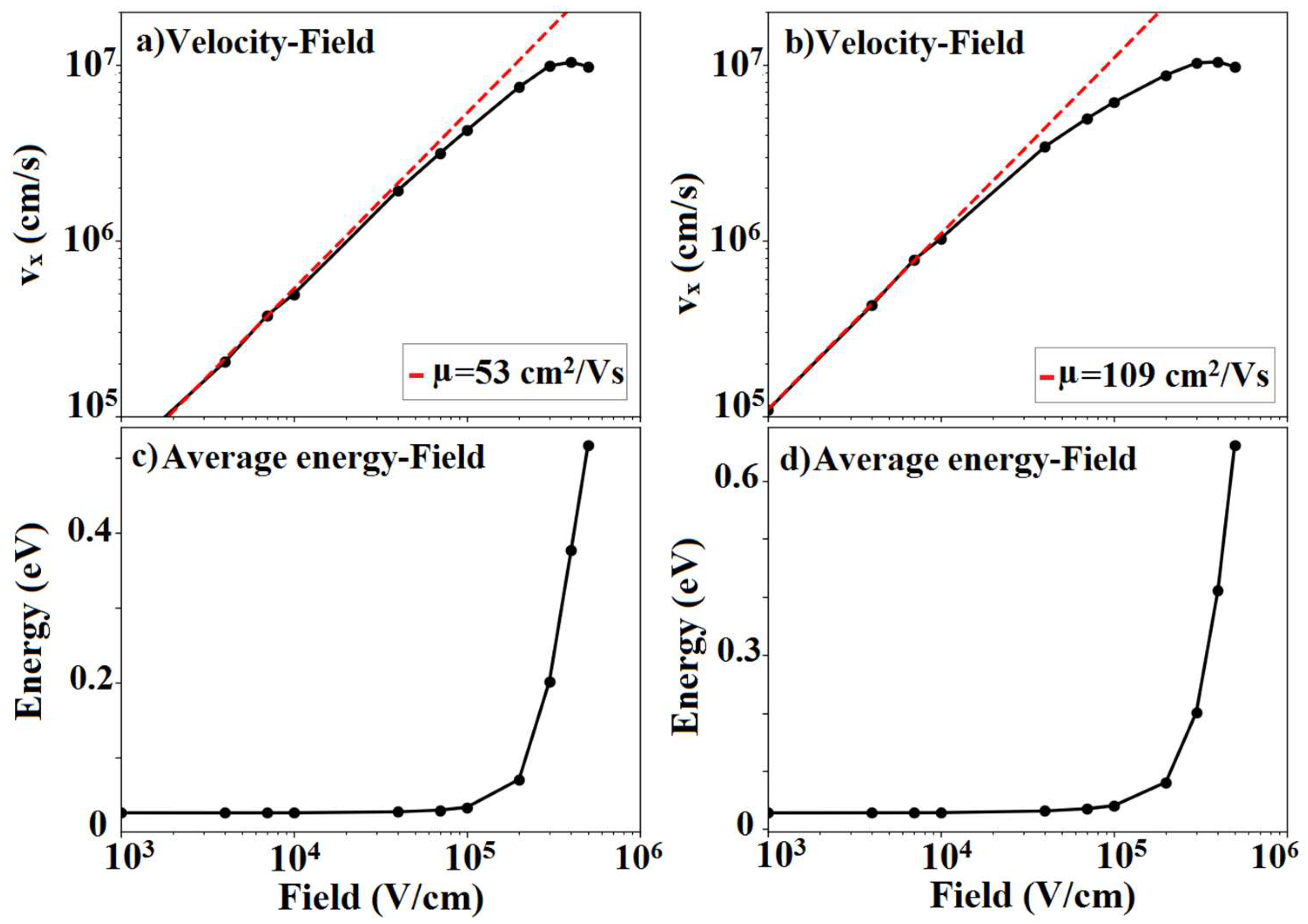
3.5. Velocity Field Calculations
3.6. Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Fischetti, M.V.; Fu, B.; Vandenberghe, W.G. Theoretical study of the gate leakage current in sub-10-nm field-effect transistors. IEEE Trans. Electron Devices 2013, 60, 3862–3869. [Google Scholar] [CrossRef]
- Neugebauer, P.; Orlita, M.; Faugeras, C.; Barra, A.L.; Potemski, M. How perfect can graphene be? Phys. Rev. Lett. 2009, 103, 136403. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.S.; Zhao, Y.; Jang, H.; Lee, S.Y.; Kim, J.M.; Kim, K.S.; Ahn, J.H.; Kim, P.; Choi, J.Y.; Hong, B.H. Large-scale pattern growth of graphene films for stretchable transparent electrodes. Nature 2009, 457, 706–710. [Google Scholar] [CrossRef]
- Reina, A.; Jia, X.; Ho, J.; Nezich, D.; Son, H.; Bulovic, V.; Dresselhaus, M.S.; Kong, J. Large Area, Few-Layer Graphene Films on Arbitrary Substrates by Chemical Vapor Deposition. Nano Lett. 2009, 9, 30–35. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Lee, E.K.; Joo, W.; Jang, Y.; Kim, B.; Lim, J.Y.; Choi, S.; Ahn, S.J.; Ahn, J.R.; Park, M.; et al. Wafer-Scale Growth of Single-Crystal Monolayer Graphene on Reusable Hydrogen-Terminated Germanium. Science 2014, 344, 286–289. [Google Scholar] [CrossRef] [PubMed]
- Schwierz, F. Graphene transistors. Nat. Nanotechnol. 2010, 5, 487–496. [Google Scholar] [CrossRef] [PubMed]
- The International Technology Roadmap for Semiconductors (ITRS). Available online: http://www.itrs2.net (accessed on 9 September 2019).
- Tao, L.; Cinquanta, E.; Chiappe, D.; Grazianetti, C.; Fanciulli, M.; Dubey, M.; Molle, A.; Akinwande, D. Silicene field-effect transistors operating at room temperature. Nat. Nanotechnol. 2015, 10, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Fischetti, M.V.; Vandenberghe, W.G. Mermin-Wagner theorem, flexural modes, and degraded carrier mobility in two-dimensional crystals with broken horizontal mirror symmetry. Phys. Rev. B 2016, 93, 155413. [Google Scholar] [CrossRef]
- Matthes, L.; Pulci, O.; Bechstedt, F. Massive Dirac quasiparticles in the optical absorbance of graphene, silicene, germanene, and tinene. J. Phys. Condens. Matter 2013, 25, 395305. [Google Scholar] [CrossRef]
- Shao, Z.G.; Ye, X.S.; Yang, L.; Wang, C.L. First-principles calculation of intrinsic carrier mobility of silicene. J. Appl. Phys. 2013, 114, 093712. [Google Scholar] [CrossRef]
- Yeoh, K.H.; Ong, D.S.; Ooi, C.H.R.; Yong, T.K.; Lim, S.K. Analytical band Monte Carlo analysis of electron transport in silicene. Semicond. Sci. Technol. 2016, 31, 065012. [Google Scholar] [CrossRef]
- Li, X.; Mullen, J.T.; Jin, Z.; Borysenko, K.M.; Buongiorno Nardelli, M.; Kim, K.W. Intrinsic electrical transport properties of monolayer silicene and MoS2 from first principles. Phys. Rev. B 2013, 87, 115418. [Google Scholar] [CrossRef]
- Seol, J.H.; Jo, I.; Moore, A.L.; Lindsay, L.; Aitken, Z.H.; Pettes, M.T.; Li, X.; Yao, Z.; Huang, R.; Broido, D.; et al. Two-Dimensional Phonon Transport in Supported Graphene. Science 2010, 328, 213–216. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Moore, A.L.; Zhu, Y.; Li, X.; Chen, S.; Shi, L.; Ruoff, R.S. Thermal transport in suspended and supported monolayer graphene grown by chemical vapor deposition. Nano Lett. 2010, 10, 1645–1651. [Google Scholar] [CrossRef] [PubMed]
- Gaddemane, G.; Vandenberghe, W.G.; Van De Put, M.L.; Chen, S.; Tiwari, S.; Chen, E.; Fischetti, M.V. Theoretical studies of electronic transport in monolayer and bilayer phosphorene: A critical overview. Phys. Rev. B 2018, 98, 115416. [Google Scholar] [CrossRef]
- Liu, G.; Wu, M.S.; Ouyang, C.Y.; Xu, B. Strain-induced semimetal-metal transition in silicene. EPL Europhysics Lett. 2012, 99, 17010. [Google Scholar] [CrossRef]
- Mohan, B.; Kumar, A.; Ahluwalia, P.K. Electronic and optical properties of silicene under uni-axial and bi-axial mechanical strains: A first principle study. Physica E 2014, 61, 40–47. [Google Scholar] [CrossRef]
- Qin, R.; Wang, C.H.; Zhu, W.; Zhang, Y. First-principles calculations of mechanical and electronic properties of silicene under strain. AIP Adv. 2012, 2, 022159. [Google Scholar] [CrossRef]
- Ni, Z.; Liu, Q.; Tang, K.; Zheng, J.; Zhou, J.; Qin, R.; Gao, Z.; Yu, D.; Lu, J. Tunable bandgap in silicene and germanene. Nano Lett. 2012, 12, 113–118. [Google Scholar] [CrossRef] [PubMed]
- Drummond, N.D.; Zólyomi, V.; Fal’Ko, V.I. Electrically tunable band gap in silicene. Phys. Rev. B 2012, 85, 075423. [Google Scholar] [CrossRef]
- Yan, J.A.; Gao, S.P.; Stein, R.; Coard, G. Tuning the electronic structure of silicene and germanene by biaxial strain and electric field. Phys. Rev. B 2015, 91, 245403. [Google Scholar] [CrossRef]
- Restrepo, O.D.; Mishra, R.; Goldberger, J.E.; Windl, W. Tunable gaps and enhanced mobilities in strain-engineered silicane. J. Appl. Phys. 2014, 115, 033711. [Google Scholar] [CrossRef]
- Low, K.L.; Huang, W.; Yeo, Y.C.; Liang, G. Ballistic Transport Performance of Silicane and Germanane Transistors. IEEE Trans. Electron Devices 2014, 61, 1590–1598. [Google Scholar] [CrossRef]
- Zólyomi, V.; Wallbank, J.R.; Fal’ko, V.I. Silicane and germanane: Tight-binding and first-principles studies. 2D Mater. 2014, 1, 011005. [Google Scholar]
- Zhang, P.; Li, X.D.; Hu, C.H.; Wu, S.Q.; Zhu, Z.Z. First-principles studies of the hydrogenation effects in silicene sheets. Phys. Lett. A 2012, 376, 1230–1233. [Google Scholar] [CrossRef]
- Lew Yan Voon, L.C.; Sandberg, E.; Aga, R.S.; Farajian, A.A. Hydrogen compounds of group-IV nanosheets. Appl. Phys. Lett. 2010, 97, 163114. [Google Scholar] [CrossRef]
- Houssa, M.; Scalise, E.; Sankaran, K.; Pourtois, G.; Afanas’ev, V.V.; Stesmans, A. Electronic properties of hydrogenated silicene and germanene. Appl. Phys. Lett. 2011, 98, 223107. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. Quantum Espresso: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with QUANTUM ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Hamann, D.R. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 2013, 88, 085117. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillonin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Baroni, S.; de Gironcoli, S.; Corso, A.D.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. [Google Scholar] [CrossRef]
- Poncé, S.; Margine, E.R.; Verdi, C.; Giustino, F. EPW: Electron–phonon coupling, transport and superconducting properties using maximally localized Wannier functions. Comput. Phys. Commun. 2016, 209, 116–133. [Google Scholar] [CrossRef]
- Vandenberghe, W.G.; Fischetti, M.V. Deformation potentials for band-to-band tunneling in silicon and germanium from first principles from first principles. Appl. Phys. Lett. 2015, 106, 013505. [Google Scholar] [CrossRef]
- Elahi, M.; Pourfath, M. Ab initio effective deformation potentials of phosphorene and consistency checks. J. Phys. Condens. Matter 2018, 30, 225701. [Google Scholar] [CrossRef]
- Sohier, T.; Calandra, M.; Mauri, F. Two-dimensional Fröhlich interaction in transition-metal dichalcogenide monolayers: Theoretical modeling and first-principles calculations. Phys. Rev. B 2016, 94, 085415. [Google Scholar] [CrossRef]
- Marzari, N.; Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 1997, 56, 12847. [Google Scholar] [CrossRef]
- Giustino, F.; Cohen, M.L.; Louie, S.G. Electron-phonon interaction using Wannier functions. Phys. Rev. B 2007, 76, 165108. [Google Scholar] [CrossRef]
- Jacoboni, C.; Reggiani, L. The Monte Carlo method for the solution of charge transport in semiconductors with applications to covalent materials. Rev. Mod. Phys. 1983, 55, 645–705. [Google Scholar] [CrossRef]
- Cahangirov, S.; Topsakal, M.; Akturk, E.; Sahin, H.; Ciraci, S. Two- and one-dimensional honeycomb structures of silicon and germanium. Phys. Rev. Lett. 2009, 102, 236804. [Google Scholar] [CrossRef] [PubMed]
- Carrete, J.; Li, W.; Lindsay, L.; Broido, D.A.; Gallego, L.J.; Mingo, N. Physically founded phonon dispersions of few-layer materials and the case of borophene. Mater. Res. Lett. 2016, 4, 204–211. [Google Scholar] [CrossRef]
- Mermin, N.D.; Wagner, H. Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Phys. Rev. Lett. 1966, 17, 1133. [Google Scholar] [CrossRef]
- Amorim, B.; Guinea, F. Flexural mode of graphene on a substrate. Phys. Rev. B 2013, 88, 115418. [Google Scholar] [CrossRef]
- Ong, Z.Y.; Pop, E. Effect of substrate modes on thermal transport in supported graphene. Phys. Rev. B 2011, 84, 075471. [Google Scholar] [CrossRef]
- Jin, Z.; Li, X.; Mullen, J.T.; Kim, K.W. Intrinsic transport properties of electrons and holes in monolayer transition-metal dichalcogenides. Phys. Rev. B 2014, 90, 045422. [Google Scholar] [CrossRef]
- Gaddemane, G.; Vandenberghe, W.G.; Van De Put, M.L.; Chen, E.; Fischetti, M.V. Monte-Carlo study of electronic transport in non-σh-symmetric two-dimensional materials: Silicene and germanene. J. Appl. Phys. 2018, 124, 044306. [Google Scholar] [CrossRef]
- Li, W. Electrical transport limited by electron-phonon coupling from Boltzmann transport equation: An ab initio study of Si, Al, and MoS2. Phys. Rev. B 2015, 92, 075405. [Google Scholar]
- Kaasbjerg, K.; Thygesen, K.S.; Jacobsen, K.W. Phonon-limited mobility in n-type single-layer MoS2 from first principles. Phys. Rev. B 2012, 85, 115317. [Google Scholar] [CrossRef]
- Jacoboni, C.; Canali, C.; Ottaviani, G.; Alberigi Quaranta, A. A review of some charge transport properties of silicon. Solid State Electron. 1977, 20, 77–89. [Google Scholar] [CrossRef]
- Gamiz, F.; Fischetti, M.V. Monte Carlo simulation of double-gate silicon-on-insulator inversion layers: The role of volume inversion. J. Appl. Phys. 2001, 89, 5478. [Google Scholar] [CrossRef]
- Poncé, S.; Margine, E.R.; Giustino, F. Towards predictive many-body calculations of phonon-limited carrier mobilities in semiconductors. Phys. Rev. B 2018, 97, 121201. [Google Scholar]
| Parameter | This Work | [26] | [25] |
|---|---|---|---|
| Lattice constant (Å) | 3.887 | 3.84 | 3.889 |
| Si–Si bond (Å) | 2.44 | 2.34 | 2.358 |
| Si–H bond (Å) | 1.502 | 1.51 | 1.501 |
| Buckling height Δ (Å) | 0.715 | 0.74 | 0.719 |
| me,x (m0) | 0.13 | 0.12 | 0.123 |
| me,y (m0) | 3.5 | 3.79 | 3.23 |
| mlh,x (m0) | 0.12 | 0.13 | 0.151 |
| mlh,y (m0) | 0.12 | - | 0.142 |
| mhh,x (m0) | 0.57 | 0.52 | 0.573 |
| mhh,y (m0) | 0.58 | - | 0.603 |
| Indirect gap (eV) | 2.19 | - | 2.19 |
| Direct gap (eV) | 2.335 | - | 2.33 |
| Phonon Branch Number | Γ | K | M |
|---|---|---|---|
| 1 | 0 | 13.8 | 10.8 |
| 2 | 0 | 13.8 | 13.8 |
| 3 | 0 | 24.0 | 18.4 |
| 4 | 47.5 | 47.0 | 50.5 |
| 5 | 60.5 | 47.0 | 50.7 |
| 6 | 60.5 | 57.0 | 56.6 |
| 7 | 63.1 | 59.0 | 60.0 |
| 8 | 63.1 | 81.9 | 76.8 |
| 9 | 89.3 | 81.9 | 87.7 |
| 10 | 89.3 | 92.5 | 91.0 |
| 11 | 262.5 | 262.1 | 262.0 |
| 12 | 264.3 | 262.1 | 262.4 |
| Cut-Off Wavelength (nm) | ||
|---|---|---|
| 0.58 | 53 | 109 |
| 1 | 31 | 109 |
| 4 | 24 | 101 |
| 16 | 5 | 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khatami, M.M.; Gaddemane, G.; Van de Put, M.L.; Fischetti, M.V.; Moravvej-Farshi, M.K.; Pourfath, M.; Vandenberghe, W.G. Electronic Transport Properties of Silicane Determined from First Principles. Materials 2019, 12, 2935. https://doi.org/10.3390/ma12182935
Khatami MM, Gaddemane G, Van de Put ML, Fischetti MV, Moravvej-Farshi MK, Pourfath M, Vandenberghe WG. Electronic Transport Properties of Silicane Determined from First Principles. Materials. 2019; 12(18):2935. https://doi.org/10.3390/ma12182935
Chicago/Turabian StyleKhatami, Mohammad Mahdi, Gautam Gaddemane, Maarten L. Van de Put, Massimo V. Fischetti, Mohammad Kazem Moravvej-Farshi, Mahdi Pourfath, and William G. Vandenberghe. 2019. "Electronic Transport Properties of Silicane Determined from First Principles" Materials 12, no. 18: 2935. https://doi.org/10.3390/ma12182935
APA StyleKhatami, M. M., Gaddemane, G., Van de Put, M. L., Fischetti, M. V., Moravvej-Farshi, M. K., Pourfath, M., & Vandenberghe, W. G. (2019). Electronic Transport Properties of Silicane Determined from First Principles. Materials, 12(18), 2935. https://doi.org/10.3390/ma12182935





