Defects, Diffusion, and Dopants in Li2Ti6O13: Atomistic Simulation Study
Abstract
1. Introduction
2. Computational Methods
3. Results and Discussion
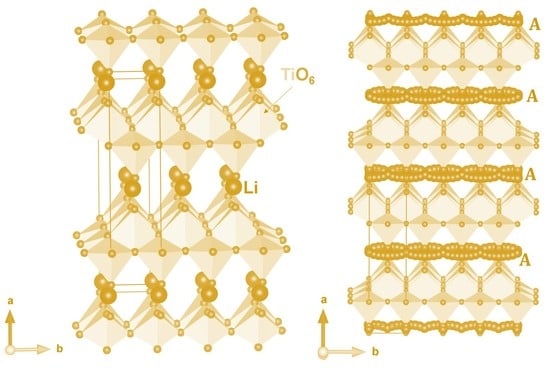
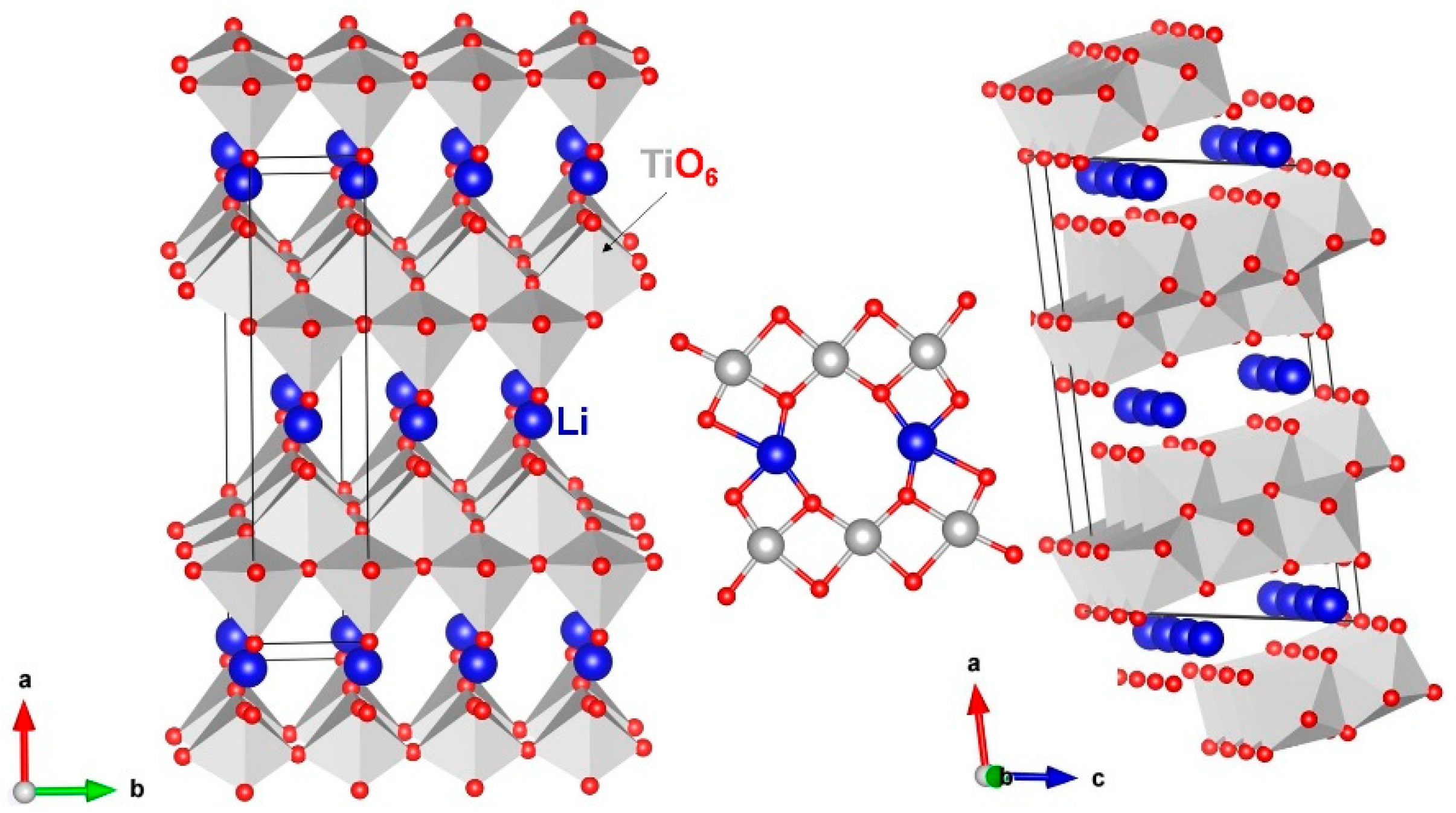
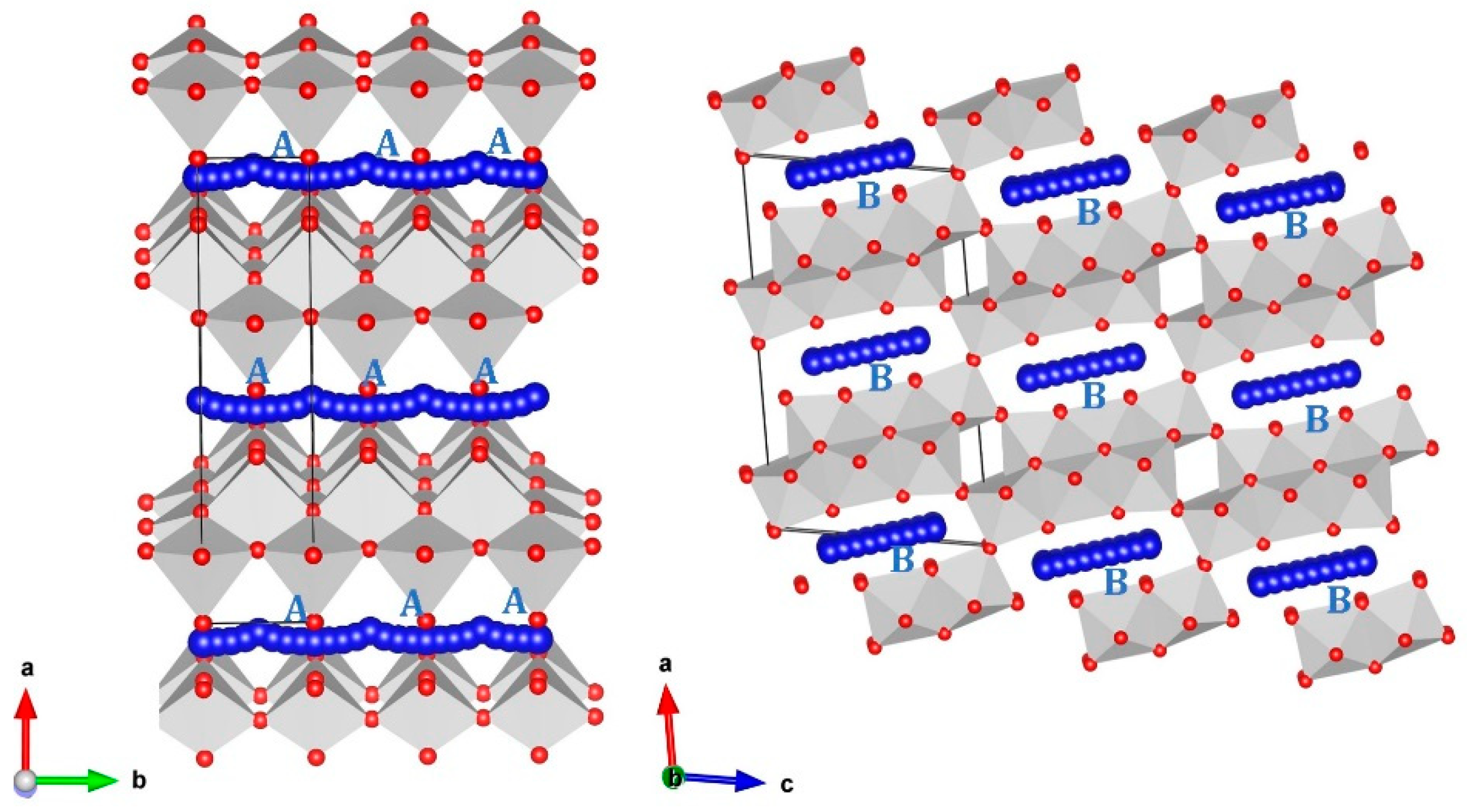
3.1. Crystal Structure of Li2Ti6O13
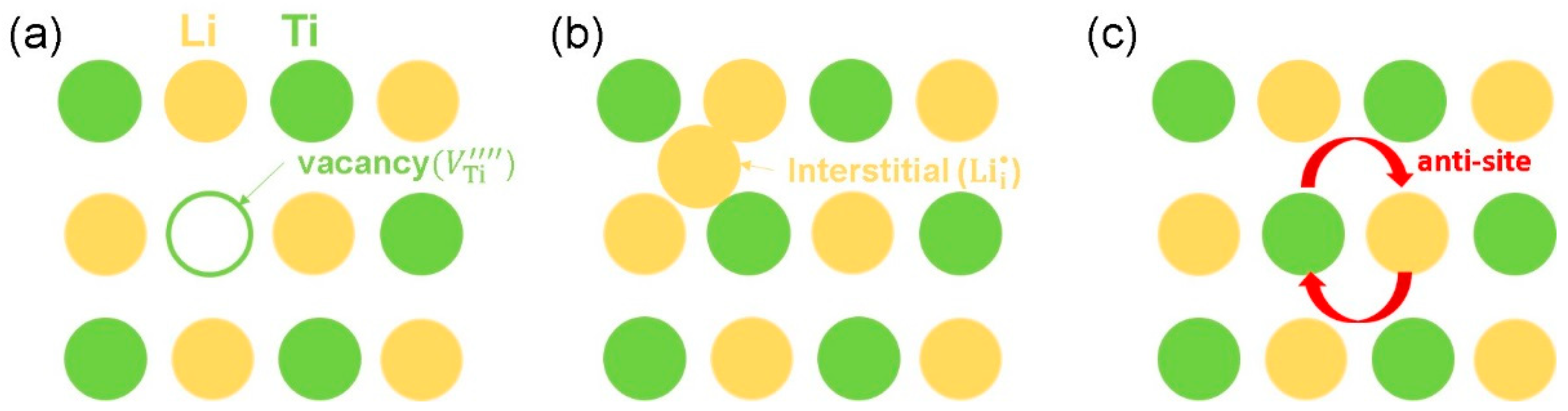
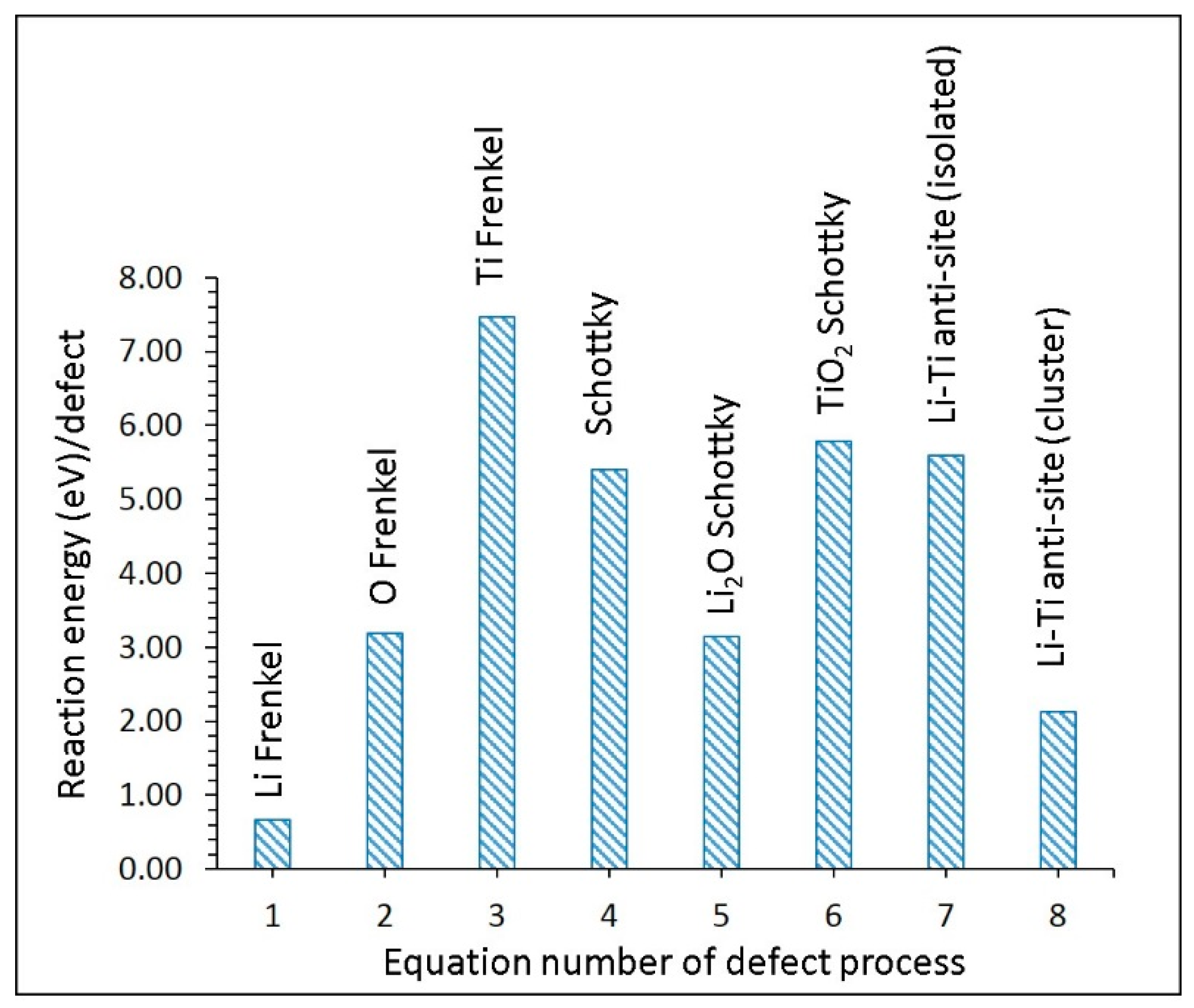
3.2. Intrinsic Defect Process
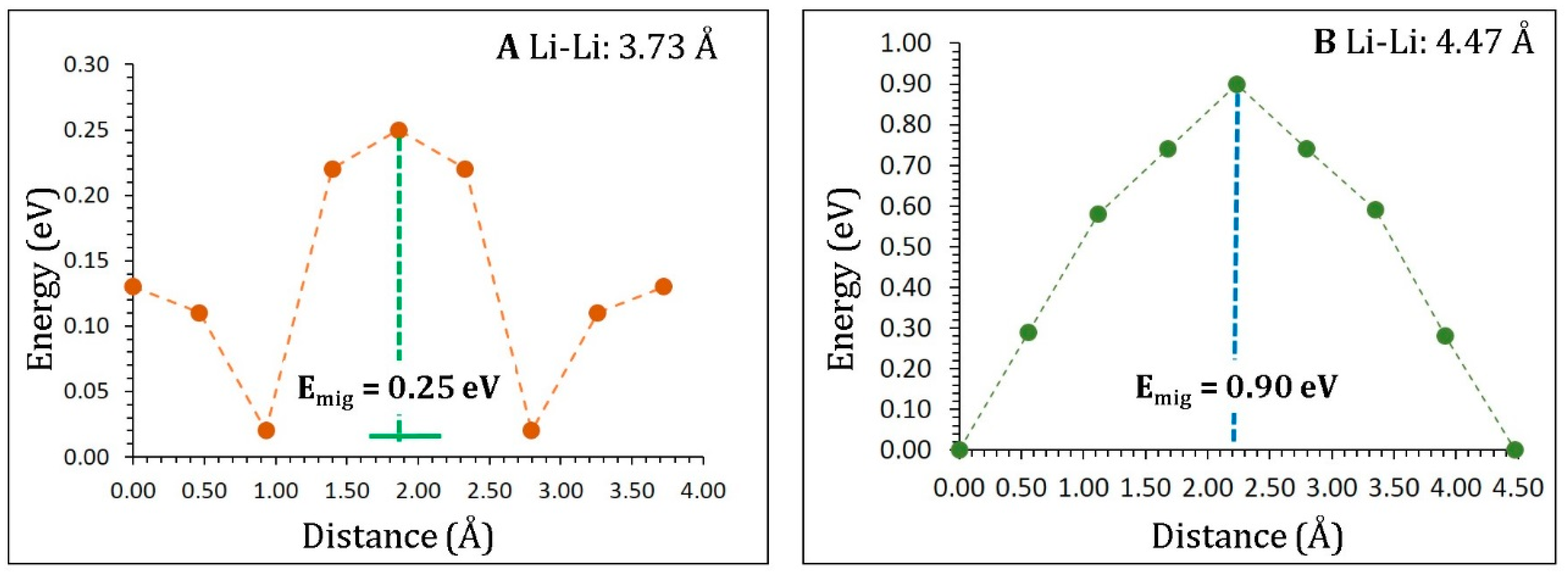
3.3. Lithium-Ion Diffusion
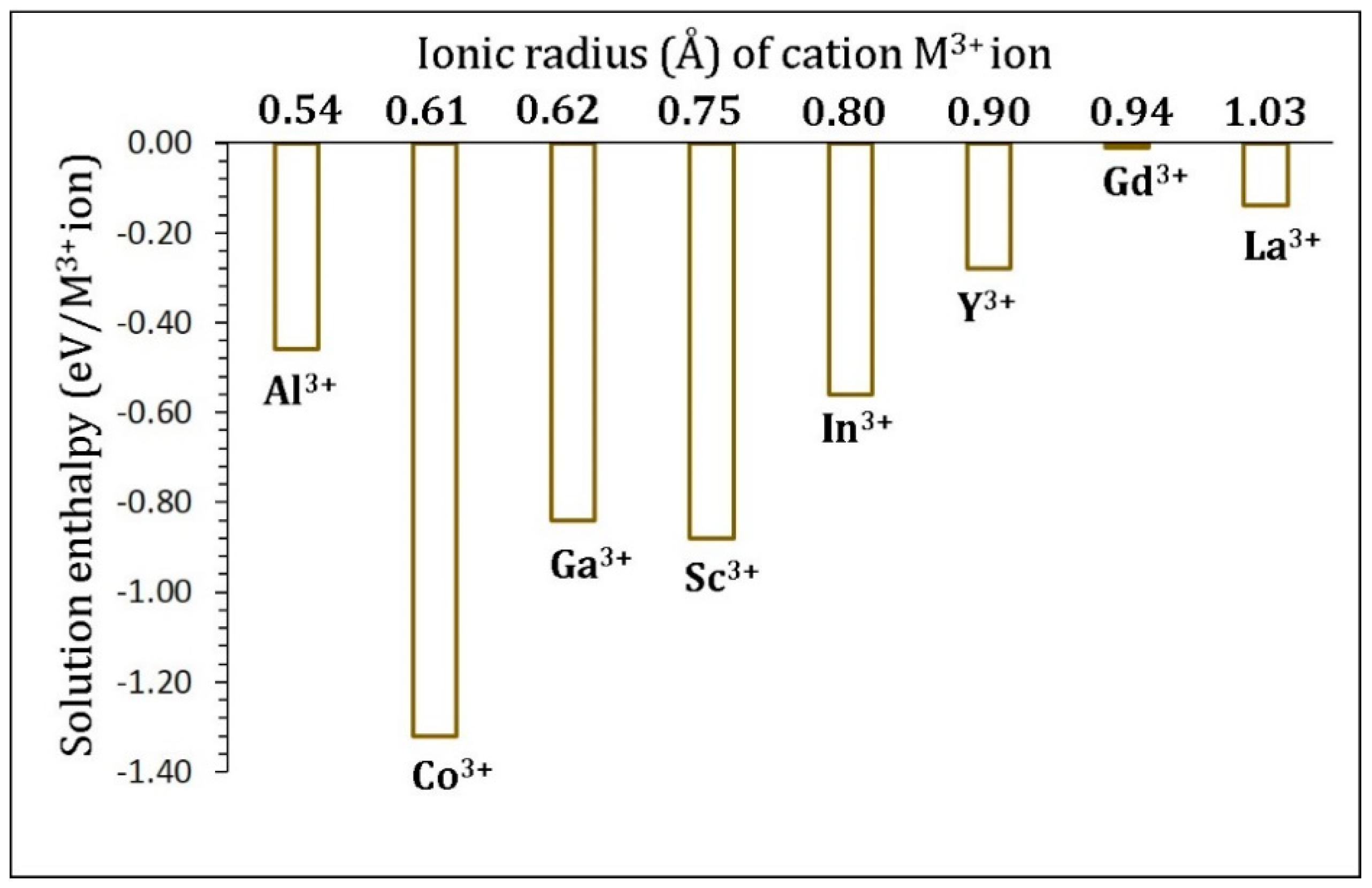
3.4. Trivalent Doping
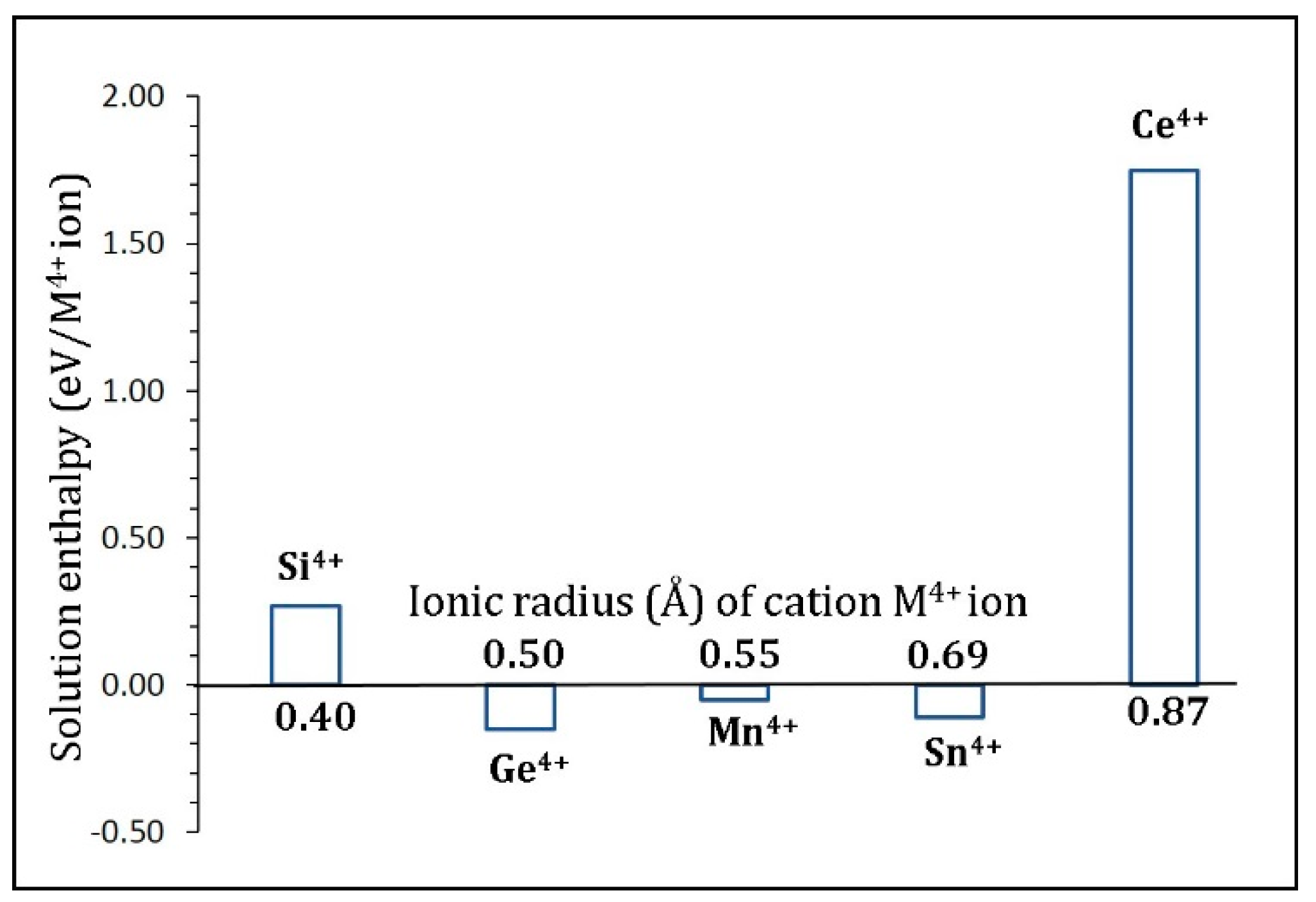
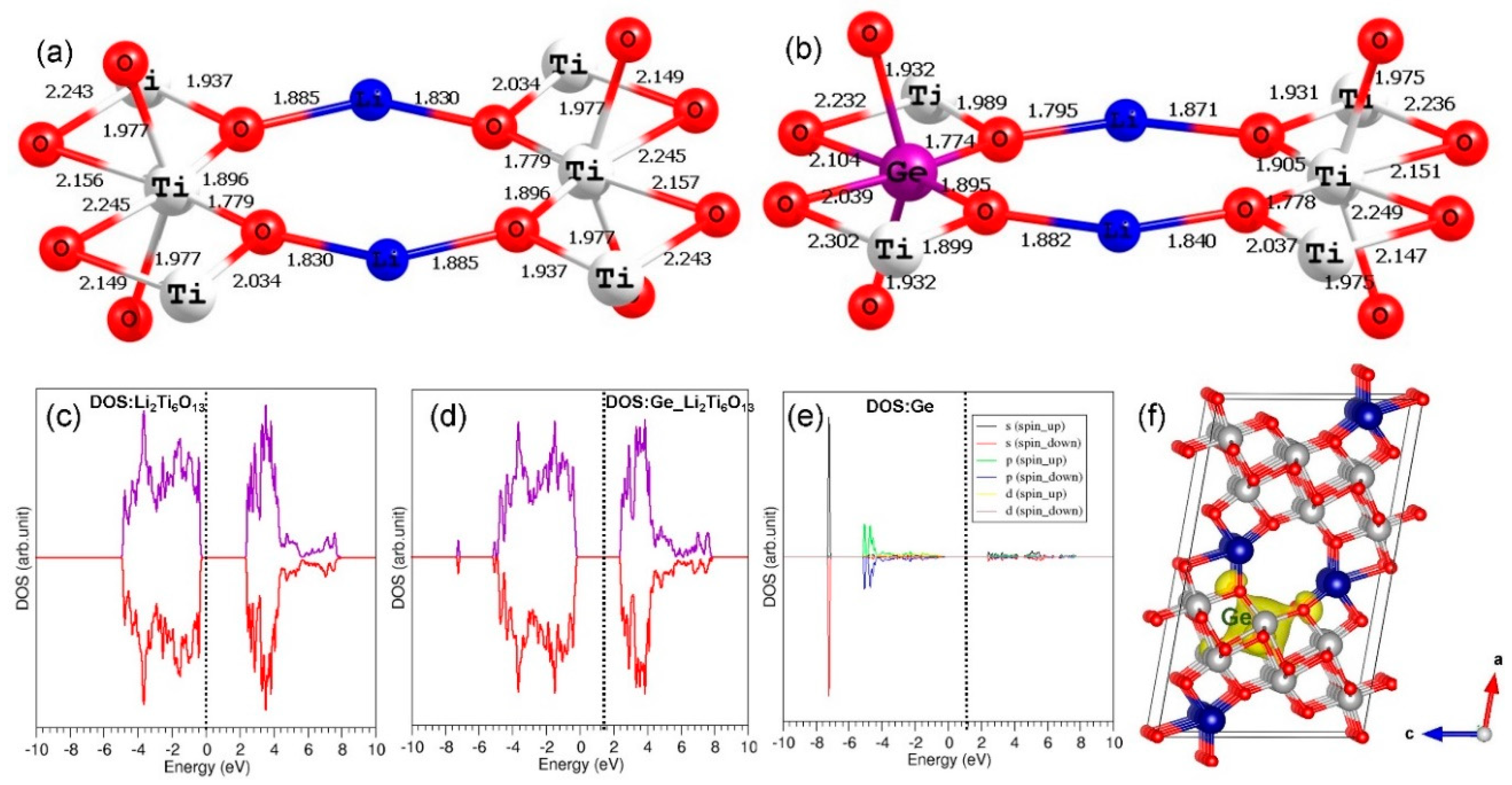
3.5. Tetravalent Doping
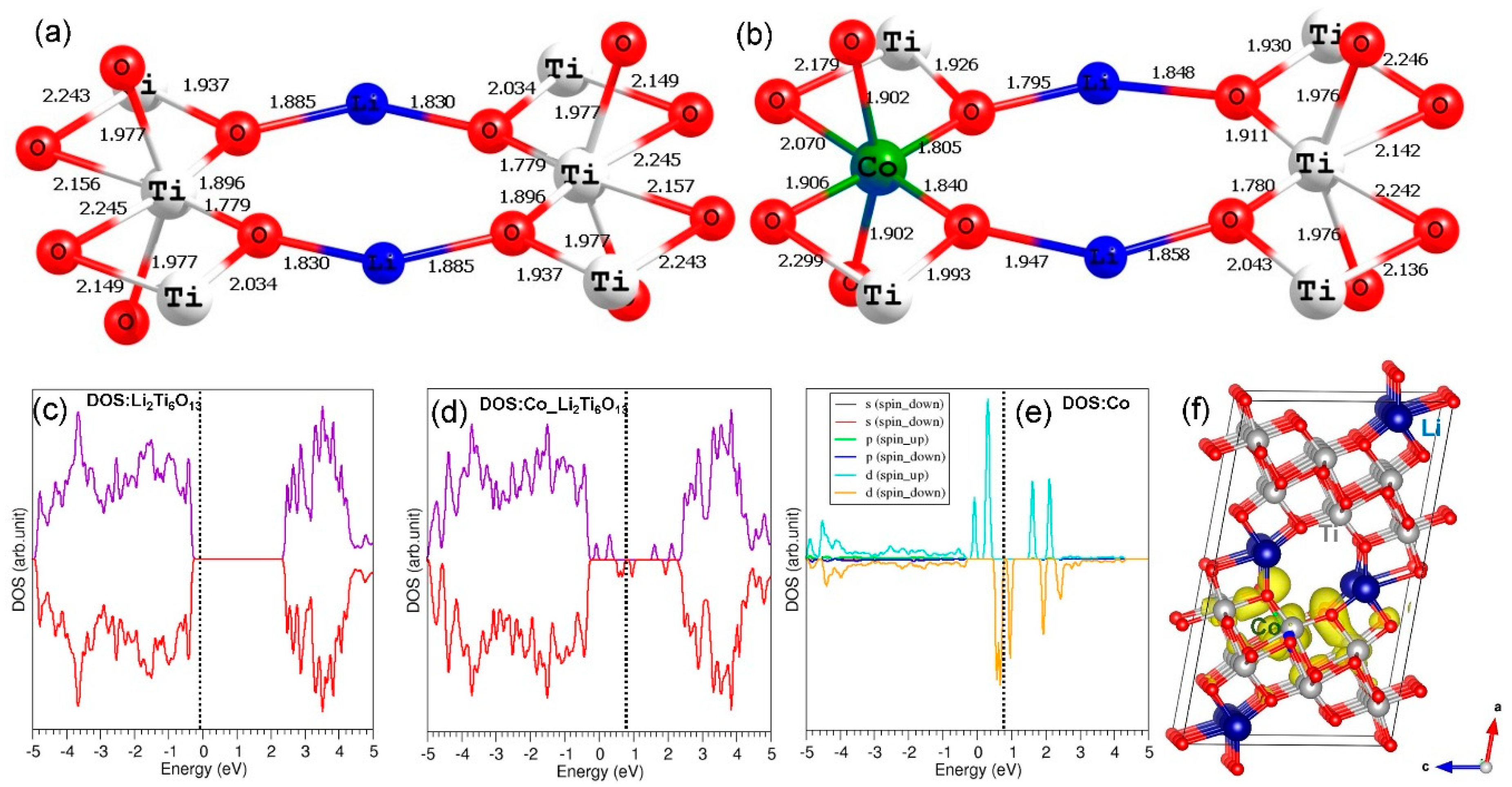
3.6. Electronic Structures of Co3+- and Ge4+-Doped Li2Ti6O13
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Armand, M.; Tarascon, J.M. Building better batteries. Nature 2008, 451, 652. [Google Scholar] [CrossRef] [PubMed]
- Whittingham, M.S. Lithium Batteries and Cathode Materials. Chem. Rev. 2004, 104, 4271–4302. [Google Scholar] [CrossRef] [PubMed]
- Padhi, A.K.; Nanjundaswamy, K.S.; Goodenough, J.B. Phospho-olivines as Positive-Electrode Materials for Rechargeable Lithium Batteries. J. Electrochem. Soc. 1997, 144, 1188–1194. [Google Scholar] [CrossRef]
- Nytén, A.; Abouimrane, A.; Armand, M.; Gustafsson, T.; Thomas, J.O. Electrochemical performance of Li2FeSiO4 as a new Li-battery cathode material. Electrochem. Commun. 2005, 7, 156–160. [Google Scholar] [CrossRef]
- Nishimura, S.-I.; Hayase, S.; Kanno, R.; Yashima, M.; Nakayama, N.; Yamada, A. Structure of Li2FeSiO4. J. Am. Chem. Soc. 2008, 130, 13212–13213. [Google Scholar] [CrossRef]
- Armstrong, A.R.; Kuganathan, N.; Islam, M.S.; Bruce, P.G. Structure and Lithium Transport Pathways in Li2FeSiO4 Cathodes for Lithium Batteries. J. Am. Chem. Soc. 2011, 133, 13031–13035. [Google Scholar] [CrossRef] [PubMed]
- Masquelier, C.; Croguennec, L. Polyanionic (Phosphates, Silicates, Sulfates) Frameworks as Electrode Materials for Rechargeable Li (or Na) Batteries. Chem. Rev. 2013, 113, 6552–6591. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, G.; Liu, Z.; Li, H.; Liu, Y.; Wang, Z.; Li, X.; Shih, K.; Mai, L. Li3V(MoO4)3 as a novel electrode material with good lithium storage properties and improved initial coulombic efficiency. Nano Energy 2018, 44, 272–278. [Google Scholar] [CrossRef]
- Recham, N.; Chotard, J.N.; Dupont, L.; Delacourt, C.; Walker, W.; Armand, M.; Tarascon, J.M. A 3.6 V lithium-based fluorosulphate insertion positive electrode for lithium-ion batteries. Nat. Mater. 2009, 9, 68. [Google Scholar] [CrossRef]
- Afyon, S.; Wörle, M.; Nesper, R. A Lithium-Rich Compound Li7Mn(BO3)3 Containing Mn2+ in Tetrahedral Coordination: A Cathode Candidate for Lithium-Ion Batteries. Angew. Chem. Inter. Ed. 2013, 52, 12541–12544. [Google Scholar] [CrossRef]
- Nishimura, S.-I.; Nakamura, M.; Natsui, R.; Yamada, A. New Lithium Iron Pyrophosphate as 3.5 V Class Cathode Material for Lithium Ion Battery. J. Am. Chem. Soc. 2010, 132, 13596–13597. [Google Scholar] [CrossRef] [PubMed]
- Jay, E.E.; Rushton, M.J.D.; Chroneos, A.; Grimes, R.W.; Kilner, J.A. Genetics of superionic conductivity in lithium lanthanum titanates. Phys. Chem. Chem. Phys. 2015, 17, 178–183. [Google Scholar] [CrossRef] [PubMed]
- De Dompablo, M.E.A.Y.; Morán, E.; Várez, A.; García-Alvarado, F. Electrochemical lithium intercalation in Li2Ti3O7-ramsdellite structure. Mater. Res. Bull. 1997, 32, 993–1001. [Google Scholar] [CrossRef]
- Kuhn, A.; Baehtz, C.; García-Alvarado, F. Structural evolution of ramsdellite-type LixTi2O4 upon electrochemical lithium insertion–deinsertion (0 ≤ x ≤ 2). J. Power Sources 2007, 174, 421–427. [Google Scholar] [CrossRef]
- Ohzuku, T.; Ueda, A.; Yamamoto, N. Zero-Strain Insertion Material of Li [Li1/3Ti5/3 ]O4 for Rechargeable Lithium Cells. J. Electrochem. Soc. 1995, 142, 1431–1435. [Google Scholar] [CrossRef]
- Colbow, K.M.; Dahn, J.R.; Haering, R.R. Structure and electrochemistry of the spinel oxides LiTi2O4 and Li43Ti53O4. J. Power Sources 1989, 26, 397–402. [Google Scholar] [CrossRef]
- Boyce, J.B.; Mikkelsen, J.C. Anisotropic conductivity in a channel-structured superionic conductor: Li2Ti3O7. Solid State Commun. 1979, 31, 741–745. [Google Scholar] [CrossRef]
- Kataoka, K.; Awaka, J.; Kijima, N.; Hayakawa, H.; Ohshima, K.-I.; Akimoto, J. Ion-Exchange Synthesis, Crystal Structure, and Electrochemical Properties of Li2Ti6O13. Chem. Mater. 2011, 23, 2344–2352. [Google Scholar] [CrossRef]
- Pérez-Flores, J.C.; Kuhn, A.; García-Alvarado, F. Synthesis, structure and electrochemical Li insertion behaviour of Li2Ti6O13 with the Na2Ti6O13 tunnel-structure. J. Power Sources 2011, 196, 1378–1385. [Google Scholar] [CrossRef]
- Pérez-Flores, J.C.; Baehtz, C.; Hoelzel, M.; Kuhn, A.; García-Alvarado, F. Full structural and electrochemical characterization of Li2Ti6O13 as anode for Li-ion batteries. Phys. Chem. Chem. Phys. 2012, 14, 2892–2899. [Google Scholar] [CrossRef]
- Zulueta, Y.A.; Nguyen, M.T. Lithium Hexastannate: A Potential Material for Energy Storage. Phys. Status Solidi (b) 2018, 255, 1700669. [Google Scholar] [CrossRef]
- Fisher, C.A.J.; Hart Prieto, V.M.; Islam, M.S. Lithium Battery Materials LiMPO4 (M = Mn, Fe, Co and Ni): Insights into Defect Association, Transport Mechanisms, and Doping Behavior. Chem. Mater. 2008, 20, 5907–5915. [Google Scholar] [CrossRef]
- Islam, M.S.; Driscoll, D.J.; Fisher, C.A.J.; Slater, P.R. Atomic-Scale Investigation of Defects, Dopants, and Lithium Transport in the LiFePO4 Olivine-Type Battery Material. Chem. Mater. 2005, 17, 5085–5092. [Google Scholar] [CrossRef]
- Kuganathan, N.; Islam, M.S. Li2MnSiO4 Lithium Battery Material: Atomic-Scale Study of Defects, Lithium Mobility, and Trivalent Dopants. Chem. Mater. 2009, 21, 5196–5202. [Google Scholar] [CrossRef]
- Fisher, C.A.J.; Kuganathan, N.; Islam, M.S. Defect chemistry and lithium-ion migration in polymorphs of the cathode material Li2MnSiO4. J. Mater. Chem. A 2013, 1, 4207–4214. [Google Scholar] [CrossRef]
- Kuganathan, N.; Sgourou, E.N.; Panayiotatos, Y.; Chroneos, A. Defect Process, Dopant Behaviour and Li Ion Mobility in the Li2MnO3 Cathode Material. Energies 2019, 12, 1329. [Google Scholar] [CrossRef]
- Kuganathan, N.; Kordatos, A.; Anurakavan, S.; Iyngaran, P.; Chroneos, A. Li3SbO4 lithium-ion battery material: Defects, lithium ion diffusion and tetravalent dopants. Mater. Chem. Phys. 2019, 225, 34–41. [Google Scholar] [CrossRef]
- Kordatos, A.; Kuganathan, N.; Kelaidis, N.; Iyngaran, P.; Chroneos, A. Defects and lithium migration in Li2CuO2. Sci. Rep. 2018, 8, 6754. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Defects and dopant properties of Li3V2(PO4)3. Sci. Rep. 2019, 9, 333. [Google Scholar] [CrossRef] [PubMed]
- Kuganathan, N.; Ganeshalingam, S.; Chroneos, A. Defects, Dopants and Lithium Mobility in Li9V3(P2O7)3 (PO4)2. Sci. Rep. 2018, 8, 8140. [Google Scholar] [CrossRef] [PubMed]
- Kuganathan, N.; Kordatos, A.; Chroneos, A. Li2SnO3 as a Cathode Material for Lithium-ion Batteries: Defects, Lithium Ion Diffusion and Dopants. Sci. Rep. 2018, 8, 12621. [Google Scholar] [CrossRef] [PubMed]
- Kuganathan, N.; Kordatos, A.; Chroneos, A. Defect Chemistry and Li-ion Diffusion in Li2RuO3. Sci. Rep. 2019, 9, 550. [Google Scholar] [CrossRef] [PubMed]
- Kuganathan, N.; Kordatos, A.; Kelaidis, N.; Chroneos, A. Defects, Lithium Mobility and Tetravalent Dopants in the Li3NbO4 Cathode Material. Sci. Rep. 2019, 9, 2192. [Google Scholar] [CrossRef] [PubMed]
- Kuganathan, N.; Kordatos, A.; Fitzpatrick, M.E.; Vovk, R.V.; Chroneos, A. Defect process and lithium diffusion in Li2TiO3. Solid State Ion. 2018, 327, 93–98. [Google Scholar] [CrossRef]
- Kuganathan, N.; Tsoukalas, L.H.; Chroneos, A. Defects, dopants and Li-ion diffusion in Li2SiO3. Solid State Ion. 2019, 335, 61–66. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Defect Chemistry and Na-Ion Diffusion in Na3Fe2(PO4)3 Cathode Material. Materials 2019, 12, 1348. [Google Scholar] [CrossRef] [PubMed]
- Kuganathan, N.; Chroneos, A. Defects, Dopants and Sodium Mobility in Na2MnSiO4. Sci. Rep. 2018, 8, 14669. [Google Scholar] [CrossRef] [PubMed]
- Kuganathan, N.; Chroneos, A. Na3V(PO4)2 cathode material for Na ion batteries: Defects, dopants and Na diffusion. Solid State Ion. 2019, 336, 75–79. [Google Scholar] [CrossRef]
- Treacher, J.C.; Wood, S.M.; Islam, M.S.; Kendrick, E. Na2CoSiO4 as a cathode material for sodium-ion batteries: Structure, electrochemistry and diffusion pathways. Phys. Chem. Chem. Phys. 2016, 18, 32744–32752. [Google Scholar] [CrossRef]
- Kuganathan, N.; Iyngaran, P.; Chroneos, A. Lithium diffusion in Li5FeO4. Sci. Rep. 2018, 8, 5832. [Google Scholar] [CrossRef]
- Kuganathan, N.; Iyngaran, P.; Vovk, R.; Chroneos, A. Defects, dopants and Mg diffusion in MgTiO3. Sci. Rep. 2019, 9, 4394. [Google Scholar] [CrossRef] [PubMed]
- Kuganathan, N.; Dark, J.; Sgourou, E.N.; Panayiotatos, Y.; Chroneos, A. Atomistic Simulations of the Defect Chemistry and Self-Diffusion of Li-ion in LiAlO2. Energies 2019, 12, 2895. [Google Scholar] [CrossRef]
- Kaushalya, R.; Iyngaran, P.; Kuganathan, N.; Chroneos, A. Defect, Diffusion and Dopant Properties of NaNiO2: Atomistic Simulation Study. Energies 2019, 12, 3094. [Google Scholar] [CrossRef]
- Kuganathan, N.; Gkanas, E.I.; Chroneos, A. Mg6MnO8 as a Magnesium-Ion Battery Material: Defects, Dopants and Mg-Ion Transport. Energies 2019, 12, 3213. [Google Scholar] [CrossRef]
- Gale, J.D.; Rohl, A.L. The General Utility Lattice Program (GULP). Mol. Simul. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Gale, J.D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 1997, 93, 629–637. [Google Scholar] [CrossRef]
- Mott, N.F.; Littleton, M.J. Conduction in polar crystals. I. Electrolytic conduction in solid salts. Trans. Faraday Soc. 1938, 34, 485–499. [Google Scholar] [CrossRef]
- Varotsos, P. Comparison of models that interconnect point defect parameters in solids with bulk properties. J. Appl. Phys. 2007, 101, 123503. [Google Scholar] [CrossRef]
- Varotsos, P. Defect volumes and the equation of state in α-PbF2. Phys. Rev. B 2007, 76, 092106. [Google Scholar] [CrossRef]
- Varotsos, P. Point defect parameters in β-PbF2 revisited. Solid State Ion. 2008, 179, 438–441. [Google Scholar] [CrossRef]
- Chroneos, A.; Vovk, R.V. Modeling self-diffusion in UO2 and ThO2 by connecting point defect parameters with bulk properties. Solid State Ion. 2015, 274, 1–3. [Google Scholar] [CrossRef]
- Cooper, M.W.D.; Grimes, R.W.; Fitzpatrick, M.E.; Chroneos, A. Modeling oxygen self-diffusion in UO2 under pressure. Solid State Ion. 2015, 282, 26–30. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes; The Art of Scientific Computing Cambridge University Press: Cambridge, UK, 1986; 818p. [Google Scholar]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kröger, F.A.; Vink, H.J. Relations between the Concentrations of Imperfections in Crystalline Solids. In Solid State Physics; Seitz, F., Turnbull, D., Eds.; Academic Press: Cambridge, MA, USA, 1956; Volume 3, pp. 307–435. [Google Scholar]
- Nytén, A.; Kamali, S.; Häggström, L.; Gustafsson, T.; Thomas, J.O. The lithium extraction/insertion mechanism in Li2FeSiO4. J. Mater. Chem. 2006, 16, 2266–2272. [Google Scholar] [CrossRef]
- Politaev, V.V.; Petrenko, A.A.; Nalbandyan, V.B.; Medvedev, B.S.; Shvetsova, E.S. Crystal structure, phase relations and electrochemical properties of monoclinic Li2MnSiO4. J. Solid State Chem. 2007, 180, 1045–1050. [Google Scholar] [CrossRef]
- Liu, H.; Choe, M.-J.; Enrique, R.A.; Orvañanos, B.; Zhou, L.; Liu, T.; Thornton, K.; Grey, C.P. Effects of Antisite Defects on Li Diffusion in LiFePO4 Revealed by Li Isotope Exchange. J. Phys. Chem. C 2017, 121, 12025–12036. [Google Scholar] [CrossRef]
- Kempaiah Devaraju, M.; Duc Truong, Q.; Hyodo, H.; Sasaki, Y.; Honma, I. Synthesis, characterization and observation of antisite defects in LiNiPO4 nanomaterials. Sci. Rep. 2015, 5, 11041. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.M.; Heitjans, P.; Bredow, T. Structural Analysis and Li Migration Pathways in Ramsdellite Li2Ti3O7: A Theoretical Study. J. Phys. Chem. C 2016, 120, 5–10. [Google Scholar] [CrossRef]
- Arunkumar, P.; Jeong, W.J.; Won, S.; Im, W.B. Improved electrochemical reversibility of over-lithiated layered Li2RuO3 cathodes: Understanding aliovalent Co3+ substitution with excess lithium. J. Power Sources 2016, 324, 428–438. [Google Scholar] [CrossRef]
- Catlow, C.R.A. Solid State Chemistry—Techniques; Cheetham, A.K., Day, P., Eds.; Clarendon Press: Oxford, UK, 1987; p. 231. [Google Scholar]
| Parameter | Calculated | Experiment [18] | |∆| (%) | ||
|---|---|---|---|---|---|
| Force Field | DFT | Force Field | DFT | ||
| a (Å) | 15.7437 | 15.4589 | 15.3065 | 2.82 | 0.99 |
| b (Å) | 3.7254 | 3.7719 | 3.7474 | 0.59 | 0.65 |
| c (Å) | 9.0525 | 9.2499 | 9.1404 | 0.96 | 1.19 |
| α = γ (°) | 90.00 | 90.00 | 90.00 | 0.00 | 0.00 |
| β (°) | 99.2636 | 100.03 | 99.3790 | 0.12 | 0.65 |
| Migration Path | Li–Li Separation (Å) | Activation Energy (eV) |
|---|---|---|
| A | 3.73 | 0.25 |
| B | 4.47 | 0.90 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuganathan, N.; Ganeshalingam, S.; Chroneos, A. Defects, Diffusion, and Dopants in Li2Ti6O13: Atomistic Simulation Study. Materials 2019, 12, 2851. https://doi.org/10.3390/ma12182851
Kuganathan N, Ganeshalingam S, Chroneos A. Defects, Diffusion, and Dopants in Li2Ti6O13: Atomistic Simulation Study. Materials. 2019; 12(18):2851. https://doi.org/10.3390/ma12182851
Chicago/Turabian StyleKuganathan, Navaratnarajah, Sashikesh Ganeshalingam, and Alexander Chroneos. 2019. "Defects, Diffusion, and Dopants in Li2Ti6O13: Atomistic Simulation Study" Materials 12, no. 18: 2851. https://doi.org/10.3390/ma12182851
APA StyleKuganathan, N., Ganeshalingam, S., & Chroneos, A. (2019). Defects, Diffusion, and Dopants in Li2Ti6O13: Atomistic Simulation Study. Materials, 12(18), 2851. https://doi.org/10.3390/ma12182851