Abstract
In this study, an improved Fourier series method is presented for the vibration modeling and analysis of moderately thick laminated composite plates with arbitrary boundary conditions, in which the vibration displacements are sought as the linear combination of a double Fourier cosine series and auxiliary series functions. The vibration model was established using the Hamilton energy principle. To study the vibration characteristics of laminated composite plates more comprehensively, firstly, the accuracy of the current results were validated via comparison with previous results and finite element method data. A parametric study was conducted on the effects of several key parameters, such as the h/b ratio, orientation and number of layers. In this section, both solutions are applicable to various combinations of boundary constraints, including classical boundary conditions and elastic-supported boundary conditions. Secondly, in order to identify the action position of vibration and the transmission of vibration energy, the response analysis of laminated plates was studied, and the power flow field for laminated plates was analyzed. Finally, a modal test was introduced to further verify the accuracy of the method in this paper.
1. Introduction
It is generally known that laminated composite plates, as basic structural components, are commonly applied in mechanical, aerospace, astronautic and civil engineering, among other fields. This is mainly because they are superior to conventional materials when high strength-to-weight and stiffness-to-weight ratios are required. Therefore, it is attractive for engineers and designers to research the material characteristics of the laminated composite plates.
At present, there are various theories of laminated plates, distinguished according to the differences in the displacement equation; these theories can be classified as follows: classical lamination theory (CLD) [1], first-order shear deformation theory (FSDT) [2,3], higher-order shear deformation theories (HSDT) [4,5,6], layer-wise lamination theory [7,8,9,10] and the three-dimensional elastic theory [11,12,13]. After establishing the vibration equation of composite laminates, there have been many studies on the vibration and response analysis of laminated composite plates.
According to Yu et al. [14], the vibration characteristics of anisotropic rectangular plates under the mixed boundary conditions of solid support and simple support are analyzed based on the superposition principle. Ge et al. [15] studied the dynamic response of symmetrically orthogonal composite laminates on elastic foundations under in-plane preloading and transverse impact loads based on the modal superposition method. In this paper, the equation of motion for displacement description is deduced by using the higher-order shear deformation theory. Huang et al. [16] studied the free vibration characteristics of orthotropic rectangular plates subjected to internal compression on a two-parameter elastic foundation by the method of separated variables. Kshirsagar et al. [17] analyzed the free vibration and buckling of rectangular plates under arbitrary classical boundary conditions based on the superposition principle of infinite series with infinite truncation. Liu et al. [18] presented the exact closed solution of a rectangular plate by using the method of separating variables. The boundary conditions of plate structure in this paper are simply supported on one side, and have arbitrary classical boundary conditions on the other. Chung et al. [19] studied the vibration characteristics of rectangular plates under elastic boundary conditions by the Rayleigh‒Ritz method, where the Timoshenko beam function is used as the permissible deflection function. Liew et al. [20,21] presented the vibration characteristics of anisotropic plates and symmetrical composite laminates under mixed boundary conditions based on the subdomain and orthogonal polynomial methods. On this basis, they use the Reissner‒Mindlin theory and p-Ritz method to analyze the vibration characteristics of composite laminates and calculate the vibration frequencies of composite laminates under different boundary conditions, length-width ratios and width-thickness ratios. Cheung et al. [22] studied the free vibration characteristics of symmetrically laminated plates under point-supported boundary conditions by using a new displacement admissible function and the Rayleigh‒Ritz method. The allowable function is composed of a static beam function, which is different from the existing admissible function. The functions they set can satisfy both geometric boundary conditions and point-supported boundary conditions. Matsunaga et al. [23] analyzed the natural frequency and buckling stress of laminates by considering the influence of shear deformation thickness variation and moment of inertia, and expanded the vibration displacement function in power series. Mbakogu et al. [24] studied the bending problem of orthotropic rectangular plates under uniformly distributed loads by the Galerkin method. Dalaei et al. [25] solved the vibration problem of cantilever plates with anisotropic materials for the first time by using the extended Kantorovich method; they also obtained a closed-form high-precision solution in their paper. Bercin et al. [26] studied the bending and vibration of fully clamped plates by the Kantorovich method. Chen et al. [27,28,29,30] established a series of composite laminate models and studied the vibration, stability and large deformation of composite laminate plates. Luccioni et al. [31] presented the free vibration characteristics and stability of composite laminates by the finite element method, combining the classical laminate theory with the first-order shear deformation theory. Rao et al. [32] presented several finite element models to study the static, stability, impact and nonlinearity of laminated plates and shells. Shafiee et al. [33] analyzed the vibration characteristics of composite coupled plates by the finite element method. Huang et al. [34] studied the free vibration characteristics of rectangular plates with variable thickness based on the discrete method, and the characteristic equation of free vibration was obtained by the Green function. Liew et al. [35] presented the free vibration of symmetrical laminated plates by the moving least squares differential integral method. Song et al. [36,37,38] studied the free vibration of laminated plates by the local Radial Point Interpolation method; however, it is difficult to deal with the displacement boundary using a meshless method. Zhang et al. [39,40] presented an improved Fourier series method for the free vibration analysis of a moderately thick laminated composite rectangular plate with non-uniform boundary conditions. They also established a unified analysis model for vibration characteristics of composite laminated annular sector plates, circular sector plates, annular plates and circular plates with various elastic boundary conditions. Qin et al. [41] studied the free vibration analysis of composite laminated plates based on the Jacobi‒Ritz method.
Romanelli et al. [42] presented the dynamic response of a simply supported rectangular composite plate under local pressure based on the series method. Shen et al. [43,44] discussed the dynamic response of a cantilever plate on a Pastemak elastic foundation under temperature and transverse dynamic loads by the Rayleigh‒Ritz method, considering the influence of first-order shear deformation, foundation stiffness coefficient and temperature change. Khan et al. [45] presented the dynamic response of a composite cantilever plate under a uniform load by the variational method. Niyogi et al. [46] analyzed the free and forced vibration responses of composite laminates based on the nine-node element method, considering the influence of first-order transverse shear deformation and moment of inertia. Biswas et al. [47] studied the transient dynamic response behavior of multi-layered hybrid composite plates by a modified higher-order refined zigzag theory (HRZT). Zhang et al. [48] presented the free and forced vibration behaviors of thin, three-dimensionally coupled plate structures based on the dynamic stiffness method (DSM). Nefske et al. [49] presented a power flow finite element method, which is applied to the calculation of beam structures. In subsequent studies, power flow finite element method has been developed and gradually applied to the power flow analysis of coupled structures. Hambric et al. [50] calculated the structural sound intensity of a cantilever plate with stiffened members by the finite element method, and the bending, torsion and axial power flow were obtained. Li et al. [51] obtained the structural sound intensity vectors in three cases by finite element harmonic response analysis through calculating the surface admittance of a thin plate by the structural sound intensity method. Cieslik et al. [52] presented a method to introduce the bending moment and external force into the theoretical expression of structural vibration and sound intensity by using the complex mode theory. The vibration power flow of simply supported stiffened plates is calculated by the finite element method, and the energy flow distribution of stiffened plates is analyzed in this paper. Xing et al. [53] studied the power flow of structures under fluid‒structure interaction based on the substructure method. The energy flow density vector was used to represent the energy flow transmission path between substructures, and the energy flow transmission was visually shown by graphics. Wang et al. [54] studied the structural sound intensity characteristics of composite laminates under dynamic concentrated forces. An example of structural sound intensity was analyzed by using finite element software; in this paper, the results show that orthotropic laminates have different characteristics from isotropic laminates, and that the structural sound intensity characteristics of orthotropic laminates are influenced by the boundary conditions, number of layers and stacking sequence. Zhang et al. [55,56,57,58,59] presented the free and forced vibration behaviors of the laminated plate-cavity coupling system by means of the improved Fourier series method.
There have been many studies on thin plates with arbitrary boundary conditions. However, these studies have limitations for moderately thick composite plates with special supported boundary conditions, for instance, an arbitrary elastic boundary. In addition, because the Mindlin theory considers the shear deformation along the thickness direction compared with the equivalent single-layer theory used in thin plates when studying the vibration of plates, the results obtained by the Mindlin theory are more accurate. On the other hand, most of the recent research merely discusses the vibration analysis, while the research on energy transfer is insufficient. Nevertheless, in many engineering applications, such as in the design of vehicles, it is necessary to comprehend the energy transfer path in order to reduce noise and vibration. Yan [60] points out that, compared with the traditional path analysis method, power flow analysis not only describes the speed of energy transfer or transformation, but also can be used to characterize the flow of vibration energy in the system. An et al. [61] studied the transmission path in hydraulic pipelines by using vibration power flow. Inoue et al. [62,63,64] studied the relationship between the structural noise response and the total power flow transmitted to the receiving structure, and they presented that there is a certain similarity between the response spectrum of structural noise and the total power spectrum transmitted to the receiving structure in a wide frequency range. Lee et al. [65,66] used the method of measuring vibration power flow to analyze the transmission paths of occupant interior structural noise caused by vehicle transmission system; they identified the main transmission paths according to the power flow, and modified the body structure with modal analysis to reduce the structural noise. Wang [67] studied the transmission characteristic of energy flows of micro-vibrations in spacecraft structures. Therefore, the study of power flow analysis of structural component is essential.
In this paper, a mechanics model is presented, based on the Mindlin theory, in order to research its vibration characteristics with arbitrary boundary conditions. Three kinds of restraining springs (translational, rotational and torsional), attached to each edge, are introduced to establish the general structure model of laminated composite plates. In addition, a modified Fourier series method is introduced to describe the vibration displacement function of the structure to study the influences of the structural style and the boundary conditions on the vibration characteristics of laminated composite plates. Moreover, the vibration model of the laminated composite plates with arbitrary boundary conditions is established, which is based on the Hamilton energy variation principle. This paper also focuses on the effect on vibration frequency while changing various key parameters (such as the ratio between thickness and width, the number of layers, as well as the laying angle between two layers). In the following section, several numerical examples of the free vibration of a laminated composite plate with arbitrary boundary conditions are presented, which can serve as references for future engineering. The current results were checked against previous results and achieved good agreement. Moreover, to analyze the vibration characteristics of laminated composite plates more comprehensively, the present work discusses the vibration response characteristic of the laminate, in terms of energy, through harmonic response and power flow analysis. In this section, we discuss the periodic response of a continuous periodic load in a structural system; in addition, we found the distribution character of energy transfer through changing the position of actions and boundary conditions. Finally, we introduce a test to further verify the accuracy of the presented method, in which the experimental data coincide with the theoretical value.
2. Theoretical Formulations
The mechanical properties of the composite laminate structure were related to the mechanical properties and thickness of the single-layer board, as well as the fiber laying direction and sequence and the number of layers. The laminated plate shown in Figure 1 consisted of five layers. The angle of the first layer was 0°, and the other four layers were expressed as α, 90°, −α and 0°, respectively. The principal axis coordinate system of each layer in laminated composite plates was O12, and the global coordinate system was Oxy. The ply-angle of the fiber can be expressed by θ, and the positive direction was identified when the x-axis rolled towards the 1 axis in an anticlockwise direction. The material of the plate structure in this chapter was a fiber-reinforced composite material, which was composed of matrix and fiber. The matrix was mainly used to support and protect the fiber, while the fiber was enhanced and mainly supported. In addition, the coupling vibration of bending and stretching of composite laminate plates is not considered in this chapter.
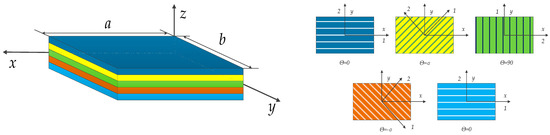
Figure 1.
Abbreviated drawing of laminated composite plates.
For the plate model based on the assumptions of the first-order shear deformation theory, the deformation of the plate was continuous. Thus, on the basis of not considering the in-plane vibration of plates, the displacement field can be expressed as
where u, v and w are the displacement in the x-, y- and z- directions, respectively, and ψx and ψy are the rotation in the x- and y- directions, respectively. Therefore, the stress‒strain relationship in coordinates, based on the small deflection theory, can be written as follows:
The corresponding stresses are obtained in terms of the generalized Hooke’s law:
where the normal stresses are and in the x and y directions, respectively, and the shear stresses are , and in the x, y and z coordinate system, respectively. The lamina stiffness coefficients are (i, j = 1, 2, 4, 5, 6), which can be expressed as follows:
where ,, in which the included angle is simply represented as θ between the principal direction of the layer and the x–axis. The lamina elastic coefficients in Equation (6) can be obtained from the material properties of the kth orthotropic lamina layer:
where and denote the longitudinal modulus and the transverse modulus, is the major Poisson’s ratio and the other Poisson’s ratio can be obtained by . , and are the shear moduli.
Through taking the unit body of unit length from the plate in the x/y direction, we can synthesize the stress component on the cross section of the unit body into an internal force per unit width. Therefore, the bending moment and , the torque and and the shear force and can be expressed as
where is the shear correction factor, and , , , and are the corresponding stresses of the kth layer.
Consider a structural model of laminated composite plates that is elastically restrained along its four edges, as shown in Figure 2. The laminated composite plates may also be loaded with three kinds of restraining springs (translational, rotational and torsional) at arbitrary locations, and the boundary conditions can be easily obtained by changing the stiffness of the springs.
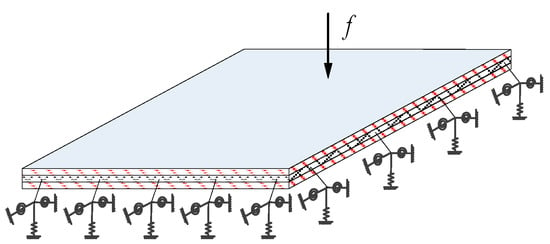
Figure 2.
A laminated composite plate with arbitrary elastic boundary support.
According to Hamilton’s principle, the vibration equation can be easily established. For a holonomic mechanical system with n generalized degrees of freedom, the generalized coordinates are qs (s = 1, 2, … n), the Lagrange function is , where T, U and W are the kinetic energy, potential energy and the external work, respectively. The Hamilton action is defined as follows:
For the laminated composite plate in Figure 2, the Hamilton equation of the plate can be expressed as follows:
where V, T and Wext, denote the total potential, the total kinetic energy and the external potential energy, respectively. The total potential includes the bending potential energy of the plate and the elastic potential energy of springs. The total potential energy can be written as follows:
where Vspring is the elastic potential energy of springs, Vplate is the bending potential energy of the plate and these terms can be explicitly expressed as follows.
The elastic potential energy of springs on the four edges can be written as follows:
The stress relationship can be evaluated according to the stress‒strain relationship. On the basis of the elastic mechanic theory, the relationship between elastic potential energy and stress‒strain is expressed as follows:
In this equation, Θ is given by
and ε1 is given by
The stiffness can be defined as
Therefore, Equation (5) can be expressed as follows:
The total kinetic energy of the laminated composite plate is given by
The external potential energy of the laminated composite plate can be expressed as
where w is the flexural displacement; a and b are the plate dimension in x direction and the plate dimension in y direction, respectively; ρ and h are the mass density and the thickness of the plate, respectively, and f (x, y) = F δ (x − x0) (y − y0), where δ is the delta function, F is the amplitude of the stresses and x0 and y0 are the position coordinates of force. kx0 and kxa (ky0 and kyb) are the transverse spring constants, Kx0 and Kxa (Ky0 and Kyb) are the rotational spring constants and Kyx0 and Kyxa (Kxy0 and Kxyb) are the torsional spring constants at x = 0 and x = a (y = 0 and y = b), respectively.
The displacement function is expanded as a single Fourier series plus an auxiliary polynomial function. The auxiliary function is used to overcome the discontinuities of the resilient boundary, the transverse displacement function w(x, y).
where p(x,y) can be expressed as
where the auxiliary polynomial based on trigonometric function can be written as follows:
where λm = mπ/a, λn = nπ/b; a is length and b is width and Amn, ,, and are the expansion coefficients.
Therefore, function w(x, y) can be rewritten as follows:
Similarly, the rotational displacement function Ψx(x, y) and Ψy (x, y) can be easily obtained as follows:
where Bmn, ,,,,Cmn, ,, and are the expansion coefficients.
Substitution of Equations (17)–(19) into Equation (11) leads to a series of equations, and these equations can be rewritten in matrix form as
where K is the stiffness matric, M is the mass matric, A is the unknown coefficient vector and F is the force vector. The detailed expressions of K and M are shown in the Appendix A.
In order to determine the modal characteristics of the laminated composite plate, one needs to solve the characteristic equation by setting the external force vector F in Equation (20) to zero. Obviously, the natural frequencies and eigenvectors of the laminated composite plate can now be easily obtained by solving a standard matrix Eigen problem. Since the components of each eigenvector are actually the expansion coefficients of the Fourier series, the corresponding mode shape can be directly determined by substituting the eigenvector in Equation (17) into Equation (19).
On the other hand, when the external force vector F is not zero, it can be used to study the response analysis of laminates. The response obtained is a harmonic response when the external excitation force is a simple harmonic force.
The lateral displacement field and the corner of the bending vibration of the plate structure at the excitation frequency by substituting the coefficient vector A in Equation (17) into Equation (19).
To solve the structural vibration and noise radiation problems, vibration power flow leads to a more comprehensive evaluation of the vibration response characteristics of the structure. It can intuitively identify the position of the vibration and the transmission path of the vibration energy, providing a better evaluation index and basis for the vibration control of the structure.
The power flow intensity I(x, y) at any point in the Mindlin plate structure can be expressed as follows:
where Ix(x,y) and Iy(x,y) are the components of I(x, y) along the x and y axes, respectively.
Therefore, the power flow intensity I(x, y) at any point can be easily obtained by substituting Equations (8)–(10) into Equation (38) and Equations (29)–(31) into Equation (39).
3. Results and Discussion
3.1. Modal Characteristics of Laminated Composite Plates
Consider a laminated composite plate with arbitrary elastic boundary support, with the dimensions of a × b, which is illustrated in Figure 2. If three kinds of restraining springs (translational, rotational and torsional) are assumed to be distributed uniformly along each edge, then all the classical boundary conditions, as well as their combinations, can be easily obtained by simply setting the spring coefficients to zero or infinity. For the sake of convenience, C denotes the clamped cases, E denotes the elastic bearing cases, F denotes the free-boundary condition and S represents the simply supported cases. Taking the edge of x = 0 as an example, the spring stiffness is shown in Table 1 when the boundary condition is F, S, C or E, respectively. (Note that the elastic boundary can be chosen arbitrarily, and the exact value of E can be transformable in different examples.)

Table 1.
Spring stiffness under different boundary conditions.
First, the relationship between the vibration solution of a rectangular plate based on the energy principle and the analytical solution based on the governing equation and the boundary condition equation was studied. The laminate was a single-layer board and the material was an isotropic material, the same as in [18].
In Table 2, the first five non-dimensional frequency parameters are shown (Ω = (ωb2/π2)(ρh/D)1/2). It can be seen from the table that the deviations of the results obtained by the present method and the analytical method were all within 0.022. The results obtained were almost identical, which verified that the energy method resulted in an exact solution when the permissible displacement function satisfied both the displacement boundary condition and the force boundary condition.

Table 2.
Natural frequency parameters for laminated plates with different methods.
In the following calculations, the laminated composite was an orthogonal symmetrical laminate, which was composed of three layers of unit plates of equal thickness—that is, the layup direction of the unit plate was 0°/90°/0°. The physical parameters are specified as Ex/Ey = 40, G12 = 3/5Ey, G23 = 1/2Ey, G13 = 3/5Ey, vy = 1/4, vx = 0.00625, S16 = S26 = S45 = 0, Poisson’s ratio μ = 0.3, shear correction factor k = 5/6.
To verify the convergence of the solution, Table 3 compares the first seven non-dimensional modal frequency parameters of the laminated composite plate under different cutoff values. For illustrative purposes, one assumes that a SSFF laminated composite plate system shown in Table 3 is defined by the dataset: D0 = Eh3/(12(1 − vxvy)); a/b = 1; h/b = 0.2; with E representing the larger value between Ex and Ey. At the same time, a comparison of the solution in [21] is also presented. It is seen that the maximum deviation of the first seven non-dimensional modal frequency parameters obtained in both cases (M = N = 4 and M = N = 16) was 1.4%; on the other hand, when the cutoff value was more than 10, the results were almost invariant. Thus, it was evident that just a few terms can lead to excellent prediction and the current solution shows remarkable convergence.

Table 3.
Convergence study of frequency for rectangular laminated plates with SSFF.
To further verify the accuracy of the method from a modal perspective, the first five non-dimensional frequency parameters are shown for the plates of various thickness–width ratios and boundary conditions in Table 4 and Table 5. Meanwhile, the results calculated by using the separate variable method in [21], the Rayleigh‒Ritz method in [18] and the results calculated by FEA are also presented in Table 4 and Table 5. It is seen that the present method has led to excellent agreement with the classical solution.

Table 4.
Natural frequency parameters for rectangular laminated plates with SSSS, CCCC, SCSC and CFFF.

Table 5.
Natural frequency parameters for rectangular laminated plates with SCSF, SSSC, SSSF and SFSF.
Figure 3 shows the mode shapes of the CCCC and FFFF moderately thick laminated composite plate. The mode shapes obtained by the present method coincide with those obtained by the finite element method. The material properties were as follows: a/b = 1, h/b = 0.2; the layup direction of the unit plate was 0°/90°/0°.
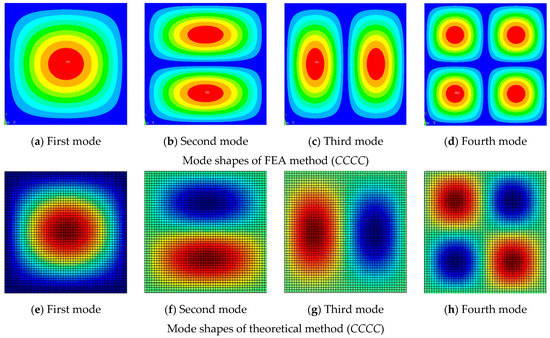
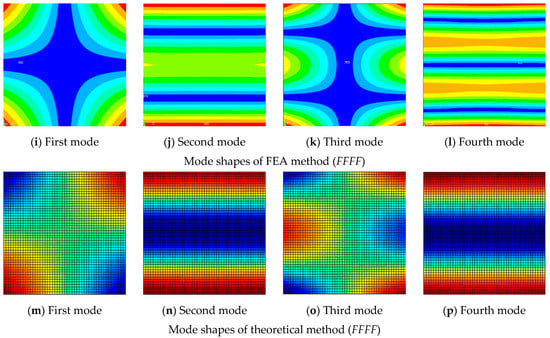
Figure 3.
Mode shapes of the composite laminated plate. (a,e,i,m) First mode, (b,f,j,n) Second mode, (c,g,k,o) Third mode, (d,h,l,p) Fourth mode.
In order to show the consistency between the results of the present method and finite element method clearly, Figure 4 shows the frequency parameter curves of the SFCF laminated composite plates. The layup direction of the unit plate was 45°/−45°/45°; a/b = 1; h/b = 0.1. Figure 5 shows the frequency parameter curves of the EFCS laminated composite plates. The spring stiffness coefficient on the elastic edge were as follows: kx0 = D0, Kx0 = 0, Kyx0 = 0.
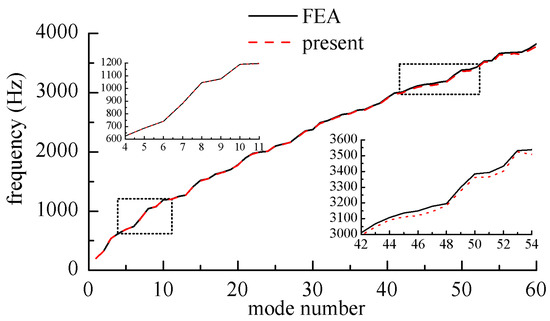
Figure 4.
Nature frequency parameters for rectangular laminated plates with CFSF.
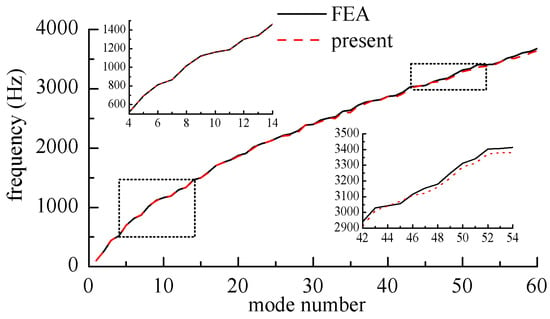
Figure 5.
Nature frequency parameters for rectangular laminated plates with ECFF.
In Figure 4 and Figure 5, the frequency curves obtained by this method coincided with those obtained by the finite element method at medium and low frequencies. At high frequencies, the results obtained by the finite element method were larger than presented results. This was because the finite element method needs finer meshes in order to get more accurate results in the high frequency band, with the workload increasing sharply.
To research the influence of different ratios between thickness and width, the first six non-dimensional frequency parameters for the SSSS and CCCC laminated composite plates are shown in Figure 6 and Figure 7, where the number of piles in the figures were three layers and five layers, respectively. As can be seen in the figures, compared with low-order frequency parameters, high-order frequency parameters showed a remarkable decrease with an increase in the ratio between thickness and width; moreover, the change was more significant when h/b was less than 0.10.
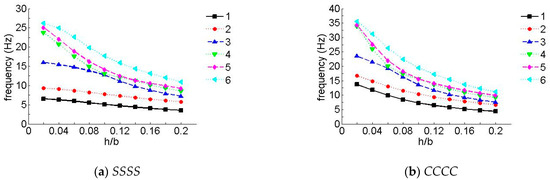
Figure 6.
Natural frequency parameters for a laminate with an arbitrary ratio between thickness and width (three layers). (a) SSSS, (b) CCCC.
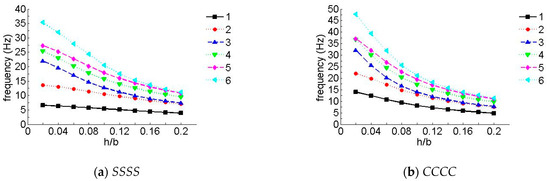
Figure 7.
Natural frequency parameters for a laminate with an arbitrary ratio between thickness and width (five layers). (a) SSSS, (b) CCCC.
To further verify the effect of the number of layers on the frequency, Figure 8 and Figure 9 show the first six non-dimensional frequency parameters for the SSSC and CCSS laminated composite plates of various layers, where h/b = 0.05 and the layup directions of the unit plates in Figure 8 and Figure 9 were 0°/45°/0° and 0°/90°/0°, respectively (when the number of layers was three), and the layup directions in Figure 8 and Figure 9, respectively were 0°/45°/0°/45°/0° and 0°/90°/0°/90°/0° (when the number of layers is five), etc. In the following figures, the data were collected when the number of layers was odd (3, 5, 7, 9, etc.).
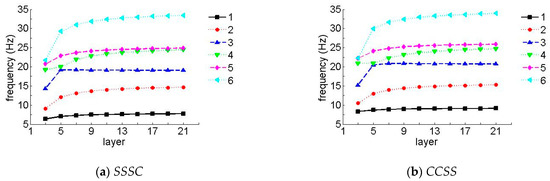
Figure 8.
Natural frequency parameters for a laminate with arbitrary layers (laying angle = 45°). (a) SSSC, (b) CCSS.
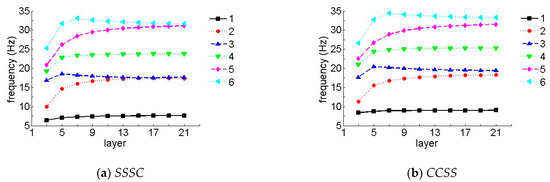
Figure 9.
Natural frequency parameters for a laminate with arbitrary layers (laying angle = 90°). (a) SSSC, (b) CCSS.
It can be seen in Figure 8 and Figure 9 that the frequency parameters increased with the increase in the number of layers, so long as the number of layers was less than 13, in which case, it stayed constant as the number of layers changed. It should be mentioned that the effect was more noticeable for higher frequencies.
In order to study the influence of the number of layers laid on the vibration frequency, Figure 10 shows the variation of the dimensionless frequency of the first order with the number of layers and the aspect ratio of the normal symmetric angled plywood structure under different boundary conditions. Among them, the laying angle of the laminate was 45°, and h/b = 0.1.
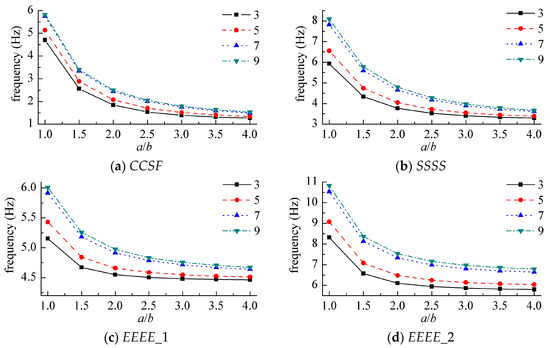
Figure 10.
Natural frequency parameters for symmetric angle-ply laminates. (a) CCSF, (b) SSSS, (c) EEEE_1, (d) EEEE_2.
In Figure 10c,d, the spring stiffness coefficients on each side of EEEE_1 were kx0 = Kx0 = Kyx0 = 106 × D0, ky0 = Ky0 = Kxy0 = 104 × D0, kxa = Kxa = Kyxa = 102 × D0, kyb = Kyb = Kxyb = 103 × D0; the spring stiffness coefficients of EEEE_2 were kx0 = ky0 = kxa = kyb = 106 × D0, Kx0 = Ky0 = Kxa = Kyb = 104 × D0, Kyx0 = Kxy0 = Kyxa = Kxyb = 102 × D0.
The laying angle was another important design parameter of the laminate. Figure 11 shows the variation of the first-order vibration frequency with the laying angle of the composite laminate under different layers.
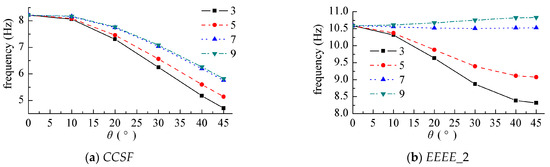
Figure 11.
Natural frequency parameters for symmetric angle-ply laminates. (a) CCSF, (b) EEEE_2.
3.2. Vibration Response Analysis of Laminated Composite Plates
In this section, the following example is focused on the vibration harmonic response of the plate. In order to avoid the numerical instability under the excitation of the plate structure resonance frequency in the numerical calculation, the structural damping factor η is introduced in the analysis, and the elastic modulus of the plate structure is correspondingly the complex elastic modulus, E’ = E(1 + jη). To avoid the instability of the response at the resonant frequency, the damping factor η (loss factor value) of the plate structure herein is η = 0.01.
The material in this section is an orthotropic plate, and the material properties of the plate were as follows: a = 1 m, b = 1 m, h = 0.1 m, E1 = 128.8 GPa, E2 = 8.3 GPa, G12 = 4.1 GPa, G23 = G12, G13 = G12, v2 = 0.355.
Figure 12 shows the displacement harmonic response curve at different points when the point force acted on the center of the cantilever plate. This part of the response curve was based on the frequency domain analysis, as the comparison map obtained by the frequency domain analysis was more intuitive, and the full text always analyzed the frequency domain part of the research, which was also to maintain the consistency of the whole article.
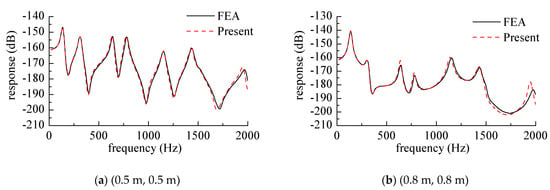
Figure 12.
Response curve while the harmonic force acted on the center of the cantilever plate. (a) (0.5 m, 0.5 m), (b) (0.8 m, 0.8 m).
The solid support edge was the edge on x = 0, and the force amplitude was F = 1 N. Figure 12a is a curve where the response point was at the center of the plate (0.5 m, 0.5 m), and Figure 12b is a curve at which the response point was at (0.8 m, 0.8 m). It can also be seen from the figure that the frequency corresponding to the peak value of the response was the modal frequency of the plate structure, and the response curves obtained by the finite element method were also given in the two figures. The mesh size was 0.02 m × 0.02 m.
In order to study the effect of the excitation on the response of the rectangular plates with different positions, Figure 13 shows the displacement response and velocity response of the composite laminate under the action of point force. The boundary condition of the laminate was CFFC. The amplitude of the point force was 1 N, the action direction was along the z-axis, the action position was (0.5 m, 0.5 m) and the action time was 0.5 s. The displacement response in the figure was the same as the position of the velocity response, with both points being (0.5 m, 0.5 m). The calculation curve obtained by the finite element method is also shown in the figure. It can be seen that the results obtained by the two methods agreed well, thus verifying the feasibility of the method for solving transient problems.
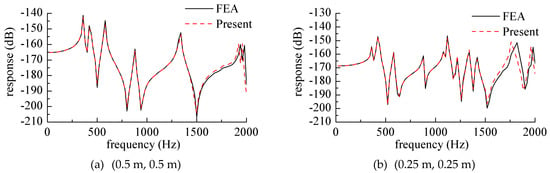
Figure 13.
Response curve while the harmonic force acted on various positions of the cantilever plate. (a) (0.5 m, 0.5 m), (b) (0.25 m, 0.25 m).
3.3. Vibration Power Flow Analysis of Laminated Composite Plates
In some engineering applications, studying the energy transfer path in structural systems is helpful for solving the problems of structural vibration and noise radiation. In recent years, as a new energy transfer analysis method, power flow studies the transmission and control of vibration in structures from the perspective of energy. Because the power flow takes into account the inherent information of both force and motion of the structure, it can evaluate the vibration response characteristics of the structure more comprehensively than the previous single description of force or displacement. In addition, energy dissipation and collection can be characterized through the study of power flow fields, having practical significance for engineering.
In order to study the influence factors and characteristics of energy transfer, the dynamical characteristics of the structures are described as the power flow field. The power flow intensity at any point can be obtained by extracting the force and displacement from Equations (37)–(39), as shown in Figure 14, Figure 15, Figure 16 and Figure 17 by using MATLAB 2017 this section, the effects of boundary conditions, the excitation frequency and the excitation location on energy transfer characteristics are presented.
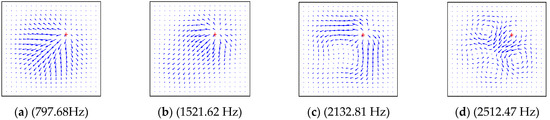
Figure 14.
The power flow field for a CCCC laminated plate excited by point force on (0.65 m, 0.65 m). (a) (797.68Hz), (b) (1521.62 Hz), (c) (2132.81 Hz), (d) (2512.47 Hz).
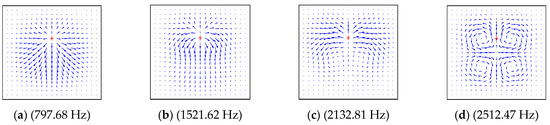
Figure 15.
The power flow field for a CCCC laminated plate excited by point force on (0.5 m, 0.65 m). (a) (797.68Hz), (b) (1521.62 Hz), (c) (2132.81 Hz), (d) (2512.47 Hz).
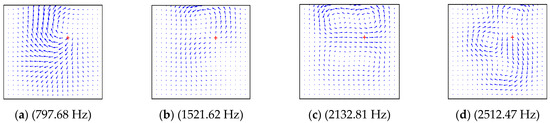
Figure 16.
The power flow field for a CSSE laminated plate excited by point force on (0.65 m, 0.65 m). (a) (797.68Hz), (b) (1521.62 Hz), (c) (2132.81 Hz), (d) (2512.47 Hz).
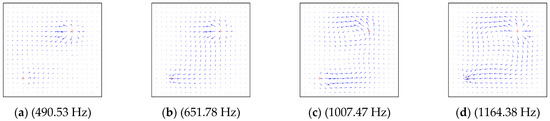
Figure 17.
The power flow field for a CSSS lamitated plate excited by point force on (0.2 m, 0.2 m) and (0.7 m, 0.7 m). (a) (490.53 Hz), (b) (651.78 Hz), (c) (1007.47 Hz), (d) (1164.38 Hz).
The material in this part was normal symmetric orthogonally laid laminate, and the material properties of the plate were as follows: a = 1 m, b = 1 m, h = 0.1 m, E1 = 128.8 GPa, E2 = 8.3 GPa, G12 = 4.1 GPa, G23 = G12, G13 = G12, v2 = 0.355. The boundary condition of Figure 14 and Figure 15 was CCCC; the four subgraphs given in each figure show the power flow field under different excitation frequencies, which were the first four natural frequencies of the composite plate. By comparing the four subgraphs, it can be seen that the distribution field and frequency of the energy flow had a significant influence. When the excitation force, action position and boundary conditions remain unchanged, the frequency change may also cause a change in the power flow distribution field.
Figure 16 shows the power flow distribution of the plate structure under different excitation frequencies when the boundary condition was CSSE and the excitation force acted on the point (0.65 m, 0.65 m). The stiffness coefficients of the three types of elastic on the elastic side were kyb = Kxyb = D0, Kyb = 0.
The excitation frequency in Figure 16 was not the first four natural frequencies of the CSSE rectangular plate, but the excitation frequency from Figure 14. It can be seen from the figure that the distribution of the power flow field had strong dependence on the position of the excitation force and the boundary condition of the rectangular plate, but there was no fixed distribution between them.
In order to study the energy transfer characteristics of plate structures subjected to multiple point forces, Figure 17 shows the distribution of vibration power flow in the whole rectangular plate structure under two-point excitation. The boundary conditions of the plate structure were CSSS. The excitation frequencies of the two point forces were the same, and the direction of action was along the z-axis, with the amplitude of 1 N. The positions of action for the two points were (0.2 m, 0.2 m) and (0.7 m, 0.7 m), respectively.
Figure 17a–d shows the power flow vector graphs at first to fourth natural frequencies. It can be seen from the figure that the vibration energy was transmitted from the excitation to the surrounding plate, but the excitation position was not always the source of vibration energy output. Under some excitation frequencies, the excitation position may also have the flow of vibration energy, which further verifies that the energy transfer was strongly dependent on the excitation frequency.
In Figure 14, Figure 15, Figure 16 and Figure 17, it can be seen that the energy transfer in the structure had an important relationship with the frequency, position, number of excitation forces and boundary conditions of the plate structure. As the excitation frequency increased, the flow path of the vibration energy in the structure became more and more complicated. When the boundary condition of one side became soft, the vibration energy rapidly flowed to this side. The vibration energy did not always transfer energy from the excitation position to the boundary according to the shortest path principle. There was also a certain form of energy circulation inside the plate structure. Through the description of the power flow, the transmission of the vibration energy could be clearly seen, thereby providing a basis for the effective control of the vibration of the structure.
3.4. Modal Test of Laminated Plates
Aiming at strengthening our understanding of the vibration behaviors of the laminated composite plate, we verified the accuracy of the present method by experimental means. Figure 18 shows the experiment to study the model characteristics of the plate. A hammer was used for excitation, and the experiment was carried out by single-point pock-up and point-by-point excitation.

Figure 18.
The test model of the laminated plate.
The composite laminate used in the experiment consisted of four layers of anisotropic single-layer plates. The material of the single-layer plate was epoxy-based composite, and the material properties of the plate were as follows: a = 0.29116 m, b = 0.19934 m, h = 0.00502 m, E1 = 135 GPa, E2 = 8.3 GPa, G12 = 4.1 GPa, G23 = G12, G13 = G12, v2 = 0.355.
In this experiment, the boundary condition of the laminated composite plate was CFFF, and the clamped boundary condition was simulated by the pressure plate and the Φ6 bolt fixed on the foundation. The laminated plate was divided into a uniform mesh, the number of grids was 9 × 9 and the excitation position of the hammer was at each grid point. According to the experimental requirements, the sampling frequency was selected to be 5000 Hz and the analysis frequency was 1950 Hz, where the sampling mode was transient and the triggering mode was signal triggering. The Donghua DH5922 data acquisition analyzer and dynamic signal acquisition system were used to analyze the excitation signal of the hammer and the response signal of the acceleration sensor. Finally, a modal analysis was performed to obtain the natural frequency in Table 6 and the mode shape of the rectangular plate in Figure 19.

Table 6.
Natural frequency of the laminate plate.
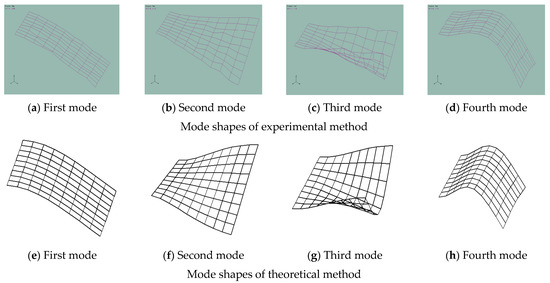
Figure 19.
Comparisons of modal shapes of the laminated plate between measured and theoretical results. (a) First mode, (b) Second mode, (c) Third mode, (d) Fourth mode, (e) First mode, (f) Second mode, (g) Third mode, (h) Fourth mode.
Table 6 shows the first eight natural frequency values obtained from the experimental composite laminate structure. The theoretical results are also given in the table. By comparing the experimental values and the theoretical values, we see that the results were in good agreement, and the maximum deviation was less than 4%, which verified the accuracy of the proposed modeling method. The results of the two methods showed a certain deviation, mainly because during the experiment the clamped boundary conditions were simulated by using multiple bolt joints, which had certain inconsistencies with the complete solidification in the theoretical calculation process. This may cause the stiffness to be less than the clamped end stiffness, resulting in the frequency of the experiment being higher than the theoretical value. Furthermore, a certain error was also generated, as the acceleration sensor introduced additional mass when it was connected to the plate structure.
Figure 19 shows the first four natural modes of the composite laminate obtained by the experimental method and theoretical method.
4. Summary
In this paper, on the basis of the improved Fourier series method, vibration modeling of a laminated composite plate was proposed to study vibration characteristics of laminates. According to the Mindlin plate theory, the mechanical models of the laminates were established and a number of functions were deduced, such as the potential energy function, as well as the function of kinetic energy. Simultaneously, according to the Hamilton principle, the vibration equations of the plates with arbitrary boundary conditions were derived by expressing the displacement as a superposition of a Fourier cosine series and four auxiliary polynomials.
Through the numerical analysis, the effectiveness of the present method was verified by a comparison between the FEA results and the results of the method proposed in relevant references and mode shapes. The natural frequency was analyzed in terms of the different boundary conditions, and the present method had the better accuracy. The effects of boundary conditions, the ratio between thickness and width, the number of layers of laminates and the laying angle on the vibration characteristics of composite laminates were studied.
It can be seen that the vibration frequency of laminate increased as the spring stiffness on the boundary increased. As the number of layers increased, the frequencies, except for the first-order frequency, showed a noticeable increase, and the frequency eventually became stable when the number of layers increased to a certain value. It can also be concluded that the effect of frequency regarding the ratio between thickness and width is significant; with the increase in h/b, the frequency of the plate vibration decreased.
Furthermore, in order to study the influencing factors and characteristics of the energy transfer, the harmonic response analysis and power flow analysis of the composited plate vibration showed that the vibration energy does not always transfer energy to the boundary according to the shortest path principle, and that there is also a certain form of energy cycle inside the plate structure. The distribution field and frequency of the energy flow had a significant influence. When the excitation force, excitation position and boundary conditions remain unchanged, the frequency change may also cause a complete change in the energy transfer.
Author Contributions
Conceptualization, Z.X., Q.L., W.H., J.W., Y.G.; methodology, Q.L., Z.X.; programming, Y.G., J.W., Z.X., W.H.; validation, Z.X., Q.L., W.H.; writing—original draft preparation, Z.X., Q.L., W.H.; writing—review and editing, Z.X., Q.L., W.H.; visualization, Z.X., Y.G.; supervision, Q.L., W.H.; project administration, Z.X., Q.L., W.H.; funding acquisition, Q.L.
Funding
This work was funded by the National Natural Science Foundation of China (No. 51405096) and the Fundamental Research Funds for the Central Universities (HEU3072019CF0706).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The detailed expressions of the submatrices Kij and Mij in Equations (34)–(35) are provided as follows.
where s = m(N + 1) + n + 1, t = m1 (N + 1) + n1 + 1, m = 0, 1, …, M, m1 = 0, 1, …, M, n = 0, 1, …, N, n1 = 0, 1, …, N, M and N are the cutoff value. And the submatrix M1,6 to M1,15 are zero matrix. Similarily, the other submatrix can be expressed as
where the submatrix M2,6 to M2,15 and M4,6 to M4,15 are zero matrix.
References
- Reddy, J.N. Mechanics of Laminated Composite Plate: Theory and Analysis; CRC Press: New York, NY, USA, 1997; pp. 30–40. [Google Scholar]
- Civalek, Ö. Free vibration analysis of symmetrically laminated composite plates with first-order shear deformation theory (FSDT) by discrete singular convolution method. Finite Elements Anal. Des. 2008, 44, 725–731. [Google Scholar] [CrossRef]
- Bhar, A.; Phoenix, S.; Satsangi, S. Finite element analysis of laminated composite stiffened plates using FSDT and HSDT: A comparative perspective. Compos. Struct. 2010, 92, 312–321. [Google Scholar] [CrossRef]
- Subramanian, P. Dynamic analysis of laminated composite beams using higher order theories and finite elements. Compos. Struct. 2006, 73, 342–353. [Google Scholar] [CrossRef]
- Alibeigloo, A.; Kari, M. Forced vibration analysis of antisymmetric laminated rectangular plates with distributed patch mass using third order shear deformation theory. Thin-Walled Struct. 2009, 47, 653–660. [Google Scholar] [CrossRef]
- Xiang, S.; Jiang, S.-X.; Bi, Z.-Y.; Jin, Y.-X.; Yang, M.-S. A nth-order meshless generalization of Reddy’s third-order shear deformation theory for the free vibration on laminated composite plates. Compos. Struct. 2011, 93, 299–307. [Google Scholar] [CrossRef]
- Reddy, J.N.; Robbins, D.H. Theories and Computational Models for Composite Laminates. Appl. Mech. Rev. 1994, 47, 147–169. [Google Scholar] [CrossRef]
- Desai, Y.; Ramtekkar, G.; Shah, A. Dynamic analysis of laminated composite plates using a layer-wise mixed finite element model. Compos. Struct. 2003, 59, 237–249. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Afsari, A.; Zahedinejad, P.; Bahadori, R. Three-dimensional layerwise-finite element free vibration analysis of thick laminated annular plates on elastic foundation. Appl. Math. Model. 2010, 34, 776–790. [Google Scholar] [CrossRef]
- Hu, M.Y.; Wang, A.W. Free vibration and stress analysis of fiber reinforced viscoelastic composite laminates. Eng. Mech. 2010, 27, 10–20. [Google Scholar]
- Ding, H.J.; Chen, W.Q.; Xu, R.Q. 3-D accurate analysis of bending, vibration and stability of transversely anisotropic laminates. Appl. Mech. Math. 2001, 22, 16–22. [Google Scholar]
- Chen, W.; Lü, C.; Chen, W. 3D free vibration analysis of cross-ply laminated plates with one pair of opposite edges simply supported. Compos. Struct. 2005, 69, 77–87. [Google Scholar] [CrossRef]
- Yang, Y.Z.; Liu, H. 3-D exact solutions of free and forced vibrations of laminated plates. Mech. Pract. 2008, 30, 23–26. (In Chinese) [Google Scholar]
- Yu, S.; Cleghorn, W. Generic Free Vibration of Orthotropic Rectangular Plates with Clamped and Simply Supported Edges. J. Sound Vib. 1993, 163, 439–450. [Google Scholar] [CrossRef]
- Ge, L.; Shen, H.S.; Lin, Z.Q. Forced vibration of symmetrical orthogonal layered plates on elastic foundation. J. Shanghai Jiaotong Univ. 2002, 1634–1639. (In Chinese) [Google Scholar]
- Huang, Y.; Liao, Y.; Xie, Y. Free vibration of orthotropic plates compressed on two-parameter elastic foundation. Eng. Mech. 2006, 23, 46–49. [Google Scholar]
- Kshirsagar, S.; Bhaskar, K. Accurate and elegant free vibration and buckling studies of orthotropic rectangular plates using untruncated infinite series. J. Sound Vib. 2008, 314, 837–850. [Google Scholar] [CrossRef]
- Liu, B.; Xing, Y. Exact solutions for free vibrations of orthotropic rectangular Mindlin plates. Compos. Struct. 2011, 93, 1664–1672. [Google Scholar] [CrossRef]
- Chung, J.; Chung, T.; Kim, K. Vibration Analysis of Orthotropic Mindlin Plates with Edges Elastically Restrained against Rotation. J. Sound Vib. 1993, 163, 151–163. [Google Scholar] [CrossRef]
- Liew, K.M.; Hung, K.; Lim, M. Method of domain decomposition in vibrations of mixed edge anisotropic plates. Int. J. Solids Struct. 1993, 30, 3281–3301. [Google Scholar] [CrossRef]
- Liew, K.M. Solving the vibrations of thick symmetric laminates by Reissner/Mindlin plate theory and the p-Ritz method. J. Sound Vib. 1996, 198, 343–363. [Google Scholar] [CrossRef]
- Cheung, Y.; Zhou, D. The free vibrations of rectangular composite plates with point-supports using static beam functions. Compos. Struct. 1999, 44, 145–154. [Google Scholar] [CrossRef]
- Matsunaga, H. Vibration and stability of cross-ply laminated composite plates according to a global higher-order plate theory. Compos. Struct. 2000, 48, 231–244. [Google Scholar] [CrossRef]
- Mbakogu, F.; Pavlović, M. Bending of clamped orthotropic rectangular plates: a variational symbolic solution. Comput. Struct. 2000, 77, 117–128. [Google Scholar] [CrossRef]
- Dalaei, M.; Kerr, A.D. Analysis of clamped rectangular orthotropic plates subjected to a uniform lateral load. Int. J. Mech. Sci. 1995, 37, 527–535. [Google Scholar] [CrossRef]
- Bercin, A.N. Free vibration solution for clamped orthotropic plates using the Kantorovich method. J. Sound Vib. 1996, 196, 243–247. [Google Scholar] [CrossRef]
- Wanji, C.; Xu, M.; Li, L. A model of a modified couplestress theory for composite laminated Reddy plate. Compos. Struct. 2012, 94, 2143–2156. [Google Scholar] [CrossRef]
- Chen, W.; Li, X. A new modified couple stress theory for anisotropic elasticity and micro-scale laminated Kirchhoff plate model. Arch. Appl. Mech. 2014, 84, 323–341. [Google Scholar] [CrossRef]
- Li, L.; Chen, W.; Zhen, N. Model of composite laminated thin plate base on modified couple stress theory and buckling analysis of scale effects. Eng. Mech. 2013, 30, 9–15. [Google Scholar]
- Yang, S.Q.; Chen, W.J. On hypotheses of composite laminated plates based on new modified couple stress theory. Compos. Struct. 2015, 133, 46–53. [Google Scholar] [CrossRef]
- Luccioni, L.X.; Dong, S.B. Levy type finite element analyses of vibration and stability of thin and thick laminated composite rectangular plates. Compos. B 1998, 29, 459–475. [Google Scholar] [CrossRef]
- Rao, K.P. Study of the behavior of laminated composite beam, plate and shell structures using some specifically developed finite elements. J. Spacecr. Technol. 2000, 10, 1–13. [Google Scholar]
- Shafiee, A.; Alizadeh, Y.; Redekop, D. Free vibration of completely free coupled orthotropic rectangular plates. J. Sound Vib. 2003, 267, 366–370. [Google Scholar] [CrossRef]
- Huang, M.; Ma, X.; Sakiyama, T.; Matuda, H.; Morita, C. Free vibration analysis of orthotropic rectangular plates with variable thickness and general boundary conditions. J. Sound Vib. 2005, 288, 931–955. [Google Scholar] [CrossRef]
- Liew, K.M.; Huang, Y.Q.; Reddy, J.N. Vibration analysis of symmetrically laminated plates based on FSDT using the moving least squares differential quadration method. Comput. Method. Appl. Mech. Eng. 2003, 192, 2203–2222. [Google Scholar] [CrossRef]
- Xiang, S.; Wang, K.-M. Free vibration analysis of symmetric laminated composite plates by trigonometric shear deformation theory and inverse multiquadric RBF. Thin-Walled Struct. 2009, 47, 304–310. [Google Scholar] [CrossRef]
- Xiang, S.; Li, G.; Zhang, W.; Yang, M. A meshless local point collocation method for free vibration analysis of laminated composite plates. Compos. Struct. 2011, 93, 280–286. [Google Scholar] [CrossRef]
- Ngo-Cong, D.; Mai-Duy, N.; Karunasena, W.; Tran-Cong, T. Free vibration analysis of laminated composite plates based on FSDT using one-dimensional IRBFN method. Comput. Struct. 2011, 89, 1–13. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, D.; Wang, Q. An improved Fourier series solution for free vibration analysis of the moderately thick laminated composite rectangular plate with non-uniform boundary conditions. Int. J. Mech. Sci. 2017, 121, 1–20. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, R.P.; Shi, D.Y.; Wang, Q.S. A simplified plate theory for vibration analysis of composite laminated sector, annular and circular plate. Thin-Walled Struct. 2019, 143, 106252. [Google Scholar] [CrossRef]
- Qin, B.; Zhong, R.; Wu, Q.Y.; Wang, T.T.; Wang, Q.S. A unified formulation for free vibration of laminated plate through Jacobi-Ritz method. Thin-Walled Struct. 2019, 144, 106354. [Google Scholar] [CrossRef]
- Romanelli, E.; Laura, P. Forced transverse vibrations of a simply supported rectangular orthotropic plate in the case where the force acts over a plate subdomain. Ocean Eng. 2001, 28, 1135–1144. [Google Scholar] [CrossRef]
- Shen, H.-S.; Yang, J.; Zhang, L. Free and forced vibration of reissner–mindlin plates with free edges resting on elastic foundations. J. Sound Vib. 2001, 244, 299–320. [Google Scholar] [CrossRef]
- Chen, Y.; Shen, H.S.; Su, W.L. Bending and vibration of cantilever plate reinforced by fiber reinforced composites. J. Shanghai Jiaotong Univ. 2003, 37, 562–565. [Google Scholar]
- Khan, Y.; Tiwari, P.; Ali, R. Application of variational methods to a rectangular clamped plate problem. Comput. Math. Appl. 2012, 63, 862–869. [Google Scholar] [CrossRef][Green Version]
- Niyogi, A.G.; Laha, M.K.; Sinha, P.K. Finite element vibration analysis of laminated composite folded plate structures. Shock Vib. 1999, 6, 273–283. [Google Scholar] [CrossRef]
- Biswas, D.; Ray, C. Comparative study on transient response analysis of hybrid laminated composite plates with experimental verification. J. Sound Vib. 2019, 453, 43–64. [Google Scholar] [CrossRef]
- Zhang, C.; Jin, G.; Ye, T.; Zhang, Y. Harmonic response analysis of coupled plate structures using the dynamic stiffness method. Thin-Walled Struct. 2018, 127, 402–415. [Google Scholar] [CrossRef]
- Nefske, D.J.; Sung, S.H. Power Flow Finite Element Analysis of Dynamic Systems: Basic Theory and Application to Beams. J. Vib. Acoust. 1989, 111, 94–100. [Google Scholar] [CrossRef]
- Hambric, S.A. Power Flow and Mechanical Intensity Calculations in Structural Finite Element Analysis. J. Vib. Acoust. 1990, 112, 542–549. [Google Scholar] [CrossRef]
- Li, Y.; Lai, J. Prediction of surface mobility of a finite plate with uniform force excitation by structural intensity. Appl. Acoust. 2000, 60, 371–383. [Google Scholar] [CrossRef]
- Cieślik, J.; Bochniak, W. Vibration energy flow in ribbed plates. Mechanics 2008, 25, 119–123. [Google Scholar]
- Xing, J.T.; Price, W.G.; Xiong, Y.P. Substructure-subdomain methods for power flow analysis of fluid-structure interaction dynamics. In Proceedings of the 10th International Congress on Sound and Vibration, Stockholm, Sweden, 7–10 July 2003; pp. 1115–1122. [Google Scholar]
- Wang, D.F.; He, P.F.; Liu, Z.S. Structural sound intensity characteristics of composite laminates under dynamic concentrated force. Chin. Q. Mech. 2007, 28, 217–222. (In Chinese) [Google Scholar]
- Zhang, H.; Shi, D.; Zha, S.; Wang, Q. A modified Fourier solution for sound-vibration analysis for composite laminated thin sector plate-cavity coupled system. Compos. Struct. 2019, 207, 560–575. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, D.; Zha, S.; Wang, Q. A simple first-order shear deformation theory for vibro-acoustic analysis of the laminated rectangular fluid-structure coupling system. Compos. Struct. 2018, 201, 647–663. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, D.; Wang, Q.; Zha, S. Vibro-acoustic analysis of the annular segment flexible plate coupled with an impedance walled enclosure. Thin-Walled Struct. 2018, 131, 205–222. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, D.; Zha, S.; Wang, Q. Parameterization study on the moderately thick laminated rectangular plate-cavity coupling system with uniform or non-uniform boundary conditions. Compos. Struct. 2018, 194, 537–554. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, D.; Zha, S.; Wang, Q. Vibro-acoustic analysis of the thin laminated rectangular plate-cavity coupling system. Compos. Struct. 2018, 189, 570–585. [Google Scholar] [CrossRef]
- Yan, J.K. General expression and measurement method of vibration power flow. Noise Vib. Control 1987, 24–29. [Google Scholar]
- An, C.L.; Ma, J.Y.; Zhang, Q.S.; Quan, L.X. Analysis of transmission path of vibration power flow in hydraulic pipelines. Noise Vib. Control 2018, 38, 36–42. [Google Scholar]
- Kim, S.; Inoue, A.; Singh, R. Experimental Study of Structure-Borne Noise Transfer Paths over the Mid-Frequency Regime; SAE Paper 2005-01-2338; SAE International: Warrendale, PA, USA, 2005. [Google Scholar]
- Inoue, A.; Kim, S.B.; Singh, R. Comparative evaluation of structure-borne noise transfer paths in a laboratory experiment. Noise Control Eng. J. 2006, 54, 382–395. [Google Scholar] [CrossRef]
- Inoue, A.; Singh, R.; Fernandes, G.A. Absolute and relative path measures in a discrete system by using two analytical methods. J. Sound Vib. 2008, 313, 696–722. [Google Scholar] [CrossRef]
- Lee, S.K. Identification of a vibration transmission path in a vehicle by measuring vibrational power flow. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2004, 218, 167–175. [Google Scholar] [CrossRef]
- Lee, S.K. Application of vibrational power flow to a passenger car for reduction of interior noise. Shock Vib. 2000, 7, 277–285. [Google Scholar] [CrossRef]
- Wang, B. Research on Transmission Characteristic of Energy Flows of Micro-Vibrations in Spacecraft Structures. Ph.D. Thesis, National University of Defense Technology, Changsha, China, September 2016. (In Chinese). [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).