Abstract
Aeronautical stiffened panels composed of thin shells and beams are prone to deformation or buckling due to the combined loading, functional boundary conditions and interface forces between joined parts in the assembly processes. In this paper, a mechanical prediction model of the multi-component panel is presented to investigate the deformation propagation, which has a significant effect on the fatigue life of built-up structures. Governing equations of Kirchhoff–Love shell are established, of which displacement expressions are transformed into Fourier series expansions of several introduced potential functions by applying the Galerkin approach. This paper presents an intermediate quantity, concentrated force at the joining interface, to describe mechanical interactions between the coupled components. Based on the Euler–Bernoulli beam theory, unknown intermediate quantity is calculated by solving a 3D stringer deformation equation with static boundary conditions specified on joining points. Compared with the finite element simulation and integrated model, the proposed method can substantially reduce grid number without jeopardizing the prediction accuracy. Practical experiment of the aircraft panel assembly is also performed to obtain the measured data. Maximum deviation between the experimental and predicted clearance values is 0.193 mm, which is enough to meet the requirement for predicting dimensional variations of the aircraft panel assembly.
1. Introduction
Stiffened panel structure composed of slender beams and a thin-walled shell is widely applied in the fields of marine and aeronautical engineering since it is lightweight and has high load-bearing capacity. Integrated stiffened panel model, regarded as a single piece structure, is generally exploited for the structural idealization of the built-up construction [1]. An aircraft fuselage panel as the built-up stiffened structure is usually assembled by riveting a skin and the stringers together. Before the riveting operation, the actual position of components (skin and stringer) may differ from the designed dimensions due to deformation resulting from the forces at joining interfaces and clamped boundary conditions with non-zero constraints. Thus, the integrated panel analysis cannot achieve an accurate evaluation of the actual profile. Moreover, numerical computation costs of a large-scale aircraft panel with real boundary conditions are also prohibitive. Therefore, a more efficient substructure model of large built-up panels, taking account of the initial variations, coupled interface force and mixed boundary conditions, should be established to achieve computational cost saving and accurate deformation prediction.
Approaches to model the multi-component structures have received attention from aeronautical engineers and mechanical experts, who focus on continuous mechanical descriptions and discrete element modeling of the beam, shell, or their combinations. The integrated one-piece models are mostly utilized in mechanical research to simplify the actual built-up structures. The Euler–Bernoulli beam (EBB) [2], Timoshenko beam [3,4], and nonlinear beam formulation [5] are usually introduced into the deformation analysis of the structures with slender and flexible components. Displacement formulae of these deformation prediction model are expressed or fitted by the Taylor-type expansion [6], Hermite interpolating polynomials [7] and Chebyshev polynomials [8]. The Kirchhoff shell [9], Reissner–Mindlin shell [10], and higher-order approximation shell theory [11] are employed for exploring the intrinsic mechanisms of thin panels. Although the deformation model generated from the single beam theory or shell theory could reduce the computational complexity, it cannot achieve the coupling analysis of structural interaction between multiple adjacent components.
To deal with the static analysis of complex thin-walled structures, Zappino and Carrera [12] built the variable kinematic models using Carrera Unified Formulation, which allows one-, two-, and three-dimensional refined structures to be connected to each other easily. Guida et al. [13] performed a finite element (FE) simulation of the lower lobe fuselage section and also conducted a drop experiment on small components for analyzing the energy absorbing ability of multi-component structures during a crash landing. The grid design for finite element method (FEM) has considerable effects on the time consumption and accuracy of results. Silva et al. [14] proposed a wave finite element method to express the dynamic stiffness matrix of the periodic structures with substructuring techniques that could yield large computational savings. Pacheco et al. [15] established aerodynamic and structural models of reinforced panels based on the principle of virtual work, which is discretized through the FE method. They found that modeling stiffeners as immovable boundaries would overestimate flutter onset conditions and underestimate post-flutter amplitudes. Thus, considering the flexibility of stiffeners is essential to the nonlinear analysis of complex aircraft configurations.
In addition, the solution of boundary value problems for the aforementioned complex mechanical system is another important challenge of multi-component structure analysis. Wesley et al. [16] solved the one- and two-dimensional structural mechanics problems by employing the Lagrange multiplier method and double exponential transformation. Tamijani and Kapania [1] utilized the element-free Galerkin approach to solving the buckling and static problems of simply supported plates with different stiffener configurations. Sapountzakis and Mokos [17] carried out a general solution to the nonlinearly coupled deflection equation of plates stiffened by doubly symmetric cross-sectional beam based on the analog equation method and boundary element method. Ahmad and Kapania [18] presented a vibration solution of integrally stiffened plates with plate-strip stiffeners with the Rayleigh–Ritz approach, which can also be applied to fully clamped, free, and cantilever supported stiffened plates. However, deformation investigations of multi-component structures, such as the previously mentioned ones, usually take no account of the initial variations. For the complex multi-component aircraft, a mechanical model with no consideration of the actual variation of boundary conditions may directly affect the aerodynamic and fatigue performance analysis of the structure.
To meet the computational saving and accuracy requirements for the numerical calculations of a large-scale aircraft stiffened panel, an efficient semi-analytical solution for mechanical substructure model of the joined beam-shell structure is firstly proposed in this paper. Based on the Kirchhoff–Love shell theory, governing equations with displacement and rotation boundary constraints are established to calculate the skin deformation resulting from the initial positioning variations and the coupling interaction between the joined parts. The solution of the shell equations is derived from the Fourier–Galerkin approach. Simultaneously, the displacement formulas of modified Euler–Bernoulli beam are developed to predict the 3D deformation of stringers caused by the positioning errors and clamping operation. For describing the interactions of coupled beam-shell structures, concentrated forces expressed as Dirac delta functions and the static boundary conditions at joining interfaces are introduced into the deformation equations. Moreover, the displacements solutions of the deformed stiffened panel are derived by adopting the Wronskian matrix and potential functions with Fourier series expansions. Finally, the accuracy and efficiency of the proposed semi-analytical method are verified by making a comparison with FE analysis results and the measured data in the practical experiment of the aircraft panel assembly.
2. Governing Equations of Stiffened Panel and Its Solution Procedure
As a typical subassembly part of aircraft, the fuselage stiffened panel is the combination of stringers and skin, as shown in Figure 1. Skin and stiffeners are first positioned and fastened to the specified location on the fixturing boards by adjusting the clamping mechanisms. Position error and the clamping variations on the contact edges could cause the initial deformations of panel components, which are the boundary value problems for governing equations of shell and beam with functional boundary conditions. Subsequently, the joining operation also induces the deflection due to the mechanical interactions between the coupled structures.
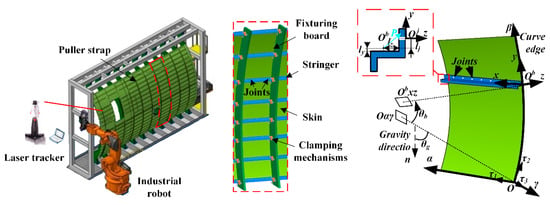
Figure 1.
Assembled aircraft stiffened panel structure.
2.1. Shell Subjected to Concentrated Force at Joining Interface and Functional Boundary Conditions
Kirchhoff–Love shell theory is utilized to establish the deformation model of single curvature skin, regarded as a thin cylindrical shell. The curvilinear coordinate system of the undeformed shell is denoted as Oαβγ. Curve edges of the panel are located on fixturing boards, which induce the position variations on boundary conditions, as shown in Figure 1.
The equilibrium equations of cylindrical shell [11] along axes of local coordinate system Oτ1τ2τ3 are established by
where , . Moreover, the third terms of second equation in Equation (1) are small enough quantities to be eliminated for thin shell [19]. The stress components are expressed in terms of the middle surface stain components, as follows:
where is a unit matrix, elements of matrix [QI] are , , , other elements of [QI] are zeroes, strains are , and , changes in curvature and twist are , and . The stress resultants and stress couples of a thin cylindrical shell are given by:
where .
Substituting Equation (3) into Equation (1), governing equations of the deformation of a thin cylindrical shell can be derived as
Differential operator matrix of the above equation is denoted by:
Since the symmetric matrix is a linear differential operator matrix, Equation (5) can be transformed into the combination of several differential equations of potential functions. The introduced potential functions have the following relations with displacements:
where is the cofactor of determinant . Substituting Equation (6) into Equation (4) yields:
The Galerkin approach is employed to derive solutions of the governing equations. According to the expressions satisfying the simply supported boundary conditions prescribed on the two straight edges of shell in [20], displacement and rotation components are assumed as:
where , . The displacements and stress acting on the straight edges of shell, and , have the following relationships:
which are also the boundary conditions on straight edges of panel.
Therefore, the variables in potential functions and the loads are decoupled by expanding the functions into the form of Fourier series as Equation (8):
and
where
Substituting Equations (8) and (11) into Equation (4), the displacements and loads with can be rewritten as:
where , is the coefficient to be determined. When , substituting the expanded Equations (10)–(12) into Equation (7) and eliminating the trigonometric terms, the following equations can be obtained:
where constant . The solution of Equation (14) must be derived to calculate , which is the functions in the displacement Equation (6), i.e., the solutions of shell deformation equation.
The complete solution is the sum of the homogeneous solution and the particular solution. Firstly, the solutions of the homogeneous equation corresponding to Equation (14) are calculated by solving the characteristic equation:
All roots of Equation (15) are obtained by:
where real and imaginary parts of complex roots are listed as Equation (A1) in Appendix A. Solutions of the homogeneous equation corresponding to Equation (14) can be expressed by:
where elements of are , , , and other elements of are zeroes, is a set of real coefficients in displacement expressions to be determined.
Secondly, the particular solutions of Equation (14) are derived by using the Wronskian determinant. The Wronskian determinant of the functions , a fundamental set of solutions to the associated homogeneous equation to Equation (14), is defined by:
The determinant is denoted by replacing the j-th column of the Wronskian with the column (0,0,…,0,1)T.
Particular solutions of Equation (14) can be derived from the following expression:
The load functions of concentrated force and uniform load encountered in the practical joining process of aircraft panel assembly are introduced to derive the explicit expressions of Eqaution (19). When the concentrated force f is imposed on the joining interface of shell at point , the associated distributed load q introduced into the deformation equation is expressed as the Dirac delta function . Using Equation (12), the following expression can be derived:
Then, the particular solution of Equation (14) with concentrated force applied on shell when is transformed as:
When the uniform load is imposed on the shell, the particular solution of Equation (14) with can be easily obtained by:
where qim is a constant or linear function of α.
Since the distributed load is a combination of concentrated force and uniform load, the complete solution of Equation (14) with should be the superposition of Equations (17), (21) and (22) as . Subsequently, substituting into Equations (10) and (6), the displacements expressions with coefficients can be obtained as Equation (A2).
Moreover, the presented displacement functions should satisfy the boundary conditions prescribed on shell edges. The initial variations on the skin curve edges are regarded as the non-zero kinematic boundary conditions imposed on edges , as follows:
where is the rotation around the axis β. Expanding , , and into Fourier series as the form of displacements expressions in Equations (A3) and (A4), a set of linear algebraic equations specific to coefficients are generated. Then, coefficients can be solved. Deformation of arbitrary point (α,β,γ) on the shell is determined by , and . Eventually, the semi-analytical expression of shell deformation with concentrated force, uniform load and arbitrary functional boundary conditions applied are achieved.
2.2. Fundamental Equation of Spatial Stiffener with Arbitrary Boundaries
Deformation of the stiffener is analyzed by the modified EBB model. Modified EBB approach introduces the transformation relations of displacements and rotations between arbitrary points on the same cross-section of the stringer entity. Cartesian coordinate system Obxyz of beam is shown in Figure 1. , and are the rotations around three coordinate axes, respectively.
With the assumptions imposed in EBB theory, the stress resultants can be described as [21,22]:
where elements of matrix [B] are , , , , , other elements of [B] are zeroes, is the axial strain, , and denote components of the curvature vector of axis x.
The governing differential equations of EBB are derived based on the principle of minimum total potential energy, which implies that the total potential energy of the system must be stationary and the stationary value is always a minimum. The total potential energy of the system is defined by:
where is a functional, is total strain energy, is the work done by external forces. To achieve the stationary total potential energy, the variation of Equation (25) should satisfy the following relations:
The strain energy of a beam is defined in terms of six components: one axial force, two bending moments, two shear forces and one torsional moment [23]. Since the shear deformation is neglected in the EBB theory, the total strain energy is expressed by the sum of the strain energy components due to tension or compression, bending and torsion force. The variation of the strain energy is described as:
The virtual work of external forces is given by:
where the notation means the minus of the function values with selected independent variable values x2 and x1. Using the Green’s theorem and method of integration by parts, Equation (26) is rewritten in the following form:
Simplifying Equation (29), the governing equations and the static boundary conditions are derived as:
The governing equation of EBB is expressed by substituting stress resultants–strain relation Equation (24) into Equation (30), as follows:
The position error and clamping variations on the edges of stiffeners are regarded as the following kinematic boundary conditions:
For each joining point on the cross section of the beam , eight supplementary boundary conditions should be added into the EBB deformation equation as:
Thus, displacements ub, vb and wb, the piecewise functions with unknown coefficient Cj, could be expressed by the polynomial functions of independent variable x since the derived governing equation is a set of the linear partial differential equation.
In particular, the modified EBB method introduces the transformation relations between the displacements of the centroid and arbitrary joining point on the cross-section of the stringer, the following expression [24] is presented by:
where the coordinate of arbitrary joining point on the cross-section with respect to Cartesian coordinate system Obxyz is , rotation matrix .
Consequently, the displacements and rotations of arbitrary points on the deformed stringer with positioning and clamping variations and the mechanical joining interaction are derived as Equations (32) and (35).
2.3. Calculation Procedure for Stiffened Panel deformation
For solving the coefficients in the explicit expressions of stiffener and shell deformation, the proposed intermediate quantities, concentrated forces at the joining interface of the coupled structure as fi in Equation (20) and fy and fz in Equation (34), still should be calculated. Moreover, force fz and f3 in the normal direction of the surface have the main effect on the actual panel profile since the automated drilling and riveting system of aircraft panel can achieve the measurement of surface normal and adjustment of machining direction. In summary, the detailed procedures for deformation calculation of stiffened panel with initial variation and joining force are illustrated in Figure 2.
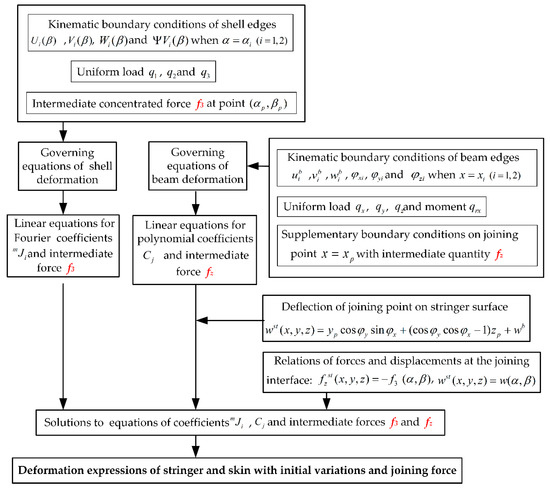
Figure 2.
Procedure of panel components deformations with initial variation and joining force.
3. Numerical Validation and Experiments
In this section, deformation propagation of fuselage stiffened panel with initial variations and mechanical interactions between the joined components are investigated. The semi-analytical calculation, FE simulation and practical experiments are performed by using the actual measured boundary conditions in engineering applications. Geometric and material properties of the stringer and shell are presented in Table 1 and Table 2.

Table 1.
Geometric and material property parameters of stringers.

Table 2.
Geometric and material property parameters of skin.
3.1. Initial Kinematic Boundary Conditions of Panel Components
To determine the value of boundary conditions prescribed on the edges of stringers and skin, initial variations of points on the surfaces of fixturing boards, stringers I and II, and clamping mechanisms are captured by the measurement device in fuselage panel assembly platform, as shown in Figure 3.

Figure 3.
Experiment platform of aircraft fuselage panel assembly. (a) Aircraft assembly platform; (b) substructure of fuselage panel.
The variations between the actual and theoretical position and orientation of the skin and stringers edges are the specified kinematic boundary conditions, as depicted in Table 3 and Table 4.

Table 3.
Actual boundary conditions prescribed on shell curve edges with respect to Cartesian coordinate Oτ1τ2τ3.

Table 4.
Actual boundary conditions prescribed on beam with respect to Cartesian coordinate Obxyz.
The measured variations are converted to the boundary conditions on curve edges of panel and with respect to curvilinear coordinate as the following expressions:
where
In addition to being imposed with the kinematic boundary constraints, the skin and stringers are also subjected to the gravity load. Load components of beam qx, qy and qz in the direction of local coordinate axes are 0, and , and . Load components of shell q1, q2 and q3 in the direction of local coordinate axes are 0, and , respectively.
3.2. Initial Deformation of Panel Components
During the positioning and clamping process, the panel components, skin and stringers, are just subjected to the initial kinematic boundary conditions listed in Equations (9) and (36) without the joining force. Substituting boundary conditions in Table 3 and Table 4 into the Fourier series expansion of shell displacement functions and beam deformation expressions, unknown coefficients and can be derived. Deformations of shell, beam I and beam II are provided by the proposed method, as shown in Figure 4 and Figure 5a. FE models of shell and beams are established by using commercial software ABAQUS® 6.14 Standard with S8R element and B33 elements, respectively. Approximate element size is 25 mm and the grid number of FE model is over 1440.
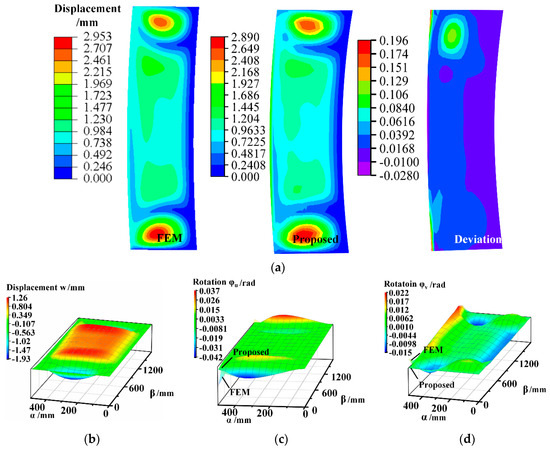
Figure 4.
Displacement and rotation of the deformed shell middle surface. (a) Magnitude of displacement; (b) displacement in direction of γ; (c) rotation around axis α; (d) rotation around axis β.
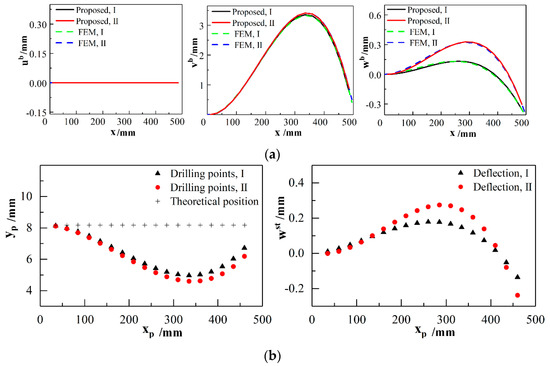
Figure 5.
Deformation of stringers and presented deflections of points to be joined. (a) Deformation of beam I and II along the centroid locus of cross-section; (b) positions and deflection of drilling points on the stringers I and II.
Besides, positions of points to be joined on the stringers I and II are predicted by solving a system of equations and by the Newton–Raphson approach. Substituting the solutions and into Equation (35), deflections wst of the points to be joined are obtained, as shown in Figure 5b. Based on the theoretical arc lengths of skin, , the actual positions of points to be joined on shell are obtained by solving a system of equations and . Solutions are substituted into Equation (A2), deflections w of the points to be joined on skin are calculated. In the practical aircraft assembly process, actual clearance between the panel components is measured to describe the relative deformation variation directly. A comparison of the predicted clearance and measured data is made to analyze the relative deformation components in the directions of surface normal, as shown in Figure 6.
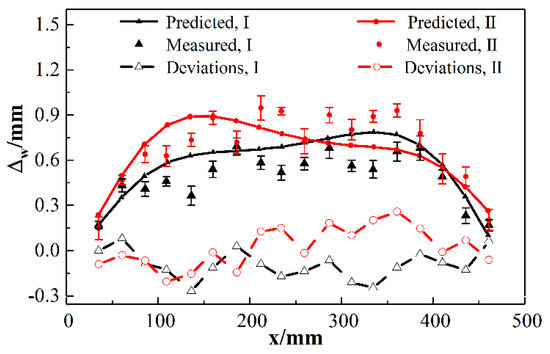
Figure 6.
Clearances between the points to be joined on stringers and adjacent skin surface.
Figure 4 and Figure 5 indicate that shell and beam deformation results provided by the proposed method are consistent with FEM result. As seen in Figure 4a, the shell displacement has increased nearly fourfold from initial variation 0.814 mm to 2.89 mm. Initial variations are obtained by , the variables of which are listed in Table 3. The functional boundary conditions cause the dramatical changes in the displacement. Maximum deviation of shell displacement between FEM and the proposed results are 0.196 mm which can verify the accuracy of the semi-analytical solutions. Figure 4b shows that deflection w in the direction of surface normal increases considerably before a decline when and then decreases finally. Displacements w and rotation φu distribute almost symmetrically with respect to section . It is noted that φu and φv provided by the FEM have distortion near the edge node while the proposed semi-analytical solution has a more stable value, as seen in Figure 4c,d.
As seen in Figure 5a, displacements wb in z-axis direction have relatively smaller values compared with the large deflection in y-axis direction. When the drilling operation is conducted by the automated robot without compensation, the positions of drilling points are skewed, as shown in Figure 5b. The skewed drilling points would be joined in the subsequent assembly process, which seriously affects the product quality. Thus, the deformation prediction of stiffened aircraft panel components has a practical significance in aeronautical engineering.
It can be observed from Figure 4b, Figure 5b and Figure 6 that clearances Δw of the regions between stringers and skin have the similar trend with the displacements w of deformed shell on sections . The major portion of clearance is the contribution from the skin deformation in the direction of surface normal. Absolute maximum deviations between predicted and measured clearances related to region I and II are 0.247 mm and 0.260 mm. Mean absolute deviations are 0.1127 mm and 0.1125 mm, respectively. It can be confirmed from the previous results that clearances provided by the proposed method and experimental approach have a good agreement.
3.3. Deformation of Stiffened Panel with Joints and Mixed Boundary Conditions
Due to the mechanical interaction of the joined parts, the stringer–skin panel will suffer the secondary deformation in the joining process. Semi-analytical calculations and FE simulation of panel substructure model with different joining points are performed to analyze the deformation propagation of stiffened panel. Measurement experiments are conducted to verify the accuracy of the proposed method, as shown in Figure 3b. The intermediate quantity, concentrated force is calculated by semi-analytical solutions, as listed in Table 5. The displacements of joining points on the stringers and skin are predicted by solving unknown coefficients and , as shown in Figure 7.

Table 5.
Calculated intermediate joining forces.
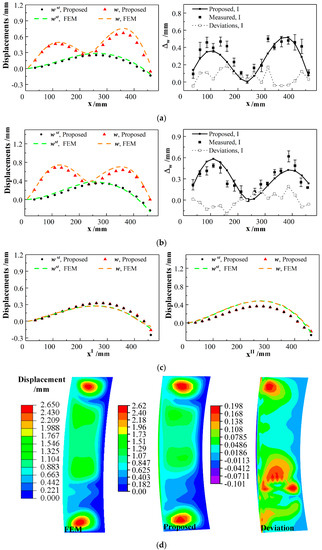
Figure 7.
Deformation of stiffened panel with joints at different positions. (a) One joining point P9I on stringer I; (b) one joining point P9II on stringer II; (c) nine joining points on stringer I and nine joining points on stringer II; (d) magnitude of displacement given by FEM and proposed method and the deviation between both
From Figure 7, it can be seen the joining operation causes dramatical deformation of shell and relatively slighter deformation of stringers. Figure 7a,b show that the absolute maximum deviations between the predicted and actual clearances are 0.180 mm and 0.193 mm when the point P9I and P9II are joined respectively. Displacements in the direction of surface normal provided by the proposed method and FEM are consistent with each other. Figure 7c,d indicates that the final positions of the stiffened panel with joints are similar to the stringers, which have higher stiffness than skin. Maximum deviation of shell displacement between FEM and the proposed results are 0.198 mm which can verify the accuracy of the semi-analytical solutions. Compared with the skin deformation shown in Figure 4a, the area of panel between two stiffeners deforms obviously with the joining operation conducted. Moreover, Table 5 shows the values of concentrated forces imposed on the same joining points, P9I and P9II, change in different situations. Figure 7 illustrates that the clearances Δw have similar values when the points on the stringer I and II are joined simultaneously or separately, but the joining forces change a lot.
It can be concluded that the concentrated force on the joining point differs by the change of joining sequences. The relationship between the changing force and joining point position cannot be expressed by the discrete stiffness model which considers stiffeners just as immovable boundaries. Besides, discrete integration models need more zero and first spatial derivatives at the ends of individual segments to be re-entered into the deformation calculations when the joining force and clearances change. Moreover, compared with the curve interpolating algorithm, the proposed semi-analytical substructure model can provide the values of changing force with no more supplementary parameters introduced when the positions of joining points are different.
4. Conclusions
An efficient semi-analytical displacement solution of stiffened panel substructure model is proposed to analyze the deformation propagation of built-up aircraft panel in assembly processes. The proposed method takes into account the initial positioning variations, clamped boundary conditions imposed on stringers and skin, and the coupling deformation at the joining interface of panel components. The displacement and rotation expressions of the deformed stringers and skin are derived based on the modified Euler–Bernoulli beam theory and Kirchhoff–Love shell theory. The accuracy of the predicted deformation is confirmed by comparison with the FEM results and the measured data in the practical experiment of the aircraft panel assembly. The deviations between the experimental and proposed values of clearances between the deformed panel components are less than 0.260 mm in the positioning and clamping process. Moreover, the absolute maximum deviation between the predicted and actual clearances is 0.193 mm when the joining operations are conducted on the panel. The proposed model can provide the joining force values with no need of introducing more supplementary parameters when the positions of joining points are different. Thus, the proposed method is more effective to analyze the multi-component structure deformation.
Author Contributions
Conceptualization, R.H.; methodology, R.H.; validation, R.H.; formal analysis, R.H.; investigation, R.H.; resources, Y.K.; data curation, R.H.; writing—original draft preparation, R.H.; writing—review and editing, Q.W.; supervision, J.L.; project administration, J.L.; funding acquisition, Q.W.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 51975520, Special scientific research for civil aircraft, grant number MJ-2015-G-081, the National Natural Science Foundation of China, grant number 51375442, and Science Fund for Creative Research Groups of National Natural Science Foundation of China, grant number 51521064.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| a, b, R, h | length of straight edge and arc edge, curvature radius, shell thickness, mm |
| q1, q2, q3 | external load components in the directions of axes τ1, τ2 and τ3, N·mm−2 |
| qx, qy, qz | external load components along the axes x, y and z, N·mm−1 |
| qrx, qry, qrz | moment components about the axes x, y and z, N·mm |
| f1, f2, f3 | concentrated force components caused by the joining interaction, N |
| N1, N2, N12, N21, Nx | normal internal forces of shell and beam, N·mm−2 |
| M1, M2, M12, M21, My, Mz, Myz | bending and twisting moments, N·mm |
| u, v, w | displacement components of local coordinate system Oτ1τ2τ3, mm |
| φu, φv | rotations around curvilinear coordinates, rad |
| ub, vb, wb | displacements along the centroid locus of the cross-section of beam, mm |
| ust, vst, wst | displacements of point P on the cross-section of the stringer, mm |
| xp, yp, zp | Coordinates of P with respect to Cartesian coordinate system Obxyz, mm |
| σ1, σ2, σ12 | normal stresses and shear stress components, N·mm−2 |
| E, Eb | modulus of elasticity of shell and beam, GPa |
| μ, μb | Poisson’s ratio |
| ρ, ρb | density, kg·m−3 |
| A, as | cross-sectional area, mm2, length of the stiffener, mm |
| Ixx, Iyy, Izz, Iyz, Izy | geometric torsional stiffness and moments of inertia for cross-section area, mm4 |
Appendix A
All real and imaginary parts in complex roots of Equation (15) are given by
Extended expressions for displacement functions are given as follows:
The Fourier series expansions of boundary conditions prescribed on shell edges are given by
where
References
- Tamijani, A.Y.; Kapania, R.K. Buckling and Static Analysis of Curvilinearly Stiffened Plates Using Mesh-Free Method. AIAA J. 2010, 48, 2739–2751. [Google Scholar] [CrossRef]
- Rodcheuy, N.; Frostig, Y.; Kardomateas, G.A. Extended High-Order Theory for Curved Sandwich Panels and Comparison with Elasticity. J. Appl. Mech. 2017, 84, 081002. [Google Scholar] [CrossRef]
- Reddy, J.N. Nonlocal Nonlinear Formulations for Bending of Classical and Shear Deformation Theories of Beams and Plates. Int. J. Eng. Sci. 2010, 48, 1507–1518. [Google Scholar] [CrossRef]
- Fernandes, R.R.; Tamijani, A.Y. Flutter Analysis of Laminated Curvilinear-Stiffened Plates. AIAA J. 2017, 55, 998–1011. [Google Scholar] [CrossRef]
- Su, W.; Cesnik, C.E.S. Strain-Based Geometrically Nonlinear Beam Formulation for Modeling Very Flexible Aircraft. Int. J. Solids Struct. 2011, 48, 2349–2360. [Google Scholar] [CrossRef]
- Carrera, E.; Pagani, A.; Petrolo, M. Component-Wise Method Applied to Vibration of Wing Structures. J. Appl. Mech. 2013, 80, 041012. [Google Scholar] [CrossRef]
- Salehi, M.; Sideris, P. A Finite-Strain Gradient-Inelastic Beam Theory and a Corresponding Force-Based Frame Element Formulation. Int. J. Numer. Methods Eng. 2018, 116, 380–411. [Google Scholar] [CrossRef]
- Tamijani, A.Y.; Kapania, R.K. Chebyshev-Ritz Approach to Buckling and Vibration of Curvilinearly Stiffened Plate. AIAA J. 2012, 50, 1007–1018. [Google Scholar] [CrossRef]
- Carrera, E.; Zappino, E. Carrera Unified Formulation for Free-Vibration Analysis of Aircraft Structures. AIAA J. 2016, 54, 280–292. [Google Scholar] [CrossRef]
- Sobota, P.M.; Dornisch, W.; Muller, R.; Klinkel, S. Implicit Dynamic Analysis Using an Isogeometric Reissner-Mindlin Shell Formulation. Int. J. Numer. Methods Eng. 2017, 110, 803–825. [Google Scholar] [CrossRef]
- Ventsel, E.; Krauthammer, T. Thin Plates and Shells: Theory, Analysis, and Applications; CRC Press: New York, NY, USA, 2001; pp. 319–332. [Google Scholar]
- Zappino, E.; Carrera, E. Multidimensional Model for the Stress Analysis of Reinforced Shell Structures. AIAA J. 2018, 56, 1647–1661. [Google Scholar] [CrossRef]
- Guida, M.; Marulo, F.; Abrate, S. Advances in Crash Dynamics for Aircraft Safety. Prog. Aerosp. Sci. 2018, 98, 106–123. [Google Scholar] [CrossRef]
- Silva, P.B.; Mencik, J.M.; Arruda, J.R.D. Wave Finite Element-Based Superelements for Forced Response Analysis of Coupled Systems via Dynamic Substructuring. Int. J. Numer. Methods Eng. 2016, 107, 453–476. [Google Scholar] [CrossRef]
- Pacheco, D.R.Q.; Marques, F.D.; Ferreira, A.J.M. Finite Element Analysis of Fluttering Plates Reinforced by Flexible Beams: An Energy-Based Approach. J. Sound Vib. 2018, 435, 135–148. [Google Scholar] [CrossRef]
- Slemp, W.C.H.; Kapania, R.K.; Mulani, S.B. Integrated Local Petrov-Galerkin Sinc Method for Structural Mechanics Problems. AIAA J. 2010, 48, 1141–1155. [Google Scholar] [CrossRef]
- Sapountzakis, E.J.; Mokos, V.G. An Improved Model for the Analysis of Plates Stiffened by Parallel Beams with Deformable Connection. Comput. Struct. 2008, 86, 2166–2181. [Google Scholar] [CrossRef]
- Ahmad, N.; Kapania, R.K. Free Vibration Analysis of Integrally Stiffened Plates with Plate-Strip Stiffeners. AIAA J. 2016, 54, 1103–1115. [Google Scholar] [CrossRef]
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Shells, 2nd ed.; McGraw-Hill: Singapore, 1959; p. 513. [Google Scholar]
- Wang, Q.; Hou, R.; Li, J.; Ke, Y. Analytical and Experimental Study on Deformation of Thin-Walled Panel with Non-ideal Boundary Conditions. Int. J. Mech. Sci. 2018, 149, 298–310. [Google Scholar] [CrossRef]
- Carrera, E.; Giunta, G.; Petrolo, M. Beam Structures: Classical and Advanced Theories; John Wiley & Sons: Chichester, UK, 2011; pp. 12–15. [Google Scholar]
- Przemieniecki, J.S. Theory of Matrix Structural Analysis; Dover Publications: New York, NY, USA, 1968; pp. 70–76. [Google Scholar]
- Shabana, A.A.; Yakoub, R.Y. Three Dimensional Absolute Nodal Coordinate Formulation for Beam Elements: Theory. J. Mech. Des. 2001, 123, 606–613. [Google Scholar] [CrossRef]
- Wang, Q.; Hou, R.; Li, J.; Ke, Y.; Maropoulos, P.G.; Zhang, X. Positioning Variation Modeling for Aircraft Panels Assembly Based on Elastic Deformation Theory. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2018, 232, 2592–2604. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).