Mix Design and Mechanical Properties of High-Performance Pervious Concrete
Abstract
:1. Introduction
2. Experimental Details
2.1. Materials
2.2. Test Variables and Experimental Design
2.3. Mix Proportions and Casting of Specimens
2.4. Test Methods and Data Analysis
3. Results and Discussion
3.1. Test Results of Matrixes
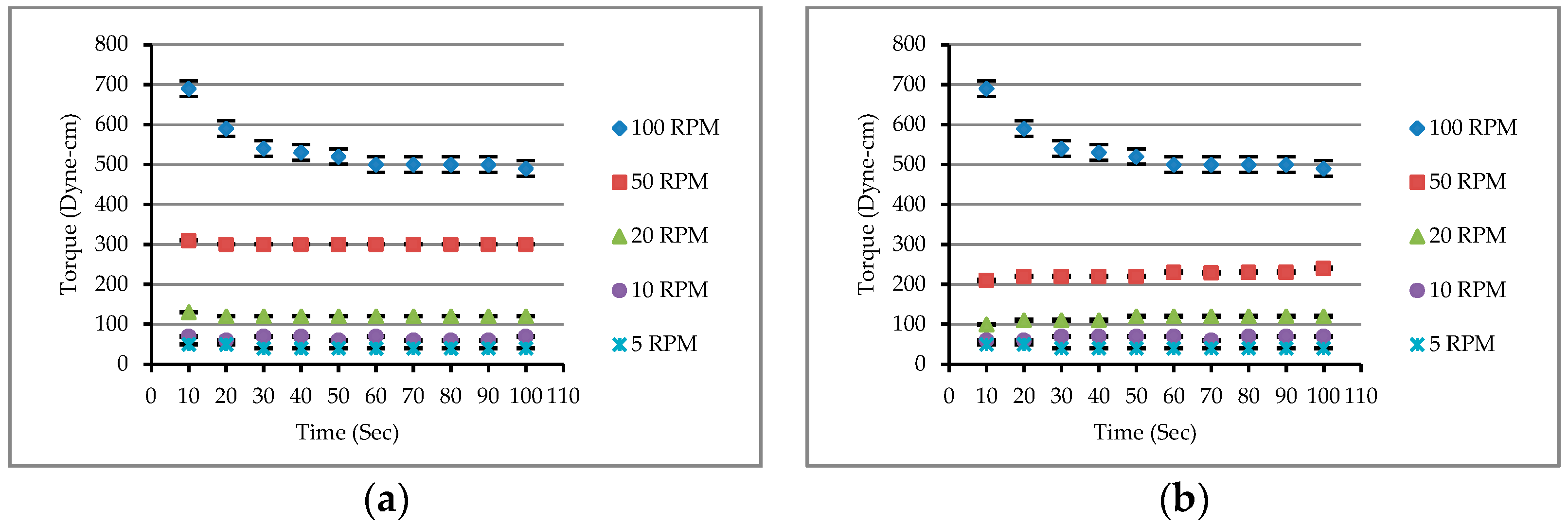
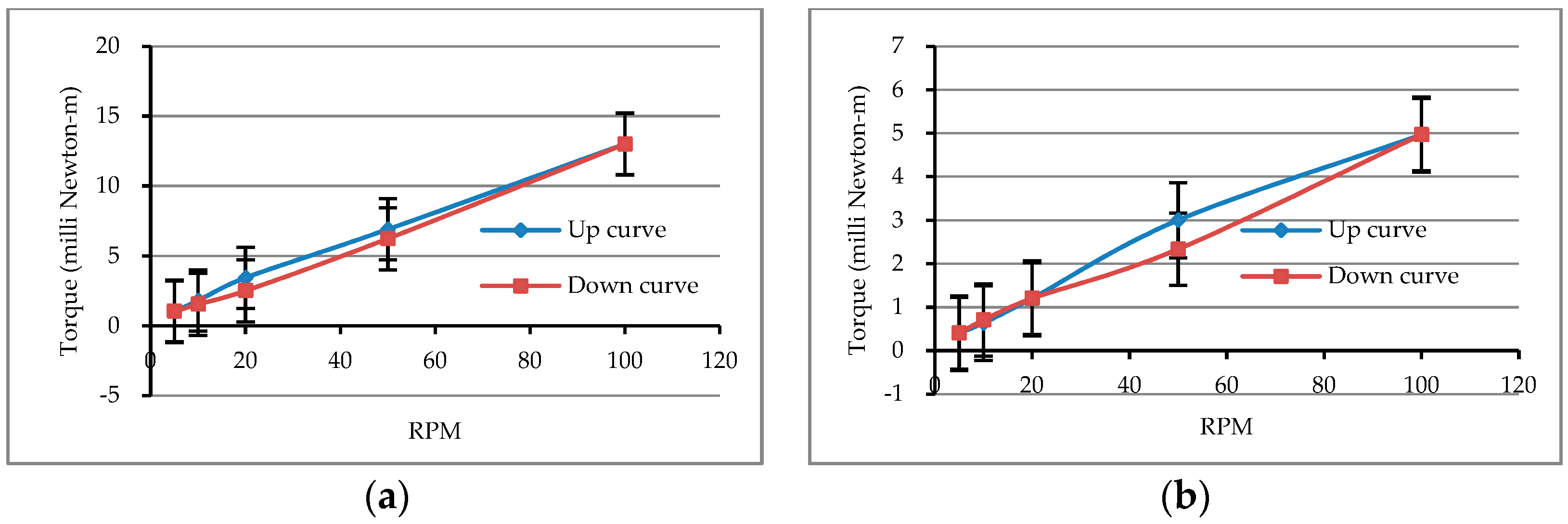
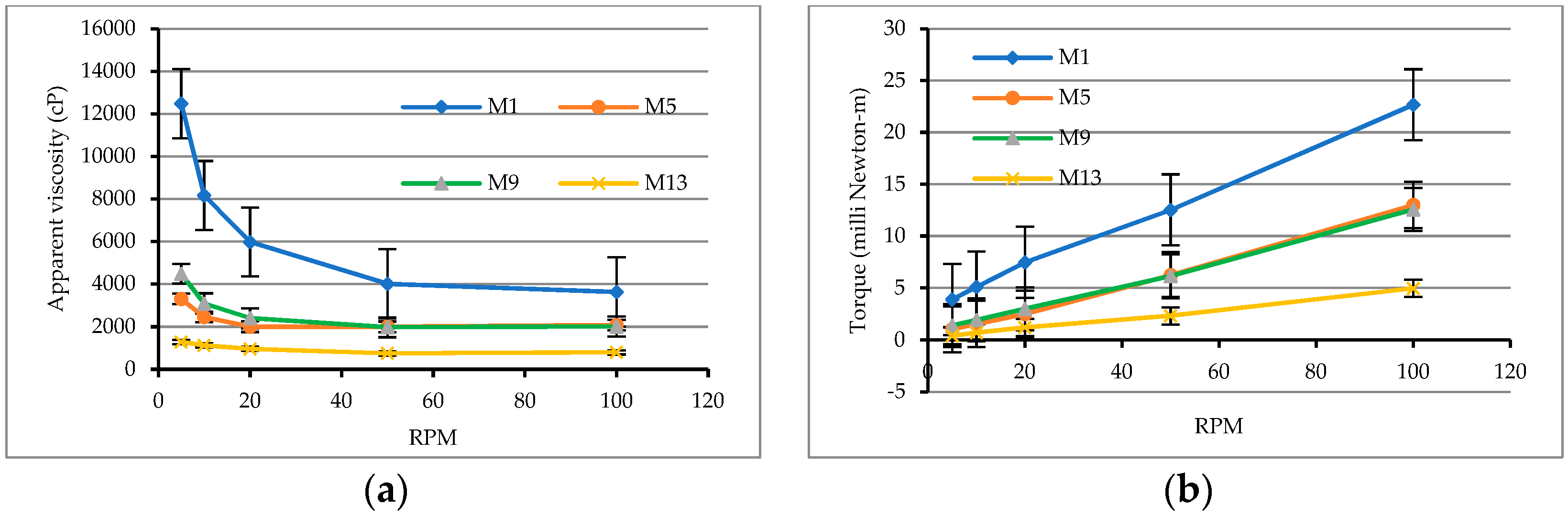
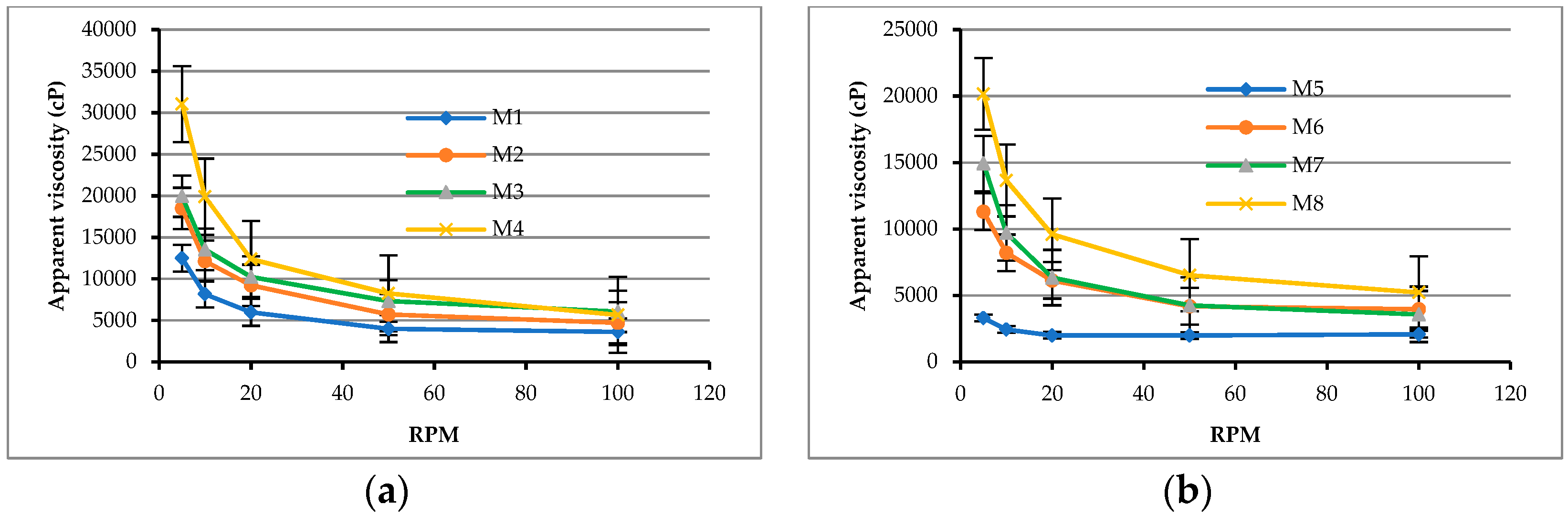
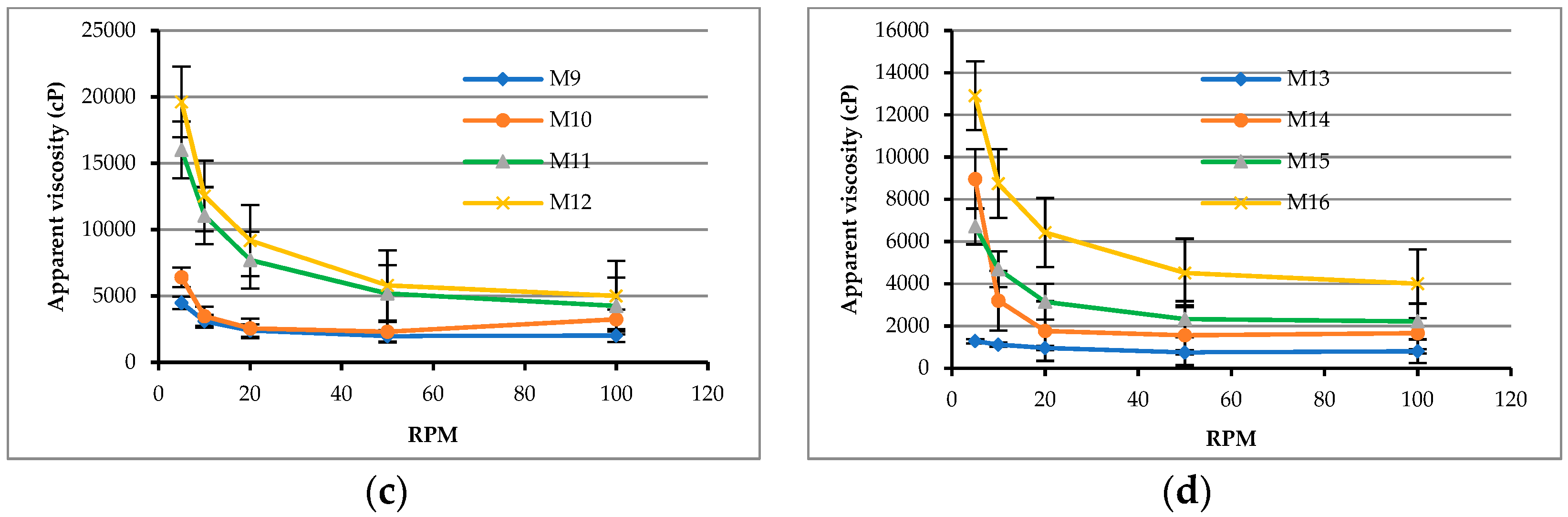
3.1.1. Rheological Behavior of Matrixes
3.1.2. Rheological Test Results of Matrixes
3.1.3. Flow Value and Compressive Strength of Matrixes
3.2. Test Results of Pervious Concretes
3.2.1. Compressive Strength
3.2.2. Elastic Modulus
3.2.3. Flexural Strength
3.2.4. Splitting Strength
3.2.5. Confirmation Tests
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chandrappa, A.K.; Biligiri, K.P. Pervious concrete as a sustainable pavement material—Research findings and future prospects: A state-of-the-art review. Constr. Build. Mater. 2016, 111, 262–274. [Google Scholar] [CrossRef]
- Barrett, M.E., Jr.; Malina, J.F.; Charbeneau, R.J. Characterization of Highway Runoff in Austin, Texas, Area. J. Environ. Eng. 1998, 124, 131–139. [Google Scholar] [CrossRef]
- United Nations. World Urbanization Prospects—The 2014 Revision; Department of Economic and Social Affairs: New York, NY, USA, 2014; p. 32. [Google Scholar]
- Zhong, R.; Wille, K. Material design and characterization of high performance pervious concrete. Constr. Build. Mater. 2015, 98, 51–60. [Google Scholar] [CrossRef]
- ACI. 522R-10 Pervious Concrete; American Concrete Institute Committee: Farmington Hills, MI, USA, 2010. [Google Scholar]
- Tennis, P.D.; Leming, M.L.; Akers, D.J. Pervious Concrete Pavements; Portland Cement Association: Skokie, IL, USA; National Ready Mixed Concrete Association: Silver Spring, MD, USA, 2004. [Google Scholar]
- United States Environmental Protection Agency, EPA. Storm Water Technology Fact Sheet: Porous Pavement; EPA: Washington, DC, USA, 1999; p. 6.
- Haselbach, L.; Boyer, M.; Kevern, J.T.; Schaefer, V.R. Cyclic heat island impacts on traditional versus pervious concrete pavement systems. J. Transp. Res. Board 2011, 2240, 107–115. [Google Scholar] [CrossRef]
- Urban Drainage and Flood Control District (UDFCD). Pervious Concrete Evaluation Materials Investigation; Thompson Materials Engineers Inc.: Denver, CO, USA, 2008. [Google Scholar]
- Houle, K.M. Winter Performance Assessment of Permeable Pavements—A Comparative Study of Porous Asphalt, Pervious Concrete, and Conventional Asphalt in a Northern Climate. Master’s Thesis, University of New Hampshire, Durham, NH, USA, September 2008. [Google Scholar]
- Olek, J.; Weiss, W.J.; Neithalath, N.; Marolf, A.; Sell, E.; Thornton, W.D. Development of Quiet and Durable Porous Portland Cement Concrete Paving Materials; Final Report SQDH 2003-5; Purdue University: West Lafayette, IN, USA, 2003. [Google Scholar]
- Park, S.; Tia, M. An experimental study on the water-purification properties of porous concrete. Cem. Concr. Res. 2004, 34, 177–184. [Google Scholar] [CrossRef]
- Bean, E.Z.; Hunt, W.F.; Bidelspach, D.A. A field survey of permeable pavement surface infiltration rates. ASCE J. Irrig. Drain. Eng. 2007, 133, 249–255. [Google Scholar] [CrossRef]
- Hesami, S.; Ahmadi, S.; Nematzadeh, M. Effects of rice husk ash and fiber on mechanical properties of pervious concrete pavement. Constr. Build. Mater. 2014, 53, 680–691. [Google Scholar] [CrossRef]
- Pilon, B.S.; Tyner, J.S.; Yoder, D.C.; Buchanan, J.R. The Effect of Pervious Concrete on Water Quality Parameters: A Case Study. Water 2019, 11, 263. [Google Scholar] [CrossRef]
- Obla, K.H. Pervious concrete—An overview. Indian Concr. J. 2010, 84, 9–18. [Google Scholar]
- National Ready Mixed Concrete Association. Concrete in Practice; National Ready Mixed Concrete Association: Silver Spring, MD, USA, 2004. [Google Scholar]
- Rehder, B.; Banh, K.; Neithalath, N. Fracture behavior of pervious concretes: The effects of pore structure and fibers. Eng. Fract. Mech. 2014, 118, 1–16. [Google Scholar] [CrossRef]
- Bonicelli, A.; Giustozzi, F.; Crispino, M. Experimental study on the effects of fine sand addition on differentially compacted pervious concrete. Constr. Build. Mater. 2015, 91, 102–110. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, G. Experimental study on properties of pervious concrete pavement materials. Cem. Concr. Res. 2003, 33, 381–386. [Google Scholar] [CrossRef]
- ACI Committee. Pervious concrete mixture proportioning. In 522 Report on Pervious Concrete; American Concrete Institute Committee: Farmington Hills, MI, USA, 2010; Chapter 6; p. 522R. [Google Scholar]
- Neithalath, N.; Sumanasooriya, M.S.; Deo, O. Characterizing pore volume, sizes, and connectivity in pervious concretes for permeability prediction. Mater. Charact. 2010, 61, 802–813. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Sebaibi, N.; Boutouil, M.; Leleyter, L.; Baraud, F. A modified method for the design of pervious concrete mix. Constr. Build. Mater. 2014, 73, 271–282. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Boutouil, M.; Sebaibi, N.; Leleyter, L.; Baraud, F. Valorization of seashell by-products in pervious concrete pavers. Constr. Build. Mater. 2013, 49, 151–160. [Google Scholar] [CrossRef]
- Schaefer, V.; Wang, K.; Suleiman, M.; Kevern, J. Mix Design Development for Pervious Concrete in Cold Weather Climates; No. 2006-01; Iowa Dept. of Transportation: Ames, IA, USA, 2006.
- Ghaharia, S.A.; Mohammadib, A.; Ramezanianpourc, A.A. Performance assessment of natural pozzolan roller compacted concrete pavements. Case Stud. Constr. Mater. 2017, 7, 82–90. [Google Scholar] [CrossRef]
- Zhong, R.; Wille, K. Compression response of normal and high strength pervious concrete. Constr. Build. Mater. 2016, 109, 177–187. [Google Scholar] [CrossRef]
- Beeldens, A.; Gemert, D.V.; Caestecker, C. Porous Concrete: Laboratory Versus Field Experience. In Proceedings of the 9th International Symposium on Concrete Roads, Istanbul, Turkey, 4–7 April 2004. [Google Scholar]
- Beeldens, A. Behavior of Porous PCC Under Freeze-Thaw Cycling. In Proceedings of the Tenth International Congress on Polymers in Concrete, Honolulu, HI, USA, 21–24 May 2001. [Google Scholar]
- Kajio, S.; Tanaka, S.; Tomita, R.; Noda, E.; Hashimoto, S. Properties of Porous Concrete with High Strength. In Proceedings of the 8th International Symposium on Concrete Roads, Lisbon, Portugal, 13–16 September 1988. [Google Scholar]
- Tamai, M.; Yoshida, M. Durability of Porous Concrete. In Proceedings of the Sixth International Conference on the Durability of Concrete, Thessaloniki, Greece, 1–7 June 2003. [Google Scholar]
- Mahalingam, R.; Mahalingam, S.V. Analysis of pervious concrete properties. Građevinar 2016, 68, 493–501. [Google Scholar]
- Kovč, M.; Sičáková, A. Pervious Concrete as an Environmental Solution for Pavements: Focus on Key Properties. Environments 2018, 5, 11. [Google Scholar] [CrossRef]
- Sharif, A.A.M.; Shahidan, S.; Koh, H.B.; Kandash, A.; Zuki, S.S.M. Strength development of pervious concrete containing engineered biomass aggregate. Mater. Sci. Eng. 2017, 271, 012002. [Google Scholar] [CrossRef]
- Aoki, Y.; Ravindrarajah, R.S.; Khabbaz, H. Properties of pervious concrete containing fly ash. Road Mater. Pavement Des. 2012, 13, 1–11. [Google Scholar] [CrossRef]
- Hamdulay, H.N.; John, R.J.; Suroshe, D.R. Effect of Aggregate Grading and Cementitious Byproduct on Performance of Pervious Concrete. Int. J. Innov. Res. Sci. Eng. Technol. 2015, 4, 6890–6897. [Google Scholar]
- Chen, Y.; Wang, K.; Wang, X.; Zhou, W. Strength, fracture and fatigue of pervious concrete. Constr. Build. Mater. 2013, 42, 97–104. [Google Scholar] [CrossRef]
- Torres, A.; Hu, J.; Ramos, A. The effect of the cementitious paste thickness on the performance of pervious concrete. Constr. Build. Mater. 2015, 95, 850–859. [Google Scholar] [CrossRef]
- Arhin, S.A.; Madhi, R.; Khan, W. Optimal Mix Designs for Pervious Concrete for an Urban Area. Int. J. Eng. Res. Technol. 2014, 3, 42–50. [Google Scholar]
- Zaetang, Y.; Wongsa, A.; Sata, V.; Chindaprasirt, P. Use of coal ash as geopolymer binder and coarse aggregate in pervious concrete. Constr. Build. Mater. 2015, 96, 289–295. [Google Scholar] [CrossRef]
- Nayak, B.H.; Prasad, K.S.B.; Kumar, M.P. An Experimental Study on Strength Characteristics of Pervious Concrete by Partial Addition of Glass Fiber and Polyester Fiber. Int. J. Eng. Res. 2015, 4, 545–549. [Google Scholar] [CrossRef]
- Rehman, H.A.A. Some properties of fiber reinforced no fine concrete. Al-Qadisiya J. Eng. Sci. 2012, 5, 439–450. [Google Scholar]
- Huang, B.; Wu, H.; Shu, X.; Burdette, E.G. Laboratory evaluation of permeability and strength of polymer-modified pervious concrete. Constr. Build. Mater. 2010, 24, 818–823. [Google Scholar] [CrossRef]
- Chang, J.J.; Yeih, W.; Chung, T.J.; Huang, R. Properties of pervious concrete made with electric arc furnace slag and alkali-activated slag cement. Constr. Build. Mater. 2016, 109, 34–40. [Google Scholar] [CrossRef]
- Kevern, J.T. Advancement of Pervious Concrete Durability. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 2008. [Google Scholar]
- Fisher, R.A. Statistical Methods for Research Workers; Oliver & Boyd: London, UK, 1925. [Google Scholar]
- Taguchi, G. Introduction to Quality Engineering: Designing Quality into Products and Processes; Asian Productivity Organization: Tokyo, Japan, 1987. [Google Scholar]
- Roy, R.K. A Primer on the Taguchi Method, Competitive Manufacturing Series; Van Nostrand Reinhold: New York, NY, USA, 1990. [Google Scholar]
- Phadke, M.S. Quality Engineering Using Robust Design; Prentice Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; Wiley: New York, NY, USA, 2005. [Google Scholar]
- ASTM. C230/C230M-14 Standard Specification for Flow Table for Use in Tests of Hydraulic Cement; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- ASTM. C109/C109M-13e1 Standard Test Method for Compressive Strength of Hydraulic Cement Mortars (Using 2-in. or [50-mm] Cube Specimens); ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar]
- ASTM. C1688/C1688M-14a Standard Test Method for Density and Void Content of Freshly Mixed Pervious Concrete; ASTM International: West Conshohocken, PA, USA, 2014; Available online: http://www.astm.org (accessed on 20 May 2019).
- ASTM. C1701/C1701M-17a Standard Test Method for Infiltration Rate of In Place Pervious Concrete; ASTM International: West Conshohocken, PA, USA, 2017; Available online: http://www.astm.org (accessed on 20 May 2019).
- ASTM. C39/C39M-18 Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens; ASTM International: West Conshohocken, PA, USA, 2018; Available online: http://www.astm.org (accessed on 20 May 2019).
- ASTM. C469/C469M-14 Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- ASTM. C496/C496M-11 Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens; ASTM International: West Conshohocken, PA, USA, 2004. [Google Scholar]
- ASTM. C78/C78M-18 Standard Test Method for Flexural Strength of Concrete (Using Simple Beam with Third-Point Loading); ASTM International: West Conshohocken, PA, USA, 2018; Available online: www.astm.org (accessed on 20 May 2019).
- Neville, A.M. Properties of Concrete; Longman: Essex, UK, 1994. [Google Scholar]
- Banfill, P.F.G. The rheology of cement paste: Propress since 1973. In Rheology of Fresh Cement and Concrete; The British Society of Rheology: London, UK, 1991. [Google Scholar]

| Void Ratio (%) | Unit Weight (kg/m3) | Permeability (mm/s) | 28 day Compressive Strength (MPa) | Flexural Strength (MPa) | Reference |
|---|---|---|---|---|---|
| 15–35 | N/A * | N/A | N/A | 2.5–3.9 | [11] |
| 19–34 | 1666–2034 | 10.2–15.0 | 13.5–25.2 | N/A | [25] |
| 19 | N/A | N/A | 26.0 | 4.4 | [27] |
| 20–30 | 1890–2083 | NA | 17.6–32.1 | 3.9–5.7 | [28] |
| 11–15 | N/A | 0.25–1.78 | N/A | 4.2–7.5 | [29] |
| 18–31 | N/A | N/A | 11.0–25.0 | N/A | [30] |
| N/A | N/A | N/A | 19.0 | N/A | [12] |
| 15–25 | 1602–2002 | 2.0–5.3 | 5.5–20.7 | 1.0–3.8 | [31] |
| 18–31 | N/A | 4.3–17.0 | 3.2–18.6 | 1.1–3.1 | [6] |
| 21–28 | N/A | 8.6–19.8 | 5.1–15.9 | 1.9–3.2 | [32] |
| 23–26 | 1890–1930 | 7.5–10.2 | 14.5–17.5 | N/A | [33] |
| 15–27 | 1766–1985 | 8.9–12.2 | 2.6–13.6 | N/A | [34] |
| 28–37 | 1750–1830 | 9.2–17.3 | 5.7–10.1 | N/A | [35] |
| NA | 1965–2067 | 3.8–6.1 | 8.5–17.2 | 1.1–4.8 | [36] |
| Parameter (Experimental Control Factor) | Levels of Parameter | Performance Parameter | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| Water–Binder Ratio, A | 0.28 | 0.31 | 0.34 | 0.37 | Flow value (mm) 7-day Compressive Strength (MPa) |
| Proportion of Cementitious Materials, B | PA * | PB | PC | PD | |
| Superplasticizer Content, C (%) | 1.0 | 1.3 | 1.6 | 1.9 | |
| Viscous Agent Content, D (%) | 0.1 | 0.2 | 0.3 | 0.4 | |
| Fiber Content, E (%) | 0.025 | 0.050 | 0.075 | 0.100 | |
| Parameter (Experimental Control Factor) | Levels of Parameter | Performance Parameter | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| Coarse Aggregate Size, A (mm) | 4.75–9.5 | 9.5–12.5 | 12.5–19.0 | Compressive Strength (MPa) Elastic Modulus (MPa) Flexural Strength (MPa) Splitting Strength (MPa) |
| Fine Aggregate Content, B (%) | 0 | 5 | 10 | |
| Matrix Type, C | CM1 * | CM2 | CM3 | |
| Aggregate to Binder Ratio, D | High | Medium | Low | |
| Experiment Number | Parameter (Level) | ||||
|---|---|---|---|---|---|
| Water–Binder Ratio | Proportion of Cementitious Materials | Superplasticizers Content (%) | Viscous Agent Content (%) | Fiber Content (%) | |
| M1 | 0.28 (1) * | PA (C:SF:SFP = 10:0:0) (1) | 0.25 (1) | 0.05 (1) | 0.025 (1) |
| M2 | 0.28 (1) | PB (C:SF:SFP = 9.6:0.2:0.2) (2) | 0.50 (2) | 0.10 (2) | 0.050 (2) |
| M3 | 0.28 (1) | PC (C:SF:SFP = 9.2:0.4:0.4) (3) | 0.75 (3) | 0.15 (3) | 0.075 (3) |
| M4 | 0.28 (1) | PD (C:SF:SFP = 8.8:0.6:0.6) (4) | 1.00 (4) | 0.20 (4) | 0.100 (4) |
| M5 | 0.31 (2) | PA (C:SF:SFP = 10:0:0) (1) | 0.50 (2) | 0.15 (3) | 0.100 (4) |
| M6 | 0.31 (2) | PB (C:SF:SFP = 9.6:0.2:0.2) (2) | 0.25 (1) | 0.20 (4) | 0.075 (3) |
| M7 | 0.31 (2) | PC (C:SF:SFP = 9.2:0.4:0.4) (3) | 1.00 (4) | 0.05 (1) | 0.050 (2) |
| M8 | 0.31 (2) | PD (C:SF:SFP = 8.8:0.6:0.6) (4) | 0.75 (3) | 0.10 (2) | 0.025 (1) |
| M9 | 0.34 (3) | PA (C:SF:SFP = 10:0:0) (1) | 0.75 (3) | 0.20 (4) | 0.050 (2) |
| M10 | 0.34 (3) | PB (C:SF:SFP = 9.6:0.2:0.2) (2) | 1.00 (4) | 0.15 (3) | 0.025 (1) |
| M11 | 0.34 (3) | PC (C:SF:SFP = 9.2:0.4:0.4) (3) | 0.25 (1) | 0.10 (2) | 0.100 (4) |
| M12 | 0.34 (3) | PD (C:SF:SFP = 8.8:0.6:0.6) (4) | 0.50 (2) | 0.05 (1) | 0.075 (3) |
| M13 | 0.37 (4) | PA (C:SF:SFP = 10:0:0) (1) | 1.00 (4) | 0.10 (2) | 0.075 (3) |
| M14 | 0.37 (4) | PB (C:SF:SFP = 9.6:0.2:0.2) (2) | 0.75 (3) | 0.05 (1) | 0.100 (4) |
| M15 | 0.37 (4) | PC (C:SF:SFP = 9.2:0.4:0.4) (3) | 0.50 (2) | 0.20 (4) | 0.025 (1) |
| M16 | 0.37 (4) | PD (C:SF:SFP = 8.8:0.6:0.6) (4) | 0.25 (1) | 0.15 (3) | 0.050 (2) |
| Experiment Number | Parameter (Level) | |||
|---|---|---|---|---|
| Coarse Aggregate Size (mm) | Fine Aggregate Content (%) | Matrix Type | Aggregate-to-Binder Ratio (weight ratio) | |
| C1 | 4.75–9.5 (1) | 0 (1) | CM1 (1) | 6.2 (1) |
| C2 | 4.75–9.5 (1) | 5 (2) | CM2 (2) | 5.9 (2) |
| C3 | 4.75–9.5 (1) | 10 (3) | CM3 (3) | 5.6 (3) |
| C4 | 9.5–12.5 (2) | 0 (1) | CM2 (2) | 5.6 (3) |
| C5 | 9.5–12.5 (2) | 5 (2) | CM3 (3) | 6.2 (1) |
| C6 | 9.5–12.5 (2) | 10 (3) | CM1 (1) | 5.9 (2) |
| C7 | 12.5–19 (3) | 0 (1) | CM3 (3) | 5.9 (2) |
| C8 | 12.5–19 (3) | 5 (2) | CM1 (1) | 5.6 (3) |
| C9 | 12.5–19 (3) | 10 (3) | CM2 (2) | 6.2 (1) |
| Mix No. | W/B | W (kg/m3) | C (kg/m3) | SF (kg/m3) | UFS (kg/m3) | SP (kg/m3) | VA (kg/m3) | PP (kg/m3) |
|---|---|---|---|---|---|---|---|---|
| M1 | 0.28 | 450.24 | 1673.75 | 0.00 | 0.00 | 16.74 | 1.67 | 0.23 |
| M2 | 0.28 | 442.18 | 1601.85 | 33.37 | 33.37 | 21.69 | 3.34 | 0.45 |
| M3 | 0.28 | 434.07 | 1530.39 | 66.54 | 66.54 | 26.70 | 5.01 | 0.68 |
| M4 | 0.28 | 425.99 | 1459.37 | 99.50 | 99.50 | 31.70 | 6.65 | 0.90 |
| M5 | 0.31 | 467.45 | 1593.73 | 0.00 | 0.00 | 21.63 | 4.98 | 0.90 |
| M6 | 0.31 | 469.65 | 1525.49 | 31.78 | 31.78 | 16.58 | 6.37 | 0.68 |
| M7 | 0.31 | 459.29 | 1457.65 | 63.38 | 63.38 | 30.28 | 1.59 | 0.45 |
| M8 | 0.31 | 461.14 | 1390.20 | 94.79 | 94.79 | 25.42 | 3.17 | 0.23 |
| M9 | 0.34 | 485.47 | 1521.00 | 0.00 | 0.00 | 25.35 | 6.32 | 0.45 |
| M10 | 0.34 | 481.11 | 1456.07 | 30.33 | 30.33 | 30.02 | 4.56 | 0.23 |
| M11 | 0.34 | 496.01 | 1391.51 | 60.50 | 60.50 | 15.21 | 3.03 | 0.90 |
| M12 | 0.34 | 512.10 | 1387.63 | 90.50 | 90.50 | 19.72 | 1.51 | 0.68 |
| M13 | 0.37 | 506.34 | 1454.63 | 0.00 | 0.00 | 28.74 | 3.14 | 0.68 |
| M14 | 0.37 | 510.22 | 1392.70 | 29.01 | 29.01 | 25.10 | 1.45 | 0.90 |
| M15 | 0.37 | 510.62 | 1331.11 | 57.87 | 57.87 | 18.91 | 5.80 | 0.23 |
| M16 | 0.37 | 536.42 | 1327.56 | 86.58 | 86.58 | 14.51 | 4.34 | 0.45 |
| Mix No. | W/B | W (kg/m3) | C (kg/m3) | SF (kg/m3) | UFS (kg/m3) | SP (kg/m3) | VA (kg/m3) | PP (kg/m3) | CA (kg/m3) | FA (kg/m3) |
|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 0.28 | 51.76 | 177.32 | 11.96 | 11.96 | 3.85 | 0.81 | 0.11 | 1249.31 | 0.00 |
| C2 | 0.28 | 59.24 | 220.23 | 0.00 | 0.00 | 2.20 | 0.22 | 0.03 | 1234.39 | 64.70 |
| C3 | 0.31 | 69.38 | 220.19 | 9.57 | 9.57 | 4.57 | 0.24 | 0.07 | 1206.25 | 134.03 |
| C4 | 0.28 | 60.35 | 224.36 | 0.00 | 0.00 | 2.24 | 0.22 | 0.03 | 1256.43 | 0.00 |
| C5 | 0.31 | 61.82 | 196.18 | 8.53 | 8.53 | 4.08 | 0.21 | 0.06 | 1256.01 | 66.11 |
| C6 | 0.28 | 60.25 | 206.42 | 14.07 | 14.07 | 4.48 | 0.94 | 0.13 | 1245.54 | 138.39 |
| C7 | 0.31 | 62.57 | 198.59 | 8.63 | 8.63 | 4.13 | 0.22 | 0.06 | 1273.57 | 0.00 |
| C8 | 0.28 | 61.03 | 209.08 | 14.26 | 14.26 | 4.54 | 0.95 | 0.13 | 1263.97 | 66.52 |
| C9 | 0.28 | 61.42 | 228.34 | 0.00 | 0.00 | 2.28 | 0.23 | 0.03 | 1274.15 | 141.57 |
| Mix No. | W/B | Proportion of Cementitious Materials | Apparent Viscosity (centi-Poise, cP) | ||||
|---|---|---|---|---|---|---|---|
| Rotational Speed of Spindle (RPM) | |||||||
| 100 | 50 | 20 | 10 | 5 | |||
| M1 | 0.28 | C:SF:SFP = 10:0:0 | 3627 | 4011 | 5973 | 8160 | 12480 |
| M2 | 0.28 | C:SF:SFP = 9.6:0.2:0.2 | 4720 | 5717 | 9227 | 12147 | 18480 |
| M3 | 0.28 | C:SF:SFP = 9.2:0.4:0.4 | 6085 | 7328 | 10247 | 13547 | 19947 |
| M4 | 0.28 | C:SF:SFP = 8.8:0.6:0.6 | 5664 | 8256 | 12400 | 19893 | 31040 |
| M5 | 0.31 | C:SF:SFP = 10:0:0 | 2080 | 1995 | 2000 | 2453 | 3307 |
| M6 | 0.31 | C:SF:SFP = 9.6:0.2:0.2 | 3969 | 4192 | 6133 | 8213 | 11307 |
| M7 | 0.31 | C:SF:SFP = 9.2:0.4:0.4 | 3580 | 4267 | 6347 | 9707 | 14933 |
| M8 | 0.31 | C:SF:SFP = 8.8:0.6:0.6 | 5237 | 6528 | 9600 | 13653 | 20160 |
| M9 | 0.34 | C:SF:SFP = 10:0:0 | 2011 | 1973 | 2400 | 3093 | 4480 |
| M10 | 0.34 | C:SF:SFP = 9.6:0.2:0.2 | 3248 | 2304 | 2560 | 3467 | 6400 |
| M11 | 0.34 | C:SF:SFP = 9.2:0.4:0.4 | 4251 | 5184 | 7707 | 11053 | 16000 |
| M12 | 0.34 | C:SF:SFP = 8.8:0.6:0.6 | 5000 | 5792 | 9173 | 12533 | 19627 |
| M13 | 0.37 | C:SF:SFP = 10:0:0 | 795 | 747 | 960 | 1120 | 1280 |
| M14 | 0.37 | C:SF:SFP = 9.6:0.2:0.2 | 1653 | 1557 | 1760 | 3200 | 8960 |
| M15 | 0.37 | C:SF:SFP = 9.2:0.4:0.4 | 2213 | 2325 | 3147 | 4693 | 6720 |
| M16 | 0.37 | C:SF:SFP = 8.8:0.6:0.6 | 4000 | 4512 | 6427 | 8747 | 12907 |
| Mix No. | Experimental Results | S/N Ratio (dB) | ||
|---|---|---|---|---|
| Flow Value (mm) | 7-Day Compressive Strength (MPa) | Flow Value | 7 Day Compressive Strength | |
| M1 | 97.3 | 87.3 | −17.27 | 38.82 |
| M2 | 54.5 | 85.7 | −31.00 | 38.66 |
| M3 | 51.0 | 79.1 | −31.82 | 37.96 |
| M4 | 70.0 | 69.1 | −26.02 | 36.79 |
| M5 | 207.0 | 82.5 | −41.36 | 38.33 |
| M6 | 79.0 | 69.5 | −20.83 | 36.84 |
| M7 | 116.7 | 76.5 | −28.53 | 37.67 |
| M8 | 43.7 | 67.0 | −33.31 | 36.52 |
| M9 | 145.9 | 64.2 | −34.95 | 36.15 |
| M10 | 241.5 | 85.7 | −43.61 | 38.66 |
| M11 | 88.5 | 79.2 | −3.52 | 37.97 |
| M12 | 95.0 | 65.0 | −13.98 | 36.26 |
| M13 | 265.5 | 78.7 | −44.89 | 37.92 |
| M14 | 249.5 | 67.1 | −44.06 | 36.53 |
| M15 | 132.6 | 64.0 | −32.59 | 36.12 |
| M16 | 67.1 | 61.3 | −27.20 | 35.75 |
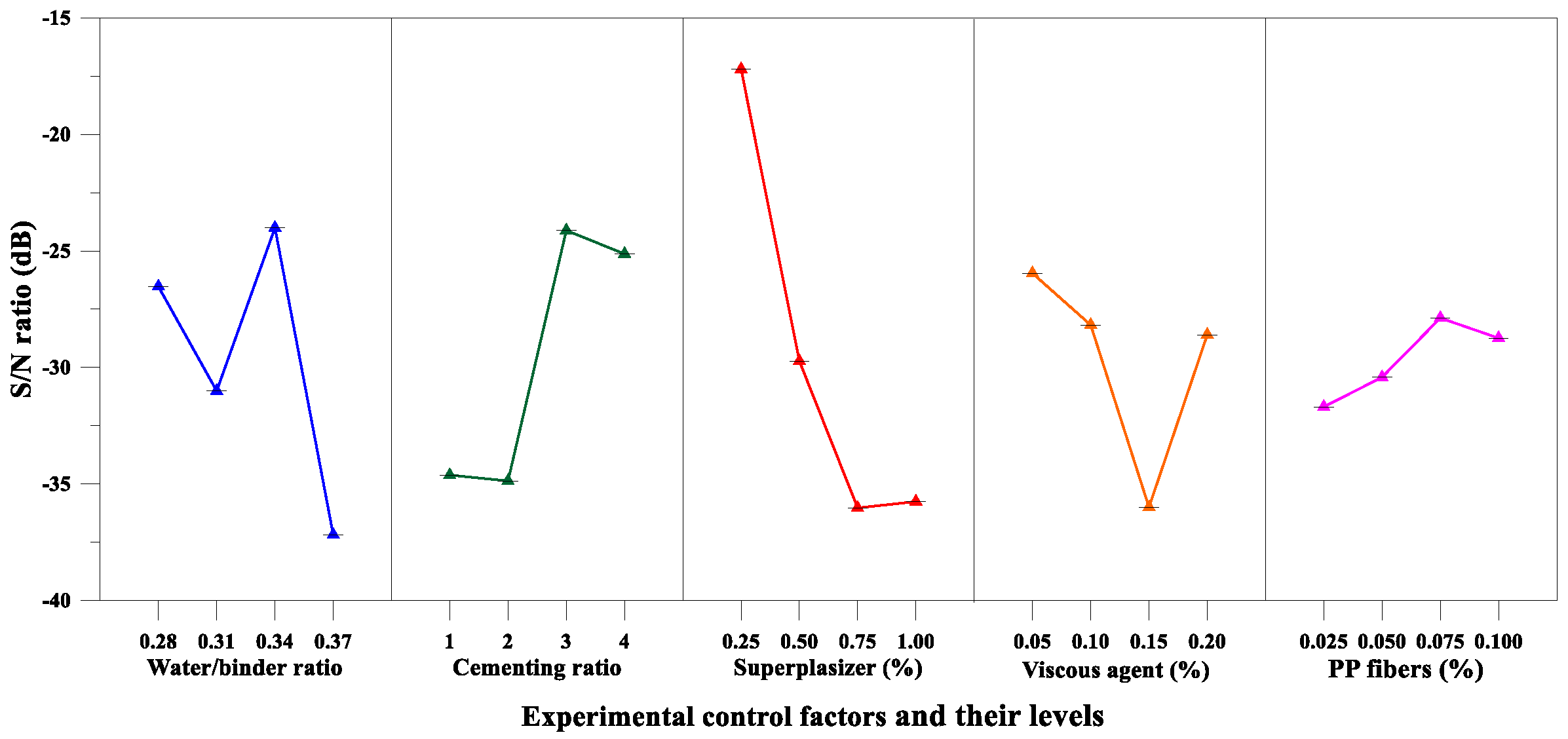
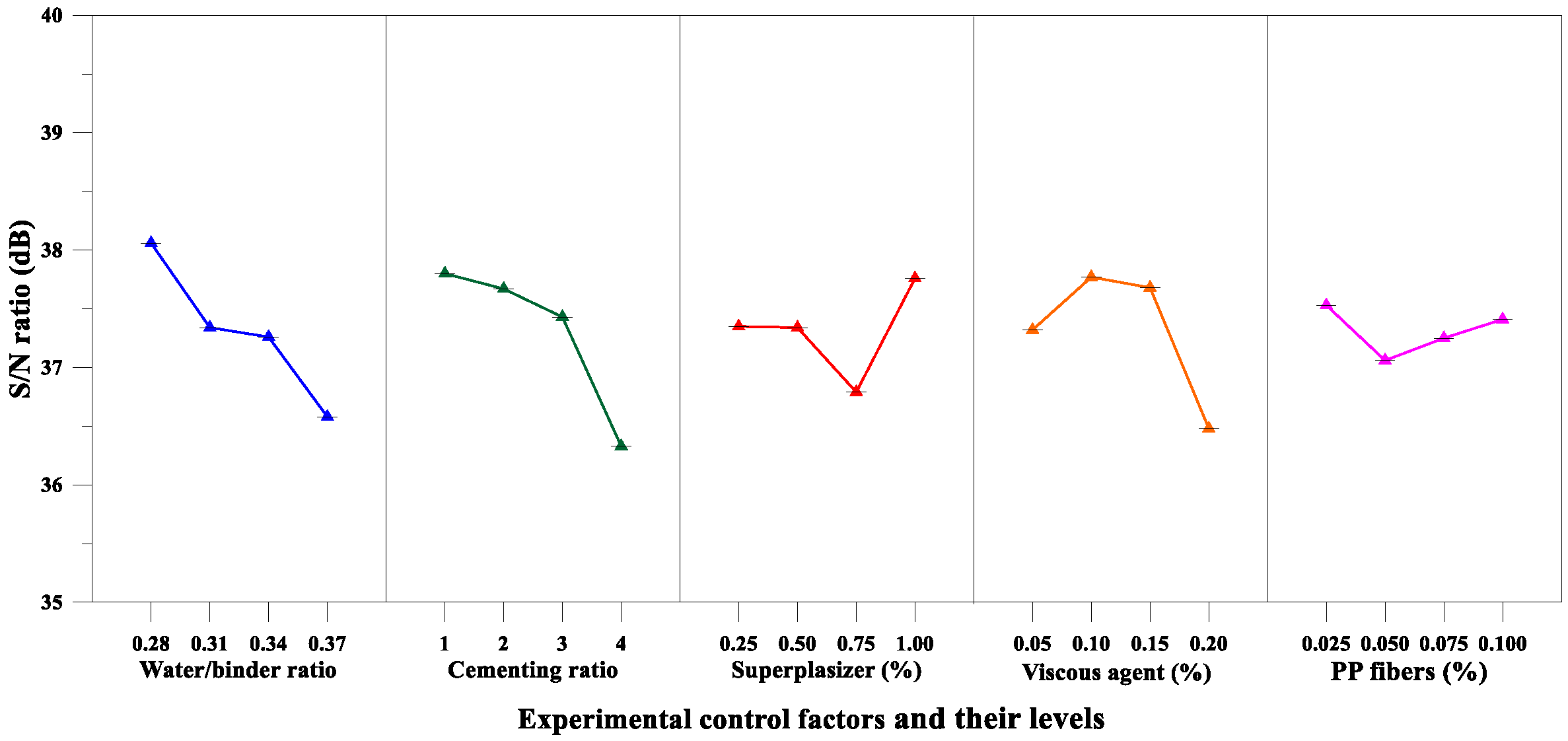
| Performance Parameter | Parameter (Experimental Control Factor) | Mean S/N Ratio (η, Unit: dB) | Delta (Max. η − Min. η) | Rank | |||
|---|---|---|---|---|---|---|---|
| Level 1 | Level 2 | Level 3 | Level 4 | ||||
| Flow Value | Water–Binder Ratio, A | −26.53 | −31.01 | −24.01 | −37.18 | 13.167 | 2 |
| Proportion of Cementitious Materials, B | −34.62 | −34.87 | −24.12 | −25.13 | 10.759 | 3 | |
| Superplasticizer Content, C (%) | −17.20 | −29.73 | −36.03 | −35.76 | 18.831 | 1 | |
| Viscous Agent Content, D (%) | −25.96 | −28.18 | −36.00 | −28.60 | 10.040 | 4 | |
| Fiber Content, E (%) | −31.69 | −30.42 | −27.88 | −28.74 | 3.815 | 5 | |
| Compressive Strength | Water–Binder Ratio, A | 38.06 | 37.34 | 37.26 | 36.58 | 1.477 | 1 |
| Proportion of Cementitious Materials, B | 37.80 | 37.67 | 37.43 | 36.33 | 1.475 | 2 | |
| Superplasticizer Content, C (%) | 37.35 | 37.34 | 36.79 | 37.76 | 0.968 | 4 | |
| Viscous Agent Content, D (%) | 37.32 | 37.77 | 37.68 | 36.48 | 1.293 | 3 | |
| Fiber Content, E (%) | 37.53 | 37.06 | 37.25 | 37.41 | 0.473 | 5 | |
| Performance Parameter | Parameter (Experimental Control Factor) | Sum of Square (SSZ) | Degree of Freedom | Variance (MSZ) | F Value (FZ) | Percentage Contribution (PZ) |
|---|---|---|---|---|---|---|
| Flow Value | Water–Binder Ratio, A | 400.27 | 3 | 133.42 | 11.46 | 18.19 |
| Proportion of Cementitious Materials, B | 412.14 | 3 | 137.38 | 11.80 | 18.78 | |
| Superplasticizer Content, C (%) | 932.11 | 3 | 310.70 | 26.69 | 53.37 | |
| Viscous Agent Content, D (%) | 228.75 | 3 | 76.25 | 6.55 | 9.65 | |
| Fiber Content, E (%) | 34.92 | 3 | 11.64 | 1.00 | 0.00 | |
| All Other/Error | 34.92 | 3 | 11.64 | – | – | |
| Total | 2008.20 | 15 | 669.40 | – | 100 | |
| Compressive Strength | Water–Binder Ratio, A | 4.37 | 3 | 1.46 | 8.68 | 23.69 |
| Proportion of Cementitious Materials, B | 5.41 | 3 | 1.80 | 10.75 | 30.04 | |
| Superplasticizer Content, C (%) | 1.89 | 3 | 0.63 | 3.76 | 23.91 | |
| Viscous Agent Content, D (%) | 4.16 | 3 | 1.39 | 8.26 | 22.37 | |
| Fiber Content, E (%) | 0.50 | 3 | 0.17 | 1.00 | 0.00 | |
| All Other/Error | 0.50 | 3 | 0.17 | – | – | |
| Total | 16.34 | 15 | 5.45 | – | 100 |
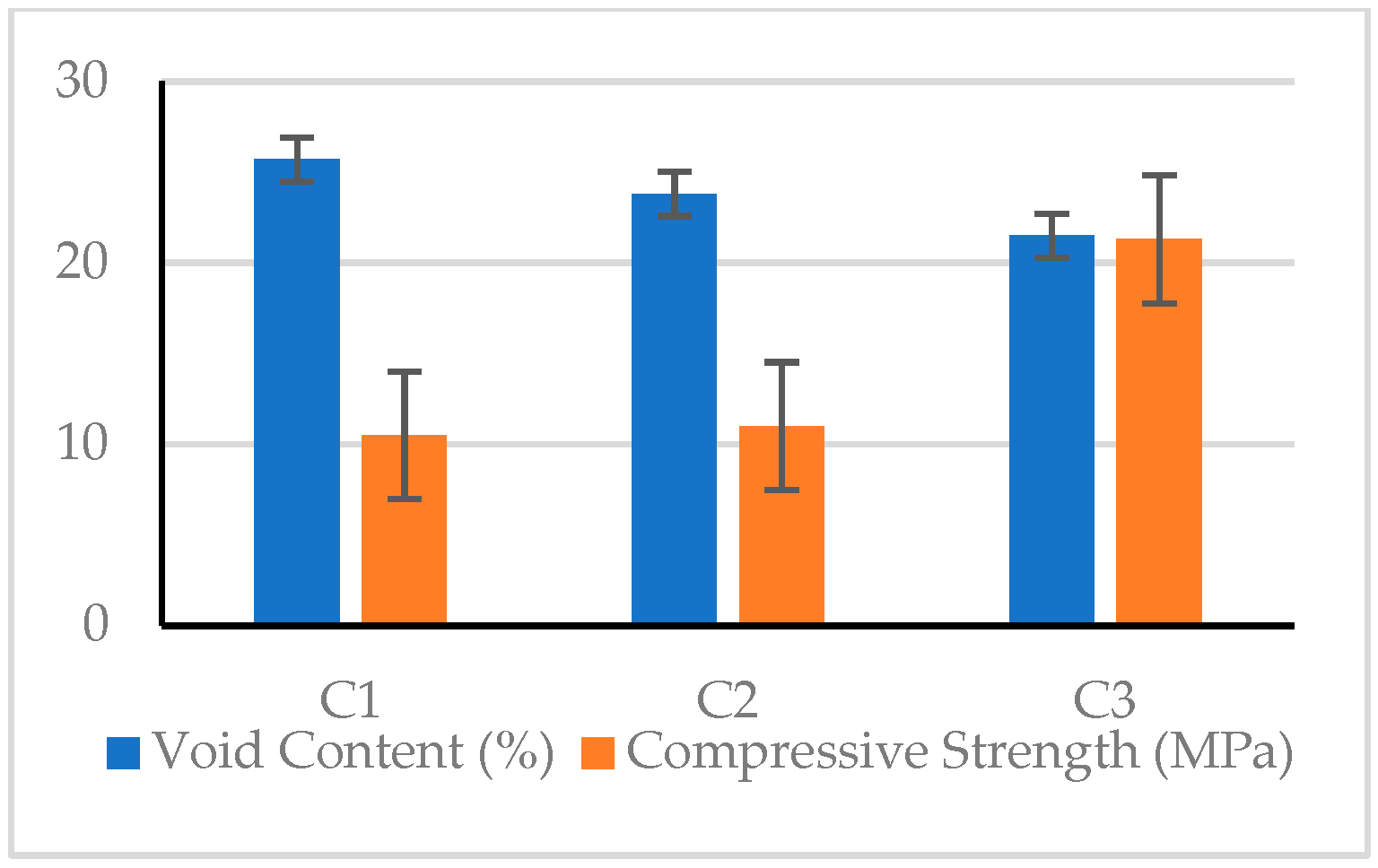
| Experiment Number | Unit Weight (kg/m3) | Vc (%) | k (mm/s) | Experimental Results (MPa) | S/N Ratio (dB) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| fc′ | Ec | fr | fs | fc′ | Ec | fr | fs | ||||
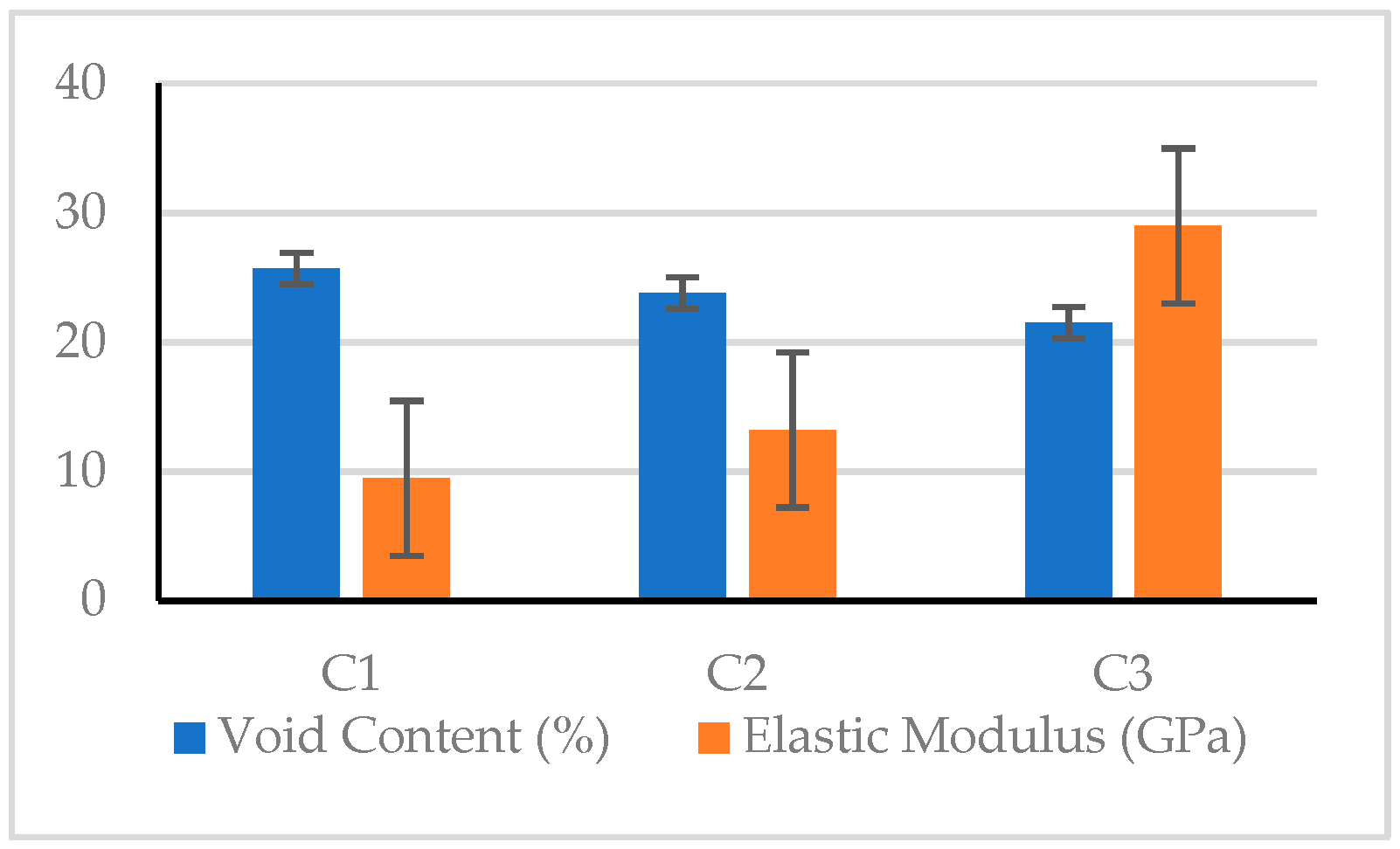
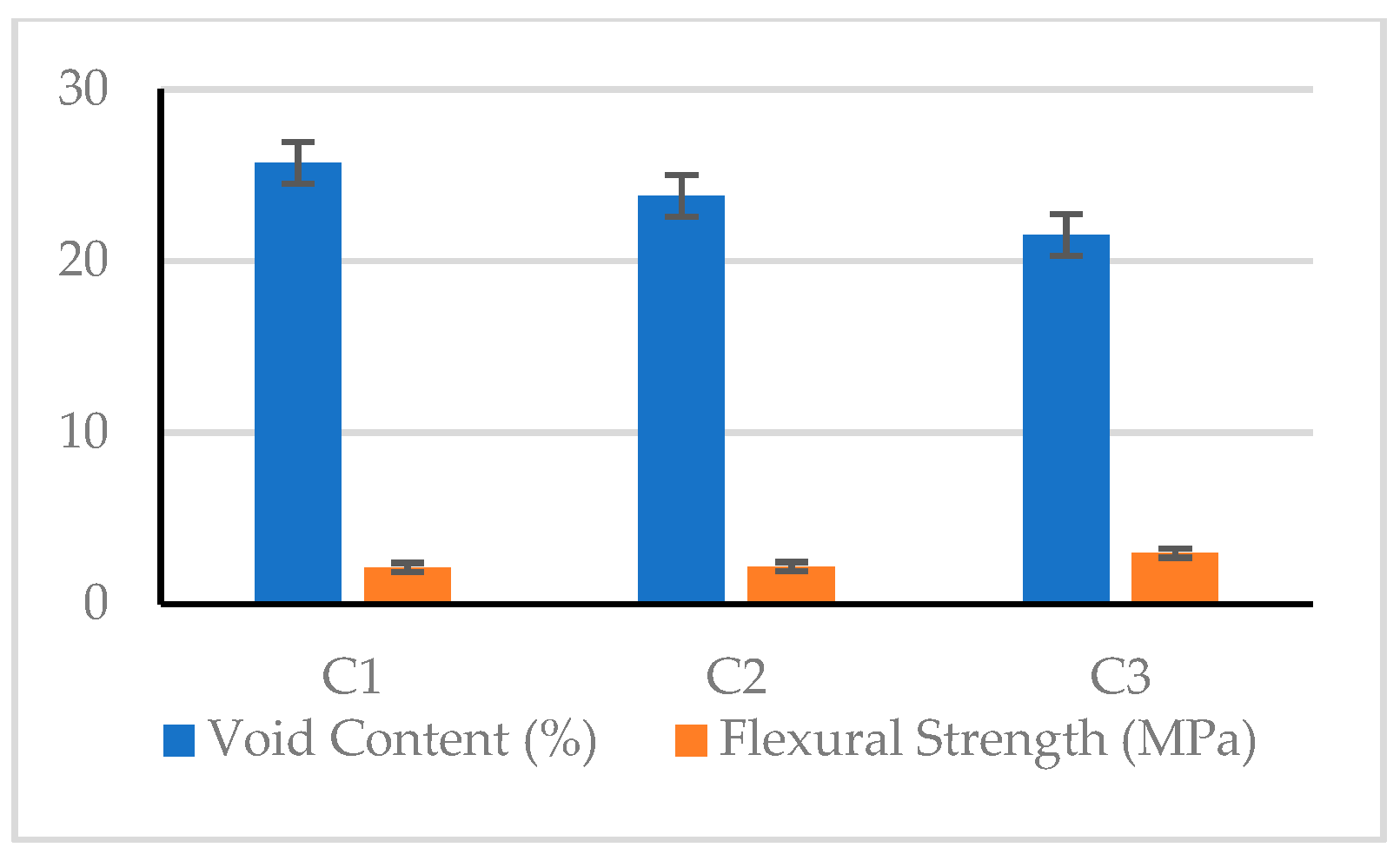
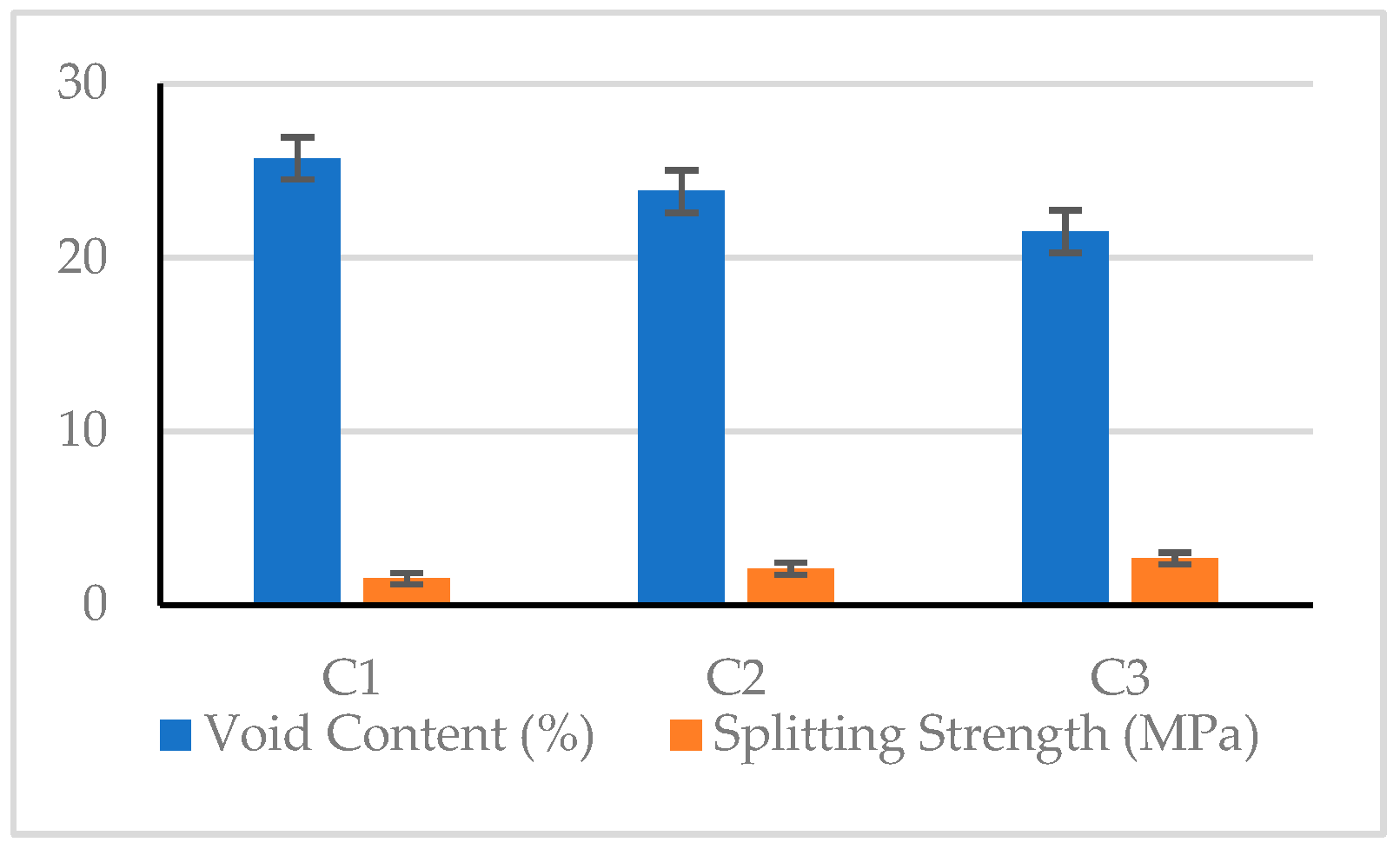
| C1 | 1507 | 25.7 | 24.2 | 10.5 | 9479.2 | 2.14 | 1.53 | 20.42 | 79.54 | 6.61 | 3.69 |
| C2 | 1581 | 23.8 | 23.1 | 11.0 | 13209.3 | 2.19 | 2.10 | 20.83 | 82.42 | 6.81 | 6.44 |
| C3 | 1654 | 21.5 | 22.1 | 21.3 | 29001.5 | 2.99 | 2.69 | 26.57 | 89.25 | 9.51 | 8.60 |
| C4 | 1544 | 24.8 | 23.6 | 12.2 | 15057.8 | 1.88 | 1.43 | 21.73 | 83.56 | 5.48 | 3.11 |
| C5 | 1602 | 23.1 | 22.8 | 14.6 | 18082.9 | 2.40 | 1.83 | 23.29 | 85.15 | 7.60 | 5.25 |
| C6 | 1684 | 21.0 | 21.8 | 15.5 | 15222.2 | 2.13 | 2.22 | 23.81 | 83.65 | 6.57 | 6.93 |
| C7 | 1556 | 24.2 | 23.3 | 13.0 | 13002.6 | 2.12 | 2.04 | 22.28 | 82.28 | 6.53 | 6.19 |
| C8 | 1635 | 22.3 | 22.4 | 17.9 | 17101.6 | 1.97 | 1.94 | 25.06 | 84.66 | 5.89 | 5.76 |
| C9 | 1708 | 20.6 | 21.6 | 10.1 | 15662.2 | 2.03 | 2.22 | 20.09 | 83.90 | 6.15 | 6.93 |
| Performance Parameter | Parameter (Experimental Control Factor) | Mean S/N Ratio (η, Unit: dB) | Delta (Max. η − Min. η) | Rank | ||
|---|---|---|---|---|---|---|
| Level 1 | Level 2 | Level 3 | ||||
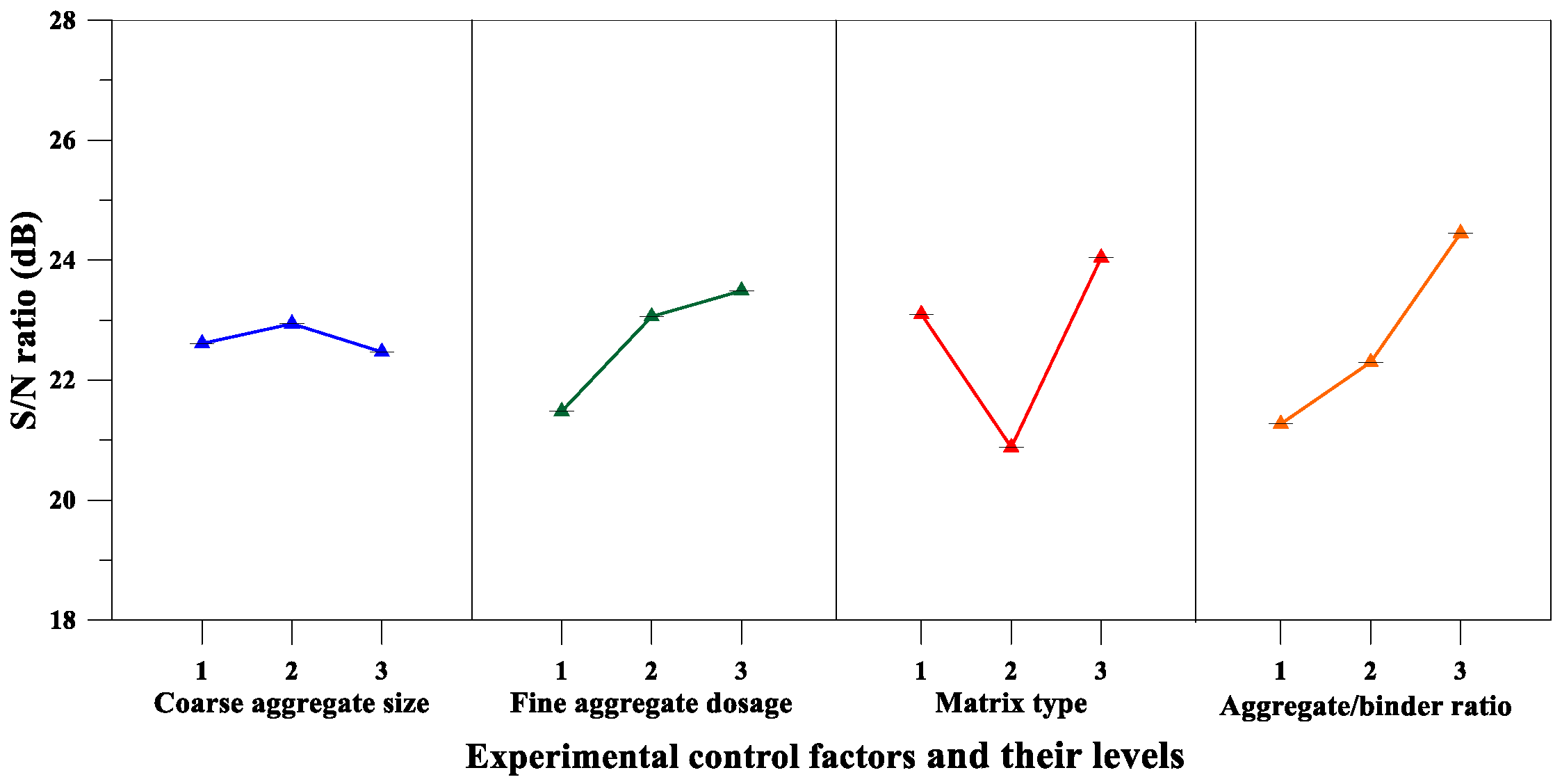
| Compressive Strength | Coarse Aggregate Size, A (mm) | 22.61 | 22.94 | 22.47 | 0.466 | 4 |
| Fine Aggregate Content, B (%) | 21.48 | 23.06 | 23.49 | 2.010 | 3 | |
| Matrix Type, C | 23.10 | 20.88 | 24.04 | 3.164 | 2 | |
| Aggregate-to-Binder Ratio, D | 21.27 | 22.30 | 24.45 | 3.185 | 1 | |
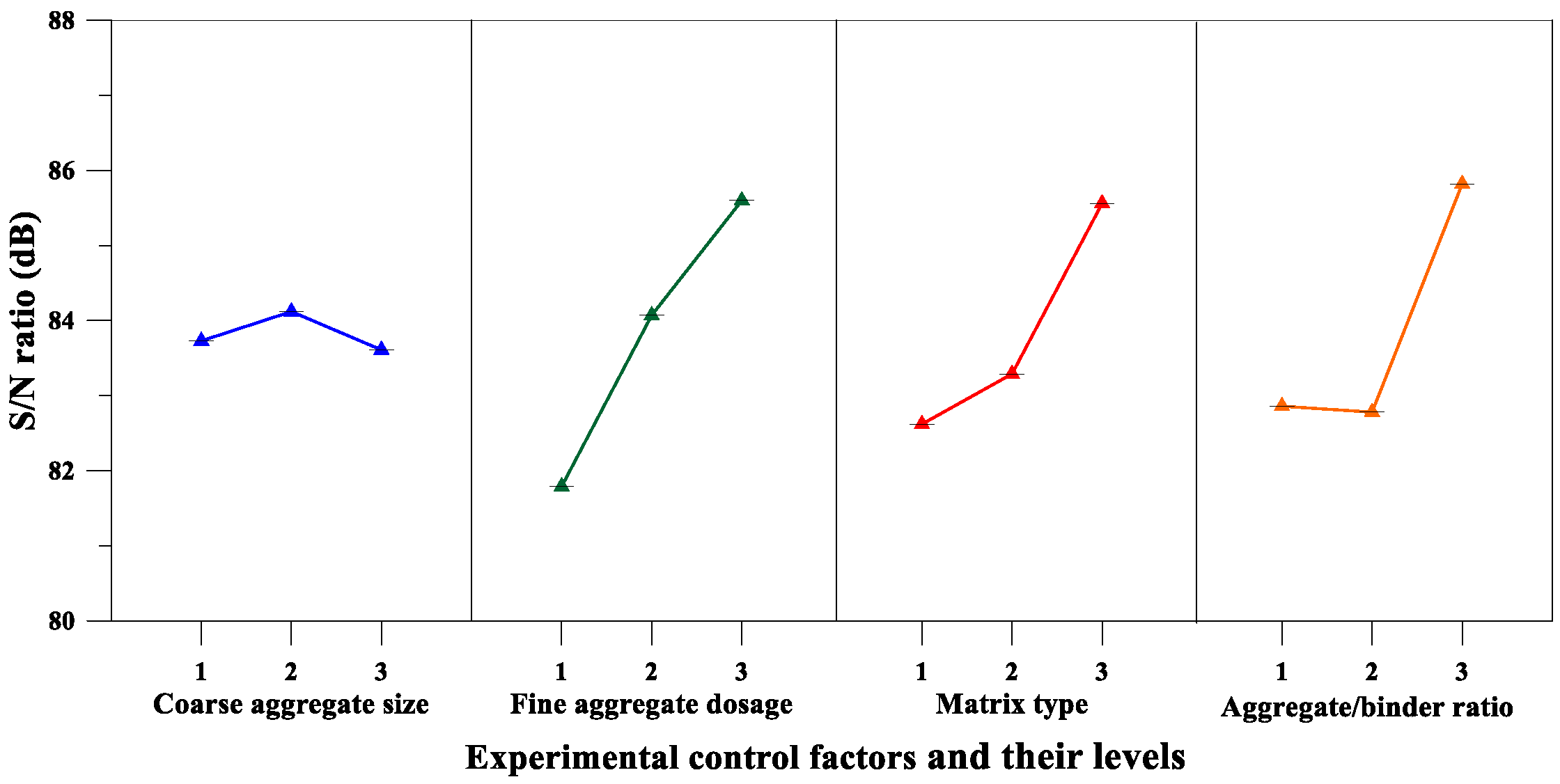
| Elastic Modulus | Coarse Aggregate Size, A (mm) | 83.73 | 84.12 | 83.61 | 0.504 | 4 |
| Fine Aggregate Content, B (%) | 81.79 | 84.07 | 85.60 | 3.808 | 1 | |
| Matrix Type, C | 82.62 | 83.29 | 85.56 | 2.943 | 3 | |
| Aggregate to Binder Ratio, D | 82.86 | 82.78 | 85.82 | 3.039 | 2 | |
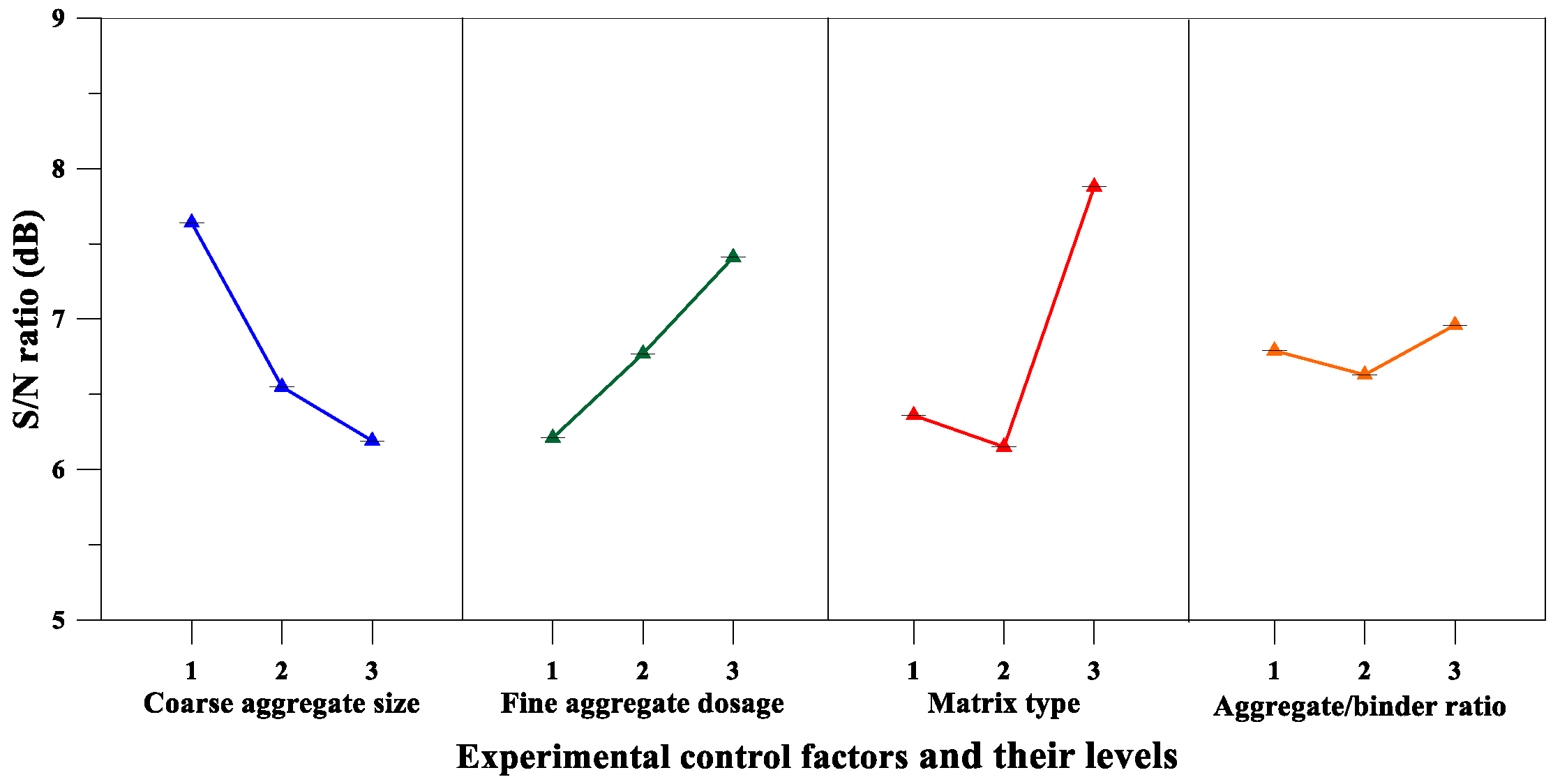
| Flexural Strength | Coarse Aggregate Size, A (mm) | 7.64 | 6.55 | 6.19 | 1.455 | 2 |
| Fine Aggregate Content, B (%) | 6.21 | 6.77 | 7.41 | 1.204 | 3 | |
| Matrix Type, C | 6.36 | 6.15 | 7.88 | 1.734 | 1 | |
| Aggregate-to-Binder Ratio, D | 6.79 | 6.63 | 6.96 | 0.328 | 4 | |
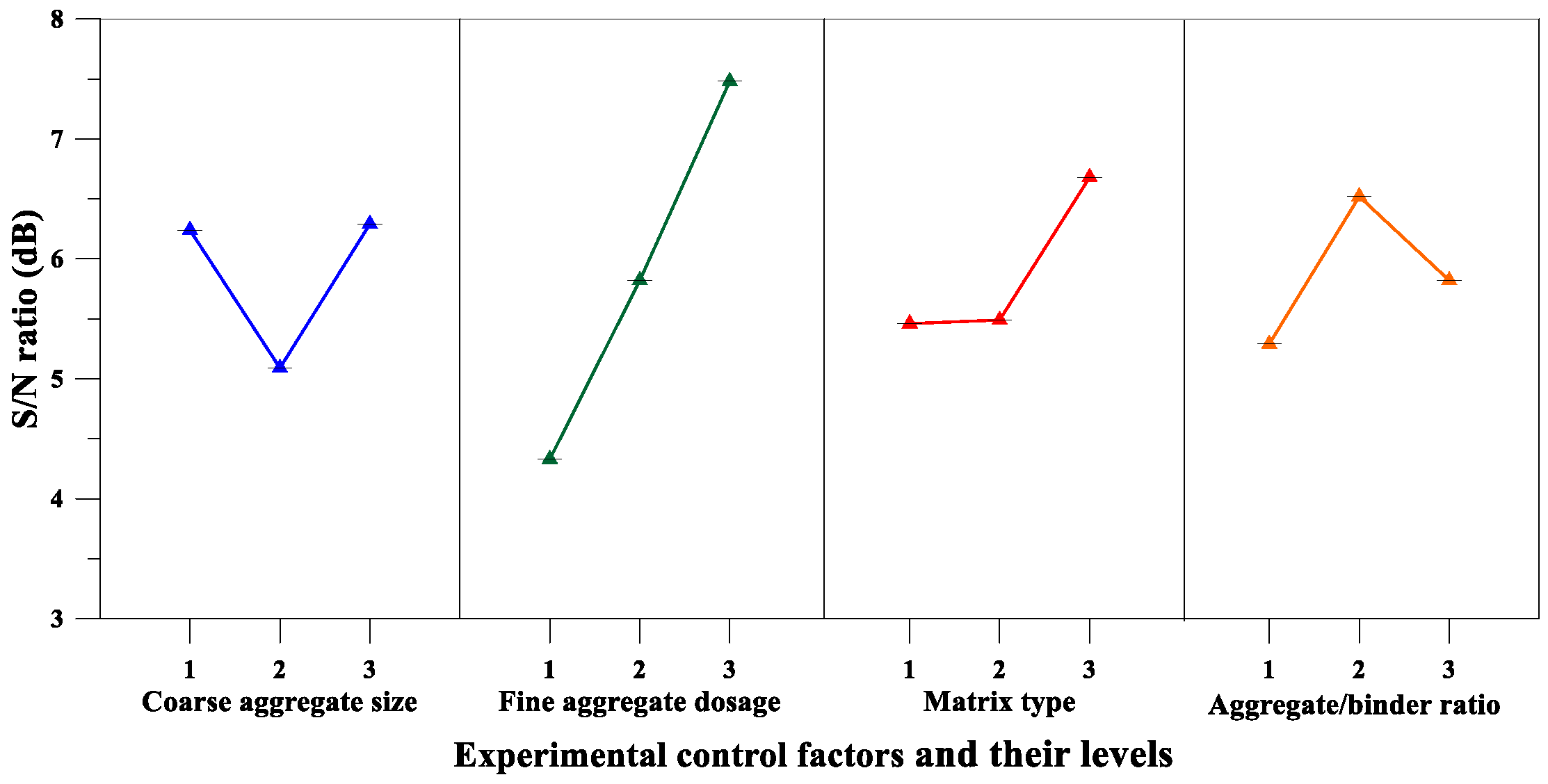
| Splitting Strength | Coarse Aggregate Size, A (mm) | 6.24 | 5.09 | 6.29 | 1.198 | 4 |
| Fine Aggregate Content, B (%) | 4.33 | 5.82 | 7.48 | 3.152 | 1 | |
| Matrix Type, C | 5.46 | 5.49 | 6.68 | 1.220 | 3 | |
| Aggregate-to-Binder Ratio, D | 5.29 | 6.52 | 5.82 | 1.231 | 2 | |
| Performance Parameter | Parameter (Experimental Control Factor) | Sum of Square (SSZ) | Degree of Freedom | Variance (MSZ) | F Value (FZ) | Percentage Contribution (PZ) |
|---|---|---|---|---|---|---|
| Compressive Strength | Coarse Aggregate Size, A (mm) | 0.35 | 3 | 0.12 | 1.00 | 0.00 |
| Fine Aggregate Content, B (%) | 6.72 | 3 | 2.24 | 19.42 | 16.47 | |
| Matrix Type, C | 15.82 | 3 | 5.27 | 45.68 | 43.54 | |
| Aggregate-to-Binder Ratio, D | 15.83 | 3 | 5.28 | 45.71 | 39.99 | |
| All Other/Error | 0.35 | 3 | 0.12 | – | – | |
| Total | 38.72 | 12 | 12.91 | – | 100.00 | |
| Elastic Modulus | Coarse Aggregate Size, A (mm) | 0.42 | 3 | 0.14 | 1.00 | 0.00 |
| Fine Aggregate Content, B (%) | 22.04 | 3 | 7.35 | 53.08 | 39.51 | |
| Matrix Type, C | 14.26 | 3 | 4.75 | 34.35 | 28.33 | |
| Aggregate-to-Binder Ratio, D | 18.02 | 3 | 6.01 | 43.39 | 32.16 | |
| All Other/Error | 0.42 | 3 | 0.14 | – | – | |
| Total | 54.73 | 12 | 18.24 | – | 100.00 | |
| Flexural Strength | Coarse Aggregate Size, A (mm) | 3.44 | 3 | 1.15 | 21.35 | 29.38 |
| Fine Aggregate Content, B (%) | 2.18 | 3 | 0.73 | 13.52 | 18.08 | |
| Matrix Type, C | 5.38 | 3 | 1.79 | 33.38 | 52.54 | |
| Aggregate-to-Binder Ratio, D | 0.16 | 3 | 0.05 | 1.00 | 0.00 | |
| All Other/Error | 0.16 | 3 | 0.05 | – | – | |
| Total | 11.16 | 12 | 3.72 | – | 100.00 | |
| Splitting Strength | Coarse Aggregate Size, A (mm) | 2.76 | 3 | 0.92 | 1.21 | 2.06 |
| Fine Aggregate Content, B (%) | 14.92 | 3 | 4.97 | 6.52 | 55.24 | |
| Matrix Type, C | 2.90 | 3 | 0.97 | 1.27 | 42.71 | |
| Aggregate-to-Binder Ratio, D | 2.29 | 3 | 0.76 | 1.00 | 0.00 | |
| All Other/Error | 2.29 | 3 | 0.76 | – | – | |
| Total | 22.86 | 12 | 7.62 | – | 100.00 |
| Performance Parameter | Initial Combination | Test Results (MPa) | Optimal Combination | Test Results (MPa) |
|---|---|---|---|---|
| Compressive Strength | A1B3C3D3 | 21.3 | A2B3C3D3 | 22.1 |
| Elastic Modulus | A1B3C3D3 | 29001.5 | A2B3C3D3 | 29843.2 |
| Flexural Strength | A1B3C3D3 | 2.99 | A1B3C3D3 | 3.02 |
| Splitting Strength | A1B3C3D3 | 2.69 | A3B3C3D2 | 2.75 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, C.-W.; Cheng, C.-K.; Tsai, C.-Y. Mix Design and Mechanical Properties of High-Performance Pervious Concrete. Materials 2019, 12, 2577. https://doi.org/10.3390/ma12162577
Tang C-W, Cheng C-K, Tsai C-Y. Mix Design and Mechanical Properties of High-Performance Pervious Concrete. Materials. 2019; 12(16):2577. https://doi.org/10.3390/ma12162577
Chicago/Turabian StyleTang, Chao-Wei, Chiu-Kuei Cheng, and Ching-Yuan Tsai. 2019. "Mix Design and Mechanical Properties of High-Performance Pervious Concrete" Materials 12, no. 16: 2577. https://doi.org/10.3390/ma12162577
APA StyleTang, C.-W., Cheng, C.-K., & Tsai, C.-Y. (2019). Mix Design and Mechanical Properties of High-Performance Pervious Concrete. Materials, 12(16), 2577. https://doi.org/10.3390/ma12162577






