Interfacial Stress Analysis of Adhesively Bonded Lap Joint
Abstract
1. Introduction
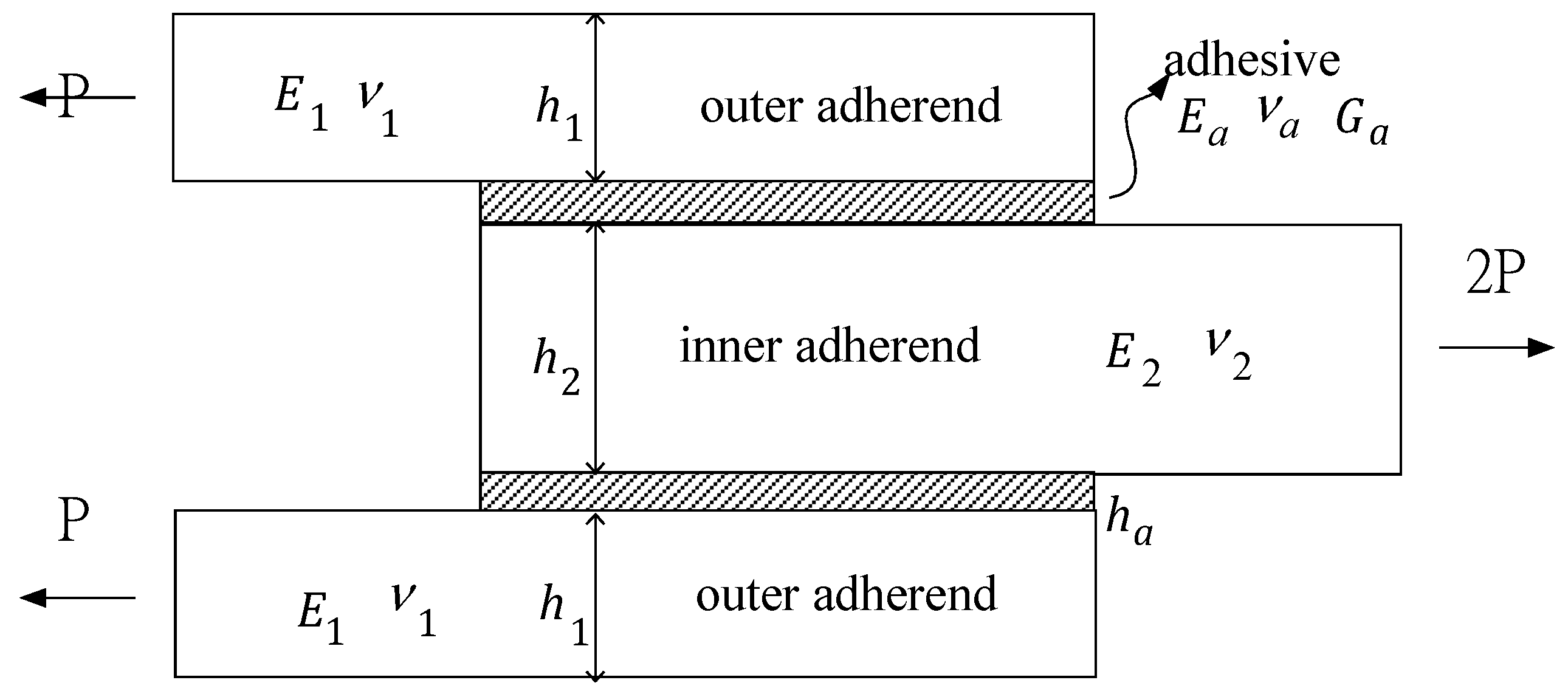
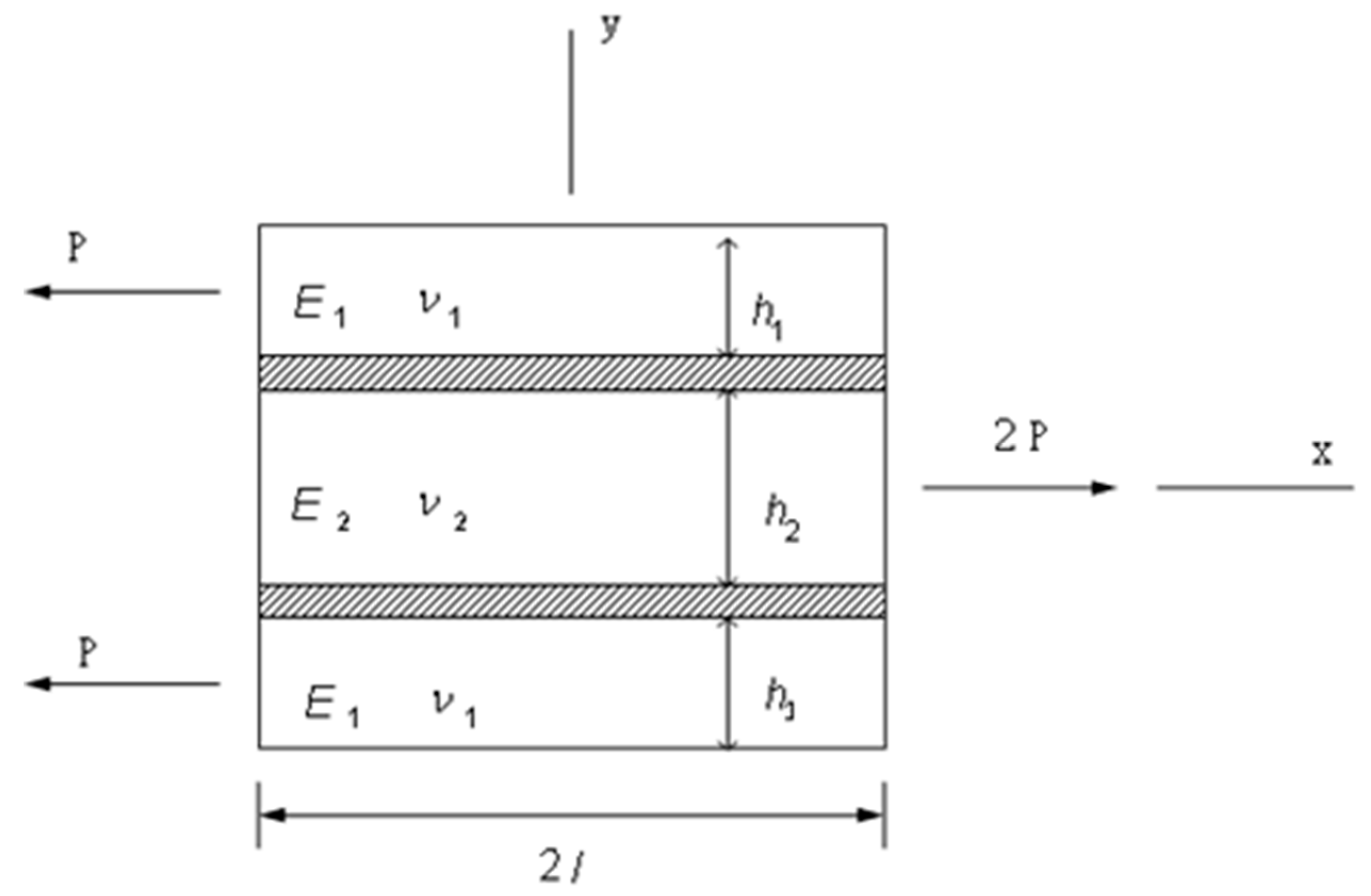
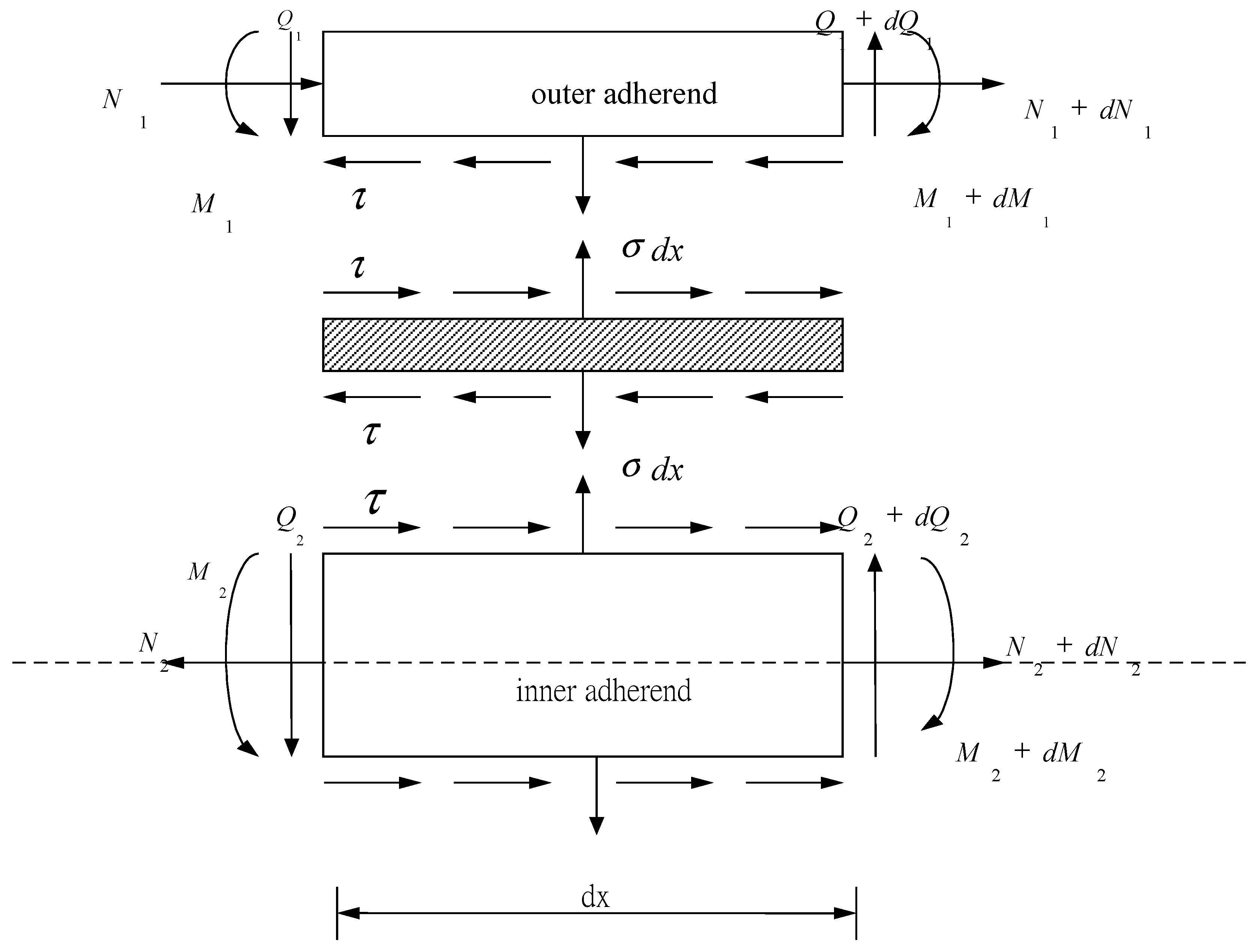
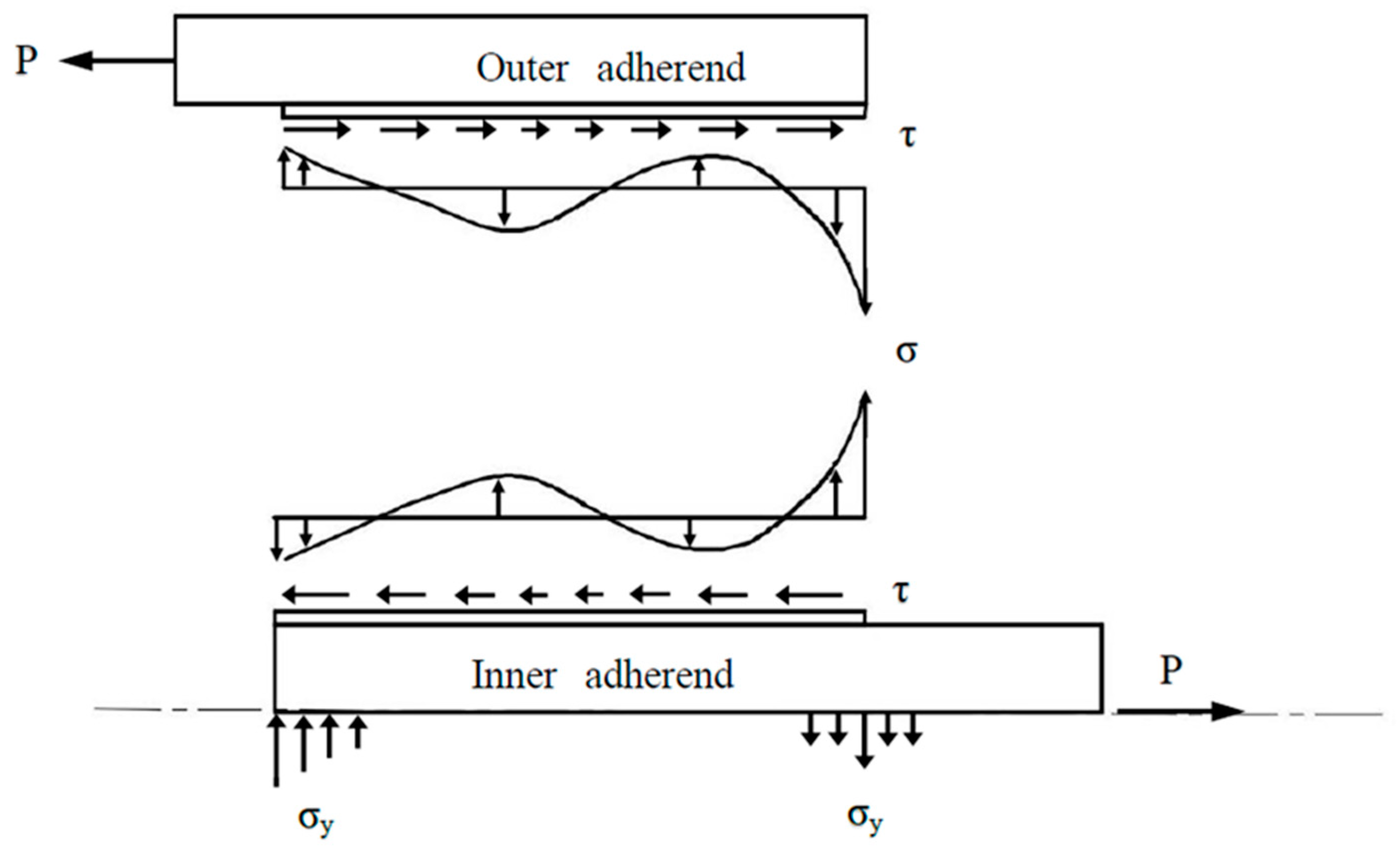
2. Stress Analysis of Double Lap Joint
3. Boundary Conditions
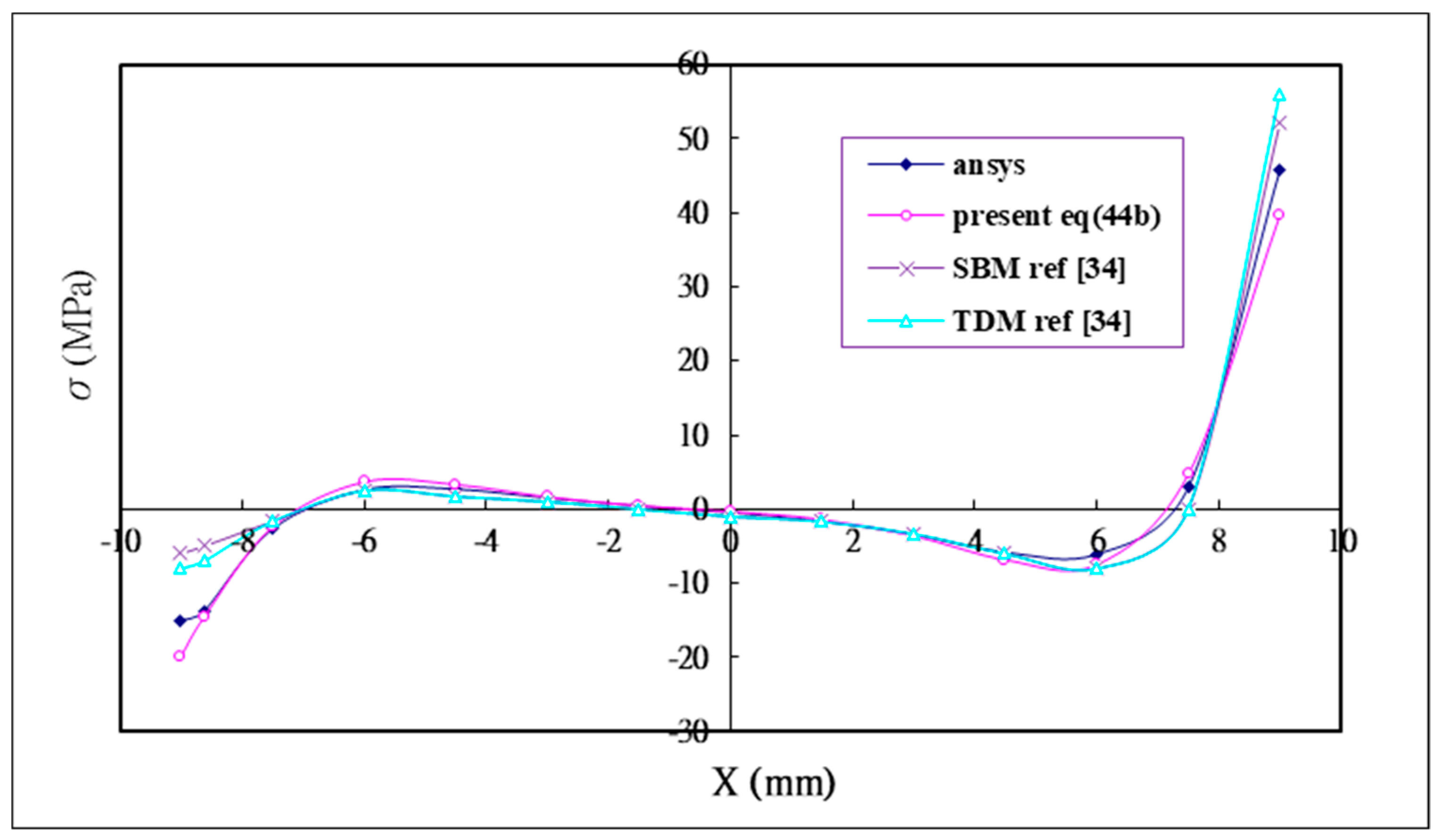
4. Verification
5. Parametric Study
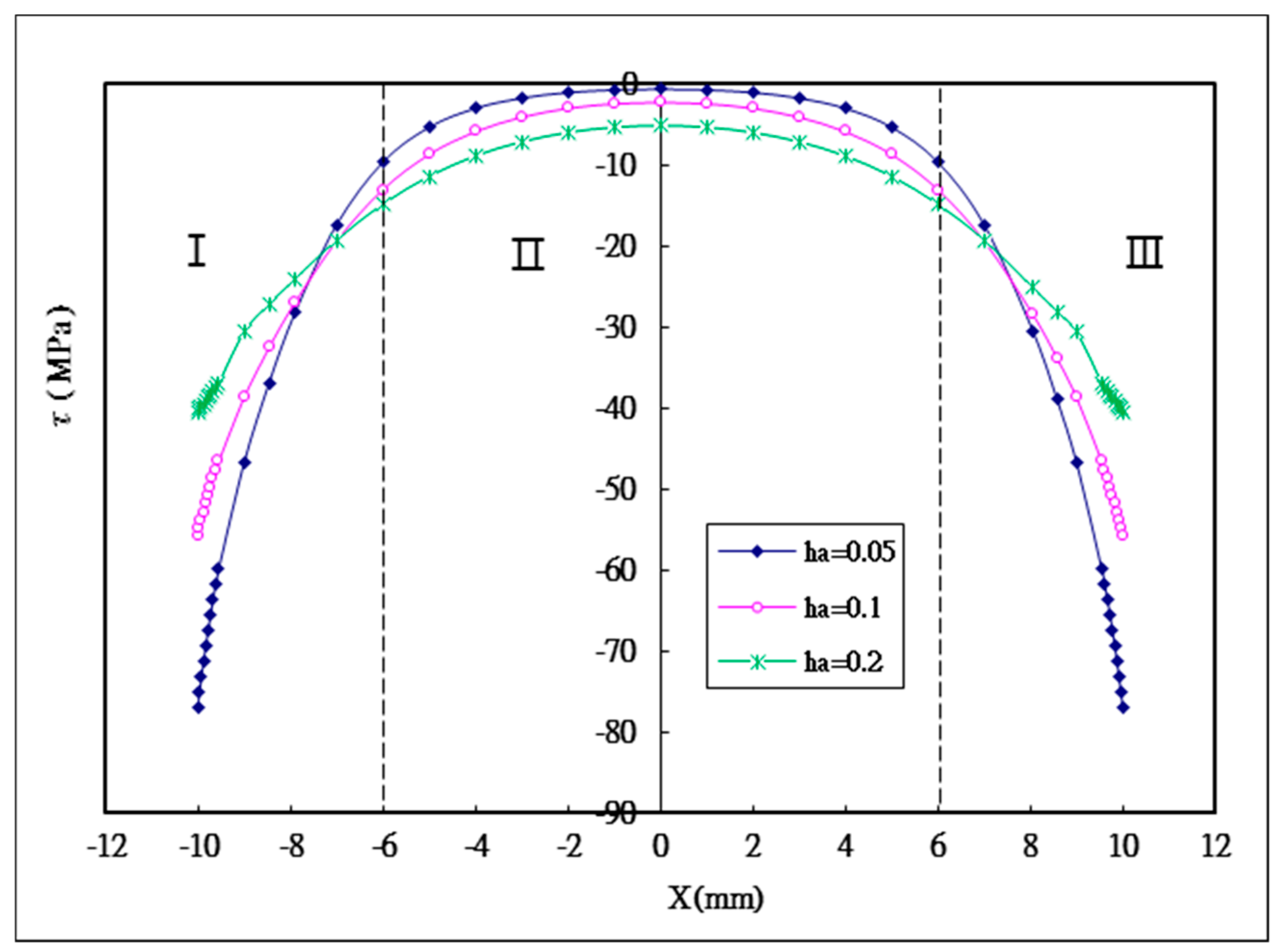
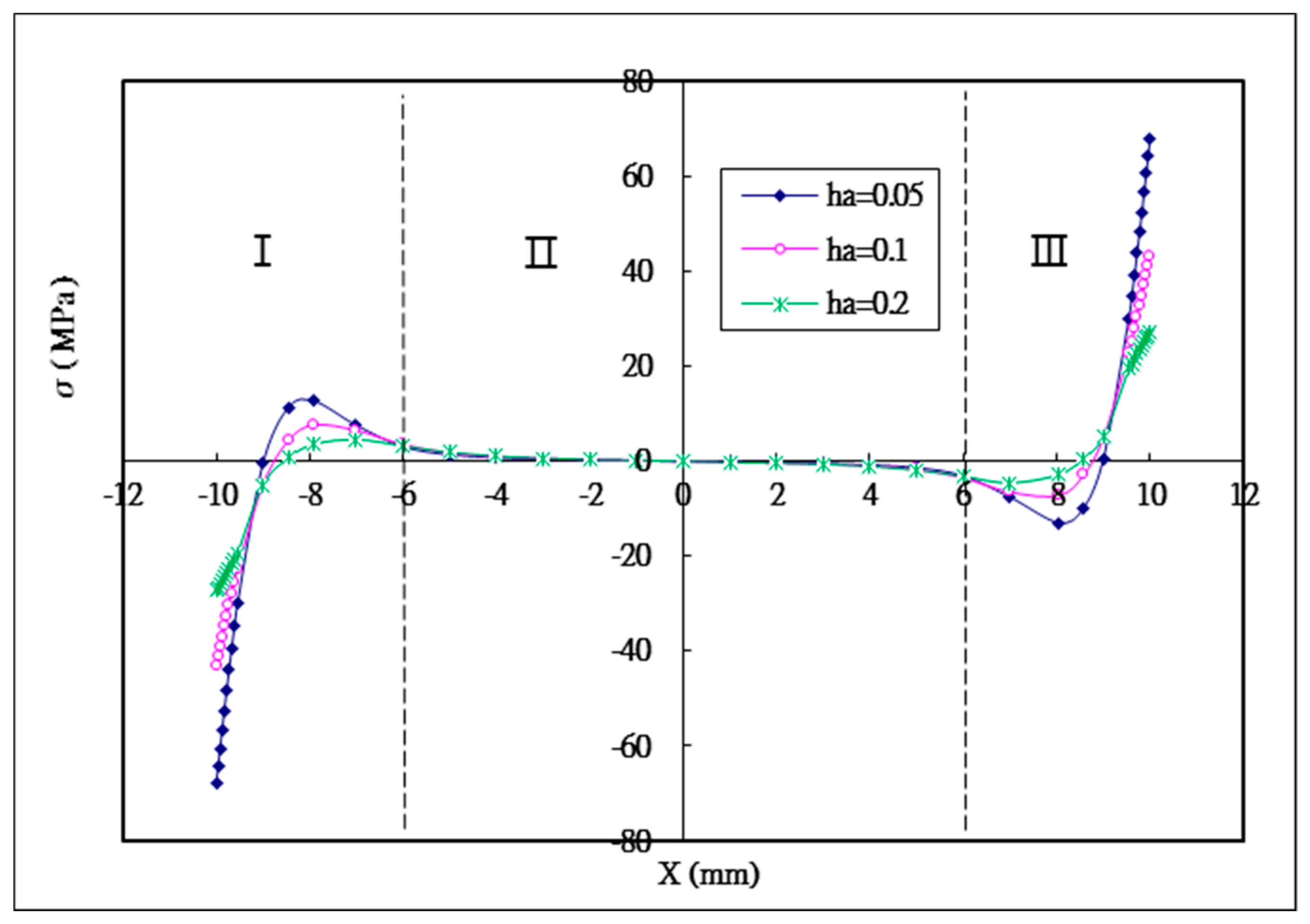
5.1. The Effect of the Thickness of the Adhesive
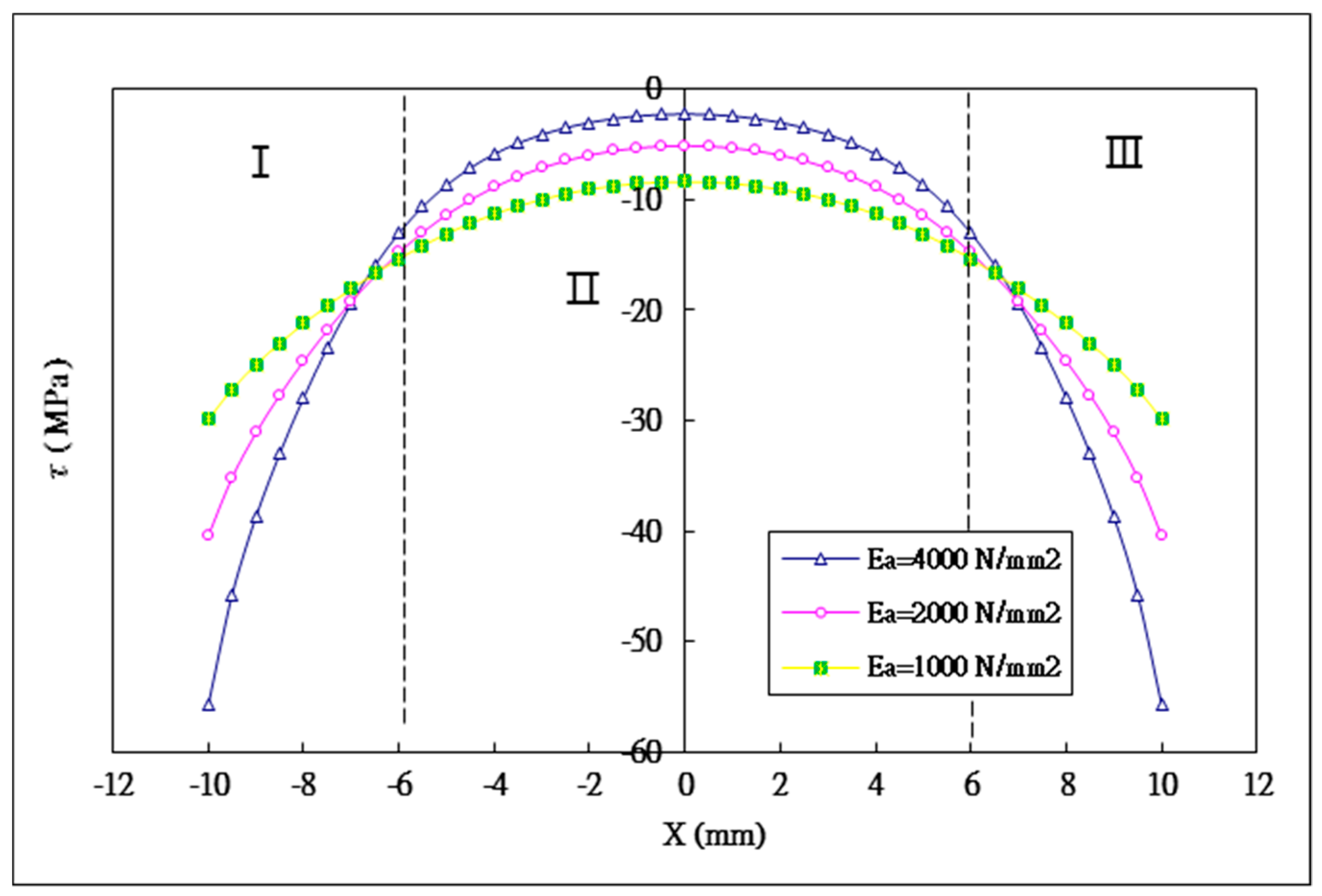
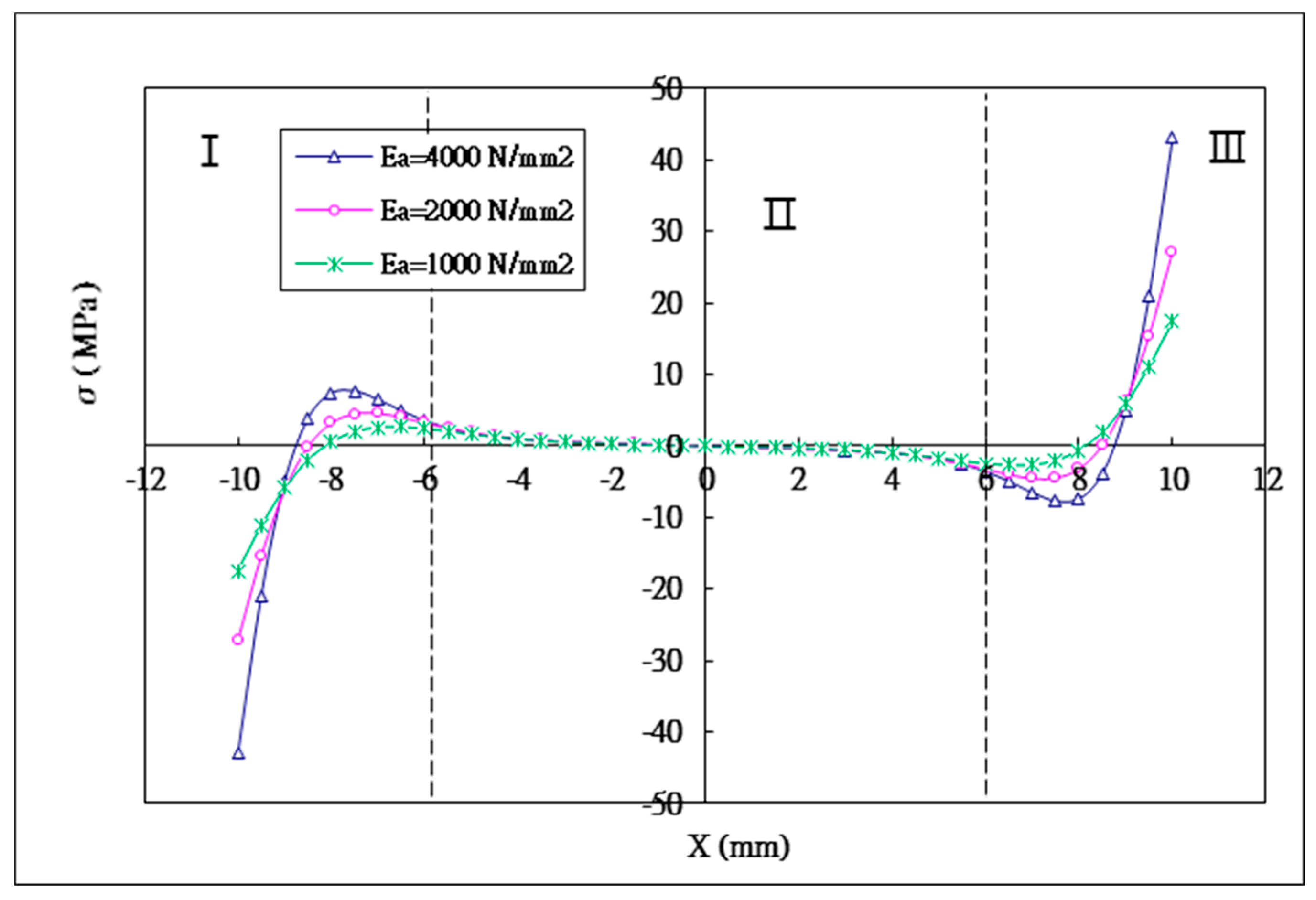
5.2. The Effect of the Young’s Modulus of the Adhesive
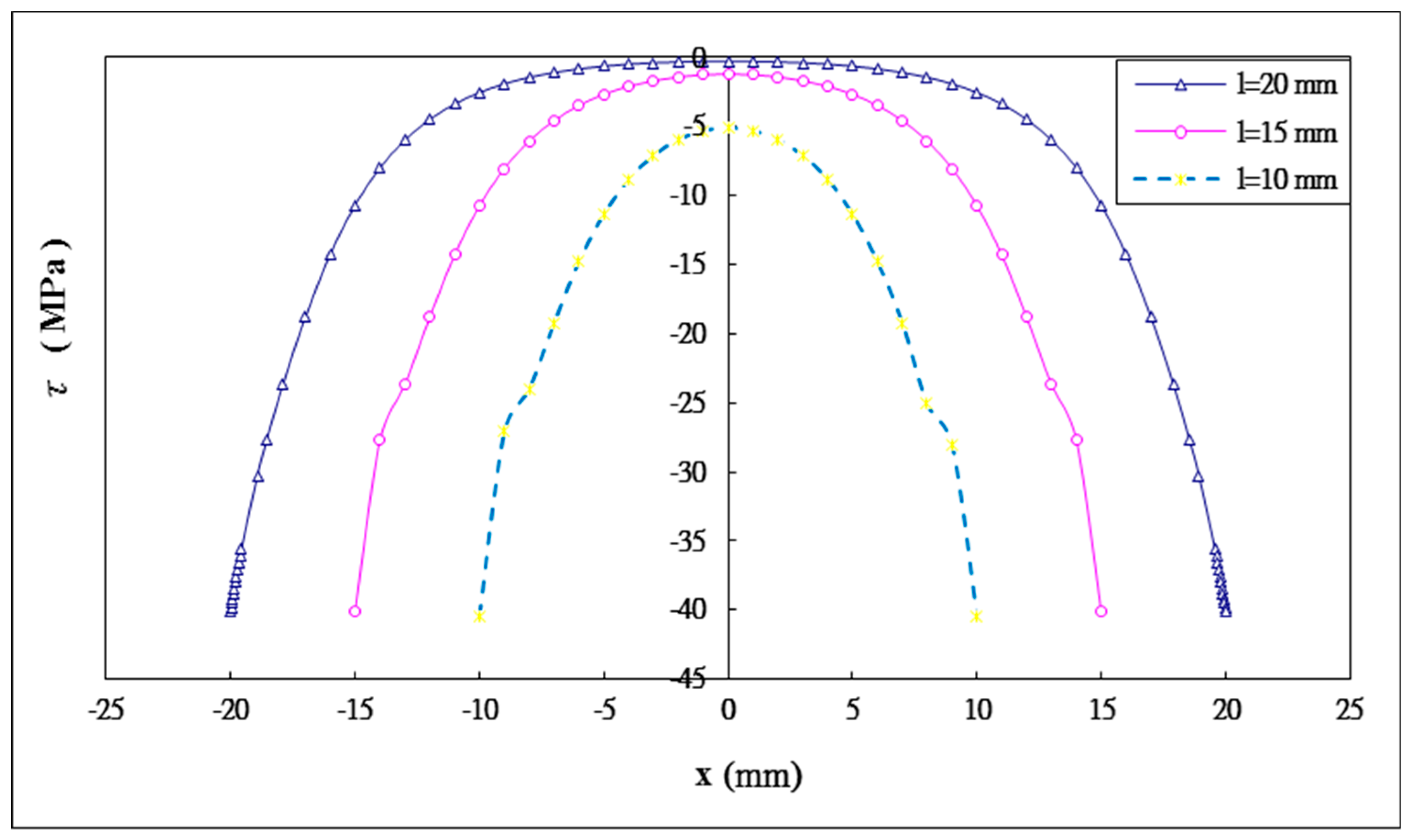
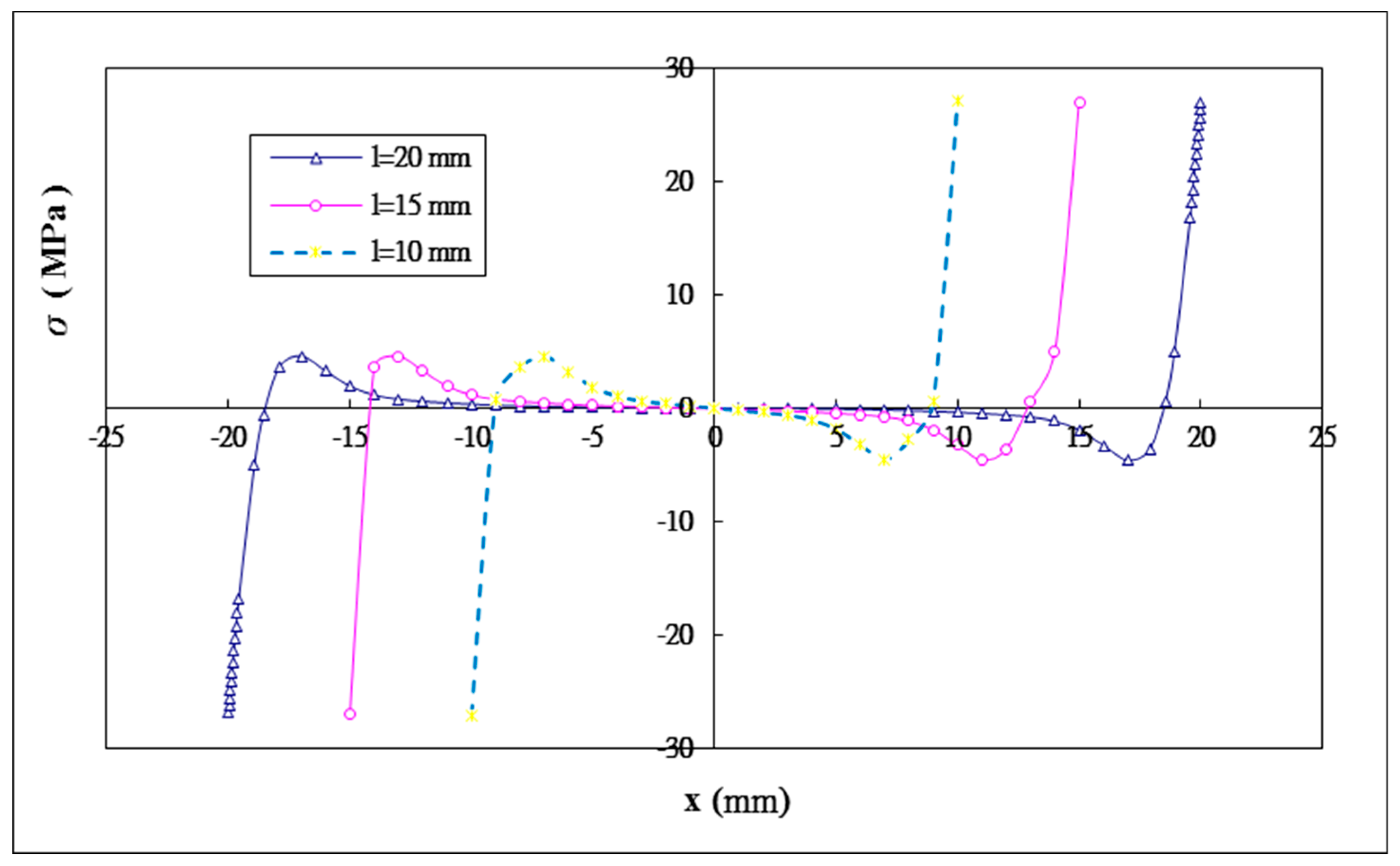
5.3. The Effect of the Bonding Length
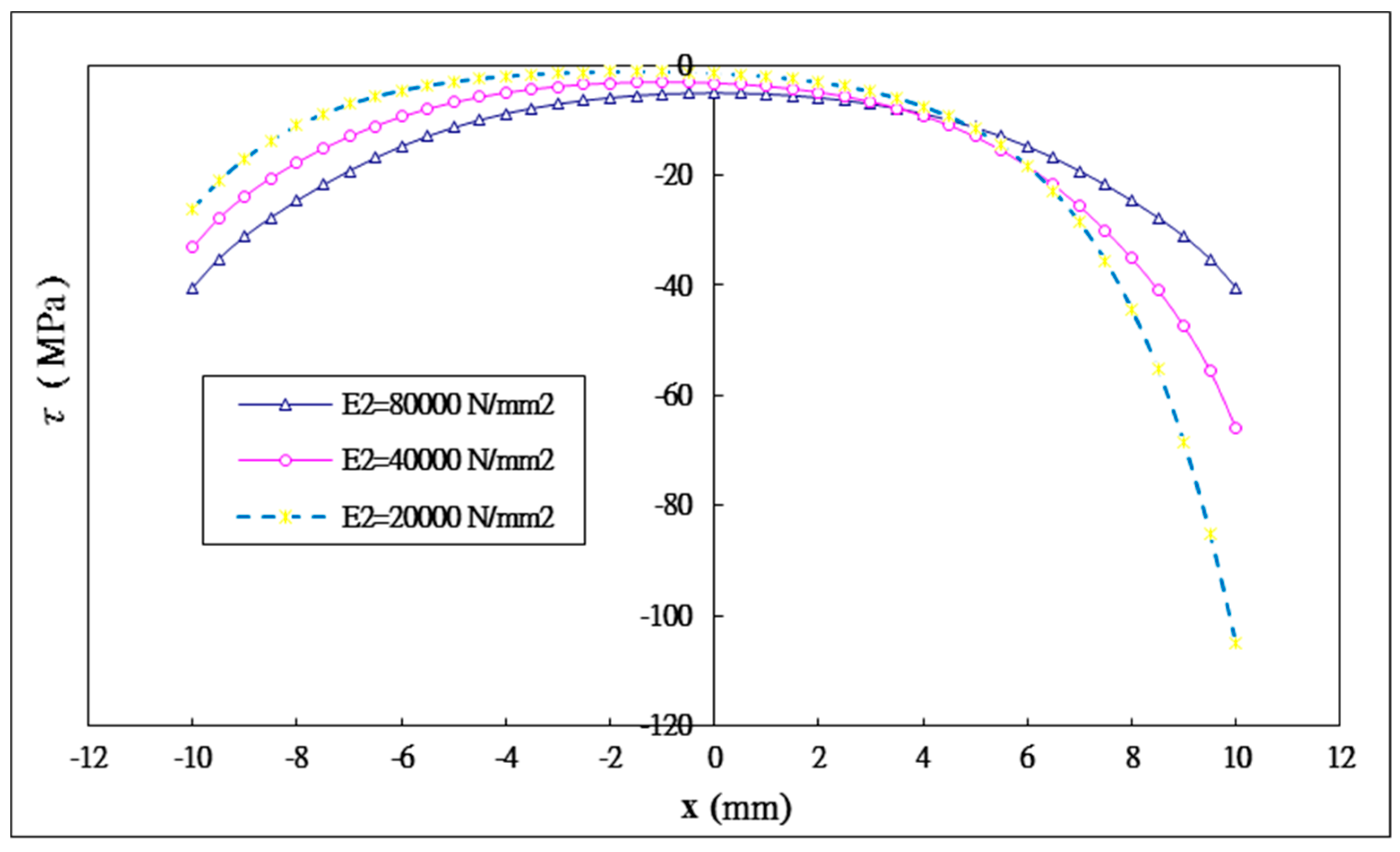
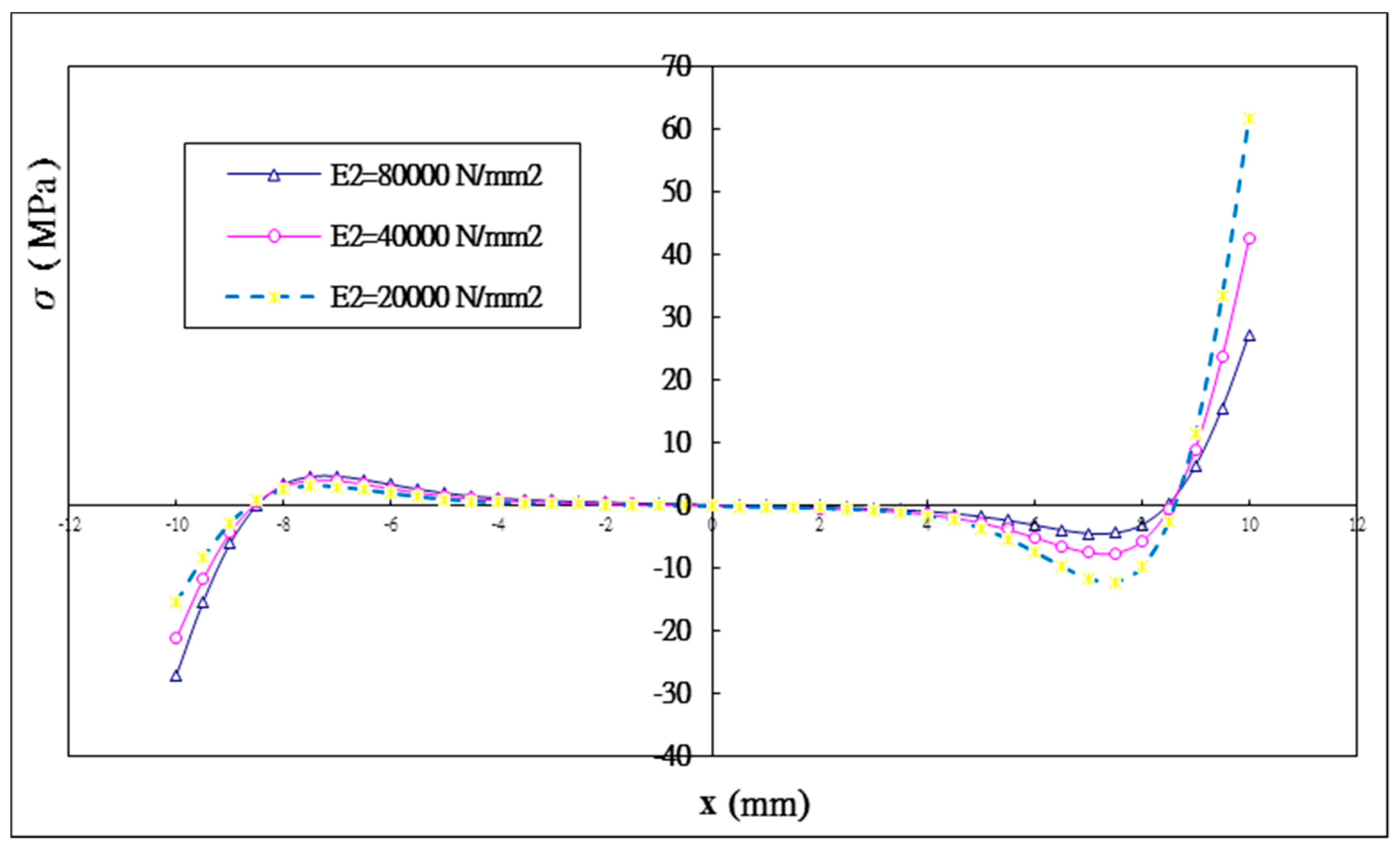
5.4. The Effect of the Young’s Modulus of the Inner Adherend
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mortensen, F.; Thomsen, O.T. Coupling effects in adhesive bonded joints. Compos. Struct. 2002, 56, 165–174. [Google Scholar] [CrossRef]
- Campilho, R.D.S.G.; Fernandes, T.A.B. Comparative evaluation of single-lap joints bonded with different adhesives by cohesive zone modeling. Procedia Eng. 2015, 114, 102–109. [Google Scholar] [CrossRef]
- Santos, T.F.; Campilho, R.D.S.G. Numerical modelling of adhesively-bonded double-lap joints by the eXtended Finite Element Method. Finite Elem. Anal. Des. 2017, 133, 1–9. [Google Scholar] [CrossRef]
- Fernandes, T.A.B.; Campilho, R.D.S.G.; Banea, M.D.; da Silva, L.F.M. Adhesive selection for single lap bonded joints: Experimentation and advanced techniques for strength prediction. J. Adhes. 2015, 91, 841–862. [Google Scholar] [CrossRef]
- Zhao, B.; Lu, Z.-H.; Lu, Y.-N. Two-dimensional analytical solution of elastic stresses for balanced single-lap joints—Variational method. Int. J. Adhes. Adhes. 2014, 49, 115–126. [Google Scholar] [CrossRef]
- Shishesaz, M.; Bavi, N. Shear stress distribution in adhesive layers of a double-lap joint with void or bond separation. J. Adhes. Sci. Technol. 2013, 27, 1197–1225. [Google Scholar] [CrossRef]
- Liao, L.; Sawa, T.; Huang, C. Numerical analysis on load-bearing capacity and damage of double scarf adhesive joints subjected to combined loadings of tension and bending. Int. J. Adhes. Adhes. 2014, 53, 65–71. [Google Scholar] [CrossRef][Green Version]
- Grant, L.D.R.; Adams, R.D.; da Silva, L.F.M. Experimental and numerical analysis of single lap joints for the automotive industry. Int. J. Adhes. Adhes. 2009, 29, 405–413. [Google Scholar] [CrossRef]
- Higgins, A. Adhesive bonding of aircraft structures. Int. J. Adhes. Adhes. 2000, 20, 367–376. [Google Scholar] [CrossRef]
- Akpinar, S. The strength of the adhesively bonded step-lap joints for different step numbers. Compos. Part B 2014, 67, 170–178. [Google Scholar] [CrossRef]
- Volkersen, O. Die Nietkraftverteilung in Zugbeanspruchten Nietverbindungen mit Konstanten Laschenquerschnitten. Luftfahrtforschung 1938, 15, 41–47. [Google Scholar]
- Goland, M.; Reissner, E. The stresses in cemented joints. J. Appl. Mech. 1944, 11, A17–A27. [Google Scholar]
- Hart-Smith, L.J. Joints Adhesive-bonded Double-lap joints. NASA Contractor Rep. 1973, 112235. [Google Scholar]
- Klarbring, A.; Movchan, A.B. Asymptotic modelling of adhesive joints. Mech. Mater. 1998, 28, 137–145. [Google Scholar] [CrossRef]
- Raous, M.; Cangemi, L.; Cocu, M. A consistent model coupling adhesion, friction, and unilateral contact. Comput. Methods Appl. Mech. Eng. 1999, 177, 383–399. [Google Scholar] [CrossRef]
- Yousefsani, S.A.; Tahani, M. Analytical solutions for adhesively bonded composite single-lap joints under mechanical loadings using full layerwise theory. Int. J. Adhes. Adhes. 2013, 43, 32–41. [Google Scholar] [CrossRef]
- Wu, X.F.; Zhao, Y. Stress-function variational method for interfacial stress analysis of adhesively bonded joints. Int. J. Solids Struct. 2013, 50, 4305–4319. [Google Scholar] [CrossRef]
- Fernlund, G. Stress analysis of bonded lap joints using fracture mechanics and energy balance. Int. J. Adhes. Adhes. 2007, 27, 584–592. [Google Scholar] [CrossRef]
- Oplinger, D.W. Effects of adherend deflection on single lap joints. Int. J. Solids Struct. 1994, 31, 2565–2587. [Google Scholar] [CrossRef]
- Tsai, M.Y.; Oplinger, D.W.; Morton, J. Improved theoretical solutions for adhesive lap joints. Int. J. Solids Struct. 1998, 35, 1163–1185. [Google Scholar] [CrossRef]
- Her, S.C. Stress analysis of adhesively-bonded lap joints. Compos. Struct. 1999, 47, 673–678. [Google Scholar] [CrossRef]
- He, X. A review of finite element analysis of adhesively bonded joints. Int. J. Adhes. Adhes. 2011, 31, 248–264. [Google Scholar] [CrossRef]
- Mokhtari, M.; Madani, K.; Belhouari, M.; Touzain, S.; Feaugas, X.; Ratwani, M. Effects of composite adherend properties on stresses in double lap bonded joints. Mater. Des. 2013, 44, 633–639. [Google Scholar] [CrossRef]
- Stuparu, F.A.; Apostol, D.A.; Constantinescu, D.M.; Picu, C.R.; Sandu, M.; Sorohan, S. Cohesive and XFEM evaluation of adhesive failure for dissimilar single-lap joint. Struct. Integr. Procedia 2016, 2, 316–325. [Google Scholar] [CrossRef]
- Moya-Sanz, E.M.; Ivañez, I.; Garcia-Castillo, S.K. Effect of the geometry in the strength of single-lap adhesive joints of composite laminates under uniaxial tensile load. Int. J. Adhes. Adhes. 2017, 72, 23–29. [Google Scholar] [CrossRef]
- Hou, X.; Kanani, A.Y.; Ye, J. Double lap adhesive joint with reduced stress concentration: Effect of slot. Compos. Struct. 2018, 202, 635–642. [Google Scholar] [CrossRef]
- Panigrahi, S.K.; Pradhan, B. Onset and growth of adhesion failure and delamination induced damages in double lap joint of laminated FRP composites. Compos. Struct. 2008, 85, 326–336. [Google Scholar] [CrossRef]
- Khan, M.A.; Aglietti, G.S.; Crocombe, A.D.; Viquerat, A.D.; Hamar, C.O. Development of design allowables for the design of composite bonded double-lap joints in aerospace applications. Int. J. Adhes. Adhes. 2018, 82, 221–232. [Google Scholar] [CrossRef]
- Ozel, A.; Yazici, B.; Akpinar, S.; Aydin, M.D.; Temiz, S. A study on the strength of adhesively bonded joints with different adherends. Compos. Part B 2014, 62, 167–174. [Google Scholar] [CrossRef]
- Tsai, M.Y.; Morton, J. An investigation into the stresses in double-lap adhesive joints with laminated composite adherends. Int. J. Solids Struct. 2010, 47, 3317–3325. [Google Scholar] [CrossRef]
- Neto, J.A.B.P.; Campilho, R.D.S.G.; da Silva, L.F.M. Parametric study of adhesive joints with composites. Int. J. Adhes. Adhes. 2012, 37, 96–101. [Google Scholar] [CrossRef]
- Akhavan-Safar, A.; Ayatollahi, M.R.; da Silva, L.F.M. Strength prediction of adhesively bonded single lap joints with different bondline thicknesses: A critical longitudinal strain approach. Int. J. Solids Struct. 2017, 109, 189–198. [Google Scholar] [CrossRef]
- Gultekin, K.; Akpinar, S.; Ozel, A. The effect of the adherend width on the strength of adhesively bonded single-lap joint: Experimental and numerical analysis. Compos. Part B 2014, 60, 736–745. [Google Scholar] [CrossRef]
- Wu, G.; Crocombe, A.D. Simplified Finite Element Modelling of Structural Adhesive Joints. Comput. Struct. 1994, 61, 385–391. [Google Scholar] [CrossRef]
- Yousefsani, S.A.; Tahani, M. Edge effects in adhesively bonded composite joints integrated with piezoelectric patches. Compos. Struct. 2018, 200, 187–194. [Google Scholar] [CrossRef]
- Radice, J.; Vinson, J. On the use of quasi-dynamic modeling for composite material structures: Analysis of adhesively bonded joints with midplane asymmetry and transverse shear deformation. Compos. Sci. Technol. 2006, 66, 2528–2547. [Google Scholar] [CrossRef]
- Taib, A.A.; Boukhili, R.; Achiou, S.; Boukehili, H. Bonded joints with composite adherends. Part II. Finite element analysis of joggle lap joints. Int. J. Adhes. Adhes. 2006, 26, 237–248. [Google Scholar] [CrossRef]
- Nemes, O.; Lachaud, F. Double-lap adhesive bonded-joints assemblies modeling. Int. J. Adhes. Adhes. 2010, 30, 288–297. [Google Scholar] [CrossRef]
- Diaz Diaz, A.; Hadj-Ahmed, R.; Foret, G.; Ehrlacher, A. Stress analysis in a classical double lap, adhesively bonded joint with a layerwise model. Int. J. Adhes. Adhes. 2009, 29, 67–76. [Google Scholar] [CrossRef]
- Yousefsani, S.A.; Tahani, M. Accurate determination of stress distributions in adhesively bonded homogeneous and heterogeneous double-lap joints. Eur. J. Mech. A Solids 2013, 39, 197–208. [Google Scholar] [CrossRef]
- Adams, R.D.; Peppiatt, N.A. Stress Analysis of Adhesive-Bonded Lap Joints. J. Strain Anal. 1974, 9, 185–196. [Google Scholar] [CrossRef]


| Outer Adherend | Inner Adherend | Adhesive | |
|---|---|---|---|
| Young’s modulus | 70 GPa | 70 GPa | 2.1 GPa |
| Poisson ratio | 0.3 | 0.3 | 0.4 |
| Thickness | 2 mm | 2 mm | 0.1 mm |
| Outer Adherend | Inner Adherend | Adhesive | |
|---|---|---|---|
| Young’s modulus | 80 GPa | 80 GPa | 2 GPa |
| Poisson ratio | 0.3 | 0.3 | 0.4 |
| Thickness | 1 mm | 2 mm | 0.2 mm |
| Bonding length | 20 mm | 20 mm | 20 mm |
| Adhesive Thickness | Maximum Shear Stress (MPa) | Maximum Peeling Stress (MPa) | ||||
|---|---|---|---|---|---|---|
| Equation (44a) | ANSYS | Difference | Equation (44b) | ANSYS | Difference | |
| 0.05 mm | −77.0 | −70.4 | 8.57% | 68.0 | 76.0 | −11.76% |
| 0.1 mm | −55.7 | −54.1 | 2.87% | 43.0 | 45.1 | −4.88% |
| 0.2 mm | −40.4 | −39.1 | 3.22% | 27.1 | 29.2 | −7.75% |
| Adhesive Young’s Modulus | Maximum Shear Stress (MPa) | Maximum Peeling Stress (MPa) | ||||
|---|---|---|---|---|---|---|
| Equation (44a) | ANSYS | Difference | Equation (44b) | ANSYS | Difference | |
| 1 GPa | −29.9 | −29.8 | 0.33% | 17.4 | 19.4 | −11.49% |
| 2 GPa | −40.4 | −39.1 | 3.21% | 27.1 | 29.2 | −7.75% |
| 4 GPa | −55.7 | −51.6 | 7.36% | 43.1 | 44.8 | −3.94% |
| Bonding Length | Maximum Shear Stress (MPa) | Maximum Peeling Stress (MPa) | ||||
|---|---|---|---|---|---|---|
| Equation (44a) | ANSYS | Difference | Equation (44b) | ANSYS | Difference | |
| 20 mm | −40.13 | −38.8 | 3.31% | 26.93 | 8.9 | −7.32% |
| 30 mm | −40.15 | −38.8 | 3.36% | 26.94 | 29.0 | −7.65% |
| 40 mm | −40.41 | −39.1 | 3.24% | 27.14 | 29.2 | −7.59% |
| Inner Adherend Young’s Modulus | Maximum Shear Stress (MPa) | Maximum Peeling Stress (MPa) | ||||
|---|---|---|---|---|---|---|
| Equation (44a) | ANSYS | Difference | Equation (44b) | ANSYS | Difference | |
| 20 GPa | −105.1 | −95.1 | 9.51% | 59.4 | 61.7 | −3.87% |
| 40 GPa | −65.9 | −62.7 | 4.86% | 42.3 | 43.8 | −3.55% |
| 80 GPa | −40.4 | −39.1 | 3.22% | 27.1 | 29.2 | −7.75% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Her, S.-C.; Chan, C.-F. Interfacial Stress Analysis of Adhesively Bonded Lap Joint. Materials 2019, 12, 2403. https://doi.org/10.3390/ma12152403
Her S-C, Chan C-F. Interfacial Stress Analysis of Adhesively Bonded Lap Joint. Materials. 2019; 12(15):2403. https://doi.org/10.3390/ma12152403
Chicago/Turabian StyleHer, Shiuh-Chuan, and Cheng-Feng Chan. 2019. "Interfacial Stress Analysis of Adhesively Bonded Lap Joint" Materials 12, no. 15: 2403. https://doi.org/10.3390/ma12152403
APA StyleHer, S.-C., & Chan, C.-F. (2019). Interfacial Stress Analysis of Adhesively Bonded Lap Joint. Materials, 12(15), 2403. https://doi.org/10.3390/ma12152403




