Assessment of Validity of Selected Criteria of Fatigue Life Prediction
Abstract
:1. Introduction
2. Analyzed Fatigue Models
2.1. Models Based on Haigh Diagram
2.2. Models Based on Critical Plane Approach
2.2.1. Findley’s Model
2.2.2. Dang Van’s Fatigue Model
2.2.3. Model Based on the Carpinteri-Spagnoli Criterion
2.2.4. Model by McDiarmid
2.2.5. Model by Papadopoulos
2.2.6. Model by Matake
2.2.7. Model by Kluger-Lagoda
2.3. Models Based on Energy Approach
Smith-Watson-Topper Model
3. Experimental Study
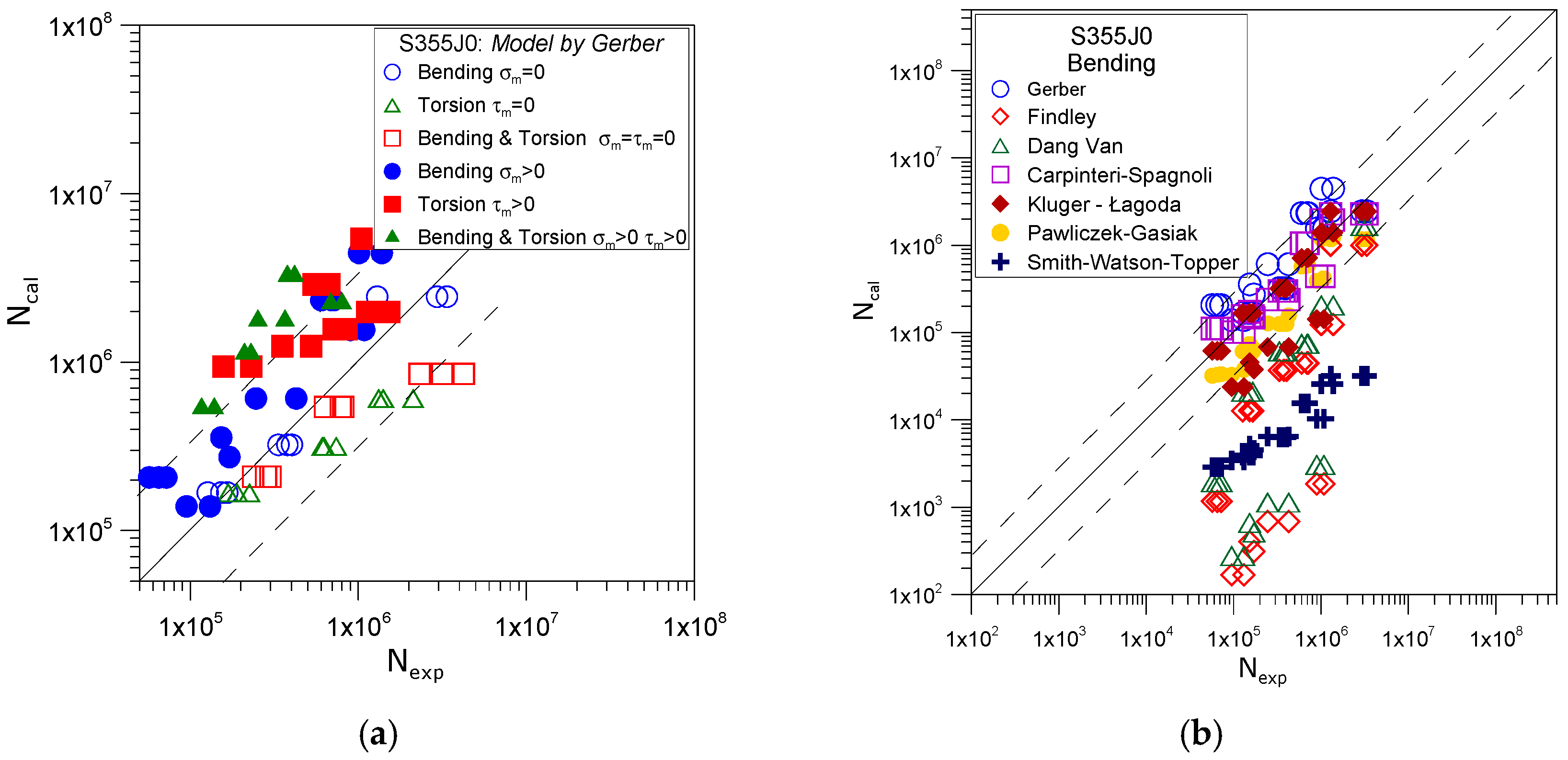
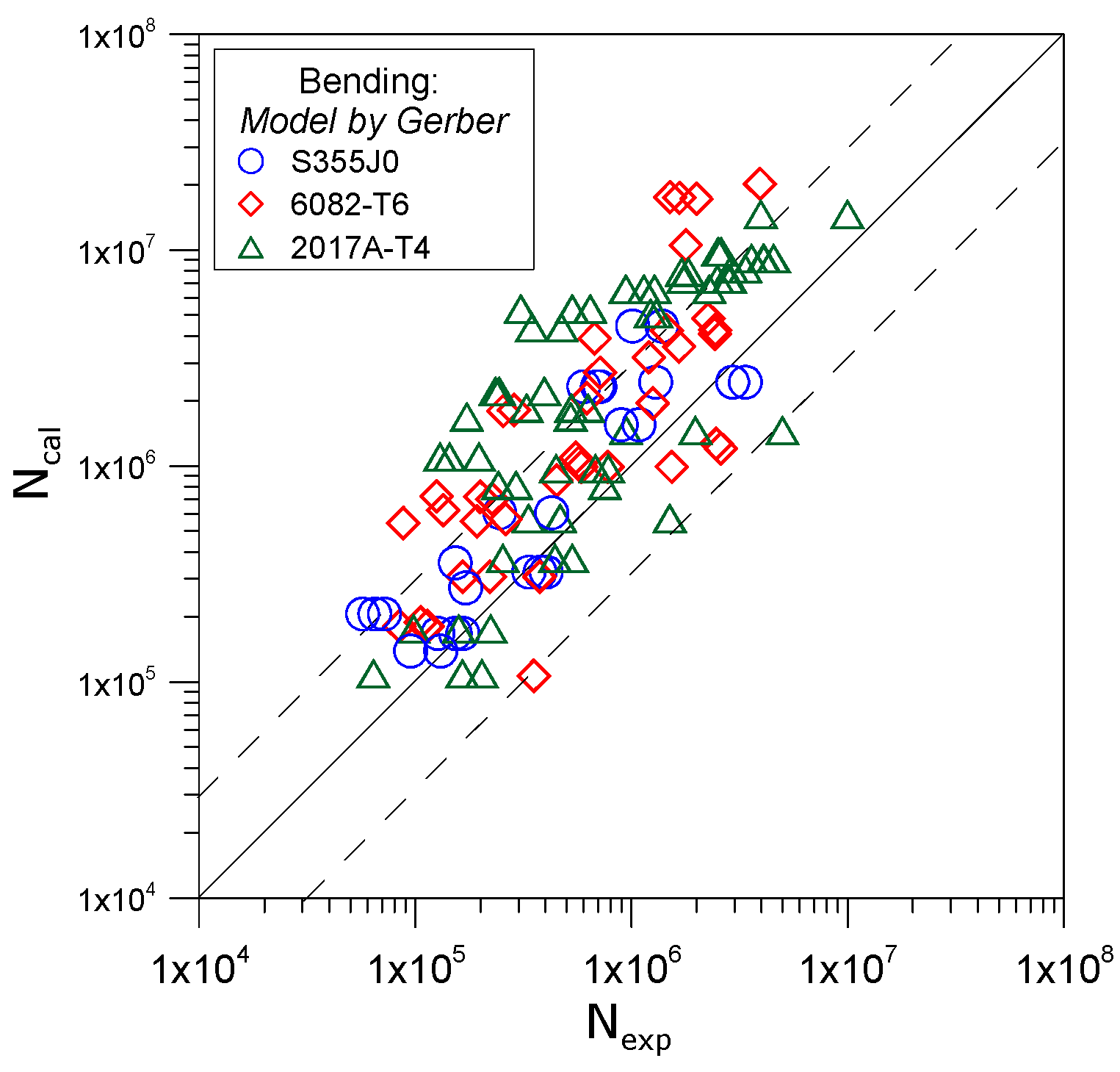
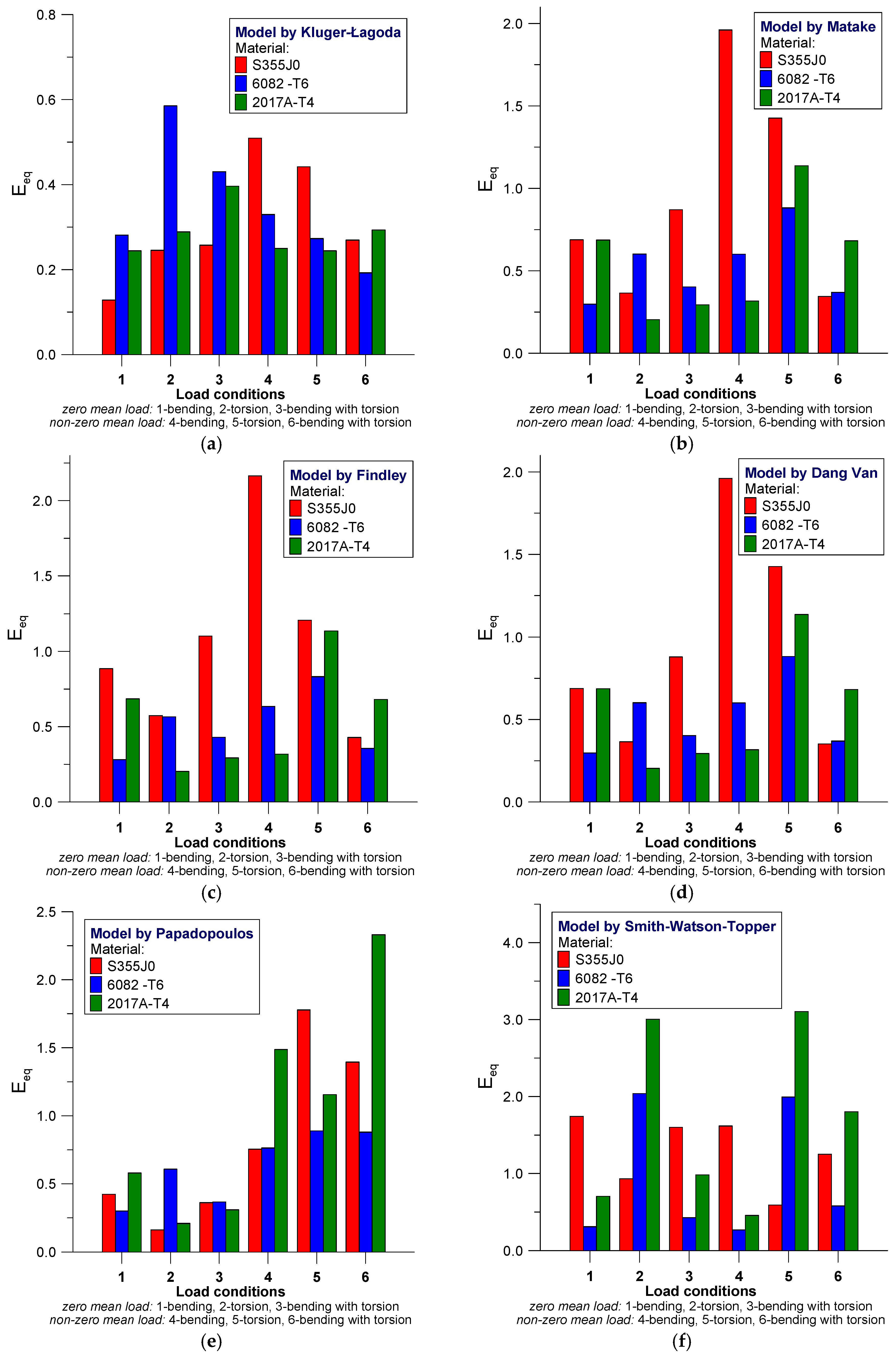
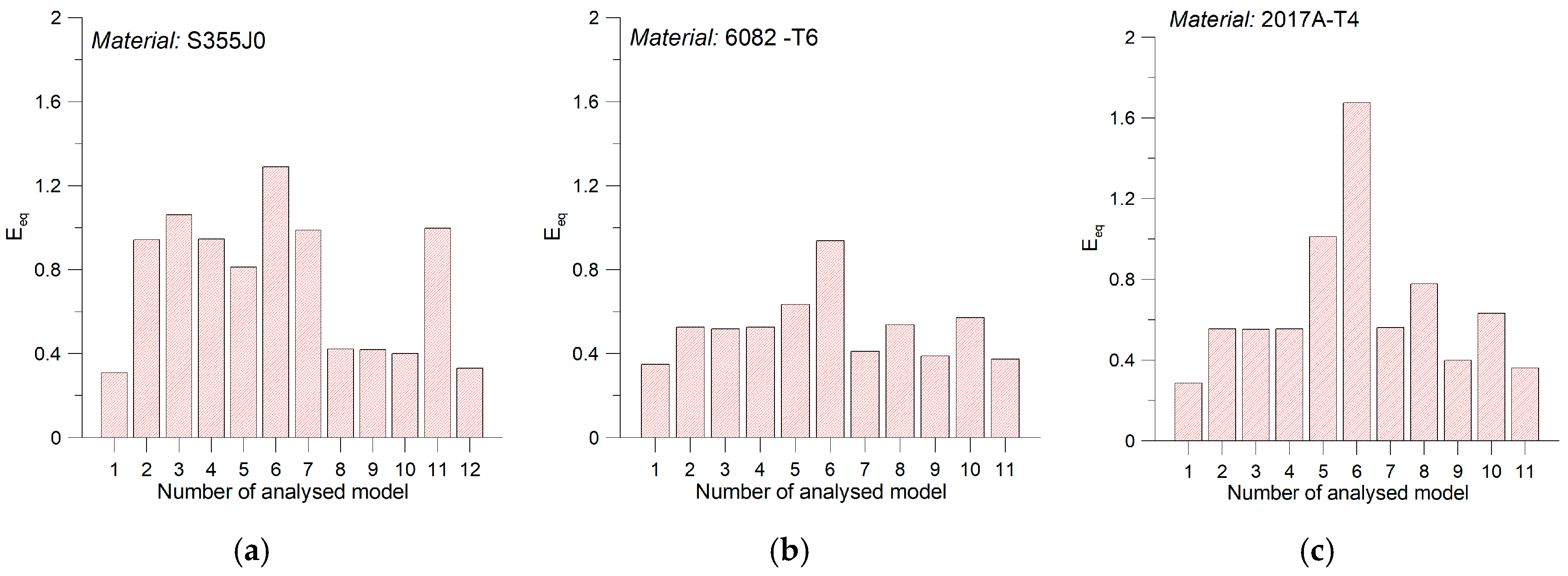
4. Analysis of Results
5. Conclusions and Finding
- For S355J0 steel the most accurate mean conformity of the calculated and experimental results was obtained for models by Kluger-Lagoda, Carpinteri-Spagnoli, Goodman, Gerber and Pawliczek-Gasiak;
- For both aluminum alloys, the models proposed by Kluger-Lagoda and also by Goodman and Soderberg proved to be most adequate, other models indicate higher discrepancies for cases of loading with load mean values;
- In the case of aluminum alloys, the Smith-Watson-Topper model demonstrates higher sensitivity in specimens subjected to torsional loading;
- Models in which the mean load is considered as a total of stress amplitude and mean stress (maximum stress as a criterion value) produce highly deteriorated fatigue life estimation results;
- For the analyzed loading conditions, the most accurate fatigue life estimations are obtained by using models that consider the material sensitivity change as the load mean value varies according to the number of cycles to failure (Pawliczek-Gasiak) and those taking into account the relationship between basic fatigue characteristics for bending and torsion (Kluger-Lagoda).
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| b | fatigue strength exponent |
| B, K | weight factors depending on the number of cycles to failure |
| c | fatigue ductility exponent |
| Eeq | computational scatter-band |
| Ei | scatter-band for the individual results |
| Em | the mean scatter-band |
| Estd | the standard deviation to mean scatter-band |
| k | weight factor |
| Nf | number of cycles to failure |
| Ni,cal | calculated fatigue life for individual specimens |
| Ni,exp | experimental fatigue life for individual specimens |
| pSWT | Smith-Watson-Topper parameter |
| pσ, pτ1, pτ2 | coefficients derived experimentally |
| amplitude of generalized shear stress | |
| α | critical plane orientation angle |
| δ | angle of rotation of the principal stress directions |
| Δε1 | normal strain range on the critical plane |
| ε′f | fatigue ductility coefficient |
| η, λ | factors determined based on the Haigh diagram for normal and shear stresses, respectively |
| σ′f | fatigue strength coefficient |
| σa | amplitude of normal stress |
| σaeq | amplitude of equivalent normal stress calculated for multiaxial stress state |
| σaf | fatigue limits for fully reversed bending |
| σaT | transformed normal stress amplitude due to the mean value |
| σeq | amplitude of equivalent stress for fully reversed uniaxial stress |
| σH,max | hydrostatic stresses |
| σm | mean value of normal stress |
| σmeq | mean value of equivalent stress calculated for multiaxial stress state |
| σn | the tensile normal stress on the plane of maximum shear stress |
| σn,a | normal stress amplitude on critical plane |
| σn,m | normal mean stress on critical plane |
| σn,max | maximal, normal stress on critical plane |
| σU | ultimate tensile strength |
| σy | yield strength |
| τaf | fatigue limit for alternating torsion |
| τμ | mesoscopic shear stresses |
| ψσ ψτ | material sensitivity factor for the asymmetry of cycle |
| τa | amplitude of shear stress |
| τaeq | amplitude of equivalent shear stress calculated for multiaxial stress state |
| τaT | transformed shear stress amplitude due to the mean value |
| τm | mean value of shear stress |
| τmax | the maximal shear stress |
| τn | shear stress on critical plane |
| τn,a | shear stress amplitude on the critical plane |
| τn,m | shear mean stress on the critical plane |
References
- Kluger, K.; Łagoda, T. Fatigue life of metallic material estimated according to selected models and load conditions. J. Theor. Appl. Mech. 2013, 51, 581–592. [Google Scholar]
- Skibicki, D.; Sempruch, J.; Pejkowski, L. Model of non-proportional fatigue load in the form of block load spectrum. Mater. Sci. Eng. Techonl. 2014, 45, 68–78. [Google Scholar] [CrossRef]
- Carpinteri, A.; Karolczuk, A.; Macha, E.; Vantadori, S. Expected position of the fatigue fracture plane by using the weighted mean principal Euler angles. Int. J. Fract. 2002, 115, 87–99. [Google Scholar] [CrossRef]
- Liu, Y.; Mahadevan, S. Multiaxial high-cycle fatigue criterion and life prediction for metals. Int. J. Fatigue 2005, 27, 790–800. [Google Scholar] [CrossRef]
- Liu, Y.; Zenner, H. The fatigue limit of ductile metals under multiaxial loading. Eur. Struct. Integr. Soc. 2003, 31, 147–164. [Google Scholar]
- Papuga, J. A survey on evaluating the fatigue limit under multiaxial loading. Int. J. Fatigue 2011, 33, 153–165. [Google Scholar] [CrossRef]
- Karolczuk, A.; Macha, E. Critical planes in multiaxial fatigue. Mater. Sci. Forum 2005, 482, 109–114. [Google Scholar] [CrossRef]
- Karolczuk, A.; Kowalski, M.; Kluger, K.; Żok, F. Identification of Residual Stress Phenomena Based on the Hole Drilling Method in Explosively Welded Steel-Titanium Composite. Arch. Metall. Mater. 2014, 59. [Google Scholar] [CrossRef]
- Youtsos, A. (Ed.) Residual Stress and Its Effects on Fatigue and Fracture: Proceedings of A Special Symposium Held within the 16th European Conference of Fracture—ECF16, Alexandroupolis, Greece, 3–7 July 2006; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Zhuang, W.; Halford, G. Investigation of residual stress relaxation under cyclic load. Int. J. Fatigue 2001, 23, 31–37. [Google Scholar] [CrossRef]
- Gerber, W. Determination of permissible stresses in iron constructions. Z Bayer Arch. Ing. Ver. 1974, 6, 101–110. (In German) [Google Scholar]
- Findley, W. A theory for the effect of mean stress on fatigue of metals under combined torsion and axial load or bending. J. Eng. Ind. 1959, 81, 301–306. [Google Scholar] [CrossRef]
- Dang Van, K.; Cailletaud, G.; Flavenot, J.; Le Douaron, A.; Lieurade, H. Criterion for high cycle fatigue failure under multiaxial loading. In Biaxial and Multiaxial Fatigue; Brown, M., Miller, K.J., Eds.; Mechanical Engineering Publication: London, UK, 1989; pp. 459–478. [Google Scholar]
- Smith, K.; Watson, P.; Topper, T. Stress-strain function for fatigue of metals. J. Mater. 1970, 5, 767–778. [Google Scholar]
- Kluger, K. Fatigue life estimation for 2017A-T4 and 6082-T6 aluminium alloys subjected to bending-torsion with mean stress. Int. J. Fatigue 2015, 80, 22–29. [Google Scholar] [CrossRef]
- Kluger, K.; Łagoda, T. New energy model for fatigue life determination under multiaxial loading with different mean values. Int. J. Fatigue 2014, 66, 229–245. [Google Scholar] [CrossRef]
- Gasiak, G.; Pawliczek, R. Application of an energetic model for fatigue life prediction of the construction steels under bending, torsion and synchronous bending and torsion. Int. J. Fatigue 2003, 25, 1339–1346. [Google Scholar] [CrossRef]
- Goodman, J. Mechanics Applied to Engineering, 9th ed.; N Y Longmans Green Co.: New York, NY, USA, 1954. [Google Scholar]
- Suresh, S. Fatigue of Materials, 2nd ed.; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Soderberg, C. Factor of Safety and Working Stress. Trans. ASME 1930, 52, 13–28. [Google Scholar]
- Szala, G.; Ligaj, B. Two-Parameter Fatigue Characteristics of Structural Steels and Their Experimental Verification; Monograph, J.S., Ed.; Scientific Publisher ITE: Bydgoszcz, Poland, 2011. (In Polish) [Google Scholar]
- Carpinteri, A.; Spagnoli, A.; Vantadori, S.; Bagni, C. Structural integrity assessment of metallic components under multiaxial fatigue: The C-S criterion and its evolution. Fatigue Fract. Eng. Mater. Struct. 2013, 36, 870–883. [Google Scholar] [CrossRef]
- McDiarmid, D. A shear stress based critical-plane criterion of multiaxial fatigue failure for design and life prediction. Fatigue Fract. Eng. Mater. Struct. 1994, 17, 475–484. [Google Scholar] [CrossRef]
- McDiarmid, D. A general criterion for high cycle multiaxial fatigue failure. Fatigue Fract. Eng. Mater. Struct. 1991, 14, 429–453. [Google Scholar] [CrossRef]
- Papadopoulos, I. Critical plane approaches in high-cycle fatigue: On the definition of the amplitude and mean value of the shear stress acting on the critical plane. Fatigue Fract. Eng. Mater. Struct. 1998, 21, 269–285. [Google Scholar] [CrossRef]
- Papadopoulos, I.; Davoli, P.; Gorla, C.; Filippini, M.; Bernasconi, A. A comparative study of multiaxial high-cycle fatigue criteria for metals. Int. J. Fatigue 1997, 19, 219–235. [Google Scholar] [CrossRef]
- Matake, T. An Explanation on Fatigue Limit under Combined Stress. Bull. JSME 1977, 20, 257–263. [Google Scholar] [CrossRef]
- Karolczuk, A.; Kluger, K. Analysis of the coefficient of normal stress effect in chosen multiaxial fatigue criteria. Theor. Appl. Fract. Mech. 2014, 73, 39–47. [Google Scholar] [CrossRef]
- Socie, D. Multiaxial fatigue damage models. ASME J. Eng. Mater. Technol. 1987, 109, 292–298. [Google Scholar] [CrossRef]
- Niesłony, A.; Łagoda, T.; Walat, K.; Kurek, M. Multiaxial fatigue behaviour of AA6068 and AA2017A aluminium alloys under in-phase bending with torsion loading condition. Mater. Sci. Eng. Technol. 2014, 45, 947–952. [Google Scholar] [CrossRef]
- Pawliczek, R. Fatigue Fracture Plane Orientation under Combined Bending and Torsion for 18G2A (S355J0) Steel; Opole University of Technology, Faculty of Mechanical Engineering: Opole, Poland, 2000. [Google Scholar]
- Karolczuk, A. Plastic strains and the macroscopic critical plane orientations under combined bending and torsion with constant and variable amplitudes. Eng. Fract. Mech. 2006, 73, 1629–1652. [Google Scholar] [CrossRef]
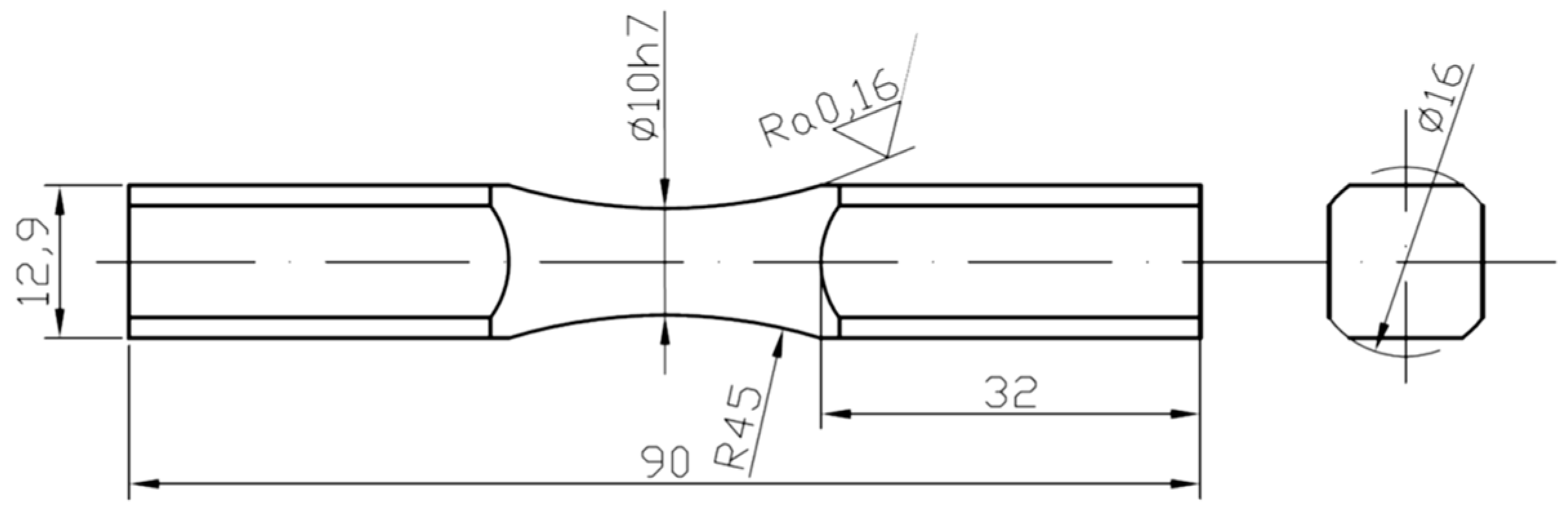

| Properties | Designation and Unit | 2017A-T4 | 6082-T6 | S355J0 |
|---|---|---|---|---|
| Young’s modulus | E, [GPa] | 72 | 72 | 213 |
| Tensile strength limit | σu, [MPa] | 545 | 385 | 611 |
| Yield strength limit | σy, [MPa] | 395 | 365 | 394 |
| Fatigue strength coefficient | σ′f, [MPa] | 643 | 651 | 880 |
| Slope factor of S-N curves (for bending) | mσ | 7.03 | 8.00 | 7.10 |
| Intercept of S-N curves (for bending) | Aσ | 21.87 | 23.83 | 23.80 |
| Slope factor of S-N curves (for torsion) | mτ | 6.87 | 7.7 | 11.7 |
| Intercept of S-N curves (for torsion) | Aτ | 19.94 | 21.4 | 32.8 |
| Fatigue limit for bending | σaf, [MPa] | 142 | 126 | 271 |
| Fatigue limit for torsion | τaf, [MPa] | 78 | 74 | 175 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kluger, K.; Pawliczek, R. Assessment of Validity of Selected Criteria of Fatigue Life Prediction. Materials 2019, 12, 2310. https://doi.org/10.3390/ma12142310
Kluger K, Pawliczek R. Assessment of Validity of Selected Criteria of Fatigue Life Prediction. Materials. 2019; 12(14):2310. https://doi.org/10.3390/ma12142310
Chicago/Turabian StyleKluger, Krzysztof, and Roland Pawliczek. 2019. "Assessment of Validity of Selected Criteria of Fatigue Life Prediction" Materials 12, no. 14: 2310. https://doi.org/10.3390/ma12142310
APA StyleKluger, K., & Pawliczek, R. (2019). Assessment of Validity of Selected Criteria of Fatigue Life Prediction. Materials, 12(14), 2310. https://doi.org/10.3390/ma12142310





