Desiccant Films Made of Low-Density Polyethylene with Dispersed Silica Gel—Water Vapor Absorption, Permeability (H2O, N2, O2, CO2), and Mechanical Properties
Abstract
1. Introduction
2. Material and Methods
2.1. Materials
2.1.1. Silica Gel
2.1.2. Polyethylene
2.2. Methods
2.2.1. Film Production
2.2.2. Density of Films and Concentration of Silica Gel in Films
2.2.3. Electron Microscopic Pictures
2.2.4. Water Vapor Absorption
2.2.5. Water Vapor Permeation
2.2.6. Nitrogen, Carbon Dioxide, and Oxygen Permeability
2.2.7. Mechanical Tests and Elongation
2.2.8. Confidence Intervals
3. Results and Discussion
3.1. Silica Gel Concentration in the Films
3.2. Microscopic Pictures
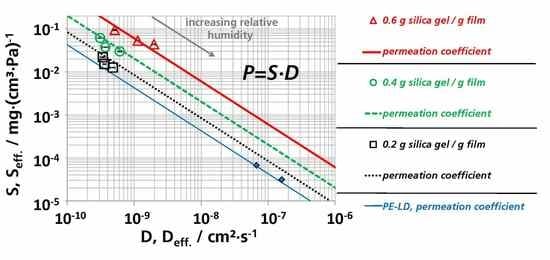
3.3. Effective Diffusion Coefficients
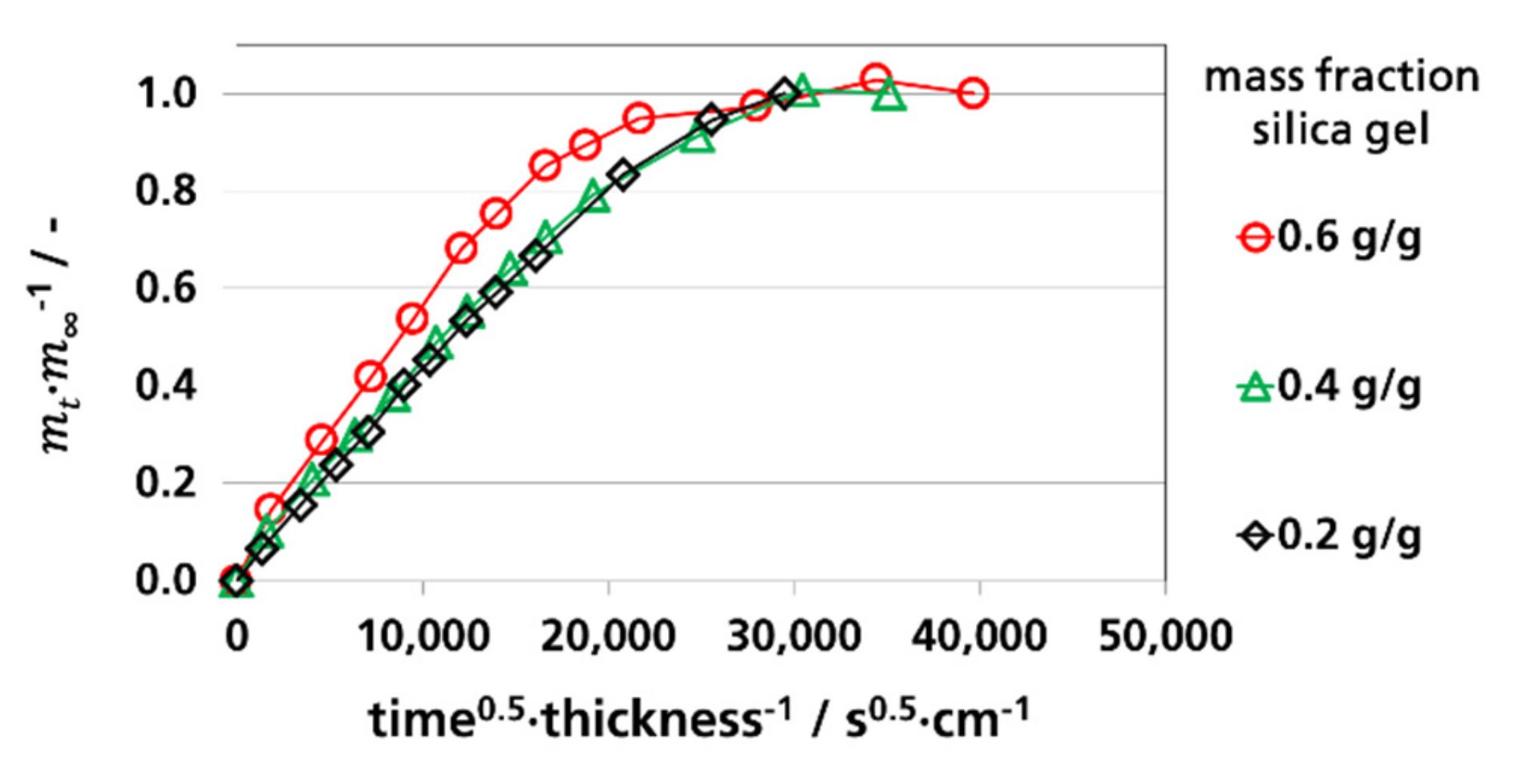
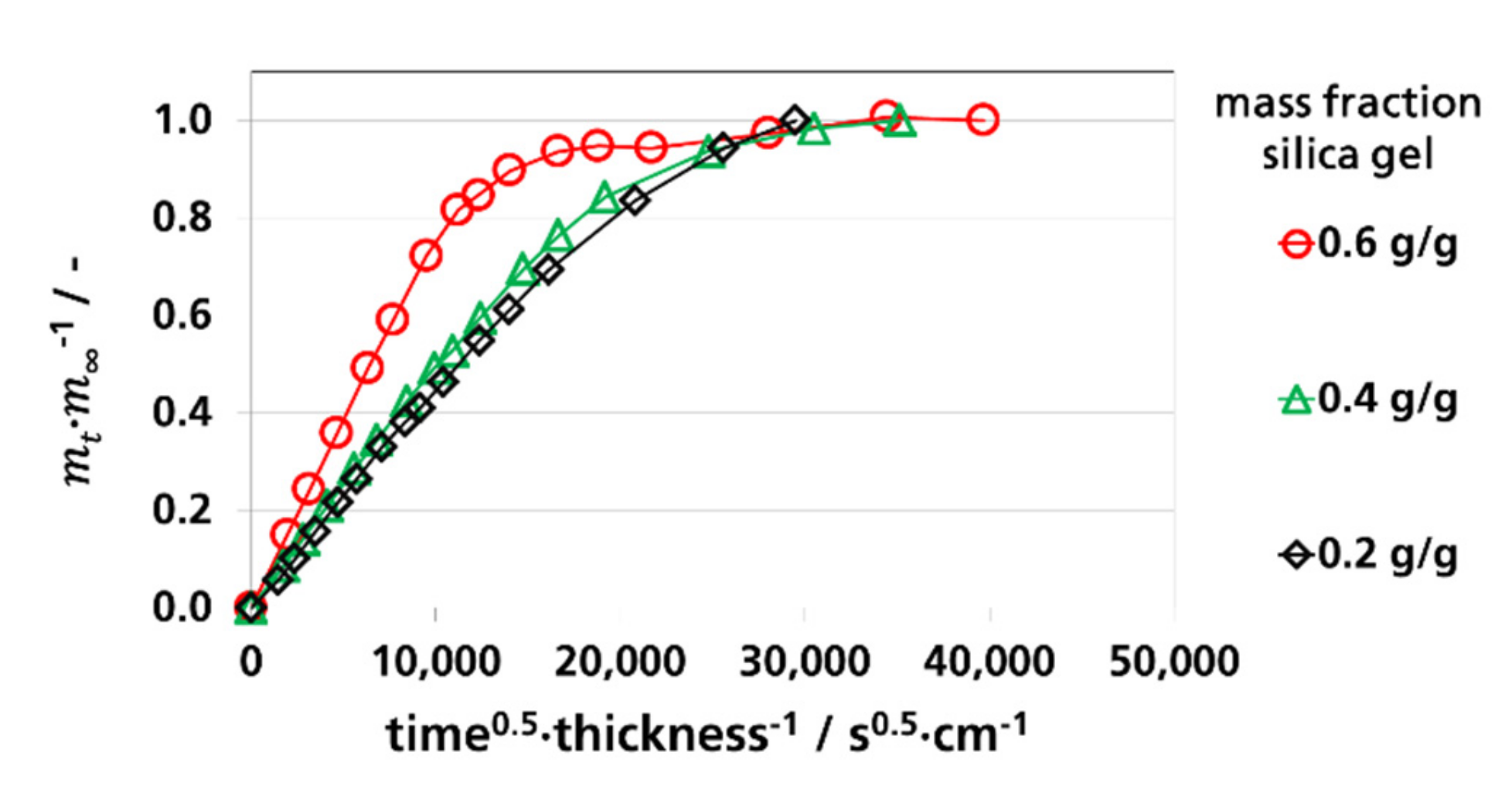
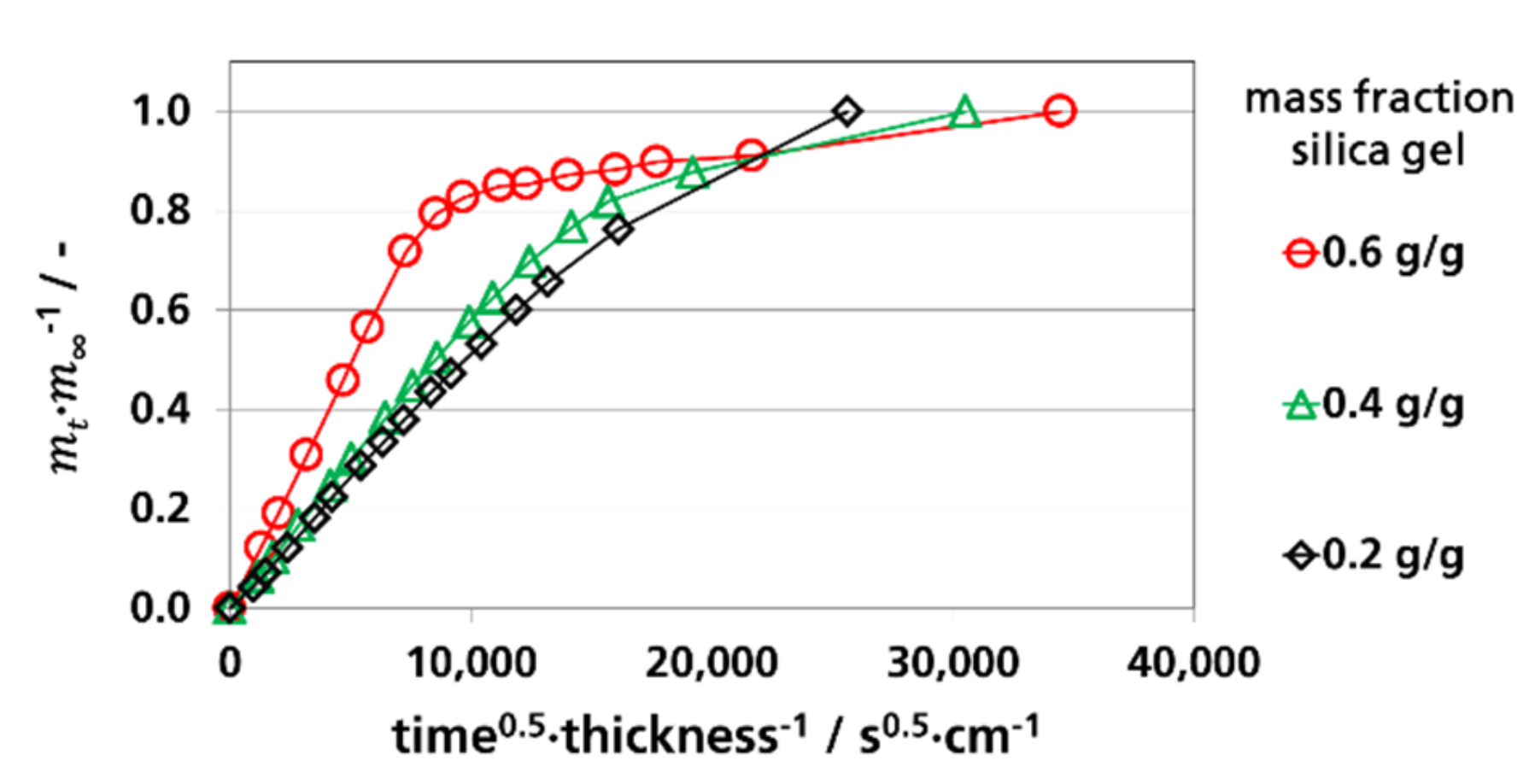
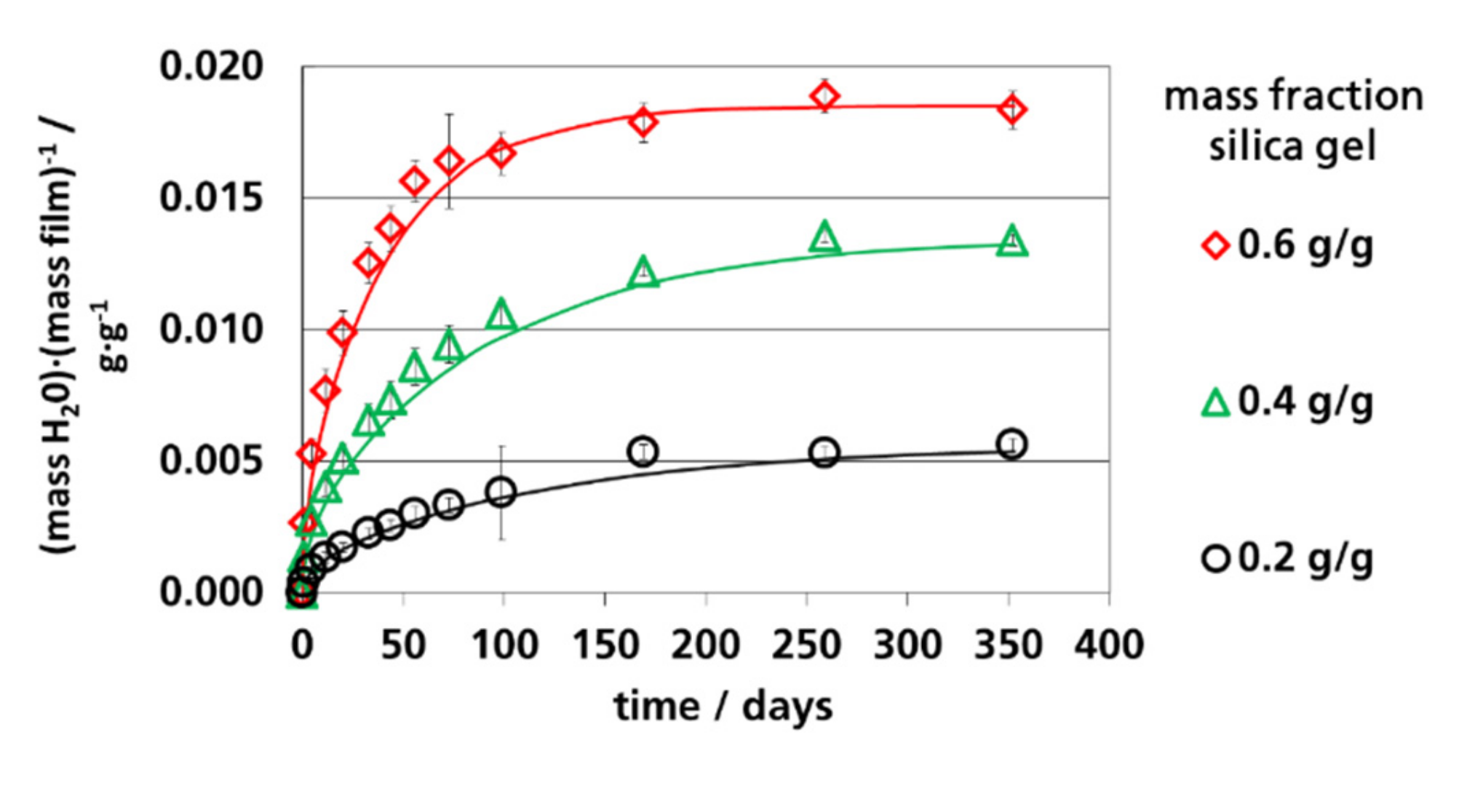
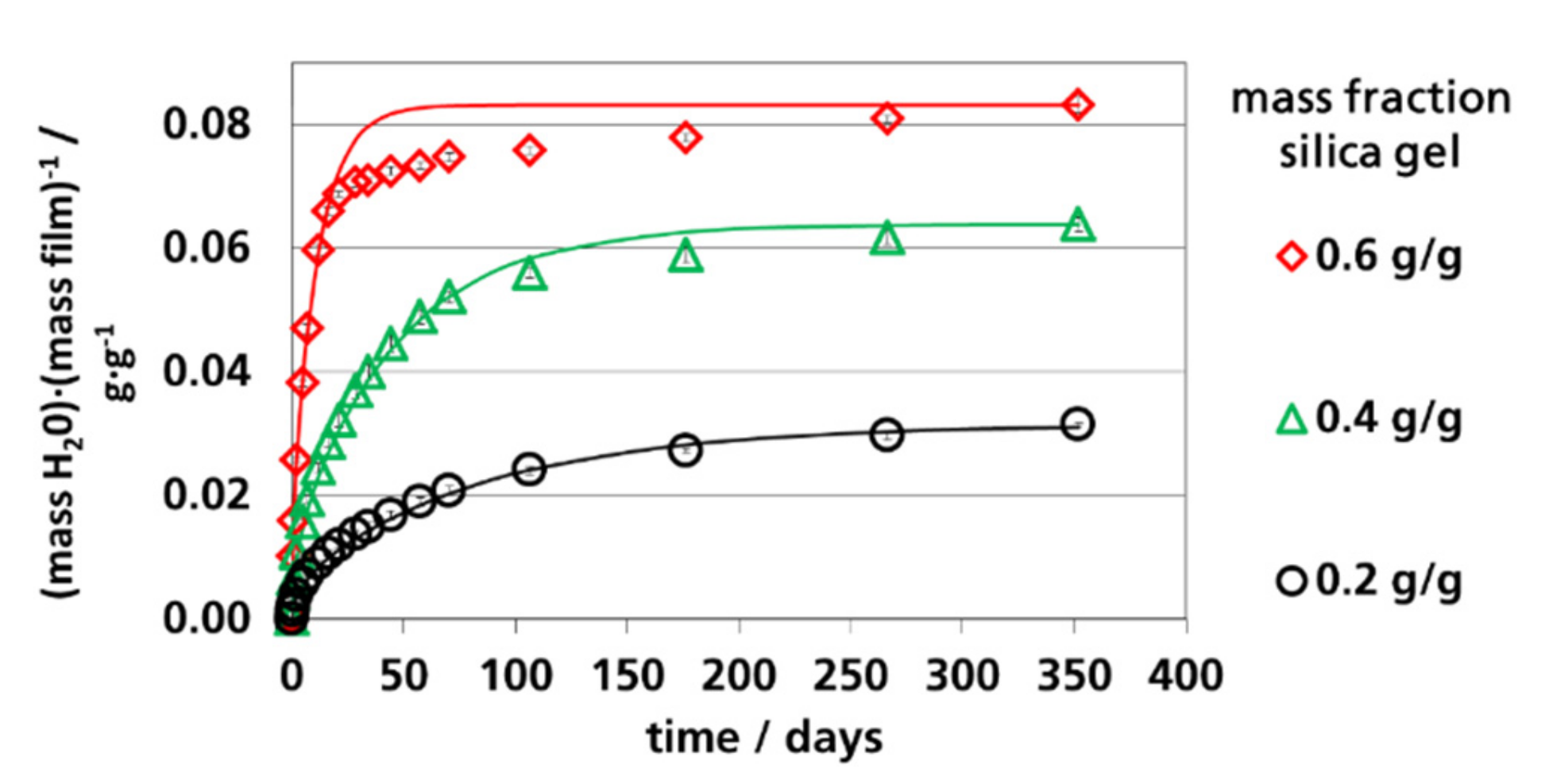
3.3.1. Effective Diffusion Coefficients by Sorption Experiments
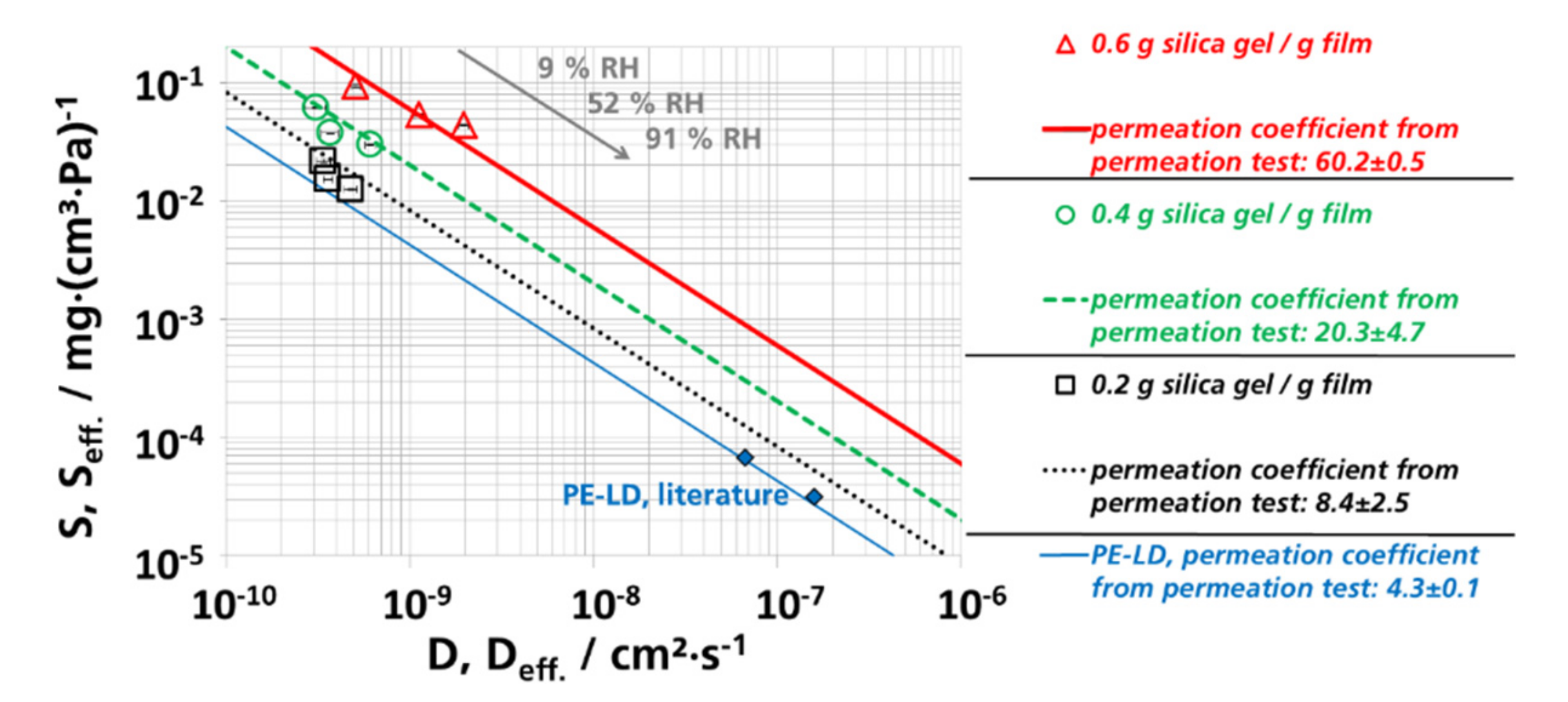
3.3.2. Effective Diffusion Coefficients by Permeation Experiments
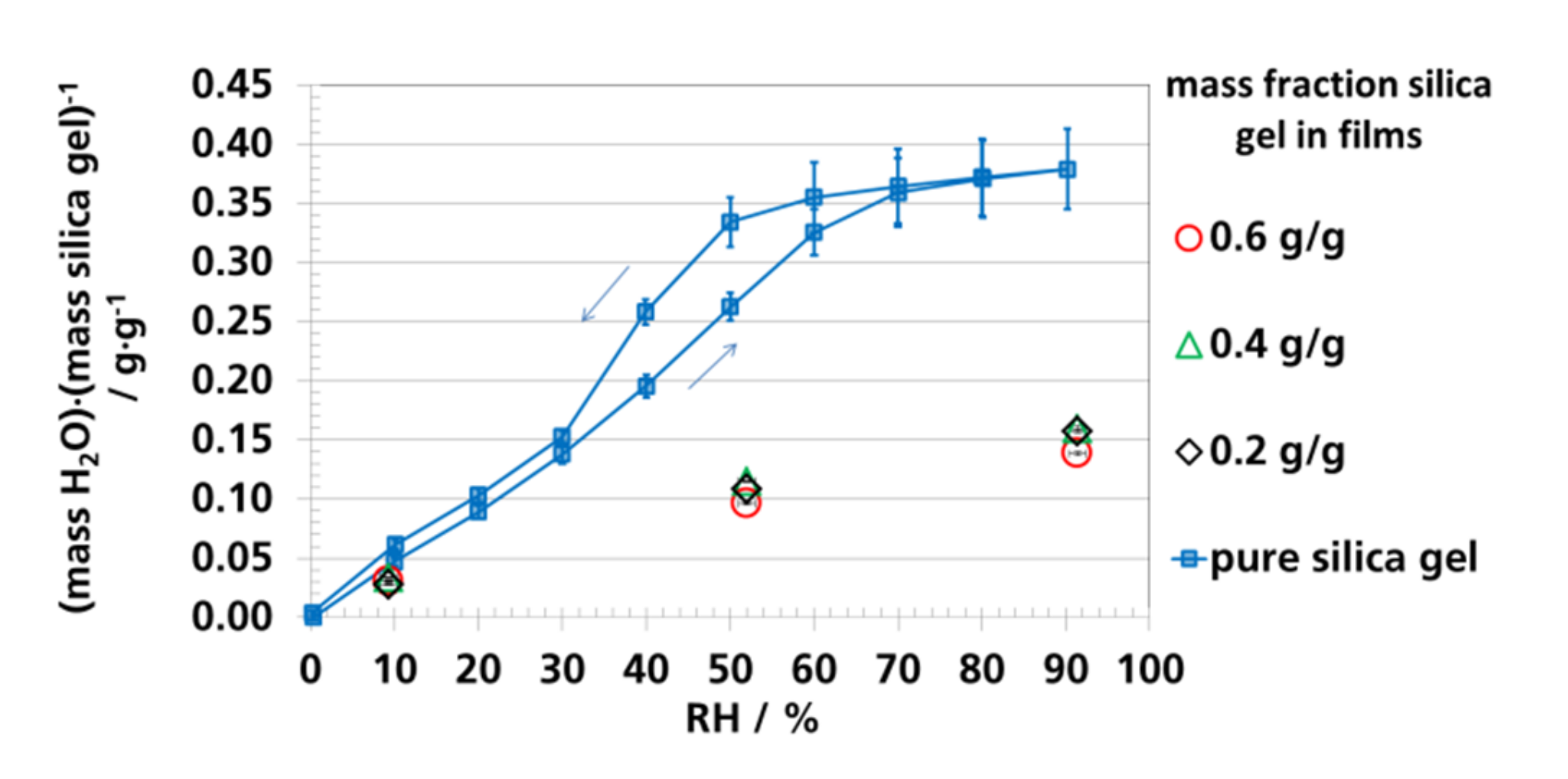
3.4. Water Vapor Absorption Capacity and Effective Sorption Coefficients
3.5. (Effective) Water Vapor Permeation Coefficients
3.6. Gas Transmission Rates
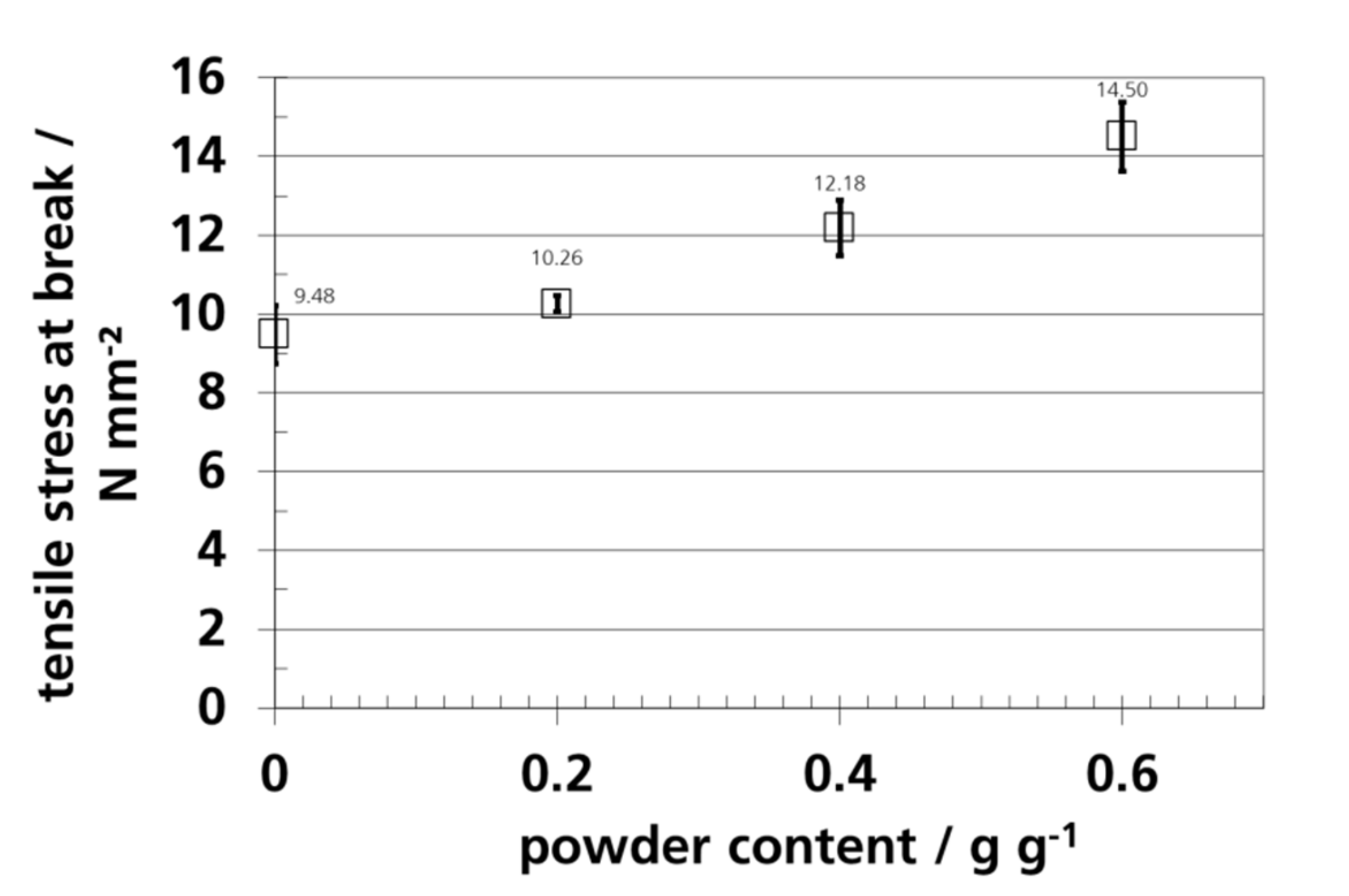
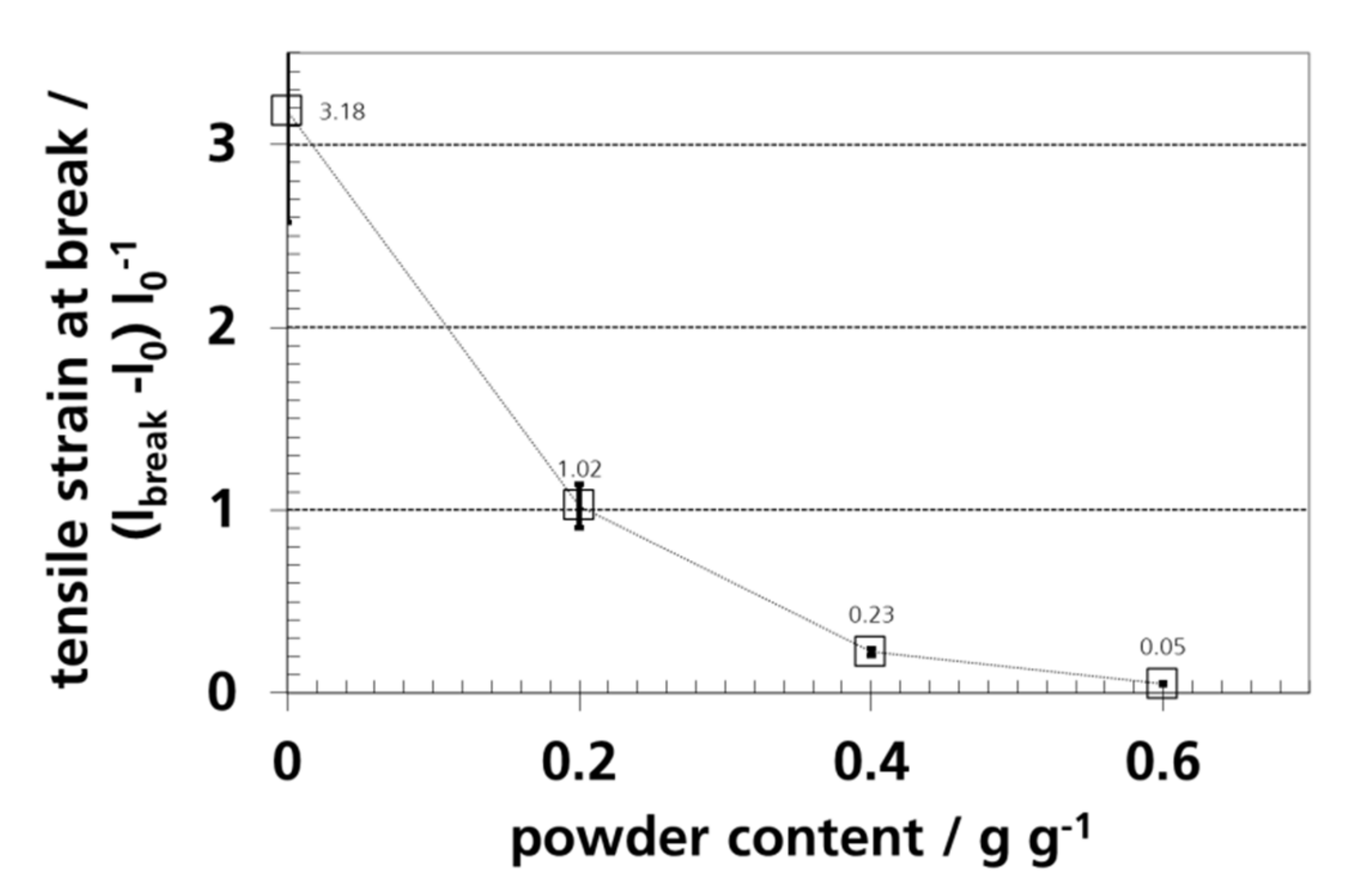
3.7. Mechanical Properties and Elongation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Remark
Conflicts of Interest
References
- Loncin, M.; Bimbenet, J.J.; Lenges, J. Influence of the activity of water on the spoilage of foodstuffs. Int. J. Food Sci. Technol. 1968, 3, 131–142. [Google Scholar] [CrossRef]
- Buchner, N.S. Gefährdung durch Wasserdampf. In Verpackung von Lebensmitteln: Lebensmitteltechnologische, Verpackungstechnische und Mikrobiologische Grundlagen; Buchner, N.S., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 145–163. [Google Scholar]
- Lück, E. Lebensmittel von mittlerer Feuchtigkeit. Zeitschrift für Lebensmittel-Untersuchung und Forschung 1973, 153, 42–52. [Google Scholar] [CrossRef]
- Labuza, T.P. The properties of water in relationship to water binding in foods: A review. J. Food Process. Preserv. 1977, 1, 167–190. [Google Scholar] [CrossRef]
- Belitz, H.-D.G.W.; Schieberle, P. Wasser. In Lehrbuch der Lebensmittelchemie: Mit Über 900 Formeln und 620 Tabellen; Belitz, H.-D.G.W., Schieberle, P., Eds.; Springer-Lehrbuch: Heidelberg, Germany, 2001; pp. 1–7. [Google Scholar]
- Iglesias, H.A.C.J. Handbook of Food Isotherms: Water Sorption Parameters for Food and Food Components; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Kessler, H.-G. Trockenprodukte—Sorptionsisothermen—Haltbarkeit. In Lebensmittel- und Bioverfahrenstechnik: Molkereitechnologie mit 109 Tabellen; Kessler, H.-G., Ed.; Kessler: München, Germany, 1996; pp. 255–264. [Google Scholar]
- Bell, L.N.; Labuza, T.P. Moisture Sorption: Practical Aspects of Isotherm Measurement and Use, 2nd ed.; American Association of Cereal Chemists: St. Paul, MN, USA, 2000. [Google Scholar]
- Esse, R.; Saari, A. An Active Moisture-Management Packaging System for Food and Other Products: A Case Study. In Smart Packaging Technologies for Fast Moving Consumer Goods; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008; pp. 129–149. [Google Scholar]
- Heiss, R. Praktische Versuche über die Feuchtigkeitsempfindlichkeit von Lebens- und Genussmitteln. In Verpackung feuchtigkeitsempfindlicher Guüter; Schruüfer, W., Ed.; Springer: Berlin, Germany, 1956; pp. 16–28. [Google Scholar]
- Waterman, K.C.; MacDonald, B.C. Package selection for moisture protection for solid, oral drug products. J. Pharm. Sci. 2010, 99, 4437–4452. [Google Scholar] [CrossRef] [PubMed]
- Redman-Furey, N.; Normand, M.D.; Peleg, M. Estimating the needed amount of desiccant, water or moistener to adjust the equilibrium water activity of dry powder mixtures. Trends Food Sci. Technol. 2013, 29, 135–141. [Google Scholar] [CrossRef]
- Kirk, J.R. Influence of Water Activity on Stability of Vitamins in Dehydrated Foods. In Water Activity: Influences on Food Quality: A Treatise on the Influence of Bound and Free Water on the Quality and Stability of Foods and Other Natural Products; Rockland, L.B., Stewart, G.F., Eds.; Academic Press: New York, NY, USA, 1981; pp. 531–566. [Google Scholar]
- Teunou, E.; Fitzpatrick, J.J.; Synnott, E.C. Characterization of food powder flowability. J. Food Eng. 1999, 39, 31–37. [Google Scholar] [CrossRef]
- Aguilera, J.; Del Valle, J.; Karel, M. Caking phenomena in amorphous food powders. Trends Food Sci. Technol. 1995, 6, 149–155. [Google Scholar] [CrossRef]
- Teunou, E.; Fitzpatrick, J.J. Effect of relative humidity and temperature on food powder flowability. J. Food Eng. 1999, 42, 109–116. [Google Scholar] [CrossRef]
- Mathlouthi, M.; Rogé, B. Water vapour sorption isotherms and the caking of food powders. Food Chem. 2003, 82, 61–71. [Google Scholar] [CrossRef]
- Salameh, A.K.; Taylor, L.S. Deliquescence-induced caking in binary powder blends. Pharm. Dev. Technol. 2006, 11, 453–464. [Google Scholar] [CrossRef]
- Langlet, M.; Benali, M.; Pezron, I.; Saleh, K.; Guigon, P.; Metlas-Komunjer, L. Caking of sodium chloride: Role of ambient relative humidity in dissolution and recrystallization process. Chem. Eng. Sci. 2013, 86, 78–86. [Google Scholar] [CrossRef]
- Leaper, M.C.; Bradley, M.S.A.; Cleaver, J.A.S.; Bridle, I.; Reed, A.R.; Abou-Chakra, H.; Tüzün, U. Constructing an engineering model for moisture migration in bulk solids as a prelude to predicting moisture migration caking. Adv. Powder Technol. 2002, 13, 411–424. [Google Scholar] [CrossRef]
- Cleaver, J.A.S.; Karatzas, G.; Louis, S.; Hayati, I. Moisture-induced caking of boric acid powder. Powder Technol. 2004, 146, 93–101. [Google Scholar] [CrossRef]
- Katz, E.E.; Labuza, T.P. Effect of Water Activity on the Sensory Crispness and Mechanical Deformation of Snack Food Products. J. Food Sci. 1981, 46, 403–409. [Google Scholar] [CrossRef]
- Azanha, A.B.; Faria, J.A.F. Use of mathematical models for estimating the shelf-life of cornflakes in flexible packaging. Packag. Technol. Sci. 2005, 18, 171–178. [Google Scholar] [CrossRef]
- Bae, Y.J.; Cho, E.S.; Qiu, F.; Sun, D.T.; Williams, T.E.; Urban, J.J.; Queen, W.L. Transparent Metal–Organic Framework/Polymer Mixed Matrix Membranes as Water Vapor Barriers. ACS Appl. Mater. Interfaces 2016, 8, 10098–10103. [Google Scholar] [CrossRef]
- Furukawa, H.; Gándara, F.; Zhang, Y.-B.; Jiang, J.; Queen, W.L.; Hudson, M.R.; Yaghi, O.M. Water Adsorption in Porous Metal–Organic Frameworks and Related Materials. J. Am. Chem. Soc. 2014, 136, 4369–4381. [Google Scholar] [CrossRef]
- Kenyó, C.; Kajtár, D.; Renner, K.; Kröhnke, C.; Pukánszky, B. Functional packaging materials: Factors affecting the capacity and rate of water adsorption in desiccant composites. J. Polym. Res. 2013, 20, 1–8. [Google Scholar] [CrossRef]
- Müller, P.; Russell, A.; Tomas, J. Einfluss des Bindemittels und der Feuchtebeladung auf die Festigkeit von Zeolith 4A-Granulaten. Influence of Binder and Moisture Content on the Strength of Zeolite 4A Granules. Chem. Ing. Tech. 2015, 87, 549–558. [Google Scholar] [CrossRef]
- Müller, P.; Russell, A.; Seidenbecher, J.; Tomas, J. Mechanische Eigenschaften zyklisch be- und entfeuchteter Zeolithgranulate. Mechanical Properties of Cyclic Moistened and Dried Zeolite Granules. Chem. Ing. Tech. 2015, 87, 1402–1411. [Google Scholar] [CrossRef]
- Cho, E.S.; Evans, C.M.; Davidson, E.C.; Hoarfrost, M.L.; Modestino, M.A.; Segalman, R.A.; Urban, J.J. Enhanced Water Vapor Blocking in Transparent Hybrid Polymer–Nanocrystal Films. ACS Macro Lett. 2015, 4, 70–74. [Google Scholar] [CrossRef]
- Kenyó, C.; Renner, K.; Móczó, J.; Fekete, E.; Kröhnke, C.; Pukánszky, B. Effect of desiccant characteristics on the properties of PS/zeolite functional packaging materials. Polym. Compos. 2014, 35, 2112–2120. [Google Scholar] [CrossRef]
- Pehlivan, H.; Özmıhçı, F.; Tıhmınlıoǧlu, F.; Balköse, D.; Ülkü, S. Water and water vapor sorption studies in polypropylene–zeolite composites. J. Appl. Polym. Sci. 2003, 90, 3069–3075. [Google Scholar] [CrossRef]
- Mathiowitz, E.; Jacob, J.S.; Jong, Y.S.; Hekal, T.M.; Spano, W.; Guemonprez, R.; Klibanov, A.M.; Langer, R. Novel desiccants based on designed polymeric blends. J. Appl. Polym. Sci. 2001, 80, 317–327. [Google Scholar] [CrossRef]
- Ferri, L.A.; Golden, D.L. Hot Melt Sealant Containing Desiccant for Use in Photovoltaic Modules. U.S. Patent WO/2009/085736, 9 July 2009. [Google Scholar]
- Kenyó, C.; Renner, K.; Móczó, J.; Fekete, E.; Kröhnke, C.; Pukánszky, B. Hips/zeolite hybrid composites as active packaging materials: Structure and functional properties. Eur. Polym. J. 2018, 103, 88–94. [Google Scholar] [CrossRef]
- Kajtár, D.A.; Kenyó, C.; Renner, K.; Móczó, J.; Fekete, E.; Kröhnke, C.; Pukánszky, B. Interfacial interactions and reinforcement in thermoplastics/zeolite composites. Compos. Part B Eng. 2017, 114, 386–394. [Google Scholar] [CrossRef]
- Sängerlaub, S.; Seibel, K.; Miesbauer, O.; Pant, A.; Kiese, S.; Rodler, N.; Schmid, M.; Müller, K. Functional properties of foamed and/or stretched polypropylene-films containing sodium chloride particles for humidity regulation. Polym. Test. 2018, 65, 339–351. [Google Scholar] [CrossRef]
- Sängerlaub, S.; Miesbauer, O.; Michael, L.; Müller, K.; Stramm, C.; Pecyna, M.; Langowski, H.C. Humidity regulation by stretched PP and PLA films with dispersed CaCl2. J. Appl. Polym. Sci. 2018, 135, 45713. [Google Scholar] [CrossRef]
- Sängerlaub, S.; Böhmer, M.; Stramm, C. Influence of stretching ratio and salt concentration on the porosity of polypropylene films containing sodium chloride particles. J. Appl. Polym. Sci. 2013, 129, 1238–1248. [Google Scholar] [CrossRef]
- Hayden, A.J.; Ozcomert, J.S. The use of calcium oxide as a desiccant in extrusion coatings. In Proceedings of the Annual Technical Conference, Nashville, TN, USA; 2004; pp. 2620–2622. [Google Scholar]
- Murray, L.; Merical, R.; Kaas, R. Moisture Scavenging Packaging for Diagnostic Test Strips, Pharmaceuticals and Other Moisture Sensitive Products. In Proceedings of the PLACE Conference and Global Hot Melt Symposium, Orlando ,FL, USA; 2003; pp. 669–675. [Google Scholar]
- Murray, L.; Johnson, R.; Sikorsky, J.; Merical, R. One-side clear active barrier packaging for moisture sensitive medical devices. In Proceedings of the TAPPI PLACE Conference, St. Louis, MO, USA; 2007; pp. 1460–1475. [Google Scholar]
- Lee, B.D.; Cho, Y.H.; Kim, W.J.; Oh, M.H.; Lee, J.H.; Zang, D.S. Effect of transparent film desiccant on the lifetime of top-emitting active matrix organic light emitting diodes. Appl. Phys. Lett. 2007, 90, 103518. [Google Scholar] [CrossRef]
- Lee, B.D.; Cho, Y.H.; Oh, M.; Kim, Y.T.; Cho, S.H.; Lee, S.Y.; Chung, Y.A.; Song, S.Y.; Lee, J.H.; Kim, S.C. Application of liquid desiccant for enhanced lifetime of active matrix organic light emitting diodes. MRS Online Proc. Libr. 2011, 1286, 78–84. [Google Scholar] [CrossRef]
- Nji, J.; Li, G. A CaO enhanced rubberized syntactic foam. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1404–1411. [Google Scholar] [CrossRef]
- Caro, J. Quo Vadis, MOF? Chem. Ing. Tech. 2018, 90, 1759–1768. [Google Scholar] [CrossRef]
- Sängerlaub, S.; Kucukpinar, E.; Kiese, S.; Bauer, K.D.; Müller, K. Desiccant films made of low-density polyethylene with dispersed calcium oxide: Water vapor absorption, permeation and mechanical properties. J. Appl. Polym. Sci. 2019, 136, 47460. [Google Scholar] [CrossRef]
- Flörke, O.W.; Graetsch, H.; Brunk, F.; Benda, L.; Paschen, S.; Bergna, H.E.; Roberts, W.O.; Welsh, W.A.; Chapman, D.M.; Ettlinger, M.; et al. Silica. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag GmbH & Co. KgaA: Weinheim, Germany, 2000. [Google Scholar]
- Foth, H.-J. Kapillarkondensation, RD-11-00472. In RÖMPP Online; Georg Thieme Verlag: Stuttgart, Germany, 2007. [Google Scholar]
- Bart, H.-J.; von Gemmingen, U. Adsorption. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag GmbH & Co. KgaA: Weinheim, Germany, 2000. [Google Scholar]
- Hauer, A. Beurteilung fester Adsorbentien in offenen Sorptionssystemen für energetische Anwendungen. Ph.D. Thesis, Berlin Techn. University, Berlin, Germany, 2002. [Google Scholar]
- Hall, M.R.; Tsang, S.C.E.; Casey, S.P.; Khan, M.A.; Yang, H. Synthesis, characterization and hygrothermal behaviour of mesoporous silica high-performance desiccants for relative humidity buffering in closed environments. Acta Mater. 2012, 60, 89–101. [Google Scholar] [CrossRef]
- Wyttenbach, H. Zur Wertbestimmung von Gastrocknungsmitteln. Ph.D. Thesis, ETH, Zürich, Switzerland, 1944. [Google Scholar]
- Goldsworthy, M.J. Measurements of water vapour sorption isotherms for RD silica gel, AQSOA-Z01, AQSOA-Z02, AQSOA-Z05 and CECA zeolite 3A. Microporous Mesoporous Mater. 2014, 196, 59–67. [Google Scholar] [CrossRef]
- Anonymous. Safety Data Sheet, Silica Gel Beads, Catalogue No. 107735; Merck KGaA: Darmstadt, Germany, 2010; p. 6. [Google Scholar]
- Anonymous. Sicherheitsdatenblatt, Silica gel weiß 0,5-1 mm, Granulat, Artikelnummer: 9376; Carl Roth GmbH + Co. KG: Karlsruhe, Germany, 2012; p. 8. [Google Scholar]
- Gey, M. Präanalytische Methoden. In Instrumentelle Analytik und Bioanalytik Biosubstanzen, Trennmethoden, Strukturanalytik, Applikationen; Gey, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 57–90. [Google Scholar]
- Anonymous. Produktinformation Lupolen® 1806 H; Basell Polyolefine GmbH: Kehl, Germany, 2005; p. 2. [Google Scholar]
- Greenspan, L. Humidity Fixed Points of Binary Saturated Aqueous Solutions. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1977, 81, 89–96. [Google Scholar] [CrossRef]
- Crank, J. Diffusion in a plane sheet. In The Mathematics of Diffusion; Crank, J., Ed.; Clarendon Press: Oxford, UK, 1975; pp. 44–68. [Google Scholar]
- Crank, J. The definition and measurement of diffusion coefficients. In The Mathematics of Diffusion; Crank, J., Ed.; Clarendon Press: Oxford, UK, 1975; pp. 44–68. [Google Scholar]
- Vieth, W.R. Theory. In Diffusion in and through Polymers: Principles and Applications; Vieth, W.R., Ed.; Hanser Pub Inc.: New York, NY, USA, 1991; pp. 15–44. [Google Scholar]
- Yang, R.M.; Tong, H.-M. Estimation of moisture diffusion coefficient in thin polymer films with piezoelectric quartz crystal resonators. J. Polym. Sci. Polym. Lett. Ed. 1985, 23, 583–586. [Google Scholar] [CrossRef]
- Grayson, M.A.; Wolf, C.J. The solubility and diffusion of water in poly(aryl-ether-ether-ketone) (PEEK). J. Polym. Sci. Part B Polym. Phys. 1987, 25, 31–41. [Google Scholar] [CrossRef]
- Jou, J.-H.; Huang, R.; Huang, P.-T.; Shen, W.-P. Structure effect on water diffusion and hygroscopic stress in polyimide films. J. Appl. Polym. Sci. 1991, 43, 857–875. [Google Scholar] [CrossRef]
- Okamoto, K.-I.; Tanihara, N.; Watanabe, H.; Tanaka, K.; Kita, H.; Nakamura, A.; Kusuki, Y.; Nakagawa, K. Sorption and diffusion of water vapor in polyimide films. J. Polym. Sci. Part B Polym. Phys. 1992, 30, 1223–1231. [Google Scholar] [CrossRef]
- Seo, J.; Han, H. Water diffusion studies in polyimide thin films. J. Appl. Polym. Sci. 2001, 82, 731–737. [Google Scholar] [CrossRef]
- Barrie, J.A.; Machin, D. Diffusion and association of water in some polyalkylmethacrylates. Part 2.-Transient state diffusion. Trans. Faraday Soc. 1971, 67, 2970–2978. [Google Scholar] [CrossRef]
- Langowski, H.-C. Permeation of Gases and Condensable Substances through Monolayer and Multilayer Structures. In Plastic Packaging; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2008; pp. 297–347. [Google Scholar]
- Barrer, R.M. Diffusion in and through Solids; The University Press: Cambridge, UK; Macmillan: New York, NY, USA, 1941. [Google Scholar]
- Krevelen, D.W.V. Properties determining mass transfer in polymeric systems. In Properties of Polymers: Their Correlation with Chemical Structure: Their Numerical Estimation and Prediction from Additive Group Contributions; Krevelen, D.W.V., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 655–702. [Google Scholar]
- Langowski, H.-C. Stofftransport durch polymere und anorganische Schichten. Transport of Substances Through Polymeric and Inorganic Layers. Vak. Forsch. Prax. 2005, 17, 6–13. [Google Scholar] [CrossRef]
- Stern, S.A.; Trohalaki, S. Fundamentals of Gas Diffusion in Rubbery and Glassy Polymers. In Barrier Polymers and Structures; ACS Symposium Series; American Chemical Society: Washington, WA, USA, 1990; Volume 423, pp. 22–59. [Google Scholar]
- Barrer, R.M. Gas flow in and through crystals and glasses. In Diffusion in and through Solids; Barrer, R.M., Ed.; The University Press: Cambridge, UK; Macmillan: New York, NY, USA, 1941. [Google Scholar]
- Barrer, R.M.; Rideal, E.K. Permeation, diffusion and solution of gases in organic polymers. Trans. Faraday Soc. 1939, 35, 628–643. [Google Scholar] [CrossRef]
- Brunauer, S. Data of adsorption. In The Adsorption of Gases and Vapors; Physical adsorption 1; Brunauer, S., Ed.; Oxford University Press: Princeton, MA, USA, 1945; pp. 7–28. [Google Scholar]
- Vieth, W.R.; Amini, M.A. Generalized dual sorption theory. In Permeability of Plastic Films and Coatings to Gases, Vapors and Liquids; Polymer Science and Technology 6; Hopfenberg, H., Ed.; Springer: New York, NY, USA; London, UK, 1974; pp. 49–61. [Google Scholar]
- Henry, W. Experiments on the Quantity of Gases Absorbed by Water, at Different Temperatures, and under Different Pressures. Philos. Trans. R. Soc. Lond. 1803, 93, 29–274. [Google Scholar] [CrossRef]
- Barrer, R.M. Solutions of the diffusion equation. In Diffusion in and through Solids; Barrer, R.M., Ed.; The University Press: Cambridge, UK; Macmillan: New York, NY, USA, 1941; pp. 1–52. [Google Scholar]
- Flynn, G.L.; Yalkowsky, S.H.; Roseman, T.J. Mass transport phenomena and models: Theoretical concepts. J. Pharm. Sci. 1974, 63, 479–510. [Google Scholar] [CrossRef]
- Steel, R.G.D. Principles and Procedures of Statistics: A Biometrical Approach, 2nd ed.; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Peacock, A.J. Introduction. Handbook of Polyethylene: Structures, Properties, and Applications; Peacock, A.J., Ed.; Dekker: New York, NY, USA, 2000; pp. 1–26. [Google Scholar]
- Placette, M.D.; Fan, X.; Zhao, J.H.; Edwards, D. A dual stage model of anomalous moisture diffusion and desorption in epoxy mold compounds. In Proceedings of the 12th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems, EuroSimE 2011, Linz, Austria, 18–20 April 2011. [Google Scholar]
- Placette, M.D.; Fan, X.; Zhao, J.H.; Edwards, D. Dual stage modeling of moisture absorption and desorption in epoxy mold compounds. Microelectron. Reliab. 2012, 52, 1401–1408. [Google Scholar] [CrossRef]
- Tagne, N.R.S.; Njeugna, E.; Fogue, M.; Drean, J.Y.; Nzeukou, A.; Fokwa, D. Study of water absorption in raffia vinifera fibres from Bandjoun, Cameroon. Sci. World J. 2014, 2014, 912380. [Google Scholar] [CrossRef]
- Fan, X.; Nagaraj, V. Finite element modeling of anomalous moisture diffusion with dual stage model. In Proceedings of the 2012 IEEE 62nd Electronic Components and Technology Conference, San Diego, CA, USA, 29 May–1 June 2012; pp. 1190–1193. [Google Scholar]
- Crank, J. Non-Fickian diffusion. In The Mathematics of Diffusion; Crank, J., Ed.; Clarendon Press: Oxford, UK, 1975; pp. 254–265. [Google Scholar]
- Hanika, M. Zur Permeation durch aluminiumbedampfte Polypropylen- und Polyethylenterephtalatfolien. Ph.D. Thesis, Lehrstuhl für Feststoff und Grenzflächenverfahrenstechnik, Technische Universität München, München, Germany, 2004. [Google Scholar]
- Moosheimer, U. Plasmavorbehandlung und Beschichtung von Kunststoffolien. Ph.D. Thesis, Fakultät Physik, Universität Regensburg, Regensburg, Germany, 1997. [Google Scholar]
- Utz, H. Barriereeigenschaften aluminiumbedampfter Kunststoffolien. Ph.D. Thesis, Lehrstuhl für Brauereianlagen und Lebensmittel-Verpackungstechnik, Technische Universität München, München, Germany, 1995. [Google Scholar]
- Comyn, J. Polymer Permeability; Elsevier: London, UK; New York, NY, USA, 1985. [Google Scholar]
- Marais, S.; Nguyen, Q.T.; Devallencourt, C.; Metayer, M.; Nguyen, T.U.; Schaetzel, P. Permeation of water through polar and nonpolar polymers and copolymers: Determination of the concentration-dependent diffusion coefficient. J. Polym. Sci. Part B Polym. Phys. 2000, 38, 1998–2008. [Google Scholar] [CrossRef]
- Paul, D.R.; Kemp, D.R. The diffusion time lag in polymer membranes containing adsorptive fillers. J. Polym. Sci. Polym. Symp. 1973, 41, 79–93. [Google Scholar] [CrossRef]
- Yang, C.; Cussler, E.L. Oxygen barriers that use free radical chemistry. AIChE J. 2001, 47, 2725–2732. [Google Scholar] [CrossRef]
- Finger, K.F.; Lemberger, A.P.; Higuchi, T.; Busse, L.W.; Wurster, D.E. Investigation and development of protective ointments IV. The influence of active fillers on the permeability of semisolids. J. Am. Pharm. Assoc. 1960, 49, 569–573. [Google Scholar] [CrossRef]
- Most, C.F. Some filler effects on diffusion in silicone rubber. J. Appl. Polym. Sci. 1970, 14, 1019–1024. [Google Scholar] [CrossRef]
- Ferrari, M.C.; Carranza, S.; Bonnecaze, R.T.; Tung, K.K.; Freeman, B.D.; Paul, D.R. Modeling of oxygen scavenging for improved barrier behavior: Blend films. J. Membr. Sci. 2009, 329, 183–192. [Google Scholar] [CrossRef]
- Yang, C.; Nuxoll, E.E.; Cussler, E.L. Reactive barrier films. AIChE J. 2001, 47, 295–302. [Google Scholar] [CrossRef]
- Nuxoll, E.E.; Cussler, E.L. The third parameter in reactive barrier films. AIChE J. 2005, 51, 456–463. [Google Scholar] [CrossRef]
- Siegel, R.A.; Cussler, E.L. Reactive barrier membranes: Some theoretical observations regarding the time lag and breakthrough curves. J. Membr. Sci. 2004, 229, 33–41. [Google Scholar] [CrossRef]
- Solovyov, S.E.; Goldman, A.Y. Optimized design of multilayer barrier films incorporating a reactive layer. I. Methodology of ingress analysis. J. Appl. Polym. Sci. 2006, 100, 1940–1951. [Google Scholar] [CrossRef]
- Lück, W. Feuchte-Messung. Handbuch der industriellen Messtechnik; Profos, P.P.T., Ed.; R. Oldenbourg: München, Germany, 1992; pp. 1015–1030. [Google Scholar]
- Pesaran, A.A. Degradation of Desiccants upon Contamination: An Experimental Study; Solar Energy Research Inst.: Golden, CO, USA, 1990. [Google Scholar]
- Bühlmann, M.R. Über die hydrothermale Alterung von Silicagelen; Juris-Verlag: Zürich, Switzerland, 1964. [Google Scholar]
- Leboda, R.; Mendyk, E.; Gierak, A.; Tertykh, V.A. Hydrothermal modification of silica gels (xerogels) 1. Effect of treatment temperature on their porous structure. Colloids Surf. A Physicochem. Eng. Asp. 1995, 105, 181–189. [Google Scholar] [CrossRef]
- Leboda, R.; Mendyk, E. Hydrothermal modification of porous structure of silica adsorbents. Mater. Chem. Phys. 1991, 27, 189–212. [Google Scholar] [CrossRef]
- Mendyk, E.; Leboda, R.; Gierak, A. Properties of hydrothermally modified silica gels—Effect of the parameters of porous structure on the course of the modification process. Mater. Chem. Phys. 1988, 20, 87–97. [Google Scholar] [CrossRef]
- Charmas, B.; Skubiszewska-Zięba, J. Application of differential scanning calorimetry to study porous structure of hydrothermally modified silicas. J. Therm. Anal. Calorim. 2017, 129, 23–32. [Google Scholar] [CrossRef]
- Langowski, H.-C. Permeation of Gases and Condensable Substances Through Monolayer and Miltilayer Structures. In Plastic Packaging: Interactions with Food and Pharmaceuticals; Piringer, O.G., Baner, A.L., Eds.; Chichester: Weinheim, Germany, 2008. [Google Scholar]
- Sängerlaub, S.; Schmid, M.; Müller, K. Comparison of water vapour transmission rates of monolayer films determined by water vapour sorption and permeation experiments. Food Packag. Shelf Life 2018, 17, 80–84. [Google Scholar] [CrossRef]
- Maxwell, C. Treatise on Electricity and Magnetism; Oxford University Press: London, UK, 1873; p. 36. [Google Scholar]
- Bruggeman, D.A.G. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen. Annalen Phys. 1935, 416, 636–664. [Google Scholar] [CrossRef]
- Higuchi, W.I. A New Relationship for the Dielectric Properties of Two Phase Mixtures. J. Phys. Chem. 1958, 62, 649–653. [Google Scholar] [CrossRef]
- Crank, J. Diffusion in heterogeneous media. In The Mathematics of Diffusion; Crank, J., Ed.; Clarendon Press: Oxford, UK, 1975; pp. 266–285. [Google Scholar]
- Bouma, R.H.B.; Checchetti, A.; Chidichimo, G.; Drioli, E. Permeation through a heterogeneous membrane: The effect of the dispersed phase. J. Membr. Sci. 1997, 128, 141–149. [Google Scholar] [CrossRef]
- Huang, Z.; Su, J.-F.; Su, X.-Q.; Guo, Y.-H.; Teng, L.-J.; Yang, C.M. Preparation and permeation characterization of β-zeolite-incorporated composite membranes. J. Appl. Polym. Sci. 2009, 112, 9–18. [Google Scholar] [CrossRef]
- Gonzo, E.E.; Parentis, M.L.; Gottifredi, J.C. Estimating models for predicting effective permeability of mixed matrix membranes. J. Membr. Sci. 2006, 277, 46–54. [Google Scholar] [CrossRef]
- Balköse, D.; Oguz, K.; Ozyuzer, L.; Tari, S.; Arkis, E.; Omurlu, F.O. Morphology, order, light transmittance, and water vapor permeability of aluminum-coated polypropylene zeolite composite films. J. Appl. Polym. Sci. 2011, 120, 1671–1678. [Google Scholar] [CrossRef]
- Friess, K.; Hynek, V.; Šípek, M.; Kujawski, W.M.; Vopička, O.; Zgažar, M.; Kujawski, M.W. Permeation and sorption properties of poly(ether-block-amide) membranes filled by two types of zeolites. Sep. Purif. Technol. 2011, 80, 418–427. [Google Scholar] [CrossRef]
- Willett, J.L. Water sorption and diffusion in starch/polyolefin blends. Polym. Eng. Sci. 1995, 35, 1184–1190. [Google Scholar] [CrossRef]
- BeMiller, J.N.; Huber, K.C. Starch. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2000. [Google Scholar]
- Peanasky, J.S.; Long, J.M.; Wool, R.P. Percolation effects in degradable polyethylene-starch blends. J. Polym. Sci. Part B Polym. Phys. 1991, 29, 565–579. [Google Scholar] [CrossRef]
- Kenny, M.; Oates, T. Lime and Limestone. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2000. [Google Scholar]
- Kanehashi, S.; Nagai, K. Analysis of dual-mode model parameters for gas sorption in glassy polymers. J. Membr. Sci. 2005, 253, 117–138. [Google Scholar] [CrossRef]
- McCall, D.W.; Douglass, D.C.; Blyler, L.L.; Johnson, G.E.; Jelinski, L.W.; Bair, H.E. Solubility and diffusion of water in low-density polyethylene. Macromolecules 1984, 17, 1644–1649. [Google Scholar] [CrossRef]
- Bendahou, D.; Bendahou, A.; Grohens, Y.; Kaddami, H. New nanocomposite design from zeolite and poly(lactic acid). Ind. Crops Prod. 2015, 72, 107–118. [Google Scholar] [CrossRef]
- Wolińska-Grabczyk, A.; Kubica, P.; Jankowski, A.; Wójtowicz, M.; Kansy, J.; Wojtyniak, M. Gas and water vapor transport properties of mixed matrix membranes containing 13X zeolite. J. Membr. Sci. 2017, 526, 334–347. [Google Scholar] [CrossRef]
- Bleisch, G.; Langowski, H.-C.; Majschak, J.-P. Lexikon Verpackungstechnik, 2nd ed.; Behr: Hamburg, Germany, 2014. [Google Scholar]
- Krevelen, D.W.V. Mechanical Properties of Solid Polymers. In Properties of Polymers: Their Correlation with Chemical Structure: Their Numerical Estimation and Prediction from Additive Group Contributions; Krevelen, D.W.V., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 383–503. [Google Scholar]
- Bigg, D.M. Mechanical properties of particulate filled polymers. Polym. Compos. 1987, 8, 115–122. [Google Scholar] [CrossRef]
- Chacko, V.P.; Farris, R.J.; Karasz, F.E. Tensile properties of CaCO3-filled polyethylenes. J. Appl. Polym. Sci. 1983, 28, 2701–2713. [Google Scholar] [CrossRef]
- Arina, M.; Honkanen, A.; Tammela, V. Mineral Fillers in Low Density-Polyethylene Films. Polym. Eng. Sci. 1979, 19, 30–39. [Google Scholar] [CrossRef]
- Shakoor, A.; Thomas, N.L. Talc as a nucleating agent and reinforcing filler in poly(lactic acid) composites. Polym. Eng. Sci. 2014, 54, 64–70. [Google Scholar] [CrossRef]
- Thiele, E.W. Relation between Catalytic Activity and Size of Particle. Ind. Eng. Chem. 1939, 31, 916–920. [Google Scholar] [CrossRef]
- Jakubith, M. Adsorption und heterogene Katalyse. In Grundoperationen und Chemische Reaktionstechnik: Einführung in Die Technische Chemie; Wiley-VCH: Weinheim, Germany, 1998; pp. 211–247. [Google Scholar]
- Fogler, H.S. Elements of Chemical Reaction Engineering; Prentice Hall PTR: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- Molga, E.J.; Westerterp, K.R. Principles of Chemical Reaction Engineering. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag GmbH & Co. KgaA: Weinheim, Germany, 2000. [Google Scholar]
- Sängerlaub, S. Wasserdampfsorption in Polymerfolien mit Dispergierten Sorbentien. In Ph.D. Thesis; Fakultät Wissenschaftszentrum Weihenstephan für Ernährung, Landnutzung und Umwelt, Technische Universität München, Fraunhofer Verlag: Stuttgart, Germany, 2019. [Google Scholar]



| Sample | Thickness/µm | ||
|---|---|---|---|
| Sorption Experiments (Extruded) | Tensile Tests (Extruded) | Permeability Tests (Extruded, Then Thermo-Pressed) | |
| PE-LD | 1754 ± 26 | 188 ± 27 | 315 ± 24 |
| 0.2 g silica gel/g film | 1868 ± 28 | 1183 ± 29 | 357 ± 46 |
| 0.4 g silica gel/g film | 1568 ± 37 | 768 ± 52 | 512 ± 72 |
| 0.6 g silica gel/g film | 1391 ± 22 | 766 ± 79 | 232 ± 25 |
| Sample | Density/g·cm−3; Measured | Density/g·cm−3; Expected |
|---|---|---|
| 0.2 g silica gel/g film | 1.02 ± 0.01 | 0.99 |
| 0.4 g silica gel/g film | 1.19 ± 0.01 | 1.04 |
| 0.6 g silica gel/g film | 1.35 ± 0.01 | 1.10 |
| comparison: PE-LD | 0.94 ± 0.01 | 0.91, 0.94* |
| comparison: Silica gel | - | 1.24 |
| comparison: SiO2 | - | 2.2 |
| Sample | D, Deff./(cm2·s−1)·10−10 | Deff. Permeation/Deff. Absorption | |||
|---|---|---|---|---|---|
| From Sorption Test | From Permeation Test; 85 → 0% RH | ||||
| 9% RH | 52% RH | 91% RH | |||
| Comparison: PE-LD | - | - | - | 627, 482, 670* | - |
| 0.2 g silica gel/g film | 3.4 ± 0.3 | 3.6 ± 0.2 | 4.8 ± 0.4 | 5.0 | 1.4 to 1.5 |
| 0.4 g silica gel/g film | 3.1 ± 0.4 | 3.7 ± 0.3 | 6.1 ± 0.4 | 4.7 | 0.8 to 1.5 |
| 0.6 g silica gel/g film | 5.1 ± 0.3 | 11.3 ± 0.7 | 19.7 ± 1.1 | 12.2 | 0.6 to 2.4 |
| Sample | |||
|---|---|---|---|
| 9% RH; 261 Pa | 52% RH; 1460 Pa | 91% RH; 2555 Pa | |
| Comparison: PE-LD | - | ~0 | - |
| 0.2 g silica gel/g film | 0.56 ± 0.02 | 2.17 ± 0.02 | 3.14 ± 0.03 |
| 0.4 g silica gel/g film | 1.34 ± 0.02 | 4.59 ± 0.05 | 6.39 ± 0.11 |
| 0.6 g silica gel/g film | 1.84 ± 0.07 | 5.78 ± 0.11 | 8.32 ± 0.11 |
| S, Seff./(mg H2O·(cm3 polymer·Pa)−1)·10−2 | |||
| Comparison: PE-LD | - | 0.0067* | - |
| 0.2 g silica gel/g film | 2.19 ± 0.09 | 1.52 ± 0.02 | 1.26 ± 0.02 |
| 0.4 g silica gel/g film | 6.12 ± 0.09 | 3.76 ± 0.04 | 2.99 ± 0.05 |
| 0.6 g silica gel/g film | 9.47 ± 0.28 | 5.33 ± 0.09 | 4.39 ± 0.05 |
| Film Samples | Permeation Measurements (mg·cm·(cm2·s·Pa)−1)·1012 | Peff. Permeation Peff.Absorption−1- | |||
|---|---|---|---|---|---|
| Permeation Test | |||||
| 9% RH | 52% RH | 91% RH | |||
| Comparison: PE-LD | - | - | - | 4.26 ± 0.11 | - |
| 0.2 g silica gel/g film | 7.4 ± 0.8 | 6.6 ± 2.9 | 6.0 ± 0.4 | 8.4 ± 2.5 | 1.1 to 1.4 |
| 0.4 g silica gel/g film | 19.0 ± 2.6 | 13.9 ± 1.0 | 18.2 ± 1.2 | 20.3 ± 4.7 | 1.1 to 1.5 |
| 0.6 g silica gel/g film | 48.0 ± 3.2 | 60.1 ± 4.8 | 86.4 ± 5.0 | 60.2 ± 0.5 | 0.7 to 1.3 |
| Sample | Permeation Coefficients/(mg·cm·(cm2·s·Pa)−1)·1014, 23 °C | (Effective) Permeation Coefficients/(mg·cm·(cm2·s·Pa)−1)·1012 | ||
|---|---|---|---|---|
| N2 | O2 | CO2 | H2O | |
| PE-LD | 6.3 ± 0.7 | 25.4 ± 2.7 | 110.6 ± 7.5 | 4.3 ± 0.1 |
| 0.2 g silica gel/g film | 2.8 | 13.8 | 60.4 | 8.4 ± 2.5 |
| 0.4 g silica gel/g film | 1.5 ± 0.2 | 7.8 ± 1.3 | 26.2 ± 7.4 | 20.3 ± 4.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sängerlaub, S.; Kucukpinar, E.; Müller, K. Desiccant Films Made of Low-Density Polyethylene with Dispersed Silica Gel—Water Vapor Absorption, Permeability (H2O, N2, O2, CO2), and Mechanical Properties. Materials 2019, 12, 2304. https://doi.org/10.3390/ma12142304
Sängerlaub S, Kucukpinar E, Müller K. Desiccant Films Made of Low-Density Polyethylene with Dispersed Silica Gel—Water Vapor Absorption, Permeability (H2O, N2, O2, CO2), and Mechanical Properties. Materials. 2019; 12(14):2304. https://doi.org/10.3390/ma12142304
Chicago/Turabian StyleSängerlaub, Sven, Esra Kucukpinar, and Kajetan Müller. 2019. "Desiccant Films Made of Low-Density Polyethylene with Dispersed Silica Gel—Water Vapor Absorption, Permeability (H2O, N2, O2, CO2), and Mechanical Properties" Materials 12, no. 14: 2304. https://doi.org/10.3390/ma12142304
APA StyleSängerlaub, S., Kucukpinar, E., & Müller, K. (2019). Desiccant Films Made of Low-Density Polyethylene with Dispersed Silica Gel—Water Vapor Absorption, Permeability (H2O, N2, O2, CO2), and Mechanical Properties. Materials, 12(14), 2304. https://doi.org/10.3390/ma12142304