Cable Tension Monitoring Based on the Elasto-Magnetic Effect and the Self-Induction Phenomenon
Abstract
1. Introduction
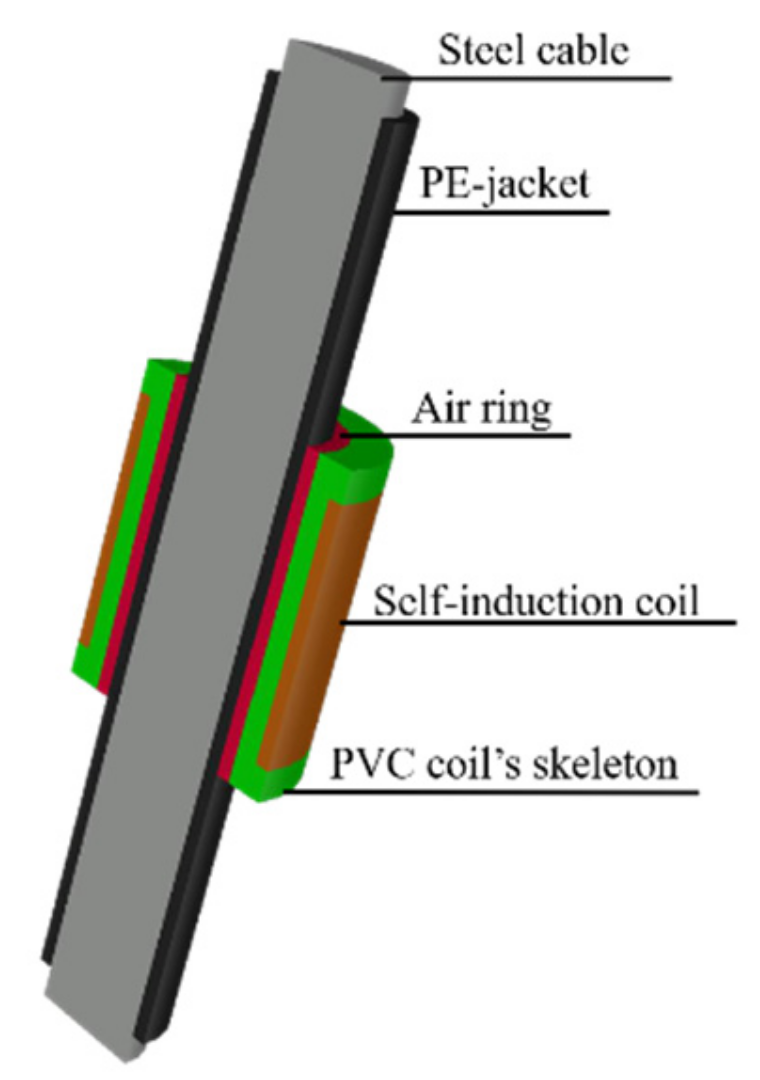
2. Working Mechanism
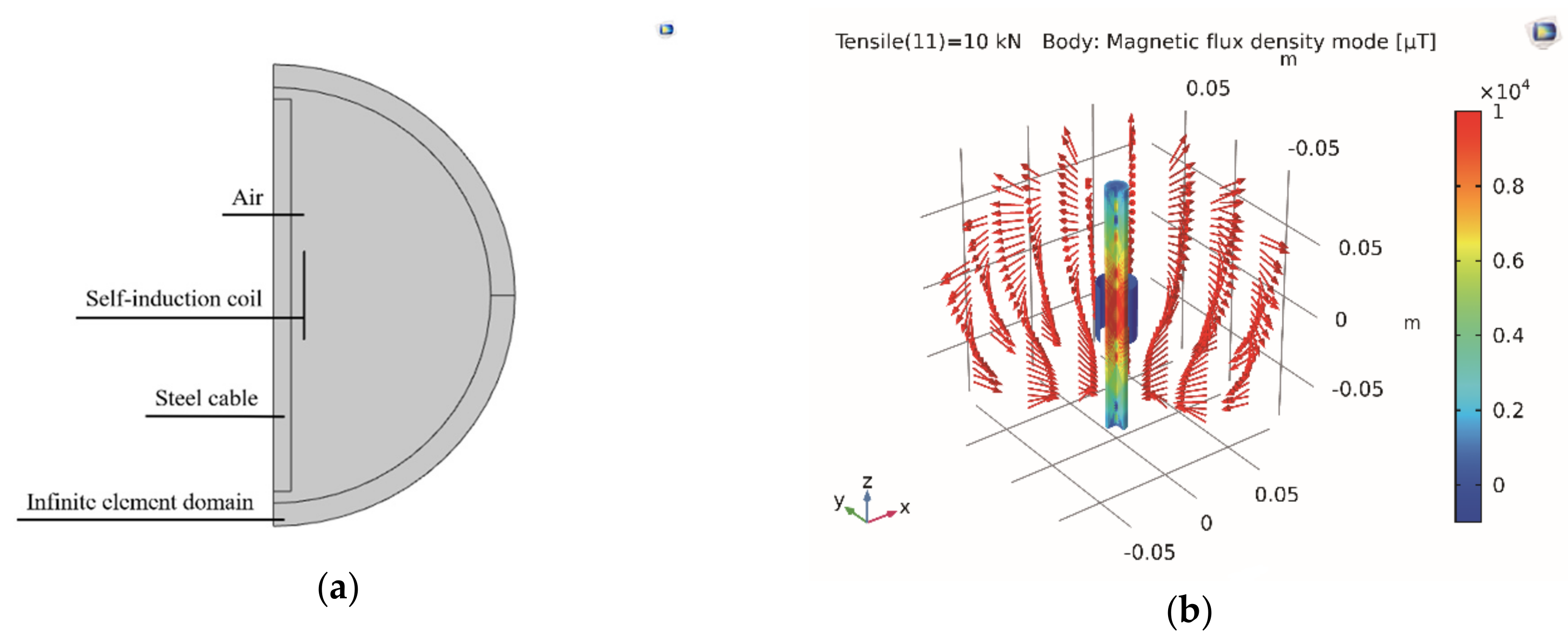
3. Numerical Analysis
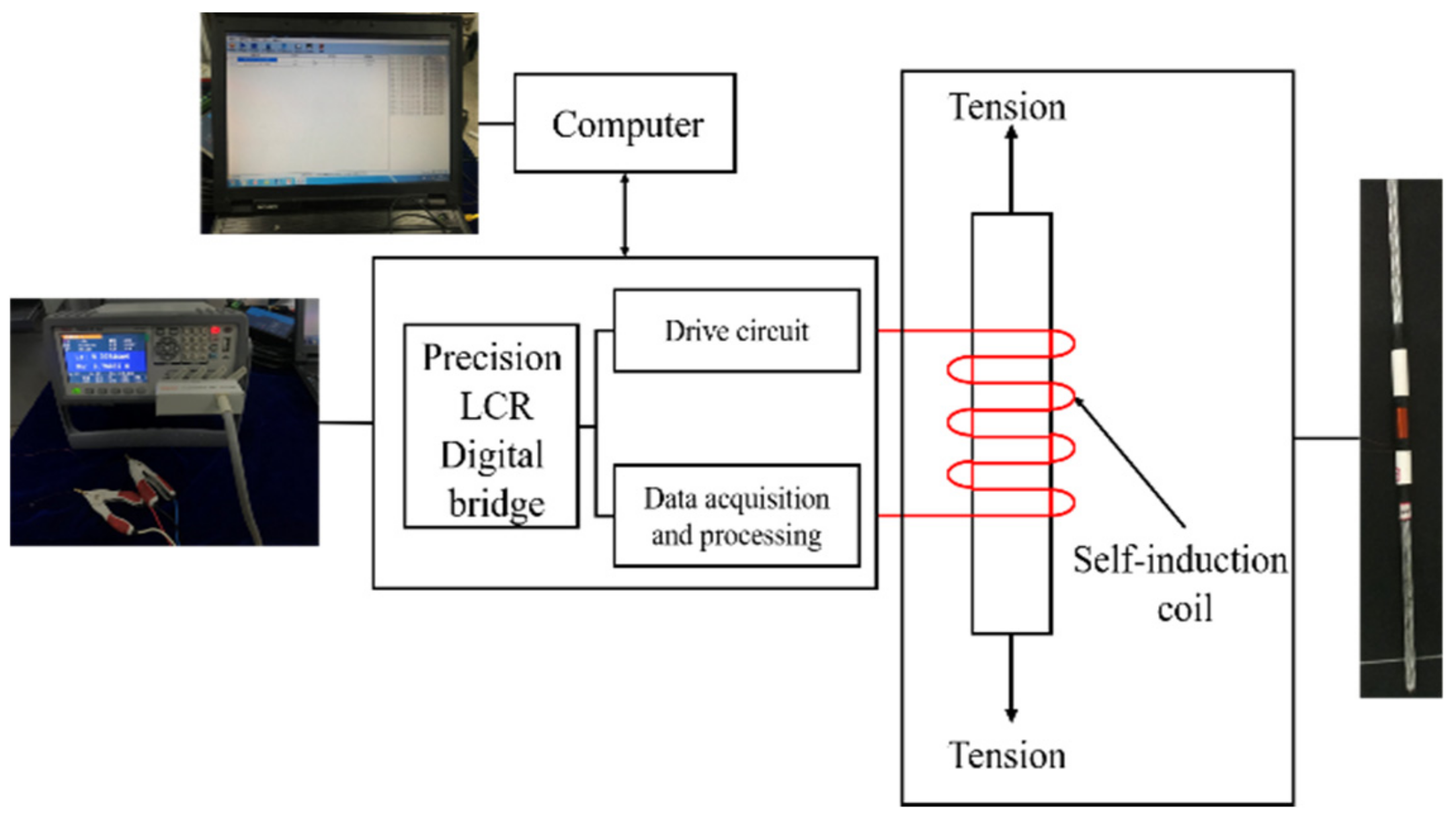
4. Experimental Verification
4.1. Materials and Methods
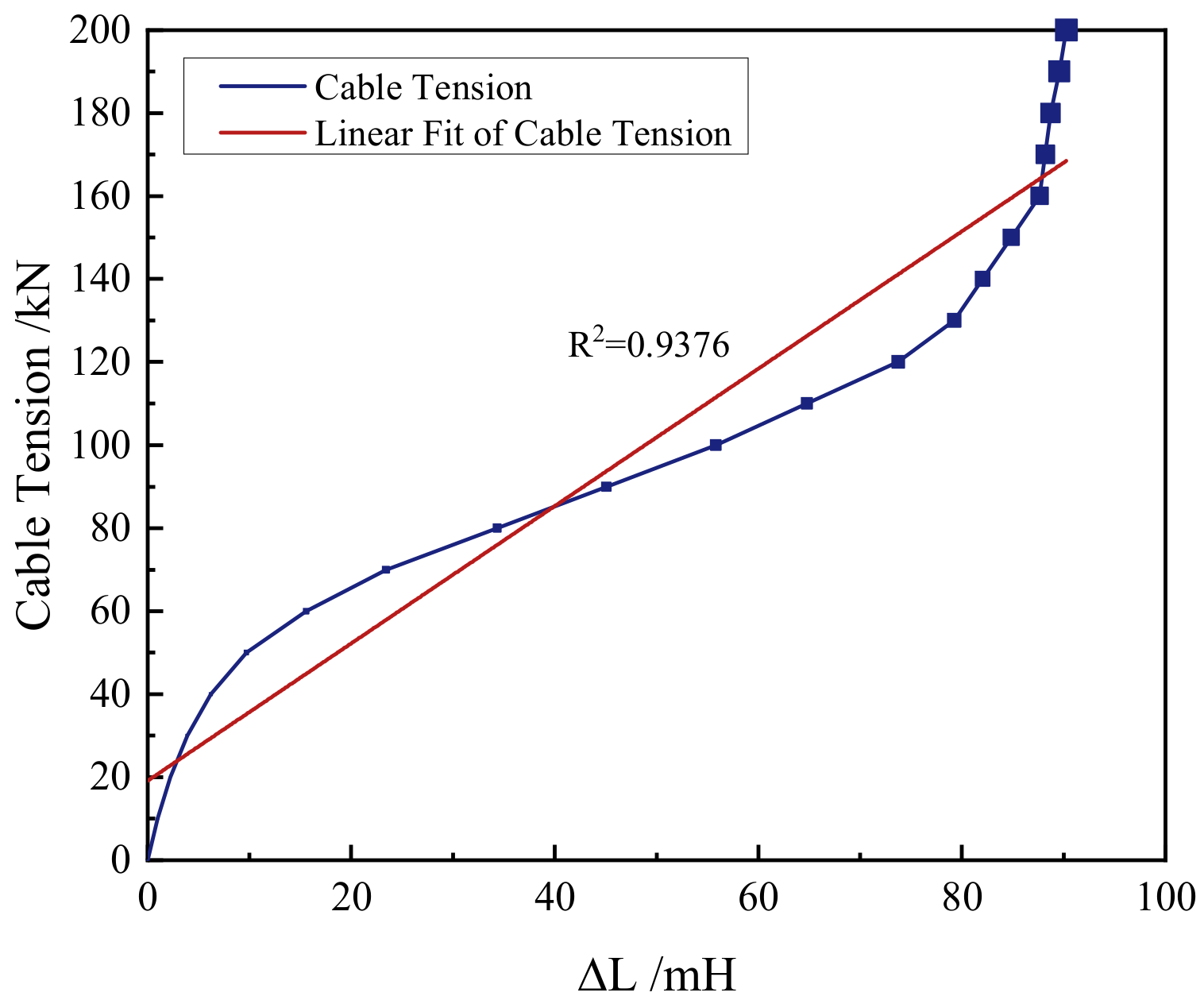
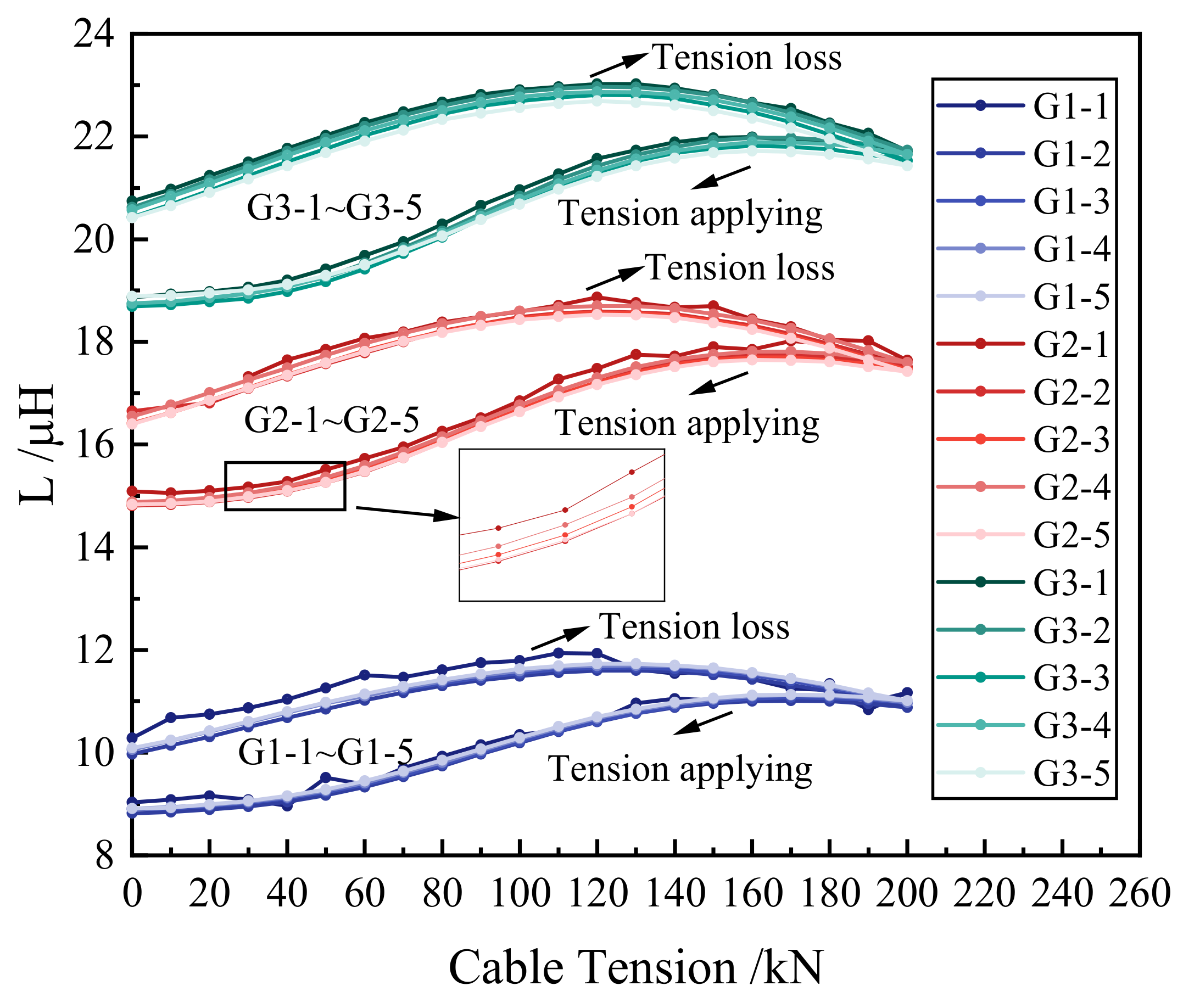
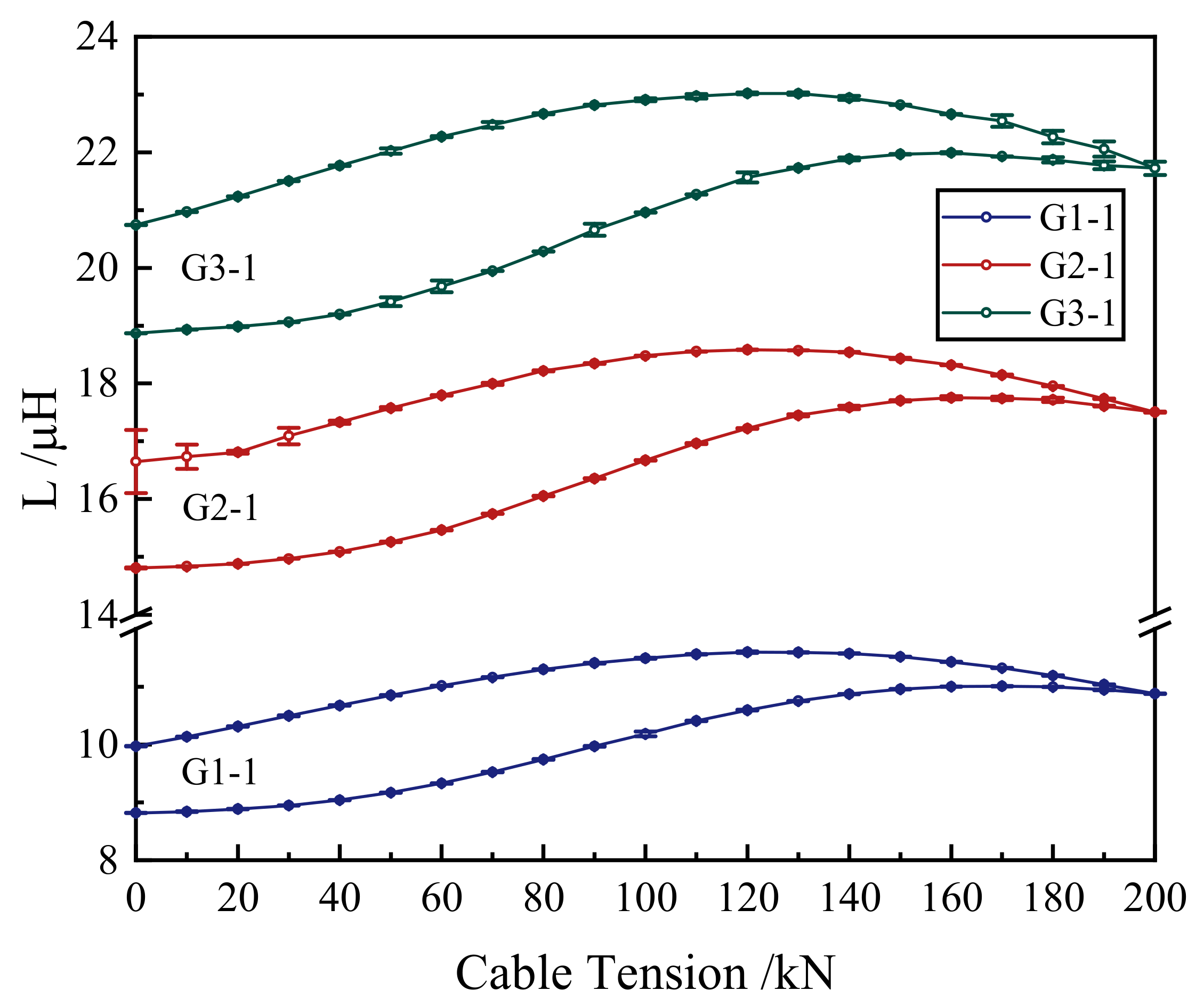
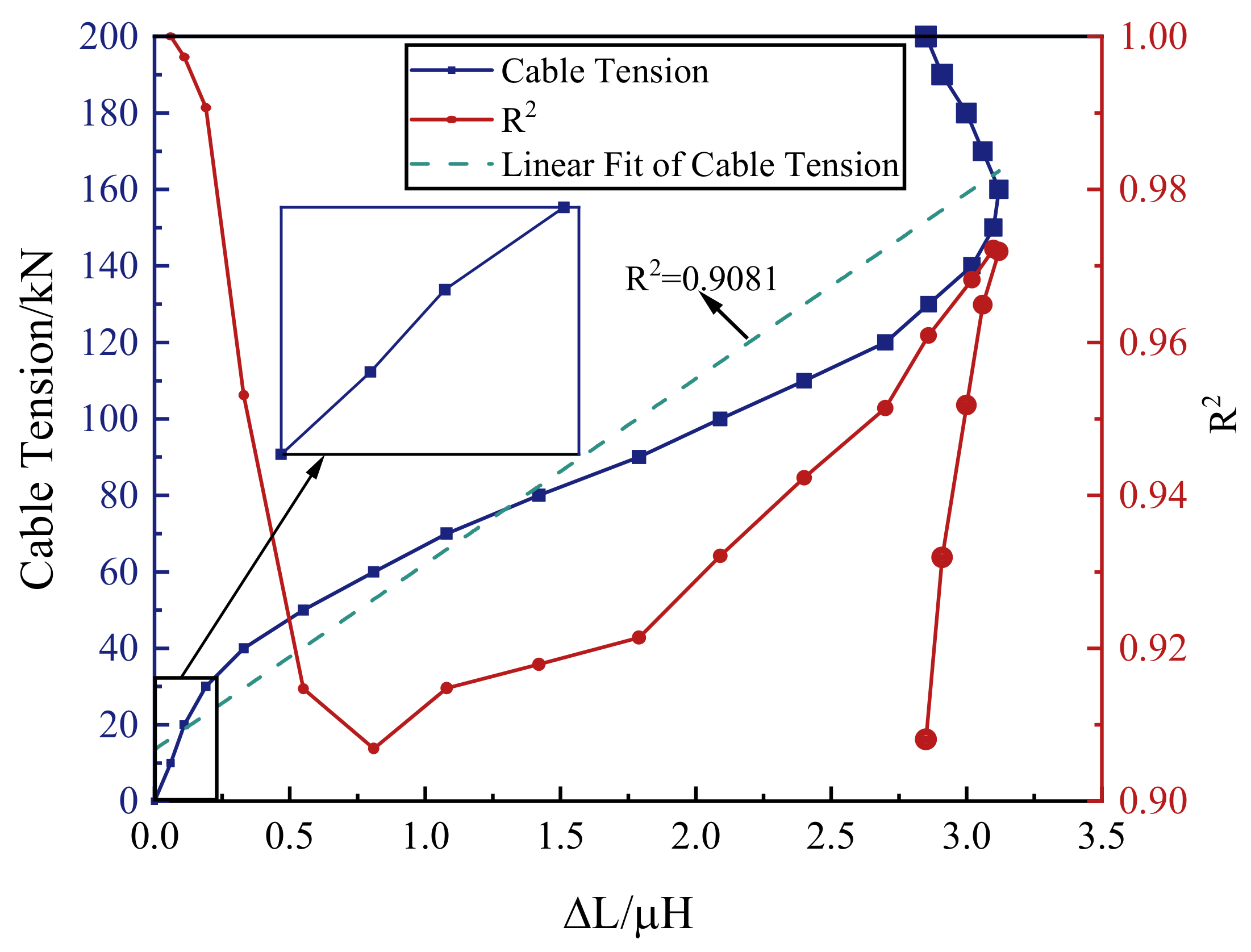
4.2. Experimental Results
5. Conclusions
- (1)
- The traditional EM sensor’s primary coil and induction unit were simplified into a self-induction coil. By analyzing the EMI method’s working mechanism, a set of cable tension monitoring systems was presented. The EMI method’s correctness was proved by the numerical analysis. The experiments were carried out to verify the results of the numerical analysis.
- (2)
- Based on the experimental results, the monitoring data processing and tension calculation methods were proposed. The methods were suitable for the tension-applying stage and the tension-loss stage. The results proved that the relation between the inductance increment and the cable tension of the tension-loss stage is different from that relation of the tension-applying stage. The results indicated that different cables of the same batch can be calibrated by one proper equation. The results demonstrated that the length of the self-induction coil has little effect on the accuracy and sensitivity of the cable tension monitoring.
- (3)
- The results of the numerical analysis and the experiments proved that the cable tension of the cable-supported structures can be monitored both at the tension-applying stage and at the tension-loss stage. The proposed EMI method and the given monitoring system are feasible to monitor the cable tension with high sensitivity, fast response, and easy installation, apart from the advantages of the traditional EM sensor.
Author Contributions
Funding
Conflicts of Interest
References
- Wong, K.Y. Instrumentation and health monitoring of cable-supported bridges. Struct. Control Health Monit. 2004, 11, 91–124. [Google Scholar] [CrossRef]
- Kim, B.H.; Park, T. Estimation of cable tension force using the frequency-based system identification method. J. Sound Vib. 2007, 304, 660–676. [Google Scholar] [CrossRef]
- Mozos, C.; Aparicio, A. Numerical and experimental study on the interaction cable structure during the failure of a stay in a cable stayed bridge. Eng. Struct. 2011, 33, 2330–2341. [Google Scholar] [CrossRef]
- Ren, W.-X.; Chen, G.; Hu, W.-H. Empirical formulas to estimate cable tension by cable fundamental frequency. Struct. Eng. Mech. 2005, 20, 363–380. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Y.; Fu, J.; Liu, A.; Gao, W. Measurement of the real-time deflection of cable-stayed bridge based on cable tension variations. Measurement 2018, 119, 218–228. [Google Scholar] [CrossRef]
- Nazarian, E.; Ansari, F.; Zhang, X.; Taylor, T. Detection of tension loss in cables of cable-stayed bridges by distributed monitoring of bridge deck strains. J. Struct. Eng. 2016, 142, 04016018. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, J.-Q. Practical formula for cable tension estimation by vibration method. J. Bridge Eng. 2010, 17, 161–164. [Google Scholar] [CrossRef]
- Zhang, Z.; He, J.; Lin, Y.; Liu, X.; Han, X. Evaluation of measurement methods for tension of parallel steel strand stay cables. Bridge Const. 2016, 46, 42–47. [Google Scholar]
- Casciati, S.; Elia, L. Estimating cable forces in a large cable-stayed bridge. In Advances in Science and Technology; Trans Tech Publications: Zurich, Switzerland, 2017; pp. 26–34. [Google Scholar]
- Li, S.; Wei, S.; Bao, Y.; Li, H. Condition assessment of cables by pattern recognition of vehicle-induced cable tension ratio. Eng. Struct. 2018, 155, 1–15. [Google Scholar] [CrossRef]
- Dan, D.; Jia, P.; Li, G.; Niu, P. Experimental Study on Mechanical and Sensing Properties of Smart Composite Prestressed Tendon. Materials 2018, 11, 2087. [Google Scholar] [CrossRef]
- Xu, F.; Chen, Y.; Zheng, X.; Ma, R.; Tian, H. Experimental Study on Corrosion and Mechanical Behavior of Main Cable Wires Considering the Effect of Strain. Materials 2019, 12, 753. [Google Scholar] [CrossRef]
- Li, H.; Ou, J. The state of the art in structural health monitoring of cable-stayed bridges. J. Civ. Struct. Health Monit. 2016, 6, 43–67. [Google Scholar] [CrossRef]
- Shu, Y.; Chen, W.-M.; Zhang, P.; Wu, J.; Liu, L.; Zhao, X. Embedding technology of Fiber Bragg Grating strain sensor for cable tension monitor. In Proceedings of the 2013 International Conference on Optical Instruments and Technology: Optical Sensors and Applications, Beijing, China, 17 November 2013; International Society for Optics and Photonics: Bellingham, WA, USA; p. 90440H. [Google Scholar]
- Lv, X.J.; Zhao, X.F.; Wang, L.; Dong, H.; Zhu, Y.F. Research on fiber Bragg grating sensing technique for cable tension monitoring of suspension bridges. In Applied Mechanics and Materials; Trans Tech Publications: New York, NY, USA, 2013; pp. 1391–1395. [Google Scholar]
- Song, Y.; Wang, J. Dynamic forces measurement of cables in structural health monitoring. In Proceedings of the Smart Sensor Phenomena, Technology, Networks, and Systems 2010, San Diego, CA, USA, 1 January 2010; International Society for Optics and Photonics: Bellingham, WA, USA, 2010; p. 764819. [Google Scholar]
- Chen, C.-C.; Wu, W.-H.; Leu, M.-R.; Lai, G. Tension determination of stay cable or external tendon with complicated constraints using multiple vibration measurements. Measurement 2016, 86, 182–195. [Google Scholar] [CrossRef]
- Zheng, G.; Ko, J.M.; Ni, Y.-Q. Multimode-based evaluation of cable tension force in cable-supported bridges. In Proceedings of the Smart Structures and Materials 2001: Smart Systems for Bridges, Structures, and Highways, Newport Beach, CA, USA, 1 January 2001; International Society for Optics and Photonics: Bellingham, WA, USA; pp. 511–523. [Google Scholar]
- Chaki, S.; Bourse, G. Stress level measurement in prestressed steel strands using acoustoelastic effect. Exp. Mech. 2009, 49, 673. [Google Scholar] [CrossRef]
- Zagrai, A.; Gigineishvili, V.; Kruse, W.A.; Murray, A.; Doyle, D.; Reynolds, W.; Arritt, B.; Gardenier, H. Acousto-elastic measurements and baseline-free assessment of bolted joints using guided waves in space structures. In Proceedings of the Health Monitoring of Structural and Biological Systems 2010, San Diego, CA, USA, 1 January 2010; International Society for Optics and Photonics: Bellingham, WA, USA, 2010; p. 765017. [Google Scholar]
- Bartoli, I.; Nucera, C.; Srivastava, A.; Salamone, S.; Phillips, R.; di Scalea, F.L.; Coccia, S.; Sikorsky, C.S. Nonlinear ultrasonic guided waves for stress monitoring in prestressing tendons for post-tensioned concrete structures. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2009, San Diego, CA, USA, 9 March 2009; International Society for Optics and Photonics: Bellingham, WA, USA, 2009; p. 729220. [Google Scholar]
- Schoenekess, H.; Ricken, W.; Becker, W.; Fehling, E.; Welz, A. Dynamic Load Inspection on Steel Tendons of Steel Reinforced Concrete Constructions by means of Eddy-Current Sensors. In Proceedings of the 9th European conference on non-destructive testing: ECNDT 2006, Berlin, Germany, September 25–29 2006; pp. 3836–3844. [Google Scholar]
- Kim, J.-M.; Lee, J.; Sohn, H. Automatic measurement and warning of tension force reduction in a PT tendon using eddy current sensing. NDT E Int. 2017, 87, 93–99. [Google Scholar] [CrossRef]
- Schoenekess, H.; Ricken, W.; Liu, J.-G.; Becker, W.-J. Eddy-current sensors and their applications to force and stress measurement in steel reinforced concrete. VDI Ber. 2002, 1685, 129–134. [Google Scholar]
- Xiu, C.; Ren, L.; Li, H. Investigation on eddy current sensor in tension measurement at a resonant frequency. Appl. Sci. 2017, 7, 538. [Google Scholar] [CrossRef]
- Duan, Y.-F.; Zhang, R.; Dong, C.-Z.; Luo, Y.-Z.; Or, S.W.; Zhao, Y.; Fan, K.-Q. Development of elasto-magneto-electric (EME) sensor for in-service cable force monitoring. Int. J. Struct. Stab. Dyn. 2016, 16, 1640016. [Google Scholar] [CrossRef]
- Joh, C.; Lee, J.W.; Kwahk, I. Feasibility study of stress measurement in prestressing tendons using Villari effect and induced magnetic field. Int. J. Distrib. Sens. Netw. 2013, 9, 249829. [Google Scholar] [CrossRef]
- Zhang, Z.J.; He, J.Q.; Lin, Y.C.; Liu, X.H.; Han, X.C. Evaluations of Measurement Methods for Parallel Strand Cables. In Applied Mechanics and Materials; Trans Tech Publications: Zurich, Switzerland, 2015; pp. 882–888. [Google Scholar]
- Wang, M.L.; Wang, G.; Zhao, Y. Application of EM stress sensors in large steel cables. In Sensing Issues in Civil Structural Health Monitoring; Springer: Berlin, Germany, 2005; pp. 145–154. [Google Scholar]
- Cappello, C.; Zonta, D.; Ait Laasri, H.; Glisic, B.; Wang, M. Calibration of elasto-magnetic sensors on in-service cable-stayed bridges for stress monitoring. Sensors 2018, 18, 466. [Google Scholar] [CrossRef]
- Deng, Y.; Li, A. Tension Force Monitoring of Main Cable. In Structural Health Monitoring for Suspension Bridges; Springer: Berlin, Germany, 2019; pp. 201–218. [Google Scholar]
- Pereira, K.; Crawford, M. Tension Sensor Assembly. U.S. Patent No. 8,766,812, 2014. [Google Scholar]
- Kim, J.; Kim, J.-W.; Park, S. Investigation of Applicability of an Embedded EM Sensor to Measure the Tension of a PSC Girder. J. Sens. 2019, 2019, 1–12. [Google Scholar] [CrossRef]
- Zhang, R.; Duan, Y.; Or, S.; Zhao, Y. Smart elasto-magneto-electric (EME) sensors for stress monitoring of steel cables: Design theory and experimental validation. Sensors 2014, 14, 13644–13660. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Gu, Y.; Wang, Y. A review of three magnetic NDT technologies. J. Magn. Magn. Mater. 2012, 324, 382–388. [Google Scholar] [CrossRef]
- Calkins, F.T.; Flatau, A.B.; Dapino, M.J. Overview of magnetostrictive sensor technology. J. Intell. Mater. Syst. Struct. 2007, 18, 1057–1066. [Google Scholar] [CrossRef]
- Duan, Y.-F.; Zhang, R.; Zhao, Y.; Or, S.-W.; Fan, K.-Q.; Tang, Z.-F. Smart elasto-magneto-electric (EME) sensors for stress monitoring of steel structures in railway infrastructures. J. Zhejiang Univ. Sci. A 2011, 12, 895–901. [Google Scholar] [CrossRef]
- Sumitro, S.; Jarosevic, A.; Wang, M. Elasto-magnetic sensor utilization on steel cable stress measurement. In Proceedings of the First fib Congress, Concrete Structures in the 21th Century, Osaka, Japan, 13–19 October; 2002; pp. 13–19. [Google Scholar]
- Xu, J.; Chen, G.; Zhou, J.; Li, Y. Effect of fatigue damage on the notch frequency of the prestressing strand based on magnetostrictive guided waves. Int. J. Appl. Electromagn. Mech. 2018, 59, 1–8. [Google Scholar] [CrossRef]
- Daniel, L.; Hubert, O.; Buiron, N.; Billardon, R. Reversible magneto-elastic behavior: A multiscale approach. J. Mech. Phys. Solids 2008, 56, 1018–1042. [Google Scholar] [CrossRef]
- Dapino, M.J.; Smith, R.C.; Calkins, F.T.; Flatau, A.B. A Magnetoelastic Model for Villari-Effect Magnetostrictive Sensors; North Carolina State University: Raleigh, NC, USA; Center for Research in Scientific Computation: Raleigh, NC, USA, 2002. [Google Scholar]
- Jiles, D.C.; Devine, M.K. Recent developments in modeling of the stress derivative of magnetization in ferromagnetic materials. J. Appl. Phys. 1994, 76, 7015–7017. [Google Scholar] [CrossRef]
- Duan, Y.F.; Zhang, R.; Zhao, Y.; Or, S.W.; Tang, Z.F. Steel stress monitoring sensor based on elasto-magnetic effect and using magneto-electric laminated composite. J. Appl. Phys. 2012, 111, 07E516. [Google Scholar] [CrossRef]
- Tiachacht, S.; Bouazzouni, A.; Khatir, S.; Wahab, M.A.; Behtani, A.; Capozucca, R. Damage assessment in structures using combination of a modified Cornwell indicator and genetic algorithm. Eng. Struct. 2018, 177, 421–430. [Google Scholar] [CrossRef]
- Khatir, S.; Wahab, M.A.; Boutchicha, D.; Khatir, T. Structural health monitoring using modal strain energy damage indicator coupled with teaching-learning-based optimization algorithm and isogoemetric analysis. J. Sound Vib. 2019, 448, 230–246. [Google Scholar] [CrossRef]
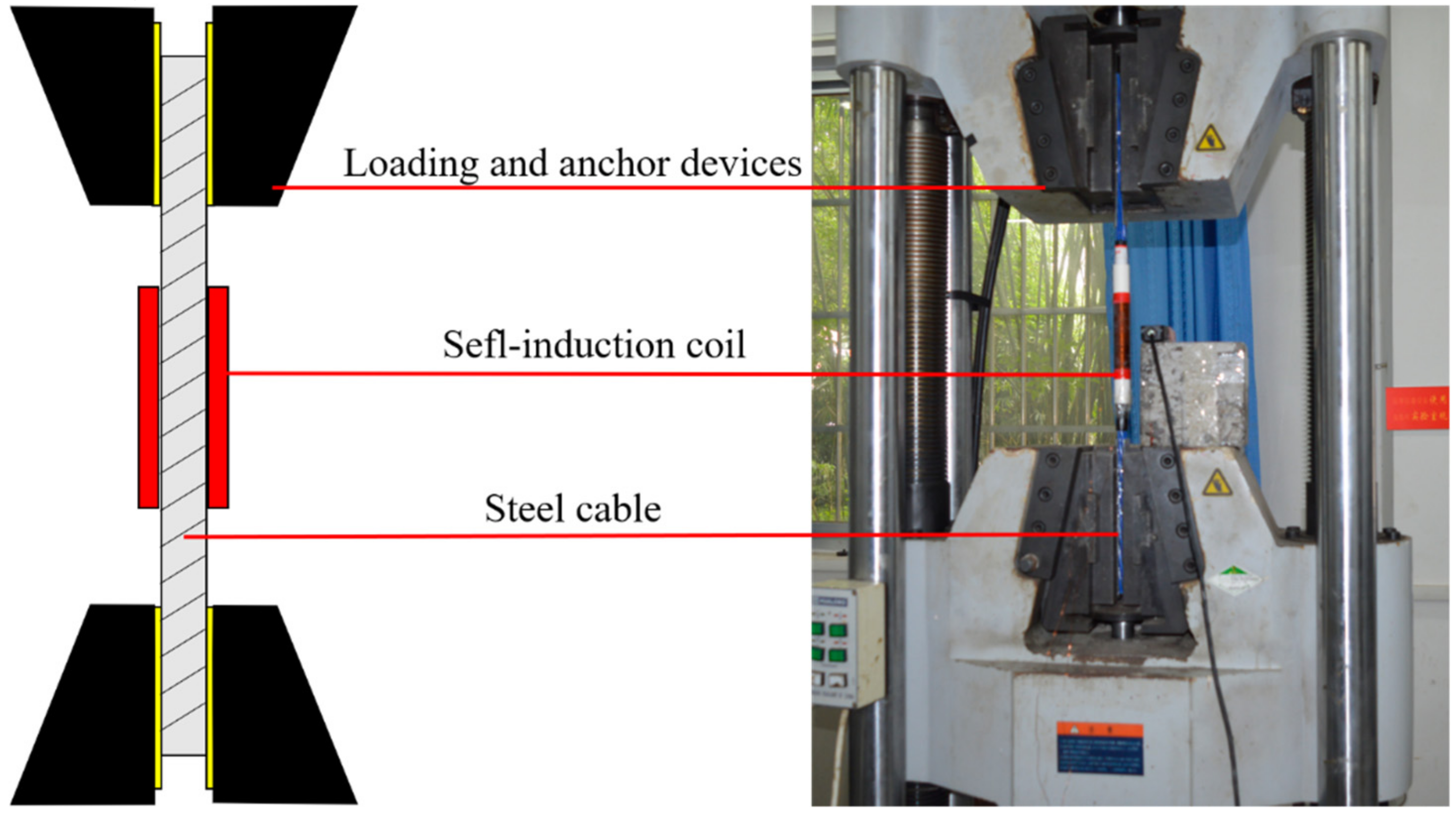
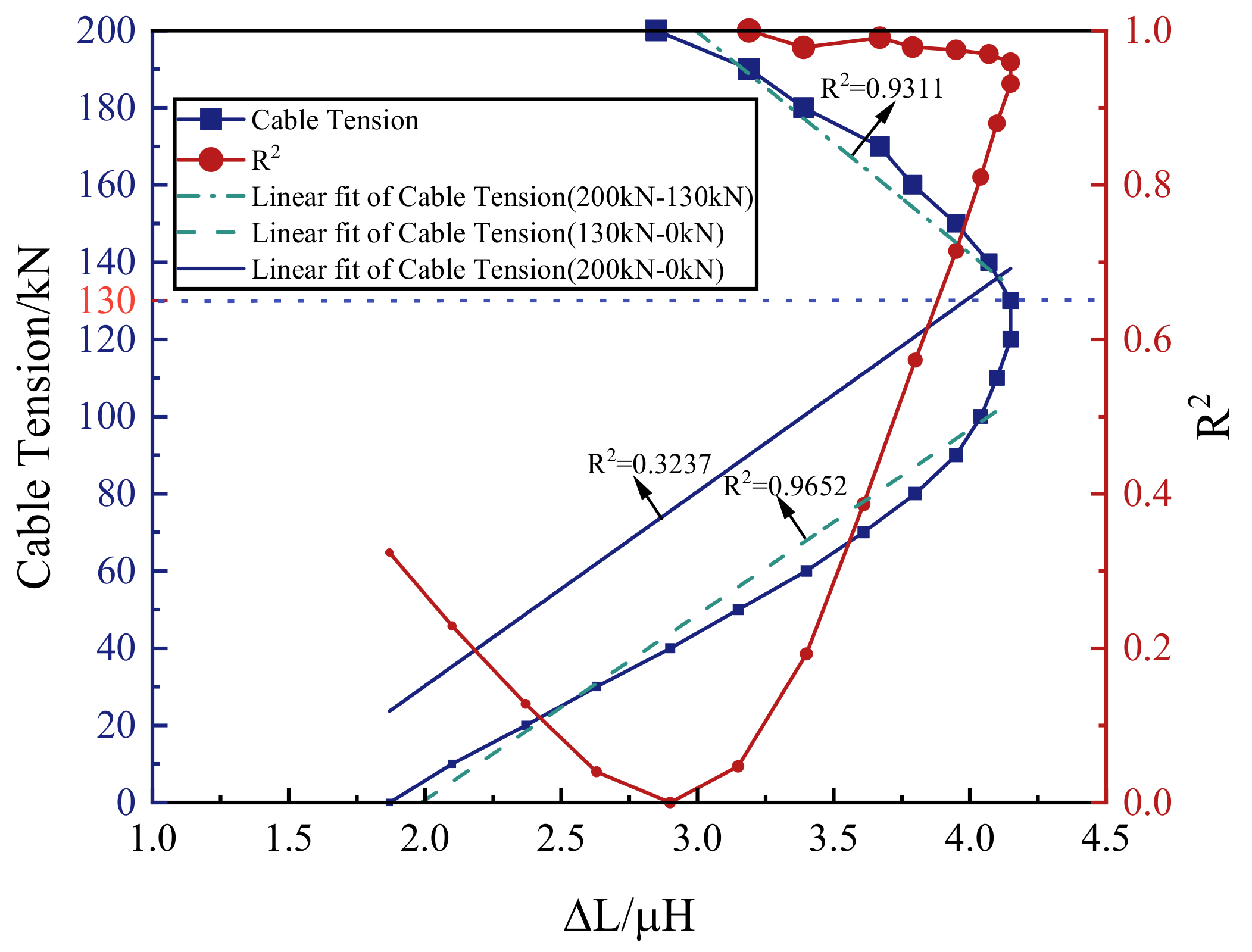
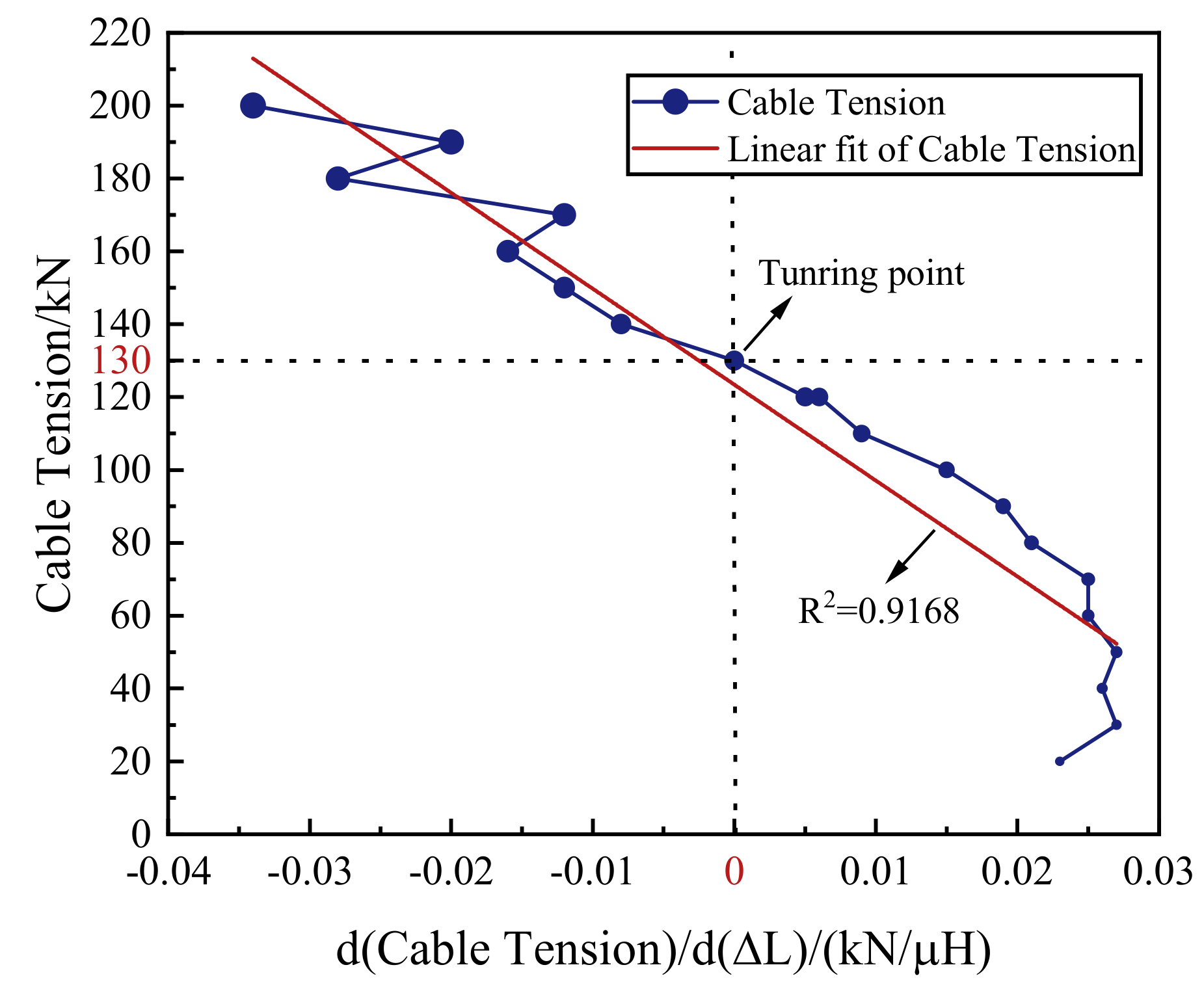
| Nominal Diameter/mm | Tensile Strength/MPa | Limit Load/kN | Yield Load/kN |
|---|---|---|---|
| 15.2 | 1860 | 259 | 220 |
| Label | Number of Turns | Number of Layers | Length/mm | Tested Specimens |
|---|---|---|---|---|
| G1 | 300 | 1 | 105 | G1-1~G1-5 |
| G2 | 300 | 2 | 52.5 | G2-1~G2-5 |
| G3 | 300 | 3 | 35 | G3-1~G3-5 |
| Specimen Label | Absolute Relative Change Rate of the Inductance to the Tension | |
|---|---|---|
| Tension-Applying Stage | Tension-Loss Stage | |
| G1-1 | 1.16% | 1.17% |
| G2-1 | 1.60% | 1.51% |
| G3-1 | 1.70% | 1.79% |
| Self-Induction Coil | Specimen | R2 of the Tension-Applying Stage | R2 of the Tension-Loss Stage | Average R2 of the Self-Induction Coil |
|---|---|---|---|---|
| G1 | G1-1 | 0.9081 | 0.9030 | 0.9215 |
| G1-2 | 0.9261 | 0.9329 | ||
| G1-3 | 0.9165 | 0.9264 | ||
| G1-4 | 0.9274 | 0.9405 | ||
| G1-5 | 0.9163 | 0.9179 | ||
| G2 | G2-1 | 0.9128 | 0.8629 | 0.9129 |
| G2-2 | 0.9249 | 0.9027 | ||
| G2-3 | 0.9217 | 0.9113 | ||
| G2-4 | 0.9273 | 0.9195 | ||
| G2-5 | 0.9219 | 0.9240 | ||
| G3 | G3-1 | 0.9307 | 0.9694 | 0.9341 |
| G3-2 | 0.9354 | 0.9244 | ||
| G3-3 | 0.9450 | 0.9324 | ||
| G3-4 | 0.9399 | 0.9205 | ||
| G3-5 | 0.9412 | 0.9020 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Zhou, J.; Zhou, Y.; Zhang, H.; Chen, J. Cable Tension Monitoring Based on the Elasto-Magnetic Effect and the Self-Induction Phenomenon. Materials 2019, 12, 2230. https://doi.org/10.3390/ma12142230
Zhang S, Zhou J, Zhou Y, Zhang H, Chen J. Cable Tension Monitoring Based on the Elasto-Magnetic Effect and the Self-Induction Phenomenon. Materials. 2019; 12(14):2230. https://doi.org/10.3390/ma12142230
Chicago/Turabian StyleZhang, Senhua, Jianting Zhou, Yi Zhou, Hong Zhang, and Jingwen Chen. 2019. "Cable Tension Monitoring Based on the Elasto-Magnetic Effect and the Self-Induction Phenomenon" Materials 12, no. 14: 2230. https://doi.org/10.3390/ma12142230
APA StyleZhang, S., Zhou, J., Zhou, Y., Zhang, H., & Chen, J. (2019). Cable Tension Monitoring Based on the Elasto-Magnetic Effect and the Self-Induction Phenomenon. Materials, 12(14), 2230. https://doi.org/10.3390/ma12142230






