A Statistical Damage Constitutive Model Based on the Weibull Distribution for Alkali-Resistant Glass Fiber Reinforced Concrete
Abstract
:1. Introduction
2. AR-GFRC Uniaxial Tensile Tests
2.1. Preparation of the AR-GFRC Specimens
2.1.1. Basic Mechanical Parameters of the AR-Glass Fibers
2.1.2. Composition and Mix Ratio of the Concrete Matrix
2.2. Test Instruments and Test Scheme of the AR-GFRC
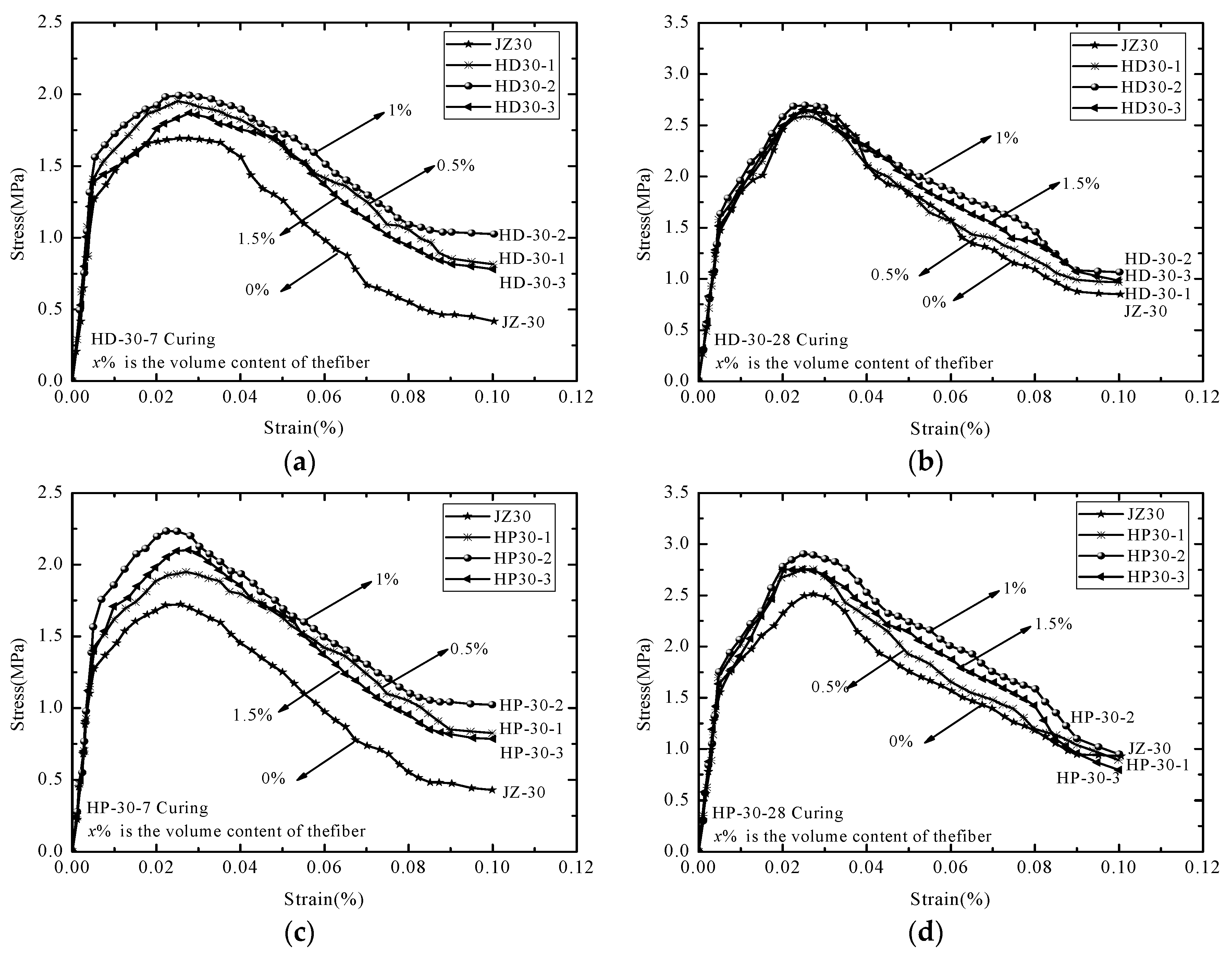
2.3. Test Results and Analysis of the AR-GFRC
2.3.1. Macroscopic Crack Failure Patterns of the Specimens
2.3.2. The Influence of the Fiber Content
3. Development of the Statistical Damage Constitutive Model for AR-GFRC
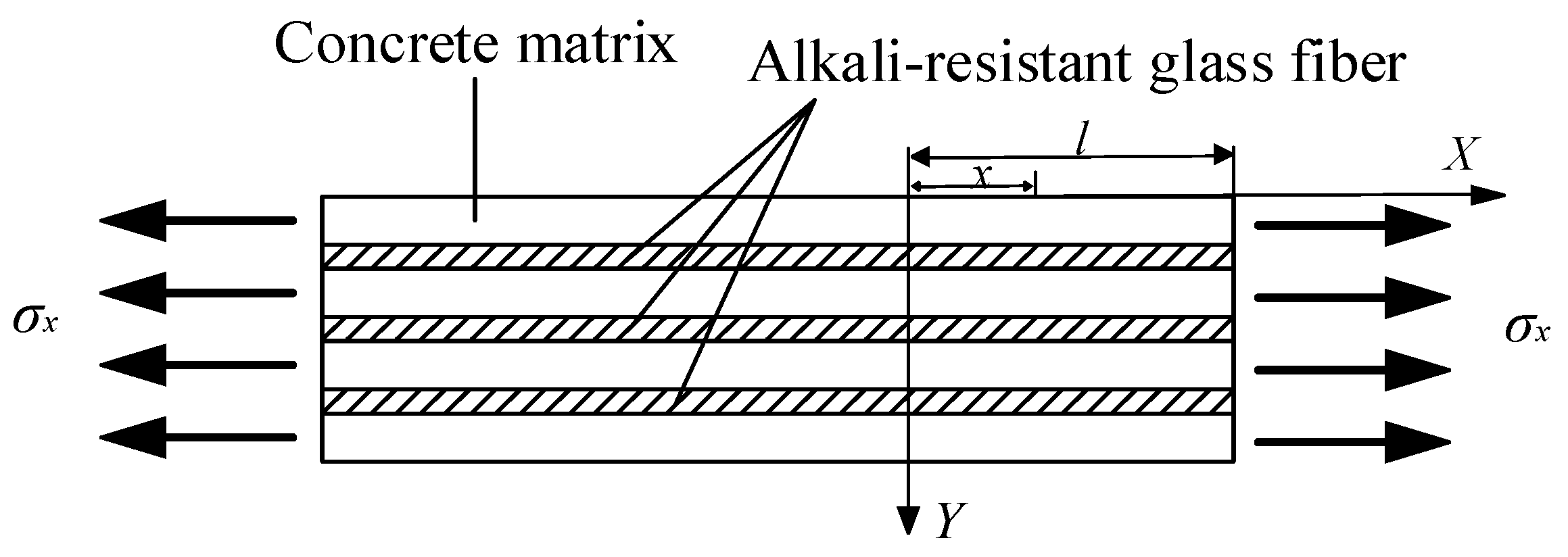
3.1. Composite Materials Theory
- (1)
- The concrete matrix and AR-glass fiber are both isotropic linear elastic materials.
- (2)
- The fibers stress direction and the distribution are parallel to the external tension load.
- (3)
- When tension deformation occurs in the concrete, the deformation is the same for the fiber and the concrete and no relative sliding or dislocation occurs. The stress of the concrete is shown in Figure 4.
3.2. Fiber Discontinuity Correction
3.3. Modified Elastic Modulus of Composites
3.4. Statistical Damage Constitutive Equation of the AR-GFRC
3.5. Determination of the Constitutive Model Parameters
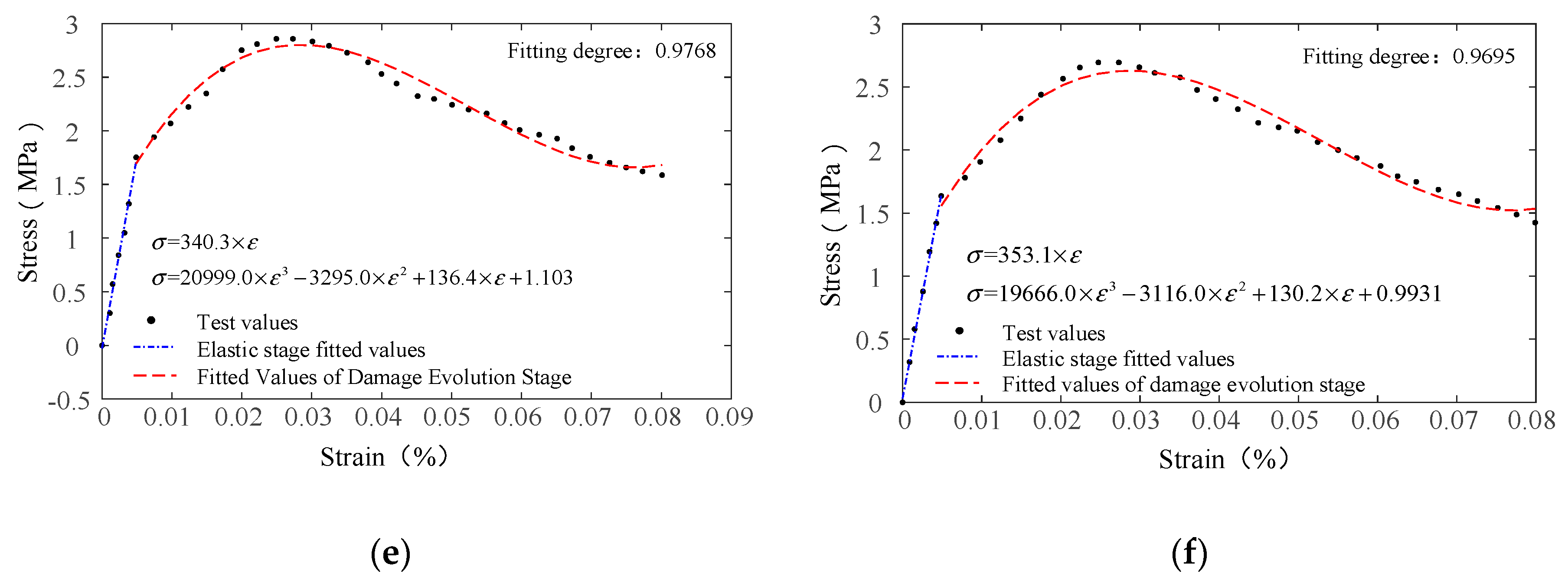
4. Verification of the Statistical Damage Constitutive Model for AR-GFC
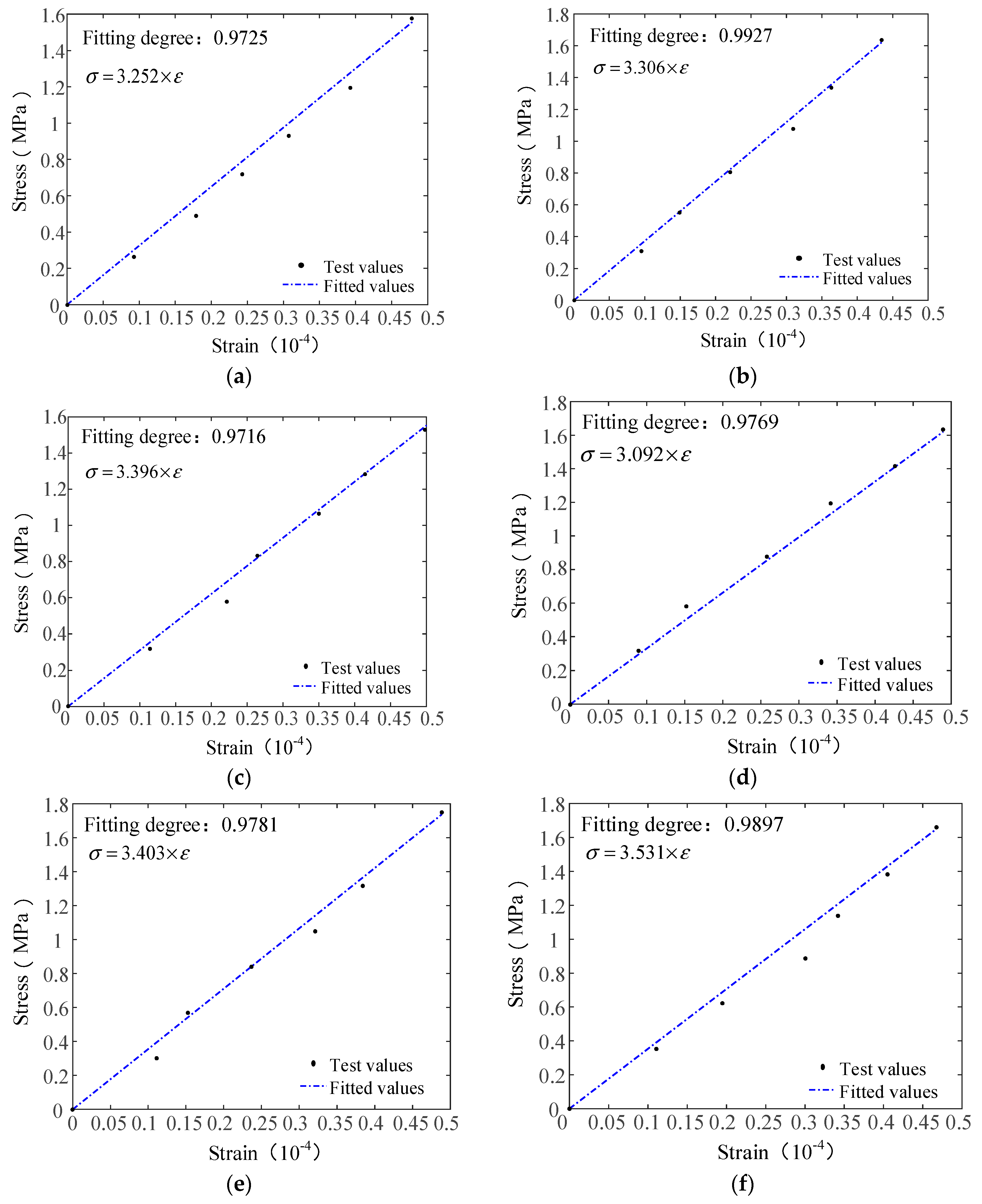
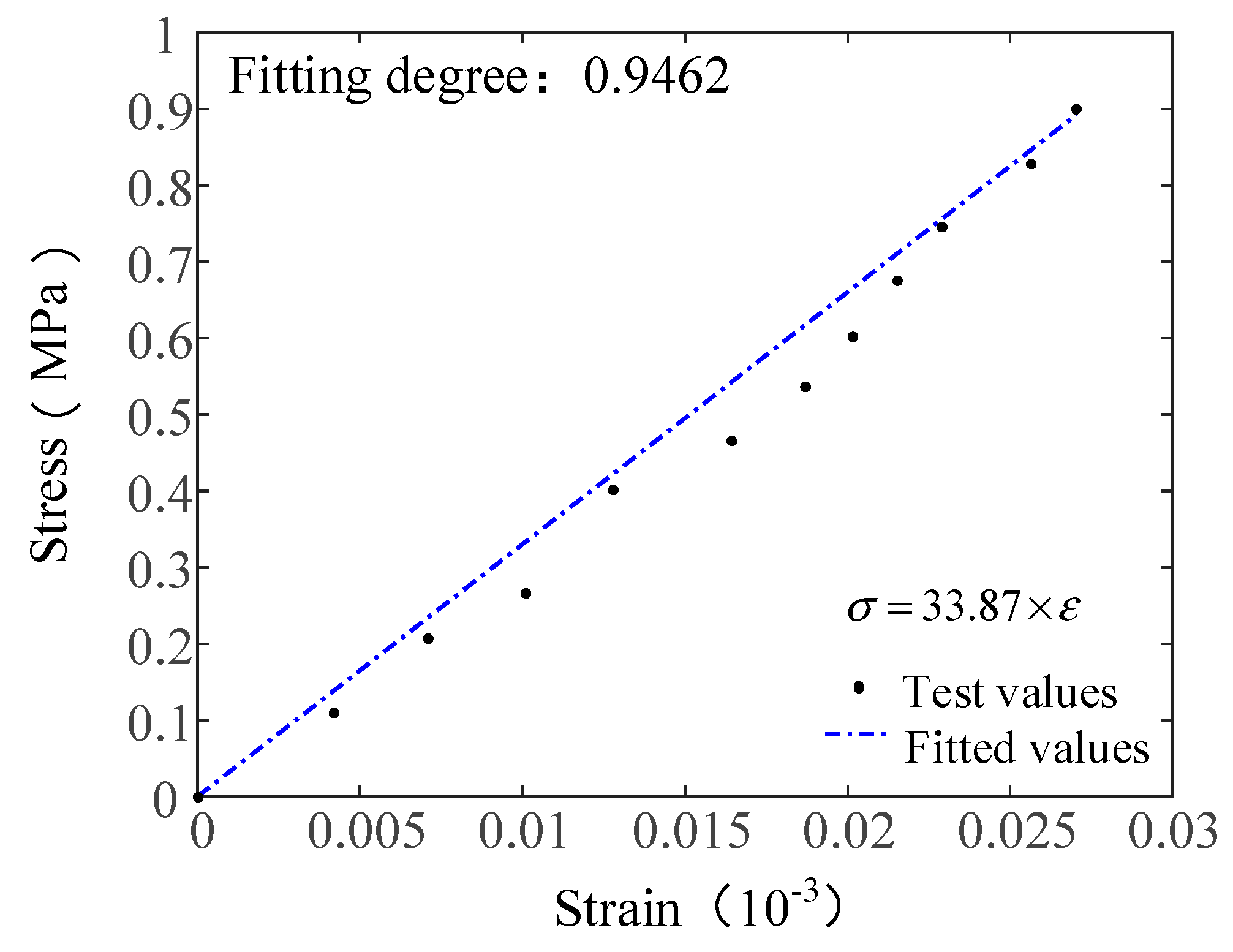
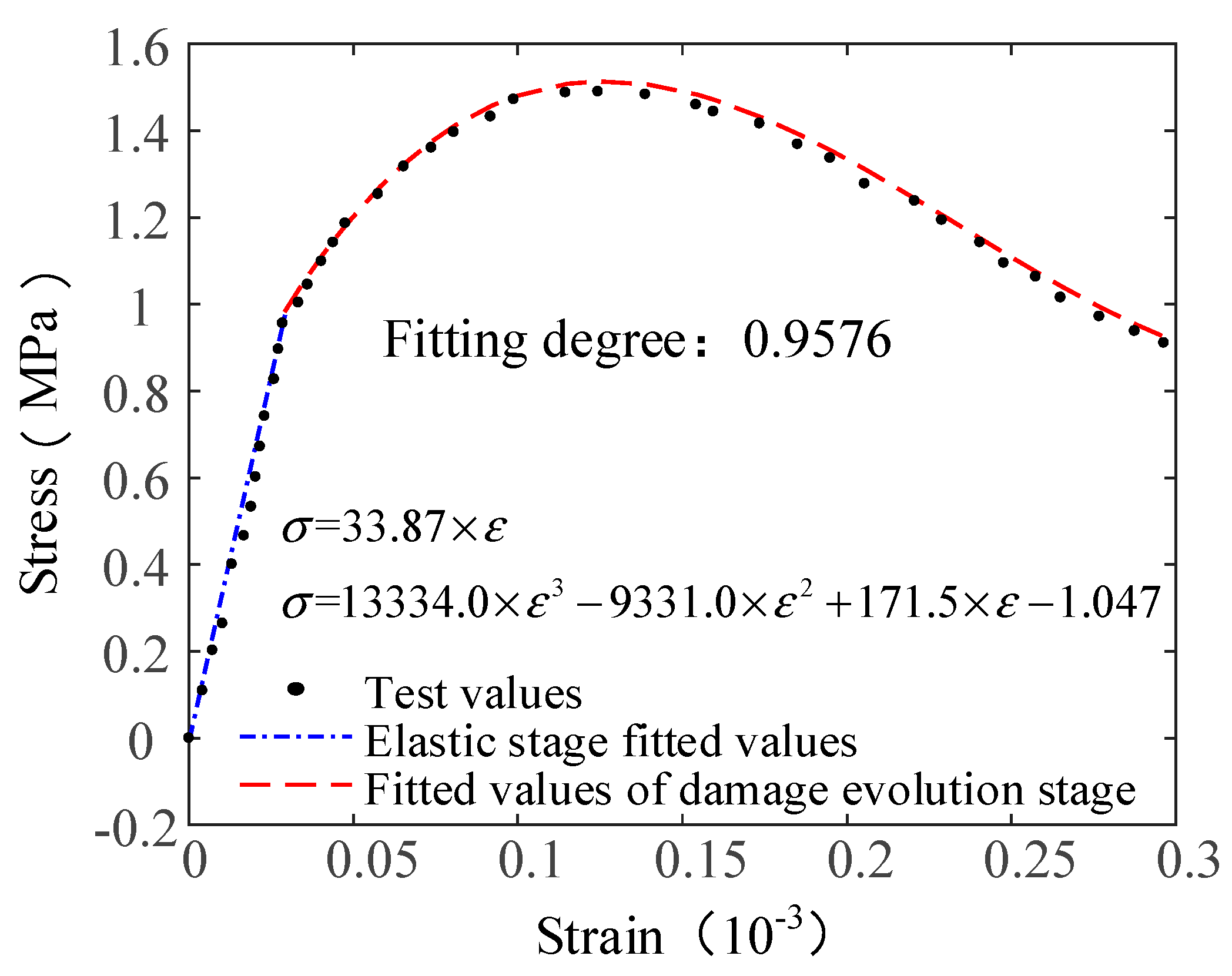
4.1. Determination and Verification of the Elastic Modulus of the Constitutive Model
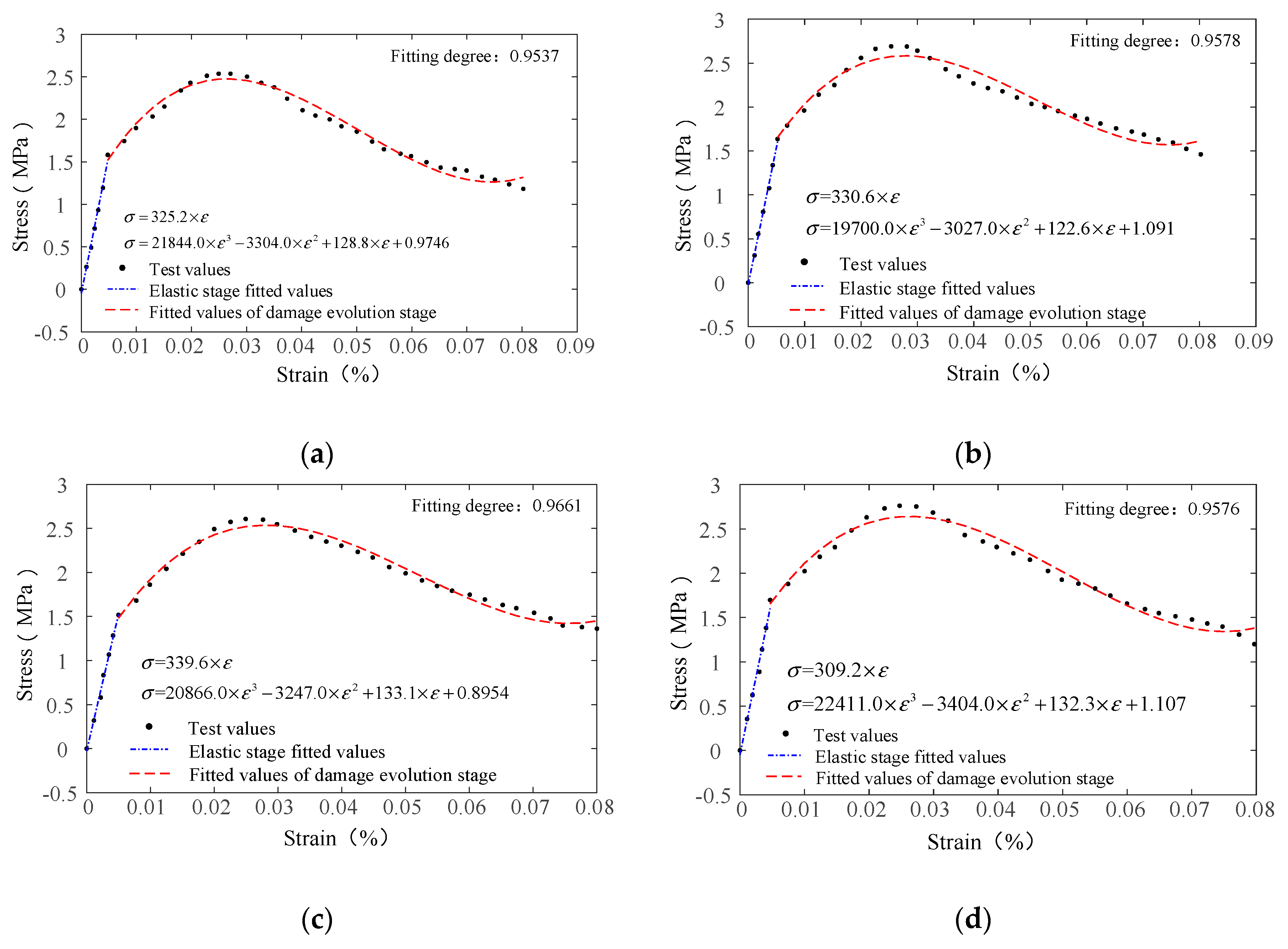
4.2. Tests and Constitutive Model Verification of the Concrete with Different Fiber Contents
4.3. The Extension and Verification of the Constitutive Model for Similar Fiber Materials
5. Conclusions
- (1)
- Indoor flat tensile tests of AR-GFRC were conducted and the macro-crack failure modes of the plain concrete and AR-GFRC specimens were analyzed to determine the occurrence and development of cracks in the material. The peak strength of different types of concrete under standard curing was quantitatively analyzed to determine the influence of the fiber content on the tensile strength of the concrete. It was determined that the tensile strength and the peak strength were highest at a fiber content of 1%.
- (2)
- The composite material theory and Krajcinovic vector damage theory were applied to modify the equations related to the fiber discontinuity and elastic modulus. The Weibull distribution function was used to derive the equation of the elastic modulus of the fiber reinforced concrete composite and the statistical damage constitutive model of the AR-GFRC was developed. The statistical parameters of the model were determined using the numerical feature method.
- (3)
- The constitutive equation was validated based on the elastic modulus and the different fiber contents obtained from indoor uniaxial tensile tests. The validation results indicated a good fit of the theoretical and experimental results of the elastic undamaged stage and damage stage with a fitting degree larger than 0.93. Tensile test data of PP fibers made of similar materials were used to extend and validate the proposed constitutive model using the same validation method. The results showed a fitting degree larger than 0.92 for the theoretical and experimental stress–strain curve before the peak value. The statistical damage constitutive model of the AR-GFRC provides reference data and theoretical support to ensure the safety and stability of concrete structures.
Author Contributions
Funding
Conflicts of Interest
References
- Fathi, H.; Lameie, T.; Maleki, M.; Yazdani, R. Simultaneous effects of fiber and glass on the mechanical properties of self-compacting concrete. Constr. Build. Mater. 2017, 133, 443–449. [Google Scholar] [CrossRef]
- Keleştemur, O.; Arıcı, E.; Yıldız, S.; Gökçer, B. Performance evaluation of cement mortars containing marble dust and glass fiber exposed to high temperature by using Taguchi method. Constr. Build. Mater. 2014, 60, 17–24. [Google Scholar] [CrossRef] [Green Version]
- Kizilkanat, A.B.; Kabay, N.; Akyüncü, V.; Chowdhury, S.; Akça, A.H. Mechanical properties and fracture behavior of basalt and glass fiber reinforced concrete: An experimental study. Constr. Build. Mater. 2015, 100, 218–224. [Google Scholar] [CrossRef]
- Abeysinghe, C.M.; Thambiratnam, D.P.; Perera, N.J. Flexural performance of an innovative hybrid composite floor plate system comprising glass–fibre reinforced cement, polyurethane and steel laminate. Compos. Struct. 2013, 95, 179–190. [Google Scholar] [CrossRef]
- Soranakom, C.; Bakhshi, M.; Mobasher, B. Role of Alkali Resistant Glass Fibers in Suppression of Restrained Shrinkage Cracking of Concrete Materials. In Proceedings of the 15th International Glass Fibre Reinforced Concrete Association Congress, GRC 2008, CD-Proceedings, Prague, Czech Republic, 20–23 April 2008; Volume 4, pp. 20–23. [Google Scholar]
- Bakhshi, M.; Mobasher, B. Simulated Shrinkage Cracking in the Presence of Alkali Resistant Glass Fibers. Available online: https://www.researchgate.net/publication/287950176 (accessed on 12 June 2019).
- Kasagani, H.; Rao, C.B.K. Effect of Short length Glass Fiber on dilated concrete in Compression and Tension. Proc. Inst. Civ. Eng. Struct. Build. 2018, 4, 1–12. [Google Scholar]
- Yildizel, S.A.; Ozturk, A.U. Micro Glass Fiber Reinforced Concrete. ICOCEE CESME 2018, 4, 24–27. [Google Scholar]
- Bentur, A.; Ben-Bassat, M.; Schneider, D. Durability of Glass-Fiber-Reinforced Cements with Different Alkali-Resistant Glass Fibers. J. Am. Ceram. Soc. 1985, 68, 203–208. [Google Scholar] [CrossRef]
- Chandramouli, K.; Rao, P.S.; Pannirselvam, N.; Sekhar, T.S.; Sravana, P. Chloride Penetration Resistance Studies on Concretes Modified with Alkali Resistant Glass Fibers. Am. J. Appl. Sci. 2010, 7, 371–375. [Google Scholar] [CrossRef]
- Eiras, J.N.; Kundu, T.; Bonilla, M. Nondestructive Monitoring of Ageing of Alkali Resistant Glass Fiber Reinforced Cement (GRC). J. Nondestruct. Eval. 2013, 32, 300–314. [Google Scholar] [CrossRef]
- Krishnan, K.A.; Anjana, R.; George, K.E. Effect of alkali-resistant glass fiber on polypropylene/polystyrene blends: Modeling and characterization. Polym. Compos. 2014, 37, 398–406. [Google Scholar] [CrossRef]
- Kwan, W.H.; Cheah, C.B.; Ramli, M.; Chang, K.Y. AR-GFR high strength concrete in simulated aggressive environment. Mater. Constr. 2018, 68, 1–14. [Google Scholar] [CrossRef]
- Dimchev, M.; Caeti, R.; Gupta, N. Effect of carbon nanofibers on tensile and compressive characteristics of hollow particle filled composites. Mater. Des. 2010, 31, 1332–1337. [Google Scholar] [CrossRef]
- Chaitanya kumar, J.D.; Abhilash, G.V.S.; Khasim Khan, P.; Manikanta sai, G.; Tarakaram, V. Experimental Studies on Glass Fiber Concrete. Am. J. Eng. Res. 2016, 5, 100–104. [Google Scholar]
- Ashori, A.; Ghiyasi, M.; Fallah, A. Glass fber-reinforced epoxy composite with surface-modifed graphene oxide: Enhancement of interlaminar fracture toughness and thermo-mechanical performance. Polym. Bull. 2018. [Google Scholar] [CrossRef]
- Ateş, A. Mechanical properties of sandy soils reinforced with cement and randomly distributed glass fibers (GRC). Compos. Part B Eng. 2016, 96, 295–304. [Google Scholar] [CrossRef]
- Fillmore, B.; Sadeghian, P. Contribution of Longitudinal GFRP Bars in Concrete Cylinders under Axial Compression. Can. J. Civ. Eng. 2018, 45, 458–468. [Google Scholar] [CrossRef]
- Mehta, P.K.; Aitcin, P.C. Microstructural basis of selection of materials and mix proportions for high-strength concrete. Spec. Publ. 1990, 121, 265–286. [Google Scholar]
- Wang, Q.-B.; Zhu, Q.-K.; Shao, T.-S.; Yu, X.-G.; Xu, S.-Y.; Zhang, J.-J.; Kong, Q.-L. The rheological test and application research of glass fiber cement slurrybased on plugging mechanism of dynamic water grouting. Constr. Build. Mater. 2018, 189, 119–130. [Google Scholar]
- Krajcinovic, D.; Fonseka, G.U. The continuous damage theory of brittle materials, part 1: General theory. J. Appl. Mech. 1981, 48, 809–815. [Google Scholar] [CrossRef]
- Krajcinovic, D. Constitutive equations for damaging materials. J. Appl. Mech. 1983, 50, 355–360. [Google Scholar] [CrossRef]
- Ghugal, Y.M.; Deshmukh, S.B. Performance of AR-GFRC. J. Reinf. Plast. Compos. 2006, 25, 617–630. [Google Scholar] [CrossRef]
- Yıldızel, S.A. Effects of Barite Sand Addition on Glass Fiber Reinforced Concrete Mechanical Behavior. Int. J. Eng. Appl. Sci. 2017, 9, 100–105. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.; Xue, H.; Qian, M. Tensile and compressive properties of epoxy syntactic foams reinforced by short glass fiber. Indian, J. Eng. Mater. Sci. 2017, 24, 283–289. [Google Scholar]
- Wang, P.; Jiang, L.; Jiang, J.; Zheng, P.; Li, W. Strata behaviors and rock-burst-inducing mechanism under the coupling effect of a hard-thick stratum and a normal fault. Int. J. Geomech. 2018, 18, 04017135. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, P.; Zheng, P.; Luan, H.; Zhang, C. Influence of Different Advancing Directions on Mining Effect Caused by a Fault. Adv. Civ. Eng. 2019, 2019. [Google Scholar] [CrossRef]
- Wang, W.; Tian, Z.; Zhu, Q. Study of statistical damage constitutive model for rock considering pore water pressure. Chin. J. Rock Mech. Eng. 2015, 34, 676-3. [Google Scholar]
- Cao, R.; He, S.; Wei, J.; Wang, F. Study of modified statistical damage softening constitutive model for rock considering residual strength. Rock Soil 2013, 34, 1652–1660. [Google Scholar]
- Wang, Z.; Li, Y.; Wang, J.G. A damage-softening statistical constitutive model considering rock residual strength. Comput. Geosci. 2007, 33, 1–9. [Google Scholar] [CrossRef]
- Wang, P.; Jiang, L.; Li, X.; Qin, G.; Wang, E. Physical Simulation of Mining Effect Caused by A Fault Tectonic. Arab. J. Geosci. 2018, 11, 741. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, Z.; Zhu, S.; He, Z.; Zhu, D.; Liu, J.; Meng, S. Nonlinear Creep Damage Constitutive Model of Concrete Based on Fractional Calculus Theory. Materials 2019, 12, 1505. [Google Scholar] [CrossRef]
- Deng, J.; Gu, D. On a statistical damage constitutive model for rock materials. Comput. Geosci. 2011, 37, 122–128. [Google Scholar] [CrossRef]
- Liang, H. Research on Mechanical Properties Test of Multi-Scale Polypropylene Fiber Concrete and the Constitutive Model of Tensile Pressure Damage. Ph.D. Thesis, University of Chongqing, Chongqing, China, 2014. [Google Scholar]


| Type | Length (mm) | Equivalent Diameter (um) | Fracture Strength | Elongation at Break (%) | Modulus (GPa) | Melting Point (°C) |
|---|---|---|---|---|---|---|
| HD | 6/12 | 30 | 1700 | 3.6 | 60 | 1580 |
| HP | 6/12 | 30 | 1700 | 3.6 | 60 | 1580 |
| Number | Cement | Sand | Stone | HD | HP | Water | Admixture |
|---|---|---|---|---|---|---|---|
| JZ30 | 370 | 758 | 1047 | 0 | 0 | 185 | 2.0% |
| HD30-1 | 370 | 758 | 1047 | 0.5 | 0 | 185 | 2.0% |
| HD30-2 | 370 | 758 | 1047 | 1.0 | 0 | 185 | 2.0% |
| HD30-3 | 370 | 758 | 1047 | 1.5 | 0 | 185 | 2.0% |
| HP30-1 | 370 | 758 | 1047 | 0 | 0.5 | 185 | 2.0% |
| HP30-2 | 370 | 758 | 1047 | 0 | 1.0 | 185 | 2.0% |
| HP30-3 | 370 | 758 | 1047 | 0 | 1.5 | 185 | 2.0% |
| Number | Cement | Sand | Stone | Fiber Contents | Water | Admixture |
|---|---|---|---|---|---|---|
| JZ30 | 370 | 758 | 1047 | 1.0 | 185 | 2.0% |
| Cem-FIL60-12 | 370 | 758 | 1047 | 1.0 | 185 | 2.0% |
| Cem-FIL60-18 | 370 | 758 | 1047 | 1.0 | 185 | 2.0% |
| HD-6 | 370 | 758 | 1047 | 1.0 | 185 | 2.0% |
| HP-12 | 370 | 758 | 1047 | 1.0 | 185 | 2.0% |
| Type | Time | |||||||
|---|---|---|---|---|---|---|---|---|
| 7 d | 28 d | |||||||
| 0% | 0.5% | 1% | 1.5% | 0% | 0.5% | 1% | 1.5% | |
| HD | 1.68 | 1.92 | 2.09 | 1.89 | 2.64 | 2.69 | 2.73 | 2.61 |
| HP | 1.66 | 1.88 | 2.24 | 2.15 | 2.51 | 2.73 | 2.98 | 2.79 |
| Number | Em (GPa) | ρm | Ef (GPa) | ρf | α | ηl | ηf |
|---|---|---|---|---|---|---|---|
| HD30-1 | 30 | 99.5% | 60 | 0.5% | 400 | 0.1 | 0.15 |
| HD30-2 | 30 | 99% | 60 | 1.0% | 400 | 0.1 | 0.15 |
| HD30-3 | 30 | 98.5% | 60 | 1.5% | 400 | 0.1 | 0.15 |
| HP30-1 | 30 | 99.5% | 60 | 0.5% | 400 | 0.1 | 0.15 |
| HP30-2 | 30 | 99% | 60 | 1.0% | 400 | 0.1 | 0.15 |
| HP30-3 | 30 | 98.5% | 60 | 1.5% | 400 | 0.1 | 0.15 |
| Number | C1 | C2 | x0(103) | m |
|---|---|---|---|---|
| HD30-1 | -4.4 | 0.44 | 9.2841 | 2.4 |
| HD30-2 | -3.77 | 0.59 | 6.958 | 3.9 |
| HD30-3 | -3.81 | 0.58 | 5.9 | 5.2 |
| HP30-1 | -4.51 | 0.42 | 10.5358 | 2.1 |
| HP30-2 | -4.02 | 0.50 | 7.1738 | 3.5 |
| HP30-3 | -3.58 | 0.49 | 5.8271 | 4.8 |
| Fiber Marking | Diameter (mm) | Length (mm) | Elastic Modulus (GPa) | Elongation at Break (%) |
|---|---|---|---|---|
| FF1 | 0.026 | 12 | 4.5 | 40 |
| FF4 | 0.1 | 19 | 4.5 | 40 |
| CF2 | 0.8 | 50 | 7.4 | 10 |
| Test Marking | Fiber Type | Cement | Sand | Stone | Water | Fiber Contents | Sand Rate |
|---|---|---|---|---|---|---|---|
| A9 | FF1+FF4+CF2 | 406 | 548 | 1221 | 207 | 6 | 23 |
| Number | C1 | C2 | x0(103) | m |
|---|---|---|---|---|
| A9 | 3.0382 | 0.298 | 5.6742 | 4.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Zhang, C.; Meng, S.; Shi, Z.; Tao, S.; Zhu, D. A Statistical Damage Constitutive Model Based on the Weibull Distribution for Alkali-Resistant Glass Fiber Reinforced Concrete. Materials 2019, 12, 1908. https://doi.org/10.3390/ma12121908
Zhu Z, Zhang C, Meng S, Shi Z, Tao S, Zhu D. A Statistical Damage Constitutive Model Based on the Weibull Distribution for Alkali-Resistant Glass Fiber Reinforced Concrete. Materials. 2019; 12(12):1908. https://doi.org/10.3390/ma12121908
Chicago/Turabian StyleZhu, Zhende, Cong Zhang, Songsong Meng, Zhenyue Shi, Shanzhi Tao, and Duan Zhu. 2019. "A Statistical Damage Constitutive Model Based on the Weibull Distribution for Alkali-Resistant Glass Fiber Reinforced Concrete" Materials 12, no. 12: 1908. https://doi.org/10.3390/ma12121908






