Mesh-Based and Meshfree Reduced Order Phase-Field Models for Brittle Fracture: One Dimensional Problems
Abstract
1. Introduction
2. Phase-Field Model for Quasi-Brittle Fracture
2.1. Governing Equations
2.2. Weak Forms and Finite Element Implementation
- the solution of two systems for each AM iteration k and
- the evaluation of the force vector and matrices and .
- Initialization: ,
- Do AM iterations: while ( is the precision)
- (a)
- Displacement sub-problem: solve for with fixed
- (b)
- Phase-field sub-problem: solve for with fixed
- (c)
- Set
- Update nodal unknowns:
3. Reduced-Order Modelling
3.1. Mesh-Based Approach
3.1.1. Parameterized and Nonlinear ROM Based on the Projection Framework
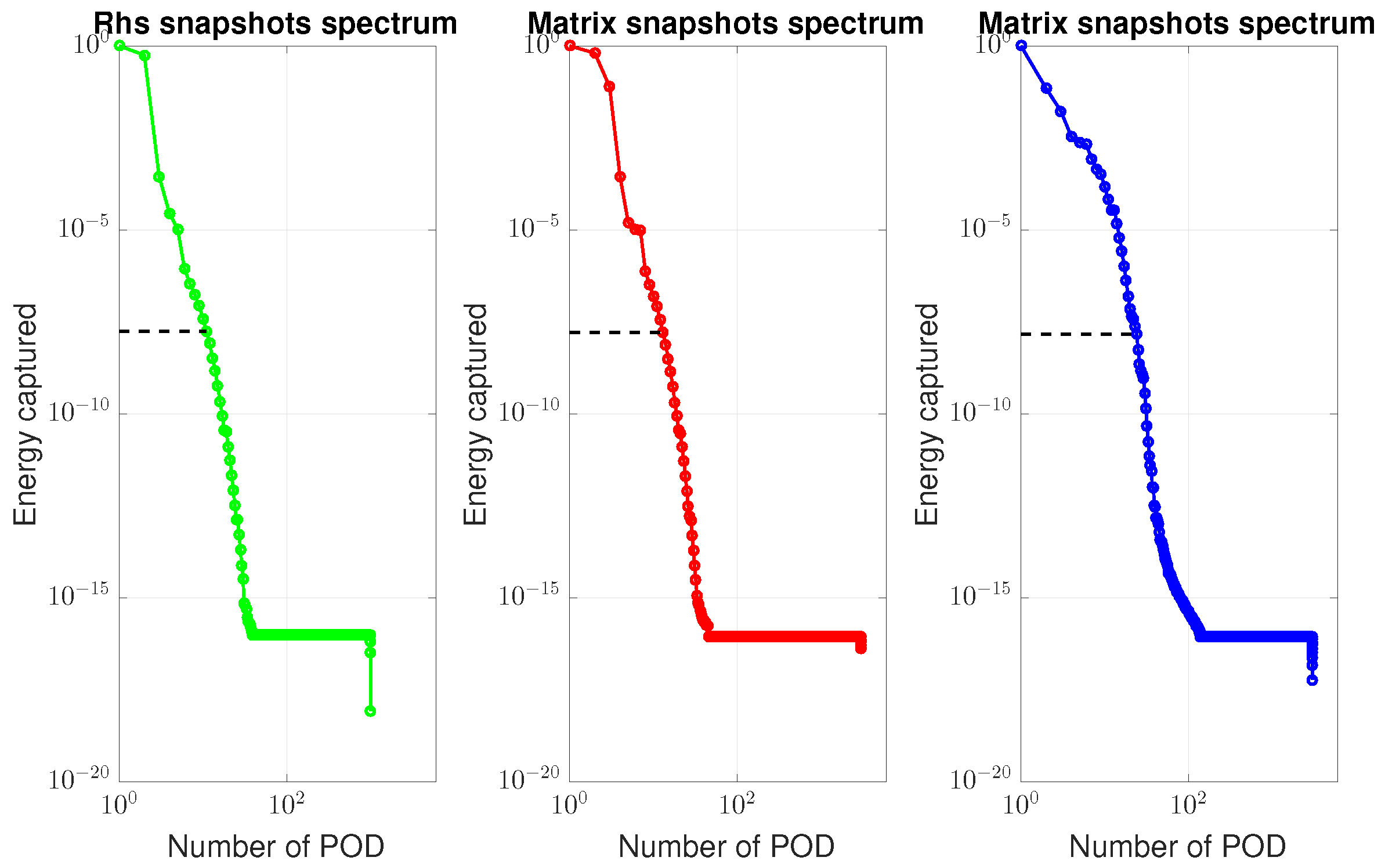
3.1.2. DEIM

3.1.3. (M)DEIM

- Initialization: ,
- Do AM iterations
- (a)
- Displacement sub-problem: solve for with fixed
- (i)
- Solve Equation (28) on the reduced mesh to obtain (replace by m).
- (ii)
- Reconstruct the reduce matrix using Equation (27) (replace by m).
- (iii)
- Obtain by reversing the operation: .
- (iv)
- Solve
- (b)
- Phase-field sub-problem: solve for with fixed
- (i)
- Solve Equation (28) on the reduced mesh to obtain .
- (ii)
- Reconstruct the reduce matrix using Equation (27).
- (iii)
- Obtain by .
- (iv)
- Obtain using Equation (23).
- (v)
- Solve
- (c)
- Set
- Update nodal unknowns:
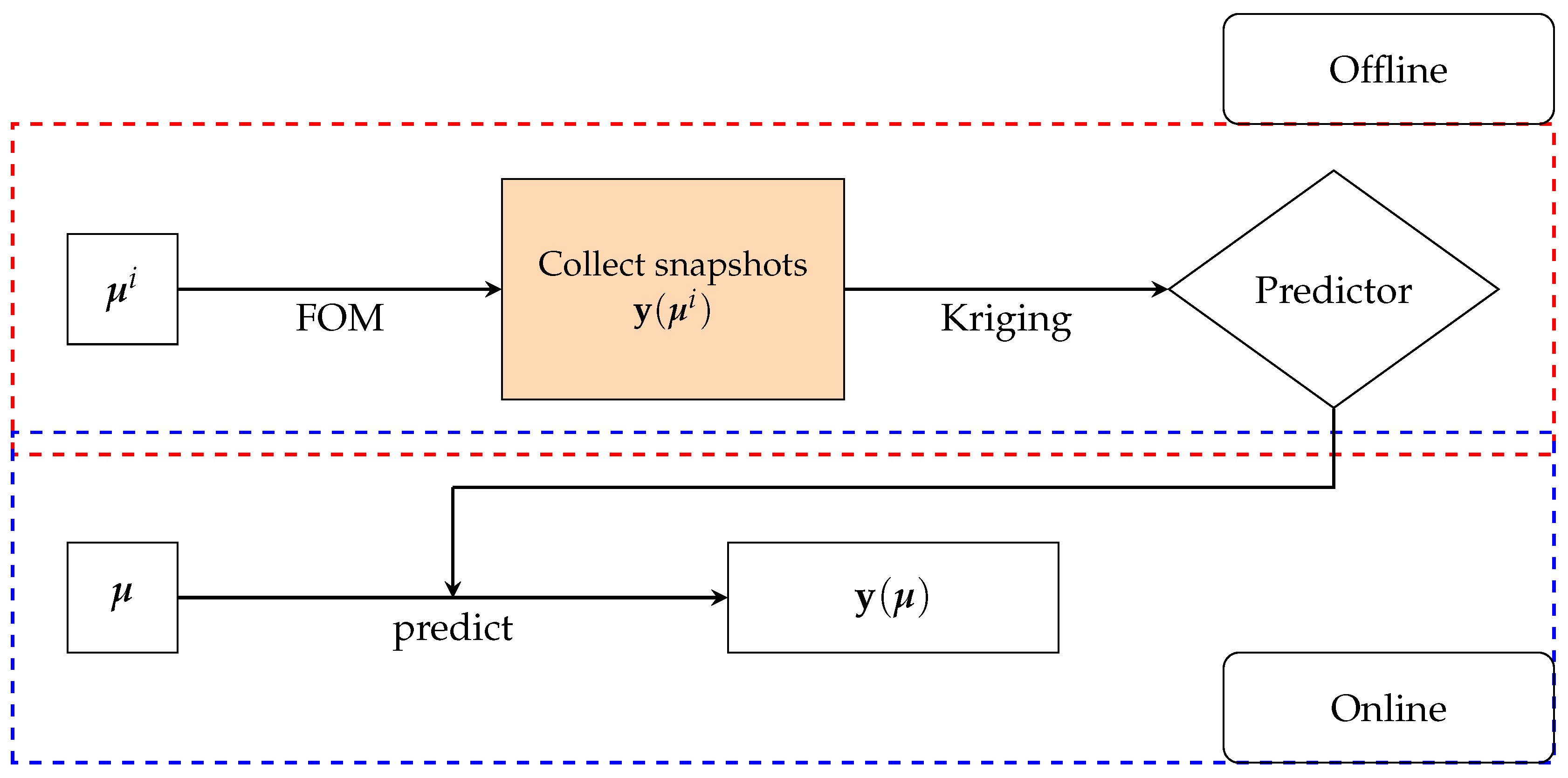
3.2. Meshfree Kriging Method
3.3. A Posteriori Error Estimations
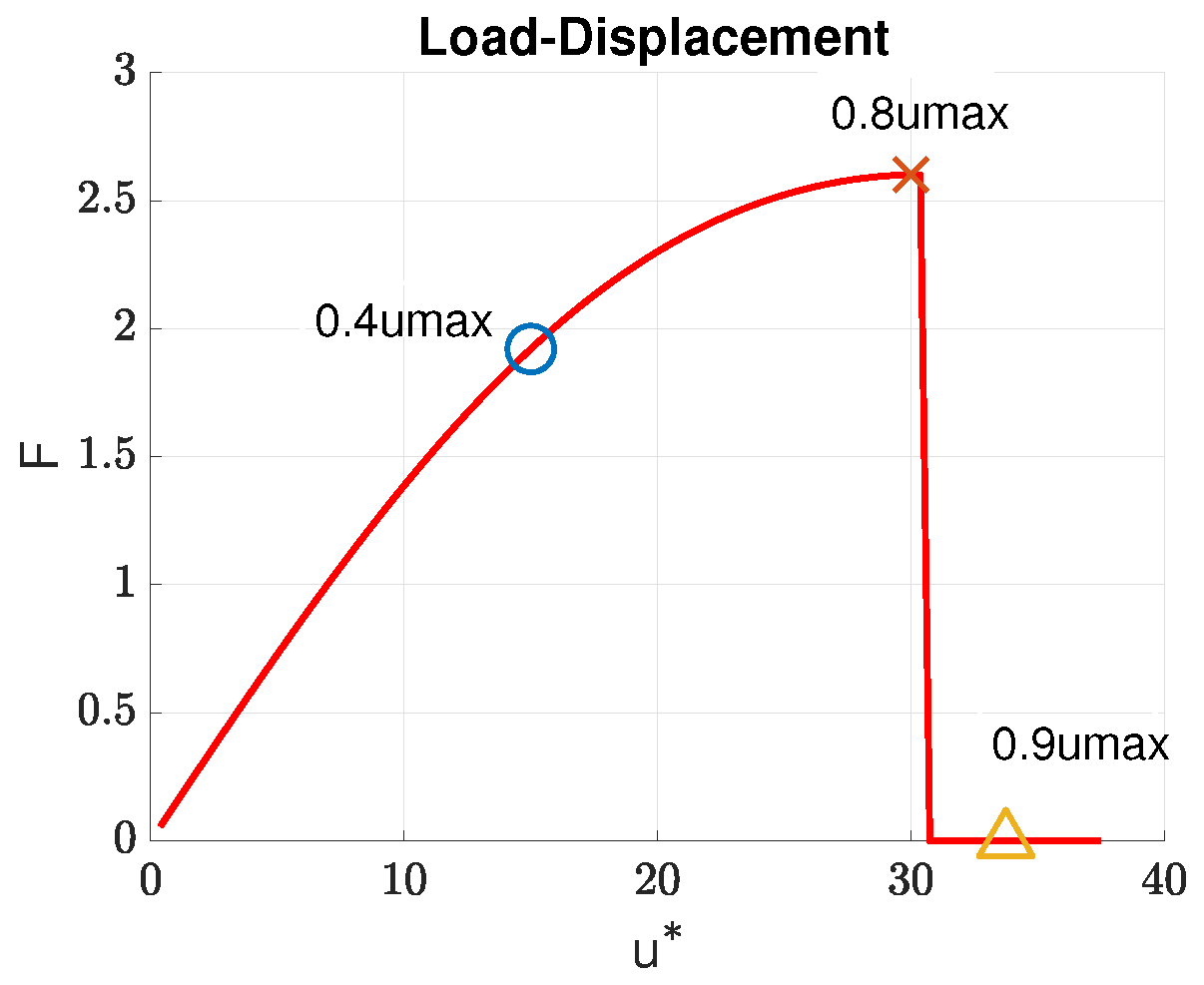
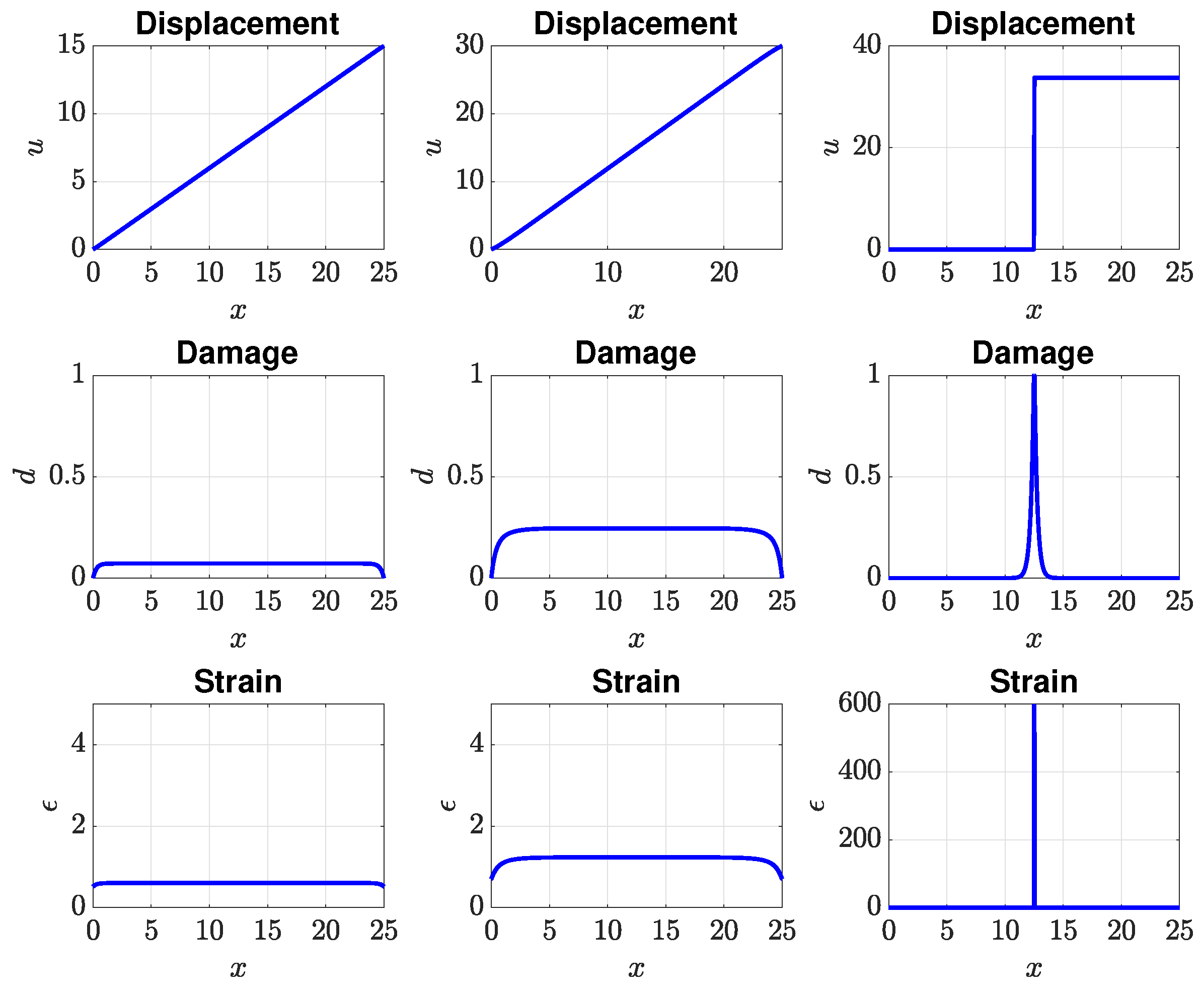
4. Numerical Examples
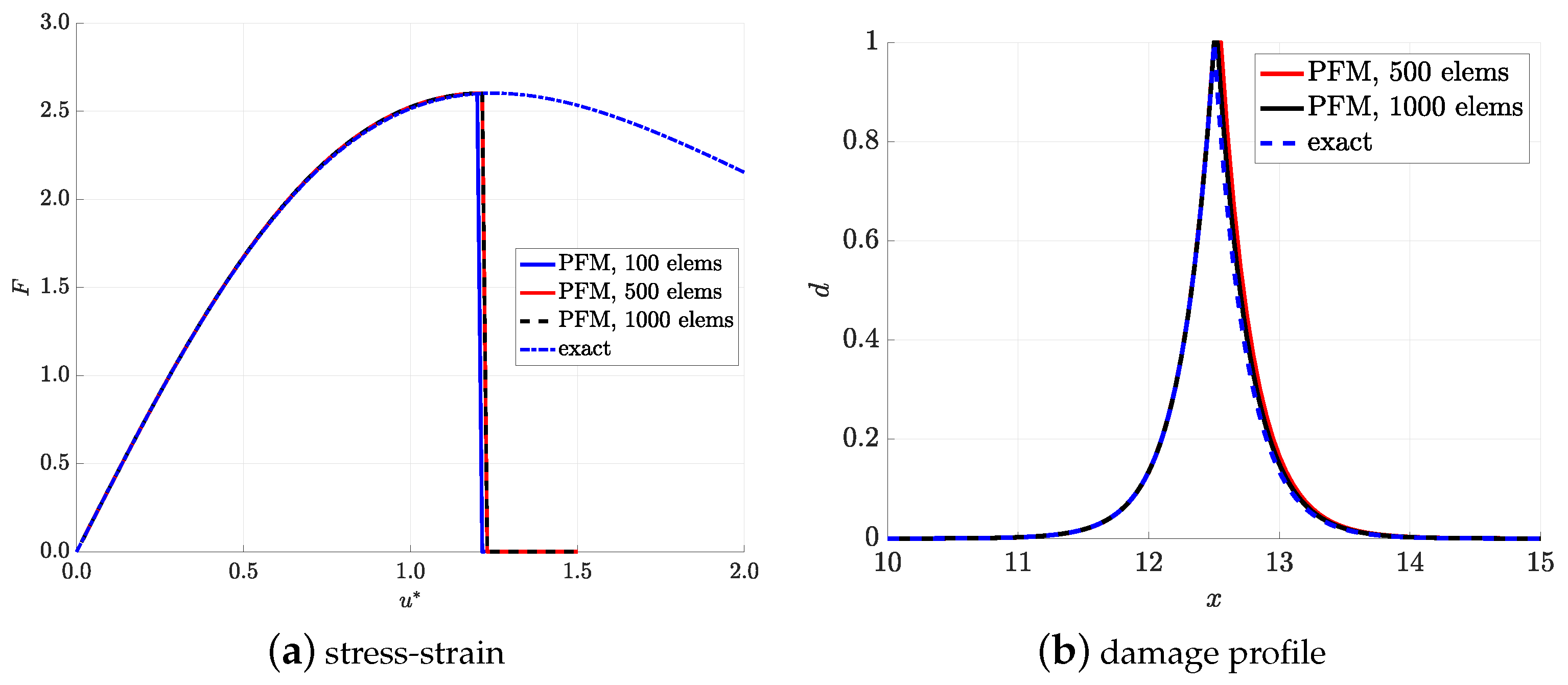
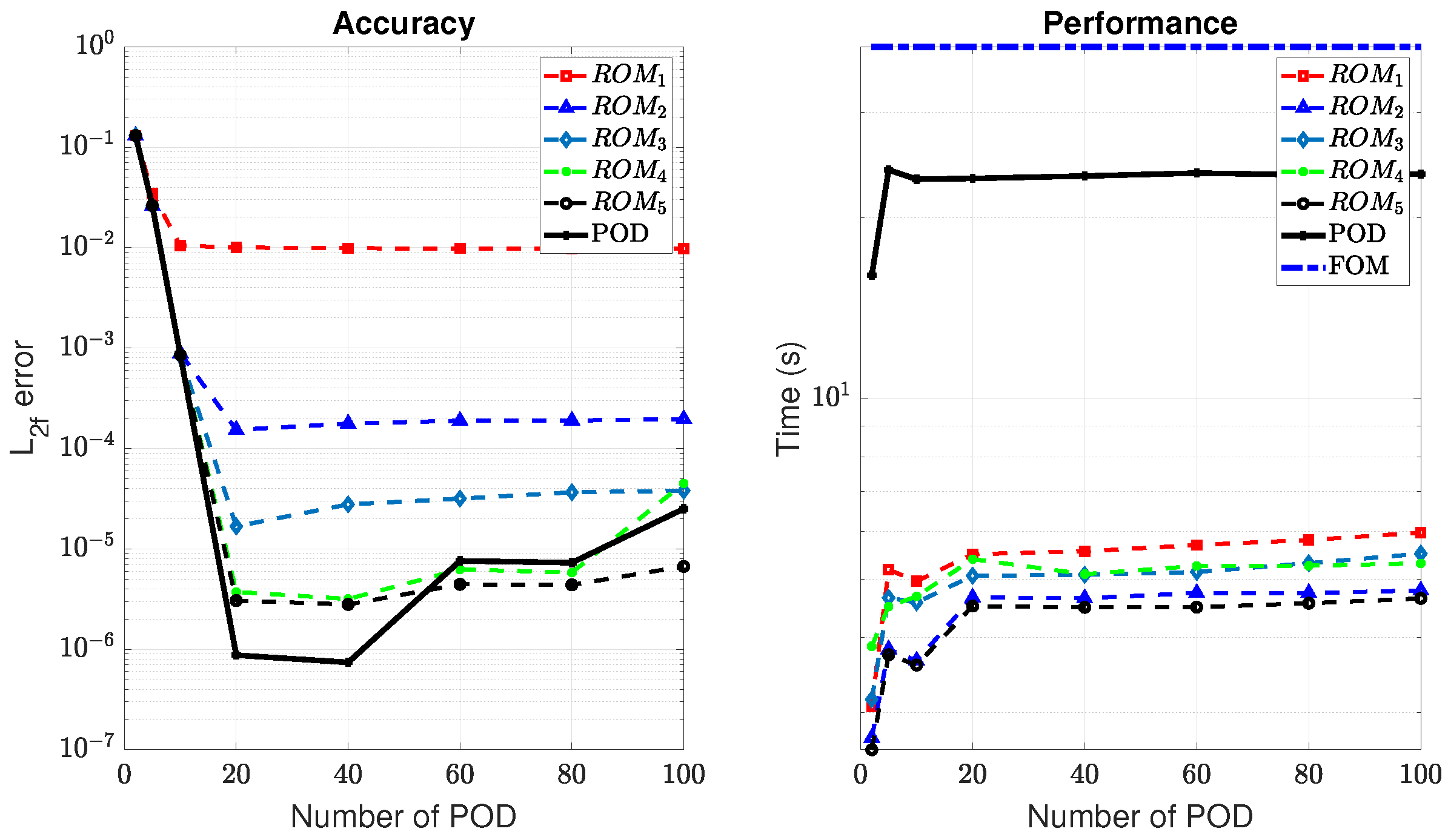
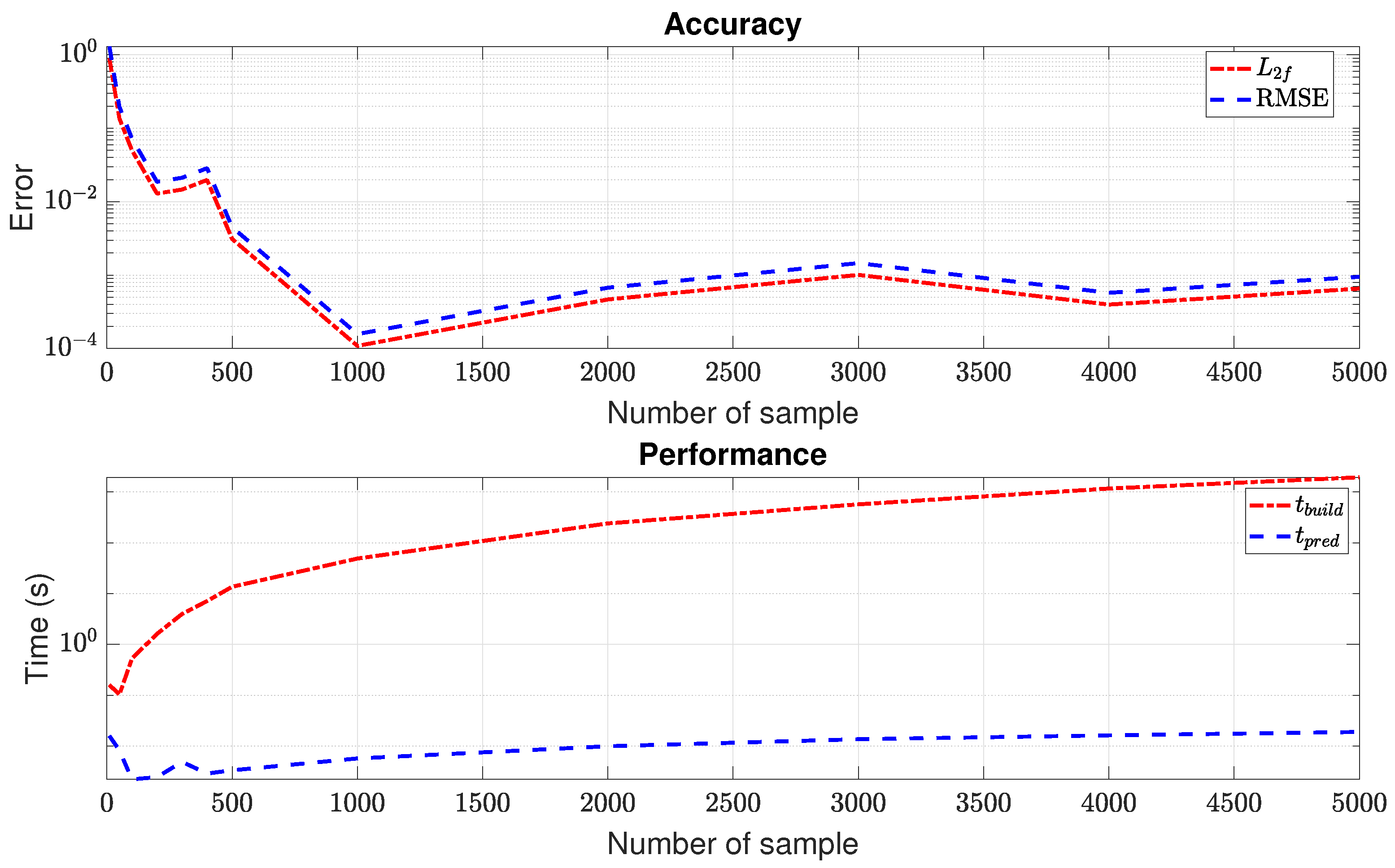
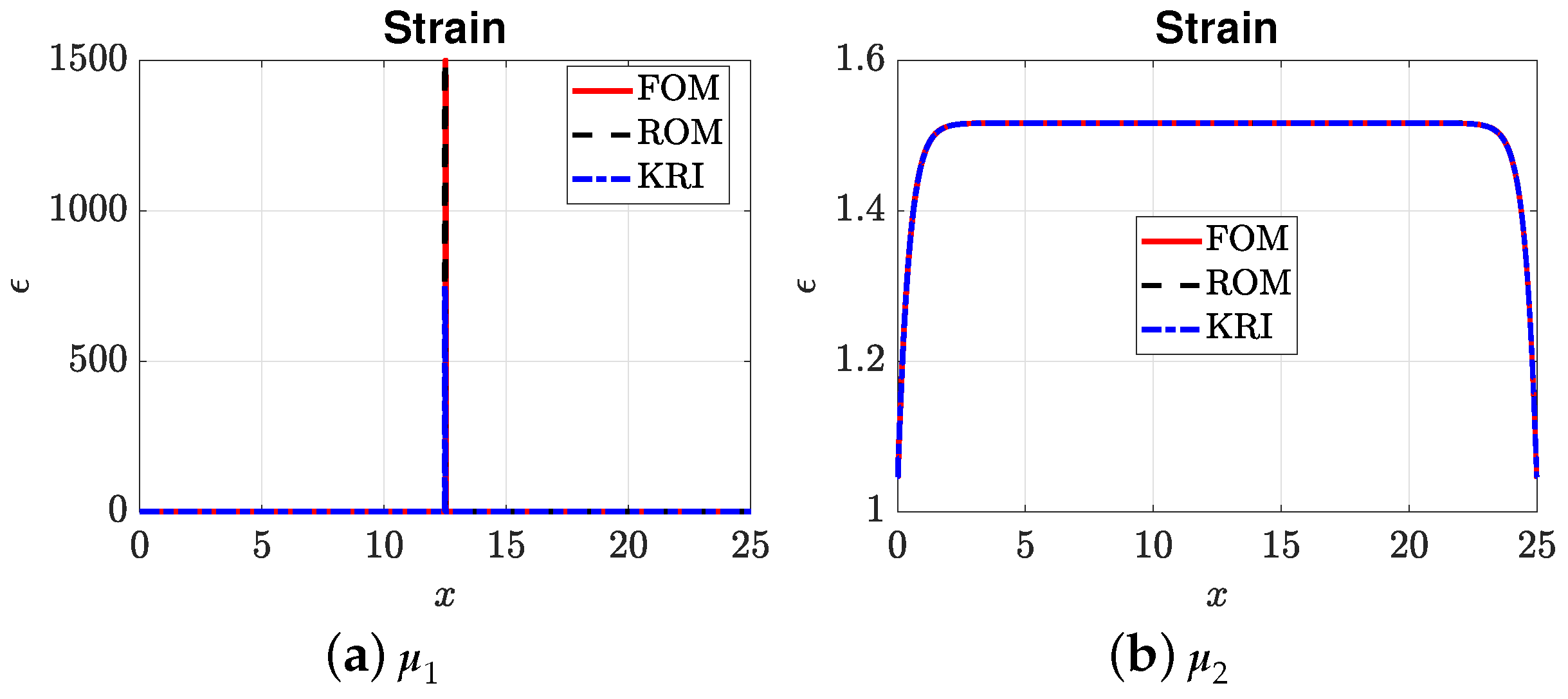
4.1. ROM Results
4.2. Kriging Results
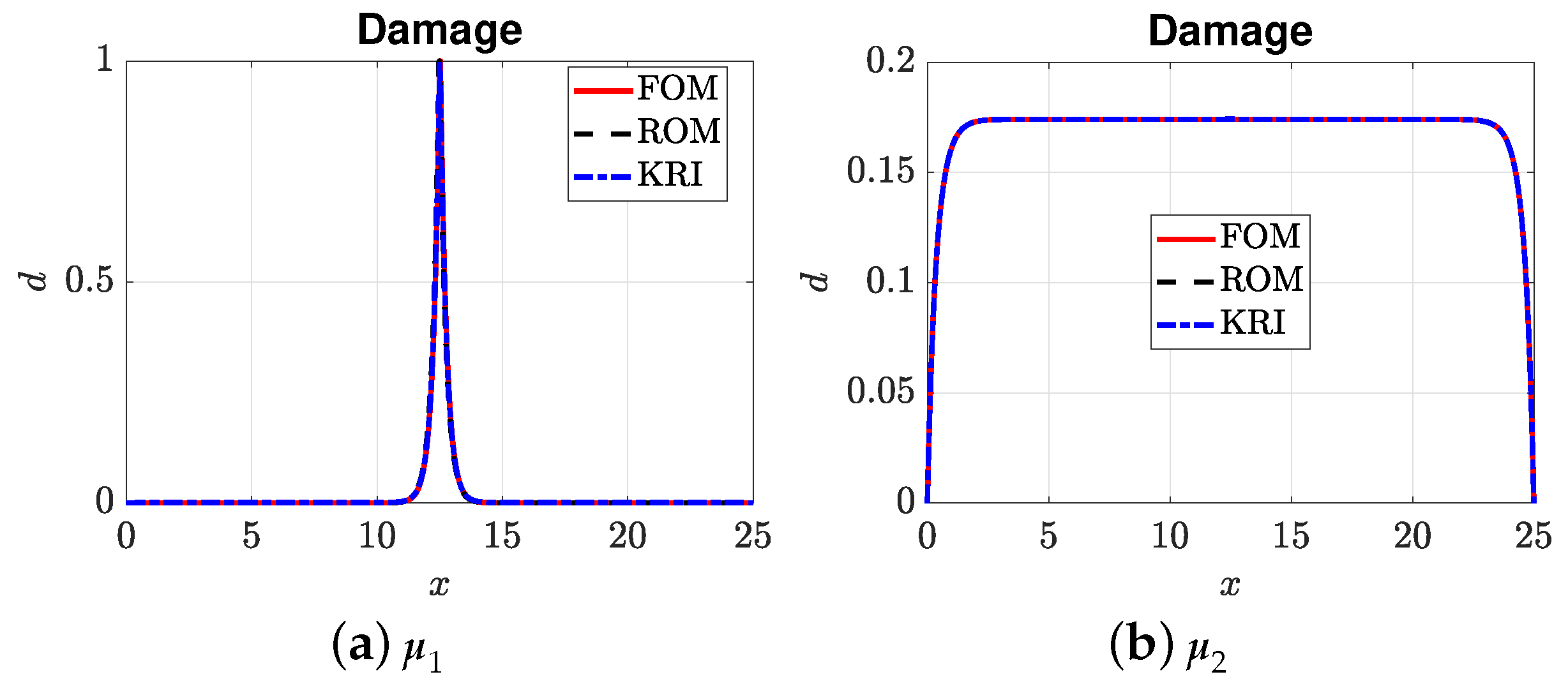
4.3. ROM vs. Kriging
5. Conclusions
- They cannot be used for extrapolation, i.e., when the parameters are out of the bounds of the considered parameter space;
- The load has not been parametrized. That is, the maximum prescribed displacement is fixed.
- The Kriging model resulted in oscillations around the damage localization point.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proper Orthogonal Decomposition Algorithm

Appendix B. Exact Solutions
References
- Quarteroni, A.; Manzoni, A.; Negri, F. Reduced Basic Methods for Partial Differential Equations; Springer: Berlin, Germany, 2016. [Google Scholar]
- Francfort, G.; Marigo, J. Revisting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.; Marigo, J.J. Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 2000, 48, 797–826. [Google Scholar] [CrossRef]
- Wu, J.Y. A unified phase-field theory for the mechanics of damage and quasi-brittle failure in solids. J. Mech. Phys. Solids 2017, 103, 72–99. [Google Scholar] [CrossRef]
- Wu, J.Y.; Qiu, J.F.; Nguyen, V.P.; Mandal, T.K.; Zhuang, L.J. Computational modelling of localized failure in solids: XFEM vs. PF-CZM. Comput. Methods Appl. Mech. Eng. 2018, 345, 618–643. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Meth. Engng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Wu, J.Y.; Nguyen, V.P. A length scale insensitive phase-field damage model for brittle fracture. J. Mech. Phys. Solids 2018, 119, 20–42. [Google Scholar] [CrossRef]
- May, S.; Vignollet, J.; de Borst, R. A numerical assessment of phase-field models for brittle and cohesive fracture: Γ-Convergence and stress oscillations. Eur. J. Mech. A/Solids 2015, 52, 72–84. [Google Scholar] [CrossRef]
- Wu, J.Y. A geometrically regularized gradient-damage model with energetic equivalence. Comput. Methods Appl. Mech. Eng. 2018, 328, 612–637. [Google Scholar] [CrossRef]
- Feng, D.C.; Wu, J.Y. Phase-field regularized cohesive zone model (CZM) and size effect of concrete. Eng. Fract. Mech. 2018, 197, 66–79. [Google Scholar] [CrossRef]
- Mandal, T.K.; Nguyen, V.P.; Heidarpour, A. Phase field and gradient enhanced damage models for quasi-brittle failure: A numerical comparative study. Eng. Fract. Mech. 2019, 207, 48–67. [Google Scholar] [CrossRef]
- Larsen, C.J.; Ortner, C.; Sali, E. Existence of Solutions to A Regularized Model of Dynamic Fracture. Math. Models Methods Appl. Sci. 2010, 20, 1021–1048. [Google Scholar] [CrossRef]
- Bourdin, B.; Larsen, C.J.; Richardson, C.L. A time-discrete model for dynamic fracture based on crack regularization. Int. J. Fract. 2011, 168, 133–143. [Google Scholar] [CrossRef]
- Schlüter, A.; Willenbücher, A.; Kuhn, C.; Müller, R. Phase field approximation of dynamic brittle fracture. Comput. Mech. 2014, 54, 1141–1161. [Google Scholar] [CrossRef]
- Borden, M.J.; Verhoosel, C.V.; Scott, M.A.; Hughes, T.J.; Landis, C.M. A phase-field description of dynamic brittle fracture. Comput. Methods Appl. Mech. Eng. 2012, 217–220, 77–95. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Wu, J. Modelling dynamic fracture of solids with a phase-field regularized cohesive zone model. Comput. Methods Appl. Mech. Eng. 2018, 340, 1000–1022. [Google Scholar] [CrossRef]
- Lee, S.; Wheeler, M.F.; Wick, T. Pressure and fluid-driven fracture propagation in porous media using an adaptive finite element phase-field model. Comput. Methods Appl. Mech. Eng. 2016, 305, 111–132. [Google Scholar] [CrossRef]
- Miehe, C.; Mauthe, S. Phase field modelling of fracture in multi-physics problems. Part III. Crack driving forces in hydro-poro-elasticity and hydraulic fracturing of fluid-saturated porous media. Comput. Methods Appl. Mech. Eng. 2016, 304, 619–655. [Google Scholar] [CrossRef]
- Badnava, H.; Msekh, M.A.; Etemadi, E.; Rabczuk, T. An h-adaptive thermo-mechanical phase-field model for fracture. Finite Elem. Anal. Des. 2018, 138, 31–47. [Google Scholar] [CrossRef]
- Zhou, S.; Zhuang, X.; Rabczuk, T. A phase-field modelling approach of fracture propagation in poroelastic media. Eng. Geol. 2018, 240, 189–203. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.; Marigo, J.J. The Variational Approach to Fracture; Springer: Berlin, Germany, 2008. [Google Scholar]
- Ambati, M.; Gerasimov, T.; de Lorenzis, L. A review on phase-field models for brittle fracture and a new fast hybrid formulation. Comput. Mech. 2015, 55, 383–405. [Google Scholar] [CrossRef]
- Wu, J.Y.; Nguyen, V.P.; Nguyen, C.T.; Sutulas, D.; Sinaie, S.; Bordas, S.P.A. Phase field model for fracture. Adv. Appl. Mech. Fract. Mech. Recent Dev. Trends. 2019. submitted for publication. [Google Scholar]
- Sirovich, L. Turbulence and the dynamics of cohenrent structures. Part 1: Coherent structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef]
- Holmes, P.; Lumley, J.; Berkooz, G. Tubulence, Cohenrent Structures, Dynamical Systems and Symmetry; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Antoulas, A.C.; Sorensen, D.C.; Gugercin, S. A survey of model reduction methods for large-scale systems. Contemp. Math. 2001, 280, 193–219. [Google Scholar]
- Haasdonk, B.; Ohlberger, M. Reduced basis method for finite volume approximations of parametrized linear evolution equations. ESAIM Math. Model. Numer. Anal. 2008, 42, 277–302. [Google Scholar] [CrossRef]
- Astrid, P.; Weiland, S.; Willcox, K.; Backx, T. Missing Point Estimation in Models Described by Proper Orthogonal Decomposition. IEEE Trans. Autom. Control 2008, 53, 2237–2251. [Google Scholar] [CrossRef]
- Carlberg, K.; Farhat, C.; Cortial, J.; Amsallem, D. The GNAT method for nonlinear model reduction: Effective implementation and application to computational fluid dynamics and turbulent flows. J. Comput. Phys. 2013, 242, 623–647. [Google Scholar] [CrossRef]
- Barrault, M.; Maday, Y.; Nguyen, N.C.; Patera, A.T. An ‘empirical interpolation’ method: Application to efficient reduced-basis discretization of partial differential equations. C. R. Math. 2004, 339, 667–672. [Google Scholar] [CrossRef]
- Chaturantabut, S.; Sorensen, D.C. Nonlinear Model Reduction via Discrete Empirical Interpolation. SIAM J. Sci. Comput. 2010, 32, 2737–2764. [Google Scholar] [CrossRef]
- Radermacher, A.; Reese, S. POD-based model reduction with empirical interpolation applied to nonlinear elasticity. Int. J. Numer. Methods Eng. 2016, 107, 477–495. [Google Scholar] [CrossRef]
- Benner, P.; Gugercin, S.; Willcox, K. A Survey of Model Reduction Methods for Parametric Systems; Preprint MPIMD/13–14; Max Planck Institute Magdeburg: Magdeburg, Germany, 2013. [Google Scholar]
- Wirtz, D.; Sorensen, D.C.; Haasdonk, B. A Posteriori Error Estimation for DEIM Reduced Nonlinear Dynamical Systems. SIAM J. Sci. Comput. 2014, 36, A311–A338. [Google Scholar] [CrossRef]
- Negri, F.; Manzoni, A.; Amsallem, D. Efficient model reduction of parametrized systems by matrix discrete empirical interpolation. J. Comput. Phys. 2015, 303, 431–454. [Google Scholar] [CrossRef]
- Amsallem, D.; Cortial, J.; Carlberg, K.; Farhat, C. A method for interpolating on manifolds structural dynamics reduced-order models. Int. J. Numer. Methods Eng. 2009, 80, 1241–1258. [Google Scholar] [CrossRef]
- Panzer, H.; Mohring, J.; Eid, R.; Lohmann, B. Parametric Model Order Reduction by Matrix Interpolation. at-Automatisierungstechnik 2010, 58, 475–484. [Google Scholar] [CrossRef]
- Degroote, J.; Vierendeels, J.; Willcox, K. Interpolation among reduced-order matrices to obtain parameterized models for design, optimization and probabilistic analysis. Int. J. Numer. Methods Fluids 2010, 63, 207–230. [Google Scholar] [CrossRef]
- Amsallem, D.; Farhat, C. An Online Method for Interpolating Linear Parametric Reduced-Order Models. SIAM J. Sci. Comput. 2011, 33, 2169–2198. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Le, T.H.H.; Khoo, B.C. Model reduction for parametric and nonlinear PDEs N by matrix interpolation. In Proceedings of the 2015 International Conference on Advanced Technologies for Communications (ATC), Ho Chi Minh City, Vietnam, 14–16 October 2015; pp. 105–110. [Google Scholar] [CrossRef]
- Nguyen, N.C.; Patera, A.T.; Peraire, J. A ‘best points’ interpolation method for efficient approximation of parametrized functions. Int. J. Numer. Methods Eng. 2008, 73, 521–543. [Google Scholar] [CrossRef]
- Nguyen, N.H. A rapid simulation of nano-particle transport in a two-dimensional human airway using POD/Galerkin reduced-order models. Int. J. Numer. Methods Eng. 2016, 105, 514–531. [Google Scholar] [CrossRef]
- Rixen, D.J. A dual Craig–Bampton method for dynamic substructuring. J. Comput. Appl. Math. 2004, 168, 383–391. [Google Scholar] [CrossRef]
- Markovic, D.; Park, K.; Ibrahimbegovic, A. Reduction of substructural interface degrees of freedom in flexibility-based component mode synthesis. Int. J. Numer. Methods Eng. 2007, 70, 163–180. [Google Scholar] [CrossRef]
- Tiso, P.; Rixen, D.J. Discrete empirical interpolation method for finite element structural dynamics. In Topics in Nonlinear Dynamics, Volume 1; Springer: Berlin, Germany, 2013; pp. 203–212. [Google Scholar]
- Galland, F.; Gravouil, A.; Malvesin, E.; Rochette, M. A global model reduction approach for 3D fatigue crack growth with confined plasticity. Comput. Methods Appl. Mech. Eng. 2011, 200, 699–716. [Google Scholar] [CrossRef]
- Ghavamian, F.; Tiso, P.; Simone, A. POD–DEIM model order reduction for strain-softening viscoplasticity. Comput. Methods Appl. Mech. Eng. 2017, 317, 458–479. [Google Scholar] [CrossRef]
- Kerfriden, P.; Passieux, J.C.; Bordas, S.P.A. Local/global model order reduction strategy for the simulation of quasi-brittle fracture. Int. J. Numer. Methods Eng. 2012, 89, 154–179. [Google Scholar] [CrossRef]
- Kerfriden, P.; Goury, O.; Rabczuk, T.; Bordas, S.P.A. A partitioned model order reduction approach to rationalise computational expenses in nonlinear fracture mechanics. Comput. Methods Appl. Mech. Eng. 2013, 256, 169–188. [Google Scholar] [CrossRef] [PubMed]
- Goury, O.; Amsallem, D.; Bordas, S.P.A.; Liu, W.K.; Kerfriden, P. Automatised selection of load paths to construct reduced-order models in computational damage micromechanics: From dissipation-driven random selection to Bayesian optimization. Comput. Mech. 2016, 58, 213–234. [Google Scholar] [CrossRef]
- Oliver, J.; Caicedo, M.; Huespe, A.E.; Hernández, J.; Roubin, E. Reduced order modelling strategies for computational multiscale fracture. Comput. Methods Appl. Mech. Eng. 2017, 313, 560–595. [Google Scholar] [CrossRef]
- Xia, L.; Da, D.; Yvonnet, J. Topology optimization for maximizing the fracture resistance of quasi-brittle composites. Comput. Methods Appl. Mech. Eng. 2018, 332, 234–254. [Google Scholar] [CrossRef]
- Krige, D.G. A Statistical Approach to Some Mine Valuations and Allied Problems at the Witwatersrand. Master’s Thesis, The University of Witwatersrand, Johannesburg, South Africa, 1951. [Google Scholar]
- Cressie, N.A.C. The Origins of Kriging. Math. Geol. 1990, 22, 239–252. [Google Scholar] [CrossRef]
- Pham, K.; Amor, H.; Marigo, J.J.; Maurini, C. Gradient damage models and their use to approximate brittle fracture. Int. J. Damage Mech. 2011, 20, 618–652. [Google Scholar] [CrossRef]
- Peerlings, R.; de Borst, R.; Brekelmans, W.; de Vree, J. Gradient-enhanced damage for quasi-brittle materials. Int. J. Numer. Methods Engng. 1996, 39, 3391–3403. [Google Scholar] [CrossRef]
- Wu, J.Y. Robust numerical implementation of non-standard phase-field damage models for failure in solids. Comput. Methods Appl. Mech. Eng. 2018, 340, 767–797. [Google Scholar] [CrossRef]
- Amor, H.; Marigo, J.; Maurini, C. Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments. J. Mech. Phys. Solids 2009, 57, 1209–1229. [Google Scholar] [CrossRef]
- Ryckelynck, D. Hyper-reduction of mechanical models involving internal variables. Int. J. Numer. Methods Eng. 2009, 77, 75–89. [Google Scholar] [CrossRef]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and Analysis of Computer Experiments. Stat. Sci. 1989, 4, 409–435. [Google Scholar] [CrossRef]
- Lophaven, S.N.; Nielsen, H.B.; Sondergaard, J. Aspects of the MATLAB Toolbox DACE; Technical Report IMM-REP-2002-13; Technical University of Denmark: Lyngby, Denmark, 2002. [Google Scholar]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]


() | () | () | () | () | |
|---|---|---|---|---|---|
| Parameter | FOM | ROM | KRI |
|---|---|---|---|
| N | 1001 | 20-20-28-16-14 | 1 |
| (s) | 64.1 | 8.1 | 5.61 × 10 |
| 1.74 × 10 | 9.63 × 10 | ||
| 4.45 × 10 | 6.41 × 10 | ||
| 2.01 × 10 | 8.21 × 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, N.-H.; Nguyen, V.P.; Wu, J.-Y.; Le, T.-H.-H.; Ding, Y. Mesh-Based and Meshfree Reduced Order Phase-Field Models for Brittle Fracture: One Dimensional Problems. Materials 2019, 12, 1858. https://doi.org/10.3390/ma12111858
Nguyen N-H, Nguyen VP, Wu J-Y, Le T-H-H, Ding Y. Mesh-Based and Meshfree Reduced Order Phase-Field Models for Brittle Fracture: One Dimensional Problems. Materials. 2019; 12(11):1858. https://doi.org/10.3390/ma12111858
Chicago/Turabian StyleNguyen, Ngoc-Hien, Vinh Phu Nguyen, Jian-Ying Wu, Thi-Hong-Hieu Le, and Yan Ding. 2019. "Mesh-Based and Meshfree Reduced Order Phase-Field Models for Brittle Fracture: One Dimensional Problems" Materials 12, no. 11: 1858. https://doi.org/10.3390/ma12111858
APA StyleNguyen, N.-H., Nguyen, V. P., Wu, J.-Y., Le, T.-H.-H., & Ding, Y. (2019). Mesh-Based and Meshfree Reduced Order Phase-Field Models for Brittle Fracture: One Dimensional Problems. Materials, 12(11), 1858. https://doi.org/10.3390/ma12111858





