Modelling of Coupled Shrinkage and Creep in Multiphase Formulations for Hardening Concrete
Abstract
1. Introduction
2. Governing Equations
2.1. Derived Thermodynamic State Variables
2.2. Hydration Model and Porosity Evolution
2.3. Desorption Isotherm
2.4. Balance Equations
2.4.1. Balance of Momentum for the Multiphase Continuum
2.4.2. Balances of Mass for the Solid Phase and the Water Phase
2.4.3. Balance of Enthalpy for the Multiphase Mixture
3. Shrinkage and Creep Models
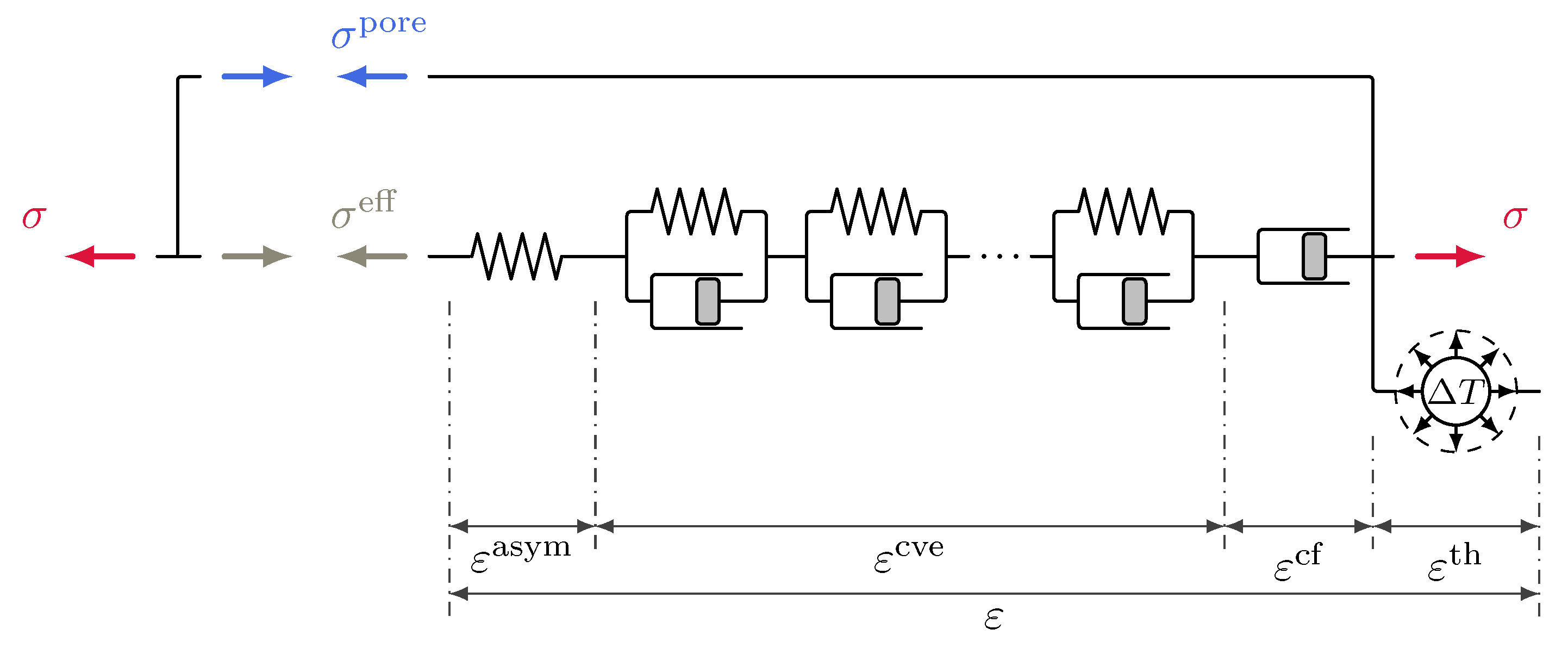
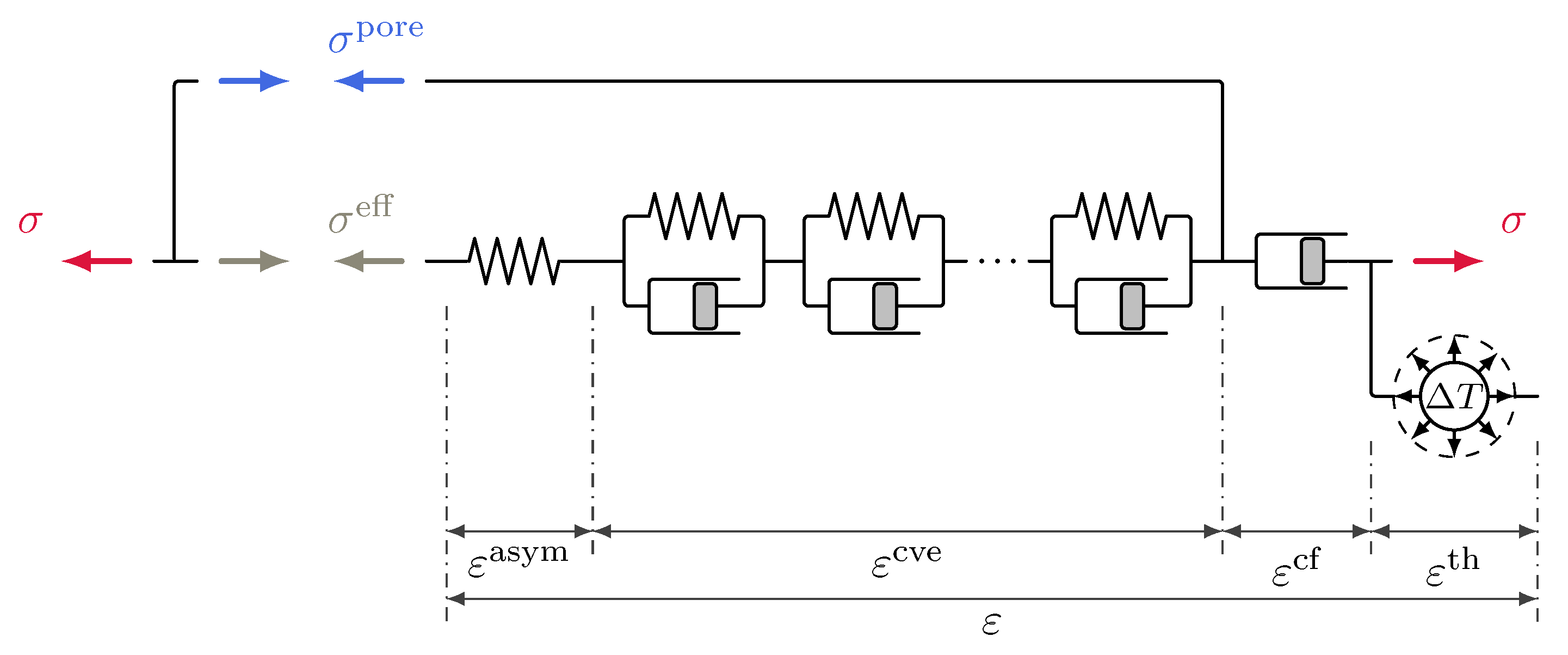
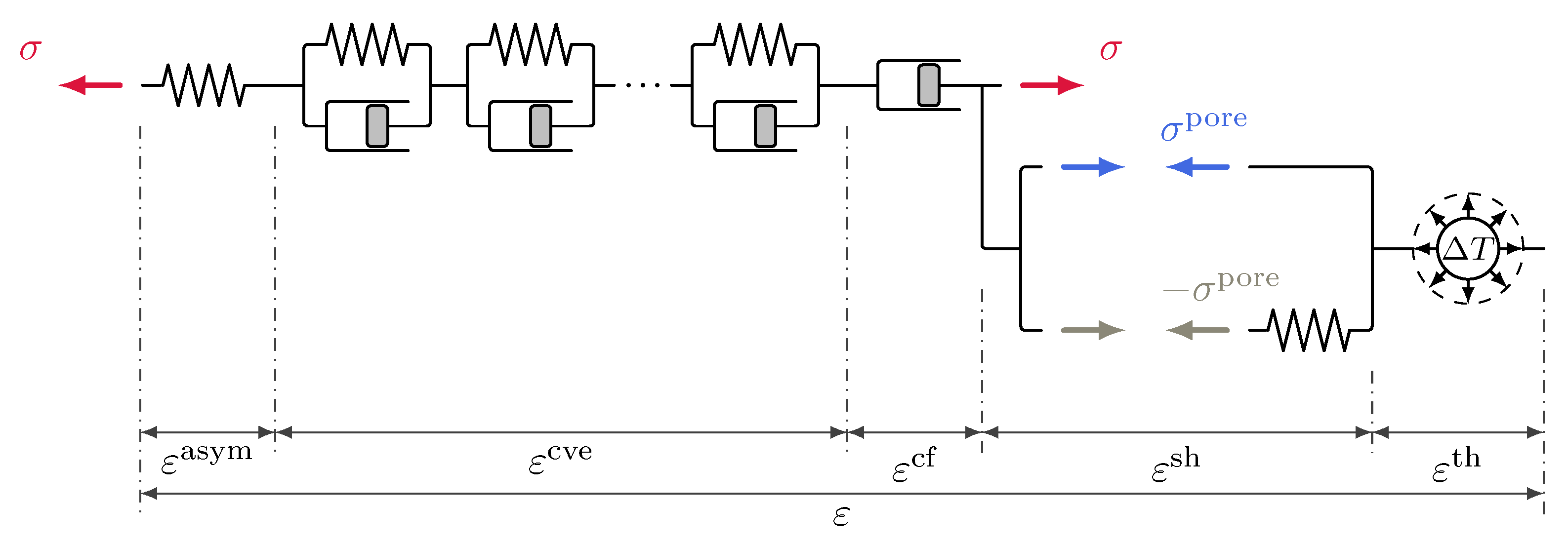
3.1. Stress Variables in Multiphase Models and Creep Driving Stress
3.2. Evolution of the Creep Strain
3.2.1. Viscoelastic Creep Strain Rate
3.2.2. Viscous Flow Creep
3.3. Stress-Strain Relationship and Effective Young’s Modulus
3.4. Coupled Multiphase Shrinkage and Creep Formulations
3.4.1. Original Multiphase Shrinkage and Creep Formulation Driven by Effective Stress
3.4.2. Multiphase Shrinkage and Creep Formulation in Terms of the Mixed Stress Concept
3.4.3. Multiphase Shrinkage and Creep Formulation in Terms of Total Stress
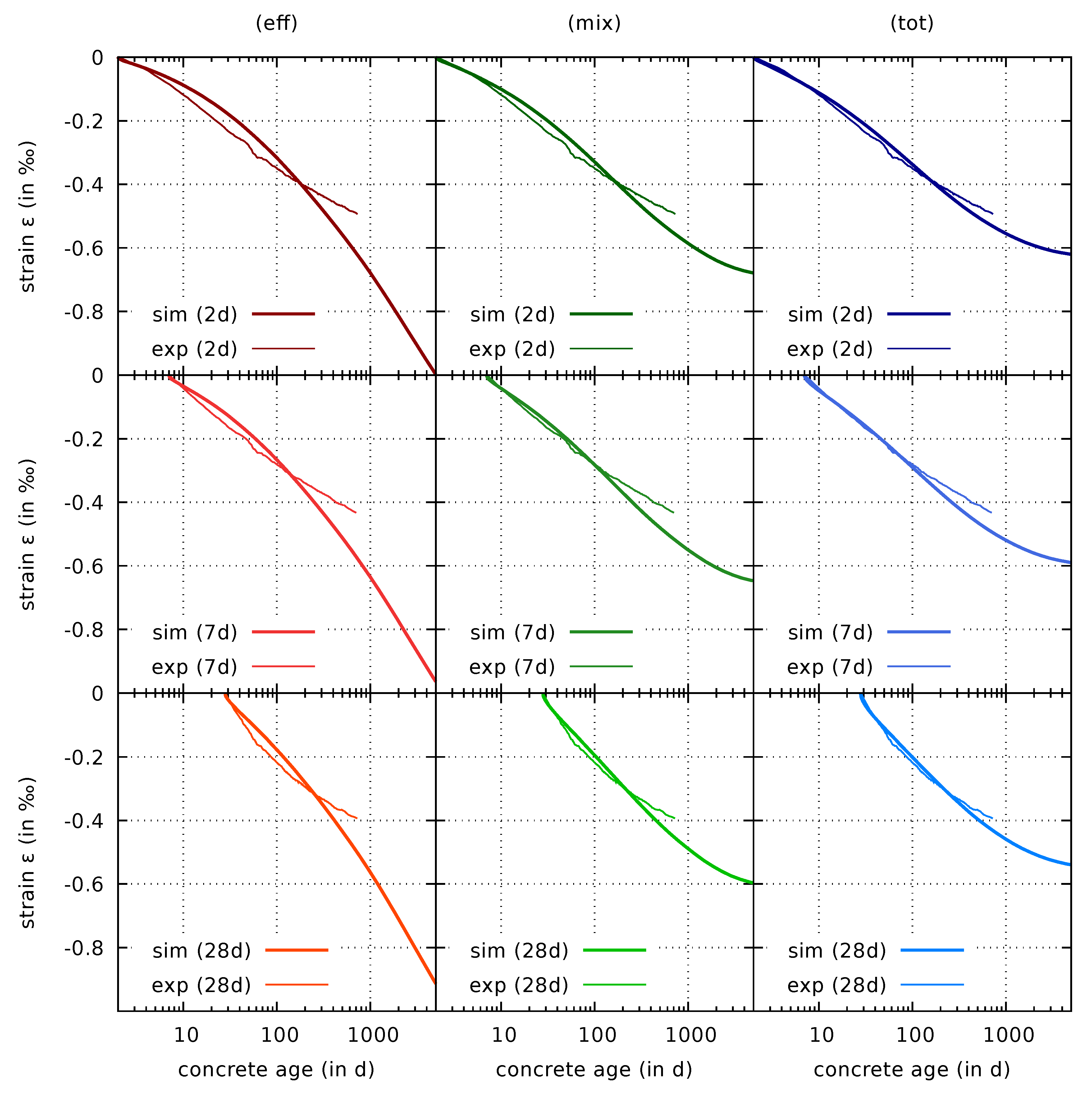
4. Comparison of the Shrinkage and Creep Formulations
4.1. Drying Shrinkage of Thin Concrete Slices
4.2. Shrinkage and Creep Tests of Cylindrical Specimens
4.2.1. Prediction of Creep Compliance Functions
4.2.2. Prediction of Autogenous Shrinkage
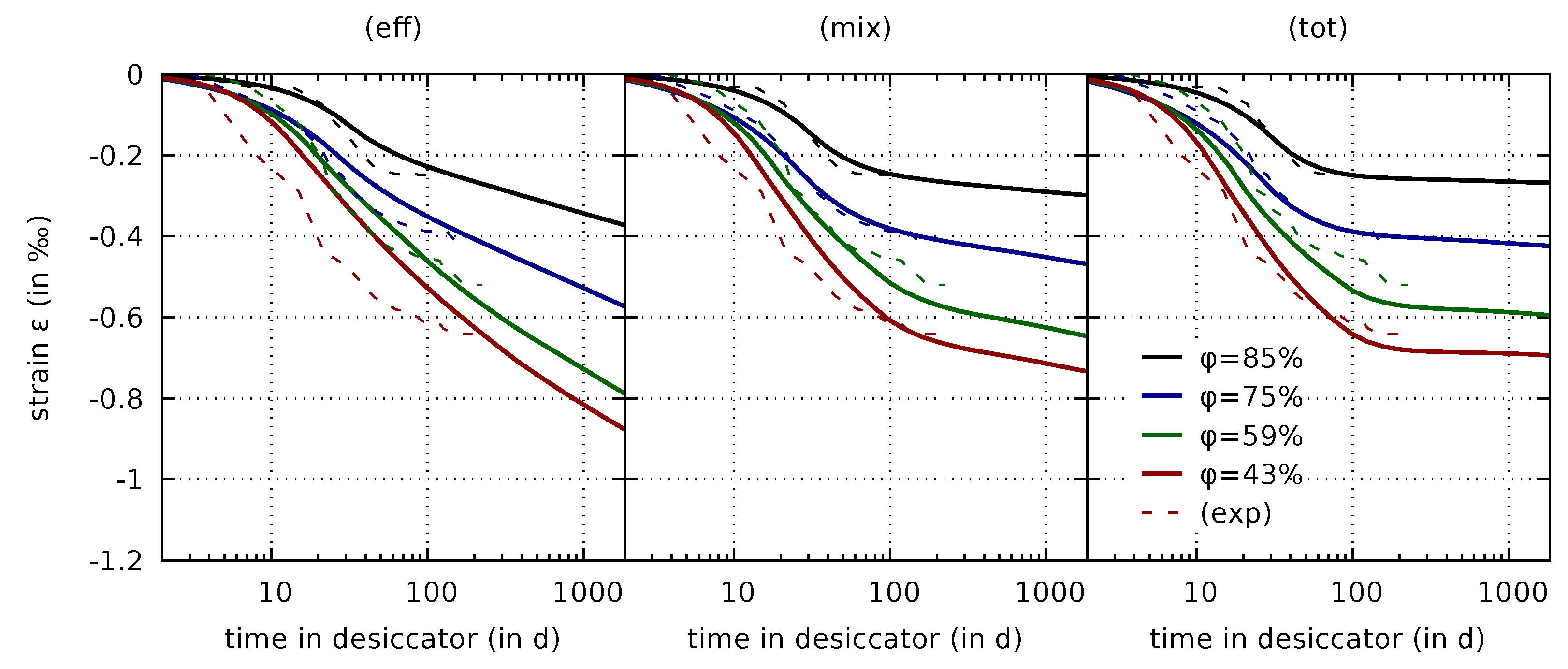
4.2.3. Predictions of Drying Shrinkage of Cylindrical Specimens
5. Conclusions
- Two new variants of a multiphase shrinkage and creep formulation are presented and are compared to the effective stress formulation by Gawin et al. [1,2]. The new formulations, termed mixed stress formulation and total stress formulation, differ from the original approach in the choice of the stress variable which drives viscous flow creep. The mixed stress formulation and the total stress formulation are based on different stress variables driving viscoelastic creep.
- The effective stress formulation predicts viscoelastic and viscous flow creep due to drying. The mixed stress formulation predicts only viscoelastic creep due to drying. For the total stress formulation, creep occurs in drying specimens only as a (minor) secondary effect related to restraint stresses resulting from inhomogeneous drying.
- The original effective stress formulation predicts significant shrinkage rates even after several years of autogenous shrinkage and drying shrinkage. Data from long-term shrinkage tests from the literature indicate that such a behavior contradicts test data. In contrast, the predicted shrinkage strains for both the mixed stress formulation and the total stress formulation, approach an ultimate value in the long term.
- The new coupled shrinkage and creep formulations are calibrated based on drying shrinkage data from experiments on thin concrete slices. Improved predictions for the evolution of these drying shrinkage strains are obtained for both the mixed and total stress formulation.
- For the new mixed and total stress formulation, the calibration of the shrinkage parameters is independent of the calibration of the long-term viscous flow creep parameters. Unlike in the original approach, shrinkage is decoupled from viscous long-term flow creep and vice versa.
- The predictions of the evolution of the shrinkage strain for sealed and unsealed cylindrical specimens are significantly improved by the mixed and the total stress formulation. It is emphasized that only the generalized Bishop parameter is recalibrated for the different formulations based on the data from thin concrete slices. All other parts of the model, and its parameters determined in [7], remain unchanged. The improved predictions for the cylindrical specimens are therefore the consequence of the modification of the coupled shrinkage and creep formulation.
Author Contributions
Funding
Conflicts of Interest
References
- Gawin, D.; Pesavento, F.; Schrefler, B.A. Hygro-thermo-chemo-mechanical modelling of concrete at early ages and beyond. Part I: hydration and hygro-thermal phenomena. Int. J. Numer. Meth. Eng. 2006, 67, 299–331. [Google Scholar] [CrossRef]
- Gawin, D.; Pesavento, F.; Schrefler, B.A. Hygro-thermo-chemo-mechanical modelling of concrete at early ages and beyond. Part II: shrinkage and creep of concrete. Int. J. Numer. Meth. Eng. 2006, 67, 332–363. [Google Scholar] [CrossRef]
- Sciumè, G.; Benboudjema, F.; De Sa, C.; Pesavento, F.; Berthaud, Y.; Schrefler, B.A. A multiphysics model for concrete at early age applied to repairs problems. Eng. Struct. 2013, 57, 374–387. [Google Scholar] [CrossRef]
- Valentini, B.; Theiner, Y.; Aschaber, M.; Lehar, H.; Hofstetter, G. Single-phase and multi-phase modeling of concrete structures. Eng. Struct. 2013, 47, 25–34. [Google Scholar] [CrossRef]
- Neuner, M.; Gamnitzer, P.; Hofstetter, G. An extended damage plasticity model for shotcrete: Formulation and comparison with other shotcrete models. Materials 2017, 10, 82. [Google Scholar] [CrossRef] [PubMed]
- Gasch, T.; Eriksson, D.; Ansell, A. On the behaviour of concrete at early-ages: A multiphase description of hygro-thermo-chemo-mechanical properties. Cem. Concr. Res. 2019, 116, 202–216. [Google Scholar] [CrossRef]
- Gamnitzer, P.; Drexel, M.; Brugger, A.; Hofstetter, G. Calibration of a multiphase model based on a comprehensive data set for a normal strength concrete. Materials 2019, 12, 791. [Google Scholar] [CrossRef] [PubMed]
- Theiner, Y.; Drexel, M.; Neuner, M.; Hofstetter, G. Comprehensive study of concrete creep, shrinkage, and water content evolution under sealed and drying conditions. Strain 2017, 53, e12223. [Google Scholar] [CrossRef]
- Drexel, M.; Theiner, Y.; Hofstetter, G. Versuche zum Schwinden und Kriechen von Beton unter Berücksichtigung des Feuchtegehalts. Bauingenieur 2018, 93, 95–102. [Google Scholar]
- Drexel, M.; Theiner, Y.; Hofstetter, G. Investigation of tensile creep of a normal strength overlay concrete. Materials 2018, 11, 993. [Google Scholar] [CrossRef]
- Drexel, M.; Smaniotto, S.; Hofstetter, G. Complementary experimental study of a normal strength overlay concrete. Mater. Today-Proc. 2019, 12, 279–287. [Google Scholar] [CrossRef]
- Alonso, E.E.; Gens, A.; Josa, A. A constitutive model for partially saturated soils. Géotechnique 1990, 40, 405–430. [Google Scholar] [CrossRef]
- Kohler, R.; Hofstetter, G. A cap model for partially saturated soils. Int. J. Numer. Anal. Meth. Geomech. 2008, 32, 981–1004. [Google Scholar] [CrossRef]
- Gamnitzer, P.; Hofstetter, G. A smoothed cap model for variably saturated soils and its robust numerical implementation. Int. J. Numer. Anal. Meth. Geomech. 2015, 39, 1276–1303. [Google Scholar] [CrossRef]
- Nuth, M.; Laloui, L. Effective stress concept in unsaturated soils: Clarification and validation of a unified framework. Int. J. Numer. Anal. Meth. Geomech. 2008, 32, 771–801. [Google Scholar] [CrossRef]
- Lewis, R.W.; Schrefler, B.A. The Finite Element Method in the Static and Dynamic Deformation and Consolidation of Porous Media; Wiley: Chichester, UK, 1998. [Google Scholar]
- Ulm, F.-J.; Coussy, O. Strength growth as chemo-plastic hardening in early age concrete. J. Eng. Mech. 1996, 122, 1123–1132. [Google Scholar] [CrossRef]
- Cervera, M.; Oliver, J.; Prato, T. Thermo-chemo-mechanical model for concrete I: Hydration and aging. J. Eng. Mech. 1999, 125, 1018–1027. [Google Scholar] [CrossRef]
- Torrenti, J.M.; Benboudjema, F. Mechanical threshold of cementitious materials at early age. Mater. Struct. 2005, 38, 299–304. [Google Scholar] [CrossRef]
- Pantazopoulou, S.J.; Mills, R.H. Microstructural aspects of the mechanical response of plain concrete. ACI Mater. J. 1995, 92, 605–616. [Google Scholar]
- Bažant, Z.P.; Jirásek, M. Creep and Hygrothermal Effects in Concrete Structures; Springer: Dordrecht, The Netherlands, 2018. [Google Scholar]
- Chitez, A.S.; Jefferson, A.D. Porosity development in a thermo-hygral finite element model for cementitious materials. Cem. Concr. Res. 2015, 78, 216–233. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Gallipoli, D.; Wheeler, S.J.; Karstunen, M. Modelling the variation of degree of saturation in a deformable unsaturated soil. Géotechnique 2003, 53, 105–112. [Google Scholar] [CrossRef]
- Gawin, D.; Pesavento, F.; Schrefler, B.A. Modelling of hygro-thermal behaviour of concrete at high temperature with thermo-chemical and mechanical material degradation. Comput. Methods Appl. Mech. Eng. 2003, 192, 1731–1771. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Gawin, D.; Majorana, C.E.; Schrefler, B.A. Numerical analysis of hygro-thermal behaviour and damage of concrete at high temperature. Mech. Cohes.-Frict. Mater. 1999, 4, 37–74. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Prasannan, A. Solidification theory for concrete creep. I: Formulation. J. Eng. Mech. 1989, 115, 1691–1703. [Google Scholar] [CrossRef]
- Carol, I.; Bažant, Z.P. Viscoelasticity with aging caused by solidification of nonaging constituent. J. Eng. Mech. 1993, 113, 2252–2269. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Hauggaard, A.B.; Baweja, S.; Ulm, F.-J. Microprestress-solidification theory for concrete creep. I: Aging and drying effects. J. Eng. Mech. 1997, 123, 1188–1194. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Hauggaard, A.B.; Baweja, S. Microprestress-solidification theory for concrete creep. II: Algorithm and Verification. J. Eng. Mech. 1997, 123, 1195–1201. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Xi, Y. Continuous retardation spectrum for solidification theory of concrete creep. J. Eng. Mech. 1995, 121, 281–288. [Google Scholar] [CrossRef]
- Jirásek, M.; Havlásek, P. Microprestress-solidification theory of concrete creep: Reformulation and improvement. Cem. Concr. Res. 2014, 60, 51–62. [Google Scholar] [CrossRef]
- Hilaire, A.; Benboudjema, F.; Darquennes, A.; Berthaud, Y.; Nahas, G. Modeling basic creep in concrete at early-age under compressive and tensile loading. Nucl. Eng. Des. 2014, 269, 222–230. [Google Scholar] [CrossRef]
- Gamnitzer, P.; Hofstetter, G. Fully coupled multi-phase modelling of pumping induced settlements, air- and water flow in multi-layered normally consolidated soils. Comput. Geotech. 2016, 79, 10–21. [Google Scholar] [CrossRef]
- Aili, A.; Vandamme, M.; Torrenti, J.; Masson, B. Is long-term autogenous shrinkage a creep phenomenon induced by capillary effects due to self-desiccation? Cem. Concr. Res. 2018, 108, 186–200. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Li, G.H. Comprehensive database on concrete creep and shrinkage. ACI Mater. J. 2008, 105, 635–637. [Google Scholar]
- Mazloom, M.; Ramezanianpoura, A.A.; Brooks, J.J. Effect of silica fume on mechanical properties of high-strength concrete. Cem. Concr. Comp. 2004, 26, 347–357. [Google Scholar] [CrossRef]
- Brooks, J.J. 30-year creep and shrinkage of concrete. Mag. Concr. Res. 2005, 57, 545–556. [Google Scholar] [CrossRef]
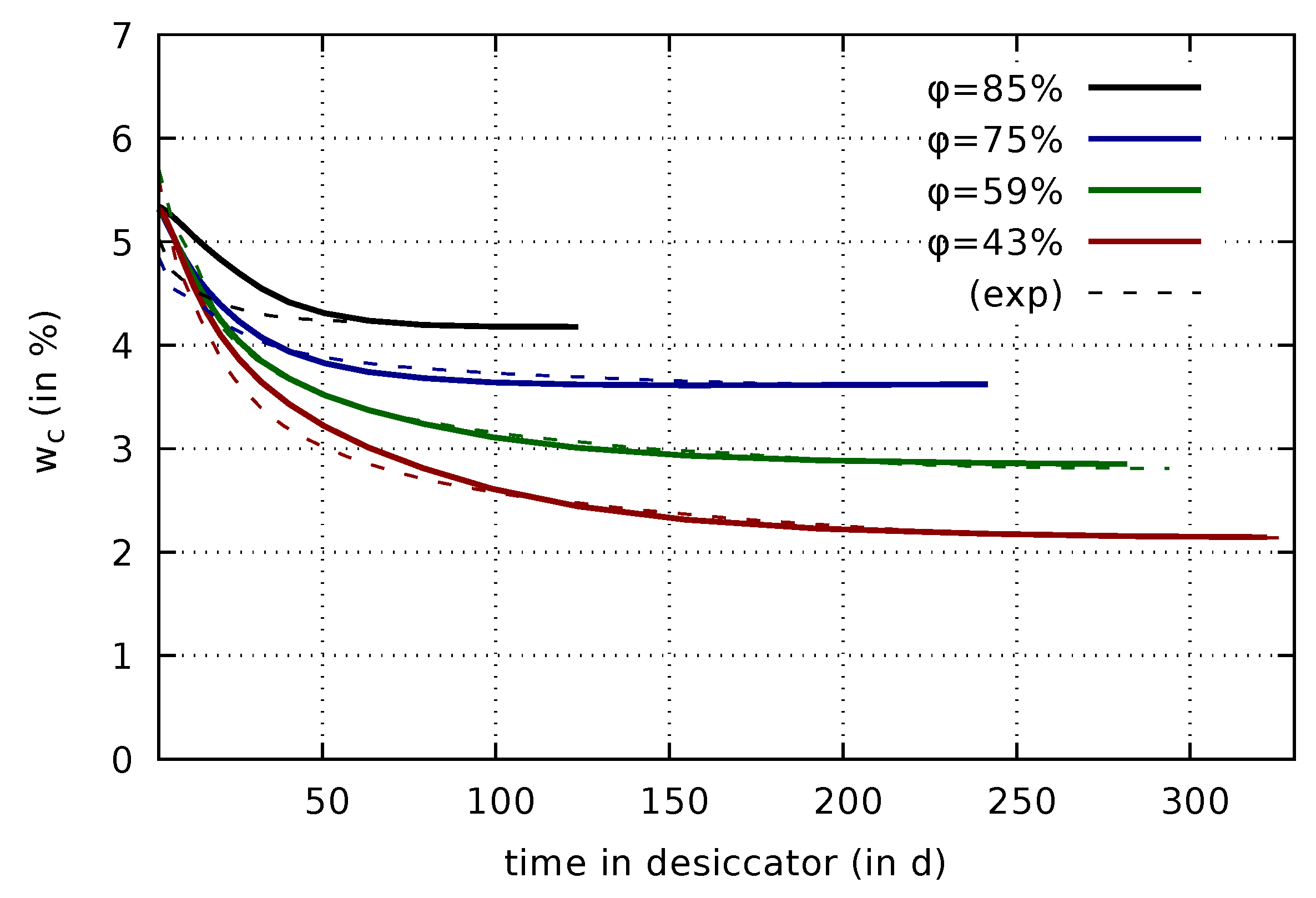
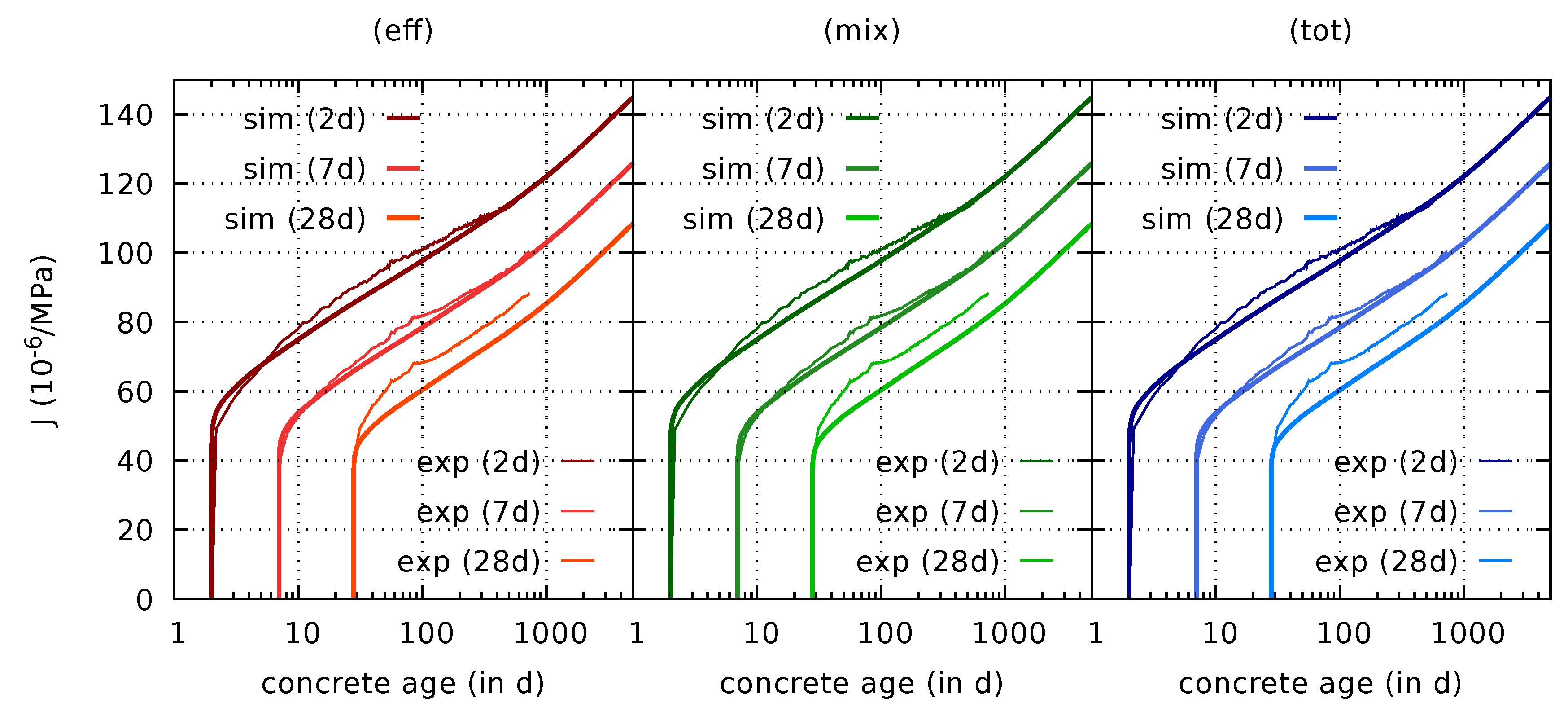
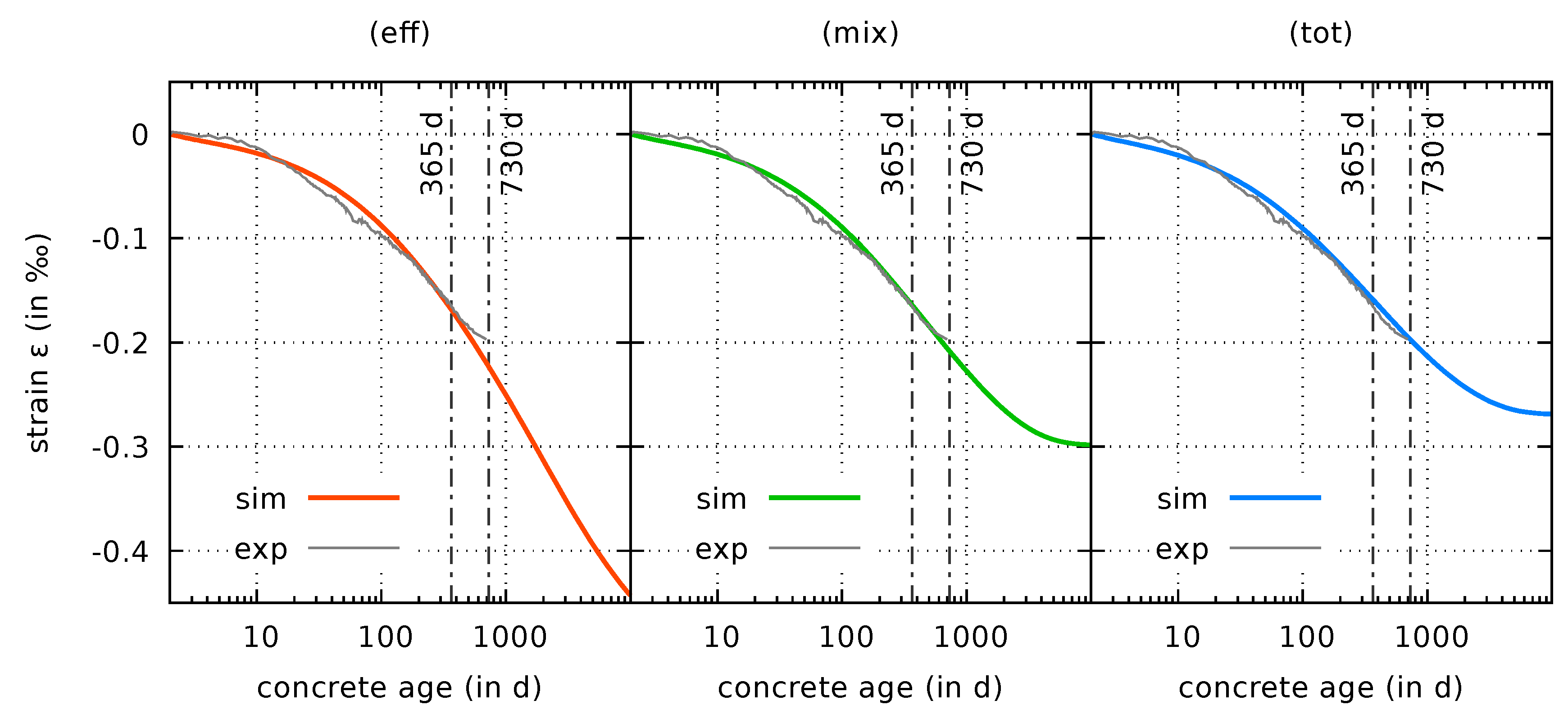
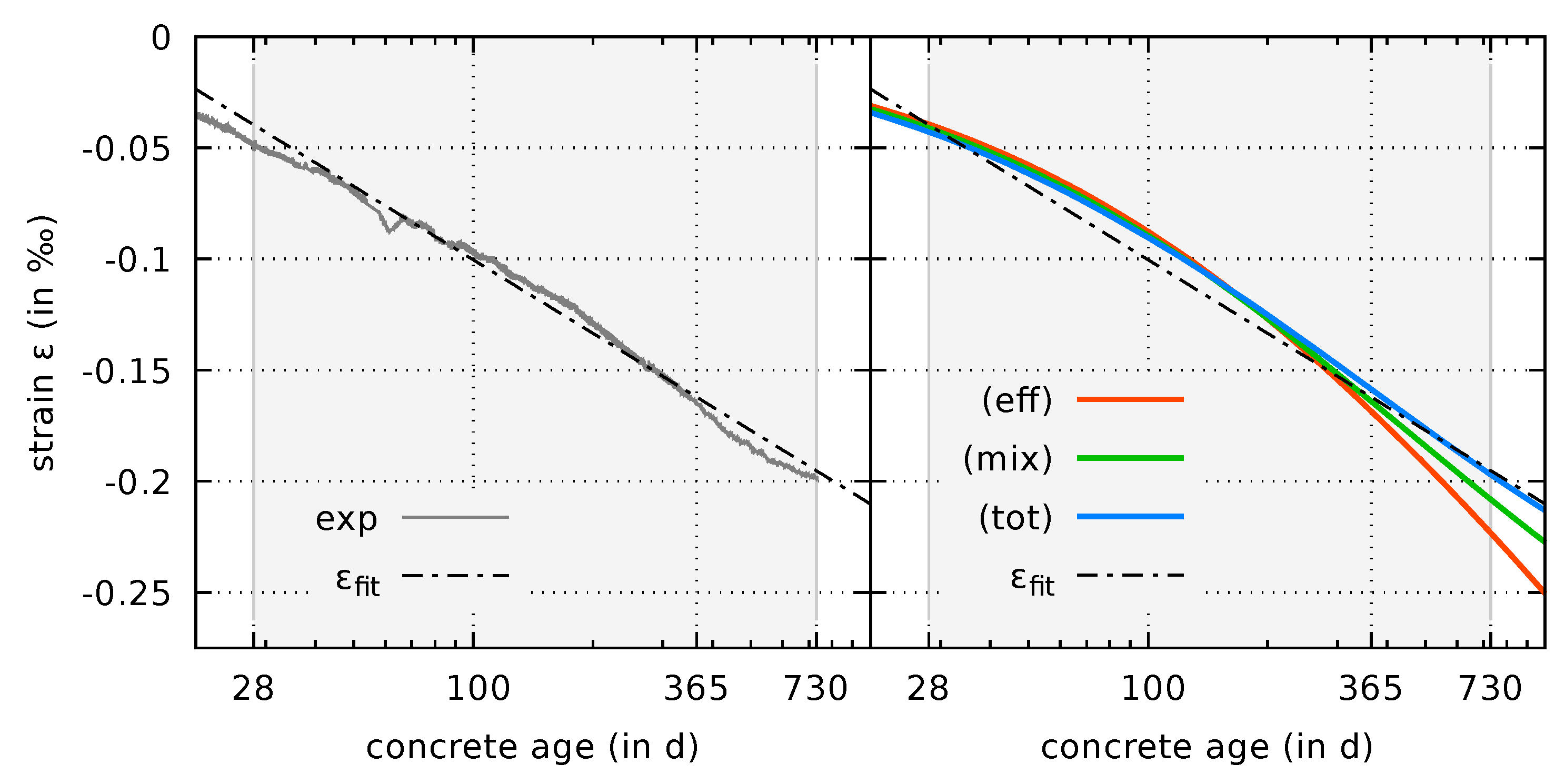
| Component | Amount |
|---|---|
| Cement CEM II A-M (S-L) 42.5 N, Lafarge | 375 |
| Added water (water/cement ratio of ) | 165 |
| Limestone sand mm | 810 |
| Limestone aggregates mm | 183 |
| Limestone aggregates mm | 457 |
| Limestone aggregates mm | 367 |
| Plasticizer Proplast 200 | 0.6% of cement mass |
| Air-entraining agent Proair NVX | 0.045% of cement mass |
| Parameter | Symbol | Value |
|---|---|---|
| Molar mass of air | kg/mol | |
| Molar mass of water | kg/mol | |
| Universal gas constant | R | 8.314 J/(K mol) |
| Atmospheric pressure | ||
| Water density | ||
| Enthalpy of evaporation | / | |
| Vapor pressure at full saturation at 293 |
| Parameter | Symbol | Value |
|---|---|---|
| General parameter for Equation (7) | / | |
| Parameter in Equation (7) governing the early-age response | ||
| Parameter in Equation (7) governing the long-term response | ||
| Estimated ultimate degree of hydration according to [20] | ||
| Activation energy (of lumped model) divided by the universal gas constant | 5000 | |
| Degree of hydration at which concrete is assumed to solidify | ||
| Ultimate amount of chemically bound water per unit volume | ||
| Solid phase density at 293 | 2606 | |
| Porosity at full hydration | % | |
| Parameter governing the decrease of porosity with increasing hydration | % |
| Parameter | Symbol | Value |
|---|---|---|
| First van Genuchten parameter | ||
| Second van Genuchten parameter | ||
| Dimensionless fitting parameter | D | |
| Parameter for porosity-dependence of the air entry value | ||
| Air entry value at full hydration | MPa |
| Parameter | Symbol | Value |
|---|---|---|
| Asymptotic intrinsic permeability at full hydration | m2 | |
| Parameter for hydration dependency of the permeability | ||
| Van Genuchten-Mualem parameter in Equation (16) | ||
| Dynamic viscosity of water | ||
| Coefficient of diffusion in the air at reference temperature | m2/ | |
| Exponent porosity dependence of resistance factor | ||
| Exponent saturation dependence of resistance factor | ||
| Convective mass transport coefficient (on boundary) | /( m2) |
| Parameter | Symbol | Value |
|---|---|---|
| Specific heat capacity of water | /() | |
| Specific heat capacity of dry air | /() | |
| Specific heat capacity of the solid phase | /() | |
| Effective heat conductivity of concrete | /() | |
| Released heat of hydration per unit volume | / | |
| Convective heat transfer coefficient | 9 /( ) |
| Parameter | Symbol | Value |
|---|---|---|
| Poisson’s ratio | ||
| Smallest retardation time in Dirichlet series | day | |
| Number of Kelvin units in Dirichlet expansion | N | 8 |
| Power-law exponent for microscopic creep compliance function | ||
| Viscoelastic compliance parameter | /MPa | |
| Viscous flow creep parameter | /MPa | |
| Initial value of the microsprestress at 1 day | 625 MPa | |
| Parameter for evolution of microprestress | /(MPa day) | |
| Parameter for dependence of evolution of microprestress on humidity changes | 10 MPa |
| Parameter | Symbol | Value |
|---|---|---|
| Asymptotic Young’s modulus at full hydration | 70,180 MPa | |
| Power-law exponent for asymptotic Young’s modulus | ||
| Thermal expansion coefficient | / |
| Parameter | Symbol | (eff) | (mix) | (tot) |
|---|---|---|---|---|
| First parameter in (25) | ||||
| Second (offset) parameter in (25) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gamnitzer, P.; Brugger, A.; Drexel, M.; Hofstetter, G. Modelling of Coupled Shrinkage and Creep in Multiphase Formulations for Hardening Concrete. Materials 2019, 12, 1745. https://doi.org/10.3390/ma12111745
Gamnitzer P, Brugger A, Drexel M, Hofstetter G. Modelling of Coupled Shrinkage and Creep in Multiphase Formulations for Hardening Concrete. Materials. 2019; 12(11):1745. https://doi.org/10.3390/ma12111745
Chicago/Turabian StyleGamnitzer, Peter, Andreas Brugger, Martin Drexel, and Günter Hofstetter. 2019. "Modelling of Coupled Shrinkage and Creep in Multiphase Formulations for Hardening Concrete" Materials 12, no. 11: 1745. https://doi.org/10.3390/ma12111745
APA StyleGamnitzer, P., Brugger, A., Drexel, M., & Hofstetter, G. (2019). Modelling of Coupled Shrinkage and Creep in Multiphase Formulations for Hardening Concrete. Materials, 12(11), 1745. https://doi.org/10.3390/ma12111745





