Scattering Theory of Graphene Grain Boundaries
Abstract
1. Introduction
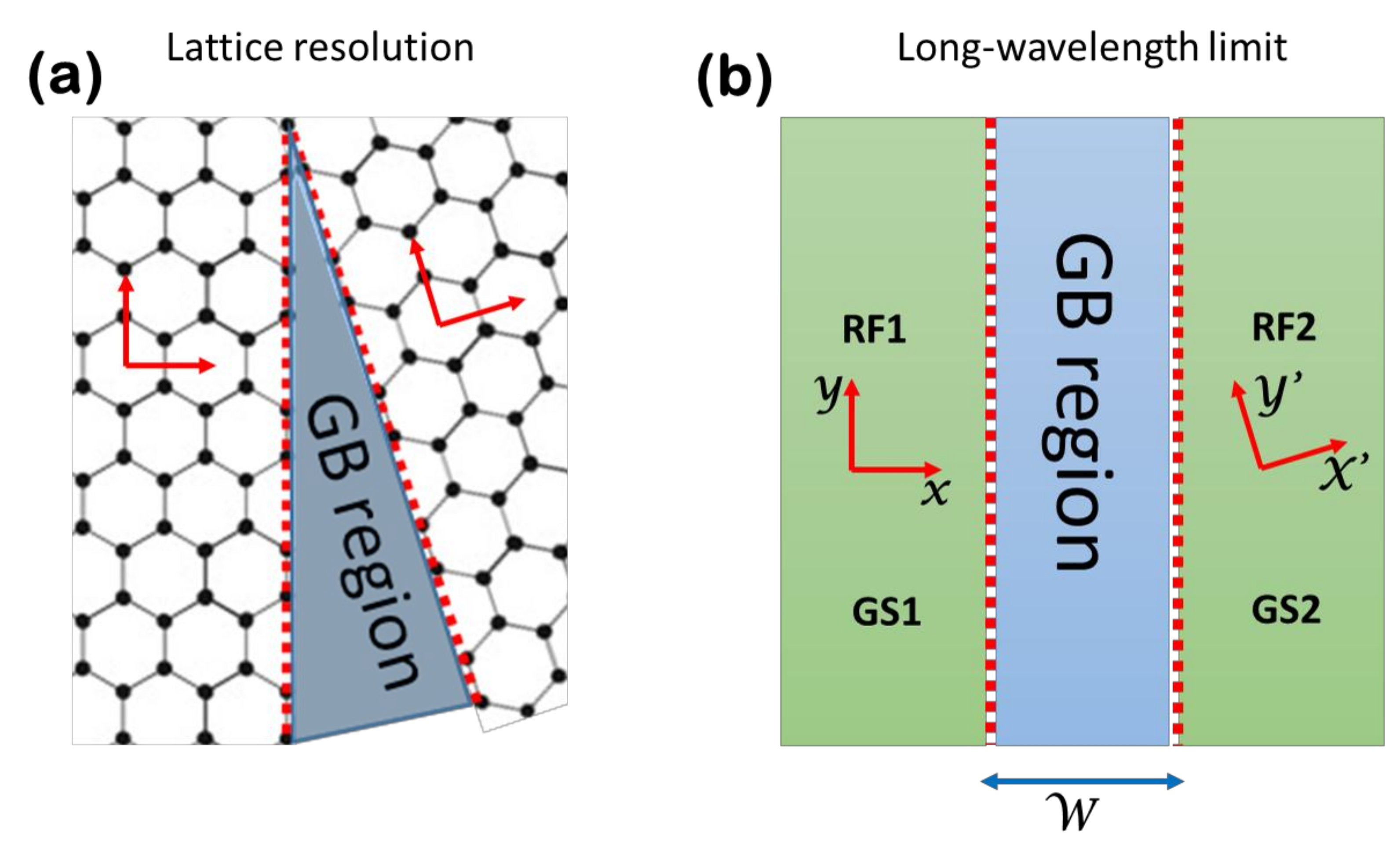
2. Dirac Hamiltonian within a Rotated Reference Frame, Current Density Conservation, and Boundary Conditions at a Grain Boundary
2.1. Dirac Hamiltonian within a Rotated Reference Frame
2.2. Current Density Conservation
2.3. The Mathematical Problem of Boundary Conditions at a Grain Boundary
2.4. Algebraic Classification of the Matching Matrix for the Grain Boundary Problem
2.5. Direct Derivation of the Matching Matrix from the Scattering Potential
3. Grain Boundary Hamiltonian Model with Position-Dependent Rotation Angle
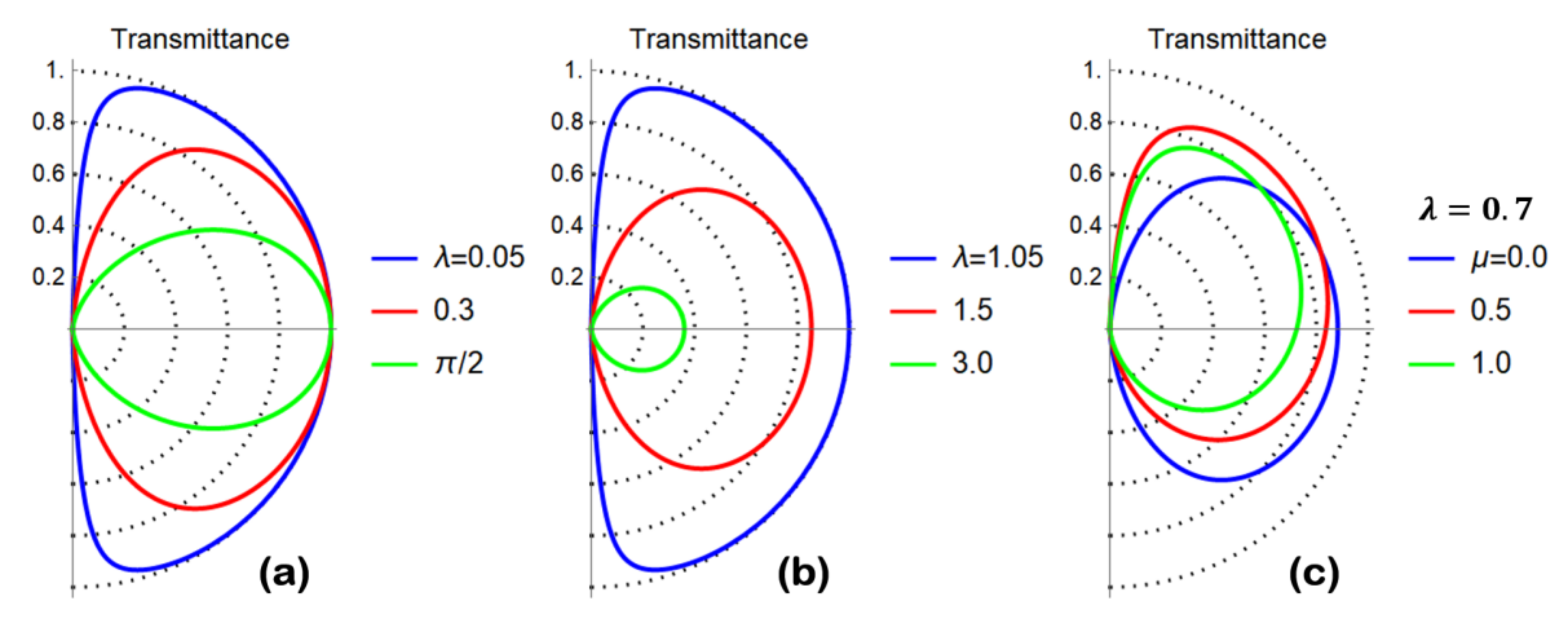
4. Results of the Scattering Theory
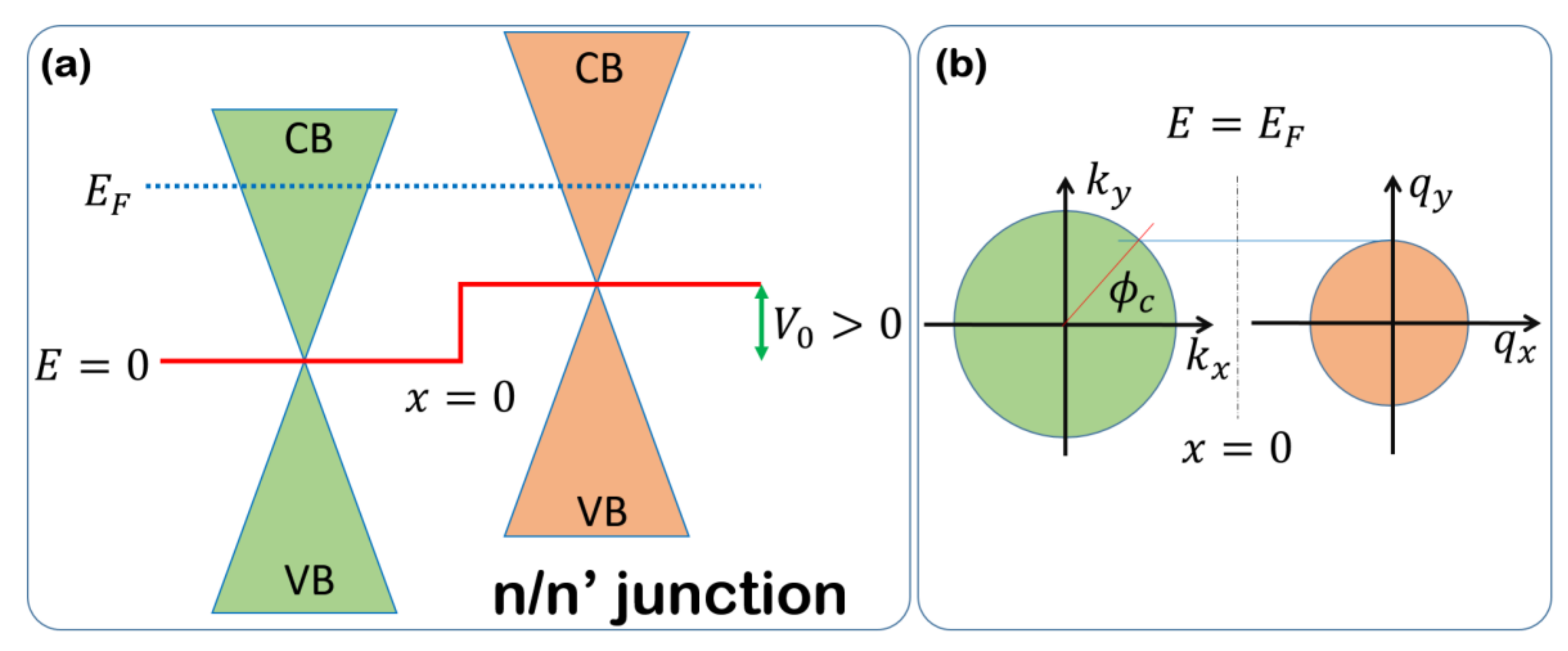
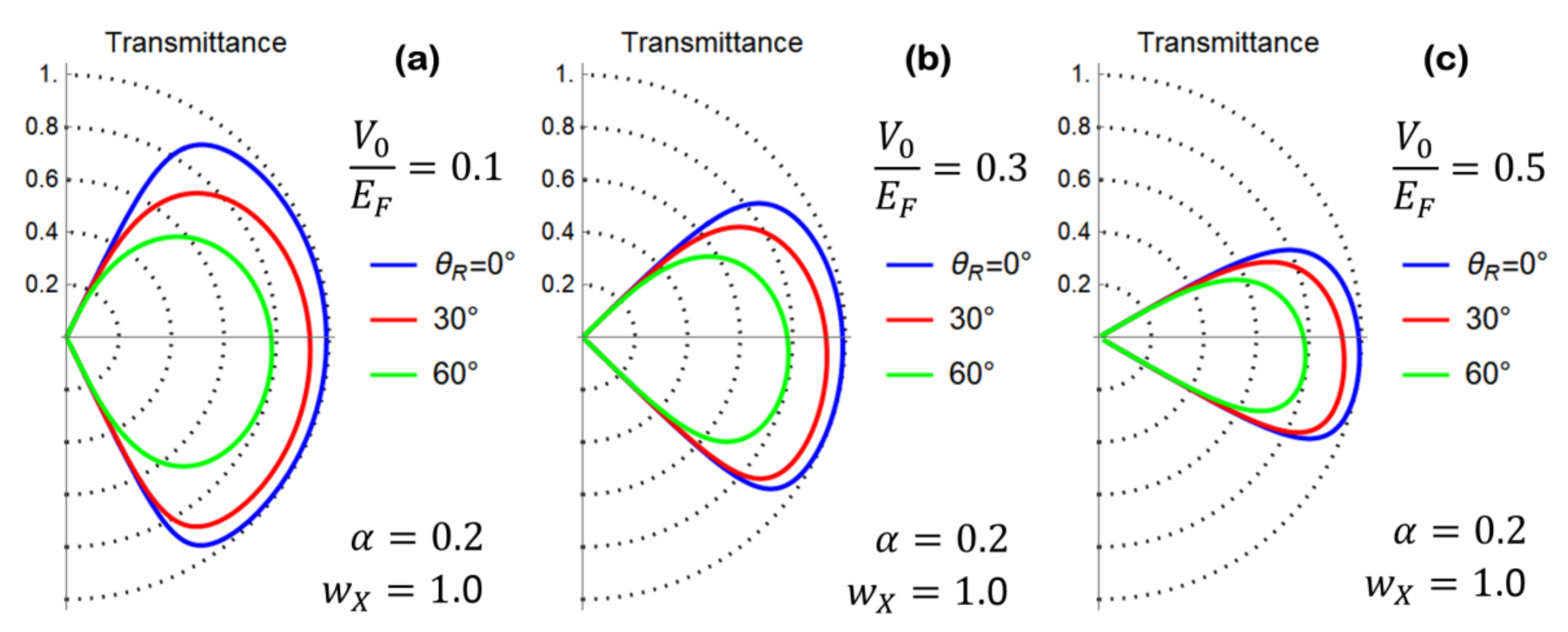
4.1. Transmission Properties of a n/n’ Grain Boundary Junction with Unconventional Boundary Conditions
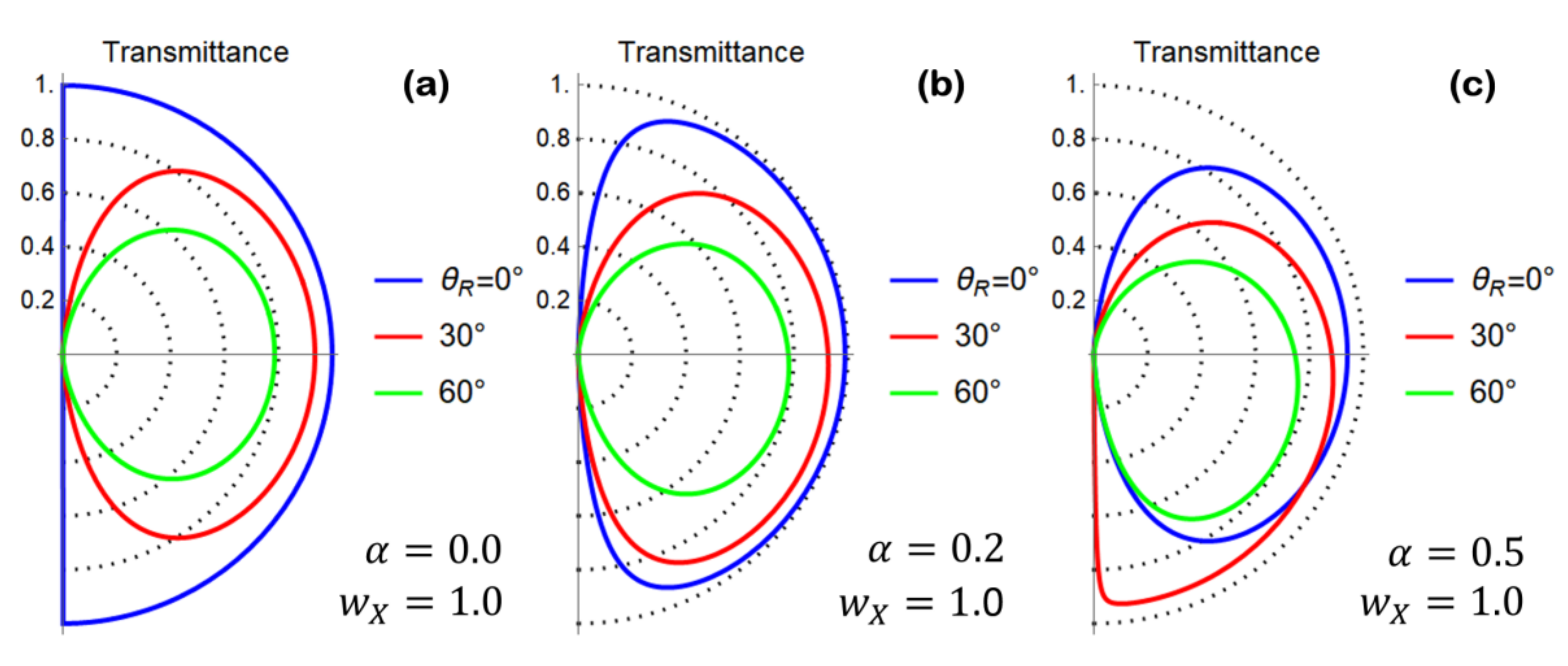
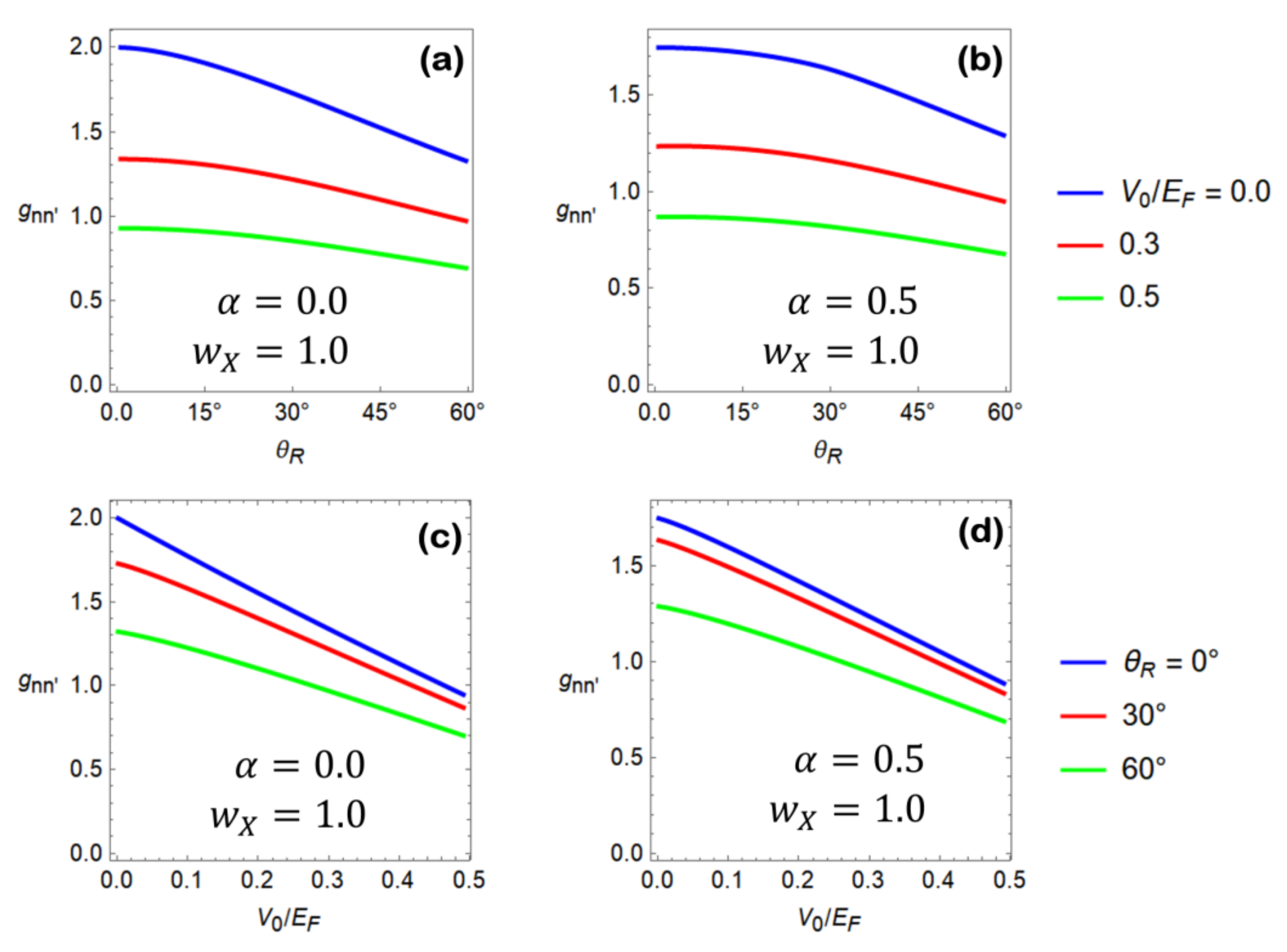
4.2. Grain Boundary Junction with -Dependent Differential Conductance
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Das Sarma, S.; Adam, S.; Hwang, E.H.; Rossi, E. Electronic transport in two-dimensional graphene. Rev. Mod. Phys. 2011, 83, 407–470. [Google Scholar] [CrossRef]
- Allain, P.E.; Fuchs, J.N. Klein tunneling in graphene: Optics with massless electrons. Eur. Phys. J. B 2011, 83, 301–317. [Google Scholar] [CrossRef]
- Rusin, T.M.; Zawadzki, W. Zitterbewegung of electrons in graphene in a magnetic field. Phys. Rev. B 2008, 78, 125419. [Google Scholar] [CrossRef]
- Tikhonenko, F.V.; Kozikov, A.A.; Savchenko, A.K.; Gorbachev, R.V. Transition between Electron Localization and Antilocalization in Graphene. Phys. Rev. Lett. 2009, 103, 226801. [Google Scholar] [CrossRef] [PubMed]
- Ostrovsky, P.M.; Gornyi, I.V.; Mirlin, A.D. Theory of anomalous quantum Hall effects in graphene. Phys. Rev. B 2008, 77, 195430. [Google Scholar] [CrossRef]
- Cheianov, V.V.; Fal’ko, V.; Altshuler, B.L. The Focusing of Electron Flow and a Veselago Lens in Graphene p-n Junctions. Science 2007, 315, 1252–1255. [Google Scholar] [CrossRef] [PubMed]
- Banszerus, L.; Schmitz, M.; Engels, S.; Dauber, J.; Oellers, M.; Haupt, F.; Watanabe, K.; Taniguchi, T.; Beschoten, B.; Stampfer, C. Ultrahigh-mobility graphene devices from chemical vapor deposition on reusable copper. Sci. Adv. 2015, 1, e1500222–e1500222. [Google Scholar] [CrossRef] [PubMed]
- Papageorgiou, D.G.; Kinloch, I.A.; Young, R.J. Mechanical properties of graphene and graphene-based nanocomposites. Prog. Mater. Sci. 2017, 90, 75–127. [Google Scholar] [CrossRef]
- Lee, S.-M.; Kim, J.-H.; Ahn, J.-H. Graphene as a flexible electronic material: Mechanical limitations by defect formation and efforts to overcome. Mater. Today 2015, 18, 336–344. [Google Scholar] [CrossRef]
- Lemme, M.C.; Echtermeyer, T.J.; Baus, M.; Kurz, H. A Graphene Field-Effect Device. IEEE Electron Device Lett. 2007, 28, 282–284. [Google Scholar] [CrossRef]
- Di Bartolomeo, A.; Santandrea, S.; Giubileo, F.; Romeo, F.; Petrosino, M.; Citro, R.; Barbara, P.; Lupina, G.; Schroeder, T.; Rubino, A. Effect of back-gate on contact resistance and on channel conductance in graphene-based field-effect transistors. Diam. Relat. Mater. 2013, 38, 19–23. [Google Scholar] [CrossRef]
- Giubileo, F.; Di Bartolomeo, A. The role of contact resistance in graphene field-effect devices. Prog. Surf. Sci. 2017, 92, 143–175. [Google Scholar] [CrossRef]
- Di Bartolomeo, A.; Giubileo, F.; Iemmo, L.; Romeo, F.; Santandrea, S.; Gambardella, U. Transfer characteristics and contact resistance in Ni- and Ti-contacted graphene-based field-effect transistors. J. Phys. Condens. Matt. 2013, 25, 155303. [Google Scholar] [CrossRef] [PubMed]
- Giubileo, F.; Di Bartolomeo, A.; Martucciello, N.; Romeo, F.; Iemmo, L.; Romano, P.; Passacantando, M. Contact Resistance and Channel Conductance of Graphene Field-Effect Transistors under Low-Energy Electron Irradiation. Nanomaterials 2016, 6, 206. [Google Scholar] [CrossRef] [PubMed]
- Di Bartolomeo, A.; Giubileo, F.; Romeo, F.; Sabatino, P.; Carapella, G.; Iemmo, L.; Schroeder, T.; Lupina, G. Graphene field effect transistors with niobium contacts and asymmetric transfer characteristics. Nanotechnology 2015, 26, 475202. [Google Scholar] [CrossRef] [PubMed]
- Di Bartolomeo, A.; Giubileo, F.; Iemmo, L.; Romeo, F.; Russo, S.; Unal, S.; Passacantando, M.; Grossi, V.; Cucolo, A.M. Leakage and field emission in side-gate graphene field effect transistors. Appl. Phys. Lett. 2016, 109, 023510. [Google Scholar] [CrossRef]
- Biró, L.P.; Lambin, P. Grain boundaries in graphene grown by chemical vapor deposition. New J. Phys. 2013, 15, 035024. [Google Scholar] [CrossRef]
- Jauregui, L.A.; Cao, H.; Wu, W.; Yu, Q.; Chen, Y.P. Electronic properties of grains and grain boundaries in graphene grown by chemical vapor deposition. Solid State Commun. 2011, 151, 1100–1104. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z.; Yuan, Q.; Xin, J.; Ding, F. The favourable large misorientation angle grain boundaries in graphene. Nanoscale 2015, 7, 20082–20088. [Google Scholar] [CrossRef] [PubMed]
- Huang, P.Y.; Ruiz-Vargas, C.S.; van der Zande, A.M.; Whitney, W.S.; Levendorf, M.P.; Kevek, J.W.; Garg, S.; Alden, J.S.; Hustedt, C.J.; Zhu, Y.; Park, J.; McEuen, P.L.; Muller, D.A. Grains and grain boundaries in single-layer graphene atomic patchwork quilts. Nature 2011, 469, 389–392. [Google Scholar] [CrossRef] [PubMed]
- Yazyev, O.V.; Chen, Y.P. Polycrystalline graphene and other two-dimensional materials. Nat. Nanotechnol. 2014, 9, 755–767. [Google Scholar] [CrossRef] [PubMed]
- Tsen, A.W.; Brown, L.; Levendorf, M.P.; Ghahari, F.; Huang, P.Y.; Havener, R.W.; Ruiz-Vargas, C.S.; Muller, D.A.; Kim, P.; Park, J. Tailoring Electrical Transport Across Grain Boundaries in Polycrystalline Graphene. Science 2012, 336, 1143–1146. [Google Scholar] [CrossRef] [PubMed]
- Cummings, A.W.; Duong, D.L.; Nguyen, V.L.; Van Tuan, D.; Kotakoski, J.; Barrios Vargas, J.E.; Lee, Y.H.; Roche, S. Charge Transport in Polycrystalline Graphene: Challenges and Opportunities. Adv. Mater. 2014, 26, 5079–5094. [Google Scholar] [CrossRef] [PubMed]
- Lahiri, J.; Lin, Y.; Bozkurt, P.; Oleynik, I.I.; Batzill, M. An extended defect in graphene as a metallic wire. Nat. Nanotechnol. 2010, 5, 326–329. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, A.; Xu, X.; Tan, C.-L.; Bae, S.-K.; Peres, N.M.R.; Hong, B.-H.; Özyilmaz, B.; Castro Neto, A.H. Transport properties of graphene with one-dimensional charge defects. Europhys. Lett. 2011, 94, 28003. [Google Scholar] [CrossRef]
- Radchenko, T.M.; Shylau, A.A.; Zozoulenko, I.V.; Ferreira, A. Effect of charged line defects on conductivity in graphene: Numerical Kubo and analytical Boltzmann approaches. Phys. Rev. B 2013, 87. [Google Scholar] [CrossRef]
- Rodrigues, J.N.B.; Peres, N.M.R.; Lopes dos Santos, J.M.B. Scattering by linear defects in graphene: A continuum approach. Phys. Rev. B 2012, 86. [Google Scholar] [CrossRef]
- Rodrigues, J.N.B.; Peres, N.M.R.; Lopes dos Santos, J.M.B. Scattering by linear defects in graphene: A tight-binding approach. J. Phys. Condens. Matt. 2013, 25, 075303. [Google Scholar] [CrossRef] [PubMed]
- Páez, C.J.; Pereira, A.L.C.; Rodrigues, J.N.B.; Peres, N.M.R. Electronic transport across linear defects in graphene. Phys. Rev. B 2015, 92. [Google Scholar] [CrossRef]
- Rodrigues, J.N.B. Intervalley scattering of graphene massless Dirac fermions at 3-periodic grain boundaries. Phys. Rev. B 2016, 94. [Google Scholar] [CrossRef]
- Foà Torres, L.E.F.; Roche, S.; Charlier, J.C. Introduction to Graphene-Based Nanomaterials: From Electronic Structure to Quantum Transport; Cambridge University Press: New York, NY, USA, 2014; ISBN 978-1-107-03083-1. [Google Scholar]
- Fleet, L. Jump across: Valleytronics. Nature Phys. 2015, 11, 620–620. [Google Scholar] [CrossRef]
- McKellar, B.H.J.; Stephenson, G.J. Relativistic quarks in one-dimensional periodic structures. Phys. Rev. C 1987, 35, 2262–2271. [Google Scholar] [CrossRef]
- Huang, M.; Yan, H.; Heinz, T.F.; Hone, J. Probing Strain-Induced Electronic Structure Change in Graphene by Raman Spectroscopy. Nano Lett. 2010, 10, 4074–4079. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romeo, F.; Di Bartolomeo, A. Scattering Theory of Graphene Grain Boundaries. Materials 2018, 11, 1660. https://doi.org/10.3390/ma11091660
Romeo F, Di Bartolomeo A. Scattering Theory of Graphene Grain Boundaries. Materials. 2018; 11(9):1660. https://doi.org/10.3390/ma11091660
Chicago/Turabian StyleRomeo, Francesco, and Antonio Di Bartolomeo. 2018. "Scattering Theory of Graphene Grain Boundaries" Materials 11, no. 9: 1660. https://doi.org/10.3390/ma11091660
APA StyleRomeo, F., & Di Bartolomeo, A. (2018). Scattering Theory of Graphene Grain Boundaries. Materials, 11(9), 1660. https://doi.org/10.3390/ma11091660





