The Effect of Alloying Elements on the Structural Stability, Mechanical Properties, and Debye Temperature of Al3Li: A First-Principles Study
Abstract
1. Introduction
2. Computational Studies
3. Results and Discussion
3.1. Site Preference and Phase Stability
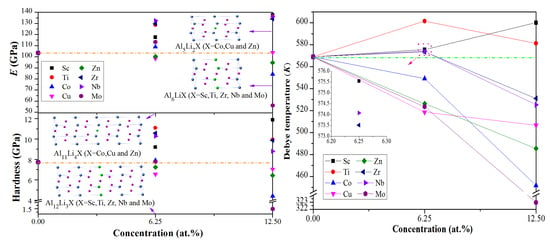
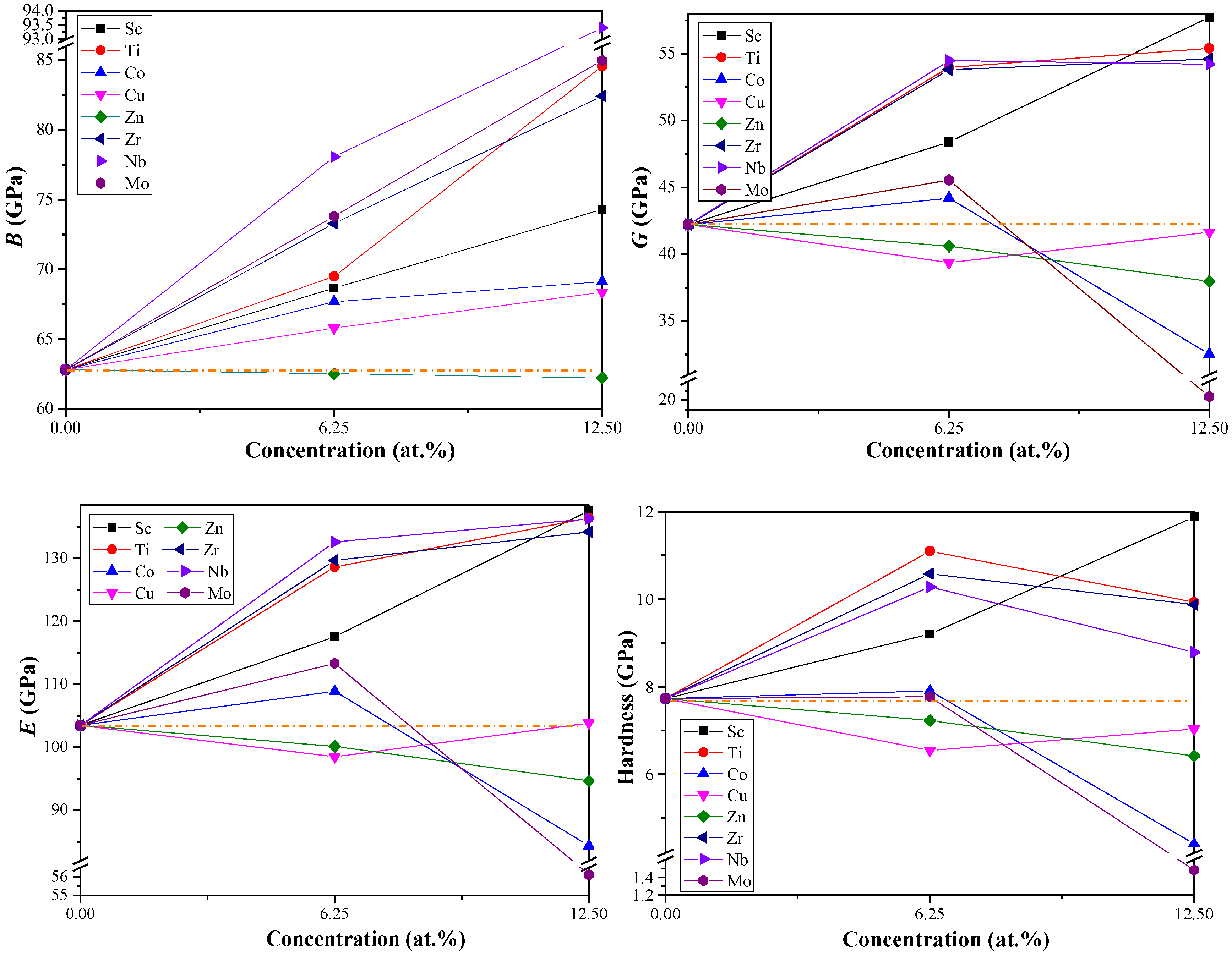
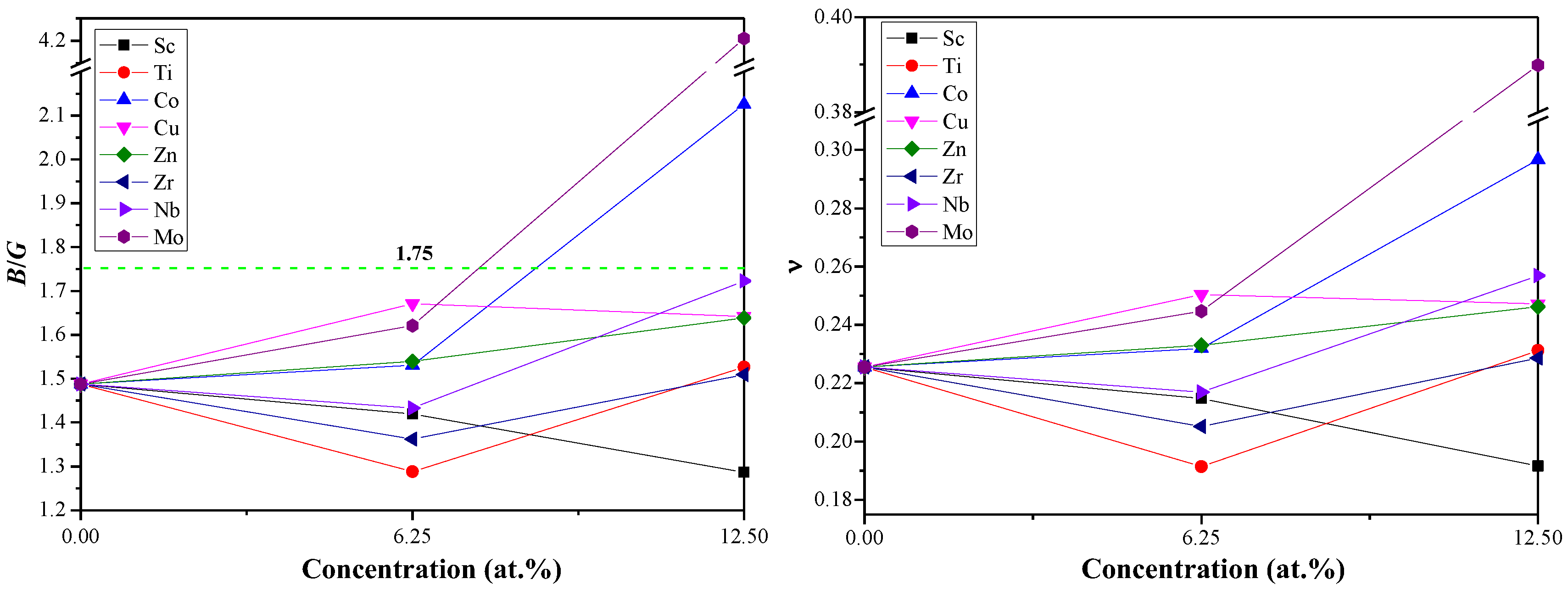
3.2. Mechanical Properties
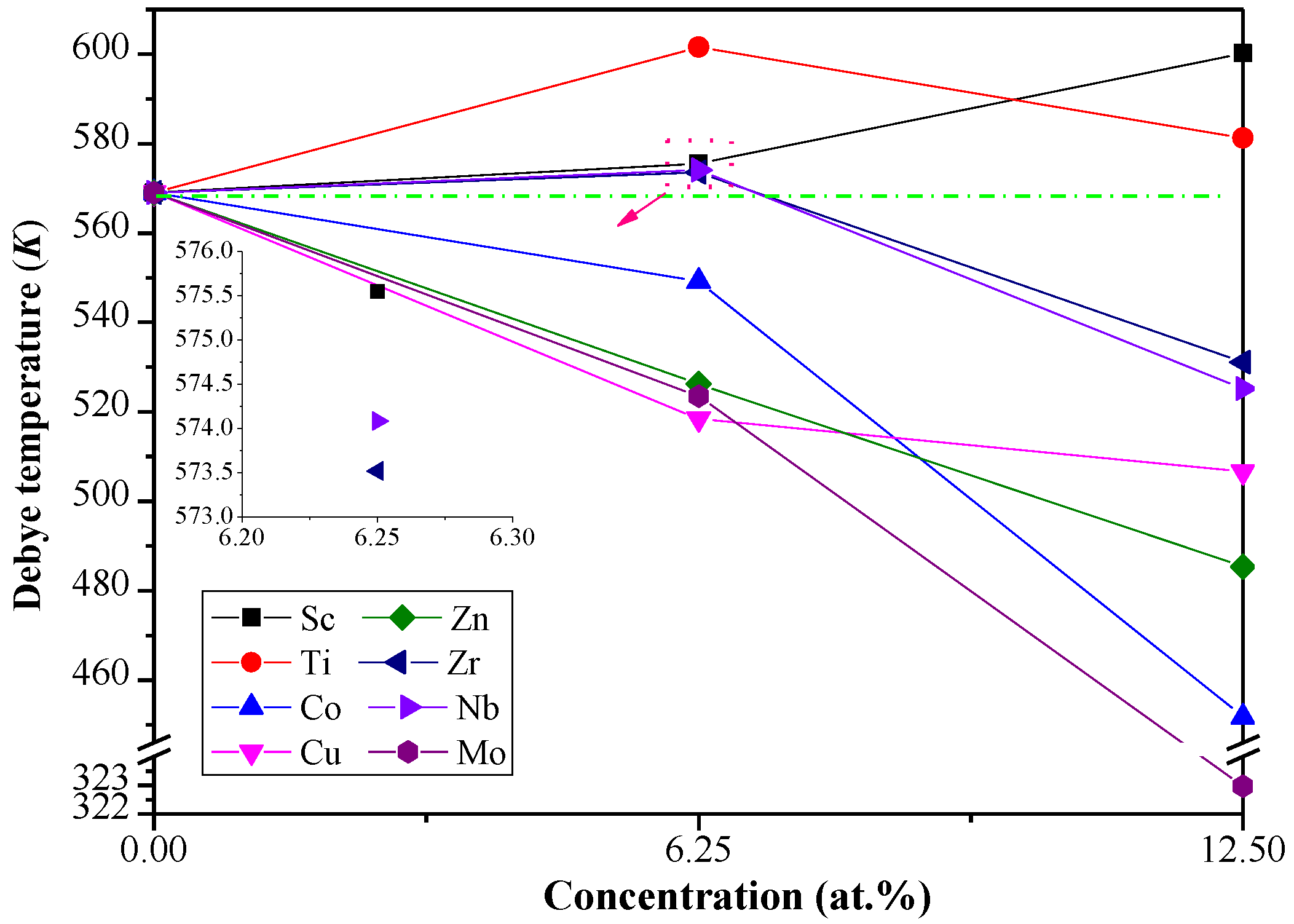
3.3. Debye Temperature
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ning, J.; Zhang, L.J.; Bai, Q.L.; Yin, X.Q.; Niu, J.; Zhang, J.X. Comparison of the microstructure and mechanical performance of 2A97 Al-Li alloy joints between autogenous and non-autogenous laser welding. Mater. Des. 2017, 120, 144–156. [Google Scholar] [CrossRef]
- Bairwa, M.L.; Date, P.P. Effect of heat treatment on the tensile properties of Al-Li alloys. J. Mater. Process. Technol. 2004, 153–154, 603–607. [Google Scholar] [CrossRef]
- Ovri, H.; Lilleodden, E.T. New insights into plastic instability in precipitation strengthened Al-Li alloys. Acta Mater. 2015, 89, 88–97. [Google Scholar] [CrossRef]
- Rösner, H.; Kalogeridis, A.; Liu, W.; Pesicka, J.; Nembach, E. Dislocation mechanisms in Al-rich Al-Li alloys. Mater. Sci. Eng. A 1997, 234–236, 298–301. [Google Scholar] [CrossRef]
- Flower, H.; Gregson, P. Solid state phase transformations in aluminium alloys containing lithium. Mater. Sci. Technol. 1987, 3, 81–90. [Google Scholar] [CrossRef]
- Williams, D.; Edington, J. The precipitation of δ′(Al3Li) in dilute aluminium–lithium alloys. Met. Sci. 1975, 9, 529–532. [Google Scholar] [CrossRef]
- Laverock, J.; Dugdale, S.B.; Alam, M.A.; Roussenova, M.V.; Wensley, J.R.; Kwiatkowska, J.; Shiotani, N. Fermi surface of an important nanosized metastable phase: Al3Li. Phys. Rev. Lett. 2010, 105, 236401. [Google Scholar] [CrossRef] [PubMed]
- Pletcher, B.A.; Wang, K.G.; Glicksman, M.E. Experimental, computational and theoretical studies of δ′ phase coarsening in Al-Li alloys. Acta Mater. 2012, 60, 5803–5817. [Google Scholar] [CrossRef]
- Mogucheva, A.; Kaibyshev, R. Microstructure and Mechanical Properties of an Al-Li-Mg-Sc-Zr Alloy Subjected to ECAP. Metals 2016, 6, 254. [Google Scholar] [CrossRef]
- Chabala, J.M.; Levi-Setti, R.; Soni, K.K.; Williams, D.B.; Newbury, D.E. Secondary ion imaging of the distribution of δ′ (Al3Li) in Al-Li alloys. Appl. Surf. Sci. 1991, 51, 185–192. [Google Scholar] [CrossRef]
- Gu, B.P.; Liedl, G.L.; Kulwicki, J.H.; Sanders, T.H., Jr. Coarsening of δ′ (Al3Li) precipitates in an Al-2.8Li0.3Mn alloy. Mater. Sci. Eng. 1985, 70, 217–228. [Google Scholar] [CrossRef]
- Hoyt, J.J.; Spooner, S. The surface energy of metastable Al3Li precipitates from coarsening kinetics. Acta Metall. Et Mater. 1991, 39, 689–693. [Google Scholar] [CrossRef]
- Lee, B.C.; Park, J.K. Effect of the addition of Ag on the strengthening of Al3Li phase in Al-Li single crystals. Acta Mater. 1998, 46, 4181–4187. [Google Scholar] [CrossRef]
- Mao, Z.; Seidman, D.N.; Wolverton, C. The effect of vibrational entropy on the solubility and stability of ordered Al3Li phases in Al-Li alloys. APL Mater. 2016, 4, 144202. [Google Scholar] [CrossRef]
- Poduri, R.; Chen, L.Q. Computer simulation of morphological evolution and coarsening kinetics of δ′ (Al3Li) precipitates in Al-Li alloys. Acta Mater. 1998, 46, 3915–3928. [Google Scholar] [CrossRef]
- Li, Z.; Tse, J.S. Ab initio studies on the vibrational and thermal properties of Al3Li. Phys. Rev. B 2000, 61, 14531–14536. [Google Scholar] [CrossRef]
- Yu, H.; Duan, X.; Ma, Y.; Zeng, M. First Principles Study of Al-Li Intermetallic Compounds. Chin. J. Chem. Phys. 2012, 25, 659–665. [Google Scholar] [CrossRef]
- Sluiter, M.; De, F.D.; Guo, X.Q.; Podloucky, R.; Freeman, A.J. First-principles calculation of phase equilibria in the aluminum lithium system. Phys. Rev. B 1990, 42, 10460–10476. [Google Scholar] [CrossRef]
- Hu, W.C.; Liu, Y.; Li, D.J.; Zeng, X.Q.; Xu, C.S. Mechanical and thermodynamic properties of Al3Sc and Al3Li precipitates in Al-Li-Sc alloys from first-principles calculations. Phys. B Condens. Matter 2013, 427, 85–90. [Google Scholar] [CrossRef]
- Wolverton, C.; Ozoliņš, V. First-principles aluminum database: Energetics of binary Al alloys and compounds. Phys. Rev. B 2006, 73, 144104. [Google Scholar] [CrossRef]
- Guo, X.; Podloucky, R.; Xu, J.; Freeman, A.J. Cohesive, electronic, and structural properties of Al3Li: An important metastable phase. Phys. Rev. B 1990, 41, 12432. [Google Scholar] [CrossRef]
- Yao, J.; Zhang, C.; Jiang, Y.; Tao, H.; Yin, D. Prediction on elastic properties of off-stoichiometric L12-Al3Li intermetallic due to point defects. Comput. Mater. Sci. 2015, 107, 184–189. [Google Scholar] [CrossRef]
- Makineni, S.K.; Sugathan, S.; Meher, S.; Banerjee, R.; Bhattacharya, S.; Kumar, S.; Chattopadhyay, K. Enhancing elevated temperature strength of copper containing aluminium alloys by forming L12 Al3Zr precipitates and nucleating θ″ precipitates on them. Sci. Rep. 2017, 7, 11154. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Wu, X.; Wang, R.; Jia, Z.; Li, W.; Liu, Q. Structural stability, mechanical properties and stacking fault energies of TiAl3 alloyed with Zn, Cu, Ag: First-principles study. J. Alloys Compd. 2016, 666, 185–196. [Google Scholar] [CrossRef]
- Gu, J.; Bai, J.; Zhu, Y.; Qin, Y.; Gu, H.; Zhai, Y.; Ma, P. First-principles study of the influence of doping elements on phase stability, crystal and electronic structure of Al2Cu (θ) phase. Comput. Mater. Sci. 2016, 111, 328–333. [Google Scholar] [CrossRef]
- Kubouchi, M.; Hayashi, K.; Miyazaki, Y. Electronic structure and thermoelectric properties of boron doped Mg2Si. Scr. Mater. 2016, 123, 59–63. [Google Scholar] [CrossRef]
- Segall, M.; Lindan, P.J.; Probert, M.A.; Pickard, C.; Hasnip, P.; Clark, S.; Payne, M. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Insights into current limitations of density functional theory. Science 2008, 321, 792–794. [Google Scholar] [CrossRef] [PubMed]
- Yoshiyama, T.; Hasebe, K.; Mannami, M. Al3Li Superlattice in Al-4.5 wt % Li Alloy. J. Phys. Soc. Jpn. 2007, 25, 908. [Google Scholar] [CrossRef]
- Sahu, B.R. Electronic structure and bonding of ultralight LiMg. Mater. Sci. Eng. B 1995, 49, 74–78. [Google Scholar] [CrossRef]
- Wang, J.-H.; Lu, Y.; Zhang, X.-L.; Shao, X.-H. The elastic behaviors and theoretical tensile strength of γ-TiAl alloy from the first principles calculations. Intermetallics 2018, 101, 1–7. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.-X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Tian, J.; Zhao, Y.; Wang, B.; Hou, H.; Zhang, Y. The structural, mechanical and thermodynamic properties of Ti-B compounds under the influence of temperature and pressure: First-principles study. Mater. Chem. Phys. 2018, 209, 200–207. [Google Scholar] [CrossRef]
- Xiao, B.; Feng, J.; Zhou, C.T.; Jiang, Y.H.; Zhou, R. Mechanical properties and chemical bonding characteristics of Cr7C3 type multicomponent carbides. J. Appl. Phys. 2011, 109, 083521. [Google Scholar] [CrossRef]
- Qi, Y.Y.; Mu, Y.; Cheng, Y.; Ji, G.F. Pressure effect on electronic, elastic and optical properties of Eu:CaF2 crystal: A first-principles study. Philos. Mag. 2015, 95, 2974–2989. [Google Scholar] [CrossRef]
- Mao, Z.; Chen, W.; Seidman, D.N.; Wolverton, C. First-principles study of the nucleation and stability of ordered precipitates in ternary Al-Sc-Li alloys. Acta Mater. 2011, 59, 3012–3023. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Watt, J.P.; Peselnick, L. Clarification of the Hashin-Shtrikman bounds on the effective elastic moduli of polycrystals with hexagonal, trigonal, and tetragonal symmetries. J. Appl. Phys. 1980, 51, 1525–1531. [Google Scholar] [CrossRef]
- Gao, F.M.; Gao, L.H. Microscopic models of hardness. J. Superhard Mater. 2010, 32, 148–166. [Google Scholar] [CrossRef]
- Chen, X.Q.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
- Yousef, E.S.; El-Adawy, A.; El-Kheshkhany, N. Effect of rare earth (Pr2O3, Nd2O3, Sm2O3, Eu2O3, Gd2O3 and Er2O3) on the acoustic properties of glass belonging to bismuth–borate system. Solid State Commun. 2006, 139, 108–113. [Google Scholar] [CrossRef]
- Zhang, W.; Chai, C.; Song, Y.; Fan, Q.; Yang, Y. Structural, Mechanical, Anisotropic, and Thermal Properties of AlAs in oC12 and hP6 Phases under Pressure. Materials 2018, 11, 740. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Shang, S.; Wang, Y.; Saengdeejing, A.; Chen, L.; Liu, Z. First-principles calculations of the elastic, phonon and thermodynamic properties of Al12Mg17. Acta Mater. 2010, 58, 4012–4018. [Google Scholar] [CrossRef]
- Nong, Z.-S.; Zhu, J.-C.; Yang, X.-W.; Cao, Y.; Lai, Z.-H.; Liu, Y.; Sun, W. First-principles calculations of the stability and hydrogen storage behavior of C14 Laves phase compound TiCrMn. Solid State Sci. 2014, 32, 1–7. [Google Scholar] [CrossRef]
- Haines, J.; Leger, J.; Bocquillon, G. Synthesis and design of superhard materials. Ann. Rev. Mater. Res. 2001, 31, 1–23. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Huang, J.; Wang, W.; Ye, Z.; Chen, S.; Zhao, Y. First-principles calculations on physical properties of Ni3Snx binary system intermetallic compounds and Ni/Ni3Sn interfaces in Nickel-Tin TLPS bonding layer. Intermetallics 2018, 101, 27–38. [Google Scholar] [CrossRef]
- Ledbetter, H.; Migliori, A. A general elastic-anisotropy measure. J. Appl. Phys. 2006, 100, 063516. [Google Scholar] [CrossRef]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal elastic anisotropy index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Wu, X.; Wang, R.; Li, W.; Liu, Q. Phase stability, mechanical properties and electronic structure of TiAl alloying with W, Mo, Sc and Yb: First-principles study. J. Alloys Compd. 2016, 658, 689–696. [Google Scholar] [CrossRef]
- Ravindran, P.; Fast, L.; Korzhavyi, P.A.; Johansson, B.; Wills, J.; Eriksson, O. Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi2. J. Appl. Phys. 1998, 84, 4891–4904. [Google Scholar] [CrossRef]
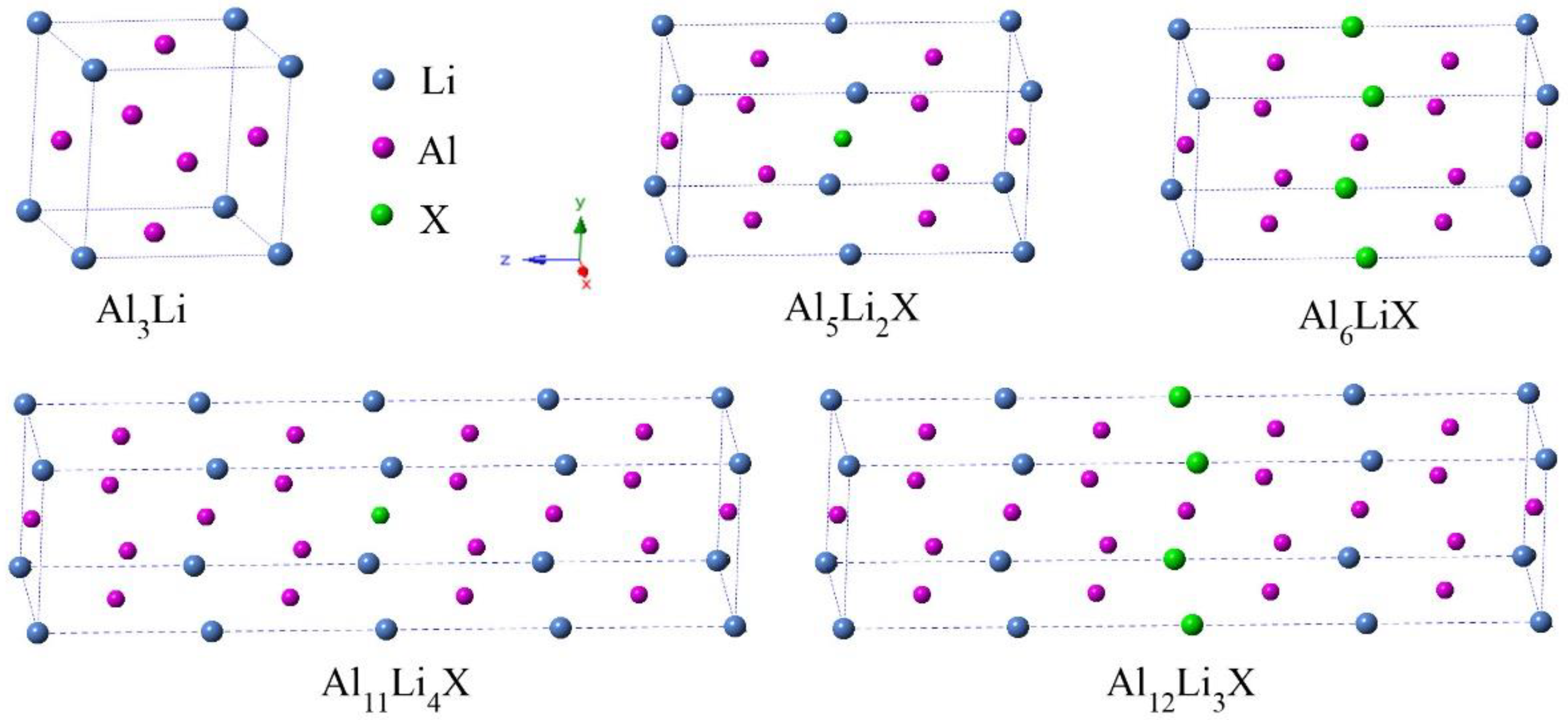
| Species | a | V | Mass Density | Hform |
|---|---|---|---|---|
| Present | 4.034 | 65.65 | 2.223 | −0.097 |
| Cal. [17] | 4.030 | 65.45 | 2.221 | - |
| Cal. [14] | 4.029 | 65.40 | - | −0.100 |
| Exp. [32] | 4.01 | 64.48 | 2.260 | - |
| Element X | ΔHf | Site Preference | Element X | ΔHf | Site Preference | ||
|---|---|---|---|---|---|---|---|
| Al6LiX | Al5Li2X | Al12Li3X | Al11Li4X | ||||
| Sc | −0.267 | −0.154 | Li | Sc | −0.180 | −0.127 | Li |
| Ti | −0.232 | −0.127 | Li | Ti | −0.169 | −0.108 | Li |
| Co | −0.185 | −0.202 | Al | Co | −0.140 | −0.152 | Al |
| Cu | −0.057 | −0.128 | Al | Cu | −0.075 | −0.111 | Al |
| Zn | −0.017 | −0.099 | Al | Zn | −0.057 | −0.098 | Al |
| Zr | −0.276 | −0.148 | Li | Zr | −0.191 | −0.118 | Li |
| Nb | −0.188 | −0.098 | Li | Nb | −0.150 | −0.094 | Li |
| Mo | −0.100 | −0.059 | Li | Mo | −0.107 | −0.075 | Li |
| Phase | Species | C11 | C33 | C44 | C66 | C12 | C13 | B | G | E | H | AU |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Al3Li | Present | 129.7 | - | 37.7 | - | 29.4 | - | 62.8 | 42.2 | 103.5 | 7.73 | 0.099 |
| Cal. [17] | 128 | - | 39 | - | 30 | - | 63.3 | 42.8 | 116.8 | - | - | |
| Exp. [39] | 123.6 | - | 42.8 | - | 37.2 | - | 66 | 43 | 105.9 | - | - | |
| Al12Li3Sc | Present | 136.2 | 130.4 | 46.1 | 51.7 | 31.0 | 38.3 | 68.7 | 48.4 | 117.6 | 9.20 | 0.019 |
| Al12Li3Ti | Present | 141.3 | 147.7 | 52.4 | 54.4 | 35.2 | 31.2 | 69.5 | 54.0 | 128.6 | 11.10 | 0.007 |
| Al11Li4Co | Present | 138.0 | 118.9 | 39.4 | 48.1 | 29.0 | 39.2 | 67.7 | 44.2 | 108.9 | 7.90 | 0.085 |
| Al11Li4Cu | Present | 126.7 | 116.2 | 37.0 | 37.5 | 37.7 | 37.0 | 65.8 | 39.4 | 98.5 | 6.55 | 0.032 |
| Al11Li4Zn | Present | 124.3 | 121.8 | 36.9 | 38.9 | 33.8 | 31.2 | 62.5 | 40.6 | 100.1 | 7.23 | 0.049 |
| Al12Li3Zr | Present | 143.4 | 147.5 | 53.1 | 55.9 | 42.2 | 35.2 | 73.3 | 53.8 | 129.7 | 10.58 | 0.008 |
| Al12Li3Nb | Present | 147.8 | 163.5 | 53.1 | 54.9 | 50.8 | 35.5 | 78.1 | 54.5 | 132.6 | 10.28 | 0.041 |
| Al12Li3Mo | Present | 118.7 | 147.0 | 52.0 | 51.5 | 66.9 | 36.6 | 73.8 | 45.4 | 113.3 | 7.77 | 0.426 |
| Al6LiSc | Present | 146.6 | 136.8 | 61.3 | 62.0 | 35.2 | 41.3 | 74.3 | 57.7 | 137.6 | 11.88 | 0.040 |
| Al6LiTi | Present | 153.7 | 157.5 | 55.0 | 62.0 | 51.8 | 48.2 | 84.6 | 55.4 | 136.4 | 9.93 | 0.020 |
| Al5Li2Co | Present | 144.9 | 76.5 | 35.9 | 34.0 | 15.6 | 58.2 | 69.1 | 32.5 | 84.3 | 4.41 | 1.534 |
| Al5Li2Cu | Present | 134.6 | 122.0 | 37.3 | 41.8 | 39.3 | 36.6 | 68.4 | 41.6 | 103.8 | 7.03 | 0.055 |
| Al5Li2Zn | Present | 123.2 | 116.4 | 33.5 | 36.4 | 37.0 | 30.9 | 62.2 | 38.0 | 94.7 | 6.42 | 0.082 |
| Al6LiZr | Present | 153.9 | 143.0 | 55.7 | 60.5 | 51.6 | 47.2 | 82.4 | 54.6 | 134.2 | 9.88 | 0.026 |
| Al6LiNb | Present | 162.0 | 156.2 | 54.2 | 64.0 | 56.4 | 61.9 | 93.4 | 54.2 | 136.3 | 8.88 | 0.047 |
| Al6LiMo | Present | 90.3 | 146.3 | 39.6 | 50.9 | 86.8 | 67.9 | 85.0 | 20.2 | 56.1 | 1.48 | 17.33 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, J.; Zhao, Y.; Hou, H.; Wang, B. The Effect of Alloying Elements on the Structural Stability, Mechanical Properties, and Debye Temperature of Al3Li: A First-Principles Study. Materials 2018, 11, 1471. https://doi.org/10.3390/ma11081471
Tian J, Zhao Y, Hou H, Wang B. The Effect of Alloying Elements on the Structural Stability, Mechanical Properties, and Debye Temperature of Al3Li: A First-Principles Study. Materials. 2018; 11(8):1471. https://doi.org/10.3390/ma11081471
Chicago/Turabian StyleTian, Jinzhong, Yuhong Zhao, Hua Hou, and Bing Wang. 2018. "The Effect of Alloying Elements on the Structural Stability, Mechanical Properties, and Debye Temperature of Al3Li: A First-Principles Study" Materials 11, no. 8: 1471. https://doi.org/10.3390/ma11081471
APA StyleTian, J., Zhao, Y., Hou, H., & Wang, B. (2018). The Effect of Alloying Elements on the Structural Stability, Mechanical Properties, and Debye Temperature of Al3Li: A First-Principles Study. Materials, 11(8), 1471. https://doi.org/10.3390/ma11081471