Enhancement Mechanism of the Dynamic Strength of Concrete Based on the Energy Principle
Abstract
1. Introduction
2. Enhancement Mechanism of the Dynamic Strength of Concrete
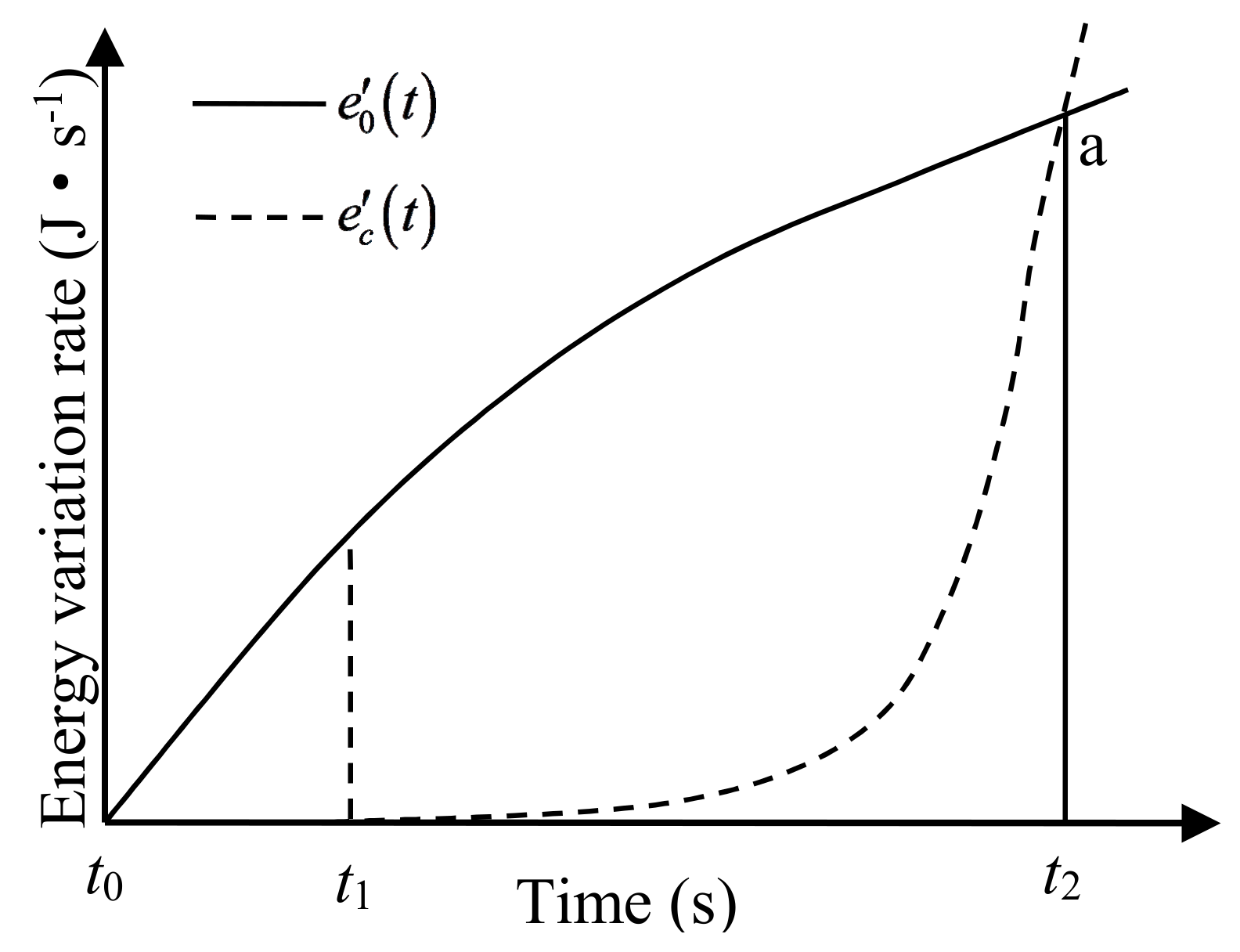
2.1. The Changing Process of Elastic Strain Energy during Loading
2.2. Enhancement Mechanism of the Dynamic Strength of Concrete
3. Dynamic Brazilian Disc Test
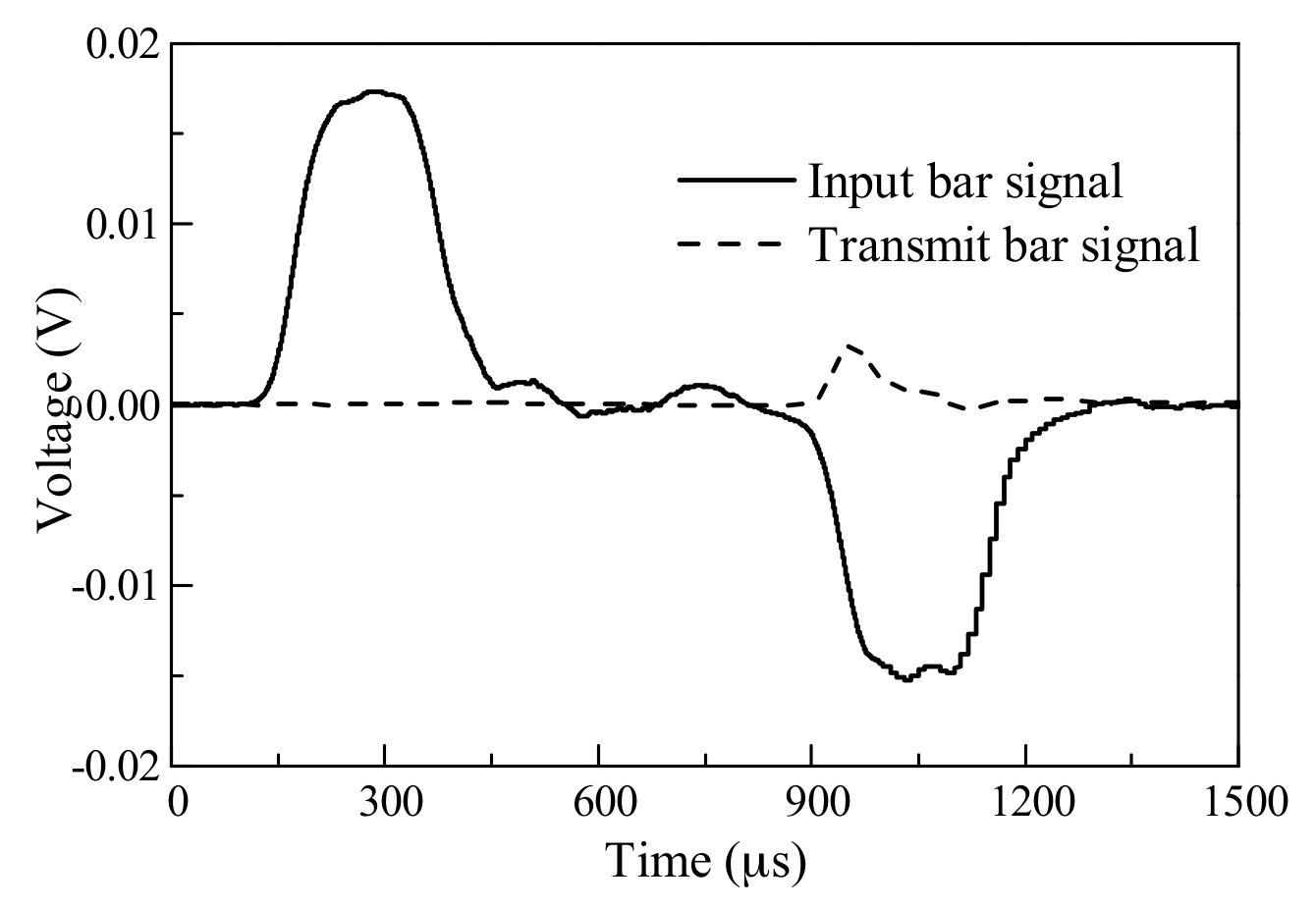
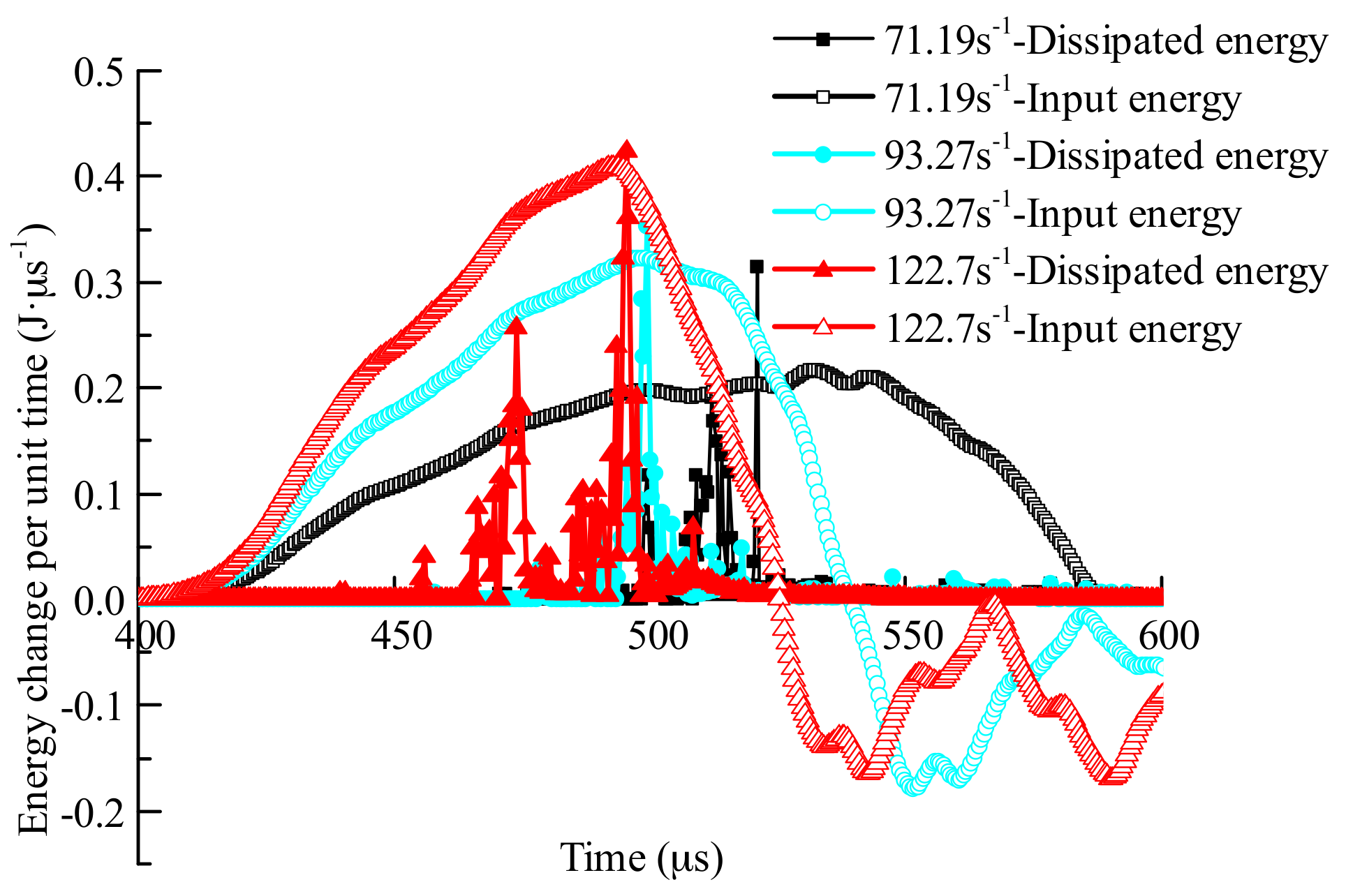
3.1. Testing Principles
3.2. Energy Calculating Method
3.3. Specimen Preparation and Experimental Arrangement
4. Analysis of Test Results
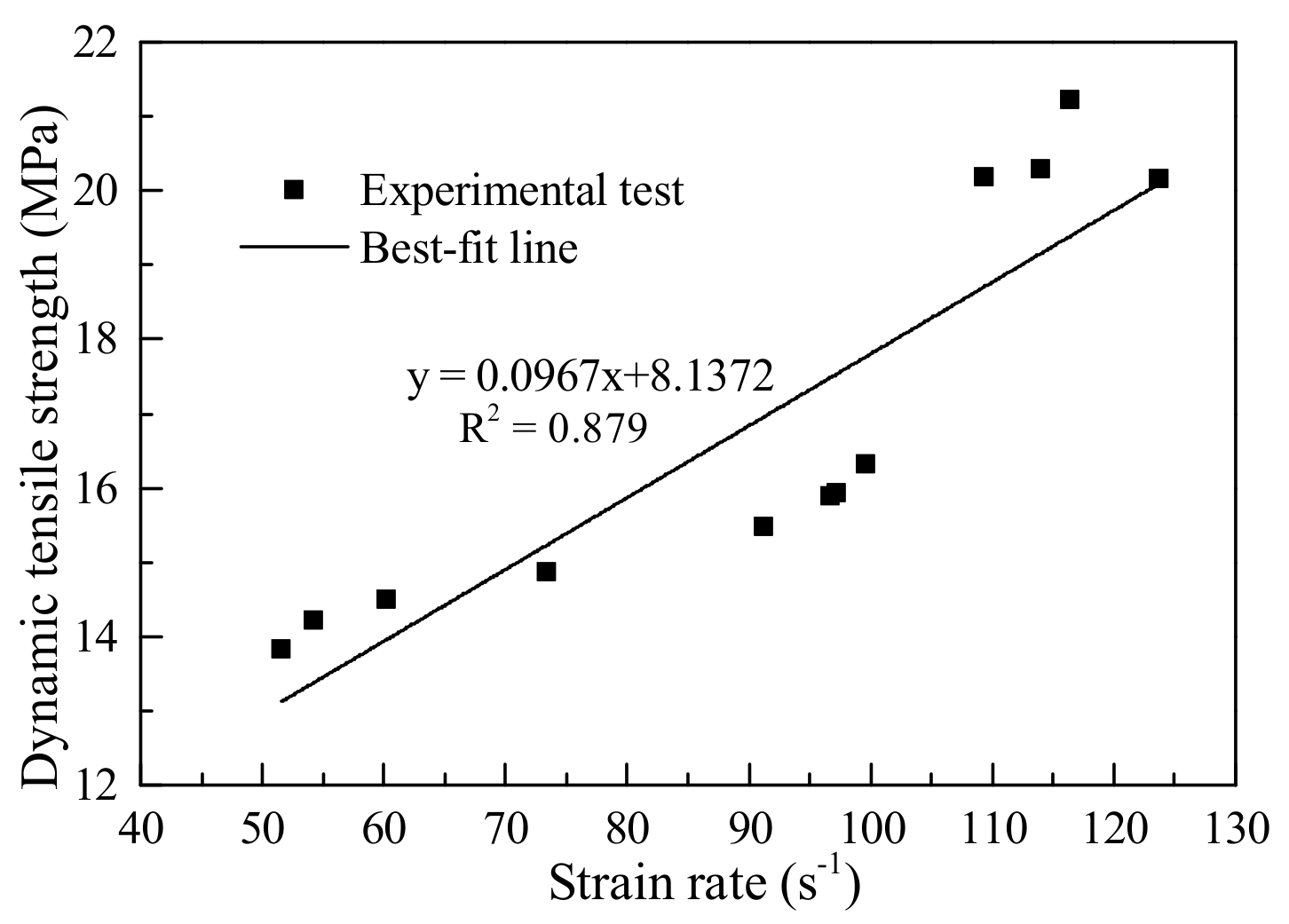
4.1. Relationship between Dynamic Tensile Strength and Strain Rate
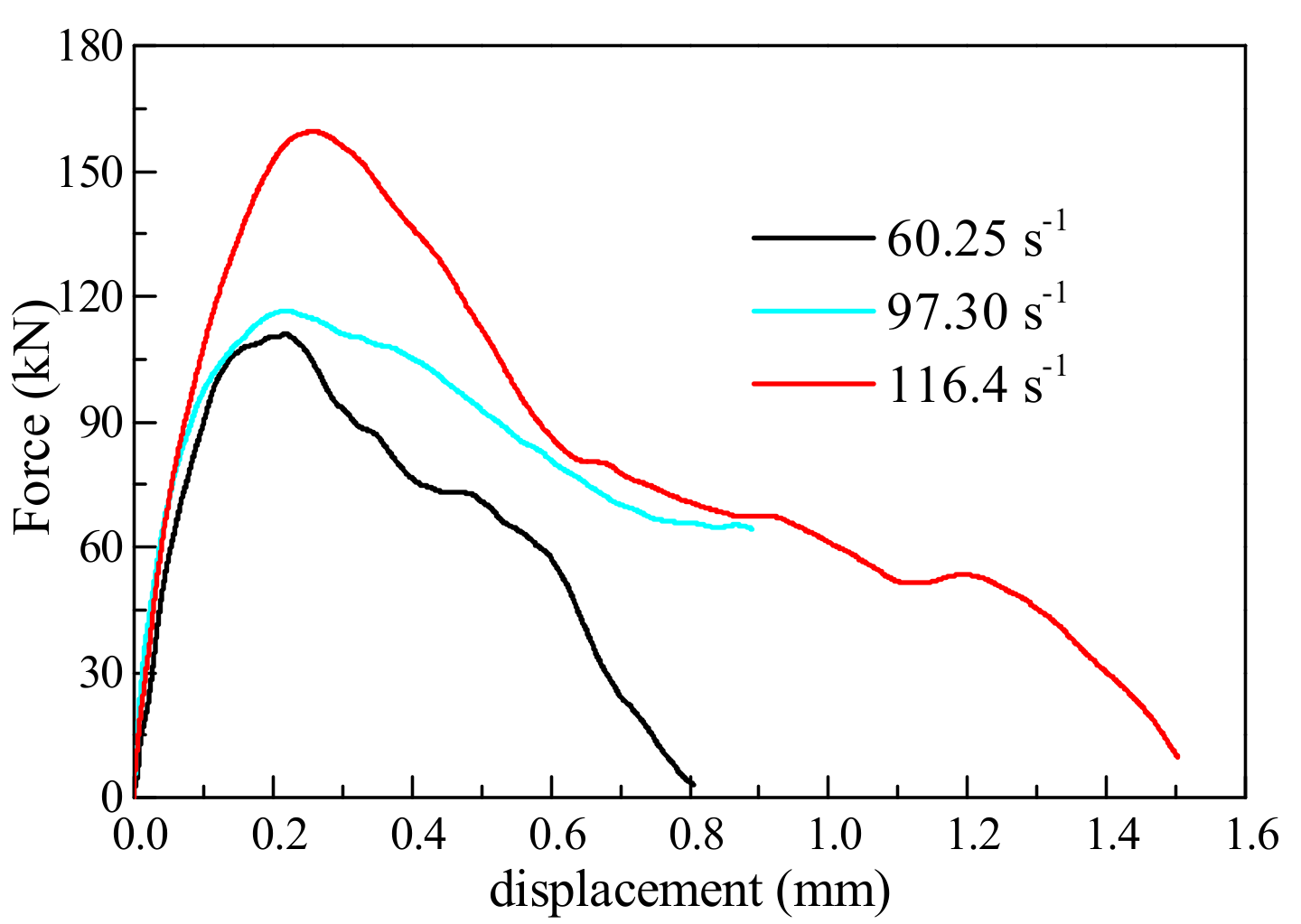
4.2. Force-Displacement Relationship
4.3. Failure Process
5. Numerical Tests of the Dynamic Brazilian Disc Test
5.1. Computational Model and Constitutive Model
5.2. Results Analysis
5.2.1. Force-Displacement Curves
5.2.2. Failure Mode
5.2.3. Energy Conversion Process
6. Conclusions
- (1)
- Through analysis of the law of energy conversion from the microscopic perspective, it was found that elastic strain energy plays a role in transmitting input energy and dissipated energy in the failure process of concrete—making it a deciding factor in concrete strength. When the rate of the change of elastic strain energy is 0, the concrete reaches peak stress.
- (2)
- By studying the energy conversion law in the failure process of concrete subjected to dynamic load, from the perspective of energy, it was proposed that the dynamic strength of concrete was due to the hysteresis effect of energy release. If the dynamic strength of concrete needs to be further enhanced, future studies from the perspective of delaying facture energy release can be conducted.
- (3)
- Through dynamic Brazilian disc tests, and numerical tests of the dynamic Brazilian disc for concrete, an analysis was carried out into the energy conversion process in the failure process of concrete. The proposed enhancement mechanism of the dynamic strength of concrete was verified by the test results. The moment of the intersection between the rate of change of input energy and the rate of change of dissipated energy was the same as the peak stress moment calculated by stress waves. After the peak stress moment, most of the excess elastic strain energy was converted into kinetic energy of the concrete fragments. Furthermore, the higher the strain rate of loading, the more the elastic strain energy was stored, and the greater the kinetic energy of the fragments.
Author Contributions
Funding
Conflicts of Interest
References
- Abrams, D.A. Effect of the Rate of Application of Load on the Compressive Strength of Concrete; American Society for Testing and Materials: West Conshohocken, PA, USA, 1917; pp. 364–377. [Google Scholar]
- Fan, X.Q.; Hu, S.W.; Lu, J.; Wei, C.J. Acoustic emission properties of concrete on dynamic tensile test. Constr. Build. Mater. 2016, 114, 66–75. [Google Scholar]
- Su, Y.; Li, J.; Wu, C.Q.; Wu, P.T.; Li, Z.X. Influences of nano-particles on dynamic strength of ultra-high performance concrete. Compos. Part B Eng. 2016, 91, 595–609. [Google Scholar] [CrossRef]
- Wu, S.X.; Chen, X.D.; Zhou, J.K. Tensile strength of concrete under static and intermediate strain rates: Correlated results from different testing methods. Nucl. Eng. Des. 2012, 250, 173–183. [Google Scholar] [CrossRef]
- Guo, Y.B.; Gao, G.F.; Jing, L.; Shim, V.P.W. Response of high-strength concrete to dynamic compressive loading. Int. J. Impact Eng. 2017, 108, 114–135. [Google Scholar] [CrossRef]
- Li, M.; Hao, H.; Shi, Y.C.; Hao, Y.F. Specimen shape and size effects on the concrete compressive strength under static and dynamic tests. Constr. Build. Mater. 2018, 161, 84–93. [Google Scholar] [CrossRef]
- Wang, C.; Chen, W.S.; Hao, H.; Zhang, S.R.; Song, R.; Wang, X.H. Experimental investigations of dynamic compressive properties of roller compacted concrete (RCC). Constr. Build. Mater. 2018, 168, 671–682. [Google Scholar] [CrossRef]
- Levi-Hevroni, D.; Kochavi, E.; Kofman, B.; Gruntman, S.; Sadot, O. Experimental and numerical investigation on the dynamic increase factor of tensile strength in concrete. Int. J. Impact Eng. 2018, 114, 93–104. [Google Scholar] [CrossRef]
- Golewski, G.L. Generalized fracture toughness and compressive strength of sustainable concrete including low calcium fly ash. Materials 2017, 10, 1393. [Google Scholar] [CrossRef] [PubMed]
- Sadowski, T.; Golewski, G.L. A failure analysis of concrete composites incorporating fly ash during torsional loading. Compos. Struct. 2018, 183, 527–535. [Google Scholar] [CrossRef]
- Qi, C.Z.; Wang, M.Y.; Qian, Q.H. Strain-rate effects on the strength and fragmentation size of rocks. Int. J. Impact Eng. 2009, 36, 1355–1364. [Google Scholar] [CrossRef]
- Rossi, P. Influence of cracking in the presence of free water on the mechanical behaviour of concrete. Mag. Concr. Res. 1991, 43, 53–57. [Google Scholar] [CrossRef]
- Hao, Y.; Hao, H.; Li, Z.X. Influence of end friction confinement on impact tests of concrete material at high strain rate. Int. J. Impact Eng. 2013, 60, 82–106. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, H.J.; Li, Q.M.; Huang, F.L. Further investigation on the dynamic compressive strength enhancement of concrete-like materials based on split Hopkinson pressure bar tests. Part I: Experiments. Int. J. Impact Eng. 2009, 36, 1327–1334. [Google Scholar] [CrossRef]
- Lee, S.; Kim, K.M.; Park, J.; Cho, J.Y. Pure rate effect on the concrete compressive strength in the split Hopkinson pressure bar test. Int. J. Impact Eng. 2018, 113, 191–202. [Google Scholar] [CrossRef]
- Zhou, Z.L.; Cai, X.; Zhao, Y.; Chen, L.; Xiong, C.; Li, X.B. Strength characteristics of dry and saturated rock at different strain rates. Trans. Nonferrous Metals Soc. China 2016, 26, 1919–1925. [Google Scholar] [CrossRef]
- Hao, Y.; Hao, H.; Zhang, X.H. Numerical analysis of concrete material properties at high strain rate under direct tension. Int. J. Impact Eng. 2012, 39, 51–62. [Google Scholar] [CrossRef]
- Hao, Y.F.; Hao, H.; Li, Z.X. Numerical analysis of lateral inertial confinement effects on impact test of concrete compressive material properties. Int. J. Prot. Struct. 2010, 1, 145–168. [Google Scholar] [CrossRef]
- Cotsovos, D.M.; Pavlovic, M.N. Numerical investigation of concrete subjected to high rates of uniaxial tensile loading. Int. J. Impact Eng. 2008, 35, 319–335. [Google Scholar] [CrossRef]
- Huang, Y.J.; Yang, Z.J.; Chen, X.W.; Liu, G.H. Monte Carlo simulations of meso-scale dynamic compressive behavior of concrete based on X-ray computed tomography images. Int. J. Impact Eng. 2016, 97, 102–115. [Google Scholar] [CrossRef]
- Peng, R.D.; Ju, Y.; Wang, J.G.; Xie, H.P.; Gao, F.; Mao, L.T. Energy Dissipation and Release during Coal Failure Under Conventional Triaxial Compression. Rock Mech. Rock Eng. 2015, 48, 509–526. [Google Scholar] [CrossRef]
- He, M.M.; Huang, B.Q.; Zhu, C.H.; Chen, Y.S.; Li, N. Energy Dissipation-Based Method for Fatigue Life Prediction of Rock Salt. Rock Mech. Rock Eng. 2018, 51, 1447–1455. [Google Scholar] [CrossRef]
- Liu, L.; Chen, Z.; Wang, Y. Elastic strain energy induced split during precipitation in alloys. J. Alloy. Compd. 2016, 661, 349–356. [Google Scholar] [CrossRef]
- Ren, X.D.; Li, J. Dynamic fracture in irregularly structured systems. Phys. Rev. E 2012, 85, 055102. [Google Scholar] [CrossRef] [PubMed]
- Lambert, D.E.; Ross, C.A. Strain rate effects on dynamic fracture and strength. Int. J. Impact Eng. 2000, 24, 985–998. [Google Scholar] [CrossRef]
- Feng, W.H.; Liu, F.; Yang, F.; Li, L.J.; Jing, L. Experimental study on dynamic split tensile properties of rubber concrete. Constr. Build. Mater. 2018, 165, 675–687. [Google Scholar] [CrossRef]
- Aliha, M.R.M.; Sistaninia, M.; Smith, D.J.; Pavier, M.J.; Ayatollahi, M.R. Geometry effects and statistical analysis of mode I fracture in guiting limestone. Int. J. Rock Mech. Min. Sci. 2012, 51, 128–135. [Google Scholar] [CrossRef]
- Kuruppu, M.D.; Chong, K.P. Fracture toughness testing of brittle materials using semi-circular bend (SCB) specimen. Eng. Fract. Mech. 2012, 91, 133–150. [Google Scholar] [CrossRef]
- Wang, Q.Z.; Xing, L. Determination of fracture toughness KIC by using the flattened Brazilian disk specimen for rocks. Eng. Fract. Mech. 1999, 64, 193–201. [Google Scholar] [CrossRef]
- Hondros, G. The evaluation of Poisson’s ratio and the modulus of materials of a low tensile resistance by the Brazilian (indirect tensile) test with particular reference to concrete. Aust. J. Appl. Sci. 1959, 10, 243–268. [Google Scholar]
- Khosravani, M.R.; Silani, M.; Weinberg, K. Fracture studies of Ultra-High Performance Concrete using dynamic Brazilian tests. Theor. Appl. Fract. Mech. 2018, 93, 302–310. [Google Scholar] [CrossRef]
- Kolsky, H. Stress Waves in Solids. J. Sound Vib. 1964, 1, 88–110. [Google Scholar] [CrossRef]
- Wang, Q.Z.; Li, W.; Xie, H.P. Dynamic split tensile test of Flattened Brazilian Disc of rock with SHPB setup. Mech. Mater. 2009, 41, 252–260. [Google Scholar] [CrossRef]
- Lu, Y.B.; Li, Q.M. About the dynamic uniaxial tensile strength of concrete-like materials. Int. J. Impact Eng. 2011, 38, 171–180. [Google Scholar] [CrossRef]
- Holmquist, T.J.; Johnson, G.R.; Cook, W.H. A Computational Constitutive Model for Concrete Subjected to Large Strains, High Strain Rates and High Pressures. In Proceedings of the 14th International Symposium Ballistics, Quebec City, QC, Canada, 26–29 September 1993; pp. 591–600. [Google Scholar]
- Shemirani, A.B.; Naghdabadi, R.; Ashrafi, M.J. Experimental and numerical study on choosing proper pulse shapers for testing concrete specimens by split Hopkinson pressure bar apparatus. Constr. Build. Mater. 2016, 125, 326–336. [Google Scholar] [CrossRef]
- Lv, T.H.; Chen, X.W.; Chen, G. The 3D meso-scale model and numerical tests of split Hopkinson pressure bar of concrete specimen. Constr. Build. Mater. 2018, 160, 744–764. [Google Scholar] [CrossRef]


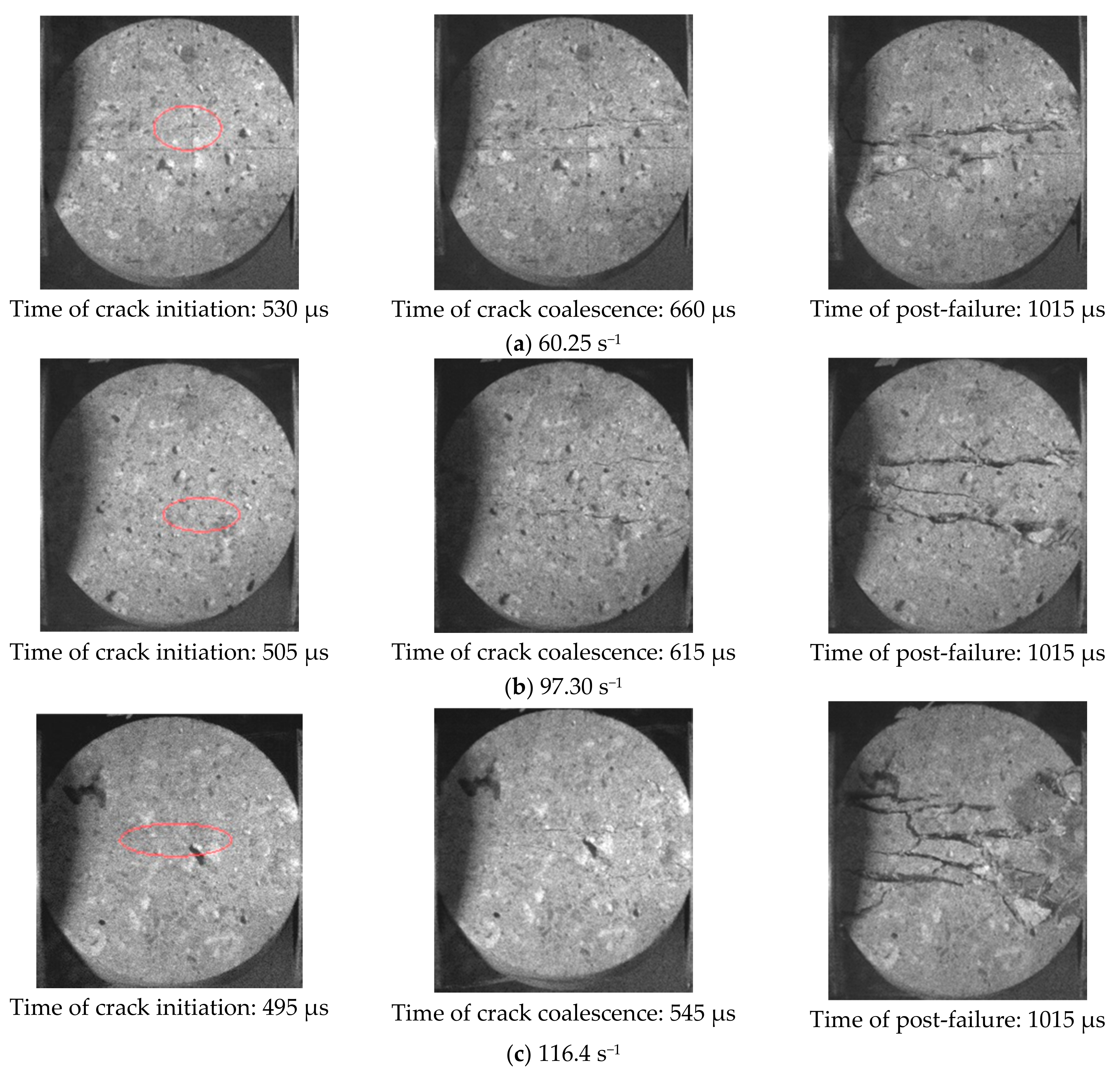
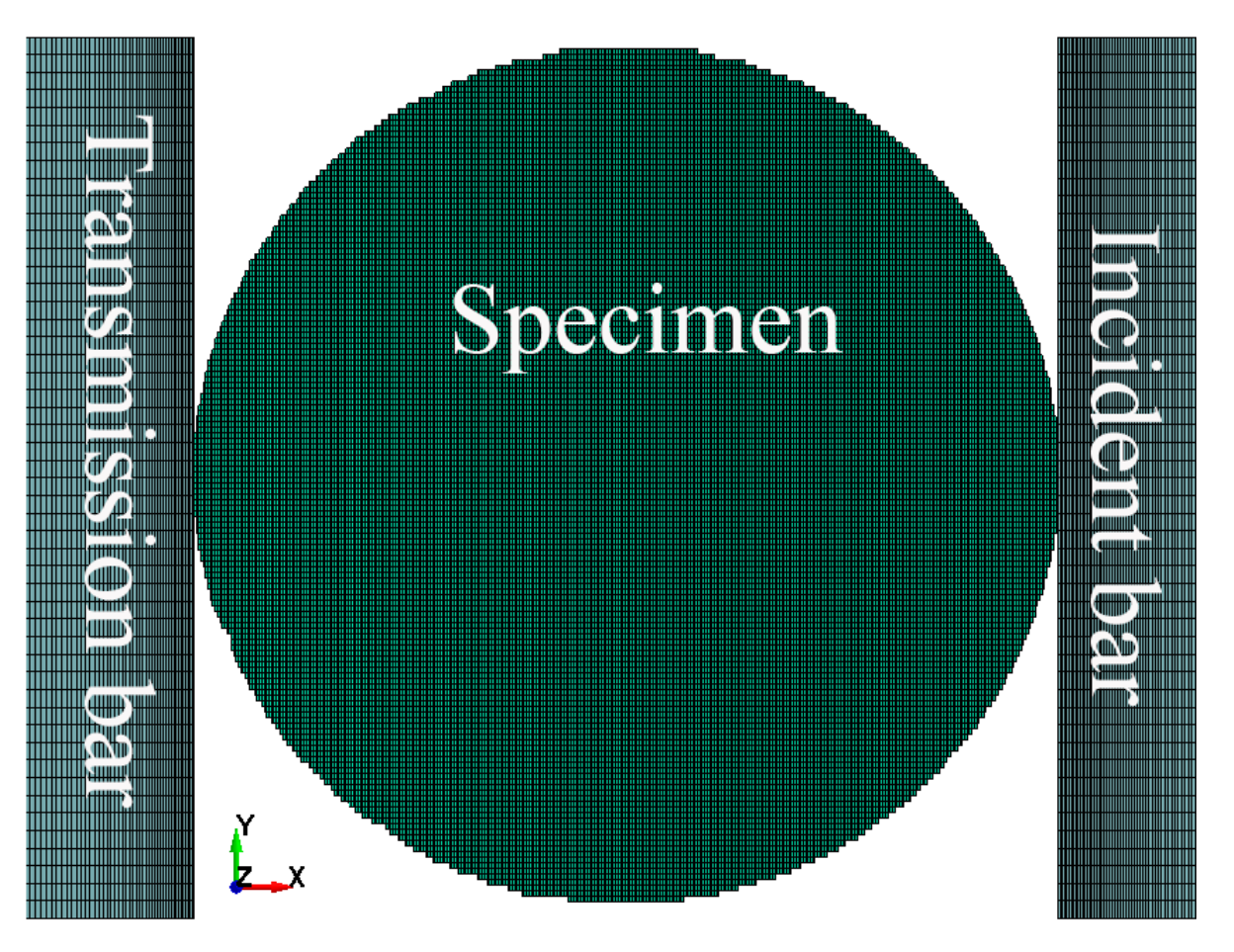
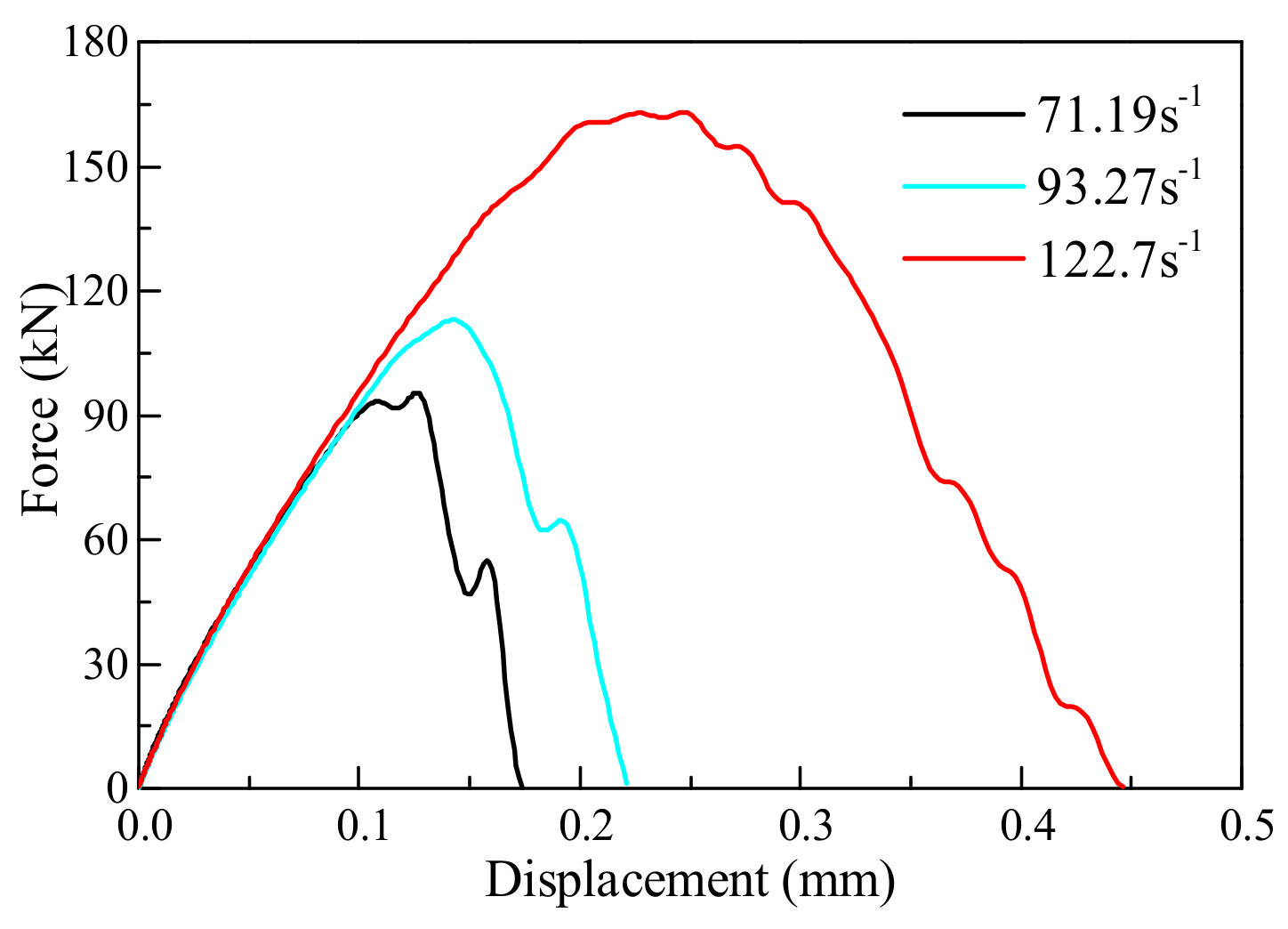
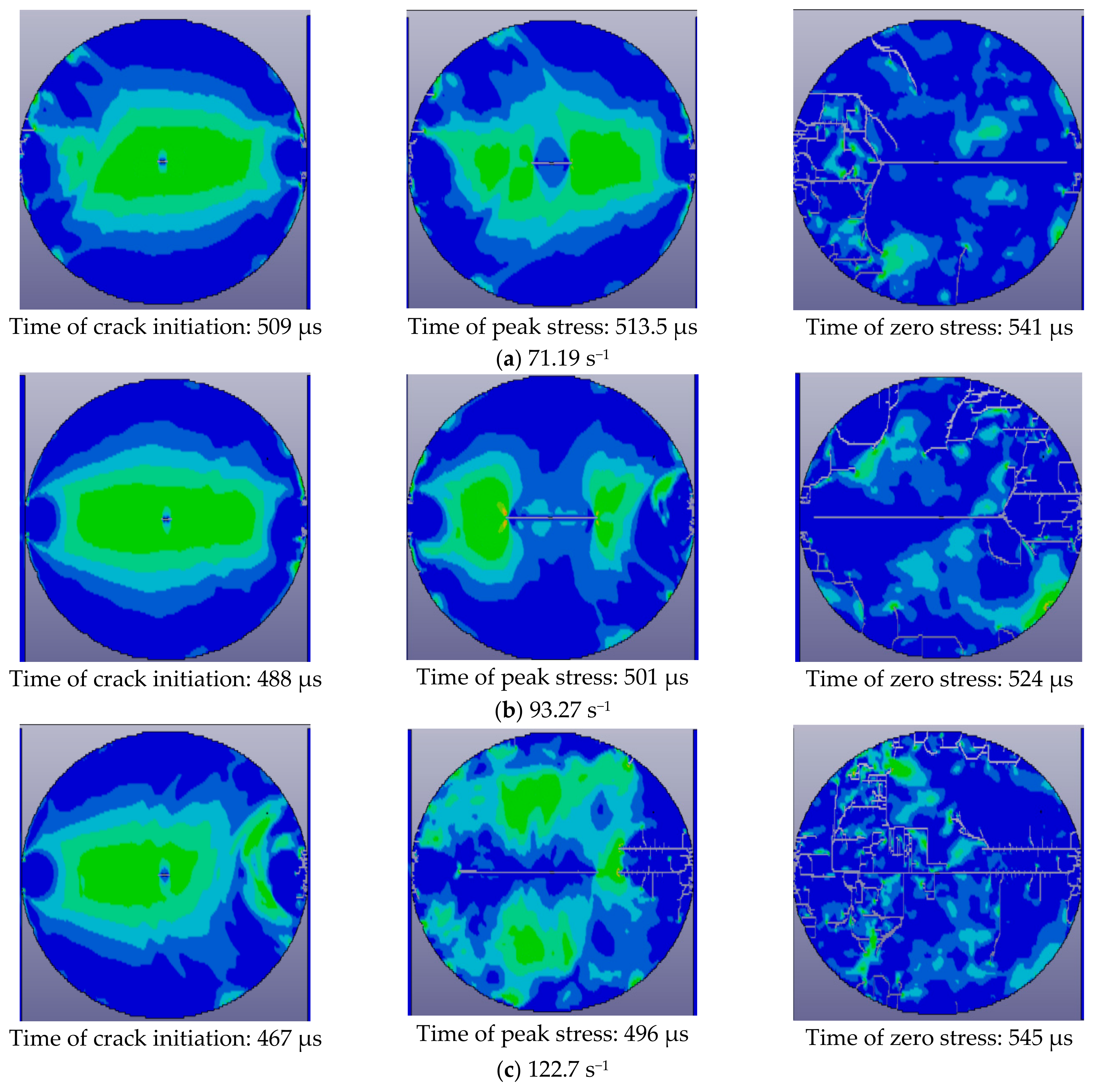
| Test No. | D (mm) | L (mm) | Impacting Pressure (MPa) | Pmax (kN) | Dynamic Tensile Strength (MPa) | Strain Rate (s−1) |
|---|---|---|---|---|---|---|
| 1 | 98.18 | 48.78 | 0.15 | 108.32 | 13.83 | 51.6 |
| 2 | 98.14 | 47.65 | 0.15 | 110.91 | 14.50 | 60.25 |
| 3 | 98.21 | 49.1 | 0.15 | 112.18 | 14.22 | 54.3 |
| 4 | 98.20 | 45.81 | 0.15 | 109.33 | 14.86 | 73.4 |
| 5 | 98.20 | 46.8 | 0.20 | 119.38 | 15.88 | 96.7 |
| 6 | 98.21 | 45.27 | 0.20 | 118.65 | 16.32 | 99.7 |
| 7 | 98.24 | 45.61 | 0.20 | 116.64 | 15.92 | 97.30 |
| 8 | 98.21 | 46.46 | 0.20 | 115.40 | 15.46 | 91.3 |
| 9 | 98.18 | 48.65 | 0.25 | 157.38 | 20.15 | 123.8 |
| 10 | 98.20 | 48.93 | 0.25 | 159.41 | 20.29 | 114.0 |
| 11 | 98.21 | 47.12 | 0.25 | 160.53 | 21.21 | 116.4 |
| 12 | 98.21 | 49.12 | 0.25 | 159.22 | 20.18 | 109.3 |
| P (kg·m−3) | G (GPa) | A | B | C | N |
| 2280 | 14.86 | 0.79 | 1.60 | 0.007 | 0.61 |
| fc (MPa) | T (MPa) | K1 (GPa) | K2 (GPa) | K3 (GPa) | Fs |
| 50 | 3 | 85 | −171 | 208 | 0.004 |
| Test No. | D (mm) | L (mm) | Impacting Pressure (MPa) | Pmax (kN) | Time of Pmax (μs) | Dynamic Tensile Strength (MPa) | Strain Rate (s−1) |
|---|---|---|---|---|---|---|---|
| 1 | 98 | 45 | 0.15 | 95.38 | 513.5 | 13.22 | 71.19 |
| 2 | 98 | 45 | 0.20 | 112.935 | 501 | 15.65 | 93.27 |
| 3 | 98 | 45 | 0.25 | 162.96 | 496 | 22.58 | 122.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Dang, F.; Wang, H.; Xue, Y.; Fang, J. Enhancement Mechanism of the Dynamic Strength of Concrete Based on the Energy Principle. Materials 2018, 11, 1274. https://doi.org/10.3390/ma11081274
Ren J, Dang F, Wang H, Xue Y, Fang J. Enhancement Mechanism of the Dynamic Strength of Concrete Based on the Energy Principle. Materials. 2018; 11(8):1274. https://doi.org/10.3390/ma11081274
Chicago/Turabian StyleRen, Jie, Faning Dang, Huan Wang, Yi Xue, and Jianyin Fang. 2018. "Enhancement Mechanism of the Dynamic Strength of Concrete Based on the Energy Principle" Materials 11, no. 8: 1274. https://doi.org/10.3390/ma11081274
APA StyleRen, J., Dang, F., Wang, H., Xue, Y., & Fang, J. (2018). Enhancement Mechanism of the Dynamic Strength of Concrete Based on the Energy Principle. Materials, 11(8), 1274. https://doi.org/10.3390/ma11081274





