Low-Temperature Superplasticity and Deformation Mechanism of Ti-6Al-4V Alloy
Abstract
1. Introduction
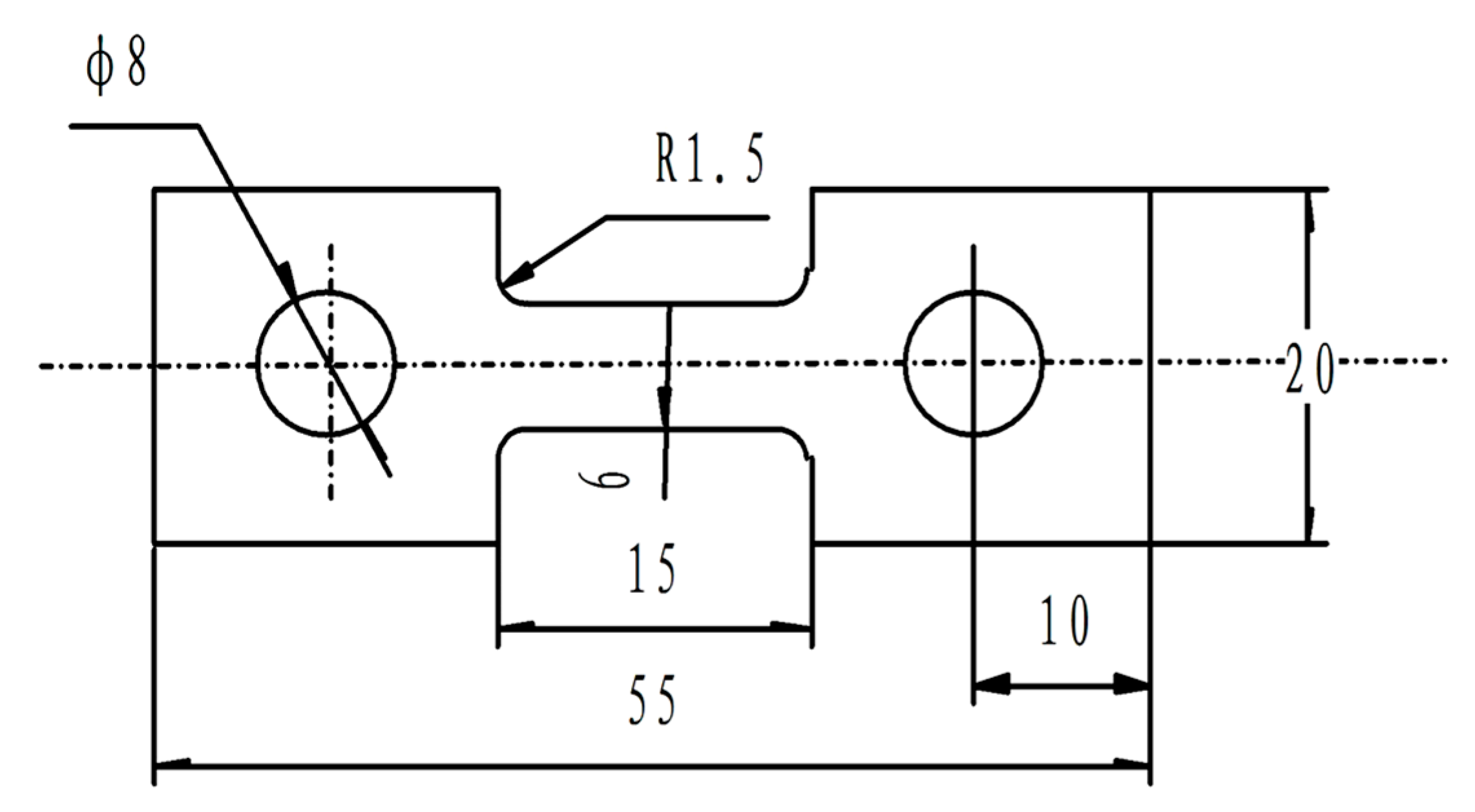
2. Experimental
3. Results and Discussion
3.1. Microstructure Prior to Deformation
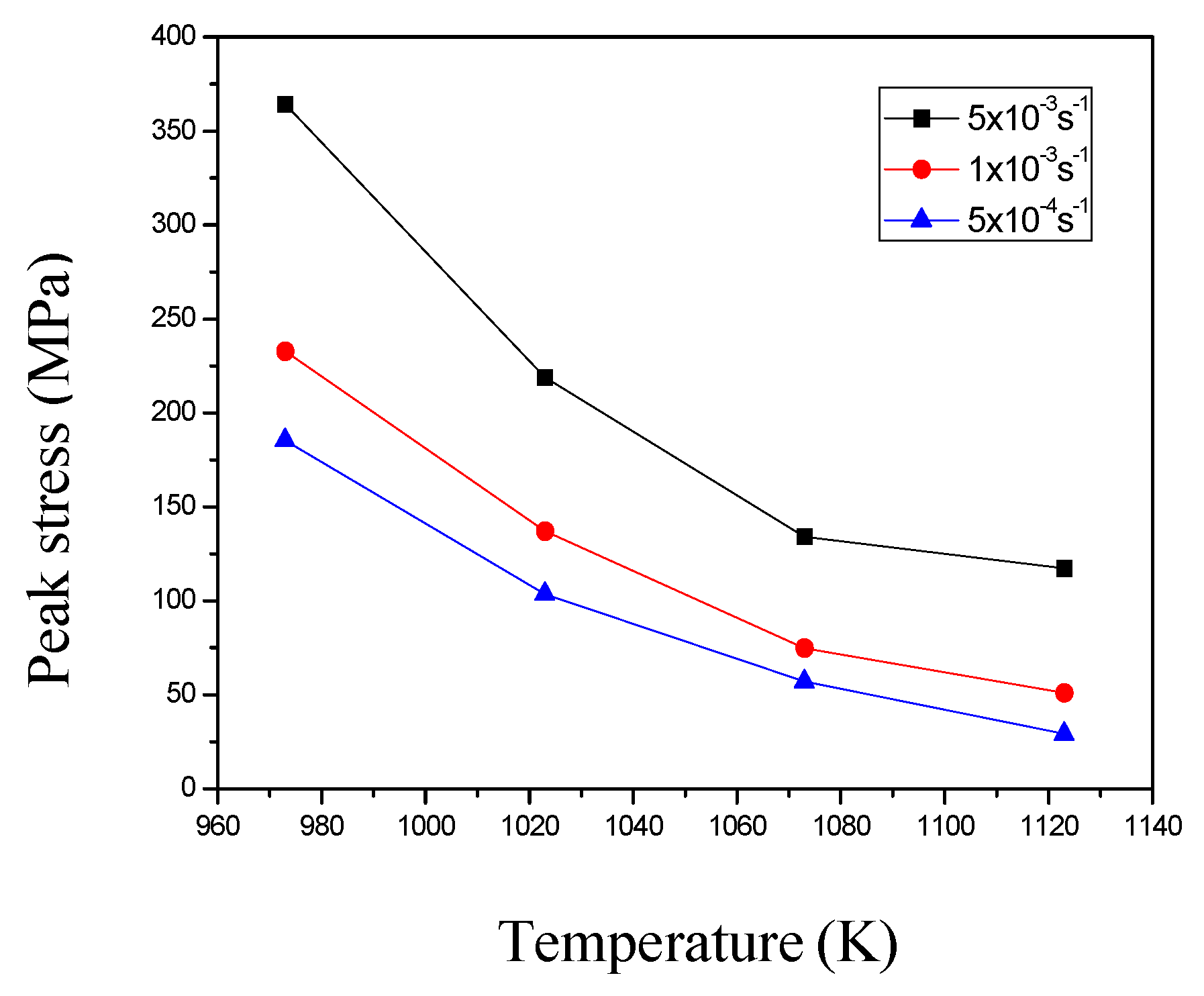
3.2. Tensile Mechanical Behavior of Ti-6Al-4V Alloy
3.3. Deformation Activation Energy of Ti-6Al-4V Alloy
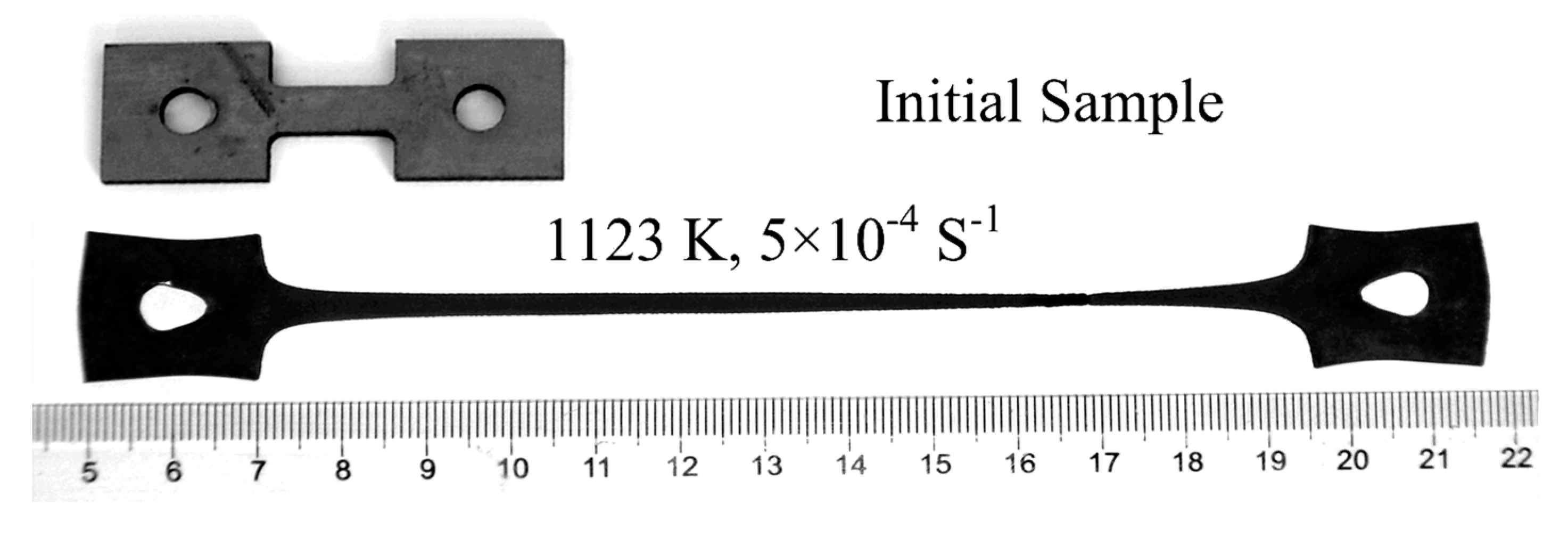
3.4. Microstructures after Tensile Deformation
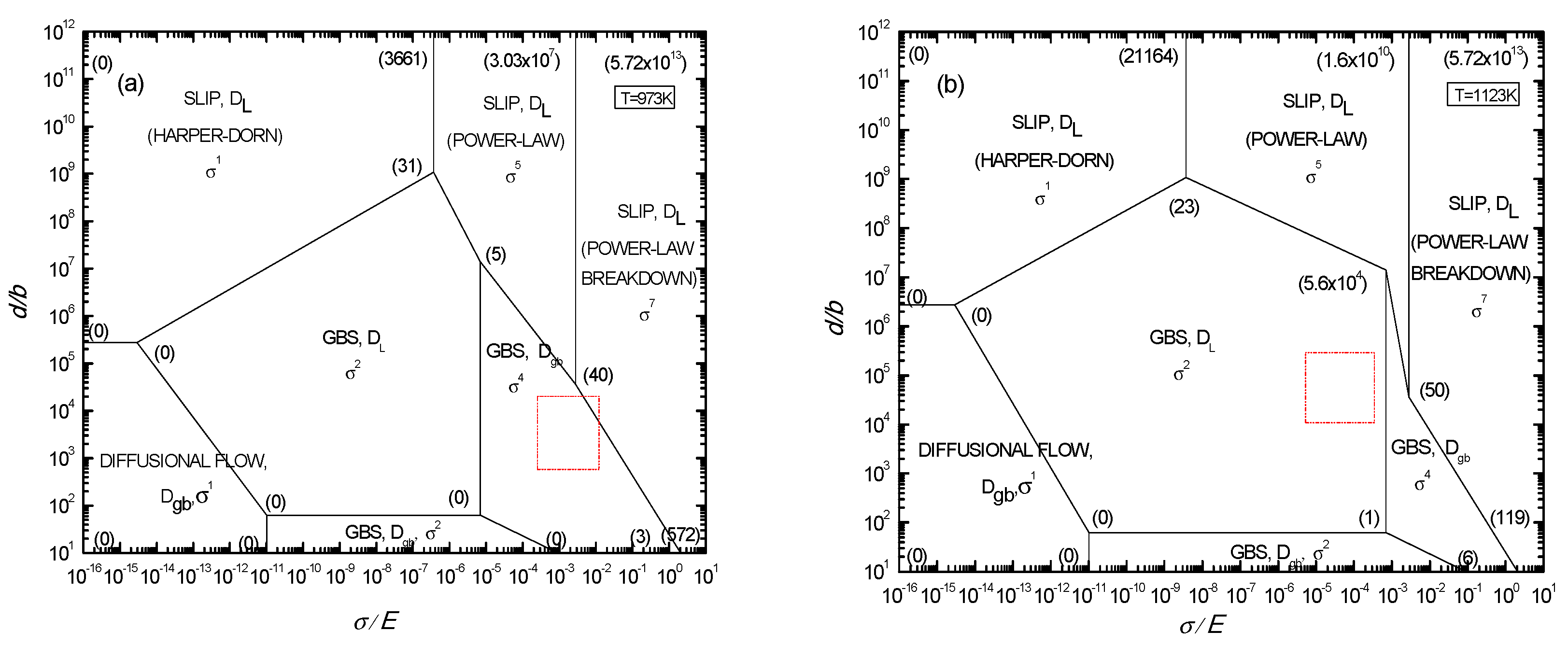
3.5. Theoretical Forecast of Low-Temperature Deformation Mechanism Maps Incorporating Dislocation Quantity
3.5.1. Construction of a Deformation Mechanism Map Incorporating the Dislocation Quantity
3.5.2. Analysis of Low-Temperature Tensile Behavior Using Deformation Mechanism Maps Containing Dislocation Quantities
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tan, Z.L.; Bai, L.S.; Bai, B.Z.; Zhao, B.; Li, Z.Q.; Hou, H.L. Fabrication of lattice truss structures by novel super-plastic forming and diffusion bonding process in a titanium alloy. Mater. Des. 2016, 92, 724–730. [Google Scholar] [CrossRef]
- Li, K.; Fu, X.S.; Chen, G.Q.; Zhou, W.L.; Li, Z.Q. Mechanical properties of strengthened surface layer in Ti-6Al-4V alloy induced by wet peening treatment. Trans. Nonferr. Met. Soc. China 2016, 26, 2868–2873. [Google Scholar] [CrossRef]
- Li, Z.Q.; Han, K.; Hou, H.L.; Wang, B.Y.; Hu, Z.H. Effect of Hydrogen on Diffusion Bonding Behavior and Mechanism of Ti-6Al-4V alloy. Rare Met. Mater. Eng. 2014, 43, 306–310. [Google Scholar]
- Chen, G.Q.; Jiao, Y.; Tian, T.Y.; Zhang, X.H.; Li, Z.Q.; Zhou, W.L. Effect of wet shot peening on Ti-6Al-4V alloy treated by ceramic beads. Trans. Nonferr. Met. Soc. China 2014, 24, 690–696. [Google Scholar] [CrossRef]
- Hamed, S.; Langdon, T.G. Using heat treatments, high-pressure torsion and post-deformation annealing to optimize the properties of Ti-6Al-4V alloys. Acta Mater. 2017, 141, 419–426. [Google Scholar]
- Ashby, M.F. A first report of deformation mechanism map. Acta Metall. 1972, 20, 887–894. [Google Scholar] [CrossRef]
- Mohamed, F.A.; Langdon, T.G. Deformation mechanism maps based on grain size. Metall. Trans. A 1974, 5, 2339–2345. [Google Scholar] [CrossRef]
- Ruano, O.A.; Wadsworth, J.; Sherby, O.D. Deformation mechanisms in an austenitic stainless steel (25Cr-20Ni) at elevated temperature. J. Mater. Sci. 1985, 20, 3735–3742. [Google Scholar] [CrossRef]
- Chung, S.W.; Higashi, K.; Kim, W.J. Supperplastic gas pressure forming of fine-grained AZ61 magnesium alloy sheet. Mater. Sci. Eng. A 2004, 372, 15–20. [Google Scholar] [CrossRef]
- Mohamed, F.A. Deformation mechanism maps for micro-grained, ultrafine-grained and nano-grained materials. Mater. Sci. Eng. A 2011, 528, 1431–1435. [Google Scholar] [CrossRef]
- Kawasaki, M.; Langdon, T.G. An Investigation of Cavity Development during Superplastic Flow in a Zinc-Aluminum Alloy Processed Using Severe Plastic Deformation. Mater. Trans. 2012, 53, 87–95. [Google Scholar] [CrossRef]
- Figueiredo, R.B.; Sabbaghianrad, S.; Giwa, A.; Greer, J.R.; Langdon, T.G. Evidence for exceptional low temperature ductility in polycrystalline magnesium processed by severe plastic deformation. Acta Mater. 2017, 1, 322–331. [Google Scholar] [CrossRef]
- Lee, D.H.; Lee, J.A.; Langdon, T.G. Annealing effect on plastic flow in nanocrystalline CoCrFeMnNi high-entropy alloy: A nanomechanical analysis. Acta Mater. 2017, 140, 443–451. [Google Scholar] [CrossRef]
- Hamed, S.; Huang, Y.; Langdon, T.G. Mechanical properties and microstructural evolution of nanocrystalline titanium at elevated temperatures. Mater. Sci. Eng. A 2016, 669, 358–366. [Google Scholar]
- Mishra, R.S.; Mukerjee, A.K. The rate controlling deformation mechanism in high strain rate superplasticity. Mater. Sci. Eng. A 1997, 234–236, 1023–1025. [Google Scholar] [CrossRef]
- Sajjadi, S.A.; Nategh, S.A. high temperature deformation mechanism map for the high performance Ni-base superalloy GTD-111. Mater. Sci. Eng. A 2001, 307, 158–164. [Google Scholar] [CrossRef]
- Tanaka, H.; Yamada, T.; Sato, E.; Jimbo, I. Distinguishing the ambient-temperature creep region in a deformation mechanism map of annealed CP-Ti. Scr. Mater. 2006, 54, 121–124. [Google Scholar] [CrossRef]
- Semenova, I.P.; Valiev, R.Z. The effect of equal-channel angular pressing on the structure and mechanical behavior of Ti-6Al-4V alloy. Mater. Sci. Eng. A 2014, 387, 805–808. [Google Scholar] [CrossRef]
- Zherebtsov, S.; Salishchev, G.A. Strength and ductility-related properties of ultrafine grained two-phase titanium alloy produced by warm multiaxial forging. Mater. Sci. Eng. A 2012, 536, 190–196. [Google Scholar] [CrossRef]
- Mallikarjun, K.; Satyam, S. Effect of prior β processing on superplasticity of (α + β) thermo mechanically treated Ti–632Si alloy. J. Mater. Process. Technol. 2003, 134, 35–44. [Google Scholar] [CrossRef]
- Bricknell, R.H.; Edington, J.W. Mechanical anisotropy and deformation mechanisms in an Al-Cu-Zr superplastic alloy. Acta Metall. 1979, 27, 1313–1318. [Google Scholar] [CrossRef]
- He, B.B.; Hu, B.; Yen, H.W.; Cheng, G.J.; Wang, Z.K.; Luo, H.W.; Huang, M.X. High dislocation density–induced large ductility in deformed and partitioned steels. Science 2017, 10, 1126. [Google Scholar] [CrossRef] [PubMed]
- Langdon, T.G. Grain boundary sliding revisited: Developments in sliding over four decades. J. Mater. Sci. 2006, 2006, 597–609. [Google Scholar] [CrossRef]
- Rao, K.P.; Hawbolt, E. Development of constitutive relationships using compression testing of a medium carbon steel. Trans. ASME J. Eng. Mater. Technol. 1992, 114, 116. [Google Scholar] [CrossRef]
- Meiler, M.L.; Lesuer, D.R.; Mukherjee, K.A. α grain size and β volume fraction aspects of the superplastictity of Ti-6Al-4V. Mater. Sci. Eng. A 1991, 136, 71. [Google Scholar]
- Kim, W.J.; Chung, S.W.; Chung, C.S.; Kum, D. Superplasticity in thin magnesium alloy sheets and deformation mechansim maps for magnesium alloys at elevated temperatures. Acta Mater. 2001, 49, 3337–3345. [Google Scholar] [CrossRef]
- Cao, F.R.; Ding, H.; Li, Y.L.; Zhao, W.J.; Guo, Y.L.; Cui, J.Z. Theoretical predicati on of dislocation-included high-temperature deformation mechanism maps for duplex magnesium lithium alloys. J. Mater. Metall. 2008, 7, 206–210. [Google Scholar]
- Frost, H.J.; Ashby, M.F. Ashby Deformation Mechanism Maps; Pergamon Press: Oxford, UK, 1982; p. 43. [Google Scholar]

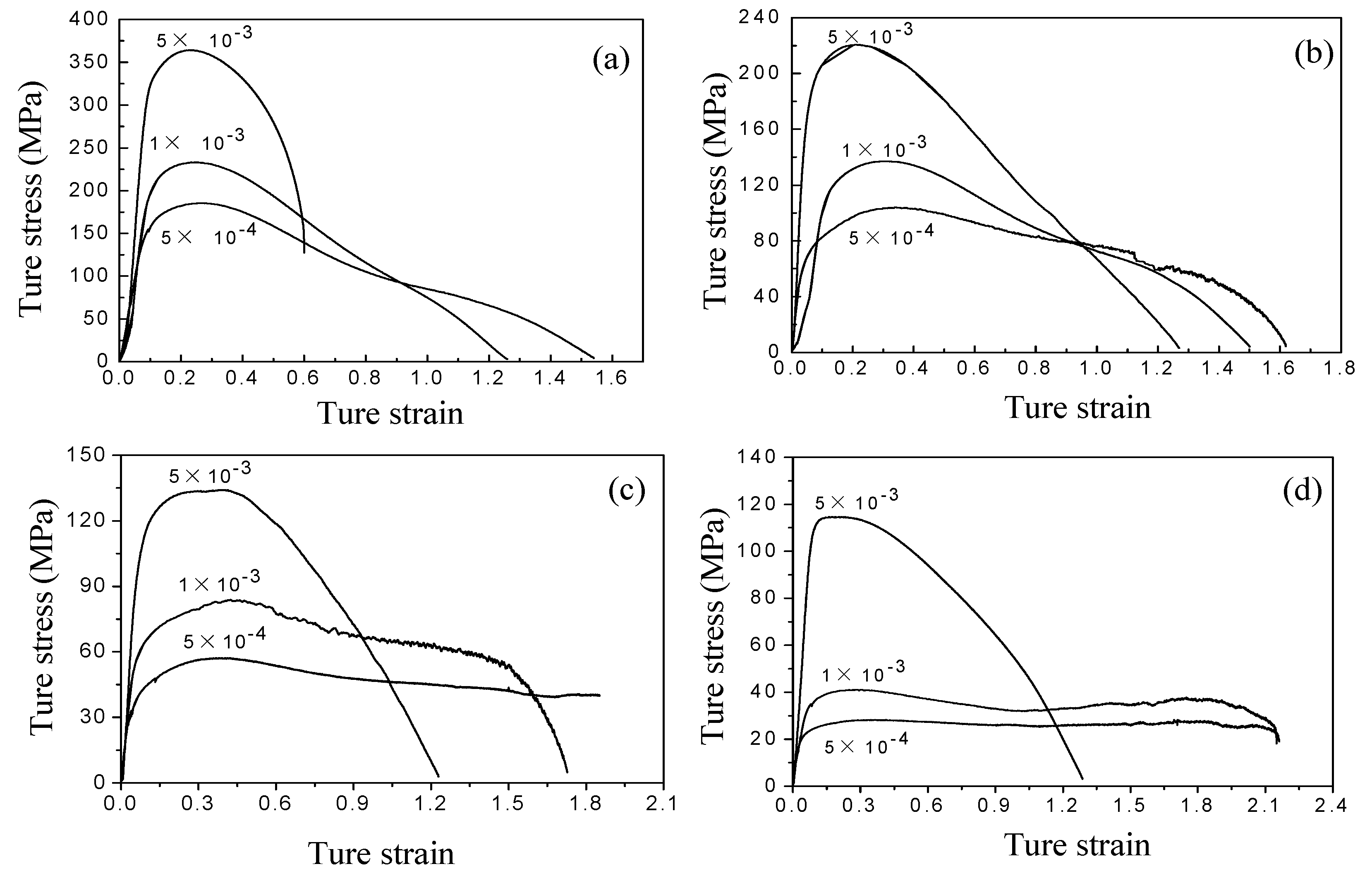



| Temperature T, (K) | Initial Strain Rate , (s−1) | Strain Rate Sensitivity Exponent m | Elongation to Failure δ, (%) |
|---|---|---|---|
| 1123 | 5 × 10−3 | 0.39 | 263 |
| 1123 | 10−3 | 0.52 | 758 |
| 1123 | 5 × 10−4 | 0.52 | 768 |
| 1073 | 5 × 10−3 | 0.38 | 240 |
| 1073 | 10−3 | 0.46 | 466 |
| 1073 | 5 × 10−4 | 0.48 | 536 |
| 1023 | 5 × 10−3 | 0.39 | 256 |
| 1023 | 10−3 | 0.43 | 347 |
| 1023 | 5 × 10−4 | 0.45 | 406 |
| 973 | 5 × 10−3 | 0.23 | 82 |
| 973 | 10−3 | 0.39 | 252 |
| 973 | 5 × 10−4 | 0.43 | 366 |
| 973 | 3 × 10−4 | 0.43 | 359 |
| Initial Strain Rate , (s−1) | Temperature T, (K) | |||
|---|---|---|---|---|
| 973 | 1023 | 1073 | 1123 | |
| 5 × 10−3 | 242.46 | 228.80 | 184.60 | 106.70 |
| 10−3 | 363.72 | 343.23 | 276.92 | 160.06 |
| 5 × 10−4 | 402.61 | 379.93 | 306.53 | 177.18 |
| Average | 336.26 | 317.32 | 256.02 | 147.98 |
| bα = 2.5 × 10−10 m | ||
| bβ = 2.86 × 10−10 m | ||
| K = 1.38 × 10−23 J/K | E = 2G(1 + ν) | |
| T (K) | (d/b) × 10−4 | (σ/E) × 104 | έ (10−4·s−1) |
|---|---|---|---|
| 973 | 0.8–7.2 | 3.2–55.1 | 5–50 |
| 1123 | 3.6–13.02 | 2.8–21.7 | 5–50 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, G.; Chen, L.; Liu, L.; Liu, H.; Peng, H.; Zhong, Y. Low-Temperature Superplasticity and Deformation Mechanism of Ti-6Al-4V Alloy. Materials 2018, 11, 1212. https://doi.org/10.3390/ma11071212
Zhou G, Chen L, Liu L, Liu H, Peng H, Zhong Y. Low-Temperature Superplasticity and Deformation Mechanism of Ti-6Al-4V Alloy. Materials. 2018; 11(7):1212. https://doi.org/10.3390/ma11071212
Chicago/Turabian StyleZhou, Ge, Lijia Chen, Lirong Liu, Haijian Liu, Heli Peng, and Yiping Zhong. 2018. "Low-Temperature Superplasticity and Deformation Mechanism of Ti-6Al-4V Alloy" Materials 11, no. 7: 1212. https://doi.org/10.3390/ma11071212
APA StyleZhou, G., Chen, L., Liu, L., Liu, H., Peng, H., & Zhong, Y. (2018). Low-Temperature Superplasticity and Deformation Mechanism of Ti-6Al-4V Alloy. Materials, 11(7), 1212. https://doi.org/10.3390/ma11071212




