Plasmon-Induced Transparency Based on Triple Arc-Ring Resonators
Abstract
1. Introduction
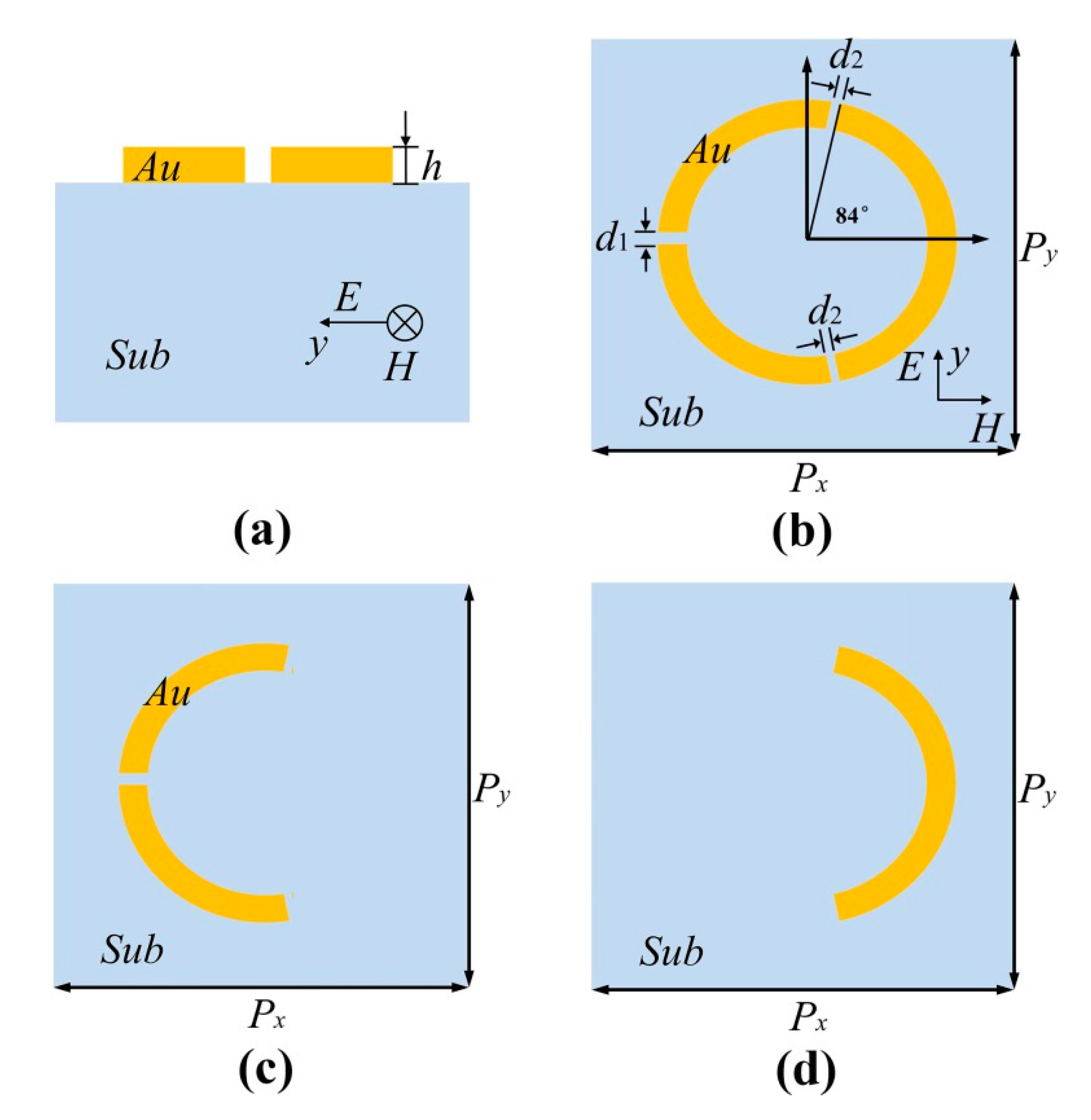
2. Materials and Method
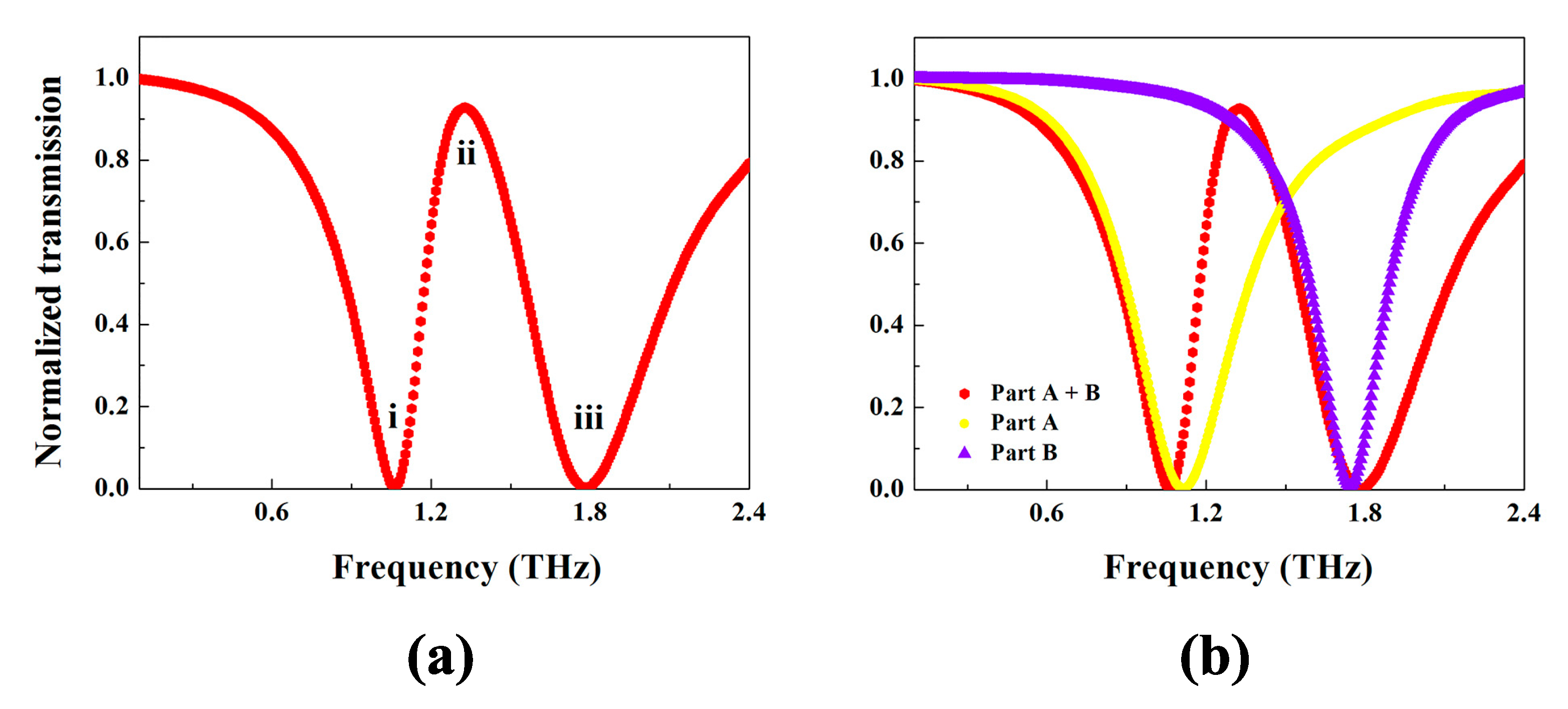
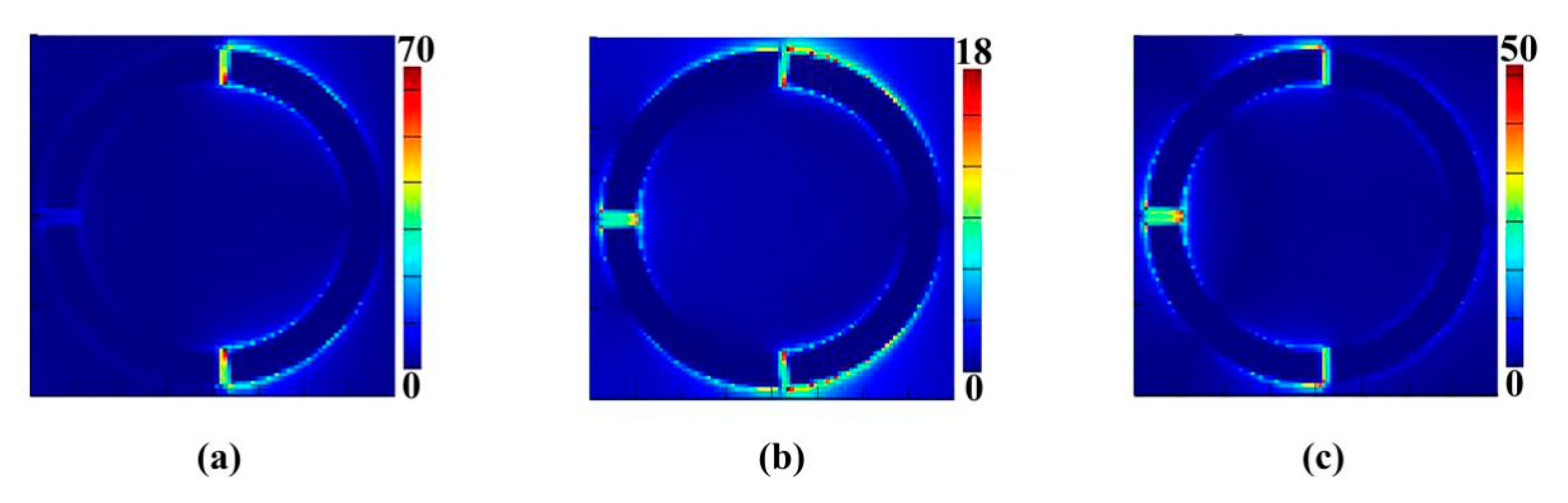
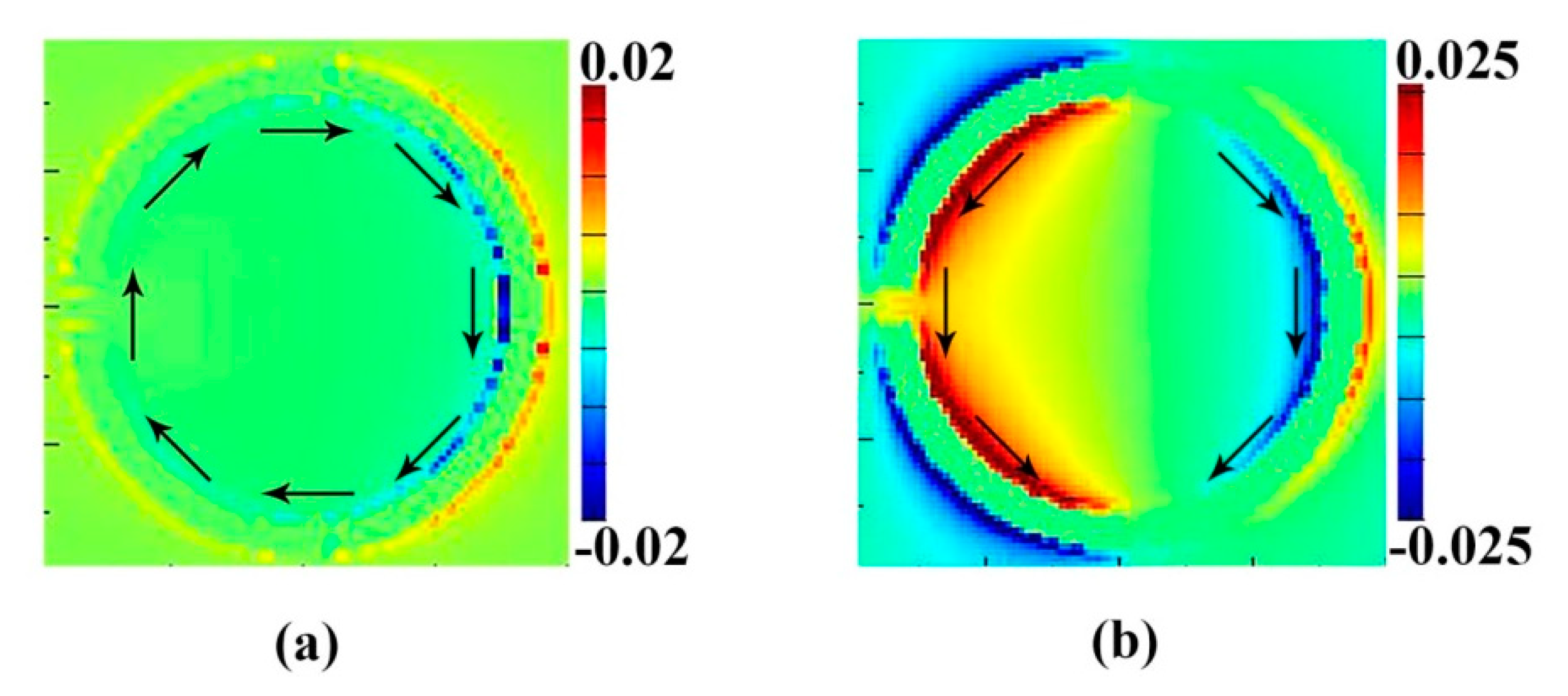
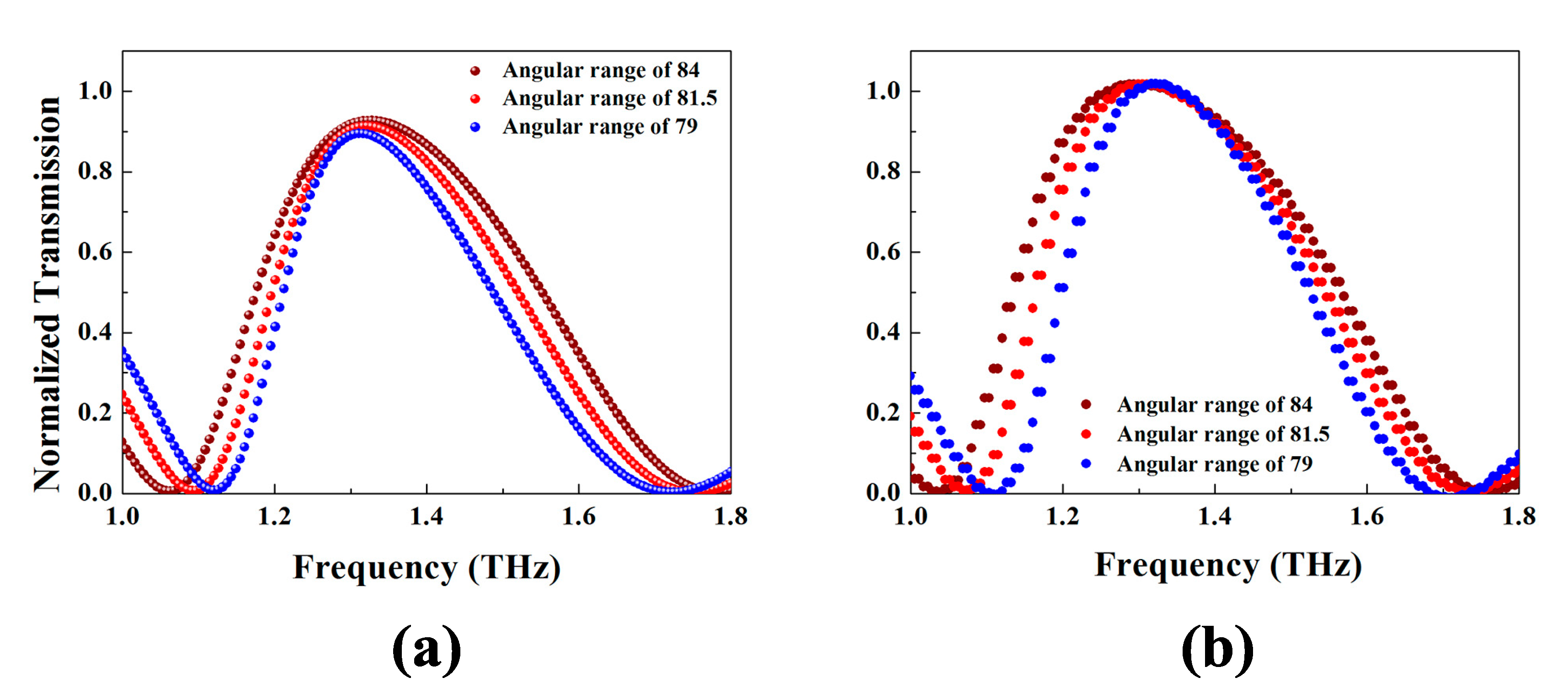
3. Simulation Results and Discussion
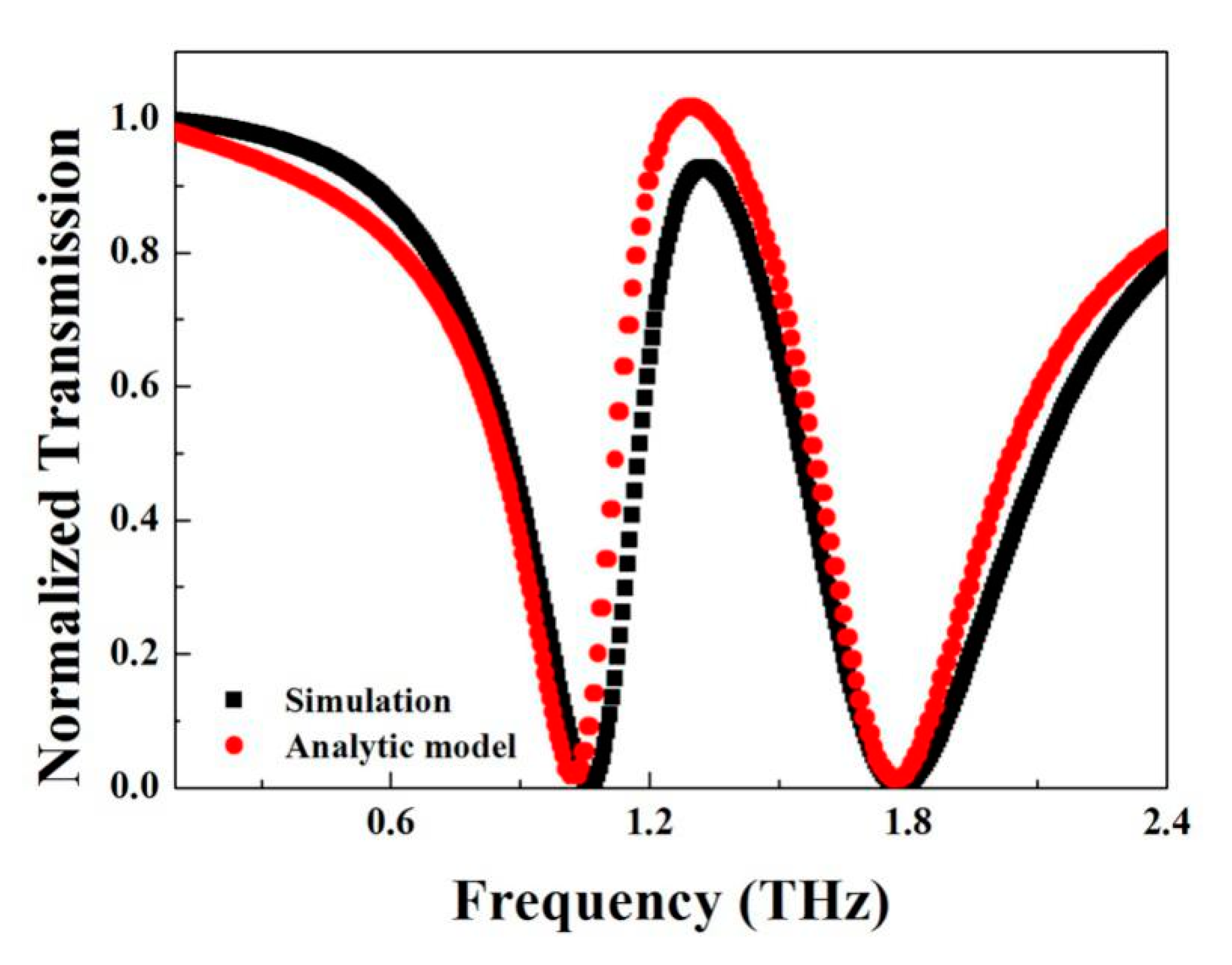
4. Theory Analyze
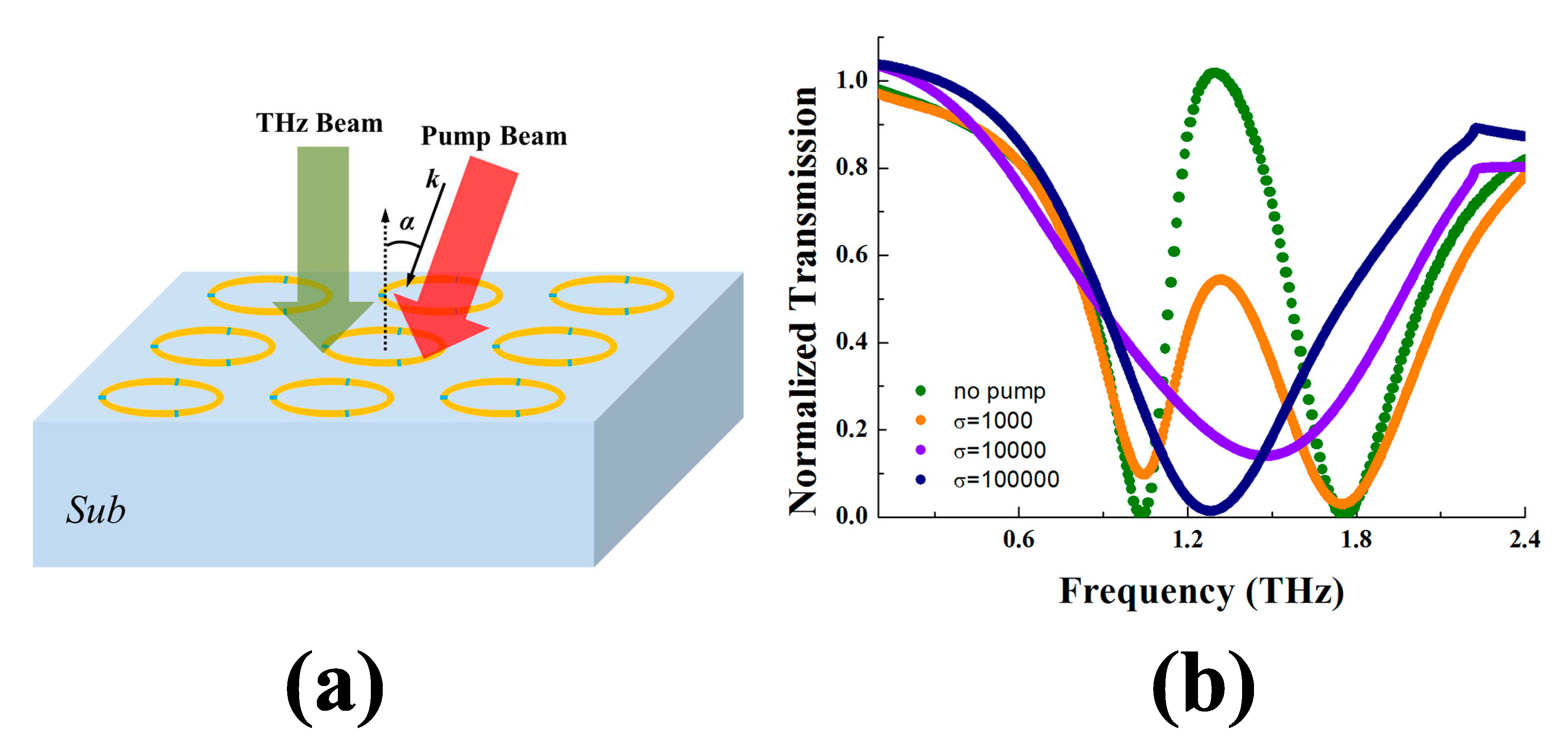
5. Potential Applications
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Smith, D.R.; Pendry, J.B.; Wiltshire, M.C.K. Metamaterials and negative refractive index. Science 2004, 305, 788–792. [Google Scholar] [CrossRef]
- Soukoulis, C.M.; Wegener, M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat. Photon. 2011, 5, 523–530. [Google Scholar] [CrossRef]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 1999, 47, 2075–2084. [Google Scholar] [CrossRef]
- Shelby, R.A.; Smith, D.R.; Schultz, S. Experimental verification of a negative index of refraction. Science 2001, 292, 77–79. [Google Scholar] [CrossRef]
- Schurig, D.; Mock, J.J.; Justice, B.J.; Cummer, S.A.; Pendry, J.B.; Starr, A.F.; Smith, D.R. Metamaterial electromagnetic cloak at microwave frequencies. Science 2006, 314, 977–980. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Sauvan, C.; Liu, H.T.; Lalanne, P. Theory of fishnet negative-index optical metamaterials. Phys. Rev. Lett. 2011, 107, 043903. [Google Scholar] [CrossRef]
- Dolling, G.; Enkrich, C.; Wegener, M.; Zhou, J.; Soukoulis, C.M.; Linden, S. Cut-wire pairs and plate pairs as magnetic atoms for optical metamaterials. Opt. Lett. 2005, 30, 3198–3200. [Google Scholar] [CrossRef]
- Grant, J.; McCrindle, I.J.H.; Cumming, D.R. Multi-spectral materials: Hybridisation of optical plasmonic filters, a mid infrared metamaterial absorber and a terahertz metamaterial absorber. Opt. Express 2016, 24, 3451–3463. [Google Scholar] [CrossRef] [PubMed]
- Bayatpur, F.; Sarabandi, K. Multipole spatial filters using metamaterial-based miniaturized-element frequency-selective surfaces. IEEE Trans. Microw. Theory Tech. 2008, 56, 2742–2747. [Google Scholar] [CrossRef]
- Wang, Z.L.; Hashimoto, K.; Shinohara, N.; Matsumoto, H. Frequency-selective surface for microwave power transmission. IEEE Trans. Microw. Theory Tech. 1999, 47, 2039–2042. [Google Scholar] [CrossRef]
- Chang, W.S.; Lassiter, J.B.; Swanglap, P.; Sobhani, H.; Khatua, S.; Nordlander, P.; Halas, N.J.; Link, S. A Plasmonic Fano Switch. Nano Lett. 2012, 12, 4977–4982. [Google Scholar] [CrossRef] [PubMed]
- Harris, S.E. Electromagnetically induced transparency. Phys. Today 1997, 50, 36–42. [Google Scholar] [CrossRef]
- Wilson, E.A.; Manson, N.B.; Wei, C. Perturbing an electromagnetic induced transparency within an inhomogeneously broadened transition. Phys. Rev. A 2003, 67, 023812. [Google Scholar] [CrossRef]
- Tassin, P.; Zhang, L.; Koschny, T.; Economou, E.N.; Soukoulis, C.M. Low-loss metamaterials based on classical electromagnetically induced transparency. Phys. Rev. Lett. 2009, 102, 053901. [Google Scholar] [CrossRef] [PubMed]
- Papasimakis, N.; Fu, Y.H.; Fedotov, V.A.; Prosvirnin, S.L.; Tsai, D.P.; Zheludev, N.I. Metamaterial with polarization and direction insensitive resonant transmission response mimicking electromagnetically induced transparency. Appl. Phys. Lett. 2009, 94, 211902. [Google Scholar] [CrossRef]
- Zhang, S.; Genov, D.A.; Wang, Y.; Liu, M.; Zhang, X. Plasmon-Induced Transparency in Metamaterials. Phys. Rev. Lett. 2008, 101, 047401. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Zhao, Z.; Shi, W.; Peng, W. Broadband terahertz plasmon-induced transparency via asymmetric coupling inside meta-molecules. Opt. Mater. Express 2017, 7, 1035–1047. [Google Scholar] [CrossRef]
- Yang, S.Y.; Xia, X.X.; Liu, Z.; Yiwen, E.; Wang, Y.J.; Tang, C.C.; Li, W.X.; Li, J.J.; Wang, L.; Gu, C.Z. Multispectral plasmon-induced transparency in hyperfine terahertz meta-molecules. J. Phys. 2016, 28, 445002. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.Q.; Li, Q.; Cao, W.; Gu, J.Q.; Singh, R.; Tian, Z.; Han, J.G.; Zhang, W.L. Polarization-Independent Plasmon-Induced Transparency in a Fourfold Symmetric Terahertz Metamaterial. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 8400707. [Google Scholar] [CrossRef]
- Luo, X.G.; Qiu, T.; Lu, W.B.; Ni, Z.H. Plasmons in graphene: Recent progress and applications. Mater. Sci. Eng. R Rep. 2013, 74, 351–376. [Google Scholar] [CrossRef]
- He, X.Y. Tunable terahertz graphene metamaterials. Carbon 2015, 82, 229–237. [Google Scholar] [CrossRef]
- Yan, X.; Yuan, L.; Wang, Y.K.; Sang, T.; Yang, G.F. Transmittance characteristics and tunable sensor performances of plasmonic graphene ribbons. AIP Adv. 2016, 6, 085301. [Google Scholar] [CrossRef]
- Jablan, M.; Buljan, H.; Solja, M. Plasmonics in graphene at infra-red frequencies. Phys. Rev. B 2009, 80, 245435. [Google Scholar] [CrossRef]
- Vasić, B.; Isić, G.; Gajić, R. Localized surface plasmon resonances in graphene ribbon arrays for sensing of dielectric environment at infrared frequencies. J. Appl. Phys. 2013, 113, 013110. [Google Scholar] [CrossRef]
- Han, X.; Wang, T.; Li, X.M.; Xiao, S.Y.; Zhu, Y.J. Dynamically tunable plasmon induced transparency in a graphene-based nanoribbon waveguide coupled with graphene rectangular resonators structure on sapphire substrate. Opt. Express 2015, 23, 31945–31955. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Han, D.Z.; Dai, Y.Y.; Yu, Z.F.; Sun, Y.; Chen, H.; Liu, X.H.; Zi, J. Plasmonic analog of electromagnetically induced transparency in nanostructure graphene. Opt. Express 2013, 21, 28438–28443. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.Y.; Wu, Q.; Erni, D.; Wu, K.; Lee, J.C. Polarization-Independent Metamaterial Analog of Electromagnetically Induced Transparency for a Refractive-Index-Based Sensor. IEEE Trans. Microw. Theory Tech. 2012, 60, 3013–3022. [Google Scholar] [CrossRef]
- Manjappa, M.; Chiam, S.Y.; Cong, L.Q.; Bettiol, A.A.; Zhang, W.L.; Singh, R. Tailoring the slow light behavior in terahertz metasurfaces. Appl. Phys. Lett. 2015, 106, 181101. [Google Scholar] [CrossRef]
- Wang, B.X.; Wang, L.L.; Wang, G.Z.; Huang, W.Q.; Li, X.F.; Zhai, X. A simple design of ultra-broadband and polarization insensitive terahertz metamaterial absorber. Appl. Phys. A 2014, 115, 1187–1192. [Google Scholar] [CrossRef]
- Wang, B.X.; Xie, Q.; Dong, G.X.; Huang, W.Q. Design of triple-band polarization controlled terahertz metamaterial absorber. Superlattices Microstruct. 2018, 114, 225–232. [Google Scholar] [CrossRef]
- Shen, N.H.; Kafesaki, M.; Koschny, T.; Zhang, L.; Economou, E.N.; Soukoulis, C.M. Broadband blueshift tunable metamaterials and dual-band switches. Phys. Rev. B 2009, 79, 161102. [Google Scholar] [CrossRef]
- Chen, H.T.; O’hara, J.F.; Azad, A.K.; Taylor, A.J.; Averitt, R.D.; Shrekenhamer, D.B.; Padilla, W.J. Experimental demonstration of frequency-agile terahertz metamaterial. Nat. Photon. 2008, 2, 295–298. [Google Scholar] [CrossRef]
- Xu, Z.C.; Gao, R.M.; Ding, C.F.; Wu, L.; Zhang, Y.T.; Xu, D.G.; Yao, J.Q. Photoexited switchable metamaterial absorber at terahertz frequencies. Opt. Commun. 2015, 344, 125–128. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, G.-X.; Xie, Q.; Zhang, Q.; Wang, B.-X.; Huang, W.-Q. Plasmon-Induced Transparency Based on Triple Arc-Ring Resonators. Materials 2018, 11, 964. https://doi.org/10.3390/ma11060964
Dong G-X, Xie Q, Zhang Q, Wang B-X, Huang W-Q. Plasmon-Induced Transparency Based on Triple Arc-Ring Resonators. Materials. 2018; 11(6):964. https://doi.org/10.3390/ma11060964
Chicago/Turabian StyleDong, Guang-Xi, Qin Xie, Qi Zhang, Ben-Xin Wang, and Wei-Qing Huang. 2018. "Plasmon-Induced Transparency Based on Triple Arc-Ring Resonators" Materials 11, no. 6: 964. https://doi.org/10.3390/ma11060964
APA StyleDong, G.-X., Xie, Q., Zhang, Q., Wang, B.-X., & Huang, W.-Q. (2018). Plasmon-Induced Transparency Based on Triple Arc-Ring Resonators. Materials, 11(6), 964. https://doi.org/10.3390/ma11060964






