Exploring the Potential of Electrical Impedance Tomography for Tissue Engineering Applications
Abstract
1. Introduction
2. Materials and Methods
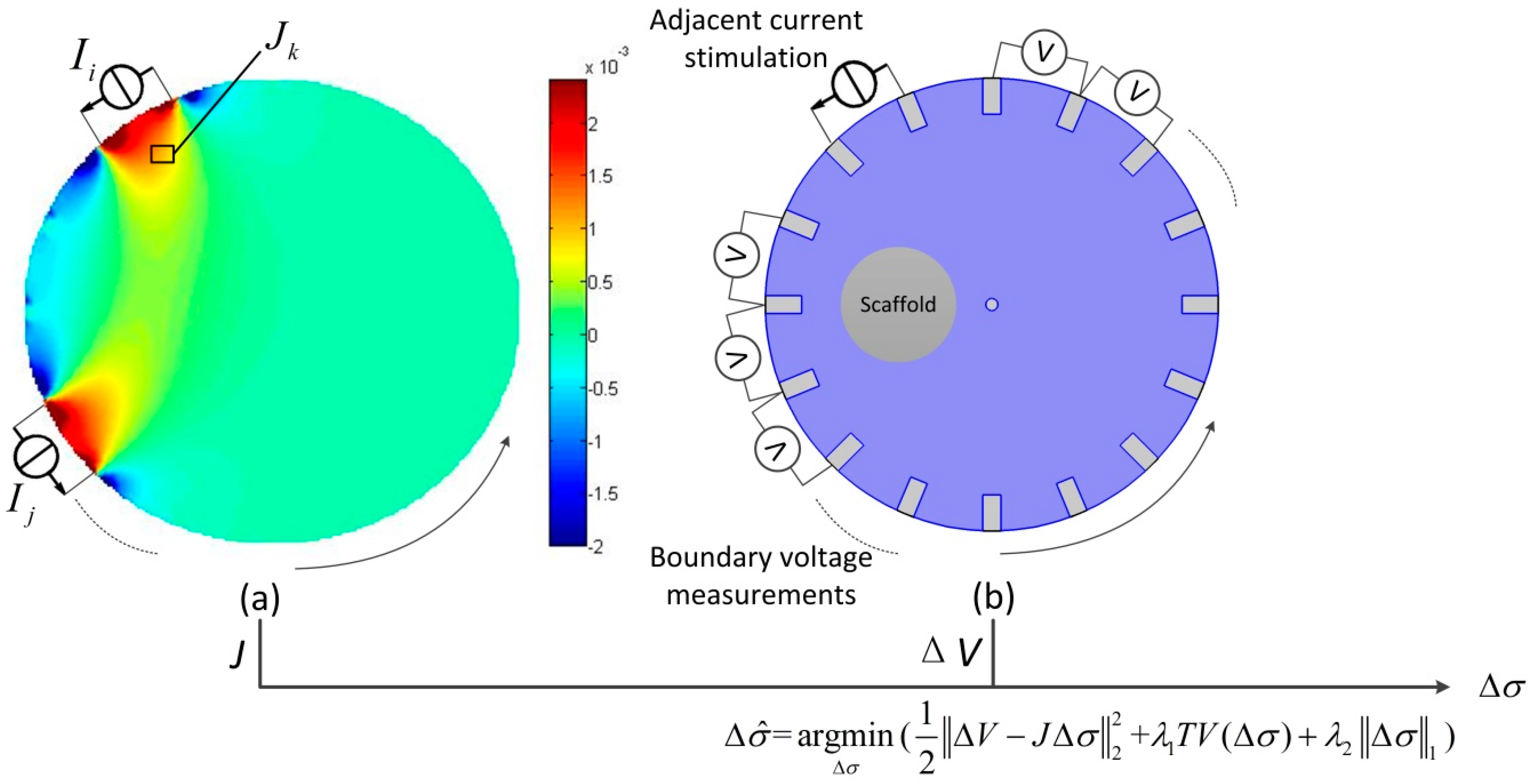
2.1. Principle of EIT
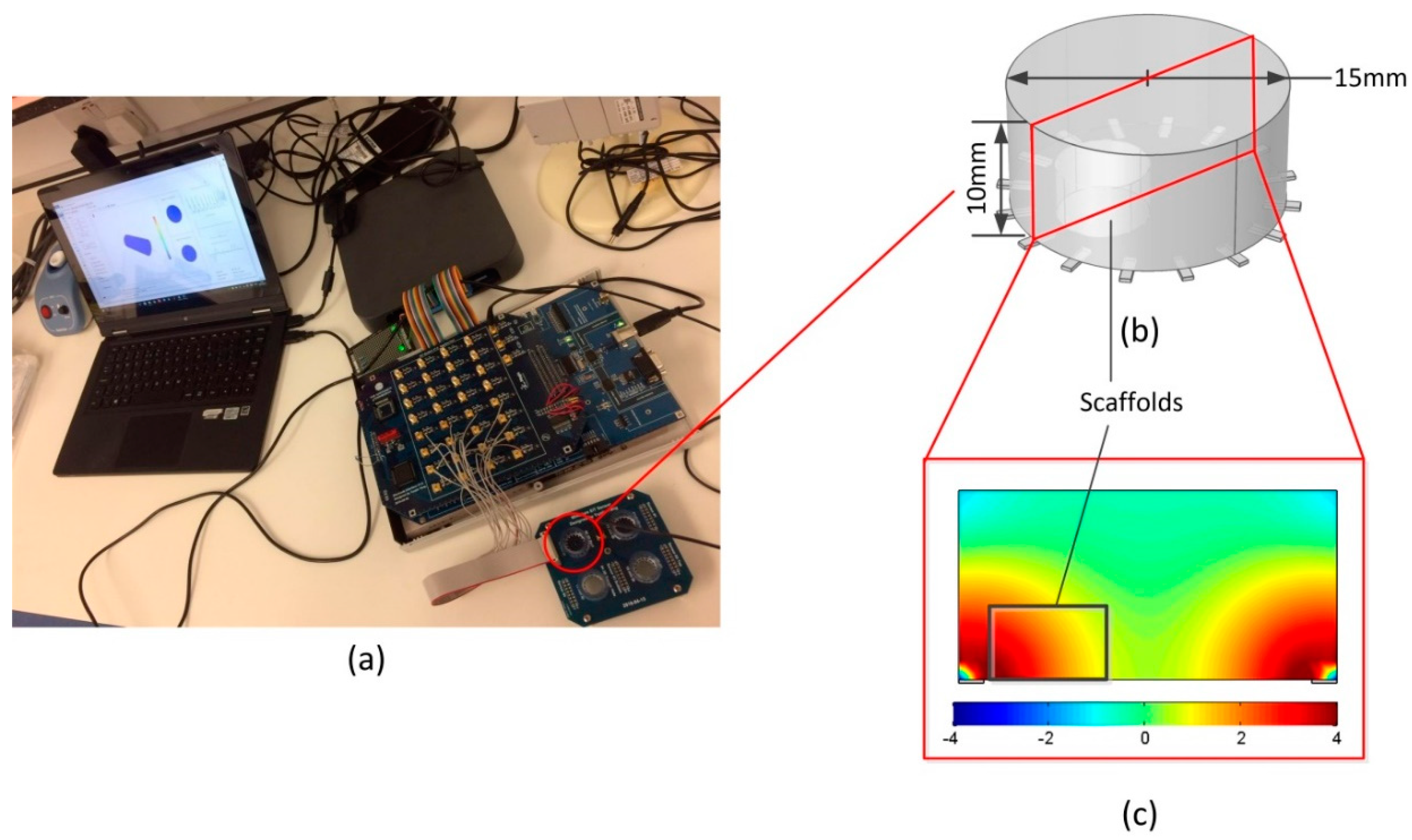
2.2. EIT Measurements in the Miniature Sensor
2.3. Cell Culture
2.4. Cell Seeding
3. Results
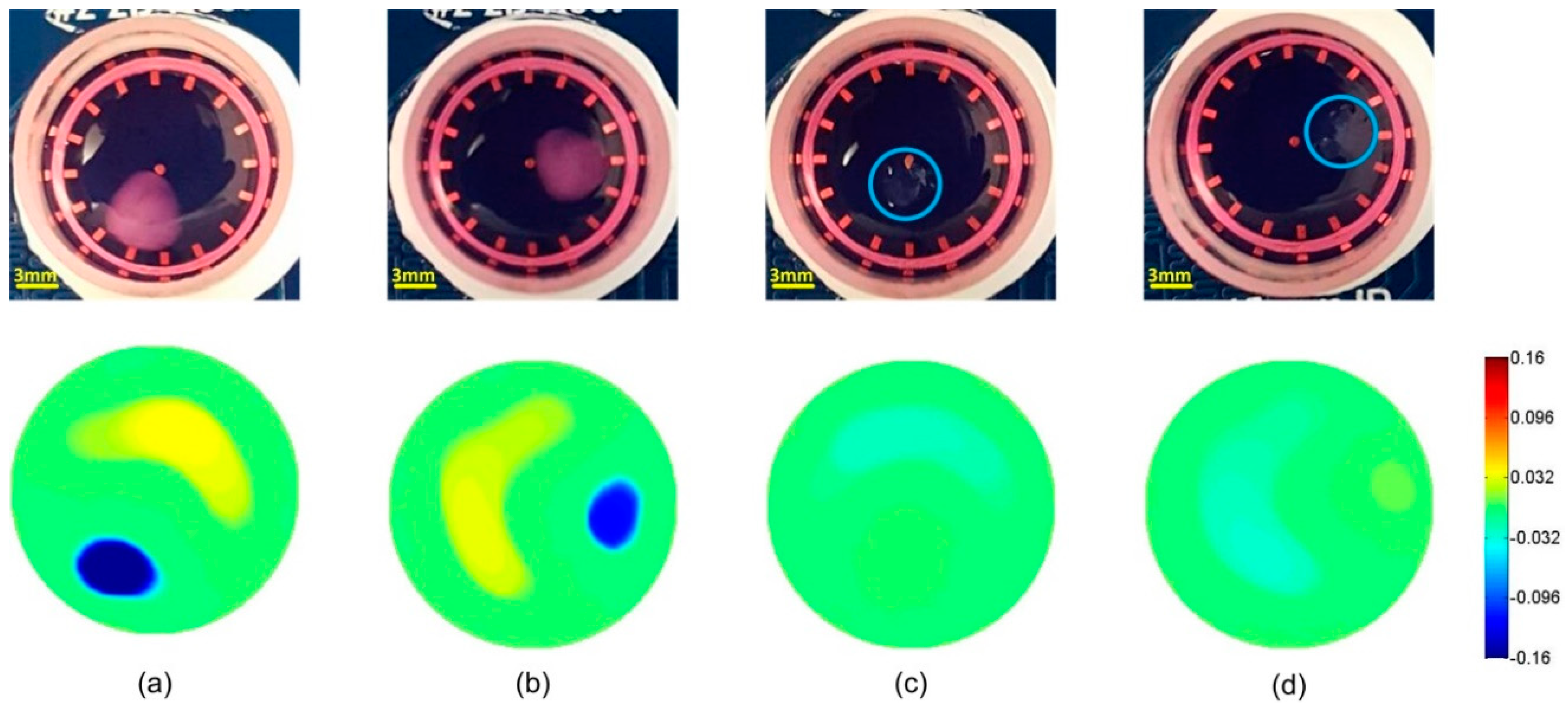
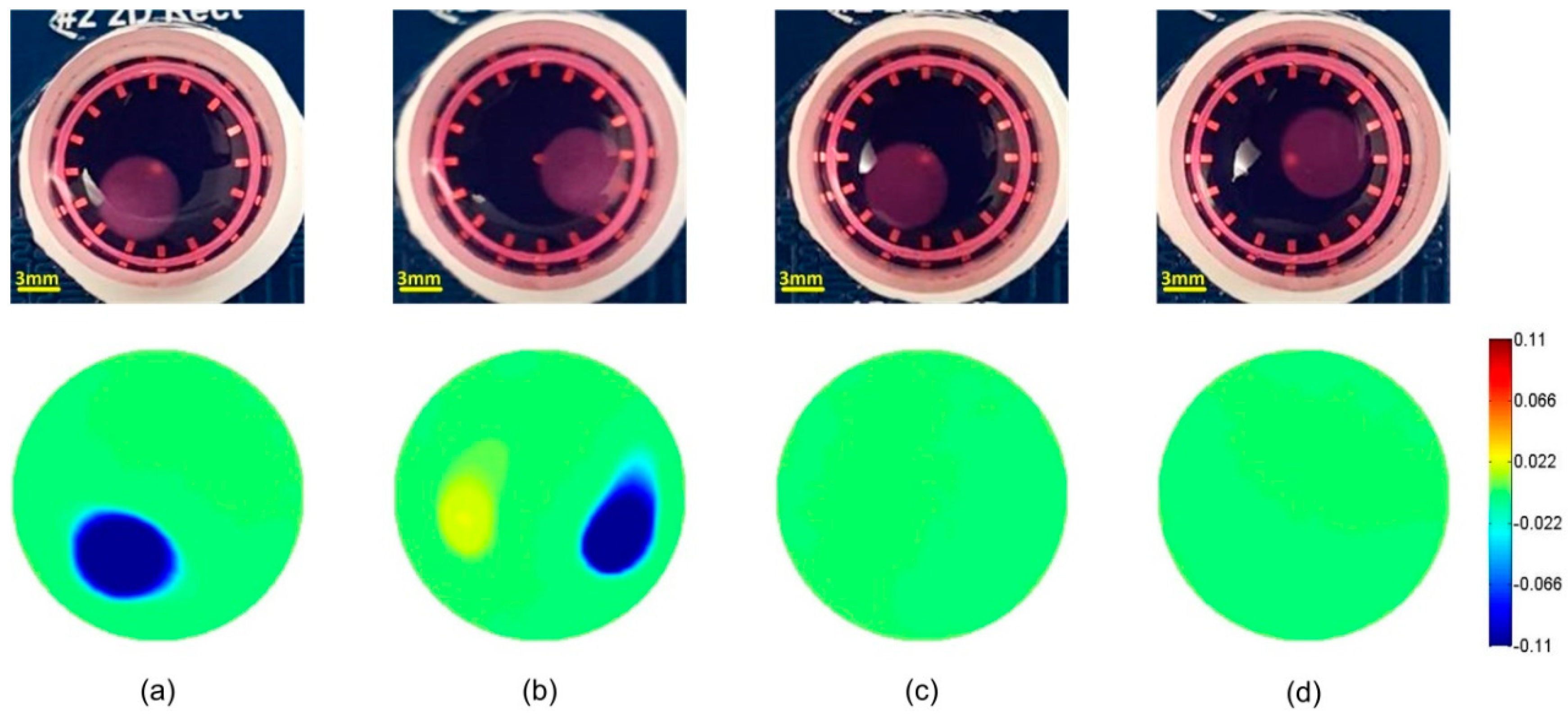
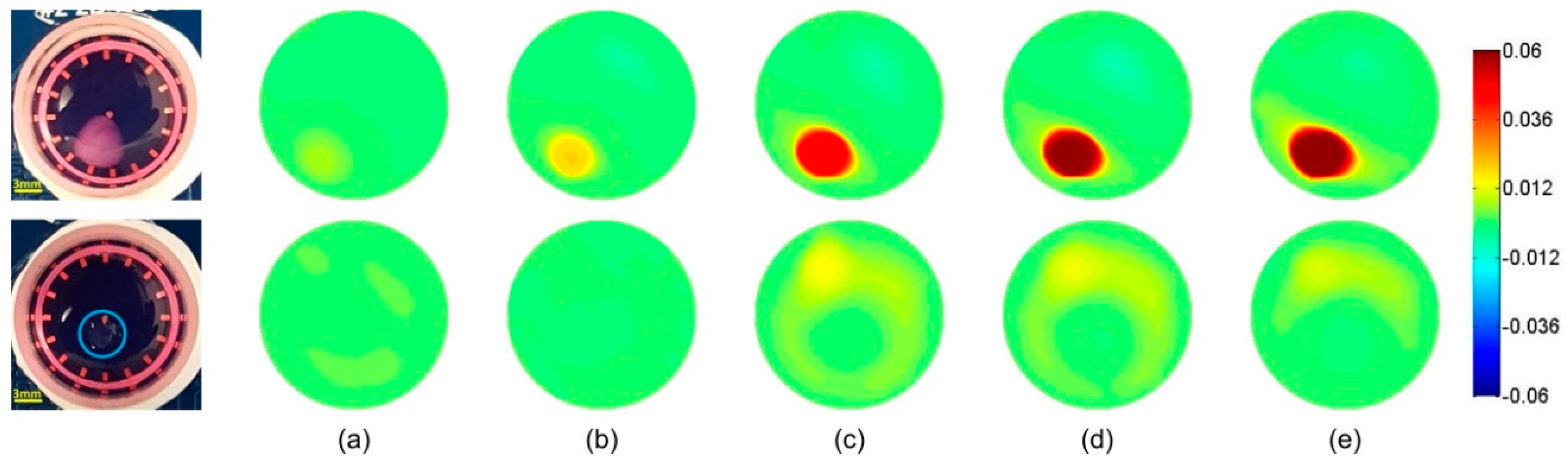
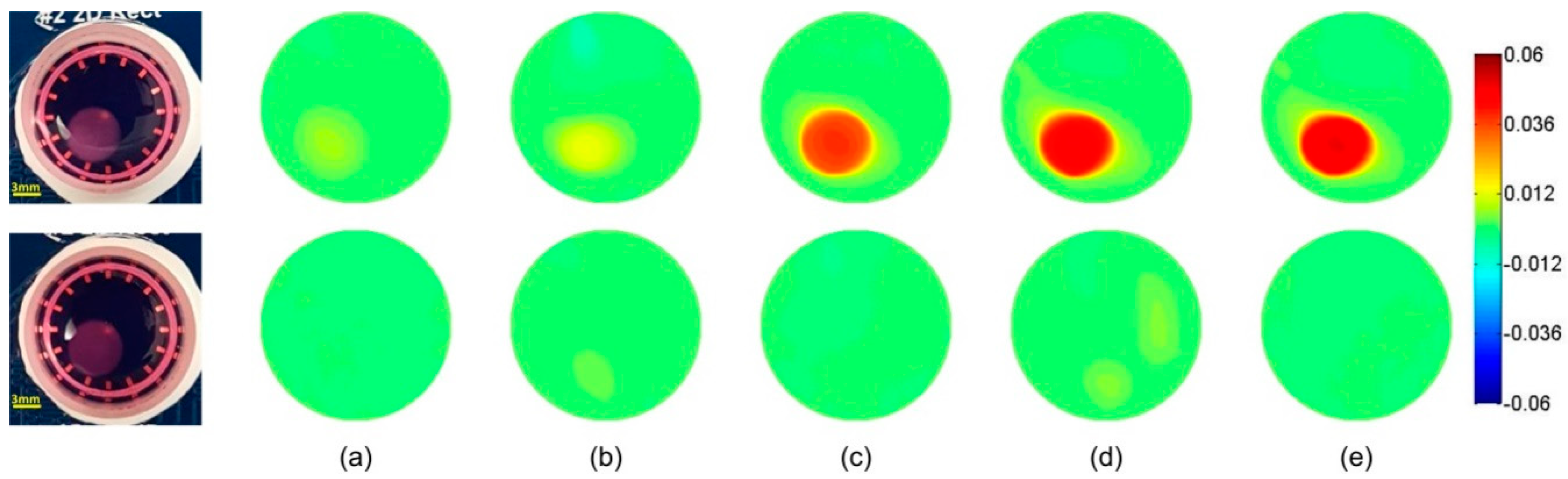
3.1. Time-Difference EIT Image Reconstruction
3.2. Frequency-Difference EIT Image Reconstruction
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Langer, R.; Vacanti, J. Tissue engineering. Science 1993, 260, 920–926. [Google Scholar] [CrossRef] [PubMed]
- Shafiee, A.; Atala, A. Tissue engineering: Toward a new era of medicine. Annu. Rev. Med. 2017, 68, 29–40. [Google Scholar] [CrossRef] [PubMed]
- Marlina, S.; Shu, M.-H.; AbuBakar, S.; Zandi, K. Development of a Real-Time Cell Analysing (RTCA) method as a fast and accurate screen for the selection of chikungunya virus replication inhibitors. Parasites Vectors 2015, 8, 579. [Google Scholar] [CrossRef] [PubMed]
- Pethig, R.; Kell, D.B. The passive electrical properties of biological systems: Their significance in physiology, biophysics and biotechnology. Phys. Med. Biol. 1987, 32, 933. [Google Scholar] [CrossRef] [PubMed]
- Ducommun, P.; Kadouri, A.; Von Stockar, U.; Marison, I. On-line determination of animal cell concentration in two industrial high-density culture processes by dielectric spectroscopy. Biotechnol. Bioeng. 2002, 77, 316–323. [Google Scholar] [CrossRef] [PubMed]
- Carvell, J.P.; Dowd, J.E. On-line measurements and control of viable cell density in cell culture manufacturing processes using radio-frequency impedance. Cytotechnology 2006, 50, 35–48. [Google Scholar] [CrossRef] [PubMed]
- Justice, C.; Brix, A.; Freimark, D.; Kraume, M.; Pfromm, P.; Eichenmueller, B.; Czermak, P. Process control in cell culture technology using dielectric spectroscopy. Biotechnol. Adv. 2011, 29, 391–401. [Google Scholar] [CrossRef] [PubMed]
- Heileman, K.; Daoud, J.; Tabrizian, M. Dielectric spectroscopy as a viable biosensing tool for cell and tissue characterization and analysis. Biosens. Bioelectron. 2013, 49, 348–359. [Google Scholar] [CrossRef] [PubMed]
- Hildebrandt, C.; Büth, H.; Cho, S.; Thielecke, H. Detection of the osteogenic differentiation of mesenchymal stem cells in 2D and 3D cultures by electrochemical impedance spectroscopy. J. Biotechnol. 2010, 148, 83–90. [Google Scholar] [CrossRef] [PubMed]
- Canali, C.; Mazzoni, C.; Larsen, L.B.; Heiskanen, A.; Martinsen, Ø.; Wolff, A.; Dufva, M.; Emnéus, J. An impedance method for spatial sensing of 3D cell constructs–towards applications in tissue engineering. Analyst 2015, 140, 6079–6088. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.-M.; Han, N.; Lee, R.; Choi, I.-H.; Park, Y.-B.; Shin, J.-S.; Yoo, K.-H. Real-time monitoring of 3D cell culture using a 3D capacitance biosensor. Biosens. Bioelectron. 2016, 77, 56–61. [Google Scholar] [CrossRef] [PubMed]
- Jamal, D.; Koji, A.; Lawrence, R.; Maryam, T. Dielectric spectroscopy for non-invasive monitoring of epithelial cell differentiation within three-dimensional scaffolds. Phys. Med. Biol. 2012, 57, 5097. [Google Scholar]
- Harikumar, R.; Prabu, R.; Raghavan, S. Electrical Impedance Tomography (EIT) and Its Medical Applications: A Review. Int. J. Soft Comput. Eng. 2013, 3, 2231–2307. [Google Scholar]
- Brown, B.; Seagar, A. The Sheffield data collection system. Clin. Phys. Physiol. Meas. 1987, 8, 91. [Google Scholar] [CrossRef] [PubMed]
- Eyuboglu, B.; Brown, B. Methods of cardiac gating applied potential tomography. Clin. Phys. Physiol. Meas. 1988, 9, 43. [Google Scholar] [CrossRef] [PubMed]
- Yerworth, R.J.; Bayford, R.; Cusick, G.; Conway, M.; Holder, D.S. Design and performance of the UCLH Mark 1b 64 channel electrical impedance tomography (EIT) system, optimized for imaging brain function. Physiol. Meas. 2002, 23, 149. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Oh, T.I.; Woo, E.J.; Holder, D. Multi-frequency EIT system with radially symmetric architecture: KHU Mark1. Physiol. Meas. 2007, 28, S183. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.M.; Oh, T.I.; Woo, E.J.; Kim, S.W.; Seo, J.K. Time- and frequency-difference imaging using KHU Mark1 EIT system. In Proceedings of the 13th International Conference on Electrical Bioimpedance and the 8th Conference on Electrical Impedance Tomography 2007, ICEBI 2007, Graz, Austria, 29 August–2 September 2007; Springer Verlag: Graz, Austria; pp. 340–343.
- Kang, S.I.; Khambampati, A.K.; Jeon, M.H.; Kim, B.S.; Kim, K.Y. A sub-domain based regularization method with prior information for human thorax imaging using electrical impedance tomography. Meas. Sci. Technol. 2016, 27, 025703. [Google Scholar] [CrossRef]
- Aristovich, K.Y.; Packham, B.C.; Koo, H.; dos Santos, G.S.; McEvoy, A.; Holder, D.S. Imaging fast electrical activity in the brain with electrical impedance tomography. NeuroImage 2016, 124, 204–213. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.; Ts, M.-E.; Seo, J.K.; Woo, E.J. Breast EIT using a new projected image reconstruction method with multi-frequency measurements. Physiol. Meas. 2012, 33, 751. [Google Scholar] [CrossRef] [PubMed]
- Cherepenin, V.; Karpov, A.; Korjenevsky, A.; Kornienko, V.; Mazaletskaya, A.; Mazourov, D.; Meister, D. A 3D electrical impedance tomography (EIT) system for breast cancer detection. Physiol. Meas. 2001, 22, 9. [Google Scholar] [CrossRef] [PubMed]
- Linderholm, P.; Braschler, T.; Vannod, J.; Barrandon, Y.; Brouard, M.; Renaud, P. Two-dimensional impedance imaging of cell migration and epithelial stratification. Lab Chip 2006, 6, 1155–1162. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.; Tsuda, S.; Zauner, K.-P.; Morgan, H. On-chip electrical impedance tomography for imaging biological cells. Biosens. Bioelectron. 2010, 25, 1109–1115. [Google Scholar] [CrossRef] [PubMed]
- Meir, A.; Rubinsky, B. Electrical impedance tomographic imaging of a single cell electroporation. Biomed. Microdevices 2014, 16, 427–437. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Wu, H.; Jia, J. Simulation study of scaffold 3D cell culture imaging using a miniature planar EIT sensor. In Proceedings of the 2017 IEEE International Conference on Imaging Systems and Techniques (IST), Beijing, China, 18–20 October 2017; pp. 1–6. [Google Scholar]
- Yin, X.; Wu, H.; Jia, J.; Yang, Y. A Micro EIT Sensor for Real-time and Non-destructive 3-D Cultivated Cell Imaging. IEEE Sens. J. 2018, 1. [Google Scholar] [CrossRef]
- Liu, X.; Cui, Y.; Yao, J.; Obara, H.; Zhao, T.; Takei, M. Development of electrical impedance tomography system for cell sedimentation detection in electrode-multilayered microchannel. In Proceedings of the 2016 IEEE International Symposium on Micro-NanoMechatronics and Human Science (MHS), Singapore, Singapore, 28–30 November 2016; pp. 1–6. [Google Scholar]
- Holder, D.S. Electrical Impedance Tomography: Methods, History and Applications; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Yang, Y.; Wu, H.; Jia, J.; Bagnaninchi, P. Scaffold-based 3-D Cell Culture Imaging Using a Miniature Electrical Impedance Tomography Sensor. Meas. Sci. Technol. under review.
- Dai, Q.; Sha, W. The physics of compressive sensing and the gradient-based recovery algorithms. arXiv, 2009arXiv:0906.1487.
- Yang, Y.; Jia, J. A multi-frequency electrical impedance tomography system for real-time 2D and 3D imaging. Rev. Sci. Instrum. 2017, 88, 085110. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Jia, J.; Smith, S.; Jamil, N.; Gamal, W.; Bagnaninchi, P.-O. A miniature electrical impedance tomography sensor and 3-D image reconstruction for cell imaging. IEEE Sens. J. 2017, 17, 514–523. [Google Scholar] [CrossRef]
- Schwan, H. Electrical properties of tissues and cell suspensions: Mechanisms and models. In Proceedings of the 16th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Engineering Advances: New Opportunities for Biomedical Engineers, Baltimore, MD, USA, 3–6 November 1994; Volume 1, pp. A70–A71. [Google Scholar]
- Xu, Y.; Xie, X.; Duan, Y.; Wang, L.; Cheng, Z.; Cheng, J. A review of impedance measurements of whole cells. Biosens. Bioelectron. 2016, 77, 824–836. [Google Scholar] [CrossRef] [PubMed]
- Solchaga, L.A.; Tognana, E.; Penick, K.; Baskaran, H.; Goldberg, V.M.; Caplan, A.I.; Welter, J.F. A rapid seeding technique for the assembly of large cell/scaffold composite constructs. Tissue Eng. 2006, 12, 1851–1863. [Google Scholar] [CrossRef] [PubMed]
- Qiao, G.; Duan, W.; Chatwin, C.; Sinclair, A.; Wang, W. Electrical properties of breast cancer cells from impedance measurement of cell suspensions. J. Phys.: Conf. Ser. 2010, 224, 012081. [Google Scholar] [CrossRef]
- Asami, K. Characterization of heterogeneous systems by dielectric spectroscopy. Prog. Polym. Sci. 2002, 27, 1617–1659. [Google Scholar] [CrossRef]
- Liu, Q.; Oh, T.I.; Wi, H.; Lee, E.J.; Seo, J.K.; Woo, E.J. Design of a microscopic electrical impedance tomography system using two current injections. Physiol. Meas. 2011, 32, 1505. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.J.; Wi, H.; McEwan, A.L.; Farooq, A.; Sohal, H.; Woo, E.J.; Seo, J.K.; Oh, T.I. Design of a microscopic electrical impedance tomography system for 3D continuous non-destructive monitoring of tissue culture. Biomed. Eng. OnLine 2014, 13, 142. [Google Scholar] [CrossRef] [PubMed]
- Lehti-Polojärvi, M.; Koskela, O.; Seppänen, A.; Figueiras, E.; Hyttinen, J. Rotational electrical impedance tomography with few electrodes. In Proceedings of the 18th International Conference on Biomedical Applications of Electrical Impedance Tomography, Hanover, NH, USA, 21–24 June 2017; p. 3. [Google Scholar]
- Wang, M. Electrode models in electrical impedance tomography. J. Zhejiang Univ. Sci. A 2005, 6, 1386–1393. [Google Scholar] [CrossRef]
- McEwan, A.; Romsauerova, A.; Yerworth, R.; Horesh, L.; Bayford, R.; Holder, D. Design and calibration of a compact multi-frequency EIT system for acute stroke imaging. Physiol. Meas. 2006, 27, S199. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Zhou, W.; Yang, Y.; Jia, J.; Bagnaninchi, P. Exploring the Potential of Electrical Impedance Tomography for Tissue Engineering Applications. Materials 2018, 11, 930. https://doi.org/10.3390/ma11060930
Wu H, Zhou W, Yang Y, Jia J, Bagnaninchi P. Exploring the Potential of Electrical Impedance Tomography for Tissue Engineering Applications. Materials. 2018; 11(6):930. https://doi.org/10.3390/ma11060930
Chicago/Turabian StyleWu, Hancong, Wenli Zhou, Yunjie Yang, Jiabin Jia, and Pierre Bagnaninchi. 2018. "Exploring the Potential of Electrical Impedance Tomography for Tissue Engineering Applications" Materials 11, no. 6: 930. https://doi.org/10.3390/ma11060930
APA StyleWu, H., Zhou, W., Yang, Y., Jia, J., & Bagnaninchi, P. (2018). Exploring the Potential of Electrical Impedance Tomography for Tissue Engineering Applications. Materials, 11(6), 930. https://doi.org/10.3390/ma11060930




