Fully Ab-Initio Determination of the Thermoelectric Properties of Half-Heusler NiTiSn: Crucial Role of Interstitial Ni Defects
Abstract
1. Introduction
2. Methods
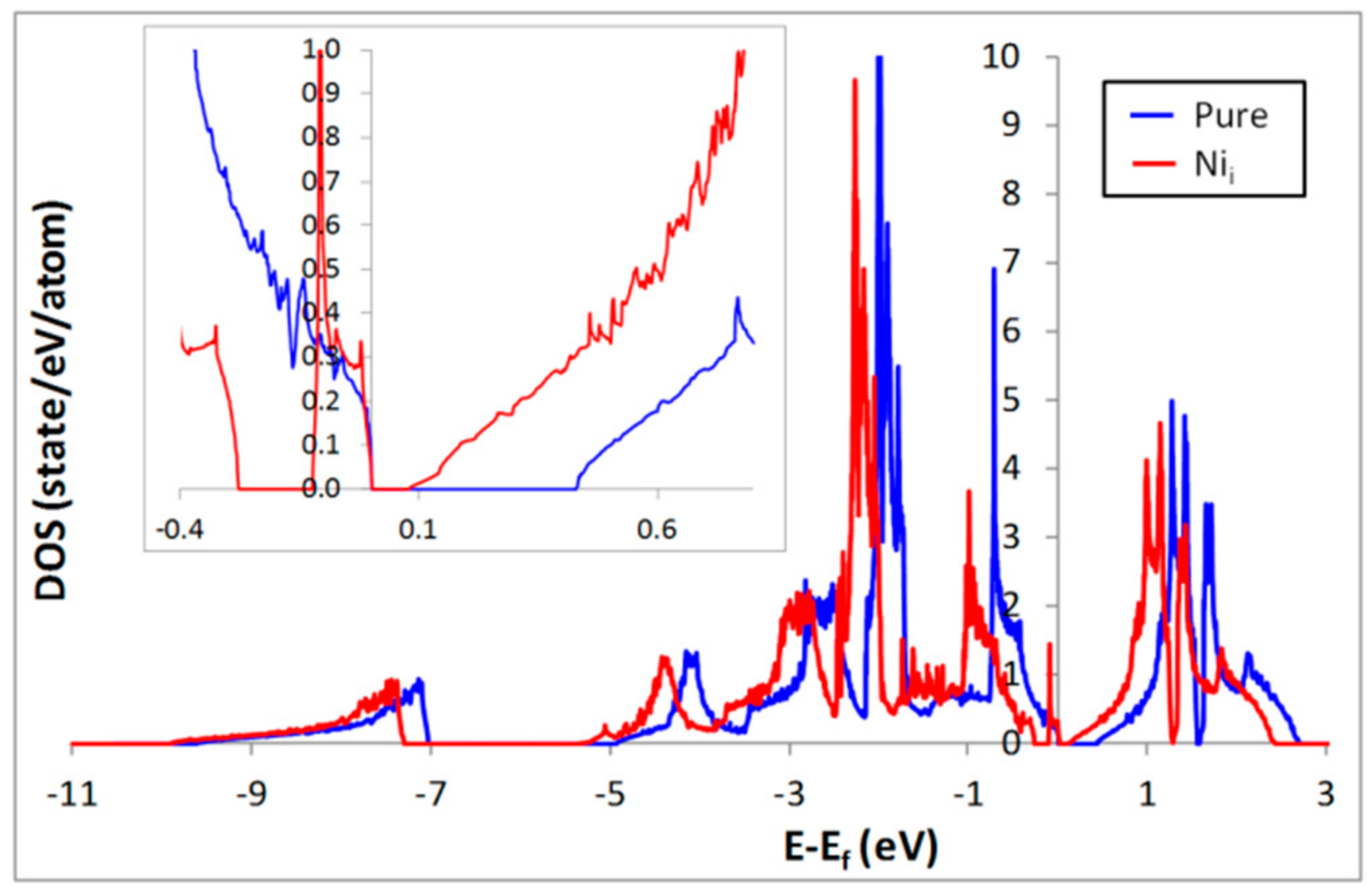
3. Influence of Interstitial Ni Defects on the Electronic Structure
4. Determination of the Energy of Formation of Defects
4.1. Case of a Non-Charged Defect
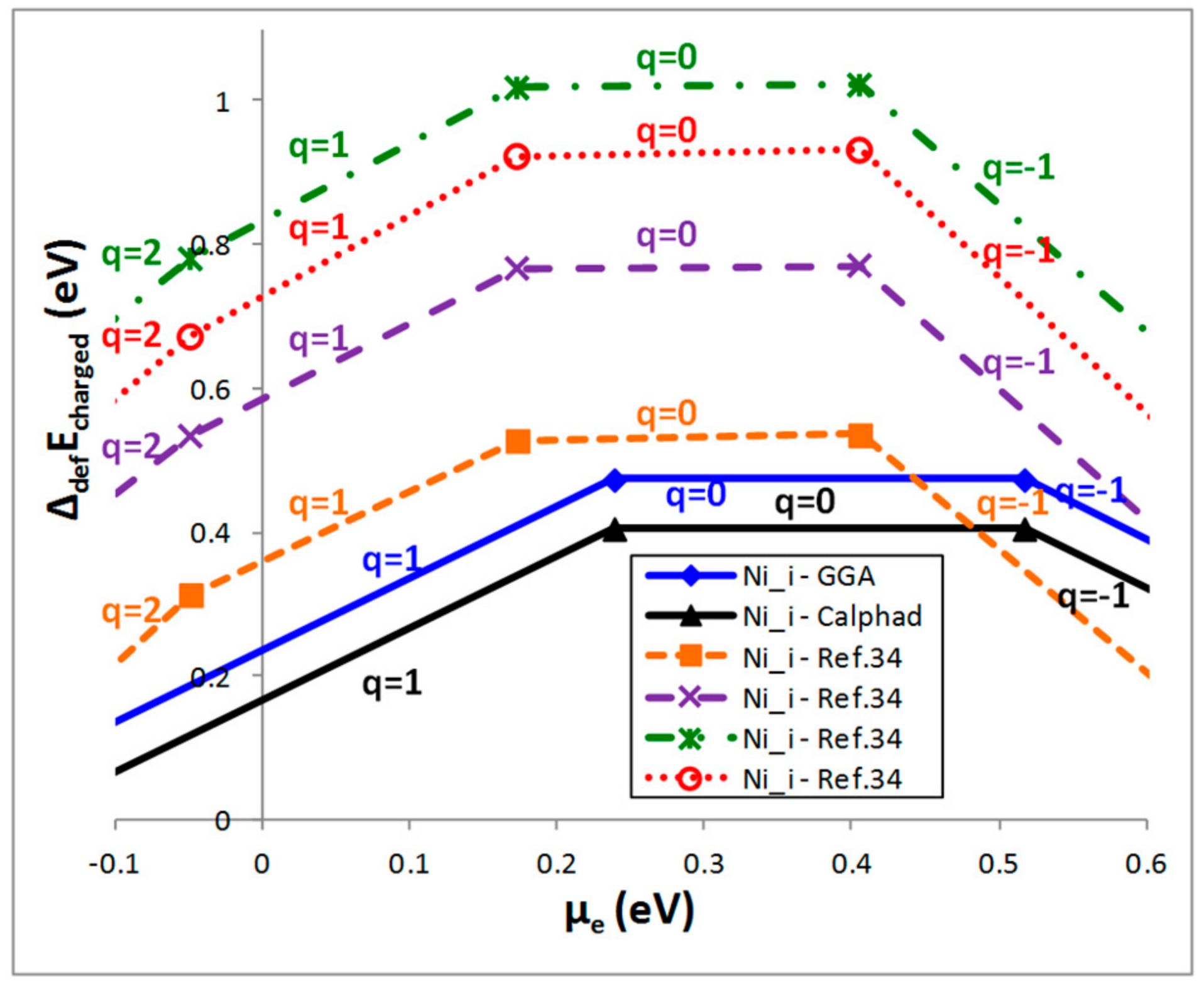
4.2. Case of a Charged Defect
5. Ab-Initio Calculation of the Thermoelectric Properties
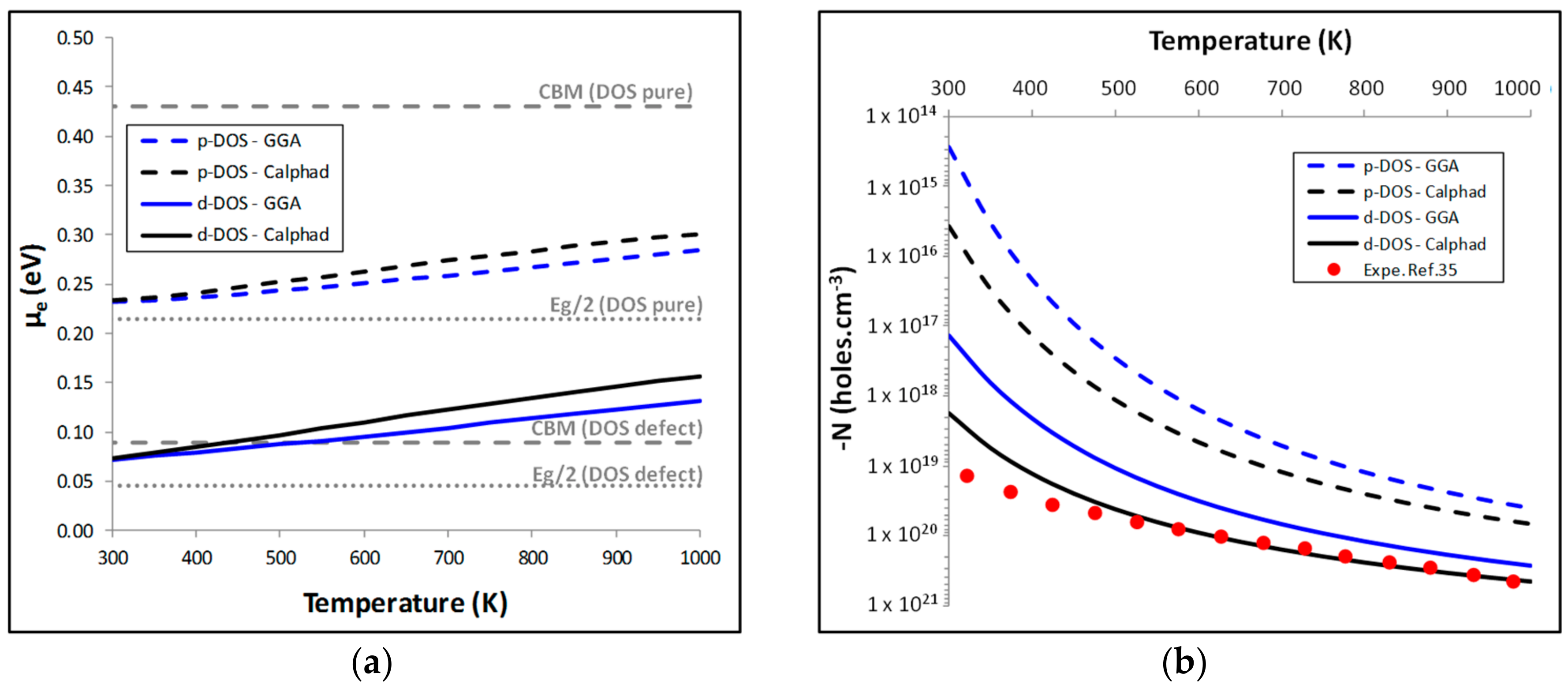
5.1. Calculation of the Carrier Concentration N
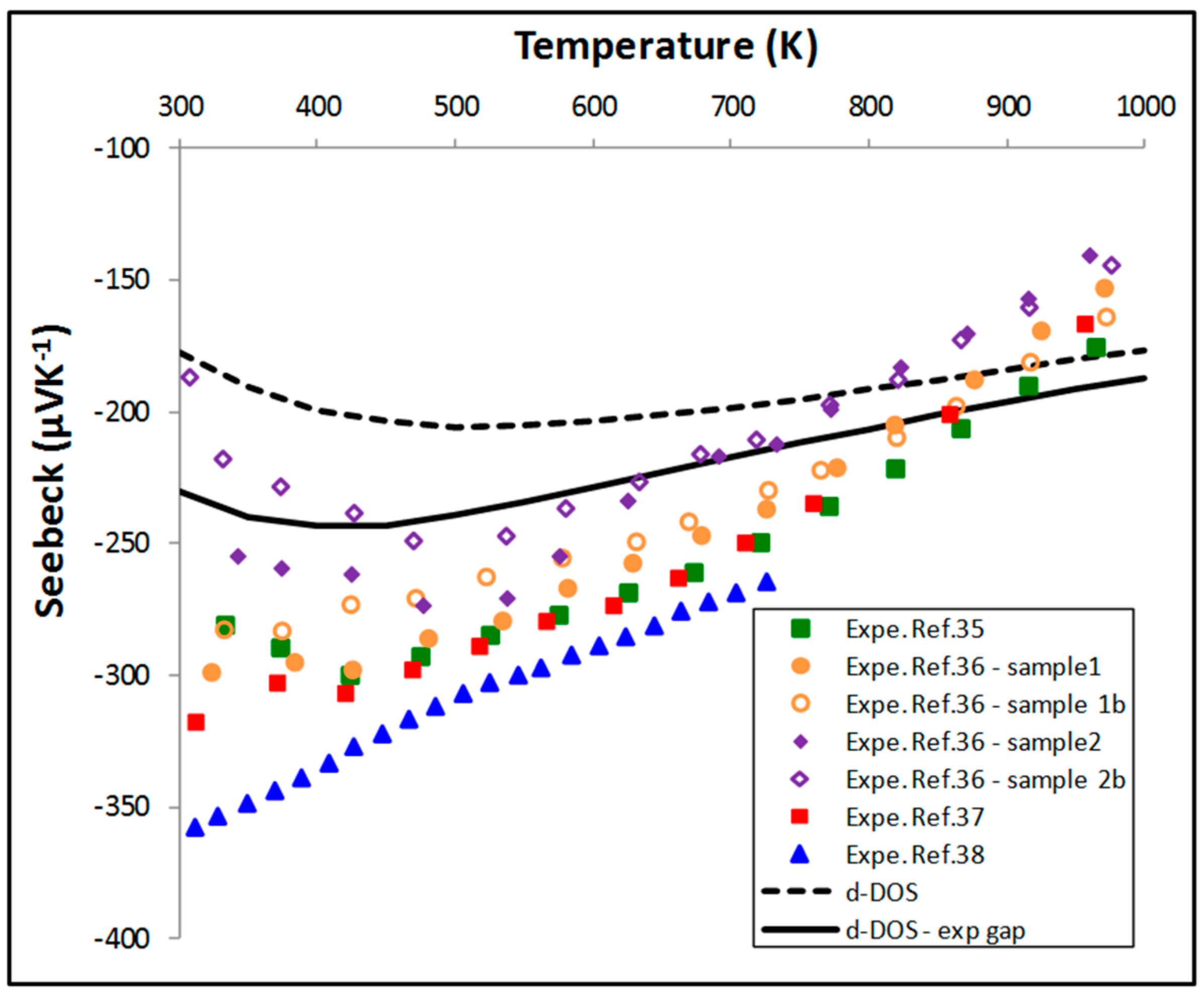
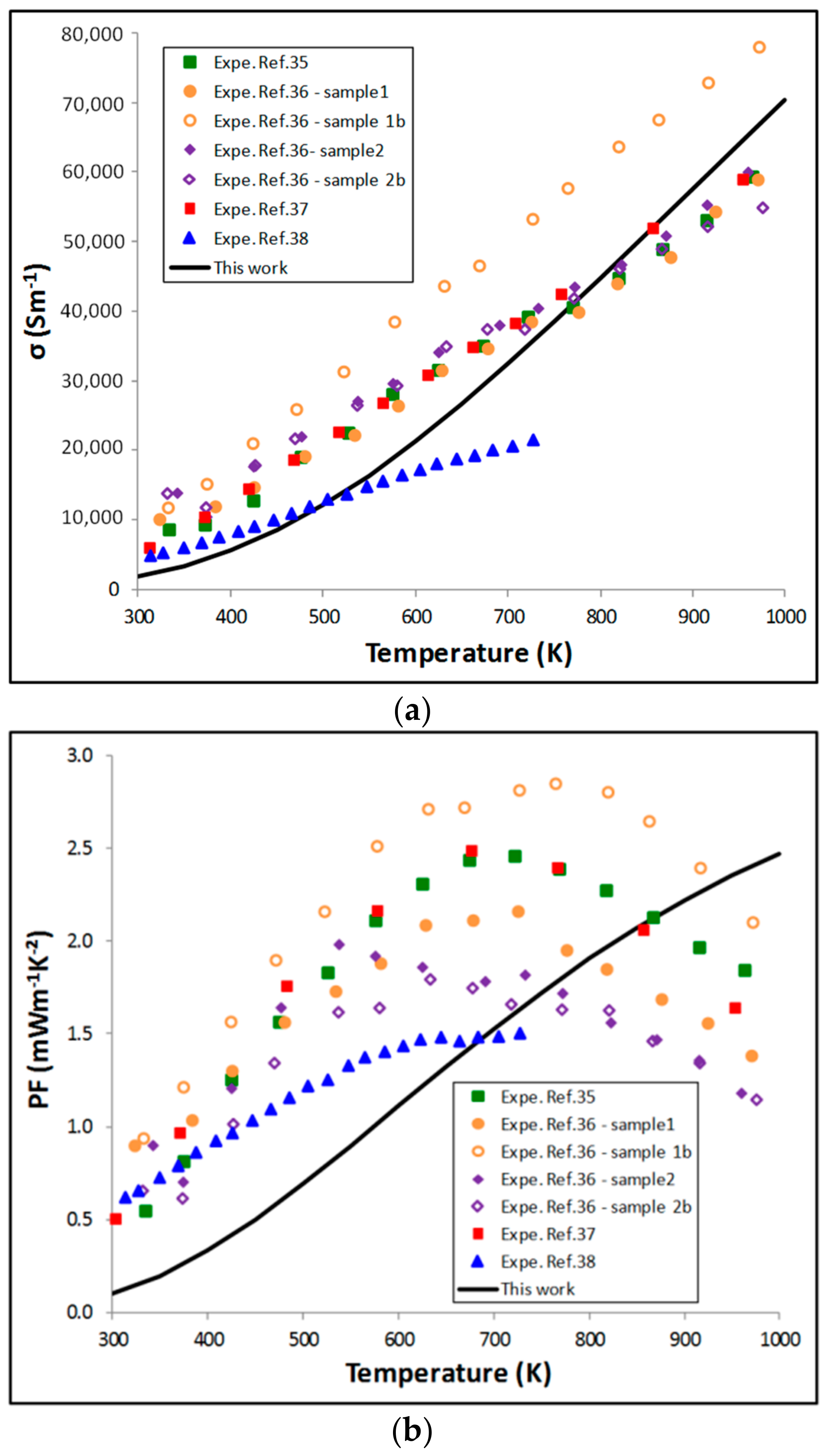
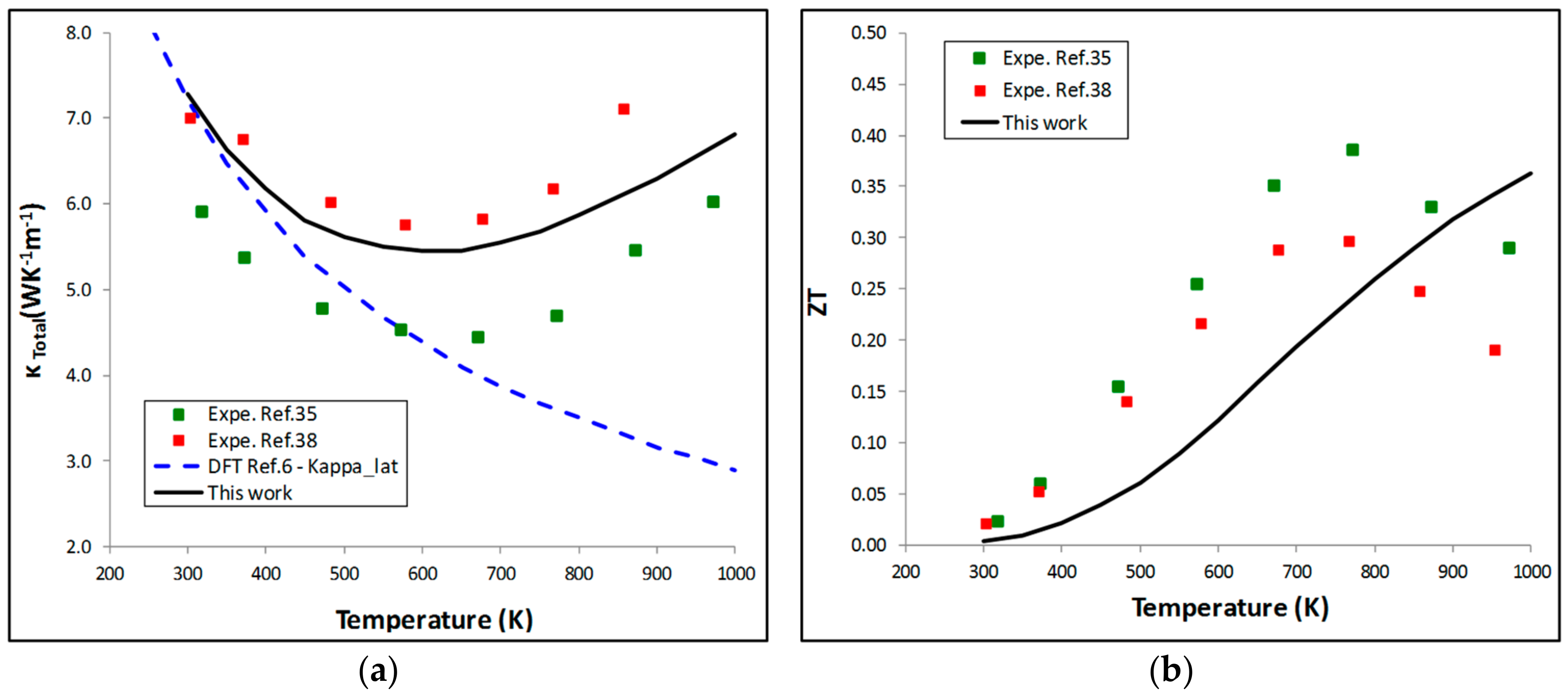
5.2. Thermoelectric Properties
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Graf, T.; Felser, C.; Parkin, S.S.P. Simple rules for the understanding of Heusler compounds. Prog. Solid State Chem. 2011, 39, 1–50. [Google Scholar] [CrossRef]
- Gelbstein, Y.; Tal, N.; Yarmek, A.; Rosenberg, Y. Thermoelectric properties of spark plasma sintered composites based on TiNiSn half-Heusler alloys. J. Mater. Res. 2011, 26, 1919–1924. [Google Scholar] [CrossRef]
- Tillard, M.; Berche, A.; Jund, P. NiTiSn by mechanical alloying: Direct formation or conversion process? Materialia 2018. submitted. [Google Scholar]
- Berche, A.; Jund, P. Oxidation of half-Heusler NiTiSn materials: Implications for thermoelectric applications. Intermeltallics 2018, 92, 62–71. [Google Scholar] [CrossRef]
- Ding, G.; Gao, G.Y.; Yao, K.L. Examining the thermal conductivity of the half-Heusler alloy TiNiSn by first-principles calculations. J. Phys. D Appl. Phys. 2015, 48, 235302. [Google Scholar] [CrossRef]
- Hermet, P.; Jund, P. Lattice thermal conductivity of NiTiSn half-Heusler thermoelectric materials from first-principles calculations. J. Alloy Compd. 2016, 688, 248–252. [Google Scholar] [CrossRef]
- Andrea, L.; Hug, G.; Chaput, L. Ab initio phonon properties of half-Heusler NiTiSn, NiZrSn and NiHfSn. J. Phys. Condens. Matter 2015, 27, 425401. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.B.; Northrup, J.E. Chemical potential dependence of defect formation energies in GaAs: Application to Ga self-diffusion. Phys. Rev. B 1991, 67, 2339–2342. [Google Scholar] [CrossRef] [PubMed]
- Colinet, C.; Jund, P.; Tedenac, J.C. NiTiSn a material of technological interest: Ab initio calculations of phase stability and defects. Intermetallics 2014, 46, 103–110. [Google Scholar] [CrossRef]
- Berche, A.; Tédenac, J.C.; Jund, P. Phase diagram and enthalpy of formation of Hf-Ni-Sn. Comput. Mater. Sci. 2016, 125, 271–277. [Google Scholar] [CrossRef]
- Gürth, M.; Grytsiv, A.; Vrestal, J.; Romaka, V.V.; Giester, G.; Bauer, E.; Rogl, P. On the constitution and thermodynamic modelling of the system Ti–Ni–Sn. RSC Adv. 2015, 112, 92270–92291. [Google Scholar] [CrossRef]
- Tang, Y.; Li, S.; Martin, L.H.J.; Reyes, E.C.; Ivas, T.; Leinenbach, C.; Anand, S.; Peters, M.; Snyder, G.F.; Battaglia, C. Impact of Ni content on the thermoelectric properties of half-Heusler TiNiSn. Energy. Environ. Sci. 2018, 11, 311–320. [Google Scholar] [CrossRef]
- Barczak, S.A.; Buckman, J.; Smith, R.I.; Baker, A.R.; Don, E.; Forbes, I.; Bos, J.W.G. Impact of Interstitial Ni on the Thermoelectric Properties of the Half-Heusler TiNiSn. Materials 2018, 11, 536. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Erratum-Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
- Madsen, G.K.H.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef]
- Chaput, L.; Tobola, J.; Pécheur, P.; Sherrer, H. Electronic structure and thermopower of Ni(Ti0.5Hf0.5)Sn and related half-Heusler phases. Phys. Rev. B 2006, 73, 045121. [Google Scholar] [CrossRef]
- Aliev, F.G.; Kozyrkov, V.V.; Moshchalkov, V.V.; Scolozdra, R.V.; Durcewski, K. Narrow band in the intermetallic compounds MNiSn (M=Ti, Zr, Hf). Phys. B Condens. Matter 1990, 80, 353–357. [Google Scholar] [CrossRef]
- Niedziolka, K.; Jund, P. Influence of the Exchange–Correlation Functional on the Electronic Properties of ZnSb as a Promising Thermoelectric Material. J. Electron. Mater. 2014, 44, 1540–1546. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Erratum: “Hybrid functionals based on a screened Coulomb potential”. J. Chem. Phys. 2006, 124, 219906. [Google Scholar] [CrossRef]
- Douglas, J.E.; Birkel, C.S.; Verma, N.; Miller, V.M.; Miao, M.S.; Stucky, G.D.; Pollock, T.M.; Seshadri, R. Phase stability and property evolution of biphasic Ti–Ni–Sn alloys for use in thermoelectric applications. J. Appl. Phys. 2014, 115, 043720. [Google Scholar] [CrossRef]
- Miyamoto, K.; Kimura, A.; Sakamoto, K.; Ye, M.; Cui, Y.; Shimada, K.; Namatame, H.; Taniguchi, M.; Fujimori, S.I.; Saitoh, Y.; et al. In-gap Electronic States Responsible for the Excellent Thermoelectric Properties of Ni-based Half-Heusler Alloys. Appl. Phys. Express 2008, 1, 081901. [Google Scholar] [CrossRef]
- Do, D.T.; Mahanti, S.D.; Pulikkoti, J.J. Electronic structure of Zr–Ni–Sn systems: Role of clustering and nanostructures in half-Heusler and Heusler limits. J. Phys. Condens. Matter 2014, 26, 275501. [Google Scholar] [CrossRef] [PubMed]
- Korzhavyi, P.A.; Ruban, A.V.; Lozovoi, A.Y.; Vekilov, Y.K.; Abrikosov, I.A.; Johansson, B. Constitutional and thermal point defects in B2NiAl. Phys. Rev. B 2000, 61, 6003–6018. [Google Scholar] [CrossRef]
- Pothin, R.; Ayral, R.M.; Berche, A.; Ziolkowski, P.; Oppitz, G.; Jund, P. Computational and experimental analysis on Te-doped ZnSb thermoelectric material. Mater. Res. Bull. 2018, 101, 90–99. [Google Scholar] [CrossRef]
- Berche, A.; Tédenac, J.C.; Fartushna, J.; Jund, P. Calphad assessment of the Ni-Sn-Ti system. Calphad 2016, 54, 67–75. [Google Scholar] [CrossRef]
- Taylor, S.E.; Bruneval, F. Understanding and correcting the spurious interactions in charged supercells. Phys. Rev. B 2011, 84, 075155. [Google Scholar] [CrossRef]
- Hermet, P.; Niedziolka, K.; Jund, P. A first-principles investigation of the thermodynamic and mechanical properties of Ni–Ti–Sn Heusler and half-Heusler materials. RSC Adv. 2013, 3, 22176. [Google Scholar] [CrossRef]
- Popovic, Z.P.; Kliche, G.; Liu, R.; Aliev, F.G. Vibrational properties of MeNiSn (Me = Ti, Zr, Hf). Solid State Commun. 1990, 74, 829–832. [Google Scholar] [CrossRef]
- Stern, R.; Dongre, B.; Madsen, G.K.H. Extrinsic doping of the half-Heusler compounds. Nanotechnology 2016, 27, 334002. [Google Scholar] [CrossRef] [PubMed]
- Muta, H.; Kanemitsu, T.; Kurosaki, K.; Yamanaka, S. High-temperature thermoelectric properties of Nb-doped MNiSn (M = Ti, Zr) half-Heusler compound. J. Alloys Compd. 2009, 469, 50–55. [Google Scholar] [CrossRef]
- Cook, A.B.; Harringa, J.L. Half-Heusler phases as prospective p-type thermoelectric materials. In Proceedings of 15th International Conference on Thermoelectrics, Pasadena, CA, USA, 26–29 March 1996; pp. 122–127. [Google Scholar]
- Katayama, T.; Kim, S.W.; Kimura, Y.; Mishima, Y. The Effects of Quaternary Additions on Thermoelectric Properties of TiNiSn-Based Half-Heusler Alloys. J. Electron. Mater. 2003, 32, 1161–1165. [Google Scholar] [CrossRef]
- Downie, R.A.; MacLaren, D.A.; Bos, J.W.G. Thermoelectric performance of multiphase XNiSn (X = Ti, Zr, Hf) half-Heusler alloys. J. Mater. Chem. A. 2014, 2, 6107–6114. [Google Scholar] [CrossRef]
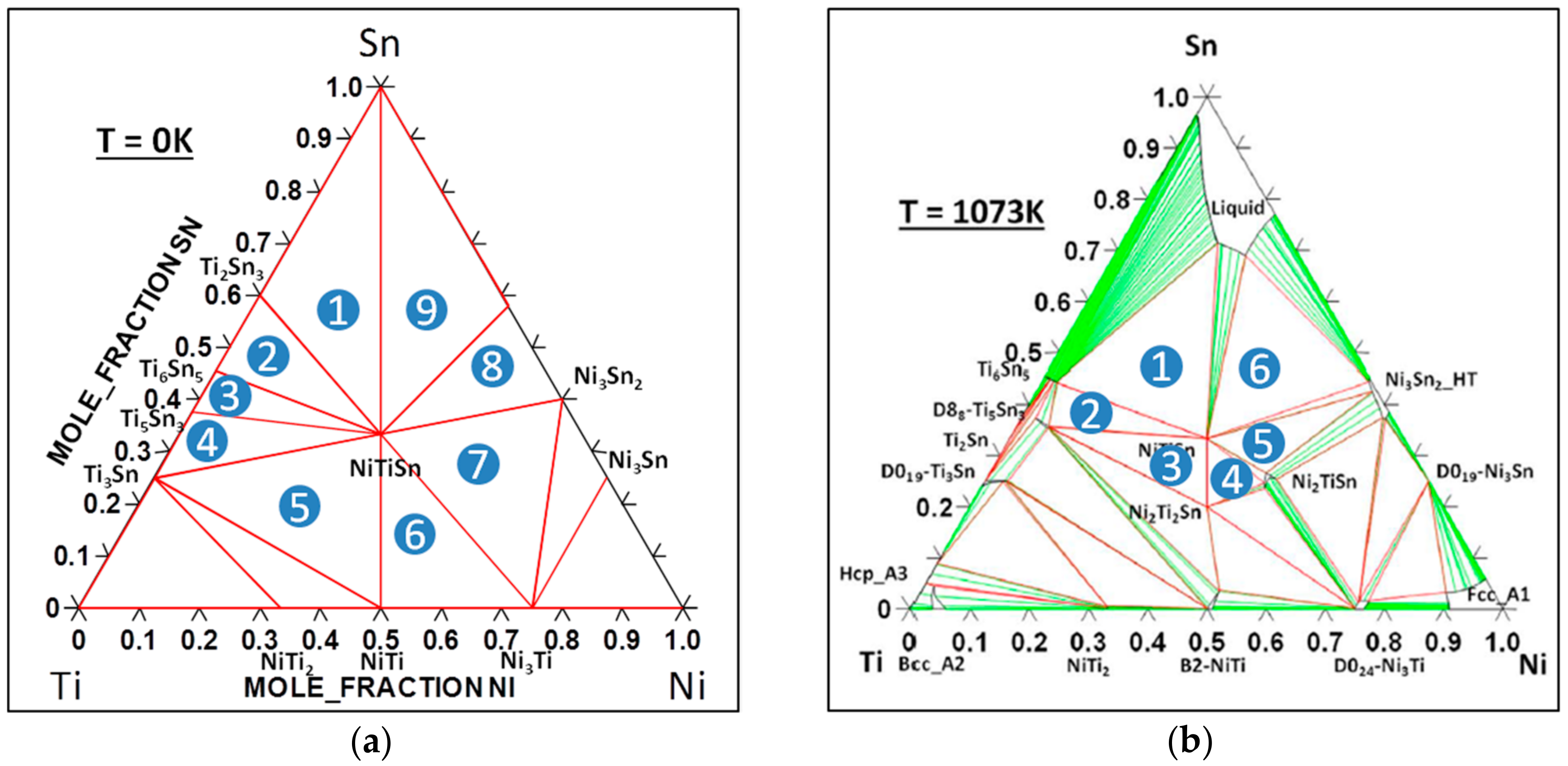
| Phase Diagram | ΔdefEs (eV) | ΔdefEμ (eV) Calculated for Each 3-Phase Region (See Figure 2) | ΔdefEmulti (eV) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||
| GGA | 0.802 | 1.053 | 1.142 | 1.079 | 1.037 | 0.860 | 0.729 | 0.473 | 0.659 | 0.847 | 0.473 |
| Calphad | 1.172 | 1.036 | 0.984 | 0.405 | 0.405 | 0.753 | - | - | - | 0.405 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berche, A.; Jund, P. Fully Ab-Initio Determination of the Thermoelectric Properties of Half-Heusler NiTiSn: Crucial Role of Interstitial Ni Defects. Materials 2018, 11, 868. https://doi.org/10.3390/ma11060868
Berche A, Jund P. Fully Ab-Initio Determination of the Thermoelectric Properties of Half-Heusler NiTiSn: Crucial Role of Interstitial Ni Defects. Materials. 2018; 11(6):868. https://doi.org/10.3390/ma11060868
Chicago/Turabian StyleBerche, Alexandre, and Philippe Jund. 2018. "Fully Ab-Initio Determination of the Thermoelectric Properties of Half-Heusler NiTiSn: Crucial Role of Interstitial Ni Defects" Materials 11, no. 6: 868. https://doi.org/10.3390/ma11060868
APA StyleBerche, A., & Jund, P. (2018). Fully Ab-Initio Determination of the Thermoelectric Properties of Half-Heusler NiTiSn: Crucial Role of Interstitial Ni Defects. Materials, 11(6), 868. https://doi.org/10.3390/ma11060868





