Pore Structure Characterization of Sodium Hydroxide Activated Slag Using Mercury Intrusion Porosimetry, Nitrogen Adsorption, and Image Analysis
Abstract
1. Introduction
2. Materials and Methods
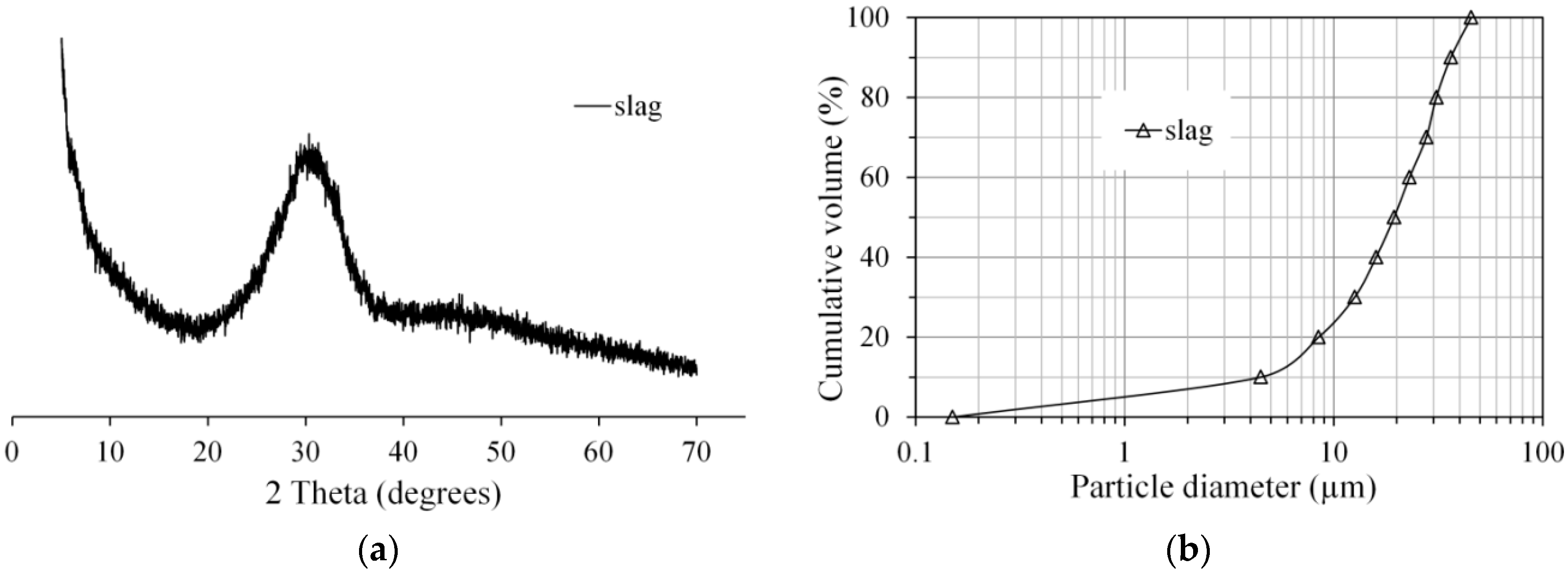
2.1. Materials and Mixtures
2.2. Methods
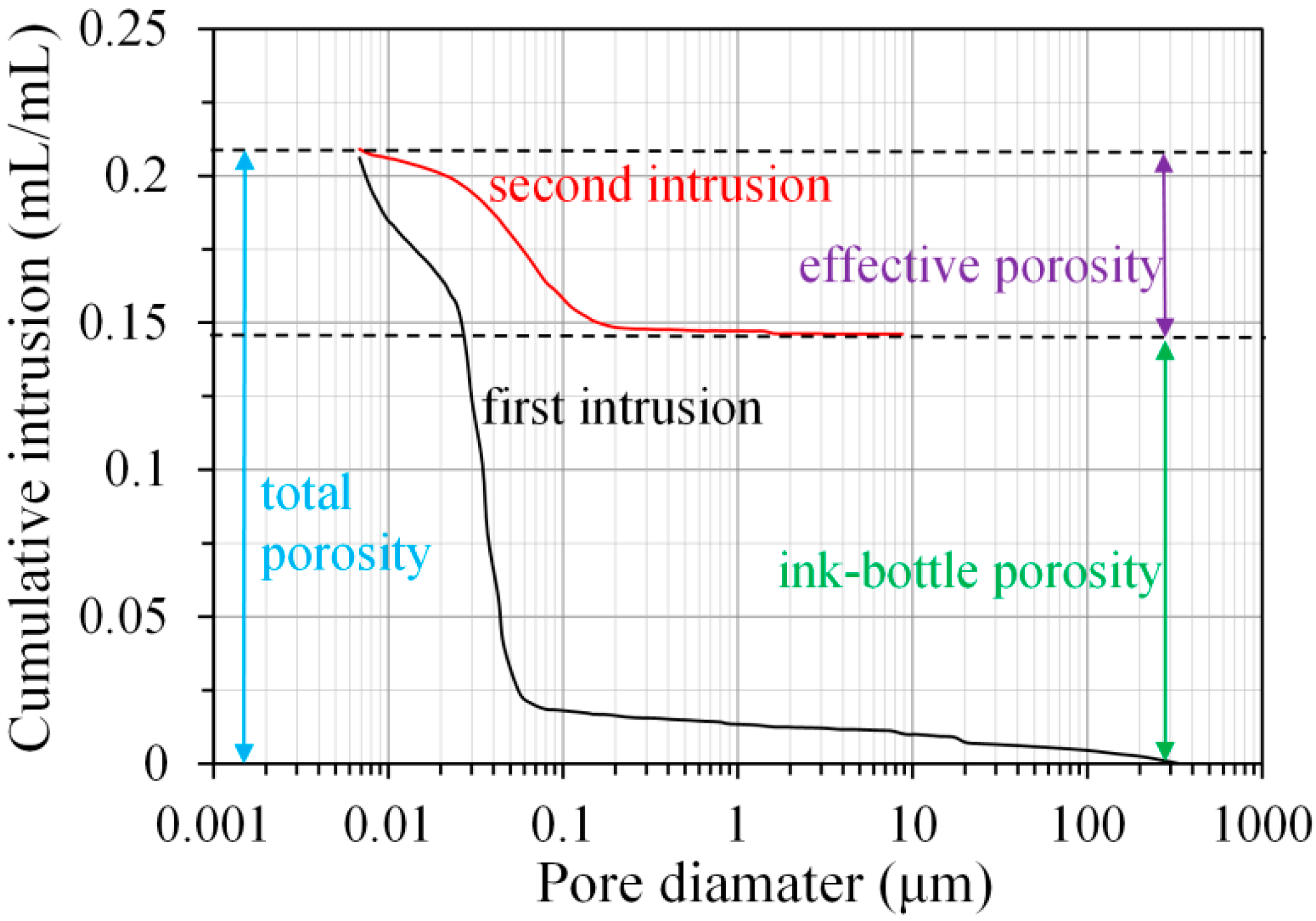
2.2.1. MIP
2.2.2. N2 Adsorption
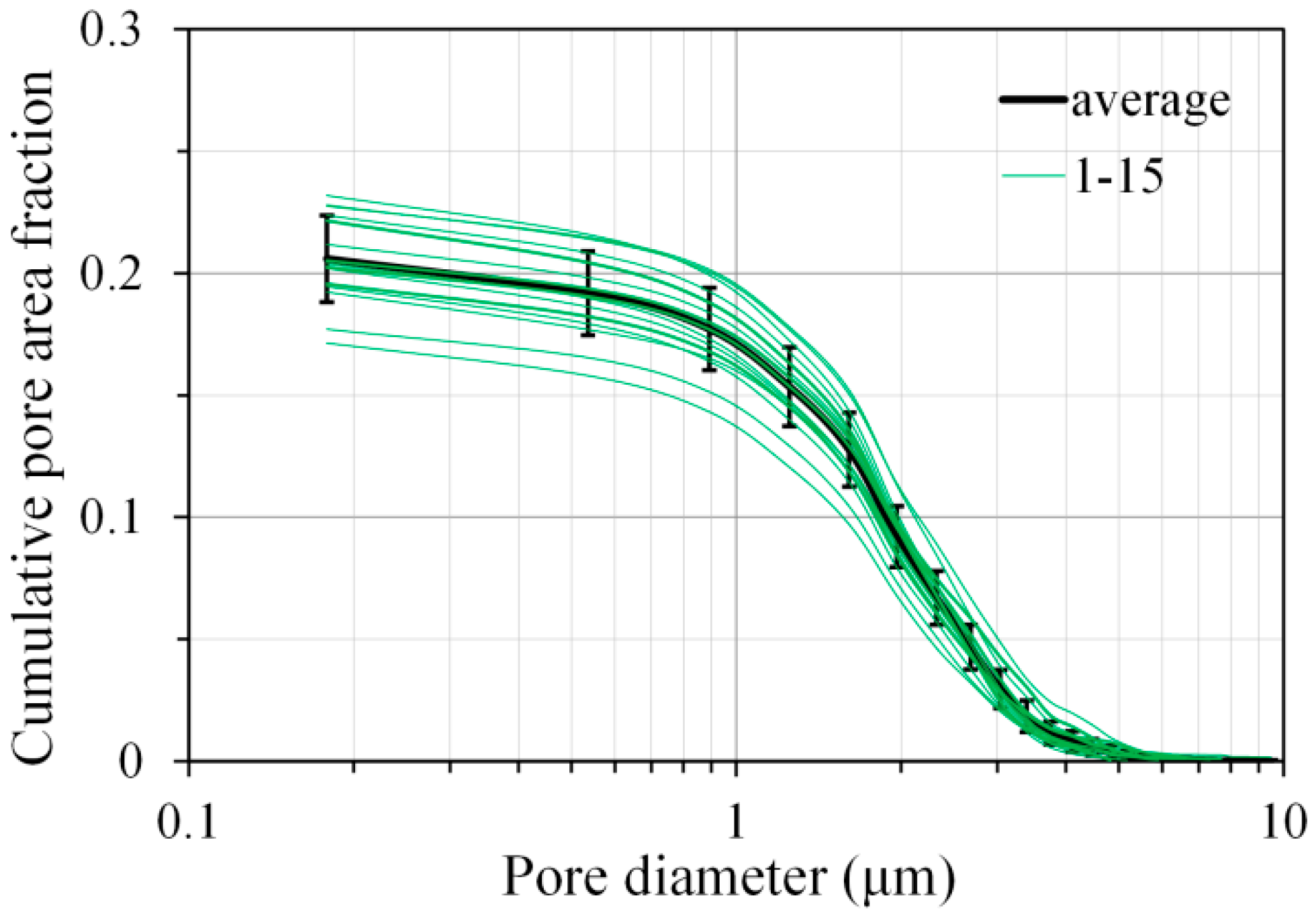
2.2.3. SEM-Image Analysis
2.2.4. Solid Phase Growth
3. Results
3.1. Morphology of Hardened Sodium Hydroxide Activated Slag Samples
3.2. Degree of Reaction of Slag
3.3. Pore Structure of Sodium Hydroxide Activated Slag Pastes Determined by MIP
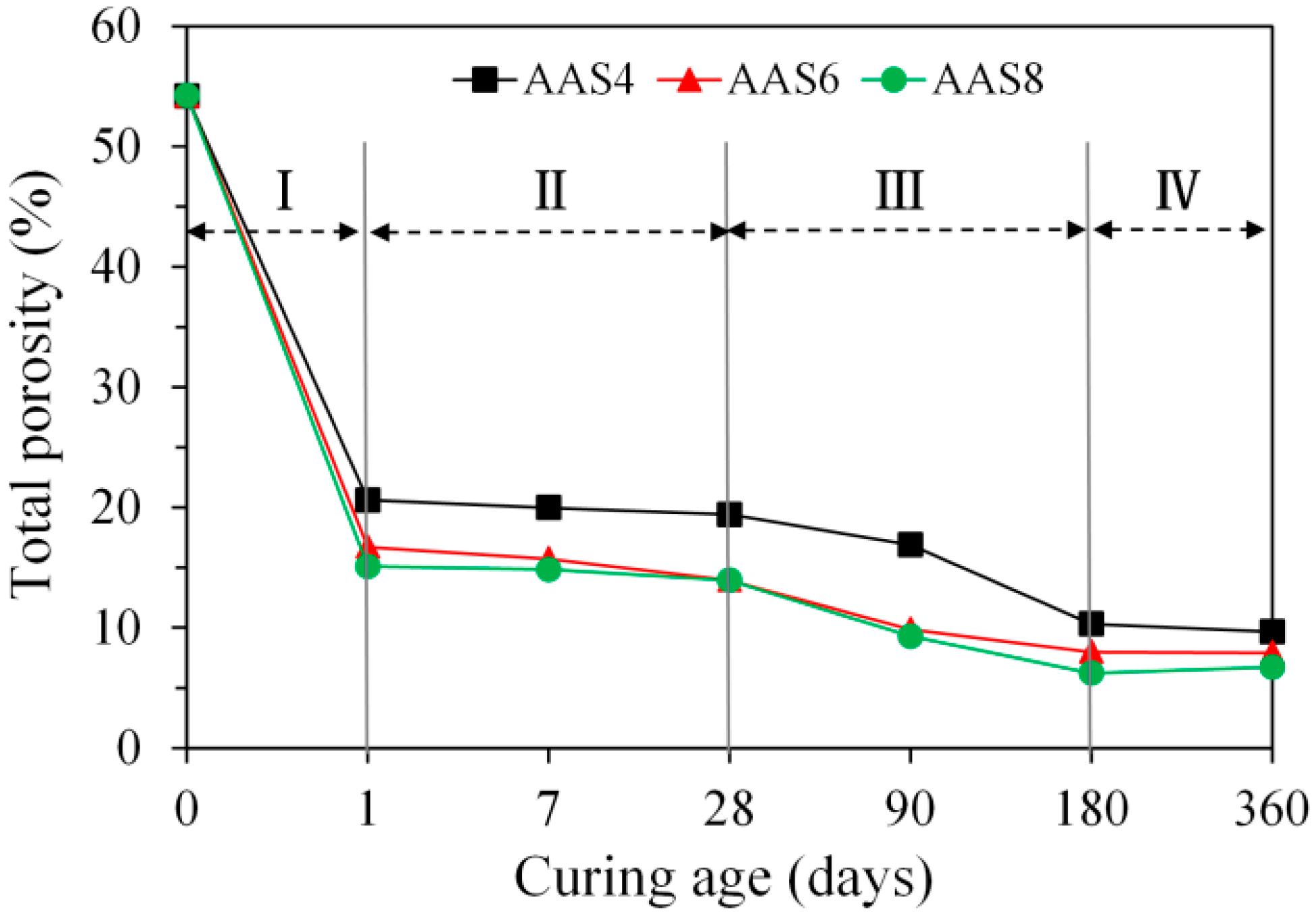
3.3.1. Total Porosity Derived from MIP
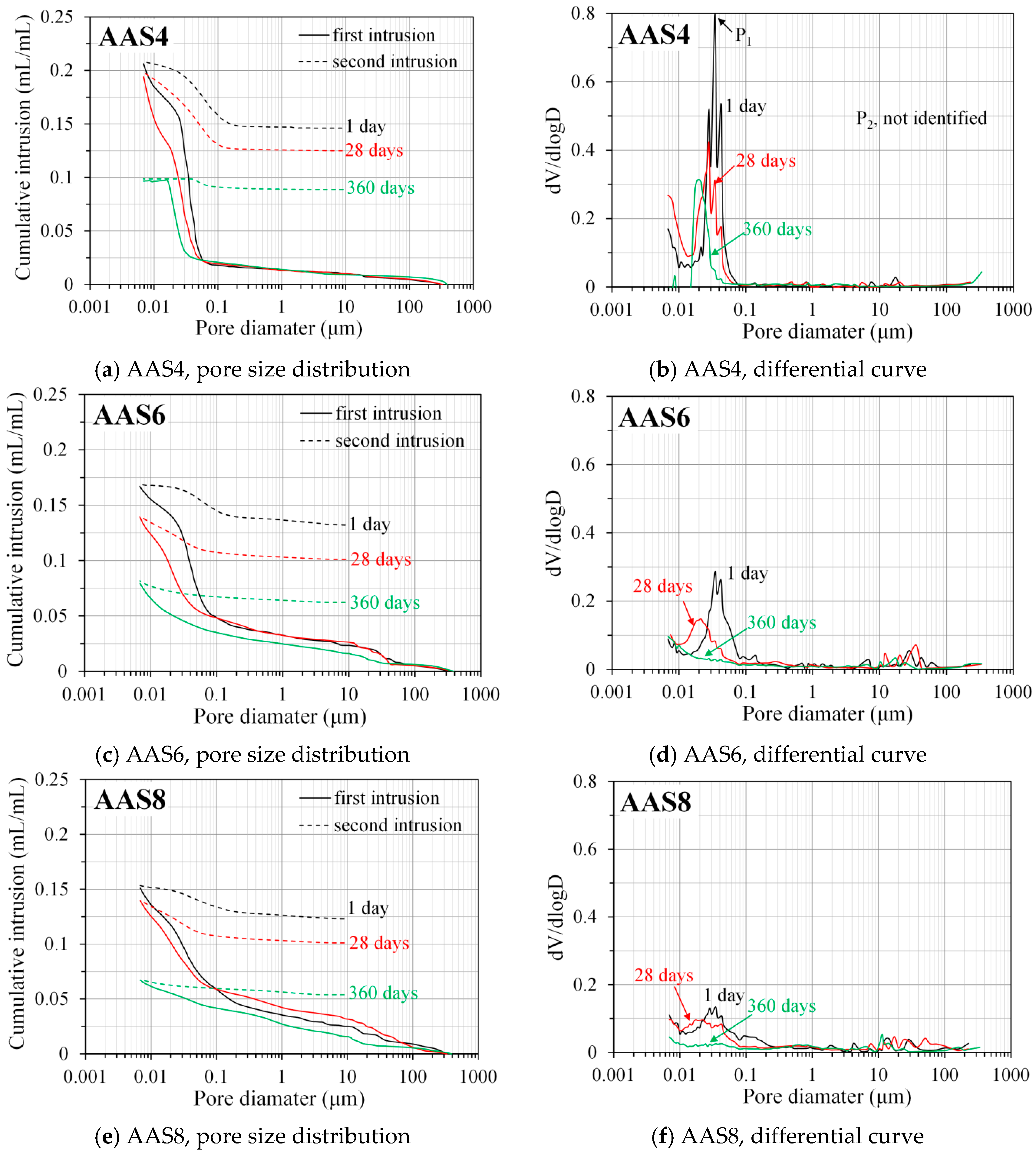
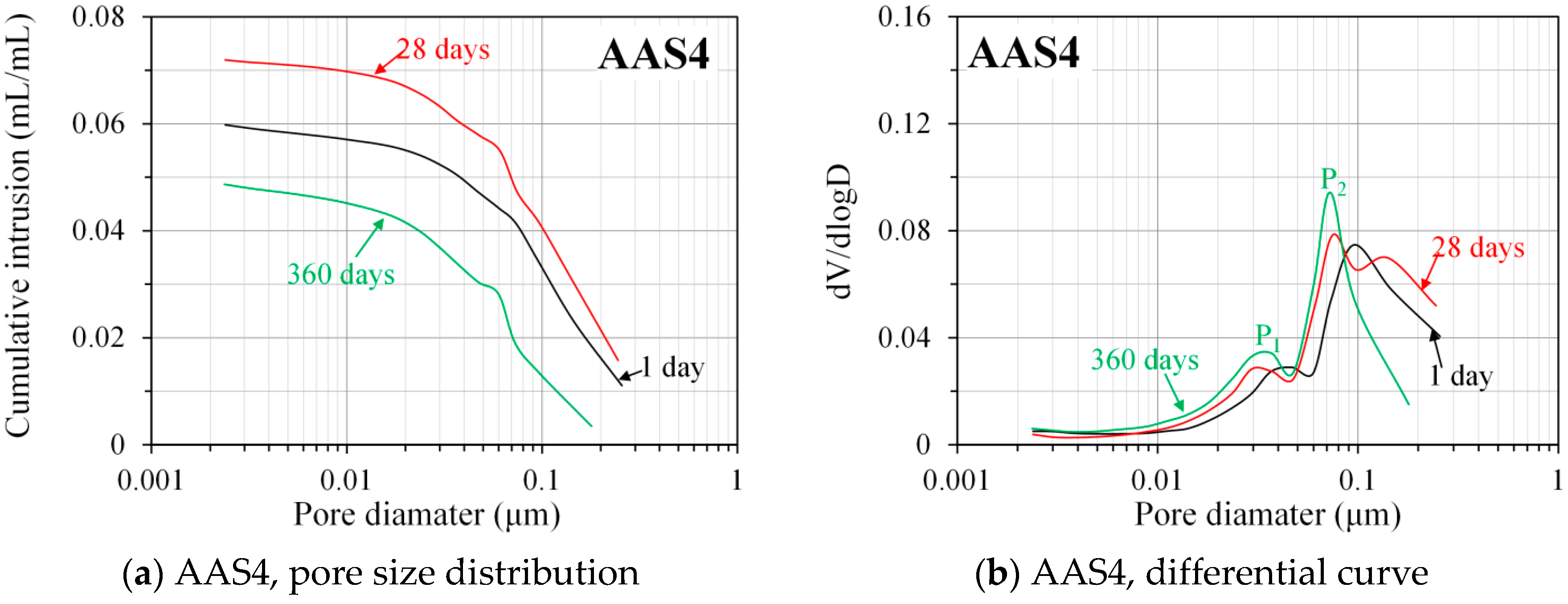
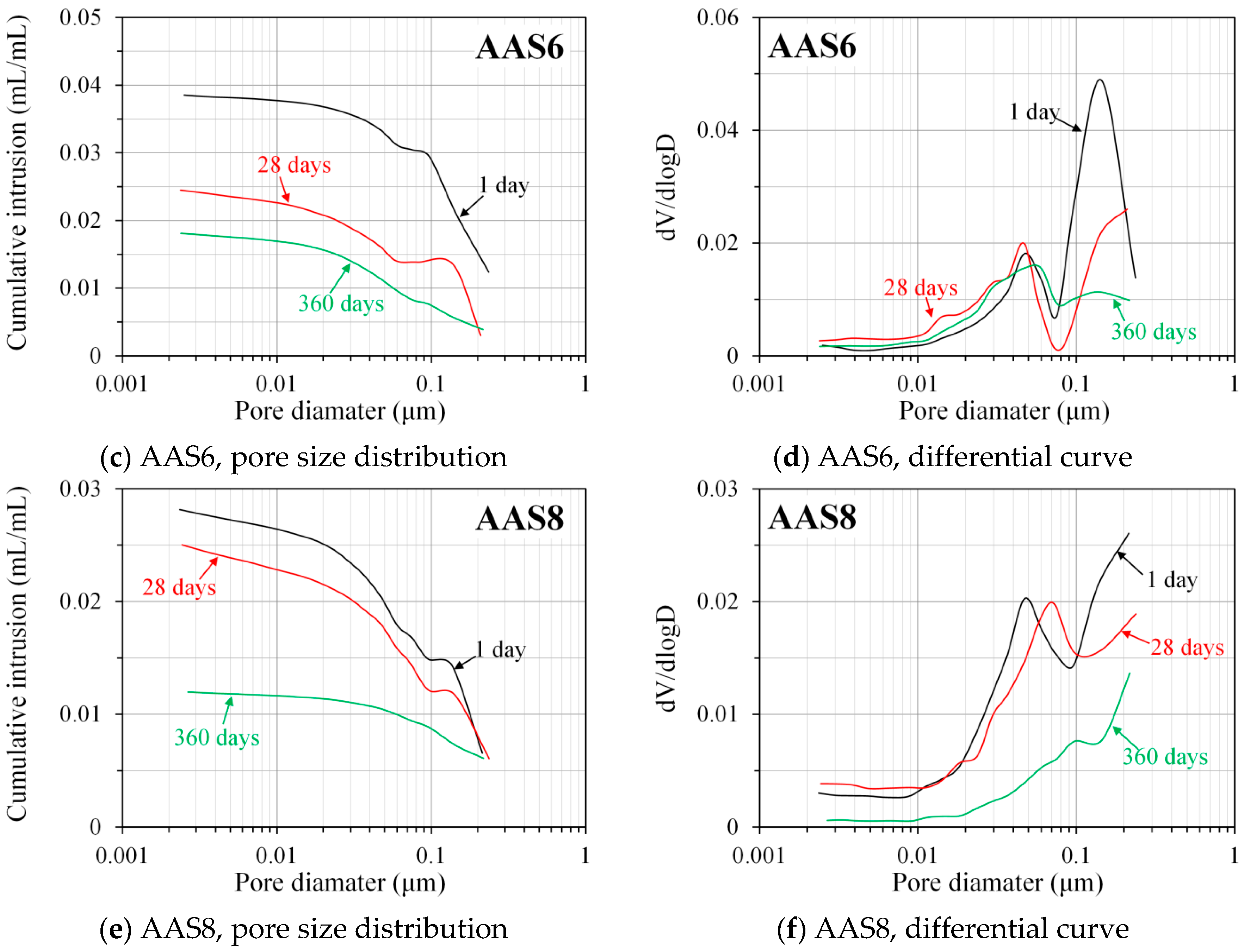
3.3.2. Pore Size Distribution Derived from MIP
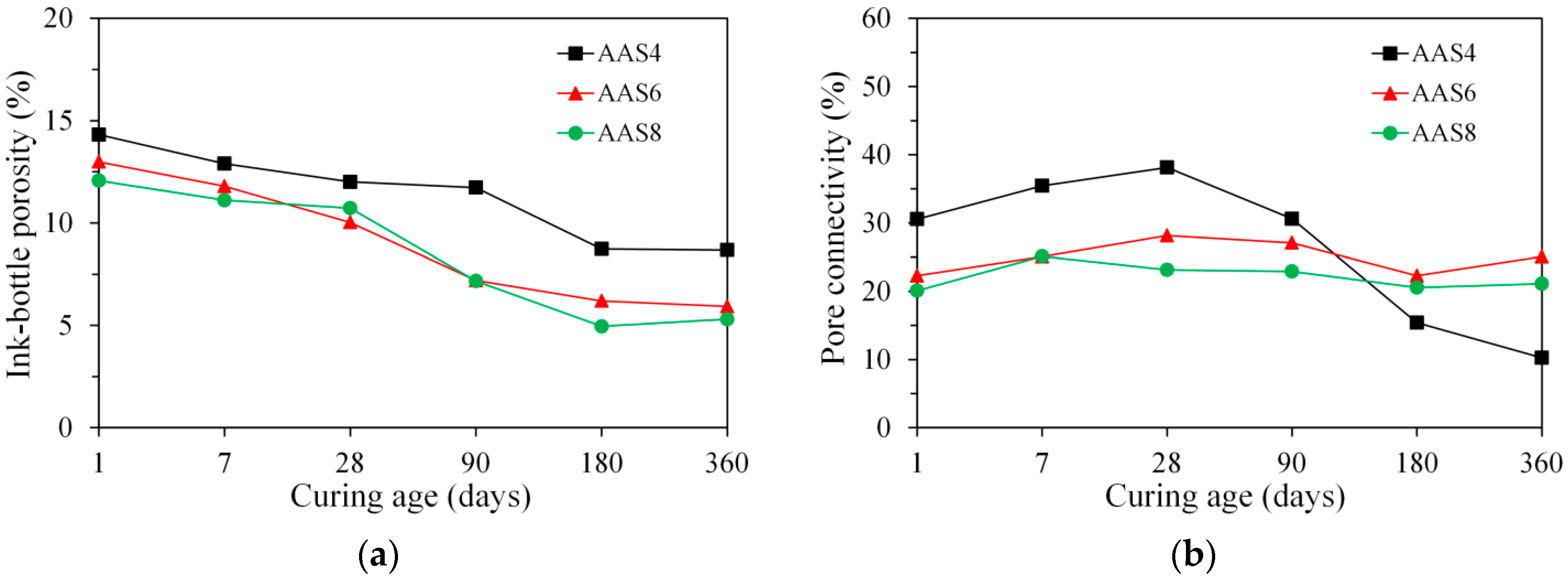
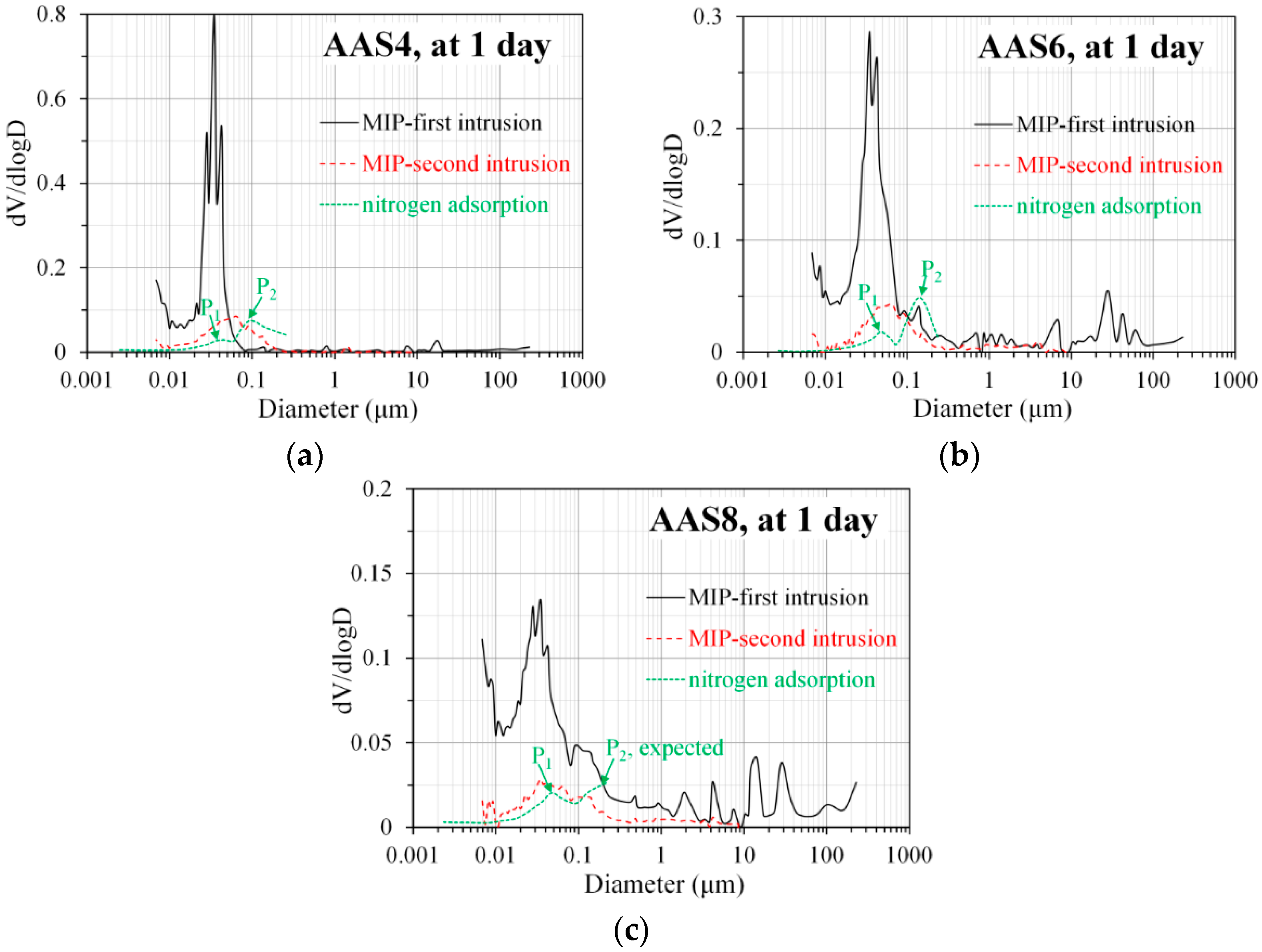
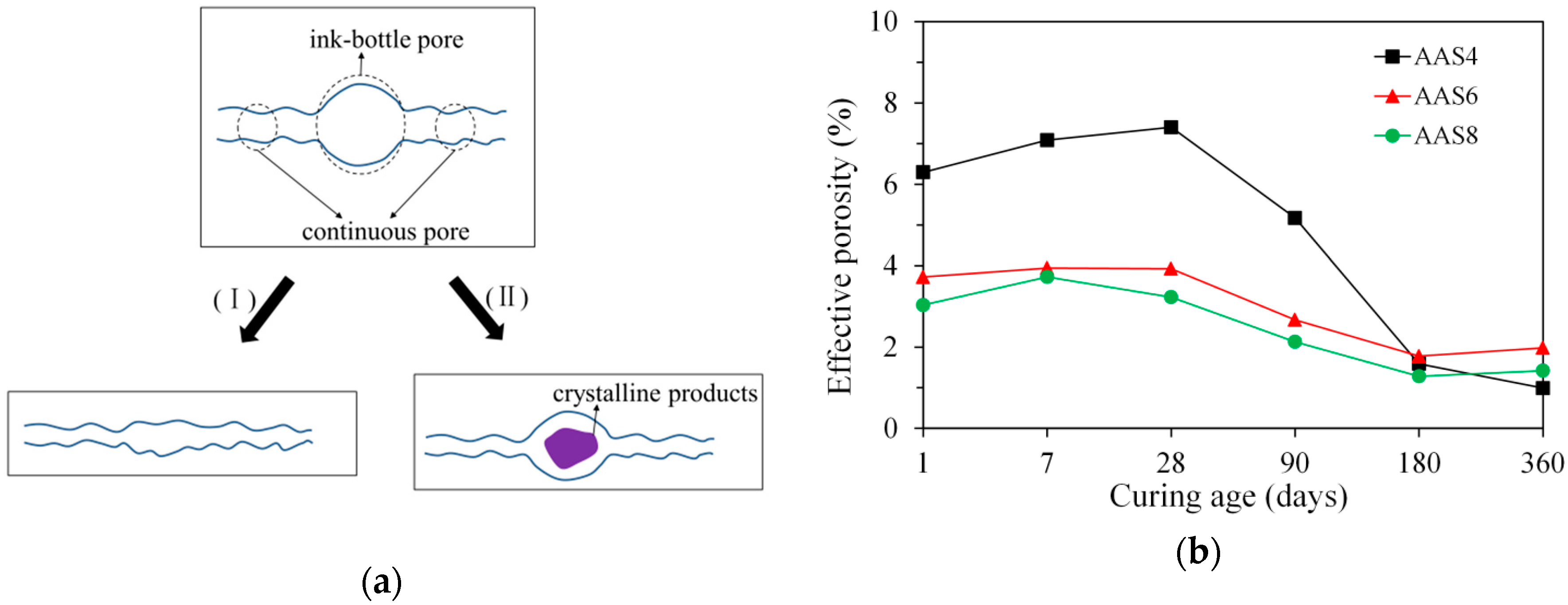
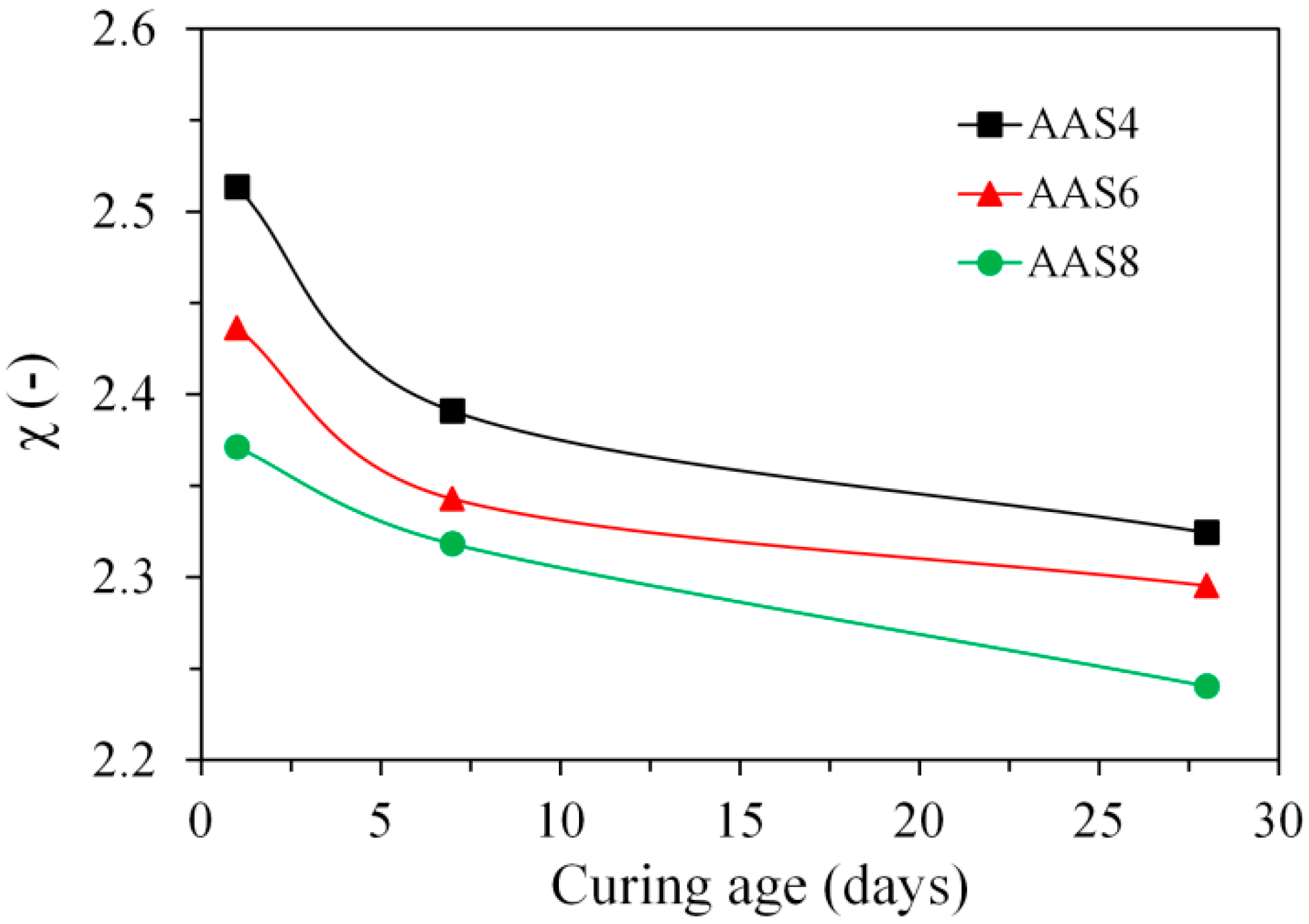
3.3.3. Ink-Bottle Pore and Pore Connectivity Derived from MIP
3.4. Pore Structure of Sodium Hydroxide Activated Slag Pastes Determined by N2 Adsorption
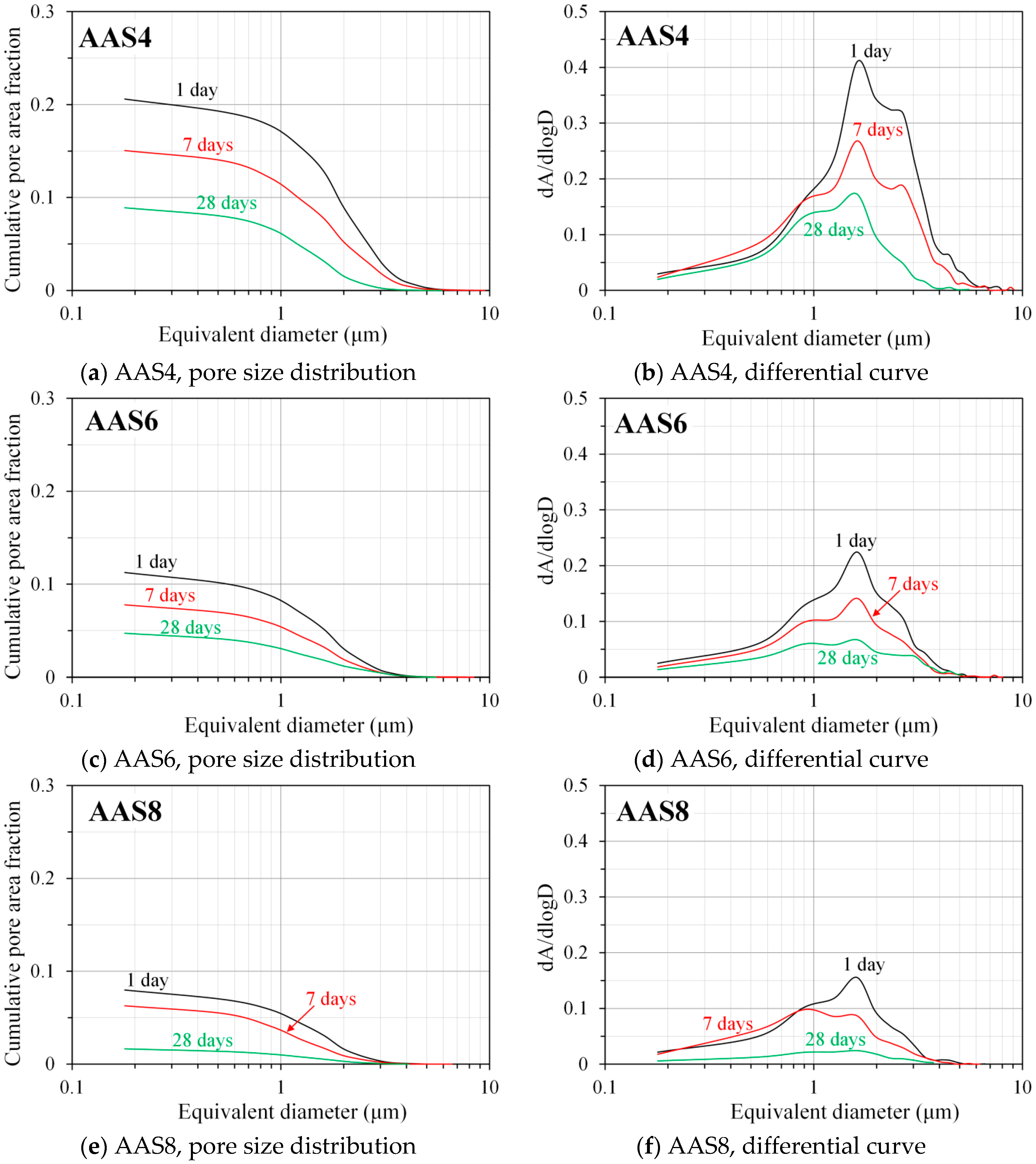
3.5. Pore Structure of Sodium Hydroxide Activated Slag Pastes Characterized by Image Analysis
4. Discussion
4.1. Comparison of Pore Structure Determined by MIP and N2 Adsorption
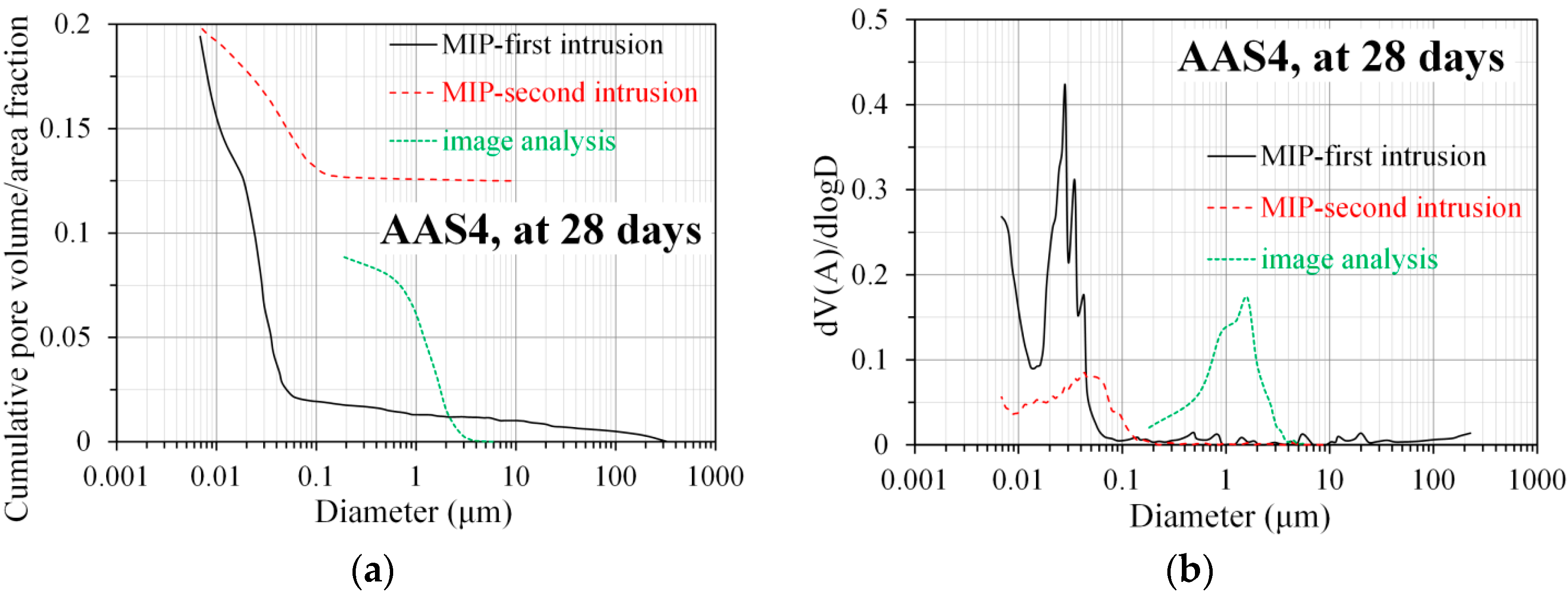
4.2. Comparison of Pore Structure Derived from MIP and Image Analysis
4.3. A Brief Summary of MIP, N2 Adsorption, and Image Analysis in Characterizing the Pore Structure of Sodium Hydroxide Activated Slag
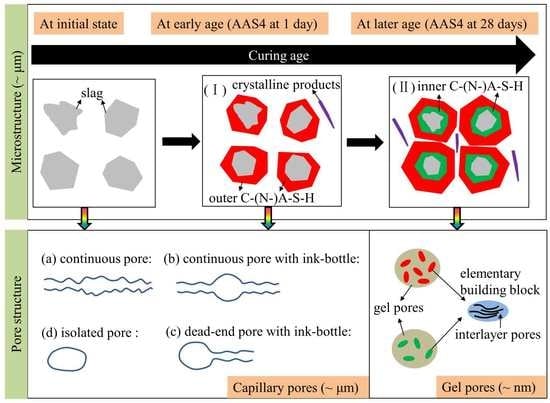
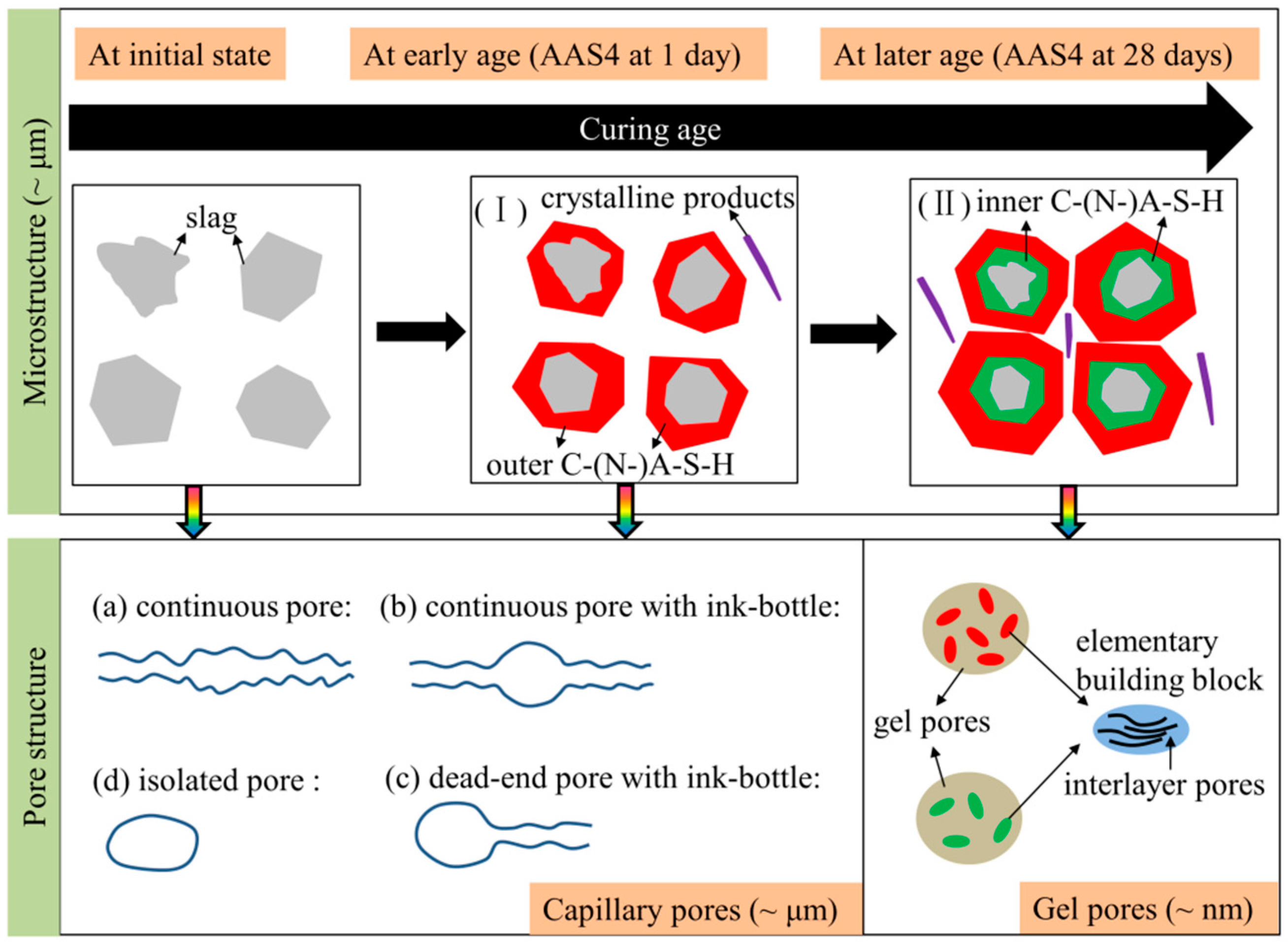
4.4. Microstructure Formation of Sodium Hydroxide Activated Slag Paste
4.5. Pore Space Filling Capacity
5. Conclusions
- MIP: The total porosity, from an initial value of 54.2%, drops about 70% within the first day and then decreases slowly with time to 7–10% at 360 days. The ink-bottle porosity decreases continuously with time, while the pore connectivity increases with time at early stages up to 28 days and then decreases until 360 days. For all the samples from 1 to 360 days, at most one peak that corresponds to gel pores was identified in the differential curves. As the Na2O content and curing age increase, the identified peak shifts to a smaller pore diameter.
- N2 adsorption: The porosity of small pores (<0.25 μm) increases with time at early stage, for example, up to 28 days for AAS4, and then decreases till 360 days. An increase of Na2O content leads to a lower porosity of small pores. In general, the differential curves show two peaks, and the trend that pore diameters of those two peaks vary with curing age depends on the content of Na2O.
- SEM-image analysis: The degree of reaction of slag is higher for samples with longer curing time and higher content of Na2O. About 50% of slag was reacted within the first day. The peak identified in the differential curves is found at about 1.6 μm, and it shows little change with increasing curing age and Na2O content.
- MIP vs. N2 adsorption: The comparison between differential curves at pore sizes smaller than 0.01 μm reveals damage resulting from high pressure during MIP measurement. The “ink-bottle” effect may lead to the absence of the second peak that corresponds to the capillary pores in the MIP results.
- Microstructure formation: The increase of Na2O content and curing age led to a reduced porosity and a refined microstructure. Conceptual models are proposed to describe the microstructure formation process, during which two layers of reaction products, e.g., outer C–(N–)A–S–H and inner C–(N)–A–S–H, grow successively around the reacting slag grains, while the secondary reaction products, such as the hydrotalcite phase, are formed in the empty coarse pore space.
- Pore space filling capacity: Sodium hydroxide activated slag has a higher pore space filling capacity than Portland cement. Along with the increases of Na2O content and curing age, the pore space filling capacity of sodium hydroxide activated slag decreases.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pacheco-Torgal, F.; Labrincha, J.; Leonelli, C.; Palomo, A.; Chindaprasit, P. Handbook of Alkali-Activated Cements, Mortars and Concretes, 1st ed.; Woodhead Publishing: Cambridge, UK, 2014. [Google Scholar]
- Provis, J.L.; Bernal, S.A. Geopolymers and related alkali-activated materials. Annu. Rev. Mater. Res. 2014, 44, 299–327. [Google Scholar] [CrossRef]
- Luukkonen, T.; Abdollahnejad, Z.; Yliniemi, J.; Kinnunen, P.; Illikainen, M. One-part alkali-activated materials: A review. Cem. Concr. Res. 2018, 103, 21–34. [Google Scholar] [CrossRef]
- Wang, S.-D.; Scrivener, K.L. Hydration products of alkali activated slag cement. Cem. Concr. Res. 1995, 25, 561–571. [Google Scholar] [CrossRef]
- Myers, R.J.; Lothenbach, B.; Bernal, S.A.; Provis, J.L. Thermodynamic modelling of alkali-activated slag cements. Appl. Geochem. 2015, 61, 233–247. [Google Scholar] [CrossRef]
- Richardson, I.G.; Brough, A.R.; Groves, G.W.; Dobson, C.M. The Characterization of Hardened Alkali-Activated Blast-Furnace Slag Pastes and the Nature of the Calcium Silicate Hydrate (C-S-H) Phase. Cem. Concr. Res. 1994, 24, 813–829. [Google Scholar] [CrossRef]
- Lothenbach, B.; Nonat, A. Calcium silicate hydrates: Solid and liquid phase composition. Cem. Concr. Res. 2015, 78 Pt A, 57–70. [Google Scholar] [CrossRef]
- Myers, R.J.; Bernal, S.A.; San Nicolas, R.; Provis, J.L. Generalized structural description of calcium–sodium aluminosilicate hydrate gels: The cross-linked substituted tobermorite model. Langmuir 2013, 29, 5294–5306. [Google Scholar] [CrossRef] [PubMed]
- Shi, C.; Roy, D.; Krivenko, P. Alkali-Activated Cements and Concretes; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Shi, C. Strength, pore structure and permeability of alkali-activated slag mortars. Cem. Concr. Res. 1996, 26, 1789–1799. [Google Scholar] [CrossRef]
- Collins, F.; Sanjayan, J. Effect of pore size distribution on drying shrinking of alkali-activated slag concrete. Cem. Concr. Res. 2000, 30, 1401–1406. [Google Scholar] [CrossRef]
- Diamond, S. A critical comparison of mercury porosimetry and capillary condensation pore size distributions of Portland cement pastes. Cem. Concr. Res. 1971, 1, 531–545. [Google Scholar] [CrossRef]
- Promentilla, M.A.B.; Sugiyama, T.; Hitomi, T.; Takeda, N. Quantification of tortuosity in hardened cement pastes using synchrotron-based X-ray computed tomography. Cem. Concr. Res. 2009, 39, 548–557. [Google Scholar] [CrossRef]
- Odler, I.; Julius Hagymassy, J.; Bodor, E.E.; Yudenfreund, M.; Brunauer, S. Hardened Portland cement pastes of low porosity IV. Surface area and pore structure. Cem. Concr. Res. 1972, 2, 577–589. [Google Scholar] [CrossRef]
- Monteilhet, L.; Korb, J.-P.; Mitchell, J.; McDonald, P.J. Observation of exchange of micropore water in cement pastes by two-dimensional T2-T2 nuclear magnetic resonance relaxometry. Phys. Rev. E 2006, 74, 061404. [Google Scholar] [CrossRef] [PubMed]
- Lange, D.A.; Jennings, H.M.; Shah, S.P. Image analysis techniques for characterization of pore structure of cement-based materials. Cem. Concr. Res. 1994, 24, 841–853. [Google Scholar] [CrossRef]
- Ye, G. Experimental Study and Numerical Simulation of the Development of the Microstructure and Permeability of Cementitious Materials; Delft University of Technology: Delft, The Netherlands, 2003. [Google Scholar]
- Ma, Y. Microstructure and Engineering Properties of Alkali Activated Fly As-As an Environment Friendly Alternative to Portland Cement; Tu Delft, Delft University of Technology: Delft, The Netherlands, 2013. [Google Scholar]
- Ma, Y.; Wang, G.; Ye, G.; Hu, J. A comparative study on the pore structure of alkali-activated fly ash evaluated by mercury intrusion porosimetry, N2 adsorption and image analysis. J. Mater. Sci. 2018, 53, 5958–5972. [Google Scholar] [CrossRef]
- Dong, H.; Zhang, H.; Zuo, Y.; Gao, P.; Ye, G. Relationship between the Size of the Samples and the Interpretation of the Mercury Intrusion Results of an Artificial Sandstone. Materials 2018, 11, 201. [Google Scholar] [CrossRef] [PubMed]
- Palacios, M.; Puertas, F. Effect of shrinkage-reducing admixtures on the properties of alkali-activated slag mortars and pastes. Cem. Concr. Res. 2007, 37, 691–702. [Google Scholar] [CrossRef]
- Ismail, I.; Bernal, S.A.; Provis, J.L.; Hamdan, S.; van Deventer, J.S. Drying-induced changes in the structure of alkali-activated pastes. J. Mater. Sci. 2013, 48, 3566–3577. [Google Scholar] [CrossRef]
- Ben Haha, M.; Le Saout, G.; Winnefeld, F.; Lothenbach, B. Influence of activator type on hydration kinetics, hydrate assemblage and microstructural development of alkali activated blast-furnace slags. Cem. Concr. Res. 2011, 41, 301–310. [Google Scholar] [CrossRef]
- Washburn, E.W. The dynamics of capillary flow. Phys. Rev. 1921, 17, 273. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Zhou, J.; Ye, G.; van Breugel, K. Characterization of pore structure in cement-based materials using pressurization–depressurization cycling mercury intrusion porosimetry (PDC-MIP). Cem. Concr. Res. 2010, 40, 1120–1128. [Google Scholar] [CrossRef]
- Garboczi, E.J. Permeability, diffusivity, and microstructural parameters: A critical review. Cem. Concr. Res. 1990, 20, 591–601. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, M.; Ye, G. Influence of moisture condition on chloride diffusion in partially saturated ordinary Portland cement mortar. Mater. Struct. 2018, 51, 36. [Google Scholar] [CrossRef]
- Gerhardt, R. As review of conventional and non-conventional pore characterization techniques. MRS Online Proc. Libr. Arch. 1988, 137. [Google Scholar] [CrossRef]
- Barrett, E.P.; Joyner, L.G.; Halenda, P.P. The determination of pore volume and area distributions in porous substances. I. Computations from nitrogen isotherms. J. Am. Chem. Soc. 1951, 73, 373–380. [Google Scholar] [CrossRef]
- Nedeljković, M.; Šavija, B.; Zuo, Y.; Luković, M.; Ye, G. Effect of natural carbonation on the pore structure and elastic modulus of the alkali-activated fly ash and slag pastes. Constr. Build. Mater. 2018, 161, 687–704. [Google Scholar] [CrossRef]
- Roels, S.; Elsen, J.; Carmeliet, J.; Hens, H. Characterisation of pore structure by combining mercury porosimetry and micrography. Mater. Struct. 2001, 34, 76–82. [Google Scholar] [CrossRef]
- Yang, Z.; Peng, X.-F.; Lee, D.-J.; Chen, M.-Y. An image-based method for obtaining pore-size distribution of porous media. Environ. Sci. Technol. 2009, 43, 3248–3253. [Google Scholar] [CrossRef] [PubMed]
- Feldman, R.F. Pore structure damage in blended cements caused by mercury intrusion. J. Am. Ceram. Soc. 1984, 67, 30–33. [Google Scholar] [CrossRef]
- Cook, R.A.; Hover, K.C. Mercury porosimetry of hardened cement pastes. Cem. Concr. Res. 1999, 29, 933–943. [Google Scholar] [CrossRef]
- Yu, Z. Microstructure Development and Transport Properties of Portland Cement-fly Ash Binary Systems: In View of Service Life Predictions. Mater. Environ. 2015. [Google Scholar] [CrossRef]
- Cui, L.; Cahyadi, J.H. Permeability and pore structure of OPC paste. Cem. Concr. Res. 2001, 31, 277–282. [Google Scholar] [CrossRef]
- Olson, R.A.; Neubauer, C.M.; Jennings, H.M. Damage to the pore structure of hardened Portland cement paste by mercury intrusion. J. Am. Ceram. Soc. 1997, 80, 2454–2458. [Google Scholar] [CrossRef]
- Zhou, J.; Ye, G.; van Breugel, K. New mercury porosimetry method for the Measurement of Pore size distribution in Cement-Based Materials. In Proceedings of the 2nd International RILEM Workshop on Concrete Durability and Service Life Planning (ConcreteLife’09), Haifa, Israel, 7–9 September 2009; pp. 490–497. [Google Scholar]
- Kaufmann, J.; Loser, R.; Leemann, A. Analysis of cement-bonded materials by multi-cycle mercury intrusion and nitrogen sorption. J. Colloid Interface Sci. 2009, 336, 730–737. [Google Scholar] [CrossRef] [PubMed]
- Garrault, S.; Finot, E.; Lesniewska, E.; Nonat, A. Study of CSH growth on C 3 S surface during its early hydration. Mater. Struct. 2005, 38, 435–442. [Google Scholar] [CrossRef]
- Chiang, W.-S.; Fratini, E.; Baglioni, P.; Liu, D.; Chen, S.-H. Microstructure determination of calcium-silicate-hydrate globules by small-angle neutron scattering. J. Phys. Chem. C 2012, 116, 5055–5061. [Google Scholar] [CrossRef]
- Thomas, J.J.; Allen, A.J.; Jennings, H.M. Density and water content of nanoscale solid C–S–H formed in alkali-activated slag (AAS) paste and implications for chemical shrinkage. Cem. Concr. Res. 2012, 42, 377–383. [Google Scholar] [CrossRef]
- Myers, R.J.; Bernal, S.A.; Provis, J.L. A thermodynamic model for C-(N-)A-S-H gel: CNASH-ss. Derivation and validation. Cem. Concr. Res. 2014, 66, 27–47. [Google Scholar] [CrossRef]
- Jennings, H.M. A model for the microstructure of calcium silicate hydrate in cement paste. Cem. Concr. Res. 2000, 30, 101–116. [Google Scholar] [CrossRef]
- Breugel, K.V. Simulation of Hydration and Formation of Structure in Hardening Cement-Based Materials; Delft University of Technology: Delft, The Netherlands, 1991. [Google Scholar]
- Ravikumar, D.; Neithalath, N. Effects of activator characteristics on the reaction product formation in slag binders activated using alkali silicate powder and NaOH. Cem. Concr. Compos. 2012, 34, 809–818. [Google Scholar] [CrossRef]



| Oxide | SiO2 | CaO | Al2O3 | MgO | Fe2O3 | SO3 | K2O | TiO2 | L.I. * |
|---|---|---|---|---|---|---|---|---|---|
| Weight (%) | 32.91 | 40.96 | 11.85 | 9.23 | 0.46 | 1.61 | 0.33 | 1.00 | 1.15 |
| Mix | Slag (g) | Na2O (g) | Water (g) |
|---|---|---|---|
| AAS4 | 100 | 4 | 40 |
| AAS6 | 100 | 6 | 40 |
| AAS8 | 100 | 8 | 40 |
| Samples | 1 Day | 7 Days | 28 Days | 180 Days | 360 Days |
|---|---|---|---|---|---|
| AAS4 | 5.98 | 6.89 | 7.19 | 6.50 | 4.87 |
| AAS6 | 3.85 | 3.46 | 2.45 | 1.57 | 1.81 |
| AAS8 | 2.82 | 3.22 | 2.50 | 1.07 | 1.19 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, Y.; Ye, G. Pore Structure Characterization of Sodium Hydroxide Activated Slag Using Mercury Intrusion Porosimetry, Nitrogen Adsorption, and Image Analysis. Materials 2018, 11, 1035. https://doi.org/10.3390/ma11061035
Zuo Y, Ye G. Pore Structure Characterization of Sodium Hydroxide Activated Slag Using Mercury Intrusion Porosimetry, Nitrogen Adsorption, and Image Analysis. Materials. 2018; 11(6):1035. https://doi.org/10.3390/ma11061035
Chicago/Turabian StyleZuo, Yibing, and Guang Ye. 2018. "Pore Structure Characterization of Sodium Hydroxide Activated Slag Using Mercury Intrusion Porosimetry, Nitrogen Adsorption, and Image Analysis" Materials 11, no. 6: 1035. https://doi.org/10.3390/ma11061035
APA StyleZuo, Y., & Ye, G. (2018). Pore Structure Characterization of Sodium Hydroxide Activated Slag Using Mercury Intrusion Porosimetry, Nitrogen Adsorption, and Image Analysis. Materials, 11(6), 1035. https://doi.org/10.3390/ma11061035