Peculiarities in the Material Design of Buckling Resistance for Tensioned Laminated Composite Panels with Elliptical Cut-Outs
Abstract
1. Introduction
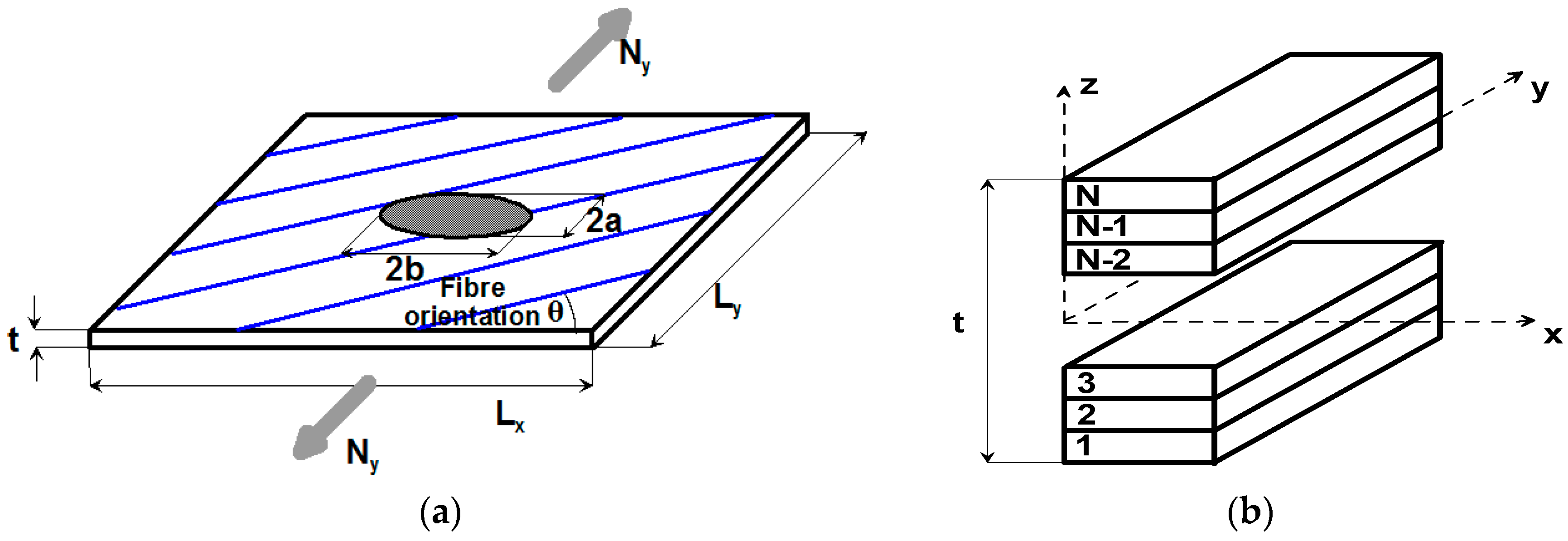
2. Formulation of the Buckling Problem and Derivation of Buckling Loads—The Rayleigh–Ritz Method
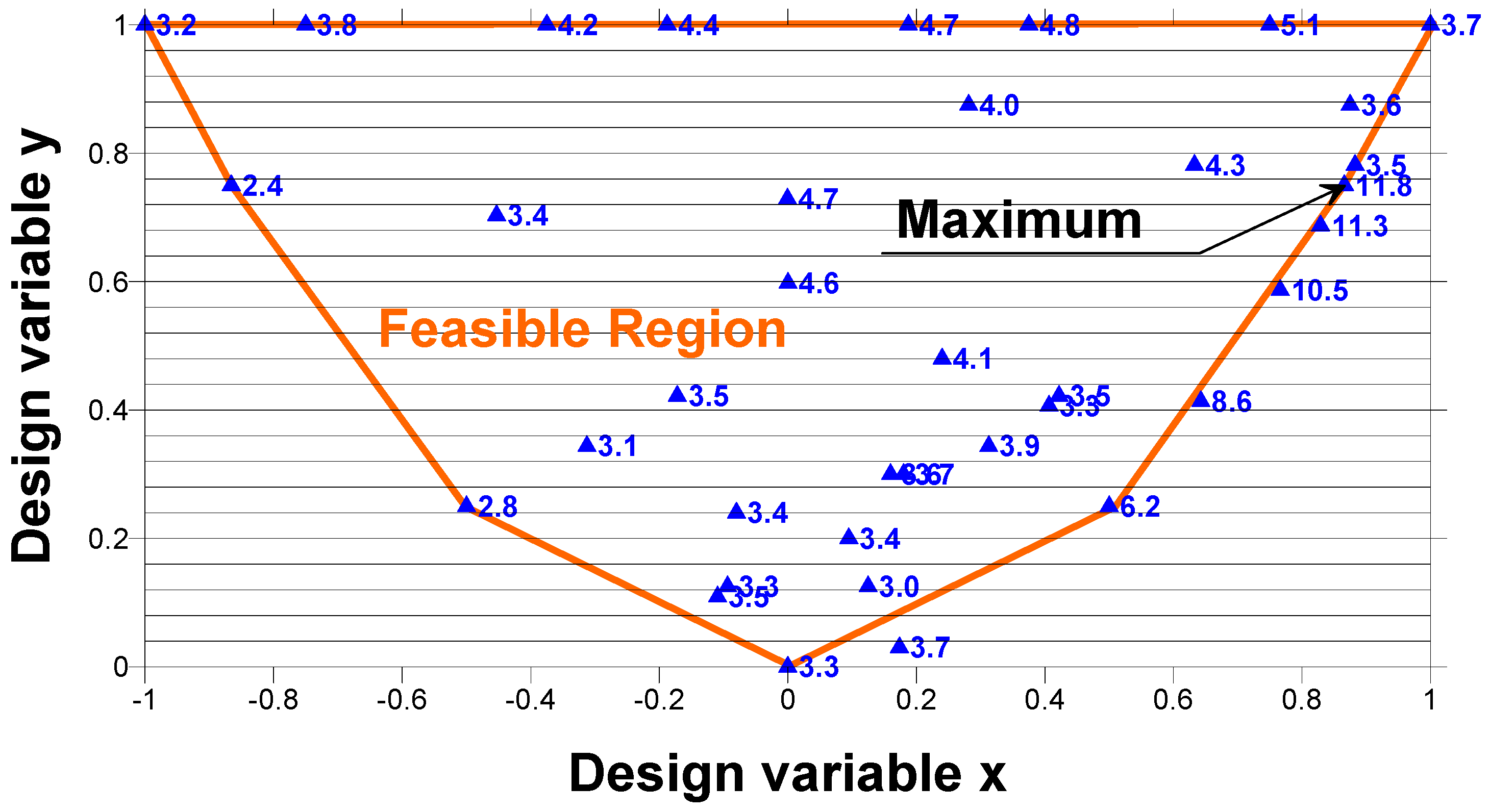
3. Optimal Design
4. Parametric Investigations
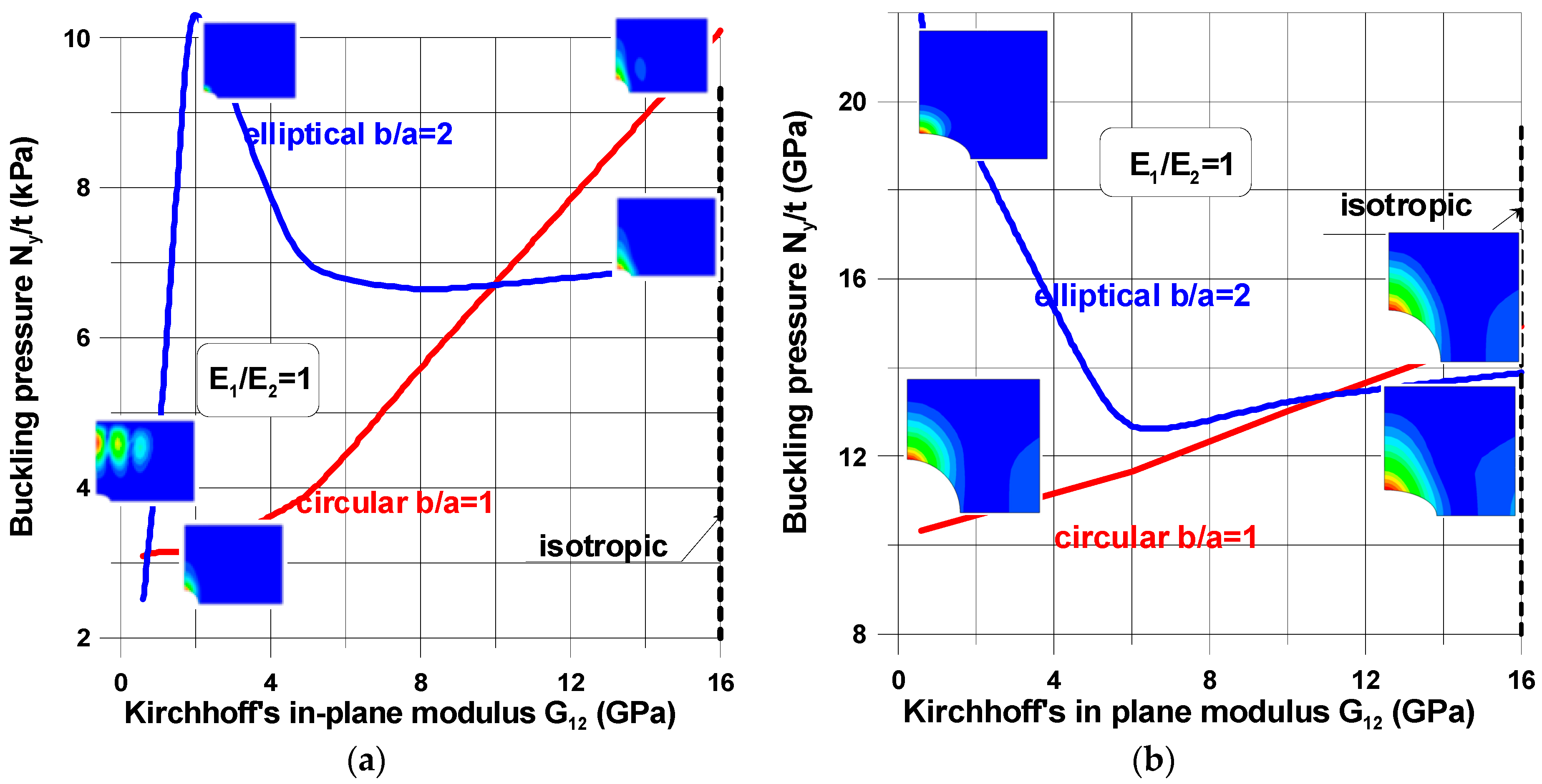
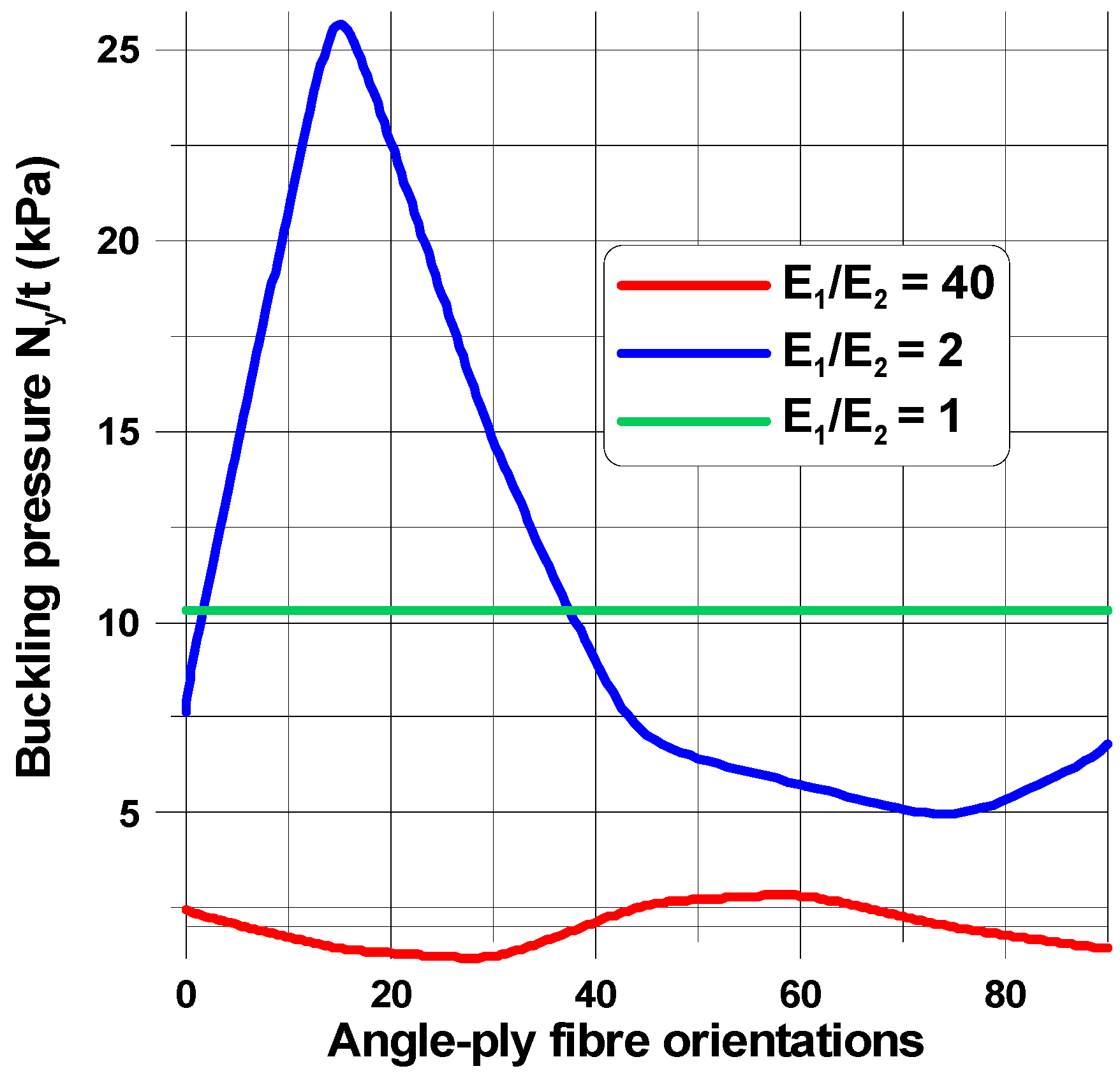
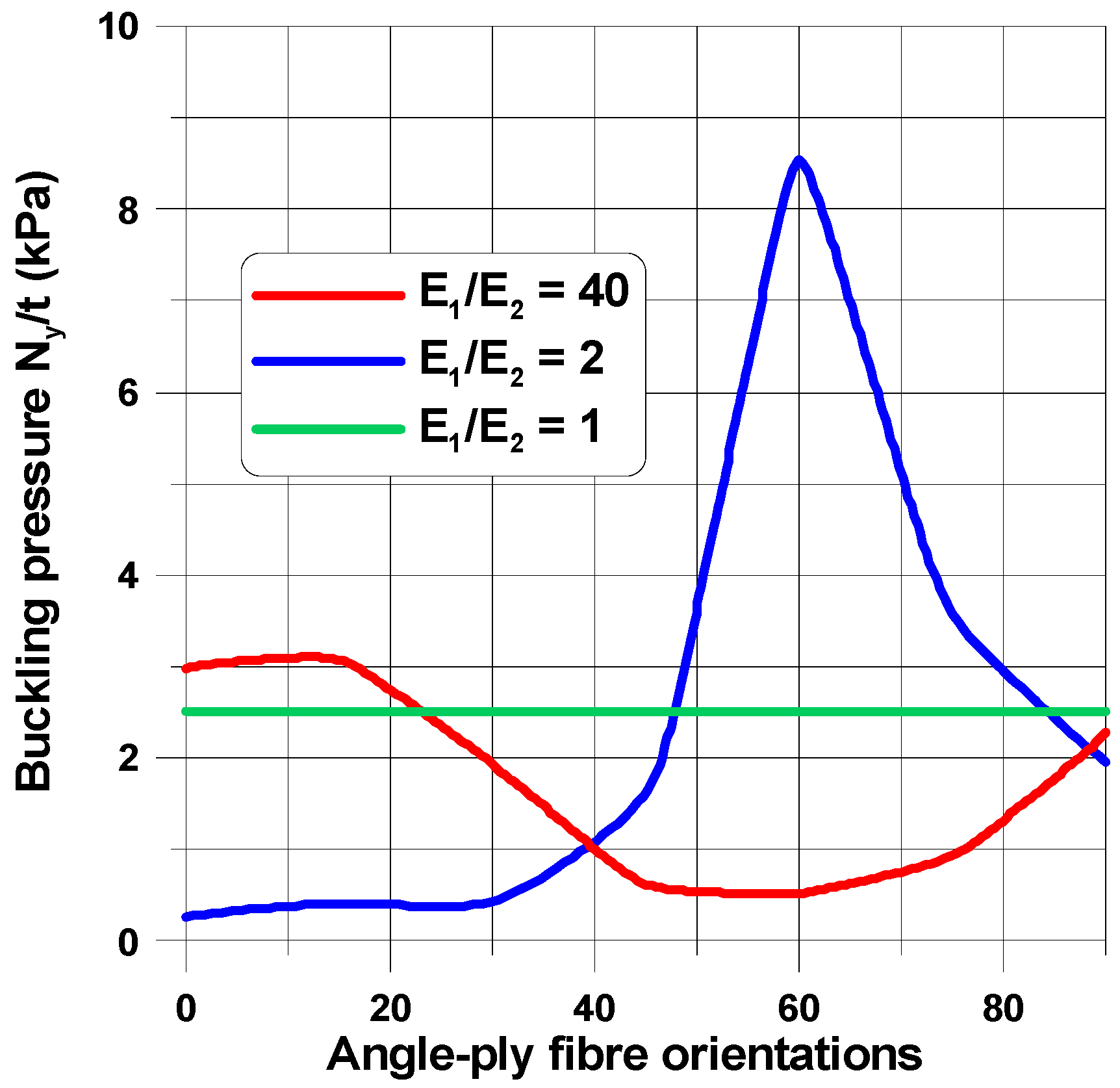
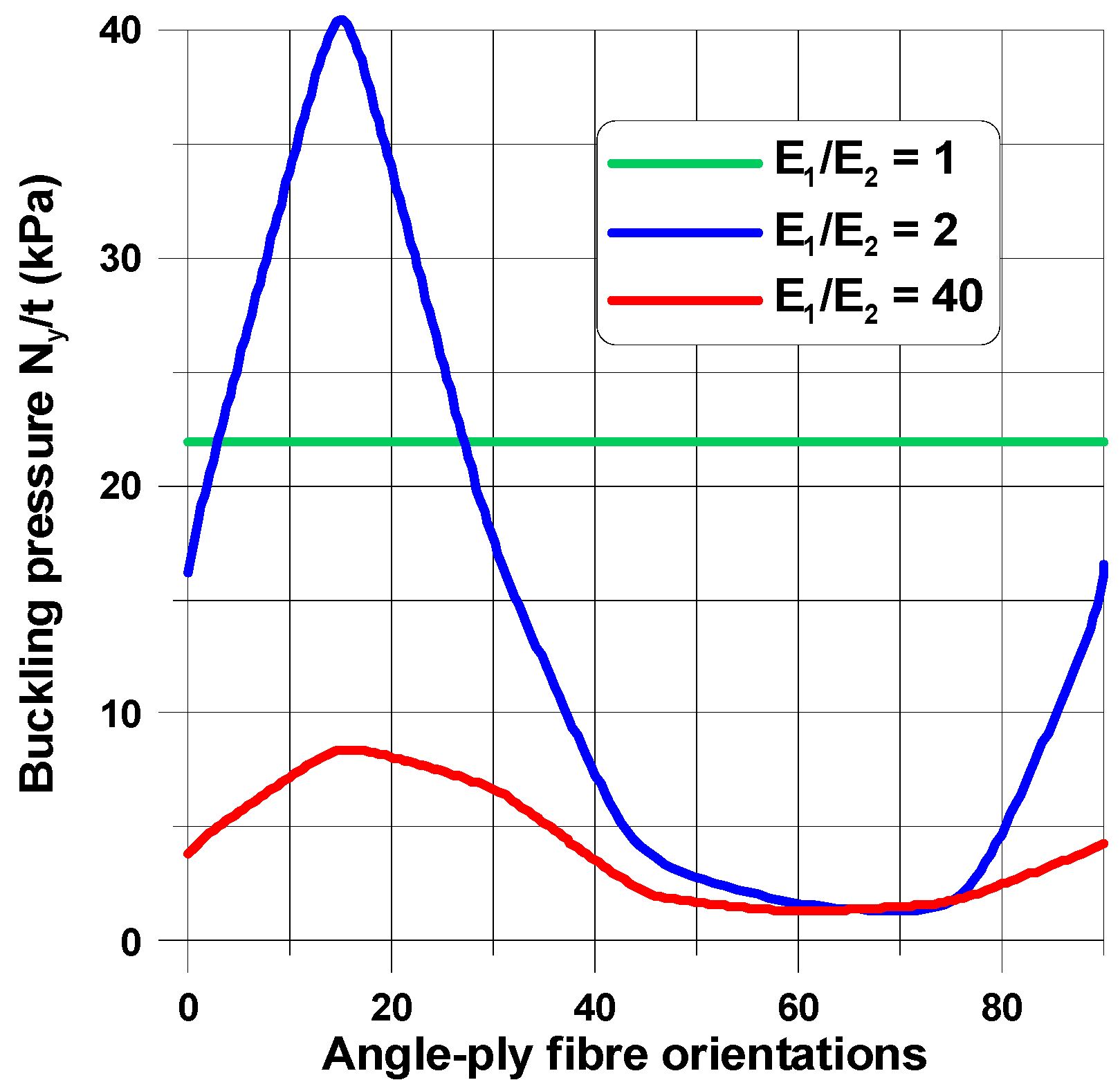
4.1. Influence of Mechanical Properties
- a single buckle at the apex of the hole (x = 0, y = a)—the characteristic buckling mode of an infinite tensioned plate;
- two buckles, one localized at the apex and the second around the point x = b, y = 0;
- three buckles located far from a cut-out—it is a characteristic behavior of buckled short tensioned panels [35].
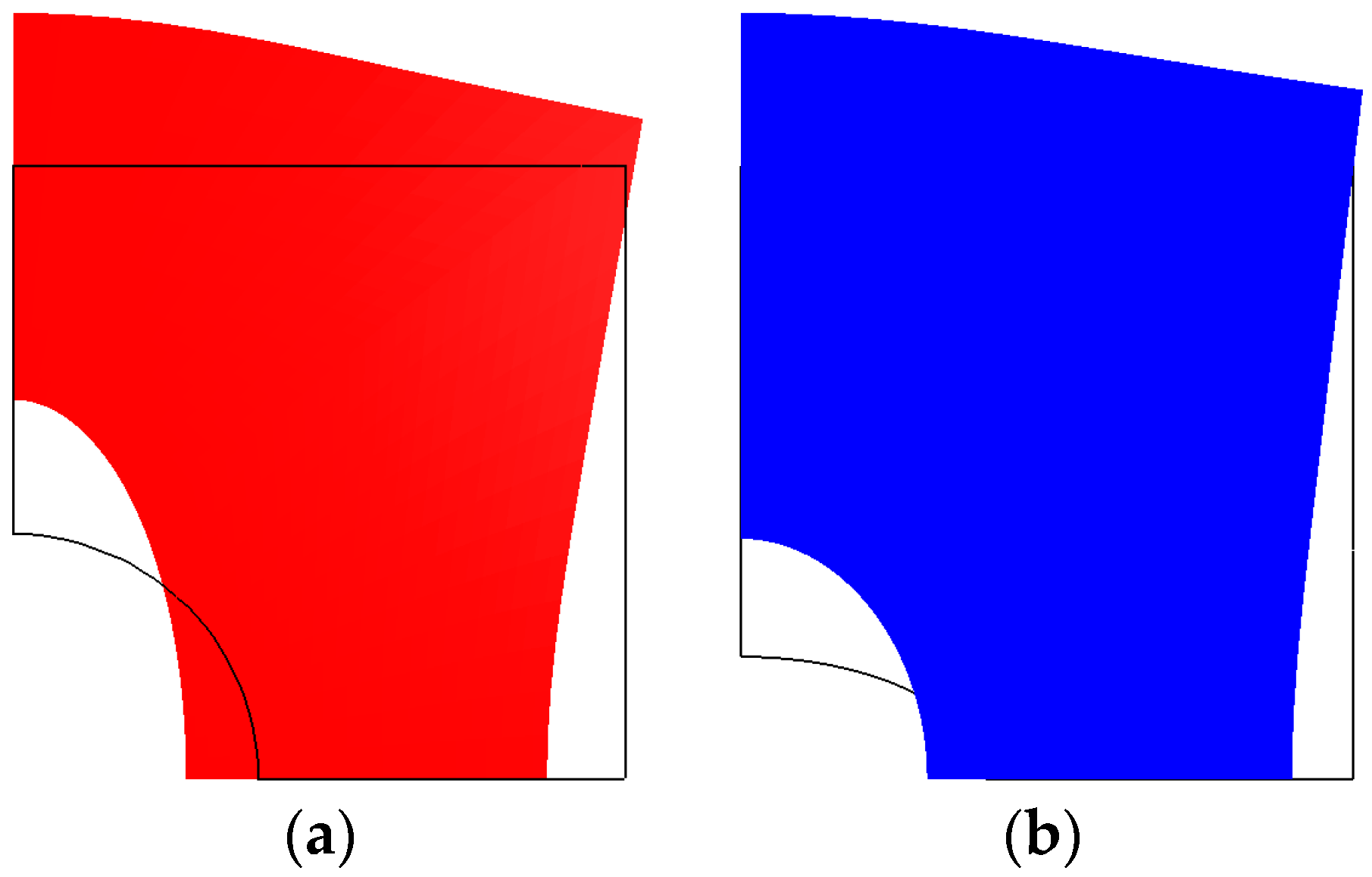
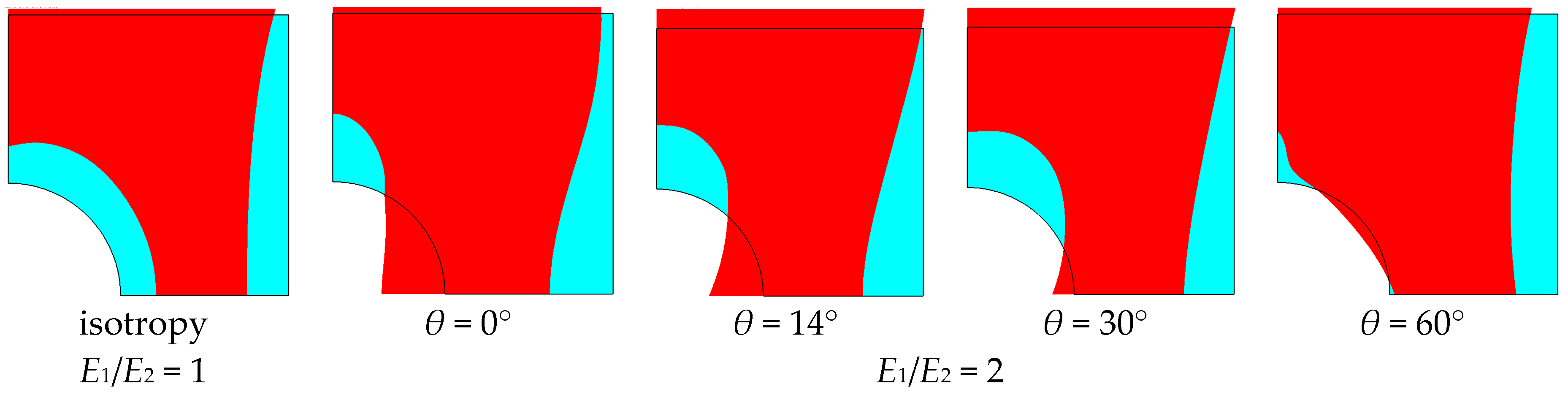
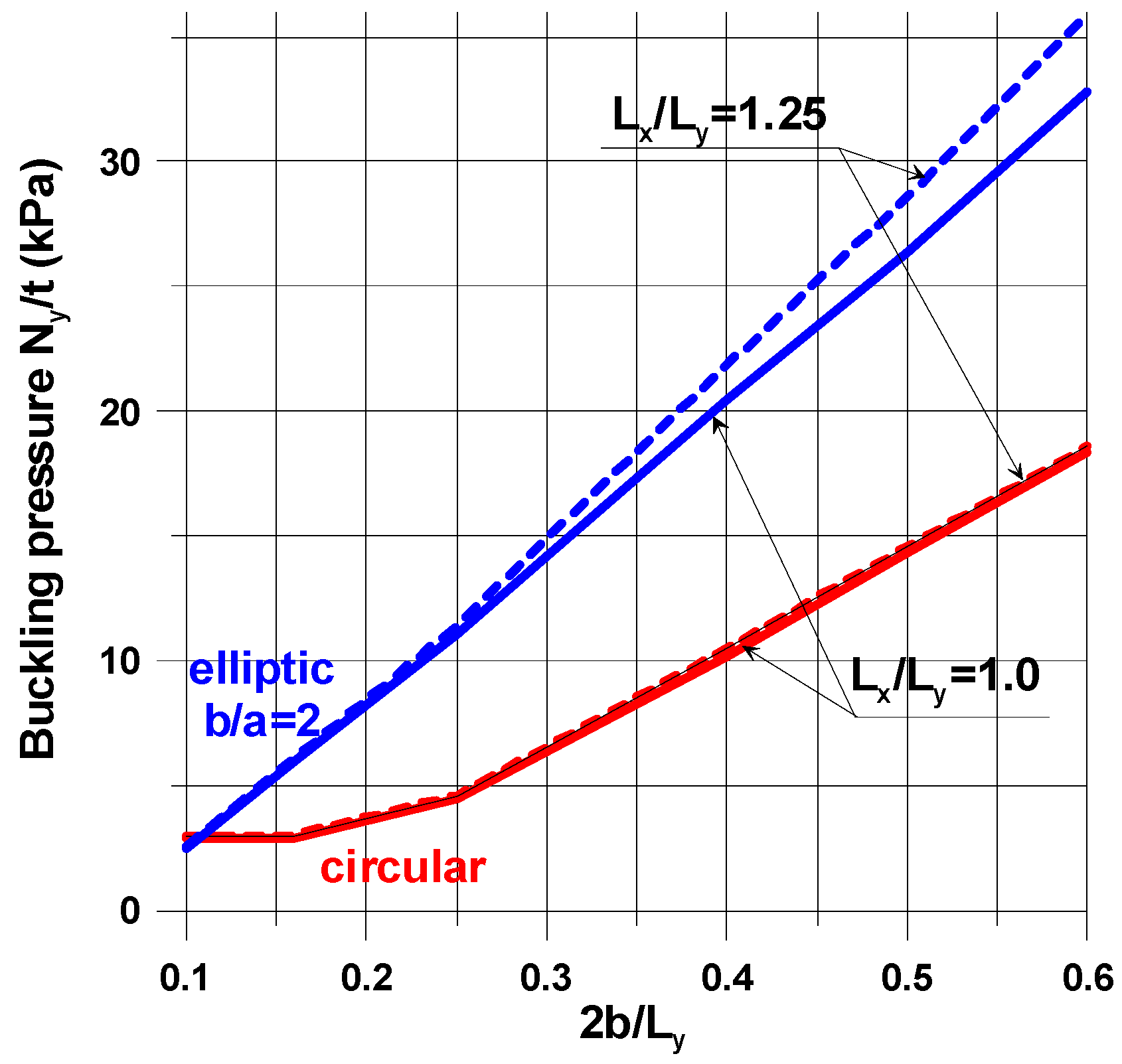
4.2. Influence of Plate and Cut-Out Geometry
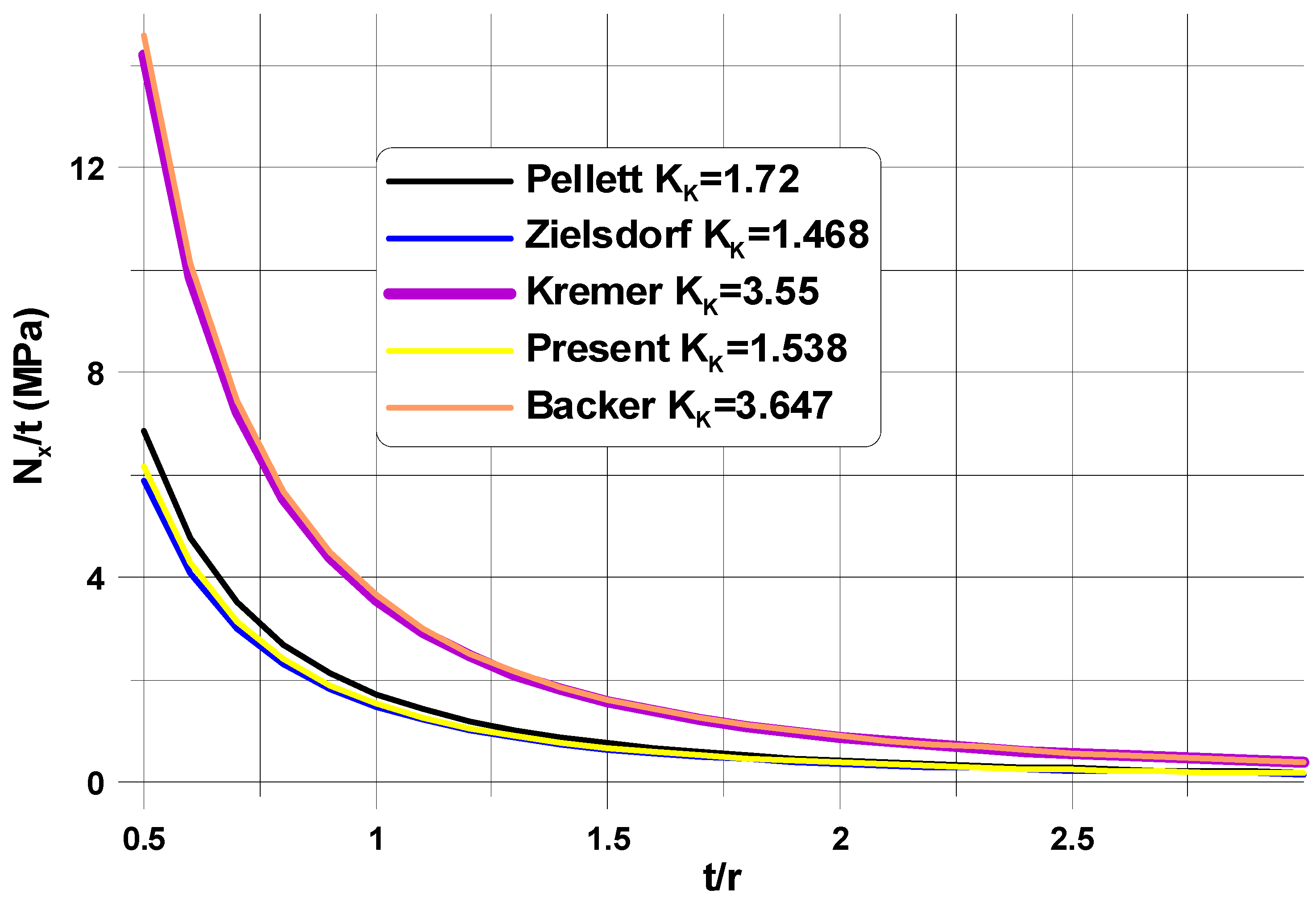
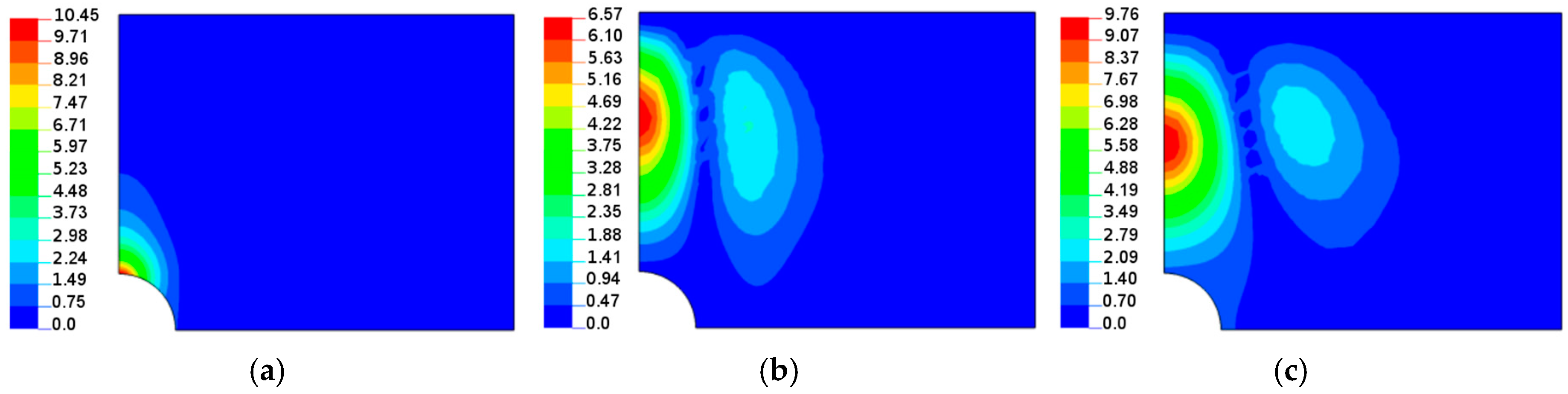
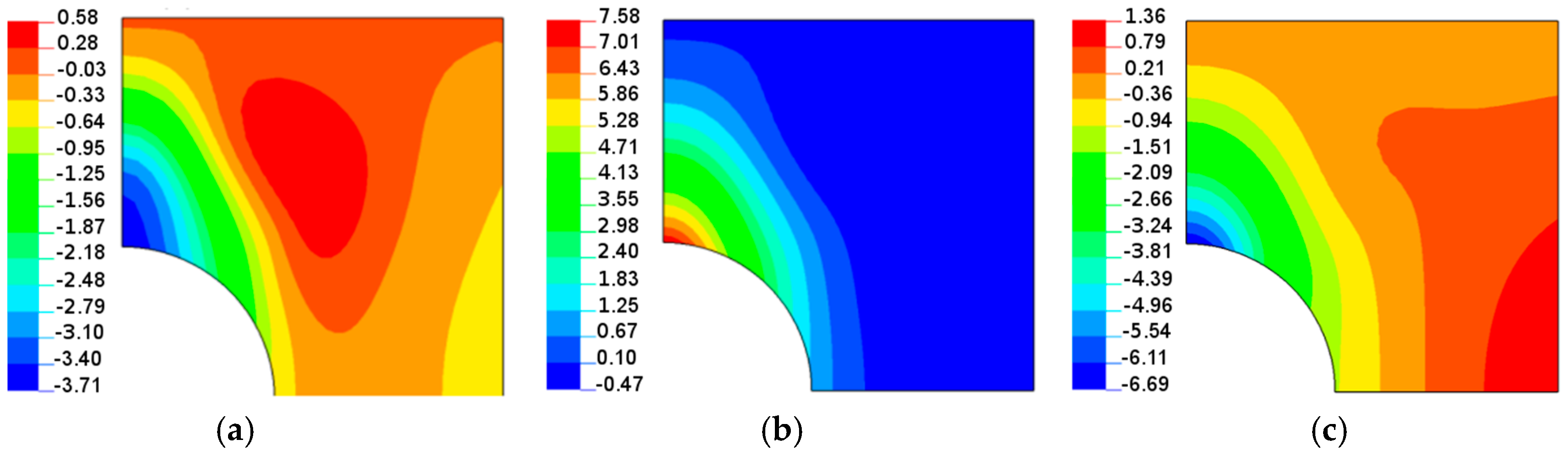
5. Comparison of Theoretical Predictions and the Finite Element Analysis
6. Concluding Remarks
Funding
Acknowledgments
Conflicts of Interest
Appendix A
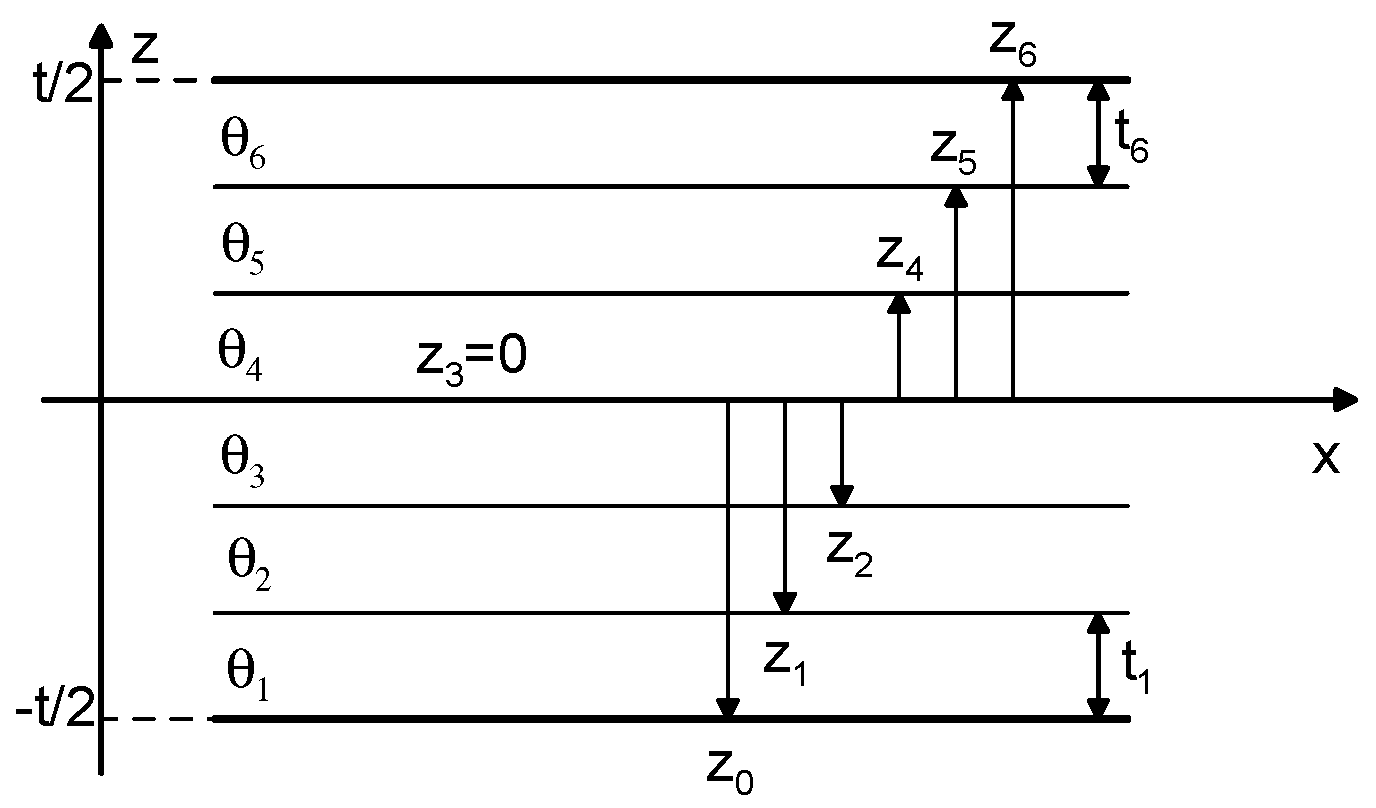
References
- Kirsch, G. Die Theorie der elastizitat und die bedurfnisse der festigkeitslehre. Zeitschrift des Vereins Deutscher Ingenieure 1898, 42, 797–807. [Google Scholar]
- Inglis, C.E. Stress in a plate due to presence of cracks and sharp corners. Trans. Inst. Naval Arch. (Lond.) 1913, 55, 219–241. [Google Scholar]
- Lekhnitskii, S.G. Anisotropic Plates; Gordon and Breach: London, UK, 1968. [Google Scholar]
- Savin, G.N. The stress distribution in a thin shell with an arbitrary hole. In Problems in Cominuum Mechanics; SIAM: Philadelphia, PA, USA, 1962; p. 382. [Google Scholar]
- Muc, A.; Ulatowska, A. Design of plates with curved fibre format. Compos. Struct. 2010, 92, 1728–1733. [Google Scholar] [CrossRef]
- Muc, A.; Ulatowska, A. Local fibre reinforcement of holes in composite multilayered plates. Compos. Struct. 2012, 94, 1413–1419. [Google Scholar] [CrossRef]
- Engels, S.; Becker, W. Optimization of hole reinforcements by doublers. Struct. Multidisc. Optim. 2000, 20, 57–66. [Google Scholar] [CrossRef]
- Muc, A. Effectiveness of optimal design with respect to computational models for laminated composite structures weakened by holes. Struct. Optim. 1998, 16, 58–67. [Google Scholar] [CrossRef]
- Parvizian, J.; Fenner, R.T. On shape optimization by the boundary element method using normal growth approach. AIAA J. 1997, 2, 1397–1403. [Google Scholar]
- Muc, A. Transverse shear effects in shape optimization of thinwalled laminated composite structures. Compos. Struct. 1995, 32, 399–408. [Google Scholar] [CrossRef]
- Gurdal, Z.; Olmedo, R. In-plane response of laminates with spatially varying fiber orientations: Variable stiffness concept. AIAA J. 1993, 31, 751–758. [Google Scholar] [CrossRef]
- Olmedo, R.; Gurdal, Z. Buckling response of laminates with spatially varying fiber orientations. In Proceedings of the AIAA/ASME/ASCE/AHS/ASC 34th SDM Conference, La Jolla, CA, USA, 19–21 April 1993; pp. 2261–2269. [Google Scholar]
- Jegley, D.C.; Tatting, B.F.; Gurdal, Z. Optimization of elastically tailored tow-placed plates with holes. In Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Conference on Structures, Structural Dynamics, and Materials, Norfolk, VA, USA, 7–10 April 2003. [Google Scholar]
- Hyer, M.W.; Charette, R.F. Use of curvilinear fiber format in composite structure design. AIAA J. 1991, 29, 1011–1015. [Google Scholar] [CrossRef]
- Hyer, M.W.; Lee, H.H. The use of curvilinear fiber format to improve buckling resistance of composite plates with central circular holes. Compos. Struct. 1991, 18, 239–261. [Google Scholar] [CrossRef]
- Parnas, L.; Oral, S.; Ceyhan, U. Optimum design of composite structures with curved fiber courses. J. Compos. Sci. Technol. 2003, 63, 1071–1082. [Google Scholar] [CrossRef]
- Cherepanov, G.P. On the buckling under tension of a membrane containing holes. J. Appl. Math. Mech. 1963, 27, 275–286. [Google Scholar] [CrossRef]
- Brock, J.E.; Costello, R.G.; Pellet, D.A. Buckling of a tensioned panel containing circular hole. AIAA J. 1968, 6, 2012–2014. [Google Scholar] [CrossRef]
- Datta, P.K.; Carlson, R.L. Buckling and vibration of a thin tensioned sheet with an elliptical hole. The results of an analytical and experimental study of both the buckling and the vibration behavior of a thin sheet with an elliptical hole in a tensile field are presented. Exp. Mech. 1973, 13, 280–286. [Google Scholar] [CrossRef]
- Carlson, R.L. An experimental study of the parametric excitation of a tensioned sheet with a crack like opening—Results of experimental studies indicate that both principal and secondary regions of instability are developed. Exp. Mech. 1974, 14, 452–458. [Google Scholar] [CrossRef]
- Datta, P.K. Parametric instability of tensioned panels with central opening and edge slot. In Proceedings of the 9th Canadian Congress of Applied Mechanics, Saskatoon, SK, Canada, 30 May–3 June 1983; pp. 99–100. [Google Scholar]
- Datta, P.K.; Biswas, S. Research Advances on Tension Buckling Behaviour of Aerospace Structures: A Review. Int. J. Aeronaut. Space Sci. 2011, 12, 1–15. [Google Scholar] [CrossRef]
- Shimizu, S. Tension buckling of plate having a hole. Thin-Walled Struct. 2007, 45, 827–833. [Google Scholar] [CrossRef]
- Larsson, P. On buckling of orthotropic stretched plates with circular holes. Compos. Struct. 1989, 11, 121–134. [Google Scholar] [CrossRef]
- Madenci, E.; Barut, P. Pre- and postbuckling response of curved thin, composite panels with cutouts under compression. Int. J. Numer. Methods Eng. 1994, 37, 1499–1510. [Google Scholar] [CrossRef]
- Kremer, T.; Schurmann, H. Buckling of tension-loaded thin-walled composite plates with cut-outs. Compos. Sci. Technol. 2009, 68, 90–98. [Google Scholar] [CrossRef]
- Muc, A.; Chwał, M.; Barski, M. Remarks on experimental and theoretical investigations of buckling loads for laminated plated and shell structures. Compos. Struct. 2018. submitted. [Google Scholar]
- Datta, P.K. On the Buckling and Vibration Behavior of a Thin Tensioned Sheet with an Elliptical Hole. Ph.D. Thesis, School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, GA, USA, June 1972. [Google Scholar]
- Zielsdorff, G. An Investigation of the Out-of-Plane Deflection Behavior of Thin Sheets with Cutouts in a Tensile Field. Ph.D. Thesis, School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, GA, USA, June 1971. [Google Scholar]
- Backer, G.C. Static and Dynamic Behaviour of Tensioned Doubly-Connected Plates. Ph.D. Thesis, School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, GA, USA, August 1972. [Google Scholar]
- Muc, A. Choice of design variables in the stacking sequence optimization for laminated structures. Mech. Compos. Mater. 2016, 52, 211–224. [Google Scholar] [CrossRef]
- Muc, A. Optimal fibre orientations for simply-supported plates under compression. Compos. Struct. 1988, 9, 161–172. [Google Scholar] [CrossRef]
- Tan, S.C. Laminated composites containing elliptical opening. J. Compos. Mater. 1987, 21, 925–948. [Google Scholar] [CrossRef]
- Seif, A.H.; Kabir, M.Z. An efficient analytical model to evaluate the first two local buckling modes of finite cracked plate under tension. Latin Am. J. Solids Struct. 2015, 12, 2078–2093. [Google Scholar] [CrossRef]
- Friedl, N.; Rammerstorfer, F.G.; Fischer, F.D. Buckling of stretched strips. Comput. Struct. 2000, 78, 185–190. [Google Scholar] [CrossRef]
- Srivastava, V.K. Notched strength prediction of laminated composite under tensile loading. Mater. Sci. Eng. A 2002, 328, 302–309. [Google Scholar] [CrossRef]
- Muc, A.; Romanowicz, P. Effect of notch on static and fatigue performance of multilayered composite structures under tensile loads. Compos. Struct. 2017, 178, 27–36. [Google Scholar] [CrossRef]
- Muc, A.; Barski, M.; Chwał, M.; Romanowicz, P.; Stawiarski, A. Fatigue damage growth monitoring for composite structures with holes. Compos. Struct. 2018, 189, 117–126. [Google Scholar] [CrossRef]
- Muc, A.; Chwał, M.; Romanowicz, P.; Stawiarski, A. Fatigue-Damage Evolution of Notched Composite Multilayered Structures under Tensile Loads. J. Compos. Sci. 2018, 2, 27. [Google Scholar] [CrossRef]
- Muc, A.; Muc-Wierzgoń, M. An evolution strategy in structural optimization problems for plates and shells. Compos. Struct. 2012, 94, 1461–1470. [Google Scholar] [CrossRef]



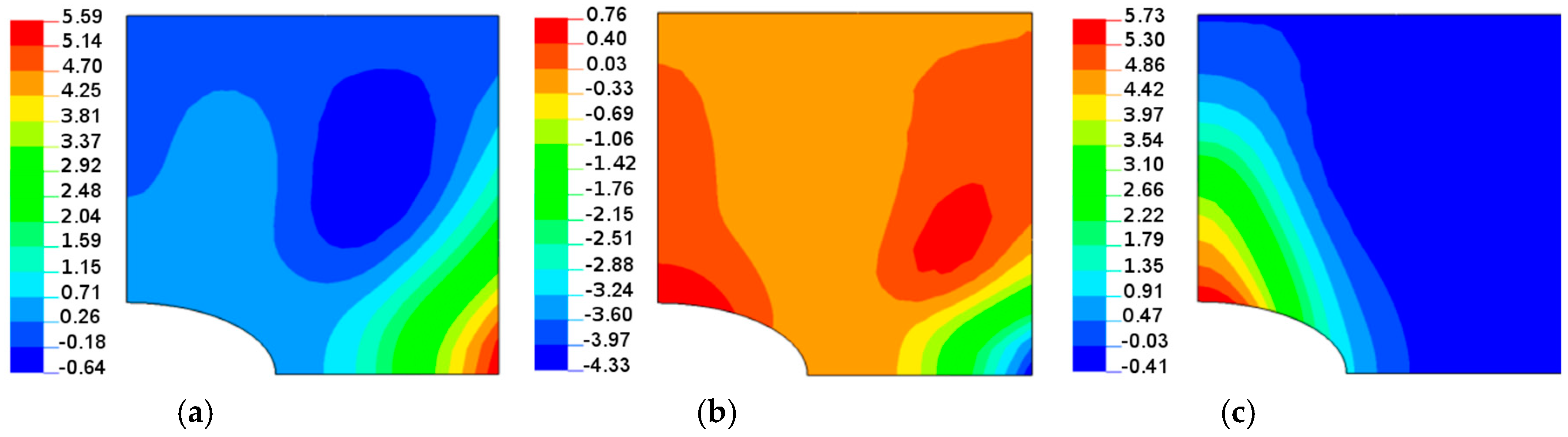
| Form of Plate and Shape of Hole | Method of Analysis | ||
|---|---|---|---|
| Kremer [26] Equation (1) | Shimizu [23] Equation (2) | Present FE | |
| Rectangular plate, circular hole, 2b/Lx = 0.4, Lx/Ly = 1.25 | 35.5 | 10.87 | 10.19 |
| Square plate, circular hole, 2b/Lx = 0.4 | 35.5 | 10.87 | 14.94 |
| Square plate, horizontal elliptical hole, 2b/Lx = 0.4, b/a = 2 | 35.5/4 = 8.88 | Not available | 13.88 |
| Rectangular plate, elliptical hole, 2b/Lx = 0.16, b/a = 2, Lx/Ly = 1.25 | 8.88 | Not available | 35.55 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muc, A. Peculiarities in the Material Design of Buckling Resistance for Tensioned Laminated Composite Panels with Elliptical Cut-Outs. Materials 2018, 11, 1019. https://doi.org/10.3390/ma11061019
Muc A. Peculiarities in the Material Design of Buckling Resistance for Tensioned Laminated Composite Panels with Elliptical Cut-Outs. Materials. 2018; 11(6):1019. https://doi.org/10.3390/ma11061019
Chicago/Turabian StyleMuc, Aleksander. 2018. "Peculiarities in the Material Design of Buckling Resistance for Tensioned Laminated Composite Panels with Elliptical Cut-Outs" Materials 11, no. 6: 1019. https://doi.org/10.3390/ma11061019
APA StyleMuc, A. (2018). Peculiarities in the Material Design of Buckling Resistance for Tensioned Laminated Composite Panels with Elliptical Cut-Outs. Materials, 11(6), 1019. https://doi.org/10.3390/ma11061019




