Effect of Temperature Distribution in Ultrasonically Welded Joints of Copper Wire and Sheet Used for Electrical Contacts
Abstract
1. Introduction
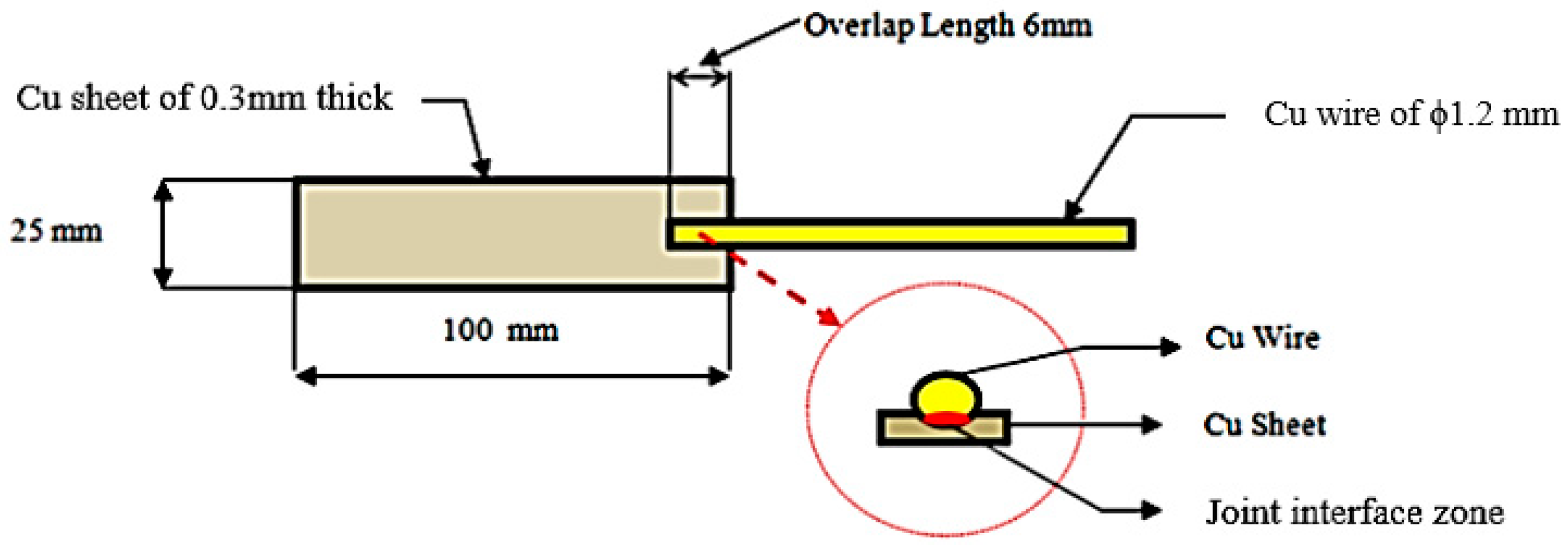
2. Experimental Details
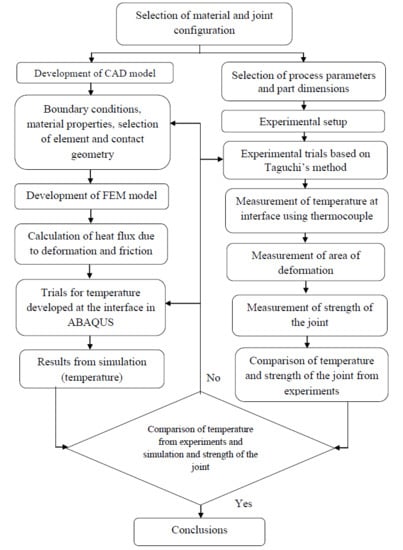
3. Finite Element Analysis
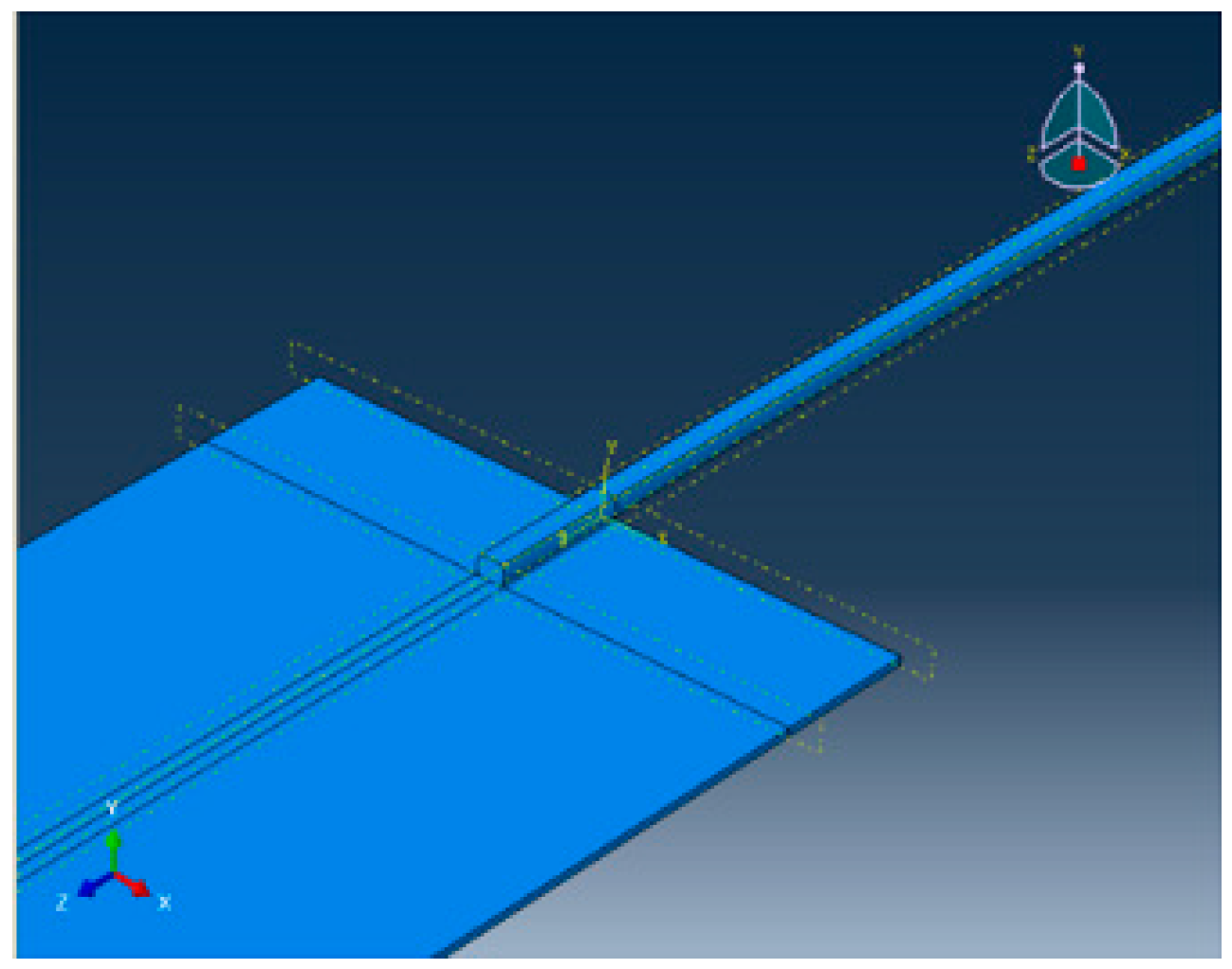
3.1. CAD Model
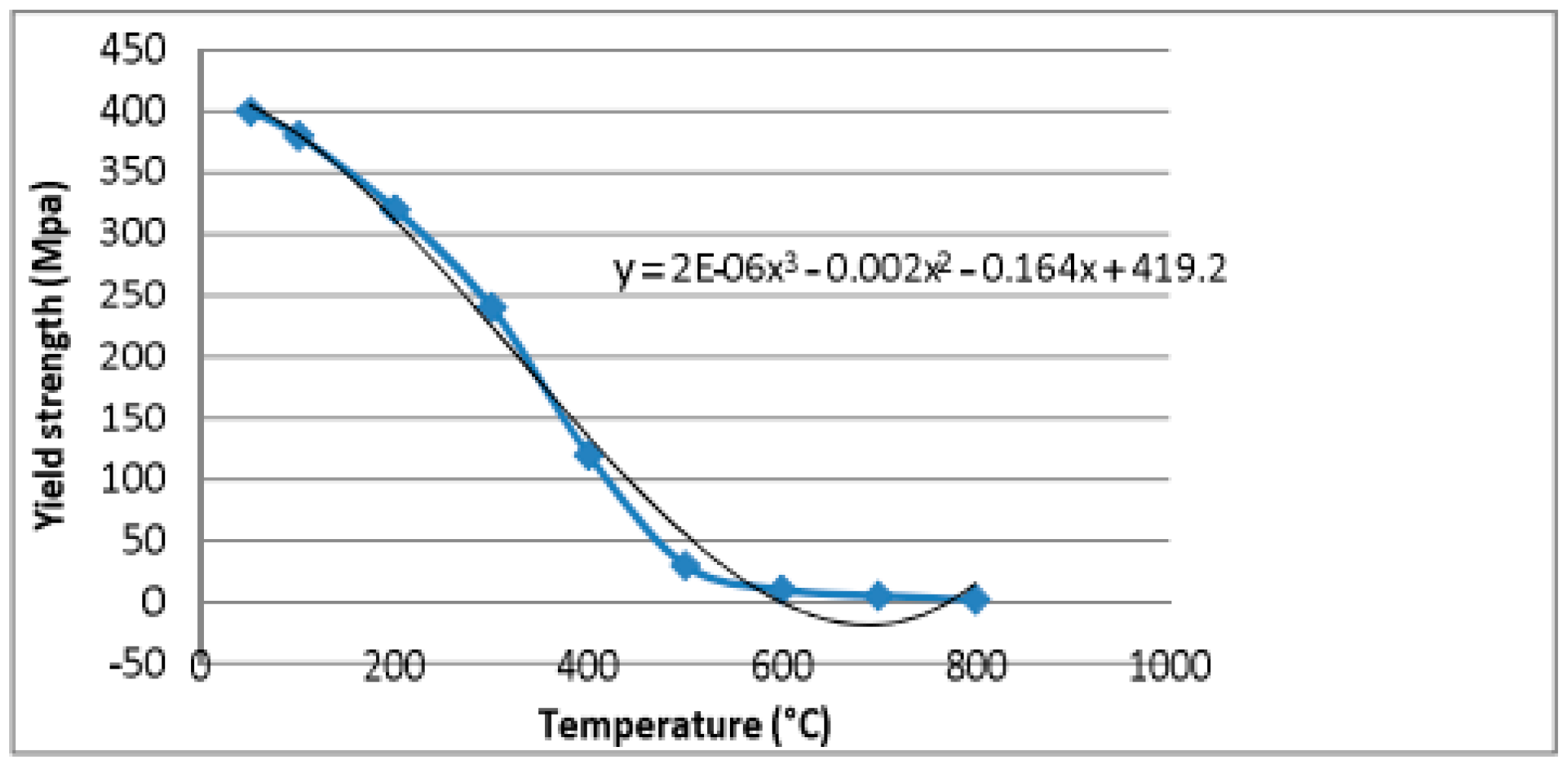
3.2. Material Properties
3.3. Element Selection and Meshing of CAD Model
3.4. Assumptions for Thermal Analysis
- Unsteady state is considered for thermal analysis.
- Full contact is established with no air gap between the specimens.
- Room temperature is 30 °C.
- The area in which the friction is effective is assumed to be the area of deformation
- Surfaces exposed to air are set under free convection.
3.5. Measurement of Area of Deformation
3.6. Calculation of Heat Flux
4. Simulation and Experimental Trials
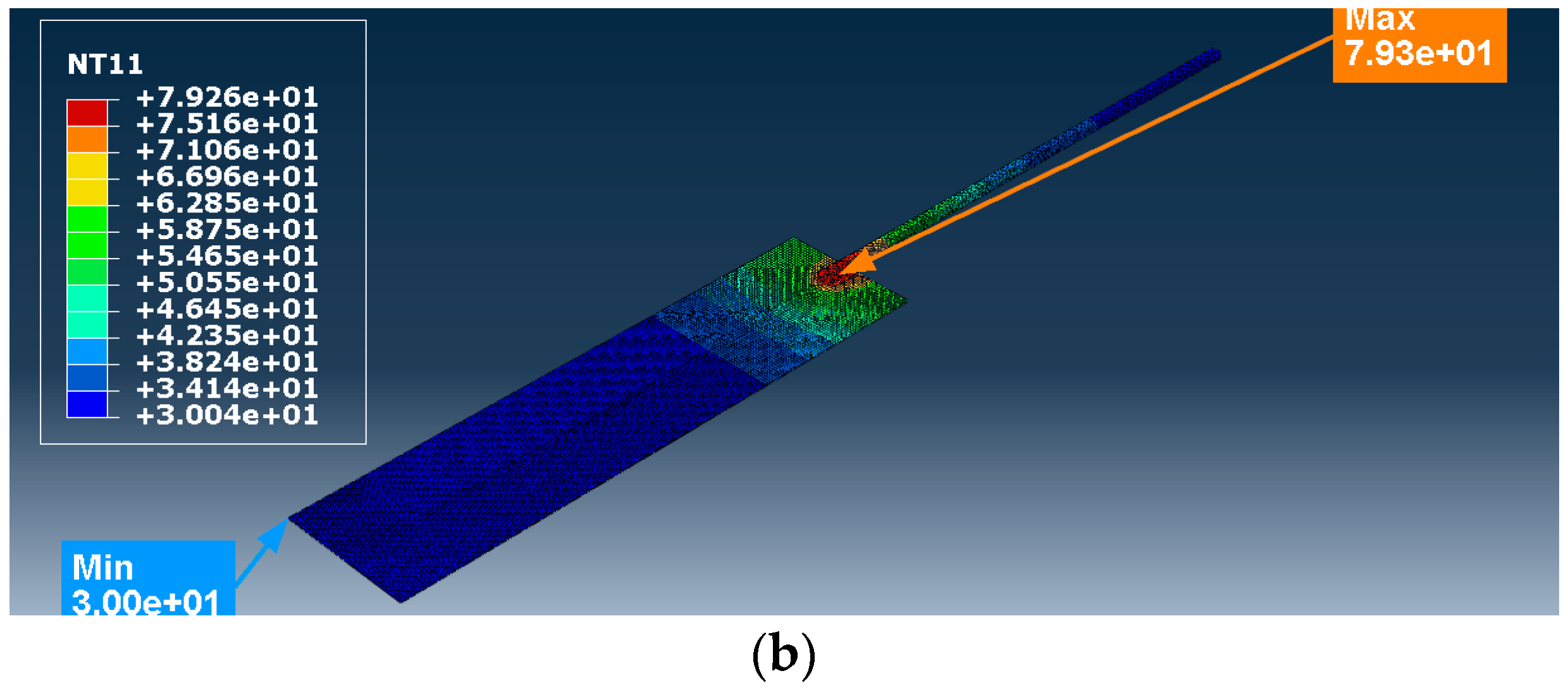
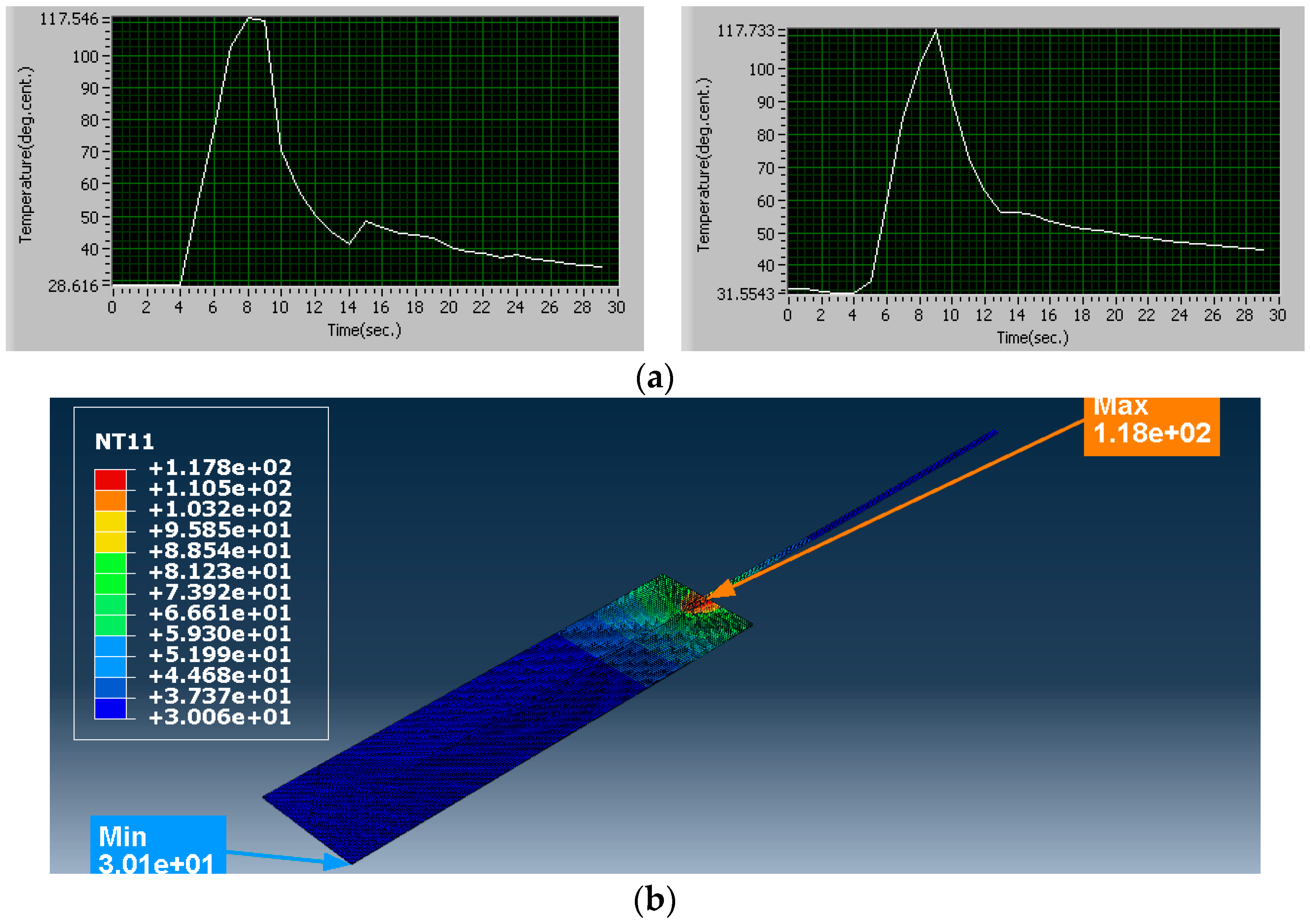
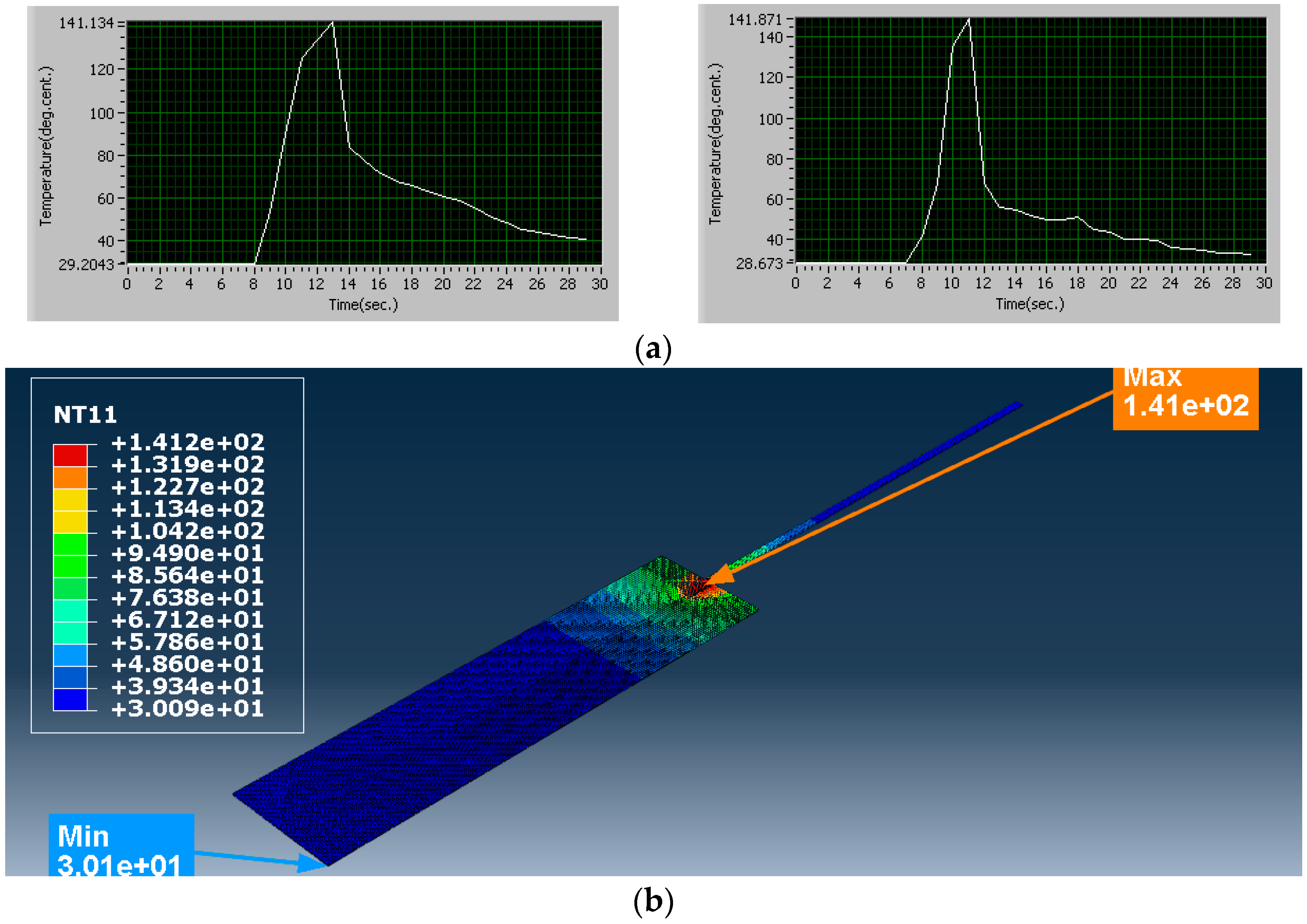
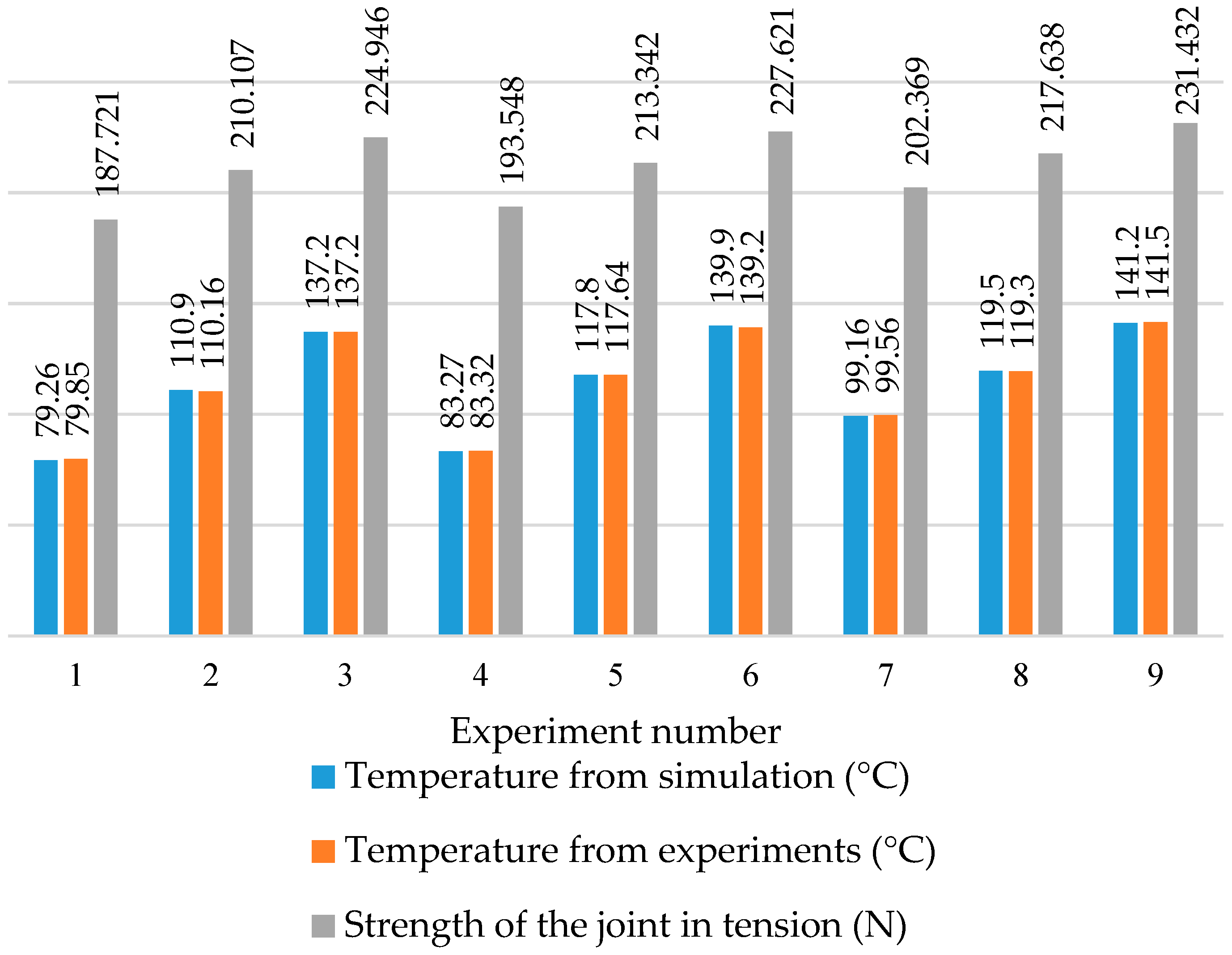
5. Results and Discussions
6. Conclusions
- The results from simulation and experiments conducted based on Taguchi’s L9 orthogonal array reveal that the maximum temperature developed during welding is less than the melting point of the work material, validating that the USMW is a solid state welding process.
- It is observed from the analysis that the influence of heat generated due to deformation and friction is significant in the process of formation of joint. The results of temperature from simulation are found to be in good agreement with results of temperature from experiments measured using thermocouple. Thus, the developed finite element model is validated.
- The results of temperature developed at the interface are compared with results of strength of the joint under tensile loading. It is inferred that the strength of the joint correlate well with the temperature developed at the interface indicating that the temperature at the interface has significant effect on strength of the joint. It is observed that the strength of the joint depends on the variations of heat generated during welding under different process parametric conditions.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yong, D.; Kim, J.-K. Numerical analysis of ultrasonic wire bonding: Part 2. Effects of bonding parameters on temperature rise. Microelectron. Reliabil. 2008, 48, 149–157. [Google Scholar]
- Elangovan, S.; Ponnayya, S.; Henry, J.; Kalakkath, P. Experimental studies on optimization of process parameters and finite element analysis of temperature and stress distribution on joining of Al–Al and Al–Al2O3 using ultrasonic welding. Int. J. Adv. Manuf. Technol. 2011, 55, 631–640. [Google Scholar]
- Jingzhou, Z.; Li, H.; Choi, H.; Cai, W.; Abell, J.A.; Li, X. Insertable thin film thermocouples for in situ transient temperature monitoring in ultrasonic metal welding of battery tabs. J. Manuf. Process. 2013, 15, 136–140. [Google Scholar]
- Hyung-Seop, S.; de Leon, M. Parametric study in similar ultrasonic spot welding of A5052-H32 alloy sheets. J. Mater. Process. Technol. 2015, 224, 222–232. [Google Scholar]
- Elangovan, S. Experimental and theoretical investigations on temperature distribution at the joint interface for copper joints using ultrasonic welding. Manuf. Rev. 2014, 1, 18. [Google Scholar] [CrossRef]
- Dongkyun, L.; Cai, W. The effect of horn knurl geometry on battery tab ultrasonic welding quality: 2D finite element simulations. J. Manuf. Process. 2017, 28, 428–441. [Google Scholar]
- Jedrasiak, P.; Shercliff, H.R.; Chen, Y.C.; Wang, L.; Prangnell, P.; Robson, J. Modeling of the thermal field in dissimilar alloy ultrasonic welding. J. Mater. Eng. Perform. 2015, 24, 799–807. [Google Scholar] [CrossRef]
- Chen, K.K.; Zhang, Y.S. Numerical analysis of temperature distribution during ultrasonic welding process for dissimilar automotive alloys. Sci. Technol. Weld. Join. 2015, 20, 522–531. [Google Scholar] [CrossRef]
- De Vries, E. Mechanics and Mechanisms of Ultrasonic Metal Welding. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2004. [Google Scholar]
- Elangovan, S.; Semeer, S.; Prakasan, K. Temperature and stress distribution in ultrasonic metal welding—An FEA-based study. J. Mater. Process. Technol. 2009, 209, 1143–1150. [Google Scholar] [CrossRef]
- Gallego-Juárez, J.A.; Graff, K.F. (Eds.) Power Ultrasonics: Applications of High-Intensity Ultrasound; Elsevier: New York, NY, USA, 2014. [Google Scholar]
- Kumar, S.; Wu, C.S.; Padhy, G.K.; Ding, W. Application of ultrasonic vibrations in welding and metal processing: A status review. J. Manuf. Process. 2017, 26, 295–322. [Google Scholar] [CrossRef]
- Mathews, P.G. Design of Experiments with MINITAB; ASQ Quality Press: Milwaukee, WI, USA, 2005. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- ASM International Handbook Committee. Properties and selection: nonferrous alloys and special-purpose materials. ASM Int. 1992, 2, 1143–1144. [Google Scholar]
- Dassault Systems. Abaqus 6.12 Analysis User’s Manual and Element Reference Guide; Dassault Systems: Vélizy-Villacoublay, France, 2013. [Google Scholar]
- Chen, K.; Zhang, Y. Thermal-mechanical analysis of ultrasonic spot welding considering acoustic softening effect. Procedia Eng. 2014, 81, 2117–2122. [Google Scholar] [CrossRef]
- Jeng, Y.-R.; Chen, J.-T.; Cheng, C.-Y. Theoretical and experimental study of a thermal contact conductance model for elastic, elastoplastic and plastic deformation of rough surfaces. Tribol. Lett. 2003, 14, 251–259. [Google Scholar] [CrossRef]
- Kim, W.; Argento, A.; Grima, A.; Scholl, D.; Ward, S. Thermo-mechanical analysis of frictional heating in ultrasonic spot welding of aluminium plates. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2011, 225, 1093–1103. [Google Scholar] [CrossRef]
- Zhou, B.; Thouless, M.D.; Ward, S.M. Determining mode-I cohesive parameters for nugget fracture in ultrasonic spot welds. Int. J. Fract. 2005, 136, 309–326. [Google Scholar] [CrossRef]







| Factors | Units | Designation | Level 1 | Level 2 | Level 3 |
|---|---|---|---|---|---|
| Clamping force | N | A | 795 | 995 | 1195 |
| Amplitude of vibration of sonotrode | µm | B | 30 | 42.5 | 57 |
| Weld time | second | C | 2 | 2.5 | 3 |
| Properties | Value |
|---|---|
| Young’s Modulus (GPa) | 115 |
| Poisson ratio | 0.3 |
| Density (kg/m3) | 8940 |
| Thermal conductivity (W/m °C) | 391 |
| Specific heat (J/Kg °C) | 385 |
| Thermal expansion co-efficient(°C−1) | 1.66 × 10−5 |
| Trial No. | Clamping Force (N) | Amplitude of Vibration of Sonotrode (μm) | Weld Time (s) | Temperature from Simulation (°C) | Temperature from Experiments (°C) | Strength of the Joint in Tension * (N) | ||
|---|---|---|---|---|---|---|---|---|
| Trial 1 | Trial 2 | Average | ||||||
| 1 | 795 | 30 | 2 | 79.26 | 79.97 | 79.73 | 79.85 | 187.721 |
| 2 | 995 | 30 | 2.5 | 110.9 | 110.06 | 110.25 | 110.16 | 210.107 |
| 3 | 1195 | 30 | 3 | 137.2 | 137.38 | 137.01 | 137.20 | 224.946 |
| 4 | 795 | 42.5 | 2 | 83.27 | 83.25 | 83.39 | 83.32 | 193.548 |
| 5 | 995 | 42.5 | 2.5 | 117.8 | 117.55 | 117.73 | 117.64 | 213.342 |
| 6 | 1195 | 42.5 | 3 | 139.9 | 139.01 | 139.38 | 139.20 | 227.621 |
| 7 | 795 | 57 | 2 | 99.16 | 99.74 | 99.37 | 99.56 | 202.369 |
| 8 | 995 | 57 | 2.5 | 119.5 | 119.60 | 119.00 | 119.30 | 217.638 |
| 9 | 1195 | 57 | 3 | 141.2 | 141.13 | 141.87 | 141.50 | 231.432 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pradeep Kumar, J. Effect of Temperature Distribution in Ultrasonically Welded Joints of Copper Wire and Sheet Used for Electrical Contacts. Materials 2018, 11, 1010. https://doi.org/10.3390/ma11061010
Pradeep Kumar J. Effect of Temperature Distribution in Ultrasonically Welded Joints of Copper Wire and Sheet Used for Electrical Contacts. Materials. 2018; 11(6):1010. https://doi.org/10.3390/ma11061010
Chicago/Turabian StylePradeep Kumar, Jeyaraj. 2018. "Effect of Temperature Distribution in Ultrasonically Welded Joints of Copper Wire and Sheet Used for Electrical Contacts" Materials 11, no. 6: 1010. https://doi.org/10.3390/ma11061010
APA StylePradeep Kumar, J. (2018). Effect of Temperature Distribution in Ultrasonically Welded Joints of Copper Wire and Sheet Used for Electrical Contacts. Materials, 11(6), 1010. https://doi.org/10.3390/ma11061010