Electronic, Magnetic, Half-Metallic, and Mechanical Properties of a New Equiatomic Quaternary Heusler Compound YRhTiGe: A First-Principles Study
Abstract
:1. Introduction
2. Computational Method
2.1. Electronic and Magnetic Behavior
2.2. Elastic Properties
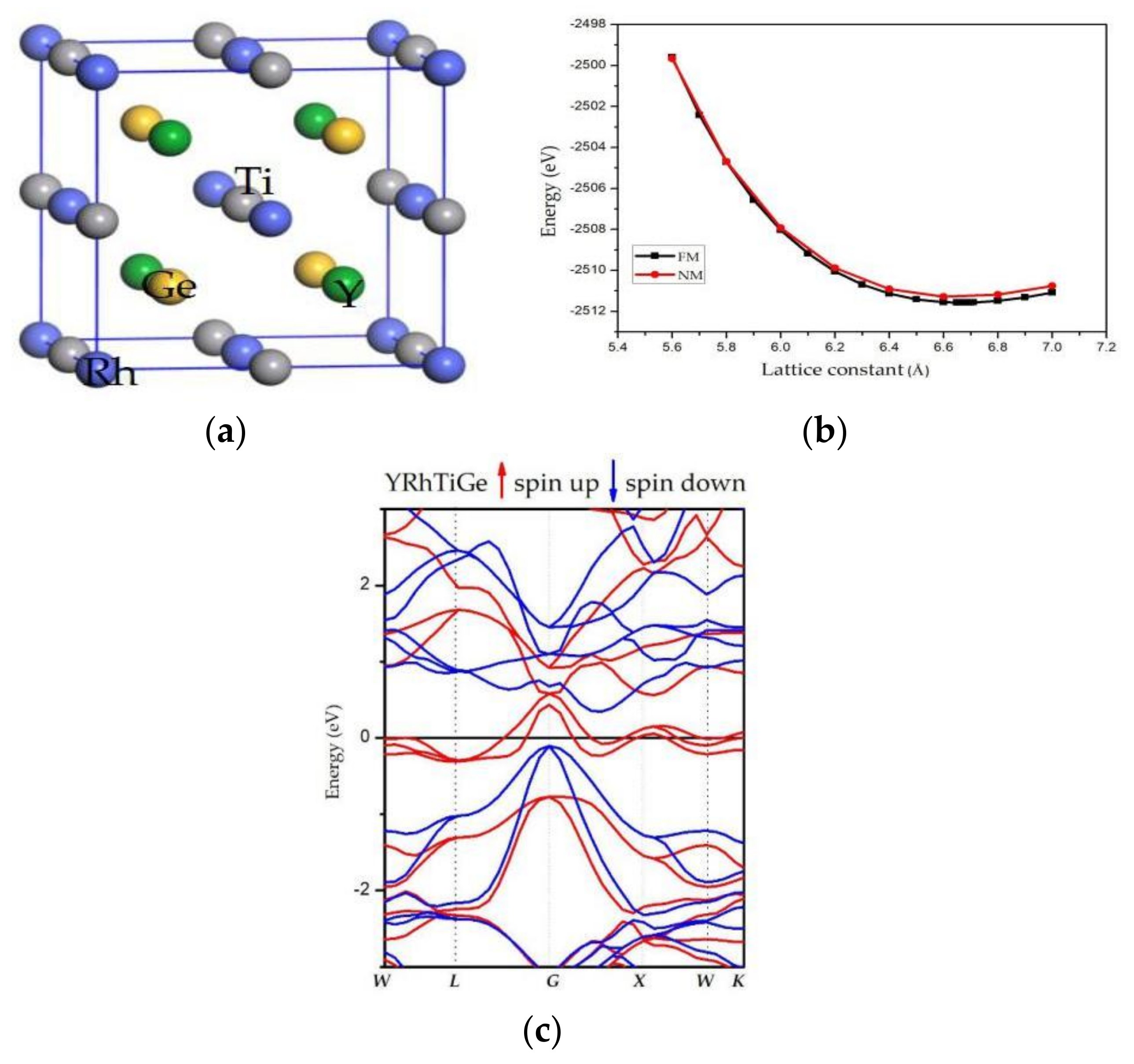
2.3. Crystal Structure
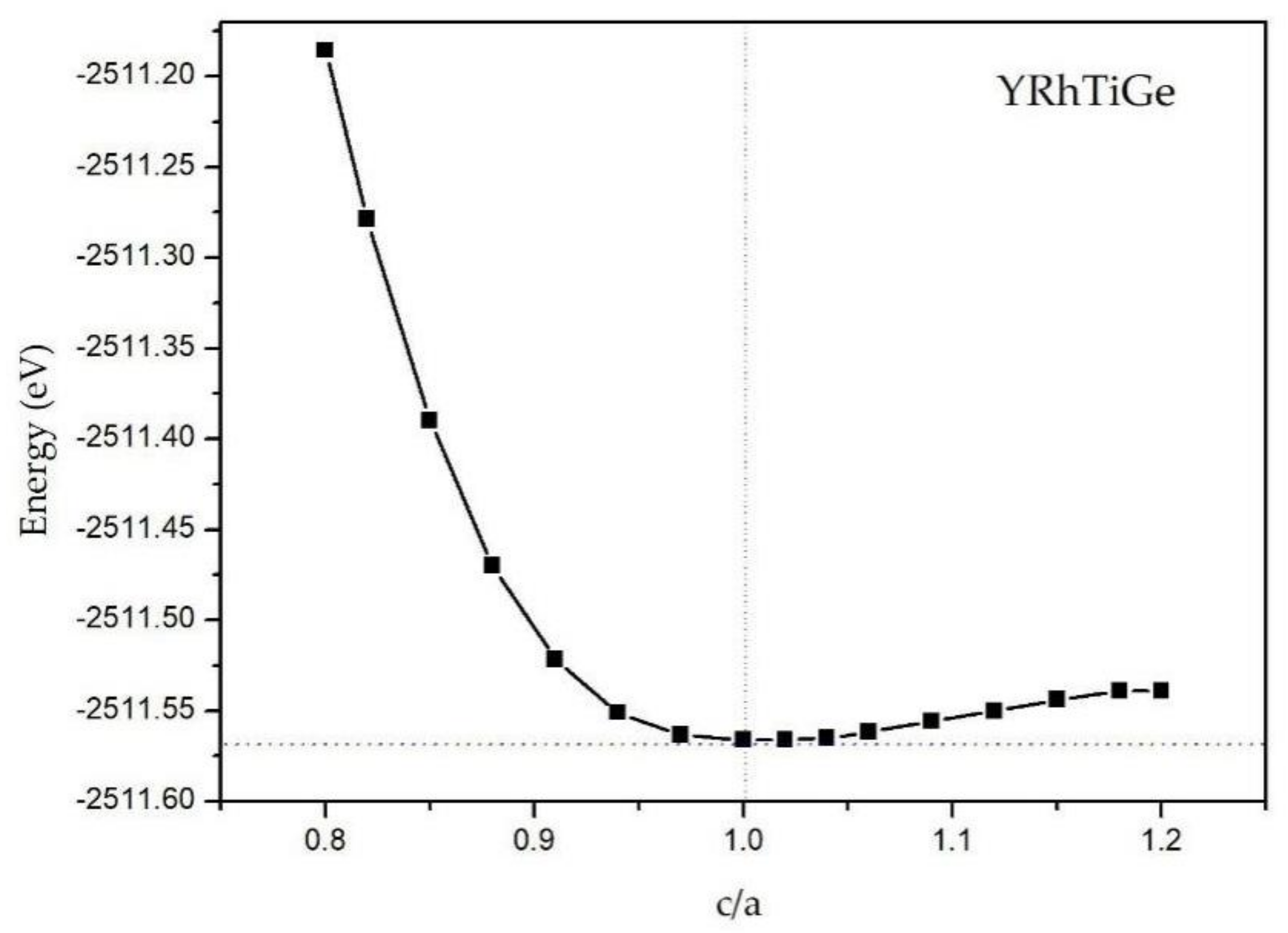
2.4. Geometry Optimization
3. Results and Discussion
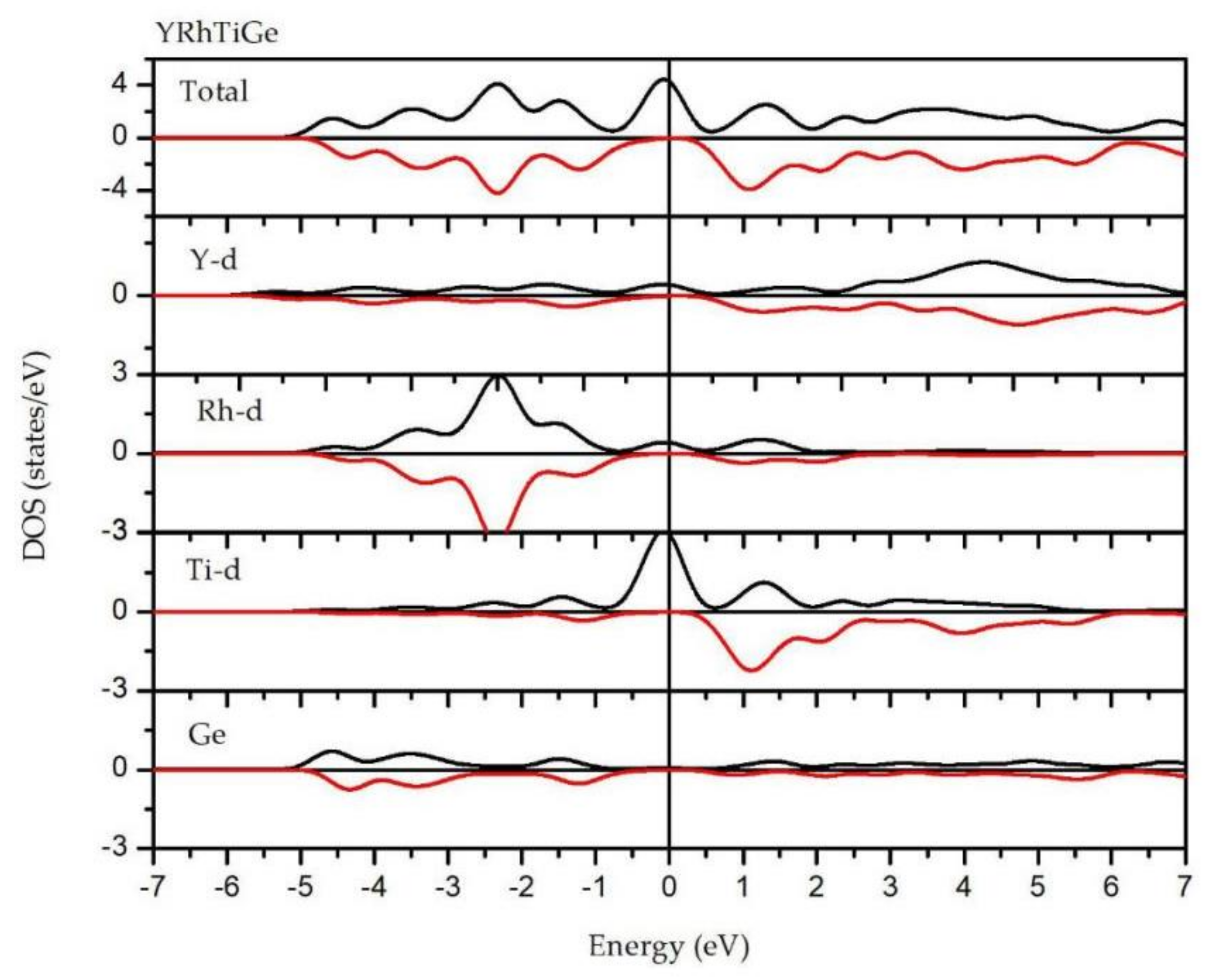
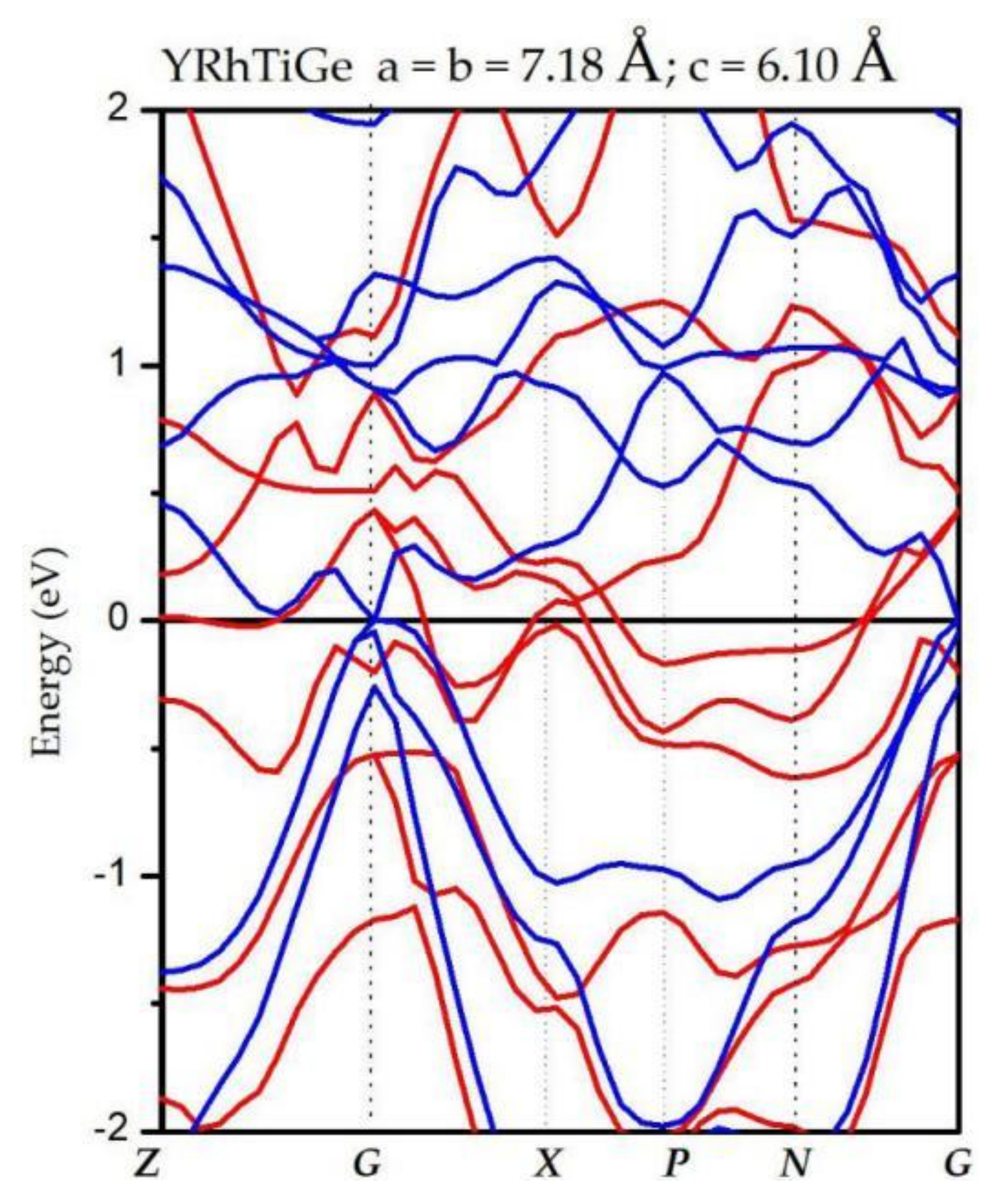
3.1. Electronic Properties
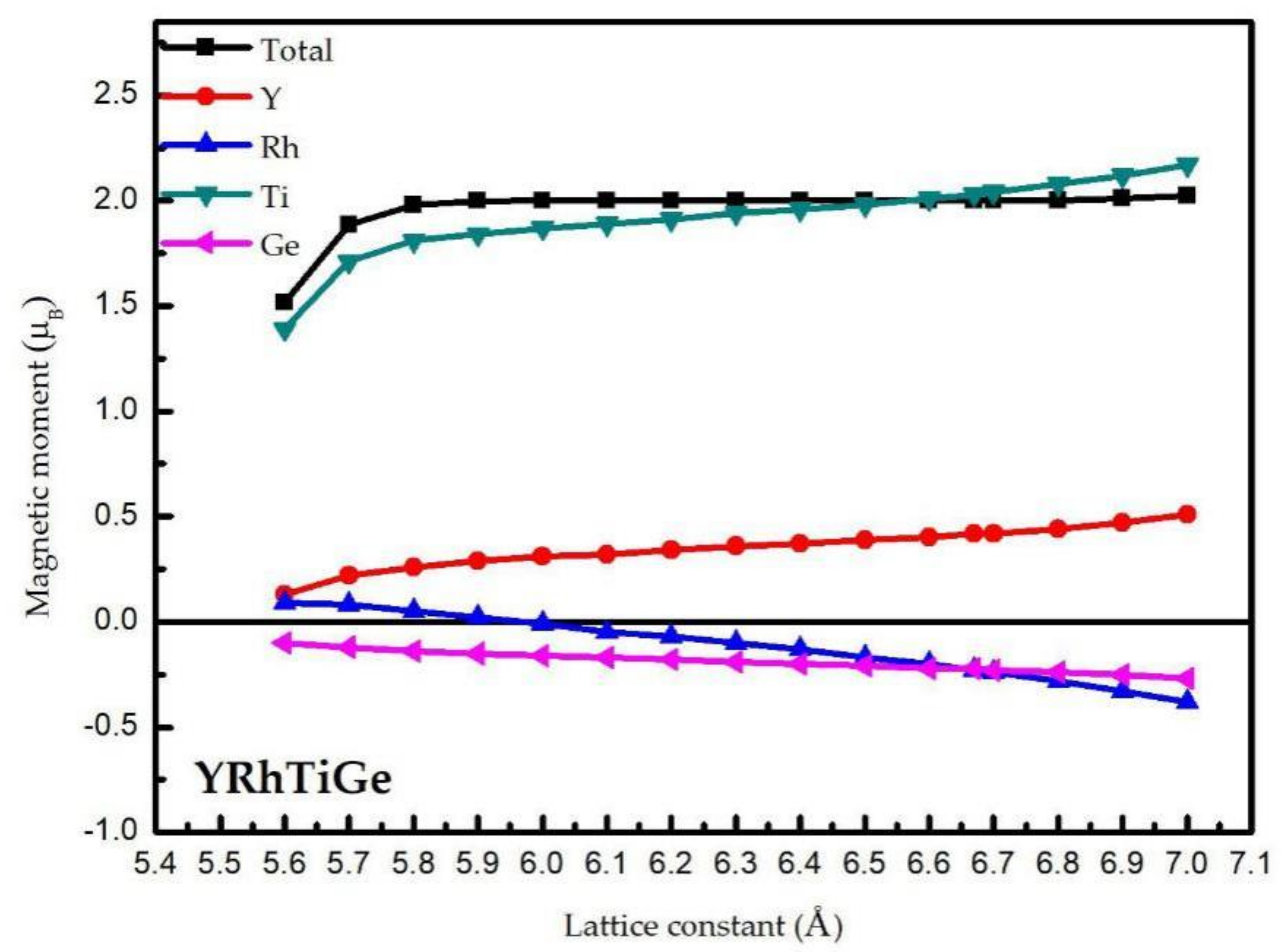
3.2. Magnetism and Slater–Pauling Rule
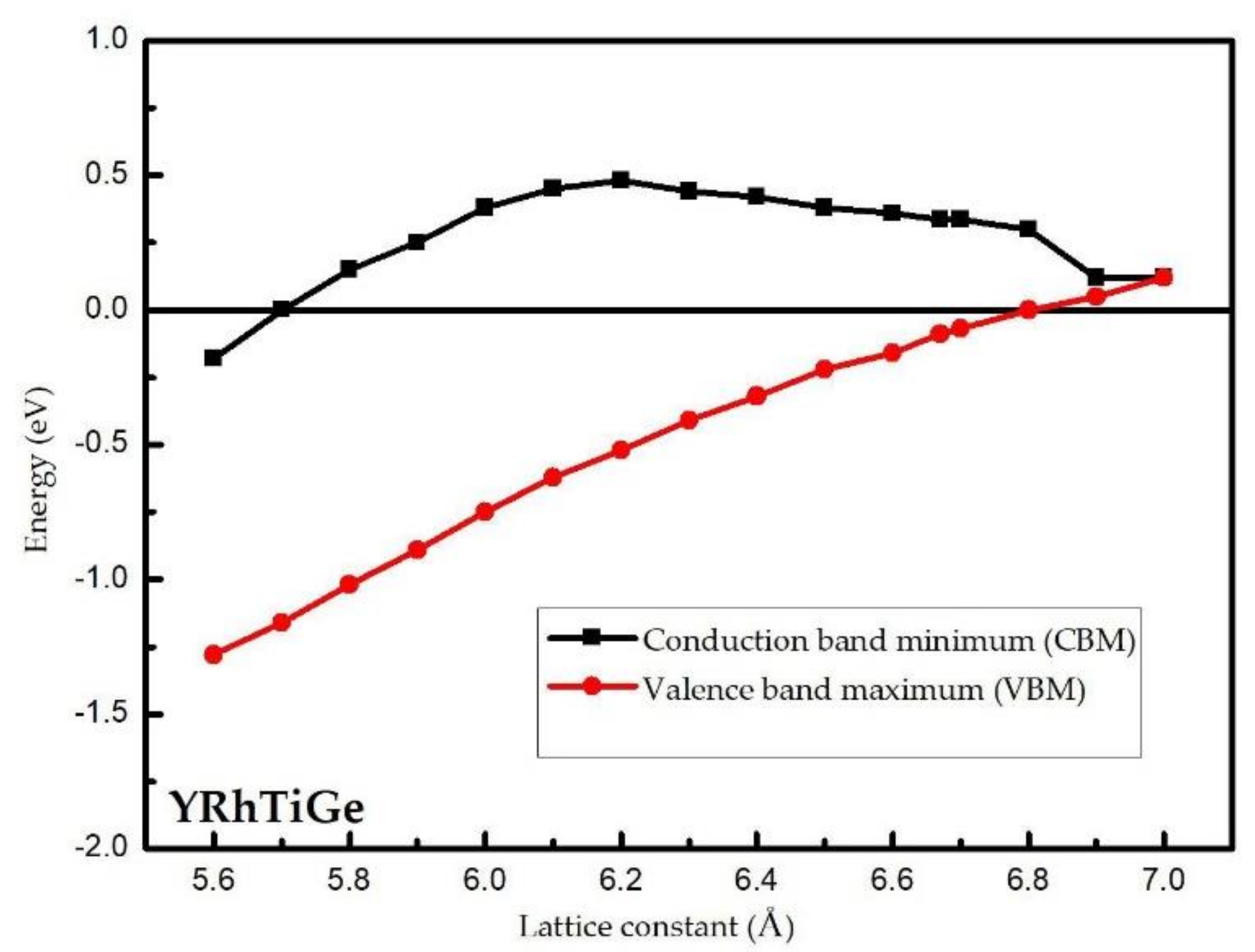
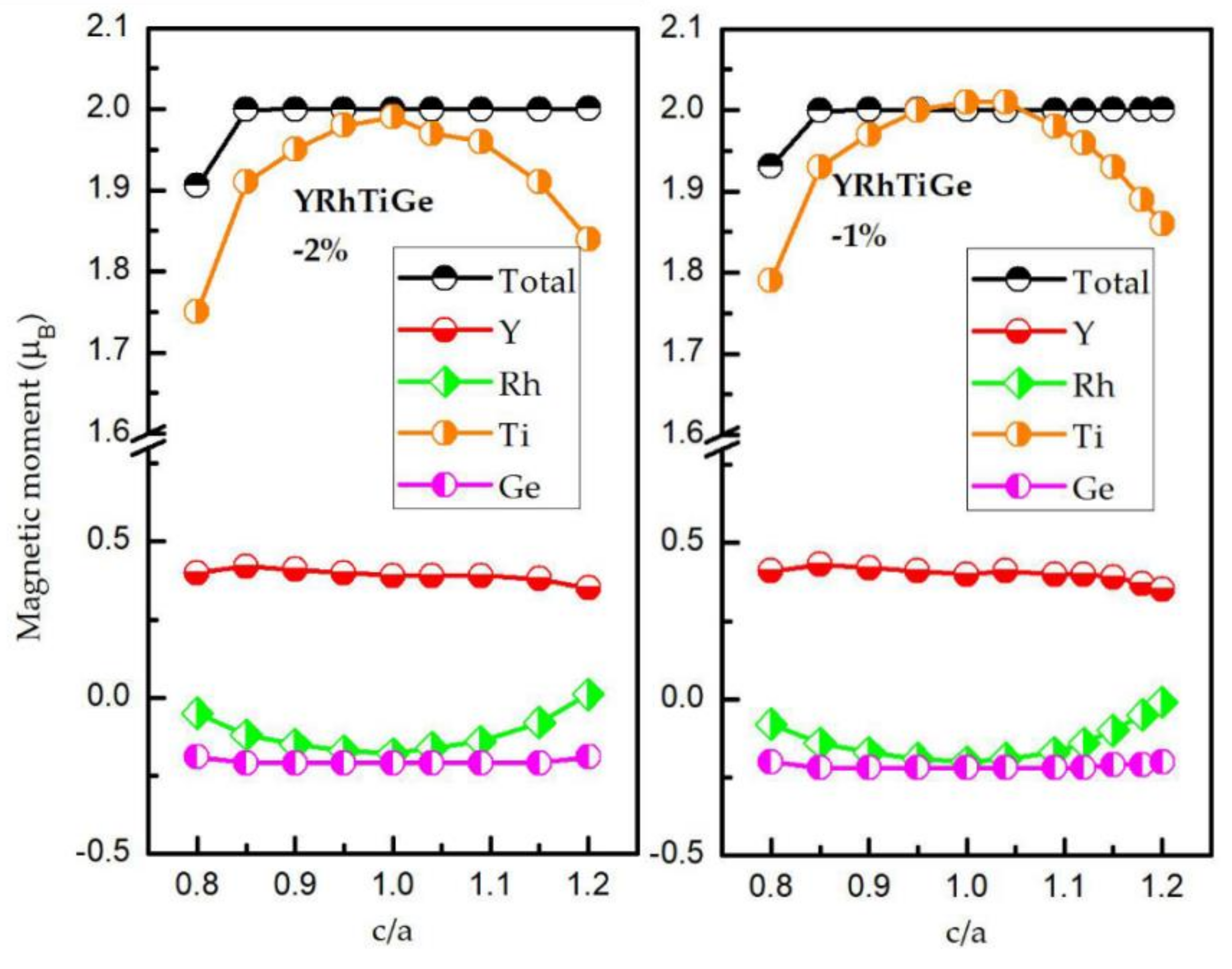
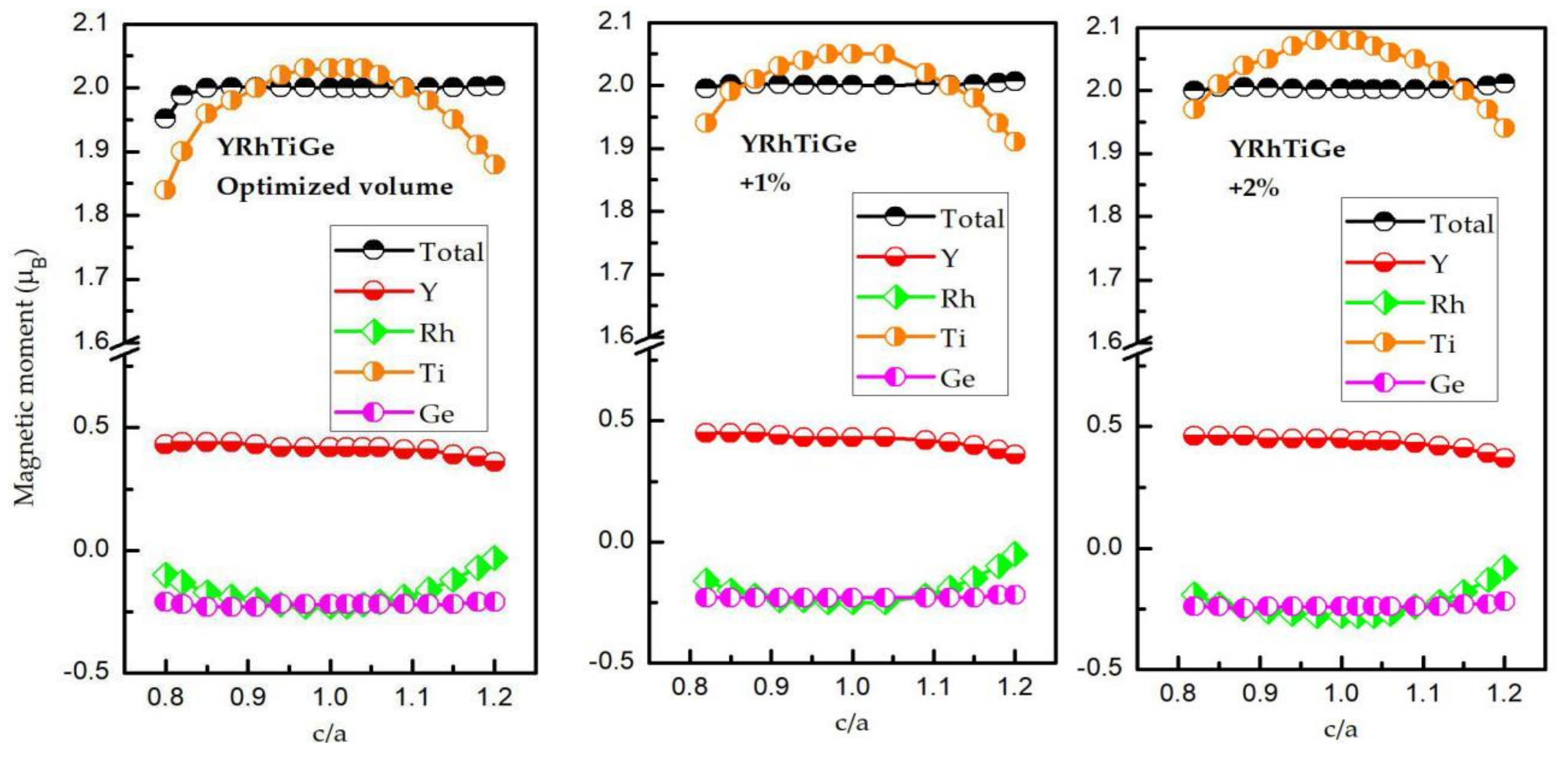
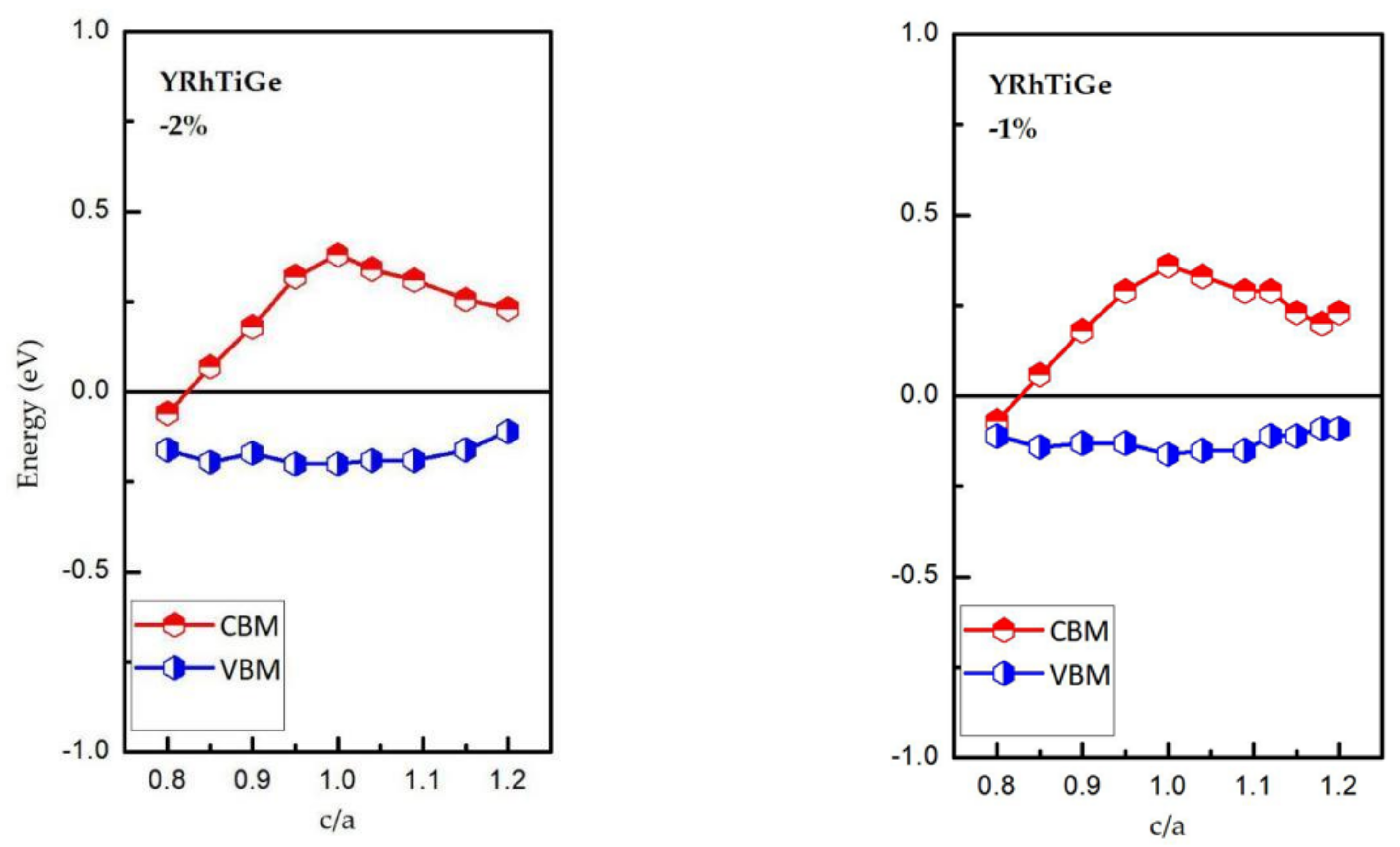
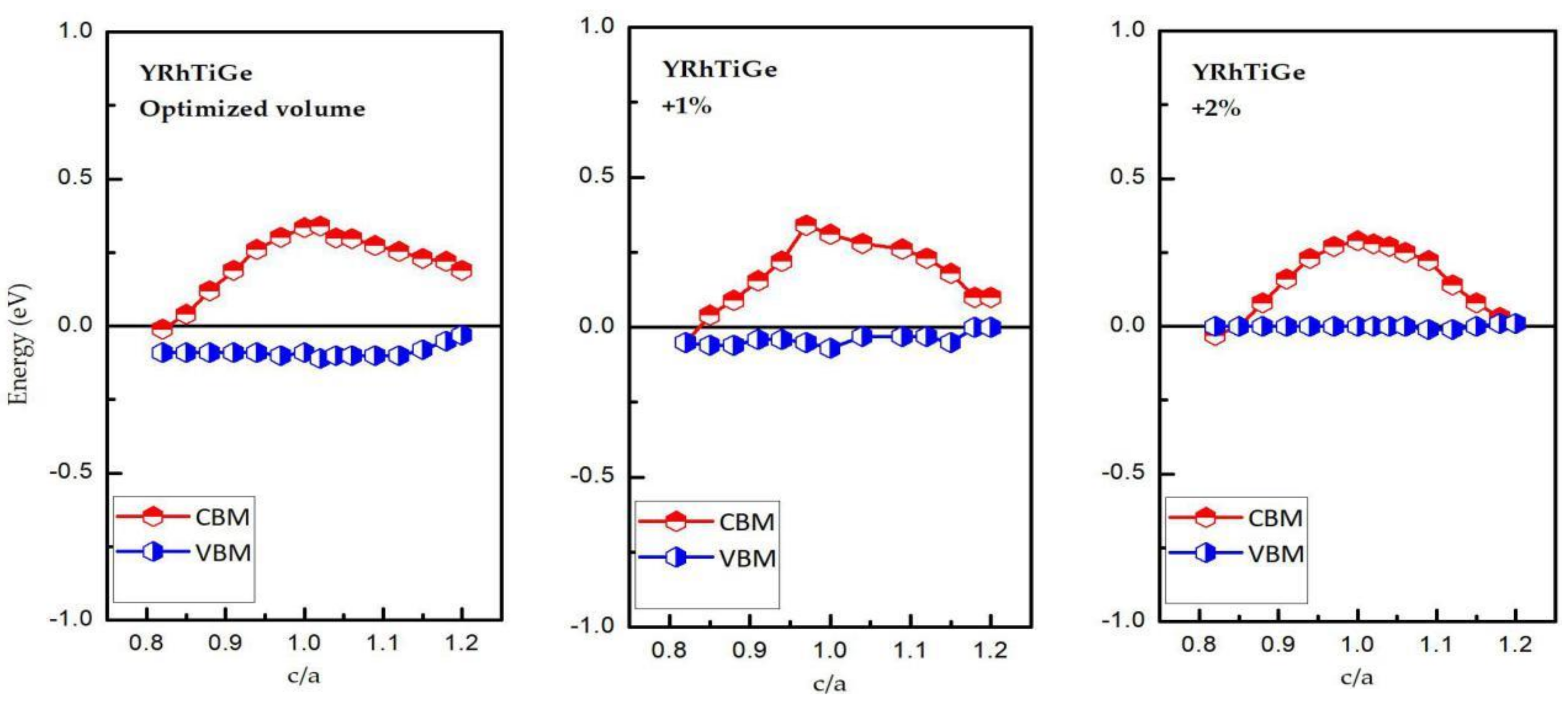
3.3. Effect of Uniform Strain and Tetragonal Deformation on the Magneto-Electronic Proprieties
- Uniform strain: For different uniform strains, although the crystal lattice maintains its cubic close-packed structure, the lattice constant tends to change.
- Tetragonal deformation: The cubic unit cell is compressed/stretched into a tetragonal one. That is, we keep the tetragonal unit cell with volume, (a = b), and the equilibrium bulk volume, , equal, while the c/a ratio changes from 0.80 to 1.20. Additionally, the tetragonal unit cell changes from −2%, −1%, 0%, 1%, and 2% Vequilibrium have also been considered into account.
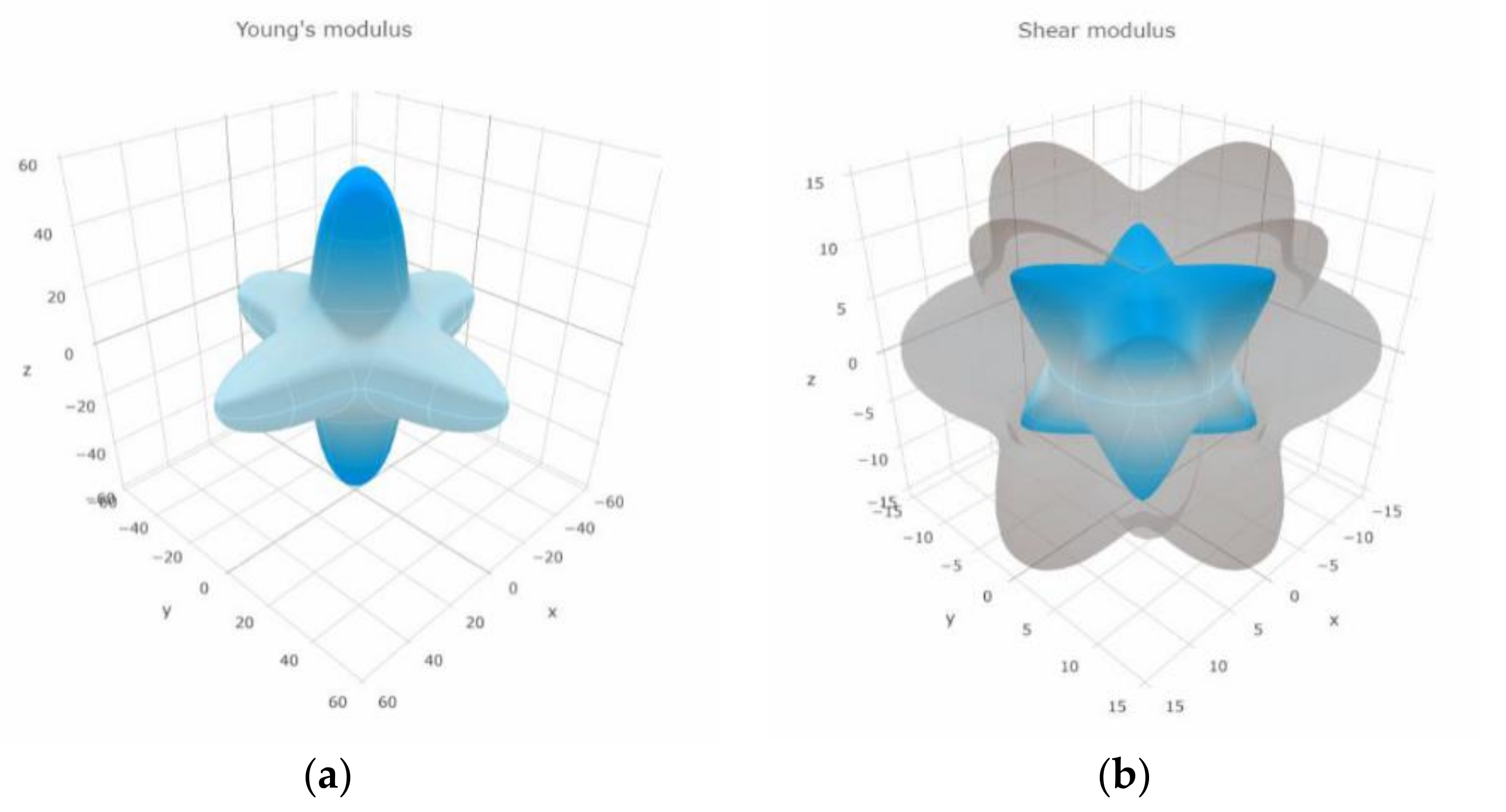
3.4. Mechanical Proprieties
3.5. Formation and Cohesive Energies
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- De Groot, R.A.; Mueller, F.M.; Van Engen, P.G.; Buschow, K.H.J. New class of materials: Half-metallic ferromagnets. Phys. Rev. Lett. 1983, 50, 2024. [Google Scholar] [CrossRef]
- Van Leuken, H.; De Groot, R.A. Half-metallic antiferromagnets. Phys. Rev. Lett. 1995, 74, 1171. [Google Scholar] [CrossRef] [PubMed]
- Gao, G.Y.; Hu, L.; Yao, K.L.; Luo, B.; Liu, N. Large half-metallic gaps in the quaternary Heusler alloys CoFeCrZ (Z = Al, Si, Ga, Ge): A first-principles study. J. Alloys Compd. 2013, 551, 539–543. [Google Scholar] [CrossRef]
- Alijani, V.; Ouardi, S.; Fecher, G.H.; Winterlik, J.; Naghavi, S.S.; Kozina, X.; Ueda, S. Electronic, structural, and magnetic properties of the half-metallic ferromagnetic quaternary Heusler compounds CoFeMnZ (Z = Al, Ga, Si, Ge). Phys. Rev. B 2011, 84, 224416. [Google Scholar] [CrossRef]
- Bainsla, L.; Mallick, A.I.; Raja, M.M.; Nigam, A.K.; Varaprasad, B.C.S.; Takahashi, Y.K.; Hono, K. Spin gapless semiconducting behavior in equiatomic quaternary CoFeMnSi Heusler alloy. Phys. Rev. B 2015, 91, 104408. [Google Scholar] [CrossRef]
- Bainsla, L.; Mallick, A.I.; Coelho, A.A.; Nigam, A.K.; Varaprasad, B.C.S.; Takahashi, Y.K.; Hono, K. High spin polarization and spin splitting in equiatomic quaternary CoFeCrAl Heusler alloy. J. Magn. Magn. Mater. 2015, 394, 82–86. [Google Scholar] [CrossRef]
- Bainsla, L.; Suresh, K.G. Equiatomic quaternary Heusler alloys: A material perspective for spintronic applications. Appl. Phys. Rev. 2016, 3, 031101. [Google Scholar] [CrossRef]
- Feng, Y.; Chen, X.; Zhou, T.; Yuan, H.; Chen, H. Structural stability, half-metallicity and magnetism of the CoFeMnSi/GaAs (0 0 1) interface. Appl. Surf. Sci. 2015, 346, 1–10. [Google Scholar] [CrossRef]
- Heusler, O. Kristallstruktur und Ferromagnetismus der Mangan-Aluminium-Kupferlegierungen. Ann. Phys. 1934, 411, 155–201. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, Z.; Liu, G. Largest magnetic moments in the half-Heusler alloys XCrZ (X = Li, K, Rb, Cs; Z= S, Se, Te): A first-principles study. Materials 2017, 10, 1078. [Google Scholar] [CrossRef] [PubMed]
- Xiao, D.; Yao, Y.; Feng, W.; Wen, J.; Zhu, W.; Chen, X.Q.; Zhang, Z. Half-Heusler compounds as a new class of three-dimensional topological insulators. Phys. Rev. Lett. 2010, 105, 096404. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Hou, Z.; Wang, Y.; Xu, G.; Shi, C.; Liu, E.; Zhang, X.X. NMR evidence for the topologically nontrivial nature in a family of half-Heusler compounds. Sci. Rep. 2016, 6, 23172. [Google Scholar] [CrossRef] [PubMed]
- Chibani, S.; Arbouche, O.; Zemouli, M.; Amara, K.; Benallou, Y.; Azzaz, Y.; Ameri, M. Ab Initio Prediction of the Structural, Electronic, Elastic, and Thermoelectric Properties of Half-Heusler Ternary Compounds TiIrX (X = As and Sb). J. Electron. Mater. 2018, 47, 196–204. [Google Scholar] [CrossRef]
- Galanakis, I.; Dederichs, P.H.; Papanikolaou, N. Slater-Pauling behavior and origin of the half-metallicity of the full-Heusler alloys. Phys. Rev. B 2002, 66, 174429. [Google Scholar] [CrossRef]
- Akriche, A.; Bouafia, H.; Hiadsi, S.; Abidri, B.; Sahli, B.; Elchikh, M.; Djebour, B. First-principles study of mechanical, exchange interactions and the robustness in Co2MnSi full Heusler compounds. J. Magn. Magn. Mater. 2017, 422, 13–19. [Google Scholar] [CrossRef]
- Babiker, S.; Gao, G.; Yao, K. Half-metallicity and magnetism of Heusler alloys Co2HfZ (Z = Al, Ga, Ge, Sn). J. Magn. Magn. Mater. 2017, 441, 356–360. [Google Scholar] [CrossRef]
- Bahramian, S.; Ahmadian, F. Half-metallicity and magnetism of quaternary Heusler compounds CoRuTiZ (Z = Si, Ge, and Sn). J. Magn. Magn. Mater. 2017, 424, 122–129. [Google Scholar] [CrossRef]
- Kang, X.H.; Zhang, J.M. The structural, electronic and magnetic properties of a novel quaternary Heusler alloy TiZrCoSn. J. Phys. Chem. Solids 2017, 105, 9–15. [Google Scholar] [CrossRef]
- Wang, J.X.; Chen, Z.B.; Gao, Y.C. Phase stability, magnetic, electronic, half-metallic and mechanical properties of a new equiatomic quaternary Heusler compound ZrRhTiIn: A first-principles investigation. J. Phys. Chem. Solids 2018, 116, 72–78. [Google Scholar] [CrossRef]
- Feng, Y.; Xu, X.; Cao, W.; Zhou, T. Investigation of cobalt and silicon co-doping in quaternary Heusler alloy NiFeMnSn. Comput. Mater. Sci. 2018, 147, 251–257. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, Z.; Jin, Y.; Wu, Y.; Dai, X.; Liu, G. Magneto-electronic properties and tetragonal deformation of rare-earth-element-based quaternary Heusler half-metals: A first-principles prediction. J. Alloys Compd. 2018, 734, 329–341. [Google Scholar] [CrossRef]
- Rasool, M.N.; Hussain, A.; Javed, A.; Khan, M.A.; Iqbal, F. Structural stability, electronic and magnetic behaviour of spin-polarized YCoVZ (Z = Si, Ge) and YCoTiZ (Z = Si, Ge) Heusler alloys. Mater. Chem. Phys. 2016, 183, 524–533. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X.; Cheng, Z. Electronic, magnetic, mechanical, half-metallic and highly dispersive zero-gap half-metallic properties of rare-earth-element-based quaternary Heusler compounds. J. Alloys Compd. 2017, 718, 63–74. [Google Scholar] [CrossRef]
- Rasool, M.N.; Mehmood, S.; Sattar, M.A.; Khan, M.A.; Hussain, A. Investigation of structural, electronic and magnetic properties of 1:1:1:1 stoichiometric quaternary Heusler alloys YCoCrZ (Z = Si, Ge, Ga, Al): An ab-initio study. J. Magn. Magn. Mater. 2015, 395, 97–108. [Google Scholar] [CrossRef]
- Xu, G.; You, Y.; Gong, Y.; Liu, E.; Xu, F.; Wang, W. Highly-dispersive spin gapless semiconductors in rare-earth-element contained quaternary Heusler compounds. J. Phys. D Appl. Phys. 2017, 50, 105003. [Google Scholar] [CrossRef]
- Rahmoune, M.; Chahed, A.; Amar, A.; Rozale, H.; Lakdja, A.; Benhelal, O.; Sayede, A. The effect of pressure and alloying on half-metallicity of quaternary Heusler compounds CoMnYZ (Z = Al, Ga, and In). Mater. Sci.-Pol. 2016, 34, 905–915. [Google Scholar] [CrossRef]
- Rasool, M.N.; Hussain, A.; Javed, A.; Khan, M.A. Study of the structural, electronic and magnetic properties of ScFeCrT (T = Si, Ge) Heusler alloys by first principles approach. J. Magn. Magn. Mater. 2017, 426, 421–428. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, Z.; Liu, G.; Dai, X.; Khenata, R.; Wang, L.; Bouhemadou, A. Rare earth-based quaternary Heusler compounds MCoVZ (M = Lu, Y; Z = Si, Ge) with tunable band characteristics for potential spintronic applications. IUCrJ 2017, 4, 758–768. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Feng, L.; Guo, R.; Liao, Y.; Khenata, R.; Liu, G.; Wang, L. New Half-Metallic Materials: FeRuCrP and FeRhCrP Quaternary Heusler Compounds. Materials 2017, 10, 1367. [Google Scholar] [CrossRef] [PubMed]
- Segall, M.D.; Lindan, P.J.; Probert, M.A.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik (mit Ausschluss der Kristalloptik); Springer: Berlin, Germany, 2014. [Google Scholar]
- Reuss, A. Calculation of the flow limits of mixed crystals on the basis of the plasticity of monocrystals. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Haines, J.; Leger, J.M.; Bocquillon, G. Synthesis and design of superhard materials. Annu. Rev. Mater. Res. 2001, 31, 1–23. [Google Scholar] [CrossRef]
- Zhang, L.; Cheng, Z.X.; Wang, X.T.; Khenata, R.; Rozale, H. First-principles investigation of equiatomic quaternary heusler alloys NbVMnAl and NbFeCrAl and a discussion of the generalized electron-filling rule. J. Superconduct. Nov. Magn. 2018, 31, 189–196. [Google Scholar] [CrossRef]
- Özdoğan, K.; Şaşıoğlu, E.; Galanakis, I. Slater-Pauling behavior in LiMgPdSn-type multifunctional quaternary Heusler materials: Half-metallicity, spin-gapless and magnetic semiconductors. J. Appl. Phys. 2013, 113, 193903. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Matori, K.A.; Zaid, M.H.M.; Sidek, H.A.A.; Halimah, M.K.; Wahab, Z.A.; Sabri, M.G.M. Influence of ZnO on the ultrasonic velocity and elastic moduli of soda lime silicate glasses. Int. J. Phys. Sci. 2010, 5, 2212–2216. [Google Scholar]
- Nye, J.F. Physical Properties of Crystals: Their Representation by Tensors and Matrices; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Luo, H.; Xin, Y.; Liu, B.; Meng, F.; Liu, H.; Liu, E.; Wu, G. Competition of L21 and XA structural ordering in Heusler alloys X2CuAl (X = Sc, Ti, V, Cr, Mn, Fe, Co, Ni). J. Alloys Compd. 2016, 665, 180–185. [Google Scholar] [CrossRef]
- Gao, Q.; Li, L.; Lei, G.; Deng, J.B.; Hu, X.R. A first-principle study on the properties of a new series of quaternary Heusler alloys CoFeScZ (Z = P, As, Sb). J. Magn. Magn. Mater. 2015, 379, 288–293. [Google Scholar] [CrossRef]
- Kundu, A.; Ghosh, S.; Banerjee, R.; Ghosh, S.; Sanyal, B. New quaternary half-metallic ferromagnets with large Curie temperatures. Sci. Rep. 2017, 2015, 7–1803. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Cheng, Z.; Wang, W. L21 and XA Ordering Competition in Hafnium-Based Full-Heusler Alloys Hf2VZ (Z = Al, Ga, In, Tl, Si, Ge, Sn, Pb). Materials 2017, 10, 1200. [Google Scholar] [CrossRef] [PubMed]
| Type/Atom | Y | Rh | Ti | Ge |
|---|---|---|---|---|
| Type 1 | D (0.75, 0.75, 0.75) | B (0.25, 0.25, 0.25) | C (0.5, 0.5, 0.5) | A (0, 0, 0) |
| Type 2 | D (0.75, 0.75, 0.75) | C (0.5, 0.5, 0.5) | B (0.25, 0.25, 0.25) | A (0, 0, 0) |
| * Type 3 | D (0.75, 0.75, 0.75) | A (0, 0, 0) | C (0.5, 0.5, 0.5) | B (0.25, 0.25, 0.25) |
| Compound | Total | Y | Rh | Ti | Ge | a (Å) |
|---|---|---|---|---|---|---|
| YRhTiGe | 2.00 | 0.42 | −0.23 | 2.03 | −0.22 | 6.67 |
| Compound | Formation Energy | Cohesive Energy | Band-Gap | Zt | S-P Rule | P (%) |
|---|---|---|---|---|---|---|
| YRhTiGe | −1.38 | 20.13 | 0.42 | 20 | Mt = Zt − 18 | 100 |
| Compound | C11 (GPa) | C12 (GPa) | C44 (GPa) | B (GPa) | G (GPa) | E (GPa) | υ |
|---|---|---|---|---|---|---|---|
| YRhTiGe | 137.2 | 96.5 | 7.74 | 110.1 | 11.53 | 33.4 | 0.44 |
| Compound | λ (GPa) | µ (GPa) | ζ | H (GPa) |
|---|---|---|---|---|
| YRhTiGe | 102.38 | 11.536 | 0.788 | 0.389 |
| Compound | Compliance (10−3 GPa−1) | η | ||
|---|---|---|---|---|
| S11 | S12 | S44 | ||
| YRhTiGe | 0.017 | 7.18 | 0.129 | 0.3803 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Wu, Y.; Li, T.; Khenata, R.; Yang, T.; Wang, X. Electronic, Magnetic, Half-Metallic, and Mechanical Properties of a New Equiatomic Quaternary Heusler Compound YRhTiGe: A First-Principles Study. Materials 2018, 11, 797. https://doi.org/10.3390/ma11050797
Han Y, Wu Y, Li T, Khenata R, Yang T, Wang X. Electronic, Magnetic, Half-Metallic, and Mechanical Properties of a New Equiatomic Quaternary Heusler Compound YRhTiGe: A First-Principles Study. Materials. 2018; 11(5):797. https://doi.org/10.3390/ma11050797
Chicago/Turabian StyleHan, Yilin, Yang Wu, Tingzhou Li, R. Khenata, Tie Yang, and Xiaotian Wang. 2018. "Electronic, Magnetic, Half-Metallic, and Mechanical Properties of a New Equiatomic Quaternary Heusler Compound YRhTiGe: A First-Principles Study" Materials 11, no. 5: 797. https://doi.org/10.3390/ma11050797
APA StyleHan, Y., Wu, Y., Li, T., Khenata, R., Yang, T., & Wang, X. (2018). Electronic, Magnetic, Half-Metallic, and Mechanical Properties of a New Equiatomic Quaternary Heusler Compound YRhTiGe: A First-Principles Study. Materials, 11(5), 797. https://doi.org/10.3390/ma11050797







