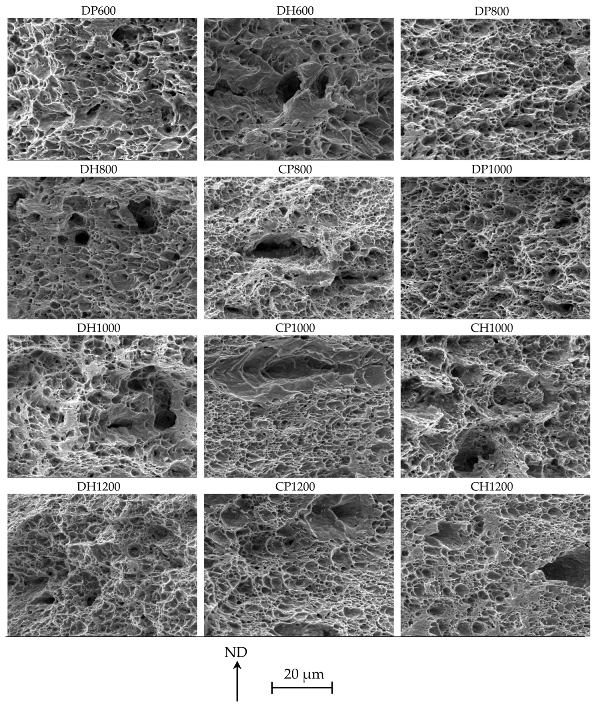
1. Introduction
Body-in-white development is strongly driven by both targets reducing CO
2 emissions and increasing crash safety. One way to reduce CO
2 emissions via lightweight design is the reduction of component thickness. This is only possible with increasing materials strength. Therefore, a wide range of high-strength multiphase steels for various applications has been developed in the last decades. Their respective mechanical properties are directly related to the underlying thermo-mechanical processing and composition dependent microstructure. Characteristics of this microstructure are: phase distribution, phase morphology, phase hardness and hardness difference between phases, grain and particle size, texture and density of geometrically necessary dislocations [
1]. These complex microstructures lead to a complex forming and fracture behaviour, which cannot be described only by the terms formability or rather ductility.
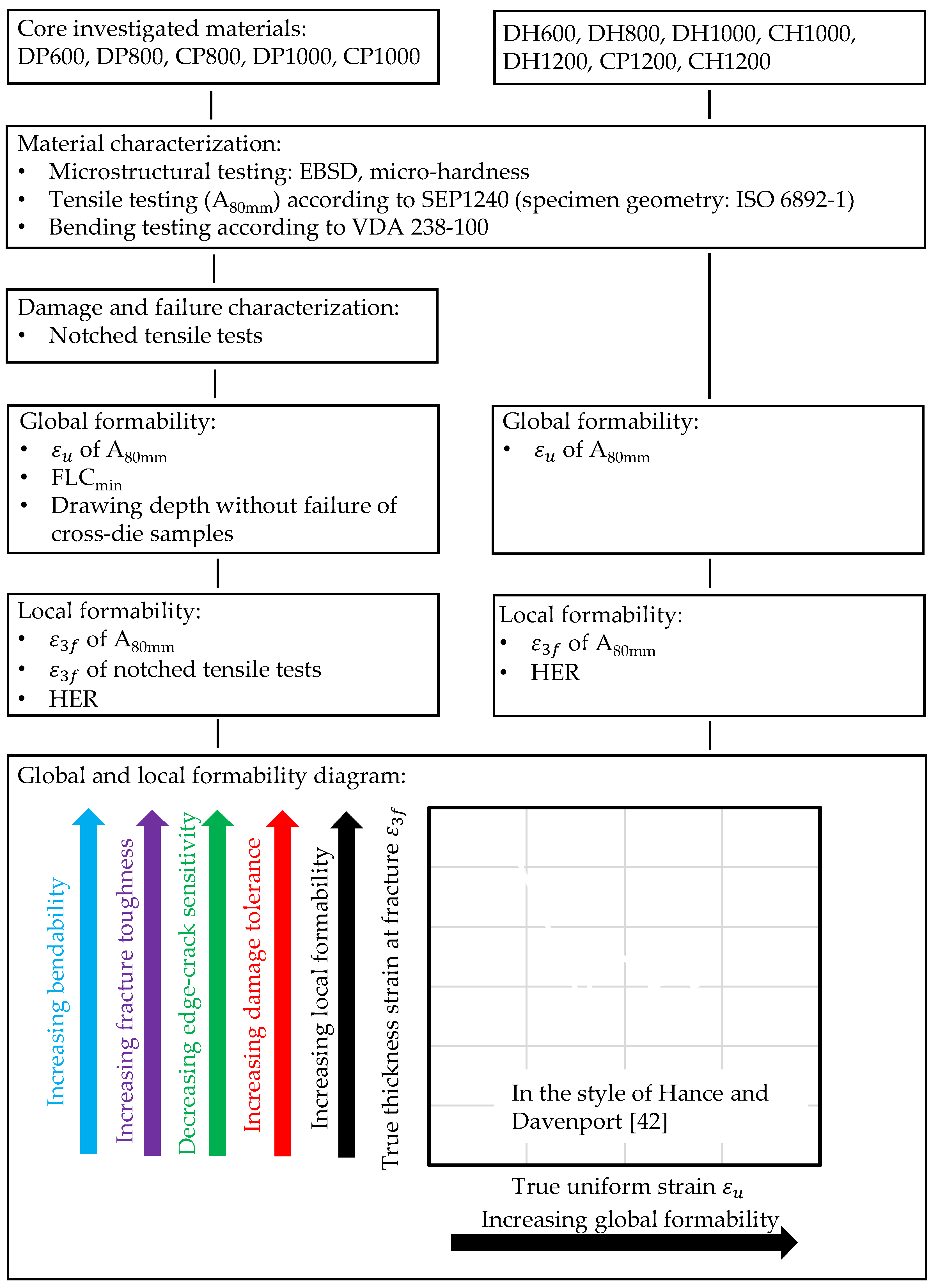
Table 1 defines therefore the terms of global formability, local formability, damage tolerance, edge-crack sensitivity and fracture toughness for sheet materials.
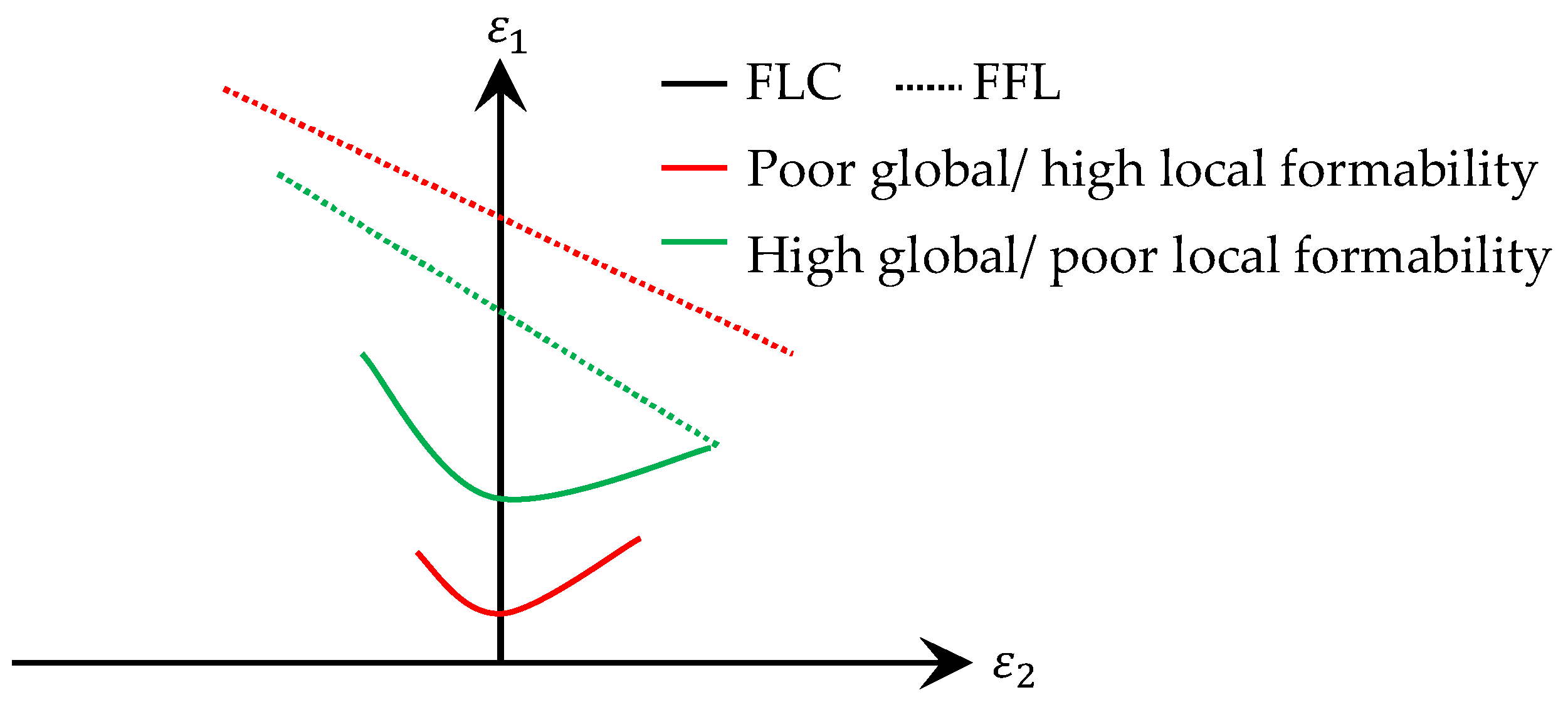
Global formability as defined above is associated with a good in-plane forming behaviour, whereas local formability is accompanied with a good out-of-plane forming behaviour, for example, bending with high strain gradients in thickness direction and high local loading at the outer fibre, as well as good stretch flangeability. As damage is not failure [
3], damage tolerance as defined here is the ability to undergo severe damage evolution during plastic flow, namely void nucleation, growth and coalescence, until rupture. Per definition, edge-crack sensitivity, with its tendency of a material to crack initiation due to further loading at a punched edge, is a special case of fracture toughness.
Multiphase steels are commonly classified according two systems. Many researchers divide them into first-, second- and third-generation AHSS (advanced high-strength steels), as displayed in
Table 2 [
4]. Another approach, displayed in
Table 3, introduced by Euro Car Body Congress [
5] is the assigning to the groups AHSS and UHSS (ultra high-strength steels).
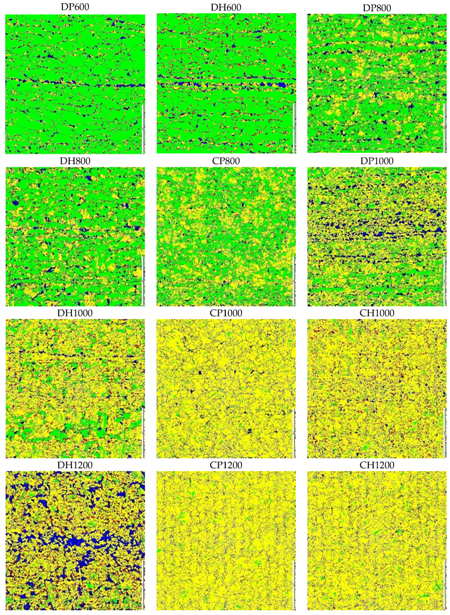
The first generation of AHSS comprises classical dual-phase (DP), complex-phase (CP), martensitic (MS) and transformation induced plasticity (TRIP) grades. Higher strength levels in comparison to conventional mild steels are gained by substitution of the softer ferrite partially or completely by harder phases like bainite and martensite. In modern car body manufacturing among the first generation of AHSS DP steels are commonly used for structural components with mainly tensile loading like B-pillars or door beams. Typical forming technologies for this class of steel with its high global formability are deep drawing, stretching or hydroforming. The microstructure of classical DP steels is based on the distribution of hard martensitic islands in a soft ferritic matrix. The differing properties of the constituent phases as well as the crystallographic and chemical heterogeneity in ferritic grains lead to stress heterogeneity during forming which favours ductile damage evolution [
1,
6]. Tasan et al. [
7] found that sharp deformation bands nucleate at ferrite grains and propagate in the softest route within the microstructure with angles of 45–50° to loading direction. This leads to very high strains in ferrite grains, which were determined by Ghadbeigi et al. using digital image correlation (DIC) and in-situ tensile testing inside a scanning electron microscope (SEM) for a DP1000 [
8] as well as for a DP600 [
9]. Ductile damage evolution is strongly dependent on the local microstructural morphology [
1,
10]. It is a dynamic process, where for example a crack of a martensite particle is followed by concentrated plastic deformation around that crack which triggers strain localization and local softening [
11]. Besides martensite cracking voids nucleate in DP steels mainly by decohesion at ferrite-martensite interfaces. Ghadbeigi et al. [
9] found martensite fracture, which is initiated at grain boundaries as main damage mechanism for a DP600. A DP800 investigated by Kadhkodapour et al. [
12] displayed void nucleation by ferrite grain boundary decohesion. Ramazani et al. [
13] classified martensite cracking as the main damage mechanism for a DP steel produced in a laboratory. Failure propagation along ferrite-martensite boundaries was found by Wang et al. [
14] for a DP800 in contrast to a combination of martensite cracking and ferrite-martensite decohesion for a DP1000. In general strain heterogeneity and thus damage evolution lead to a reduced local formability which might lead to part fracture in the forming process in the form of edge-fracture, fracture with slight necking or fracture during bending on tight radii. Bainite can be introduced to the microstructure in order to improve the susceptibility to damage evolution [
1,
15]. Among the strengthening mechanisms grain refinement is the only one that can simultaneously improve the local formability of steels [
1,
16,
17], whereas hereby the distribution of martensite becomes more critical and the ferrite-martensite morphology must be optimized [
1,
16]. Furthermore Hudgins et al. state that a reduction of hardness ratio is beneficial for improvement of classical DP-steels [
18]. CP steels consist mainly of a fine-grained bainitic or tempered martensitic matrix with small amounts of other phases. With their lower hardness ratio CP grades exhibit on the one side a high local formability and on the other side due to the higher density of dislocation pile-ups because of the harder phases a poor global formability. Pathak et al. [
19] showed for a CP800 the primary source for void nucleation at TiN (titanium nitride) particles and that secondary void nucleation takes place at martensite-bainite boundaries near the macroscopic failure strain. With its high yield strength and good local formability CP grades are used for structural parts with dominating compressive loads, for example, cross members or longitudinal members which are commonly produced by roll forming and bending operations. MS steels display an even higher yield strength than CP grades. They consist mainly of fine grained martensite and exhibit low necking strains, a poor global formability. The single phase microstructure leads to a homogenous strain distribution and thus to a good local formability with high local strains before fracture. TRIP steels were developed to achieve higher global formability in comparison to DP steels. They consist of a comparable microstructure with an added, certain amount of retained austenite, which is gained by a higher number of alloying elements. These alloying elements reduce the weldability and restrict automotive applications.
The same holds for the second generation of AHSS. The high manganese content of 15–20% enables a fully austenitic microstructure for the so-called twinning induced plasticity (TWIP) steels. The automotive applications are greatly limited by the as before mentioned poor weldability as well as by the tendency of delayed fractures.
Development of the third generation of AHSS focused on the improvement of global formability compared to 1. Gen. AHSS, without drawbacks of the 2. Gen. AHSS. Approaches to achieve this are quench and partitioning steels (Q&P) and TRIP aided bainitic ferrite steels (TBF) [
20]. The latter consist mainly of bainitic ferrite and a certain amount of martensite. TBFs are produced by rapid cooling from an austenite microstructure into the bainitic regions followed by isothermal holding. According to [
21] these steels are also named as DH steels, dual phase steels with higher global ductility/formability. The microstructure of Q&P steels consists of martensite, tempered martensite and bainite with retained austenite. One way to achieve this microstructure is by short cooling from austenite to partial martensite transformation followed by isothermal holding. According to the definition of DH steels, these steels can be also called CH, meaning complex-phase steels with higher global formability. Medium-manganese steels are under current development and therefore not yet listed in
Table 2 and
Table 3.
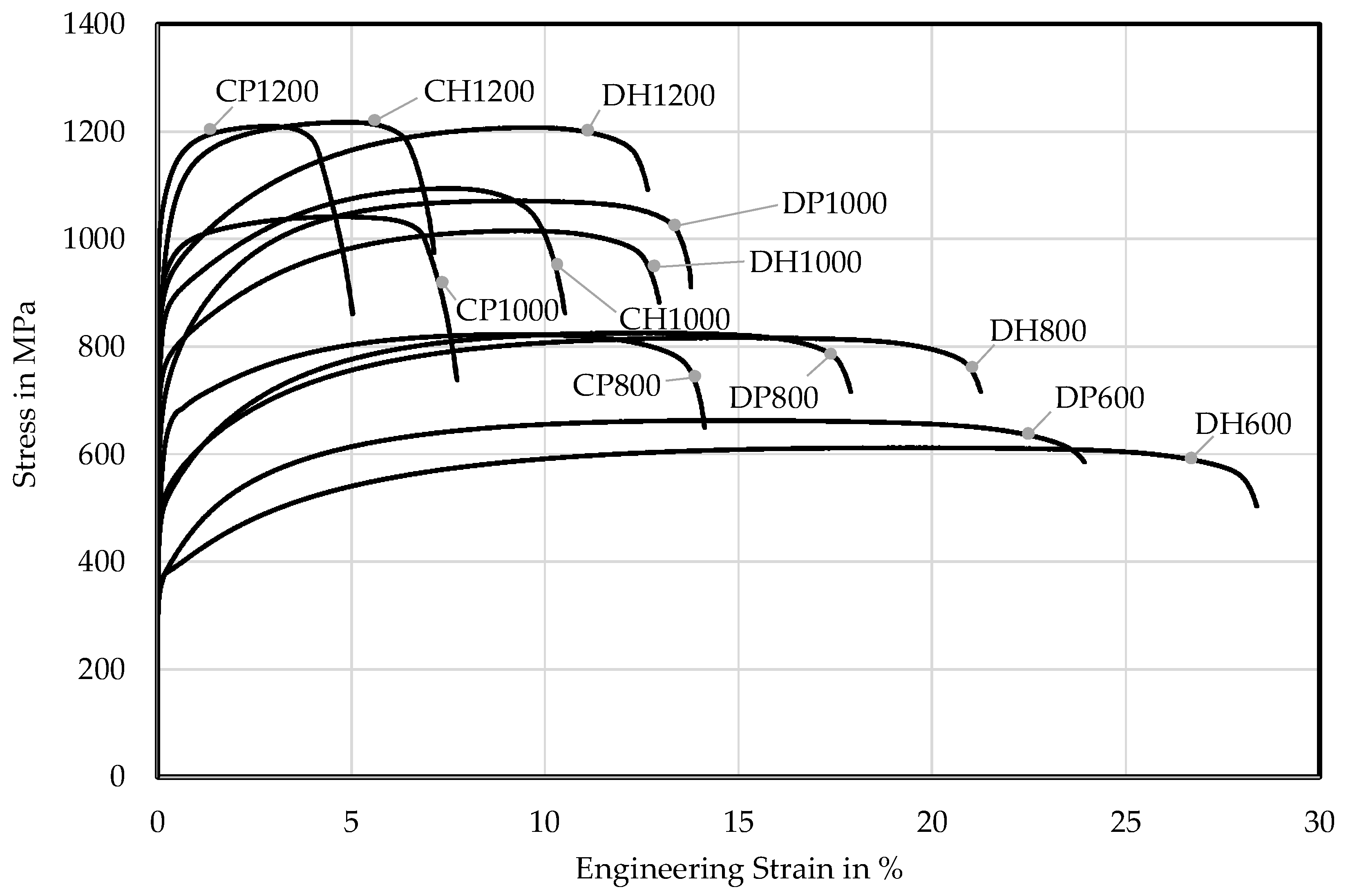
With improved microstructure of classical DP steels regarding damage effects as well as development of 3. Gen. AHSS the mechanical properties of modern AHSS are basically tailored for specific manufacturing processes and product applications. In this context, the whole set of mechanical properties related to the fracture behaviour (see
Table 1) cannot be characterized only by the classical tensile test according to ISO 6892-1 [
22].
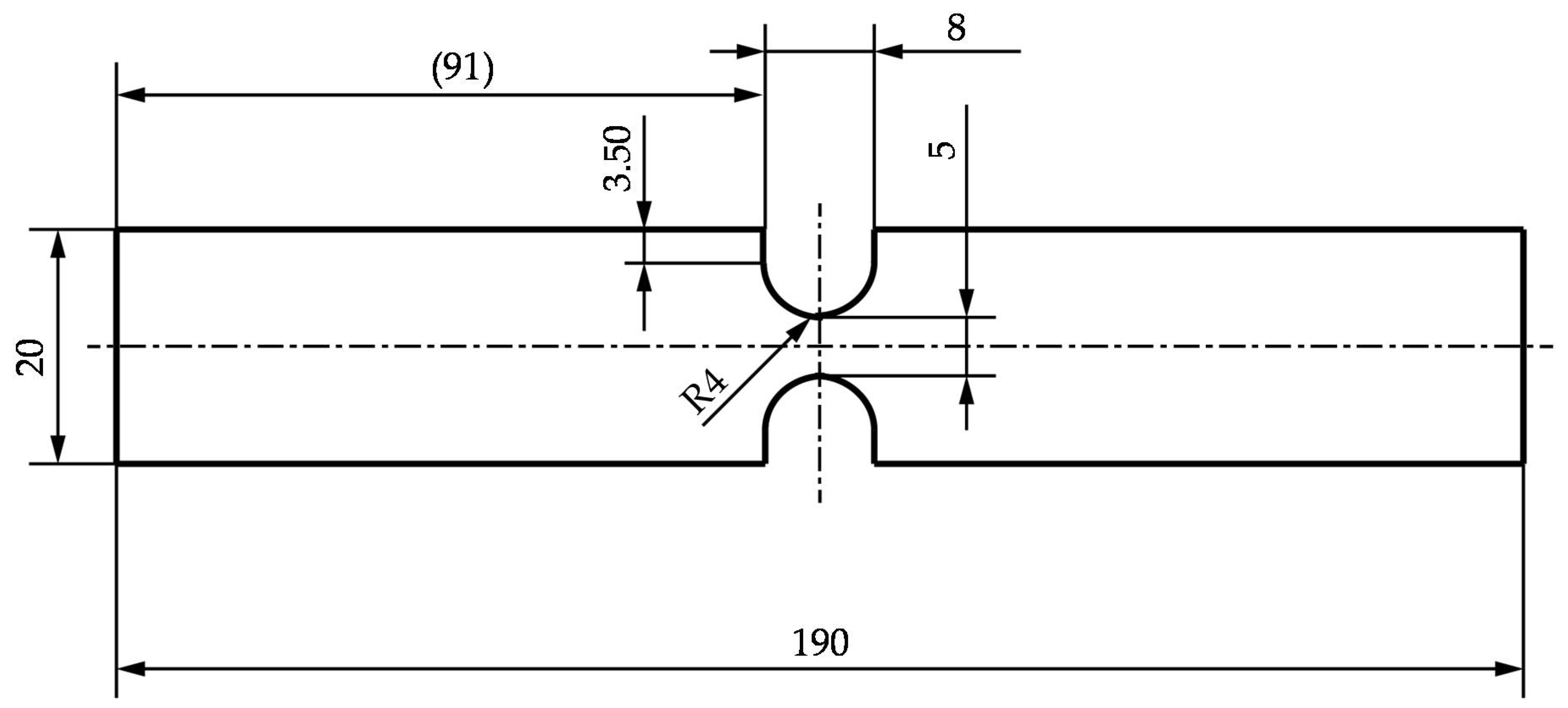
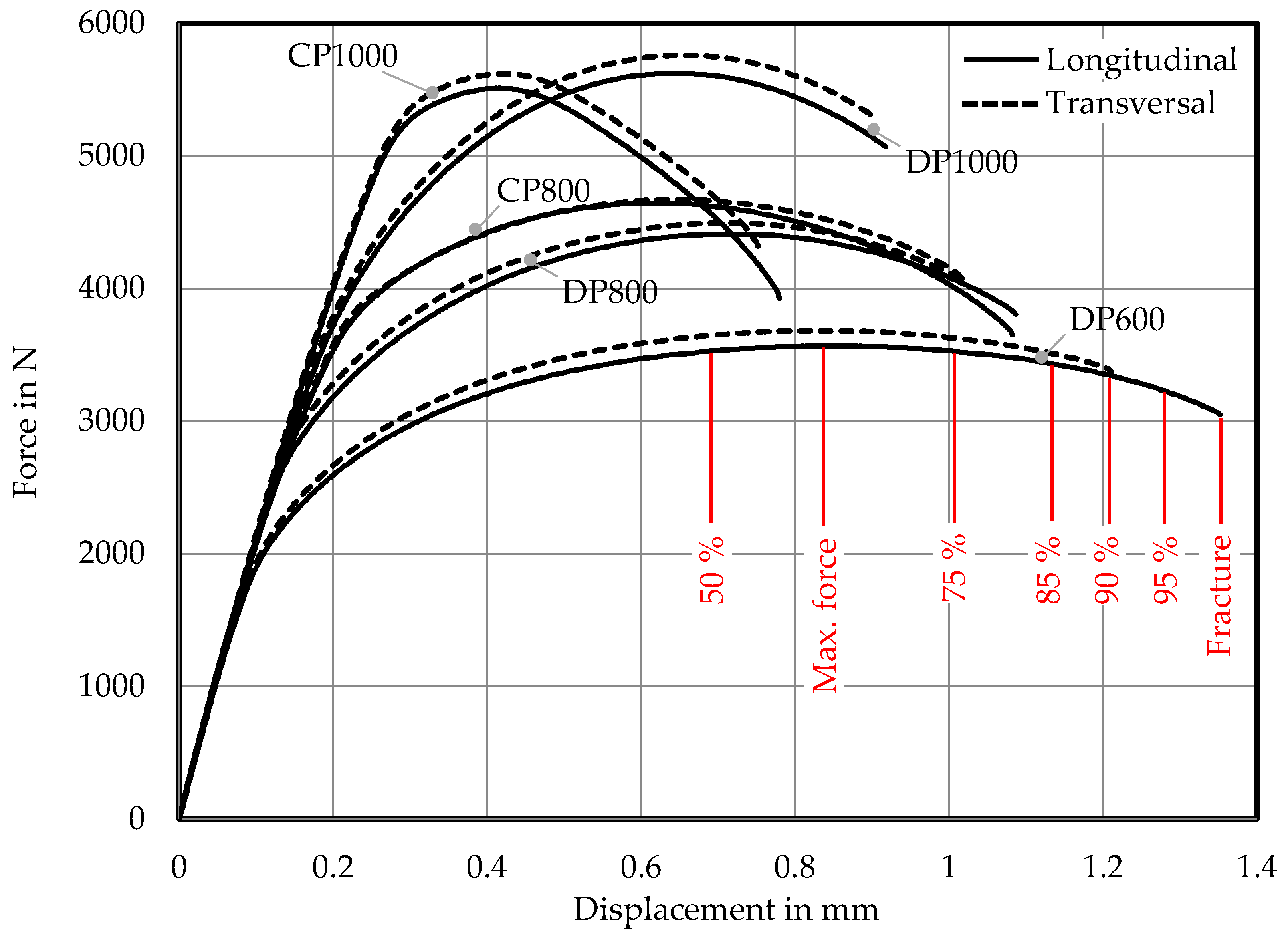
The 3-point-bending test according to VDA 238-100 [
23], originally developed for hemming assessment of aluminium alloys, has been established as state-of-the-art for characterization of bendability and crash ductility in automotive industry. Kurz et al. [
24] showed a good correlation between determined bending angles and crash behaviour of press hardened steels (PHS). In recent research, Cheong et al. [
25] improved the test set-up to determine local fracture strains for the plane-strain stress state via DIC besides the bending angle. Another way to achieve a plane-strain stress state is the usage of notched tensile specimens. For three different DP1000 grades Butcher et al. [
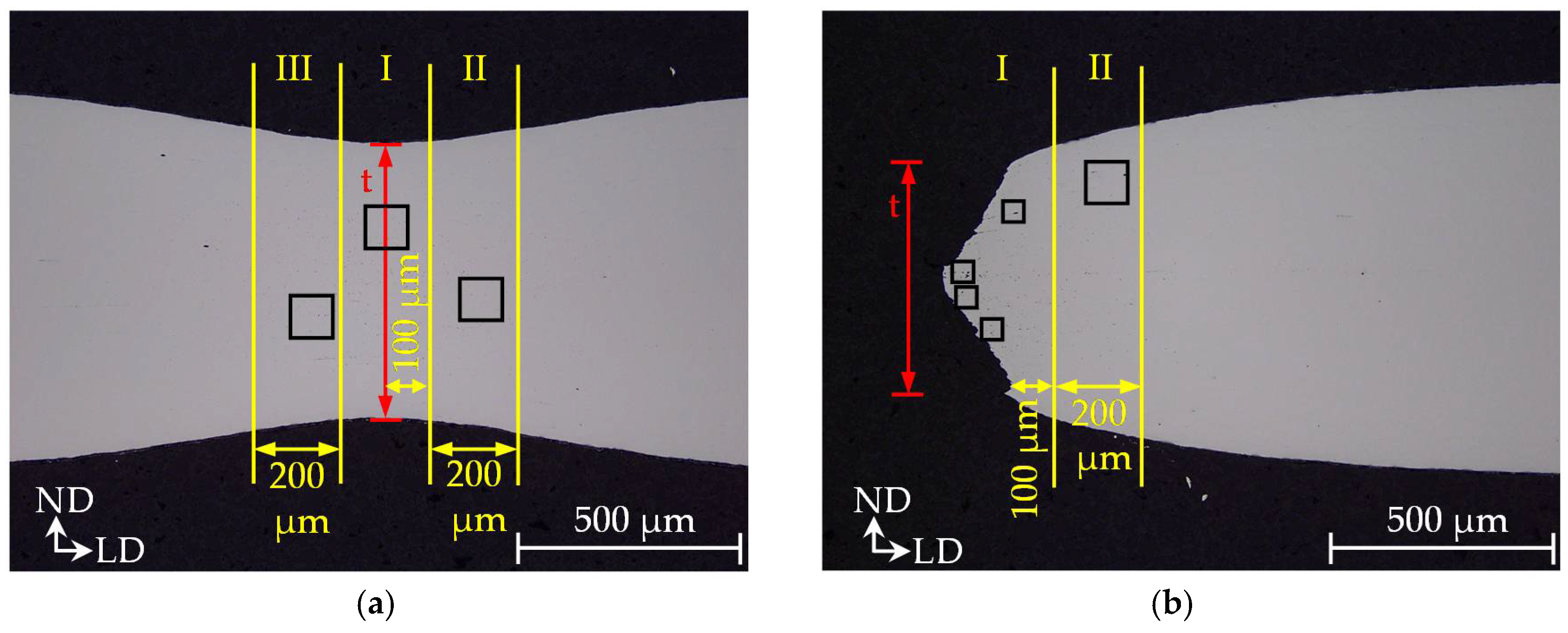
26] detect, that local failure strains of a bending specimen, determined via DIC and a notched tensile specimen, determined via a combination of DIC and thickness measurement of the fracture surface, are almost similar. Strains of the notched tensile specimen are slightly lower, because the specimen exhibits a strain gradient in thickness direction, which is averaged by thickness measurement. Similar observations are found for press hardened steels [
27]. To assess failure in bending operations in sheet metal forming simulation, Liewald et al. [
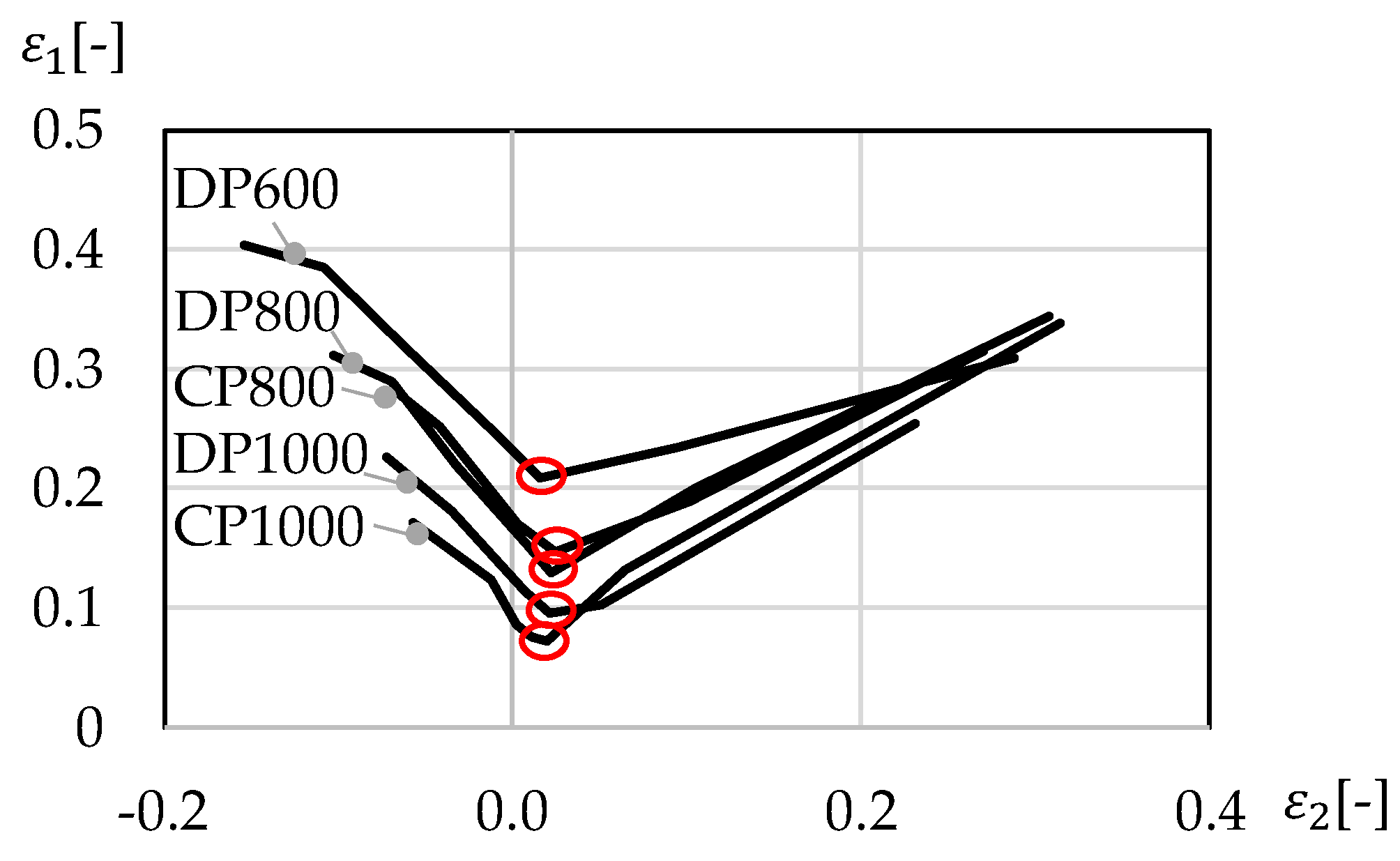
28] introduced bending limit curves (BLC), which are falling linearly from left to right in the forming limit diagram. These lines are determined by performing DIC analysis on bending specimens according to VDA 238-100 [
23] subjected to different levels of pre-straining. Another possibility for failure prediction in bending operations is using damage mechanics, for example the enhanced Lemaitre damage model, which was calibrated by Soyarslan et al. [
29] on basis of notched tensile tests and used to predict fracture in bending of a DP600.
Besides the bending test a further approach to predict the crash behaviour was introduced by Frometa et al. [
30], who showed the correlation of fracture toughness formulated in terms of essential work of fracture with crash resistance in axial impact tests for several multiphase steels. In [
31] Casellas et al. link fracture toughness of the same materials with results of hole expansion tests, which are typically conducted to access the edge-crack sensitivity. Comparable results have been published by Yoon et al. [
32], who correlated fracture toughness of AHSS with stretch-flangeability.
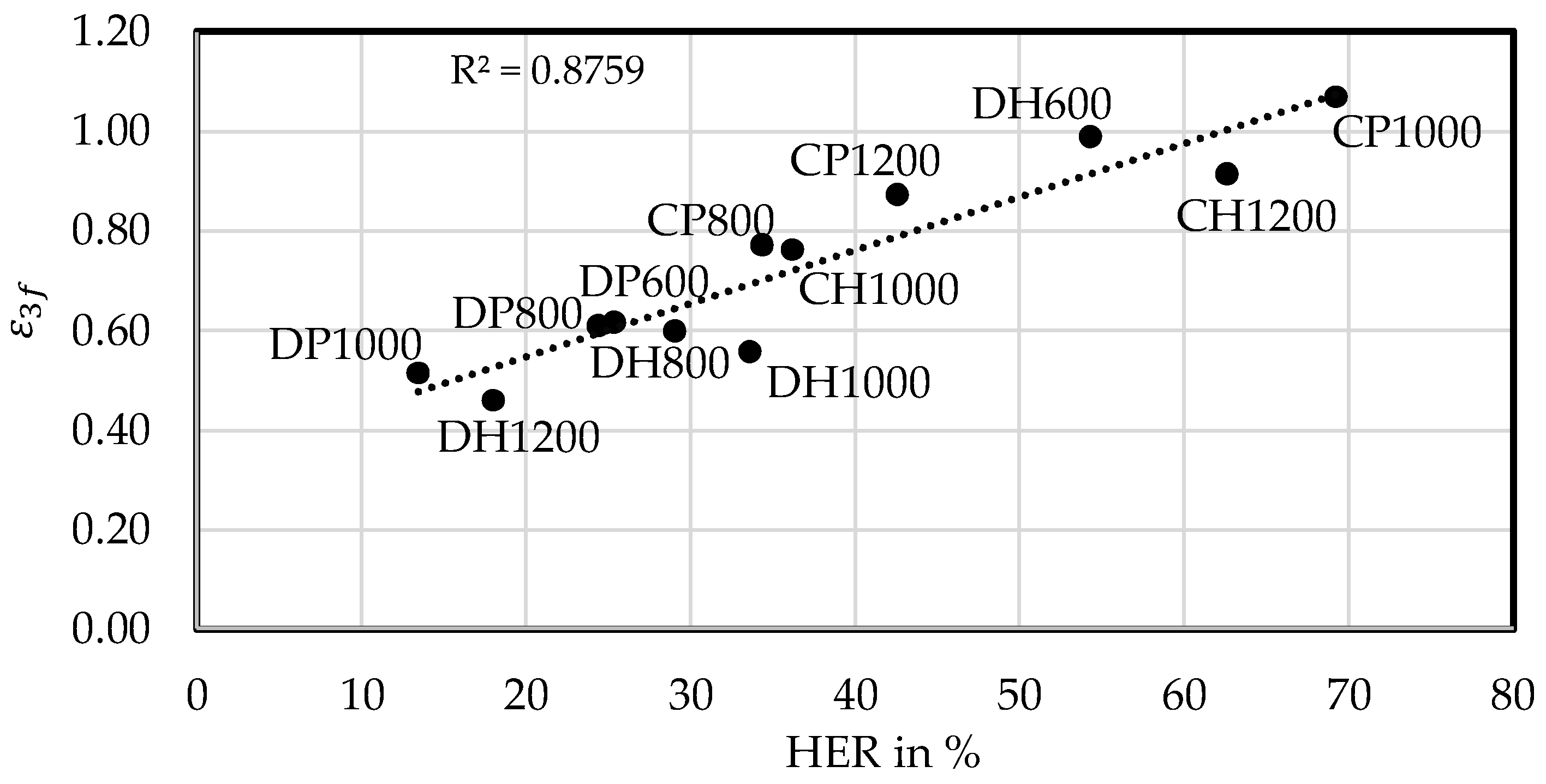
The hole expansion test according to ISO 16630 [
33] for characterizing these stretch-flangeability or rather edge-crack sensitivity itself displays several disadvantages and was therefore controversially discussed in recent research: In [
34] the influences on the hole expansion ratio (HER) from the operator over the tool up to the evaluation procedure are presented. A European round robin test [
35] revealed high deviations among several laboratories in testing of high strength steels because of the non-reproducible pre-damaged edge condition and the influence of several operators. Exemplarily, the HER showed a standard deviation of 14.6% with an average value of 58.8% for a martensitic steel [
35]. Larour et al. [
36] evaluated therefore alternative stretch flangeability testing methods.
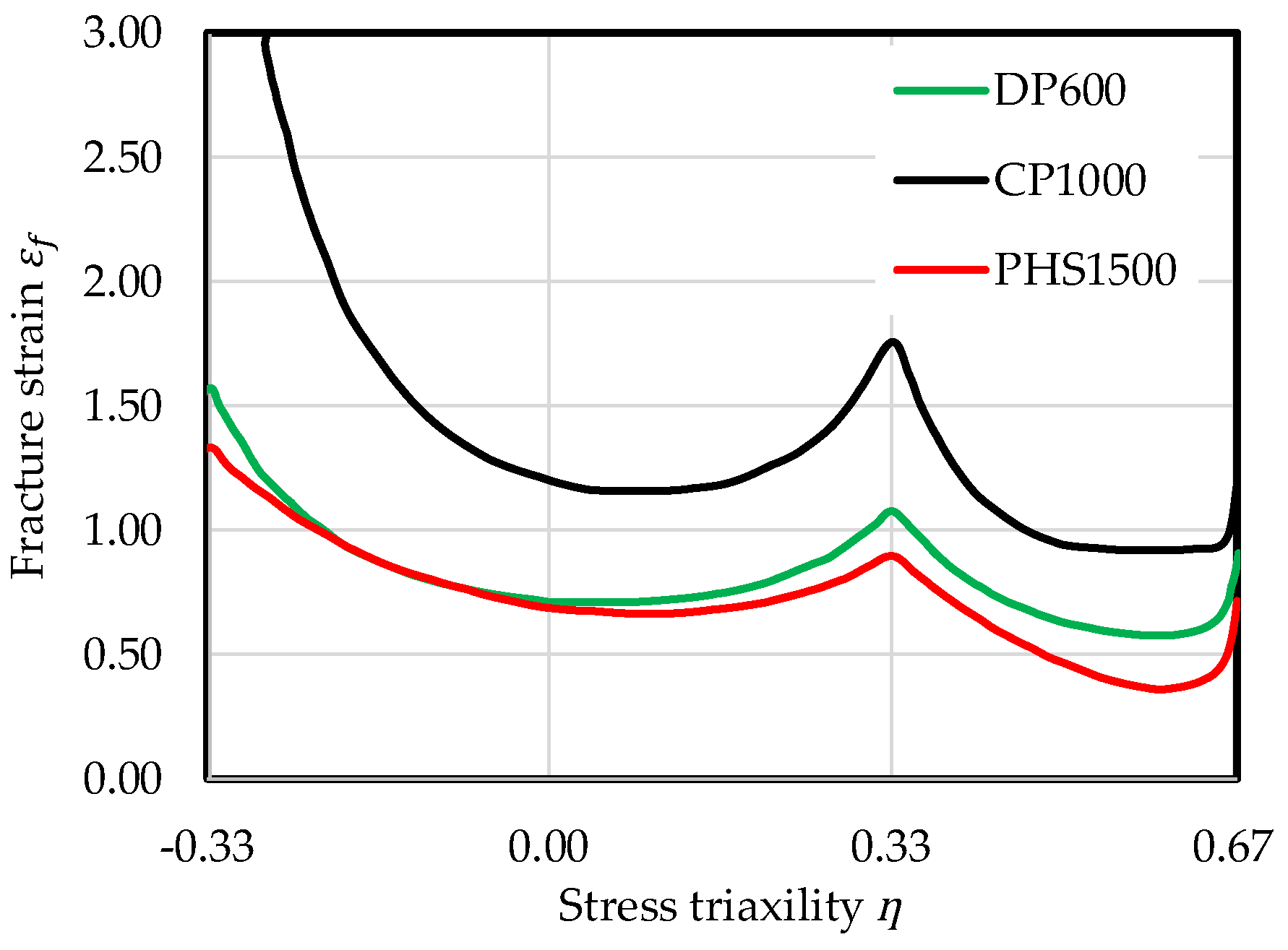
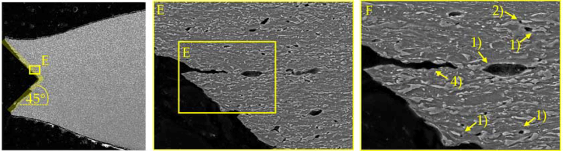
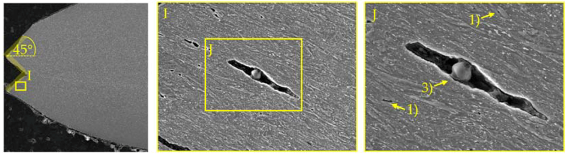
Damage tolerance as defined in
Table 1 is not characterized by a classical measure. Some damage and fracture models like Lemaitre [
2] or the fracture forming limit line (FFL) approach [
37] introduce a critical damage parameter
, which can be interpreted as following: the higher the value of
, the higher is the damage tolerance of the respective materials. The same holds for comparison of fracture strains predicted by advanced fracture criteria like the Modified-Mohr-Coulomb [
38], Lou-Huh [
39] or Hosford-Coulomb model [
40]. The higher the level of the fracture line (in case of plane stress) or fracture surface for a material is, the more damage tolerant it is. Muenstermann et al. [
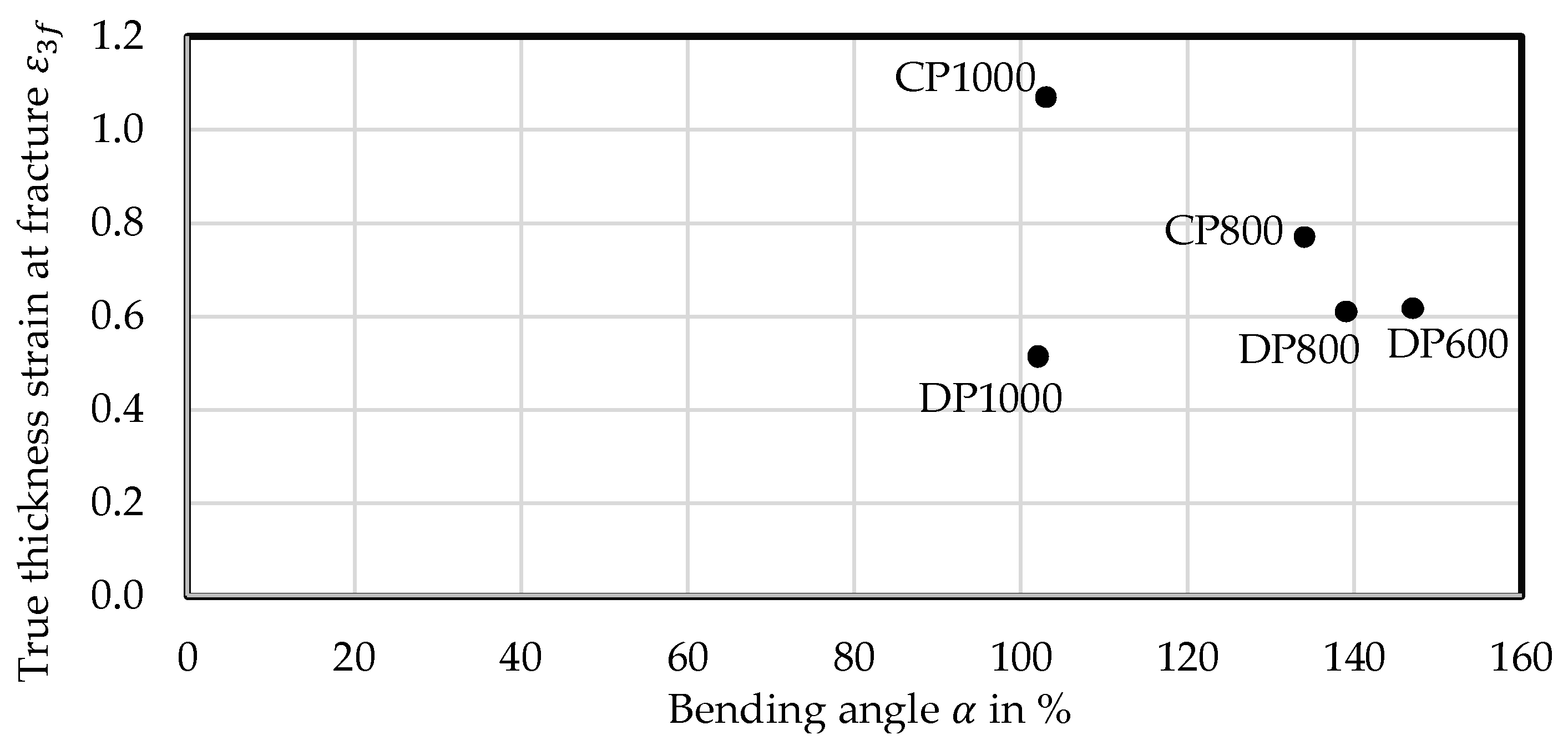
41] introduced the ratio of fracture strain over strain at damage initiation computed with a modified Bai-Wierzbicki model in analysing a DP600 and DP1000 as measure for damage tolerance. According to this study the DP600 is much more damage tolerant than the DP1000, which can be explained by the higher amount of void nucleating microstructural constituents in DP1000.
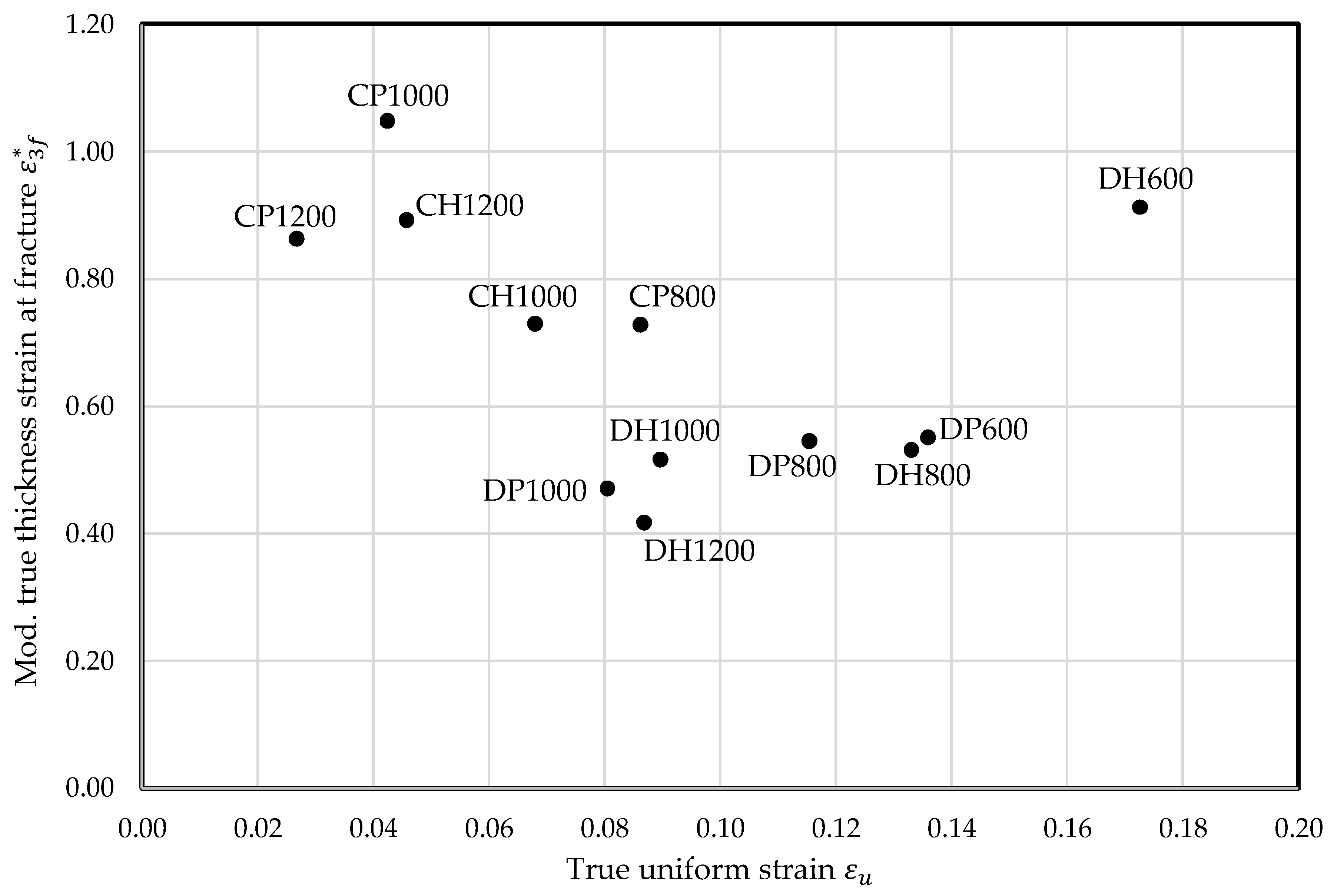
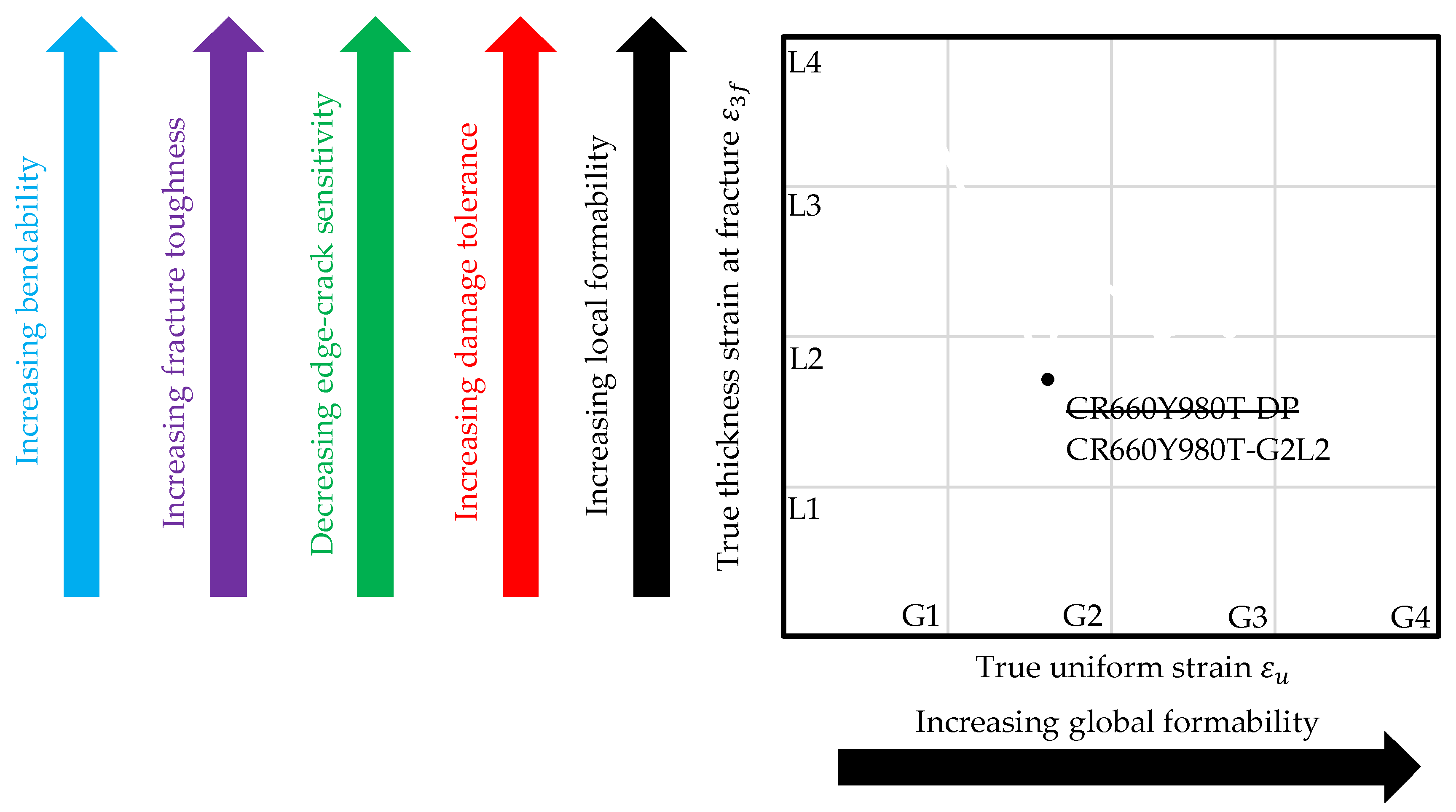
The idea of global and local formability was used by Hance and Davenport [
42] for presenting a new local and global formability map concept for application-specific material selection on examples of several AHSS of the strength class of 1000 MPa. In this proposal, the true uniform strain is used as measure for global formability. For local formability, the author suggested a so called true fracture strain, a strain measure for the reduction of area at fracture. Larour et al. [
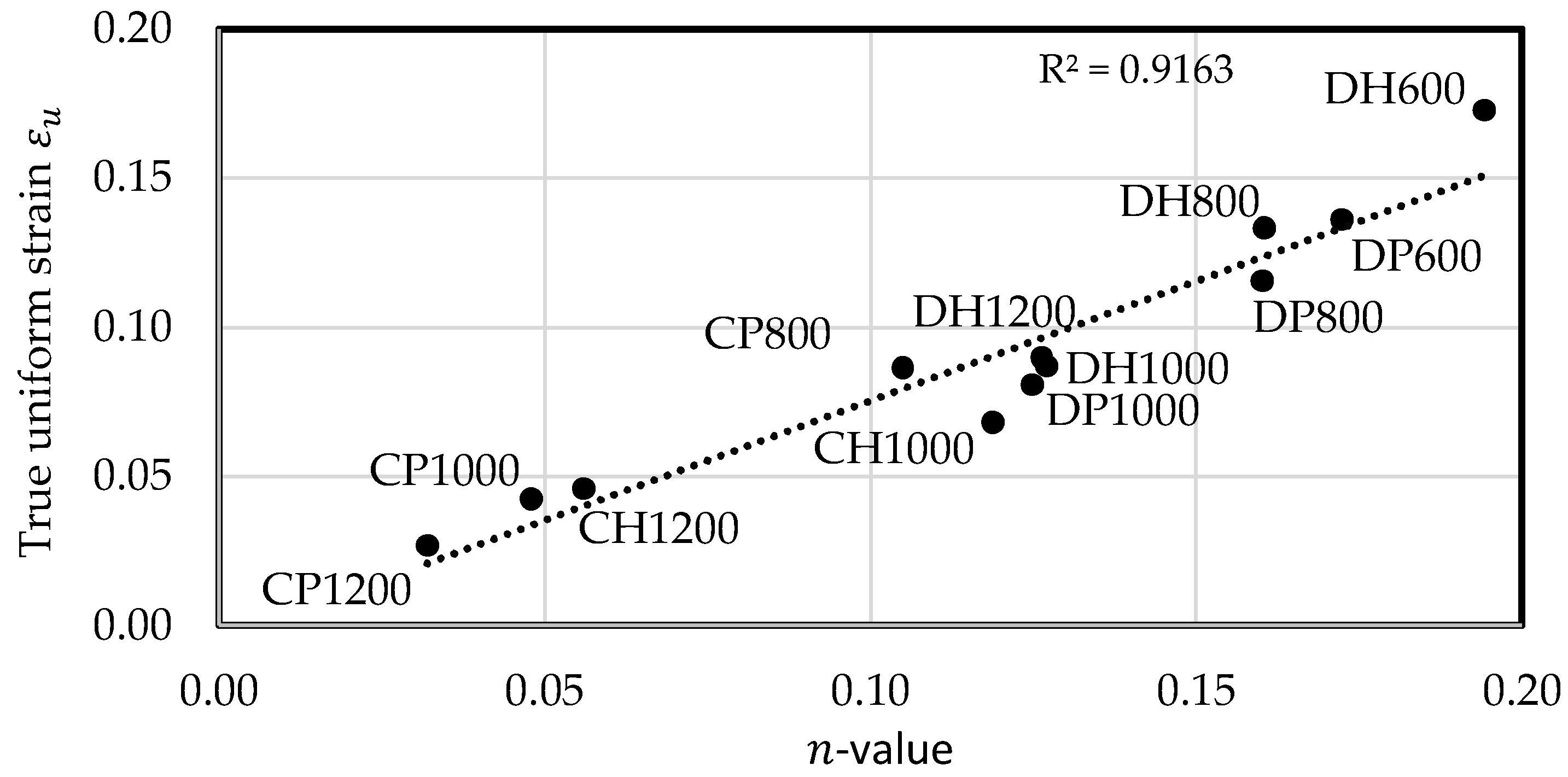
43] picked up this idea and used instead of the true fracture strain the Z-value according to ISO 6892-1 [
22] and ASTM E6 [
44] as measure for local formability. Using this measure, a good correlation to hole expansion ratios of punched as well as milled holes is obtained for a wide range of AHSS.
The aim of this contribution is to introduce a physically motivated measure for local formability, which displays the possibility to qualitatively assess the bendability, fracture toughness, edge-crack sensitivity and damage tolerance, as these material characteristics are all influenced by the same microstructural parameters. Thus, the damage behaviour of 1. Gen. AHSS is characterized and a classification scheme using global and local formability is created. These results are transferred to several steels of 3. Gen. AHSS.